Всем привет! Меня зовут Рома Смирнов. Я работаю продуктовым аналитиком в Lamoda. Как и во многих других продуктовых компаниях, решения о том, раскатывать ли новую фичу, принимаются в Lamoda на основе данных, в частности на основе результатов A/B-тестирования.

Бутстрэп — один из популярных методов обработки результатов тестов. В этой статье я расскажу о том, каким образом можно определить размер выборки при расчете результатов A/B-теста с помощью бутстрэпа.

Что такое бутстрэп 

Pull yourself up by your bootstraps – идиома, от которой произошло название метода.

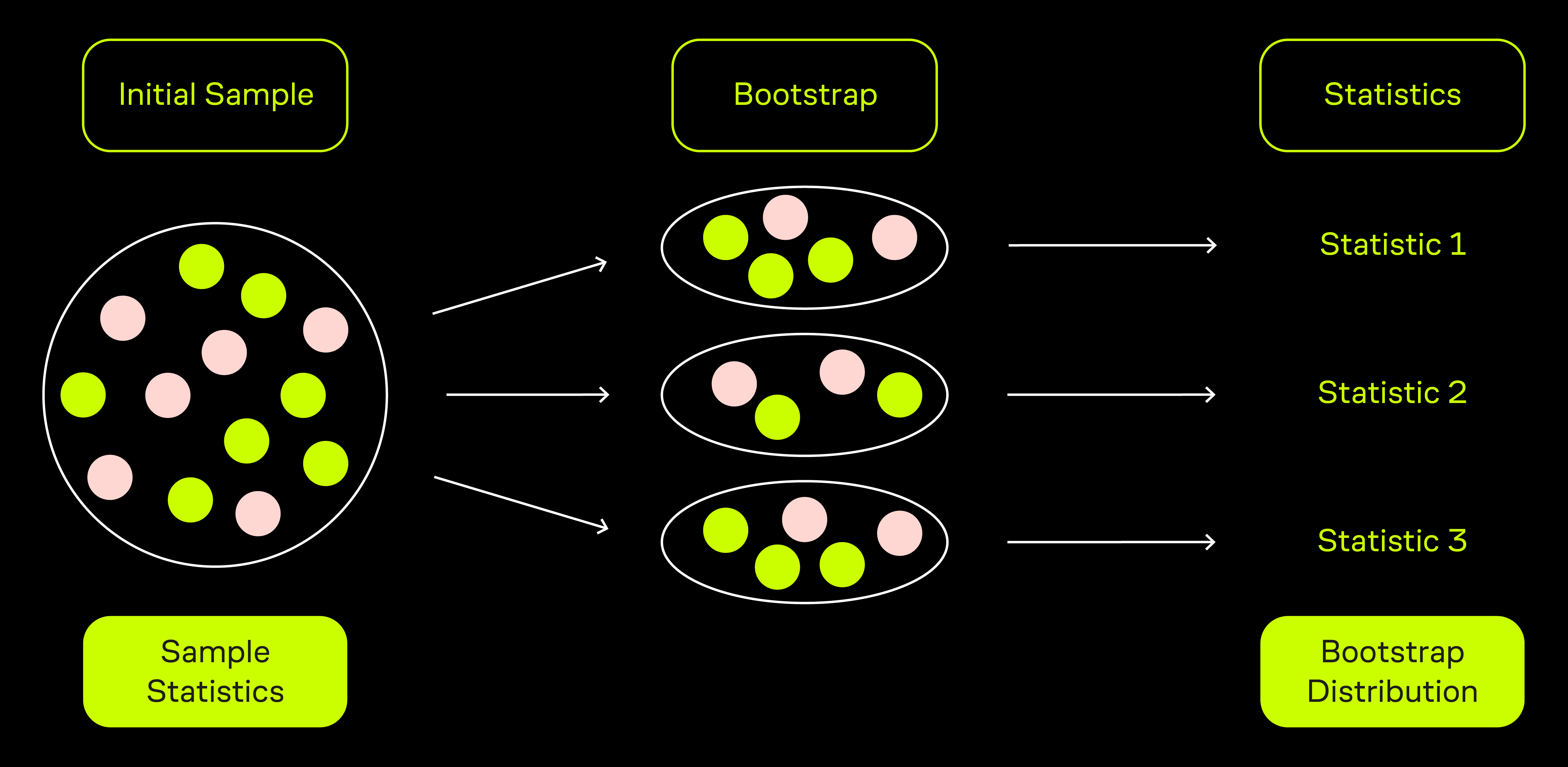
Суть бутстрэпа заключается в том, что из исходной выборки мы начинаем брать большое количество выборок с повторениями (то есть один и тот же элемент может попадать в выборку несколько раз) того же размера, что и исходная. Для каждой такой выборки мы считаем интересующую нас статистику: например, среднее. 

Это позволяет построить распределение этой статистики, имитирующее результат, который мы получили бы, если брали выборки одинакового размера не из исходной выборки, а из генеральной совокупности. На основе полученного распределения мы делаем выводы относительно того, можем ли мы отвергнуть нулевую гипотезу или нет. 

Подробнее про бутстрэп:

• Бутстреп и А/Б тестирование

• Bootstrap: виды, особенности, ограничения и способы применения (EXPF)

• Bootstrap Hypothesis Testing in Statistics with Example

Бутстрэп и размер выборки

Бутстрэп — довольно универсальный метод подсчета результатов A/B-тестов. Проблема с ним заключается в том, что это исключительно эмпирический метод.  Другими словами, нет никакой теории, которая лежала бы в его основе, как, например, для t-теста. В целом, это не было бы проблемой: работает, и пусть работает — главное, чтобы давал корректные результаты —, если бы на этапе планирования A/B-теста не нужно было определять размер выборки.

В случае с t-тестом размер выборки можно определить по формуле:

• — размер выборки для каждой из двух групп теста.

• — дисперсия группы i.

• — значения стандартного нормального распределения, соответствующие заданным уровням значимости и мощности.

• (minimum detectable effect) — минимальная разница, которую мы сможем зафиксировать между разностями математических ожиданий генеральных совокупностей, из которых были взяты исходные выборки, в рамках нулевой гипотезы и альтернативной. Обычно в рамках нулевой гипотезы такая разность предполагается равной нулю. Соответственно, MDE — это минимальный размер эффекта (разности математических ожиданий в рамках альтернативной гипотезы), который мы сможем зафиксировать, если возьмем выборки заданного размера при заданных значениях мощности и уровня значимости.

Откуда берется эта формула

Давайте представим, что у нас есть два распределения разности средних:

: ,

: ,

Пусть мы используем уровень значимости и уровень мощности

Мы отвергаем в случае, если наблюдаемая нами разница средних лежит правее 97,5-го процентиля (либо левее 2,5-го процентиля) левого распределения. Это значение отмечено вертикальной линией. Мы можем получить его, если возьмем 97,5-ый процентиль стандартного нормального распределения и проведем процедуру обратную стандартизации: умножим на стандартное отклонение и прибавим математическое ожидание.

Таким образом мы получим: 

А если вспомнить, что , получaем:

В то же время для правого распределения значение, отмеченное вертикальной линией, соответствует 20-му процентилю стандартного нормального распределения : так как мы используем уровень мощности равный 80%, вероятность ошибки второго рода будет равна 20%. 

Аналогичным образом получаем:

Теперь остается приравнять последние две формулы и выразить оттуда .

К сожалению, для бутстрэпа аналогичной формулы нет. Хочется использовать формулу для t-теста, но насколько это применимо? Давайте попробуем ответить на этот вопрос. Как мы это сделаем? С помощью симуляций, конечно же.

Синтетические данные

С самого начала составим план и будем его придерживаться:

1. Зададим две генеральные совокупности с различными математическими ожиданиями, получив таким образом MDE. Также зададим дисперсии этих генеральных совокупностей.

2. Зафиксируем уровень значимости.

3. Будем подставлять в формулу для расчета размера выборки для t-теста , а также различные значения размера выборки n, получая таким образом теоретические значения мощности.

4. Для каждого значения n будем 1000 раз брать из каждой генеральной совокупности выборки размера n и сравнивать их средние с помощью бутстрэпа. Да, мы будем делать симуляции, пока мы делаем симуляции. Если бутстрэп покажет, что средние статистически значимо различаются, будем записывать результат такого сравнения как 1, в противном случае — 0.

5. Для каждого значения n мы получим серию из 1 и 0. Посчитаем процент единиц, получив тем самым эмпирическое значение мощности — вероятность зафиксировать статистически значимое различие, там, где оно действительно есть.

6. Для каждого значения n сравним полученное эмпирическое и теоретическое значение мощности. Для этого будем использовать binominal proportion confidence interval. Пример его похожего использования можно посмотреть у коллег из Авито. Это статистический метод, который используется для того, чтобы оценить вероятность успеха в серии испытаний Бернулли. А наш список из тысячи 1 и 0, как раз и является такой серией.

Если формула для t-теста действительно пригодна для расчета размера выборки для бутстрэпа, то мы получим близкую к зависимость теоретической мощности от эмпирической

Ну что, расчехляем наших Анаконд и переходим к Питону.

Гитхаб с полным кодом

Для начала пропишем функции t-теста и бутстрэпа :

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as sps
from tqdm.notebook import tqdm as tqdm_notebook
from statsmodels.stats.proportion import proportion_confint

def ttest(sample_a, sample_b, z_sig):
    
    mean_sample_a = np.mean(sample_a)
    mean_sample_b = np.mean(sample_b)
    diff_mean = mean_sample_b - mean_sample_a
    
    std_error_a = np.var(sample_a)/len(sample_a)
    std_error_b = np.var(sample_b)/len(sample_b)
    diff_mean_std_error = std_error_a + std_error_b
    
    t_stat = diff_mean/np.sqrt(diff_mean_std_error)
    
    if t_stat >= z_sig:
        res = 1
    else:
        res = 0
    return res

def bootstrap(sample_a, sample_b, sig, n_samples=1000, func=np.mean):
    
    observed_metric = func(sample_b) - func(sample_a)
    combined_sample = np.concatenate((sample_a, sample_b), axis=None)
    combined_sample_size = len(combined_sample)
    sample_a_size = len(sample_a)
    sample_a_size = len(sample_b)
    boot_list = []
    
    for i in range(0, n_samples):
        boot_sample = np.random.choice(combined_sample, size=combined_sample_size)
        boot_sample_a = boot_sample[0:sample_a_size]
        boot_sample_b = boot_sample[sample_a_size:]
        boot_metric = func(boot_sample_a) - func(boot_sample_b)
        boot_list.append(boot_metric)
        
    final_dist = np.array(boot_list)
    p_value = sum(final_dist >= observed_metric)/len(final_dist)
    
    if p_value <= sig:
        res = 1
    else:
        res = 0
    return res

В обоих случаях для простоты я буду использовать односторонние проверки, но ничего не мешает повторить эту же процедуру для двусторонних тестов.

В качестве примера возьмем выборки из экспоненциально распределенных генеральных совокупностей (можно использовать любое другое распределение). Для начала проверим, какие результаты мы получим, если будем использовать t-тест для расчета значимости:

# Зададим исходные параметры
sig = 0.025 # уровень значимости
scale = 1900 # параметр экспоненциального распределения
mean_a = scale # мат.ожидание генеральной совокупности А
mean_b = scale*1.01 # мат.ожидание генеральной совокупности B
var_a = scale**2 # диспресия генеральной совокупности А
var_b = (scale*1.01)**2 # диспресия генеральной совокупности B
mde = mean_b-mean_a # MDE
z_sig = sps.norm.ppf(1-sig) # 97.5 процентиль стандартного нормального распределения

N = 1000

power_list = []
empirical_power_list = []
sig_list = []
sample_size_list = []
left_real_level_list = []
right_real_level_list = []

# Будем брать выборки размерами от 50000 до 275000 с шагом в 25000
for n in tqdm_notebook(range(50000, 300000, 25000)):

    # считаем теоретическую мощность
    z_power = z_sig-np.sqrt(n)*mde/np.sqrt(var_a+var_b)
    power = 1-sps.norm.cdf(z_power)

    results = []

    for i in tqdm_notebook(range(N)):

        sample_a = sps.expon(loc=0, scale=mean_a).rvs(n)
        sample_b = sps.expon(loc=0, scale=mean_b).rvs(n)

        res = ttest(sample_a, sample_b, z_sig)
        results.append(res)  

    power_list.append(power)
    empirical_power_list.append(np.mean(results)) #считаем эмпирическую мощность
    sample_size_list.append(n)
    
    # считаем доверительный интервал для вероятности успеха серии испытаний Бернулли
    left_real_level, right_real_level = proportion_confint(count=N*empirical_power_list[-1], 
                                                           nobs=N, 
                                                           alpha=0.05, 
                                                           method='wilson')
    if left_real_level < power and right_real_level > power:
        sig_list.append(1)
    else:
        sig_list.append(0)
    left_real_level_list.append(left_real_level)
    right_real_level_list.append(right_real_level)

    power_df_ttest = pd.DataFrame(columns=['power', 'empirical_power_ttest', 
                                           'sig_ttest', 'sample_size', 
                                           'left_real_level_ttest', 'right_real_level_ttest'])
    power_df_ttest['power'] = power_list
    power_df_ttest['empirical_power_ttest'] = empirical_power_list
    power_df_ttest['sig_ttest'] = sig_list
    power_df_ttest['sample_size'] = sample_size_list
    power_df_ttest['left_real_level_ttest'] = left_real_level_list
    power_df_ttest['right_real_level_ttest'] = right_real_level_list
    power_df_ttest.to_csv('ttest.csv', index=False)

Нарисуем график зависимости эмпирической мощности от теоретической:

fig, ax = plt.subplots(figsize=(10, 6), dpi=200)
ax.plot(power_df_ttest['power'], power_df_ttest['empirical_power_ttest'], '-')
ax.fill_between(power_df_ttest['power'], 
                power_df_ttest['left_real_level_ttest'], 
                power_df_ttest['right_real_level_ttest'], alpha=0.2)
plt.xlabel('Theoretical power t-test')
plt.ylabel('Empirical power t-test');

Зависимость близка к что неудивительно, ведь мы использовали в качестве критерия t-тест. Давайте посмотрим на результат немного с другой стороны, нанеся на ось X размер выборки, а на ось Y — значения теоретических и эмпирических мощностей.

fig, ax = plt.subplots(figsize=(10, 6), dpi=200)
ax.plot(power_df_ttest['sample_size'], power_df_ttest['empirical_power_ttest'], '-', 
        label='Empirical power t-test', color='blue')
ax.plot(power_df_ttest['sample_size'], power_df_ttest['power'], '-', 
        label='Theoretical power t-test', color='red')
ax.fill_between(power_df_ttest['sample_size'], power_df_ttest['left_real_level_ttest'], 
                power_df_ttest['right_real_level_ttest'], alpha=0.2, color='blue')
plt.xlabel('Sample size')
plt.ylabel('Power')
ax.legend();

Теоретические мощности почти во всех случаях лежат внутри границ доверительного интервала эмпирических мощностей.

Повторим эту же процедуру, но с использованием бутстрэпа для расчета статистической значимости.

sig = 0.025
mean_a = scale
mean_b = scale*1.01
var_a = scale**2
var_b = (scale*1.01)**2
mde = mean_b-mean_a
z_sig = sps.norm.ppf(1-sig)

N = 1000

power_list = []
empirical_power_list = []
sig_list = []
sample_size_list = []
left_real_level_list = []
right_real_level_list = []

for n in tqdm_notebook(range(50000, 300000, 25000)):

    z_power = z_sig-np.sqrt(n)*mde/np.sqrt(var_a+var_b)
    power = 1-sps.norm.cdf(z_power)

    results = []

    for i in tqdm_notebook(range(N)):

        sample_a = sps.expon(loc=0, scale=mean_a).rvs(n)
        sample_b = sps.expon(loc=0, scale=mean_b).rvs(n)

        res = bootstrap(sample_a, sample_b, sig)
        results.append(res)  

    power_list.append(power)
    empirical_power_list.append(np.mean(results))
    sample_size_list.append(n)
    left_real_level, right_real_level = proportion_confint(count=N*empirical_power_list[-1], 
                                                           nobs=N, 
                                                           alpha=0.05, 
                                                           method='wilson')
    if left_real_level < power and right_real_level > power:
        sig_list.append(1)
    else:
        sig_list.append(0)
    left_real_level_list.append(left_real_level)
    right_real_level_list.append(right_real_level)

    power_df_bootstrap = pd.DataFrame(columns=['power', 'empirical_power_bootstrap', 
                                               'sig_bootstrap', 'sample_size', 
                                               'left_real_level_bootstrap', 'right_real_level_bootstrap'])
    power_df_bootstrap['power'] = power_list
    power_df_bootstrap['empirical_power_bootstrap'] = empirical_power_list
    power_df_bootstrap['sig_bootstrap'] = sig_list
    power_df_bootstrap['sample_size'] = sample_size_list
    power_df_bootstrap['left_real_level_bootstrap'] = left_real_level_list
    power_df_bootstrap['right_real_level_bootstrap'] = right_real_level_list
    power_df_bootstrap.to_csv('bootstrap.csv', index=False)

Нарисуем график зависимости эмпирической мощности от теоретической для бутстрэпа.

fig, ax = plt.subplots(figsize=(10, 6), dpi=200)
ax.plot(power_df_bootstrap['power'], power_df_bootstrap['empirical_power_bootstrap'], '-')
ax.fill_between(power_df_bootstrap['power'], 
                power_df_bootstrap['left_real_level_bootstrap'], 
                power_df_bootstrap['right_real_level_bootstrap'], alpha=0.2)
plt.xlabel('Theoretical power t-test')
plt.ylabel('Empirical power bootstrap');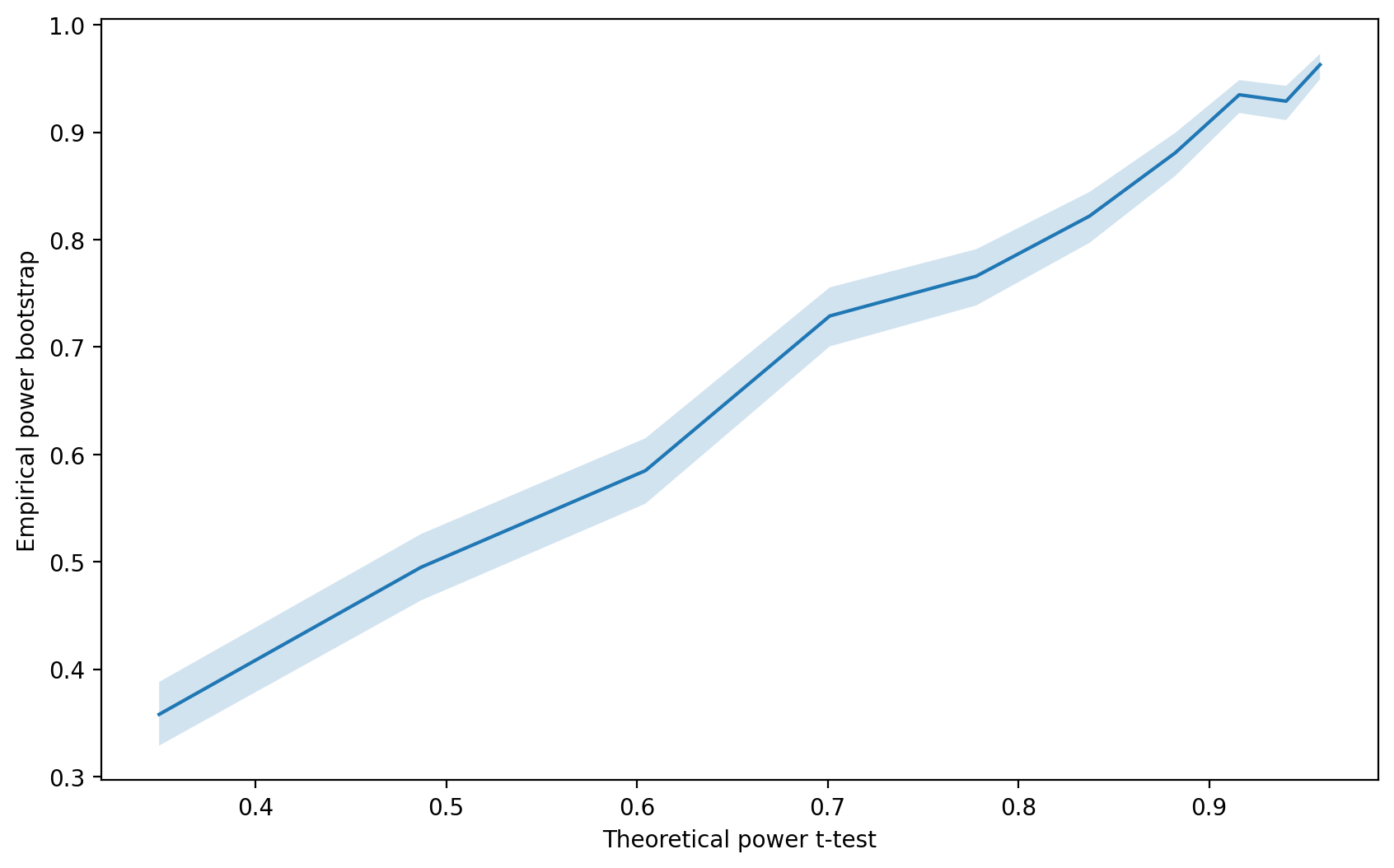

Кажется, что и в этом случае зависимость близка к Построим второй график, аналогичный тому, что строили для t-теста.

fig, ax = plt.subplots(figsize=(10, 6), dpi=200)
ax.plot(power_df_bootstrap['sample_size'], power_df_bootstrap['empirical_power_bootstrap'], '-', 
        label='Empirical power bootstrap', color='green')
ax.plot(power_df_bootstrap['sample_size'], power_df_bootstrap['power'], '-', 
        label='Theoretical power t-test', color='red')
ax.fill_between(power_df_bootstrap['sample_size'], power_df_bootstrap['left_real_level_bootstrap'], 
                power_df_bootstrap['right_real_level_bootstrap'], alpha=0.2, color='green')
plt.xlabel('Sample size')
plt.ylabel('Power')
ax.legend();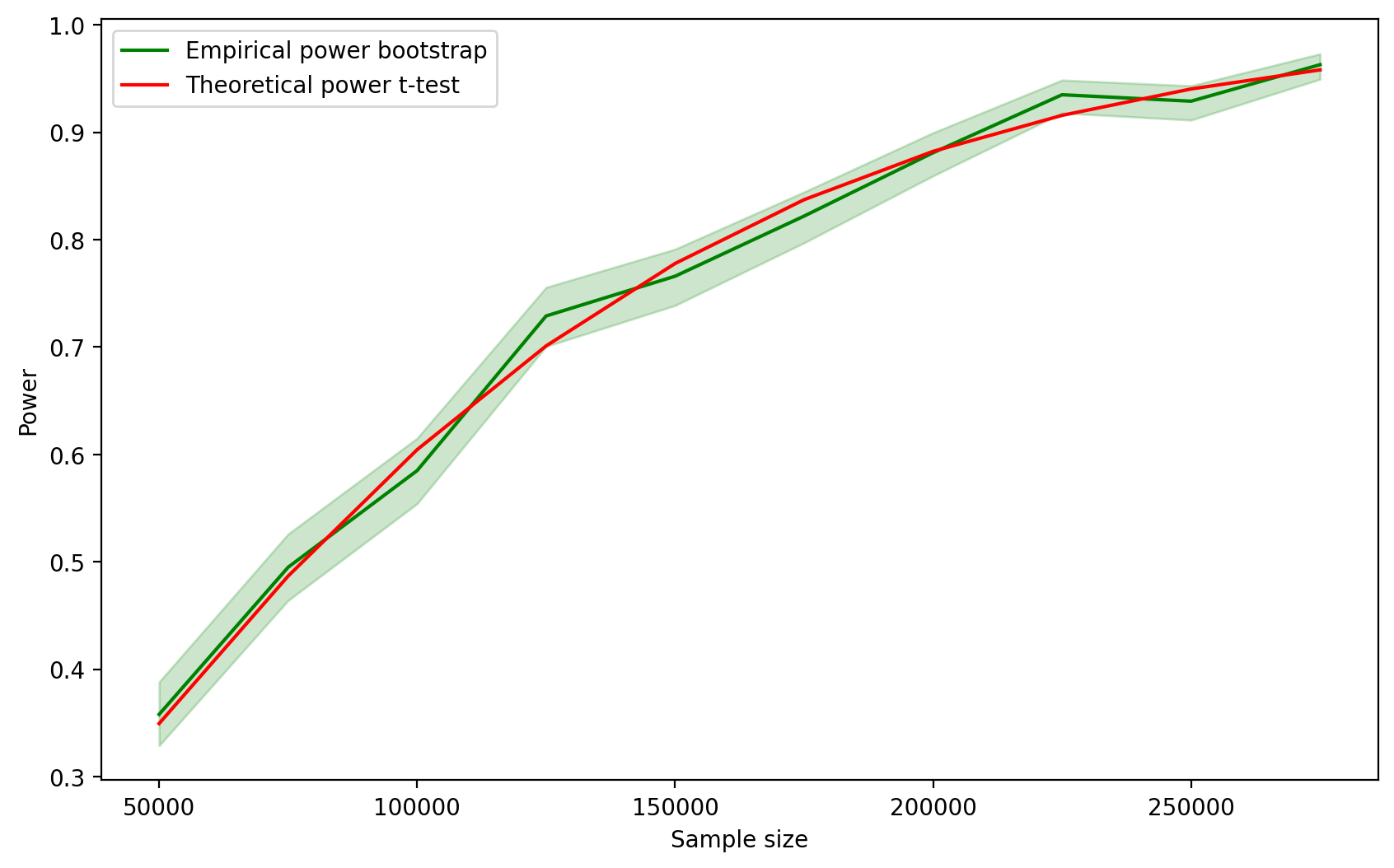

Теоретические мощности снова лежат внутри границ доверительного интервала эмпирических мощностей.

Теперь нанесем все три зависимости мощности от размера выборки на один график.

power_df = pd.merge(power_df_ttest, power_df_bootstrap, how='inner', on=['power', 'sample_size'])
power_df.set_index(pd.Index(range(50000, 300000, 25000)), inplace=True)

fig, ax = plt.subplots(figsize=(10, 6), dpi=200)
ax.plot(power_df['sample_size'], power_df['empirical_power_ttest'], '-', 
        label='Empirical power t-test', color='blue')
ax.plot(power_df['sample_size'], power_df['empirical_power_bootstrap'], '-', 
        label='Empirical power bootstrap', color='green')
ax.plot(power_df['sample_size'], power_df['power'], '-', 
        label='Theoretical power t-test', color='red')
plt.xlabel('Sample size')
plt.ylabel('Power')
ax.legend();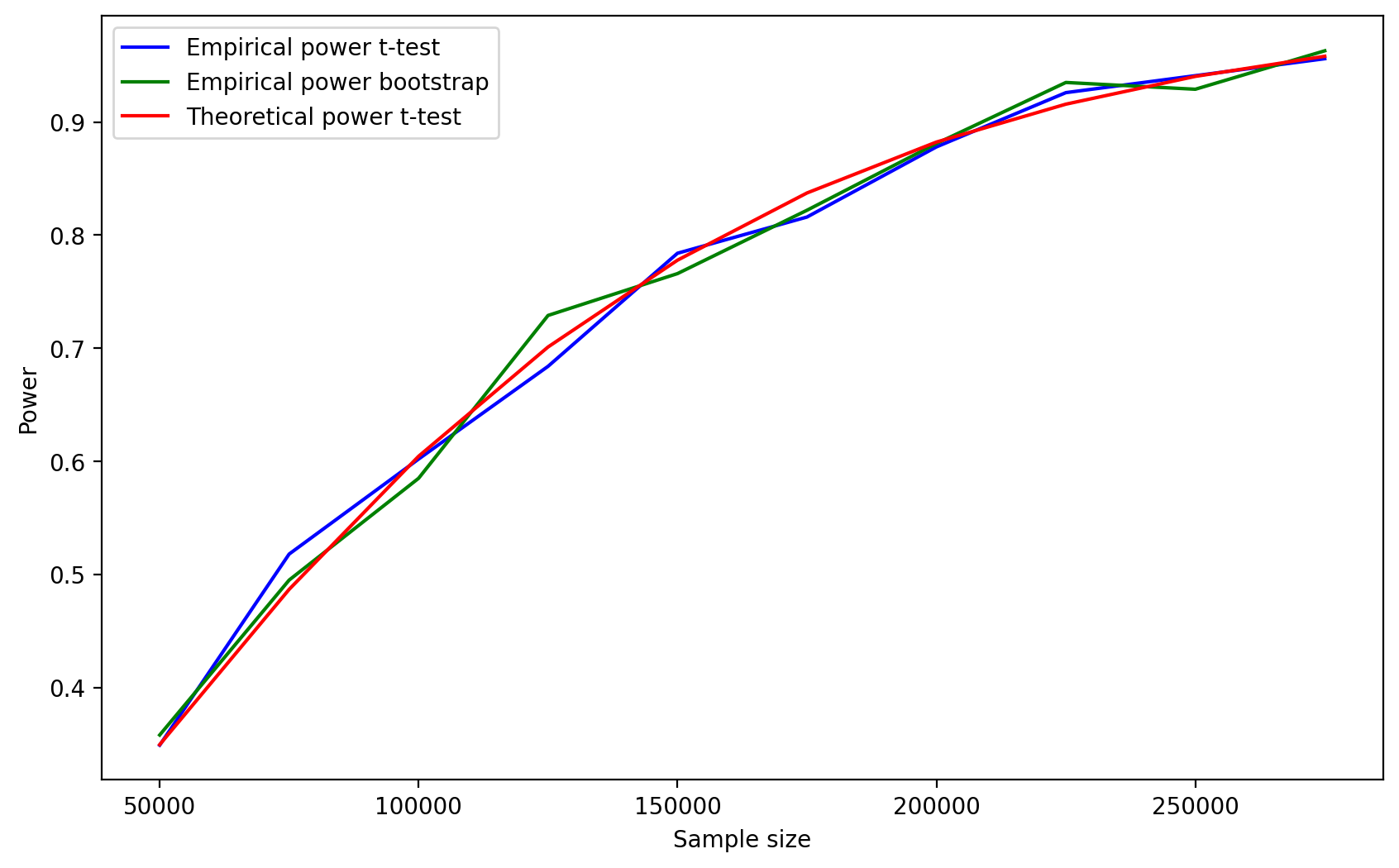

Мы получили хороший результат: формула для t-теста дает приемлемую оценку необходимого размера выборки при использовании бутстрэпа в качестве критерия для экспоненциального распределения.

Реальные данные

Допустим, формула t-теста для определения длительности сработала на синтетических данных. Но как мы можем быть уверены в том, что получим аналогичный результат на реальных данных? Например, мы можем использовать... симуляции.

Алгоритм действий будет схожим, но предлагаю подойти к этой проблеме немного с другой стороны. Обычно в компаниях есть сложившаяся практика использования конкретного уровня мощности. Поэтому давайте теперь будем варьировать не размер выборки и мощность, а размер выборки и MDE. При этом теоретический уровень мощности зафиксируем.

Но прежде чем что-то варьировать, давайте зададимся вопросом, откуда мы возьмем по 1000 выборок для каждой комбинации размера выборки и MDE? Можно взять достаточно большую выборку данных и использовать её, как фейковую генеральную совокупность для группы контроля. Тогда мы точно так же, как и в случае с синтетическими данными, сможем сдвинуть значения этой фейковой генеральной совокупности, чтобы получить фейковую генеральную совокупность тестовой группы.

Алгоритм выглядит следующим образом:

1. Запасаемся терпением, потому что ждать придется долго.

2. Фиксируем уровень значимости и уровень мощности.

3. Формируем фейковую генеральную совокупность A, взяв большой кусок исторических данных.

4. Рассчитываем для нее среднее и дисперсию.

5. Для разных значений MDE формируем фейковую генеральную совокупность B. Сформировать ее можно разными способами: прибавить константу ко всем значениям фейковой генеральной совокупности A, умножить все значения на константу или использовать любой из этих способов и добавить к ним шума (случайную величину с нулевым математическим ожиданием) – выбирайте тот способ, который по вашему мнению лучше имитирует эффекты, которые вы наблюдаете в реальности.

6. Рассчитываем для нее среднее и дисперсию.

7. Подставляем в формулу для расчета размера выборки для t-теста . Получаем необходимый размер выборки.

8. Берем 1000 раз из обеих фейковых генеральных совокупностей выборки рассчитанного размера и сравниваем их с помощью бутстрэпа. Если статистически значимое различие было зафиксировано, записываем результат как 1, в противном случае — 0.

9. Для каждого значения MDE получим серию из 1000 результатов тестов. Посчитаем эмпирическую мощность.

10. Построим доверительный интервал для каждого из полученных значений эмпирической мощности и посмотрим, попадает ли в этот интервал наше зафиксированное теоретическое значение.

sig = 0.05
power = 0.8
z_power, z_sig = sps.norm.ppf([1-power, 1-sig])

fake_population_a = np.array() # сюда вставляем выборку полученную на основе реальных данных
fake_population_a_mean = fake_population_a.mean()
fake_population_a_var = fake_population_a.var()

rel_mde_list = [0.05, 0.04, 0.03, 0.02] # относительные значения прироста (относительный MDE)

N = 1000

power_list = []
empirical_power_list = []
sig_list = []
mde_list = []
sample_size_list = []
left_real_level_list = []
right_real_level_list = []

for rel_mde in tqdm_notebook(rel_mde_list):

    # задаем фейковую генеральную совокупность B
    mde = fake_population_a_mean*rel_mde
    fake_population_b = fake_population_a + mde
    fake_population_b_mean = fake_population_a_mean + mde
    fake_population_b_var = fake_population_a_var

    n = (fake_population_a_var + fake_population_b_var)*((z_sig - z_power)**2)/(mde**2)
    n = round(n)

    results = []

    for i in tqdm_notebook(range(N)):

        sample_a = np.random.choice(fake_population_a, size=n, replace=False)
        sample_b = np.random.choice(fake_population_b, size=n, replace=False)

        res = bootstrap(sample_a, sample_b, sig)
        results.append(res)  

    power_list.append(power)
    empirical_power_list.append(np.mean(results))
    mde_list.append(rel_mde)
    sample_size_list.append(n)
    left_real_level, right_real_level = proportion_confint(count=N*empirical_power_list[-1], 
                                                           nobs=N, 
                                                           alpha=0.05, 
                                                           method='wilson')
    if left_real_level < power and right_real_level > power:
        sig_list.append(1)
    else:
        sig_list.append(0)
    left_real_level_list.append(left_real_level)
    right_real_level_list.append(right_real_level)

    power_df_bootstrap_real = pd.DataFrame(columns=['power', 'empirical_power_bootstrap', 
                                                    'sig_bootstrap', 'mde', 'sample_size', 
                                                    'left_real_level_bootstrap', 'right_real_level_bootstrap'])
    power_df_bootstrap_real['power'] = power_list
    power_df_bootstrap_real['empirical_power_bootstrap'] = empirical_power_list
    power_df_bootstrap_real['sig_bootstrap'] = sig_list
    power_df_bootstrap_real['mde'] = mde_list
    power_df_bootstrap_real['sample_size'] = sample_size_list
    power_df_bootstrap_real['left_real_level_bootstrap'] = left_real_level_list
    power_df_bootstrap_real['right_real_level_bootstrap'] = right_real_level_list
    power_df_bootstrap_real.to_csv('real_data_bootstrap.csv', index = False)

Получив значения для бутстрэпа, наносим их на график. Если результат окажется примерно таким, то формула для t-теста будет неплохим прокси-методом для расчета размера выборки для бутстрэпа.

А что если теоретическая мощность будет выходить за пределы доверительного интервала?

Расстраиваться не стоит. Доверительные интервалы тоже могут ошибаться. Ведь, по сути, когда мы строим доверительный интервал для полученных мощностей, мы задаем уровень значимости — то есть допускаем, что можем совершить ошибку первого рода. 

Если для какого-то значения MDE теоретическая мощность выходит за границы доверительного интервала, но при этом для остальных значений она лежит в пределах, то очень вероятно, что это и есть ошибка первого рода. Если хотите удостовериться в этом наверняка, то можете запастись еще большим терпением и запускать симуляции для этого конкретного уровня MDE много раз. Если только в 5% случаев вы будете наблюдать выход за границы, то это означает, что формула для t-теста дает хорошую оценку размера выборки.

Но даже если вы обнаружите, что на ваших данных рассмотренный метод стабильно дает результат, при котором формула для t-теста не работает, вы все равно можете использовать симуляции, чтобы определить необходимый размер выборки. Подробнее о том, как это сделать можно почитать у коллег из EXPF.

Давайте подведем итог:

1. Для бутстрэпа не существует теоретически обоснованного способа подсчета размера выборки. 

2. Тем не менее, скорее всего, вы можете оценить необходимый размер выборки для бутстрэпа, используя формулу для определения размера выборки для  t-теста.

3. Чтобы удостовериться в этом, вам необходимо провести симуляции на реальных данных и проверить, что заданный уровень мощности попадает в доверительные интервалы мощностей, полученных на основе симуляций для разных значений MDE.

4. Если это не так, то формулу расчета размера выборки для t-теста использовать не получится. Однако с помощью все тех же симуляций все еще можно определить минимальные размеры выборки как для бутстрэпа, так и для любого другого критерия.