Продолжаю потихоньку публиковать свои наработки к занятиям математического кружка. На этот раз речь пойдёт о до боли знакомых квадратных уравнениях и их свойствах, о которых нет времени поговорить в школе.

Геометрия квадратных уравнений

В восьмом классе мы встречаемся с квадратными уравнениями, выводим или заучиваем формулу для их решения, запоминаем страшное слово "дискримитант", в общем, становимся суровыми математиками! Либо окончательно понимаем, что "математика не моё" и наивно называем себя "гуманитариями".

Положа руку на сердце, признаю, что умение решать квадратные уравнения пригодится не всем нам во взрослой жизни. Чаще всего, мы оставляем это знание на полке со школьными тетрадками и учебниками.

Но вот какое важное универсальное знание даёт знакомство с ними: уравнение может не иметь решений, либо одно из решений может не иметь смысла, как, например, отрицательное время в какой-нибудь физической задаче.

Это важный жизненный опыт, который помогает осознавать и познавать границы возможного, применимого, разрешимого.

Квадратные уравнения могут научить ещё кое-чему, а именно, видеть алгебру, отыскивать геометрический смысл алгебраических результатов.

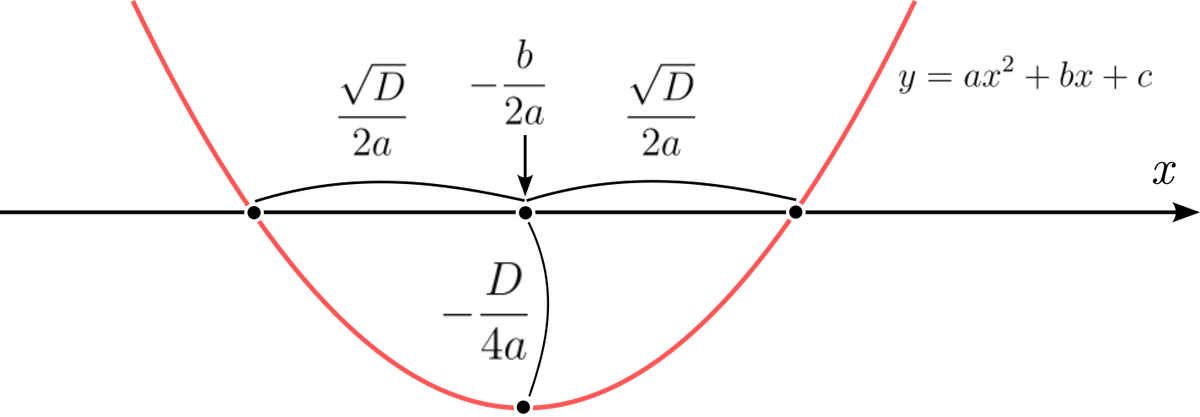
Давайте вспомним, как выглядит общий вид решения квадратного уравнения:

Что означает эта формула? Что два решения расположены по разные стороны некоторого числа  и отстоят от него на расстоянии . Какой же смысл у этих чисел?

Мы знаем, что график квадратного уравнения — это парабола. Кривая, которая имеет осевую симметрию относительно своего минимума. Эта симметрия присутствует и в решении. Число  — это положение оси симметрии, то есть, минимума, а — половина ширины отрезка, который парабола отсекает на оси. Если отсекает, конечно.

Давайте подставим в уравнение положение минимума:

Смотрите-ка, в числителе сам собой образовался дискриминант! Теперь нам легко понять его смысл — вертикальное положение минимума параболы.

Пусть, для определённости, коэффициент  будет положительным, а значит, ветви параболы будут идти наверх. Если дискриминант отрицателен, то парабола расположена над осью  и не пересекает её. В этом случае решений не будет. Если дискриминант положителен, минимум находится под осью  и парабола неизбежно пересечёт эту ось в двух точках.

Наконец, давайте посмотрим, как в само квадратное уравнение входят числа и  из которых состоят его решения. Это легко увидеть с помощью теоремы Виета:

На такой разбор может не хватить времени на школьном уроке, но он полезен для того, чтобы уравнения и их решения стали несколько более говорящими.

Пространство квадратных уравнений

Задачки в учебниках придумывают люди. И они хотят, чтобы задачи в них не просто решались, а ещё и красиво решались. Чтобы чудесным образом извлекались квадратные корни, чтобы дроби сокращались как надо.

Предположим, вам для проведения экзамена нужно сочинить десятка три задачек на решение квадратных уравнений. Вы выписываете наугад тридцать уравнений с целыми коэффициентами. Какую долю из них составят те что, не имеют вещественных решений? А сколько из них будут иметь целочисленные корни? Понятно, что во всех этих вопросах речь идет об ожидаемых величинах и долях.

Доля нерешаемых уравнений

Мы знаем, что квадратное уравнение решается, если его дискриминант  оказывается неотрицательным. А какая доля пространства троек будет удовлетворять этому условию?

На этот вопрос проще ответить не в целых числах, а в действительных, сформулировав вопрос геометрически: какой фигурой в пространстве ограничивается объём нерешаемых уравнений?

Мы знаем уравнение границы этой фигуры: . Давайте преобразуем координаты так, чтобы стало очевидным, с чем мы имеем дело. Для этого сделаем преобразование координат:

и получим:

Мы видим уравнение окружностей в координатах с радиусами . Значит, все нерешаемые уравнения попадают внутрь некоторого кругового конуса. Обратное преобразование к координатам превратит этот круговой конус в эллиптический и повернёт его, как показано на рисунке:

Нам повезло! Конус, даже эллиптический, на всех масштабах выглядит одинаково, а это значит, что можно вычислить долю его объёма в объёме всего пространства параметров. Не буду здесь вдаваться в подробности расчёта, приведу конечный результат: доля нерешаемых уравнений составляет .

Получается, что если наугад выбрать три числа и составить с их помощью квадратное уравнение, то вероятность того, что оно будет иметь вещественные решения составит чуть менее двух третей. Конечно, эта вероятность будет зависеть от конкретного способа выбора коэффициентов, но в случае их равномерного распределения результат можно ожидать таким.

Конечно, если стоит задача составить список заведомо решаемых уравнений, то наугад их сочинять не придётся. Достаточно сгенерировать нужное количество пар решений и с помощью теоремы Виета сформировать соответствующие им уравнения:

Целочисленные решения

И теперь можно перейти ко второму вопросу: как выглядит в пространстве целочисленных коэффициентов квадратных уравнений подмножество "хороших" уравнений? Хорошими будем считать квадратные уравнения с целочисленными коэффициентами, у которых и дискриминант является полным квадратом, и дроби сокращаются так, что решения тоже получаются целочисленными.

Для наглядности, эту задачу будем решать для приведённых квадратных уравнений, то есть, таких, у которых .

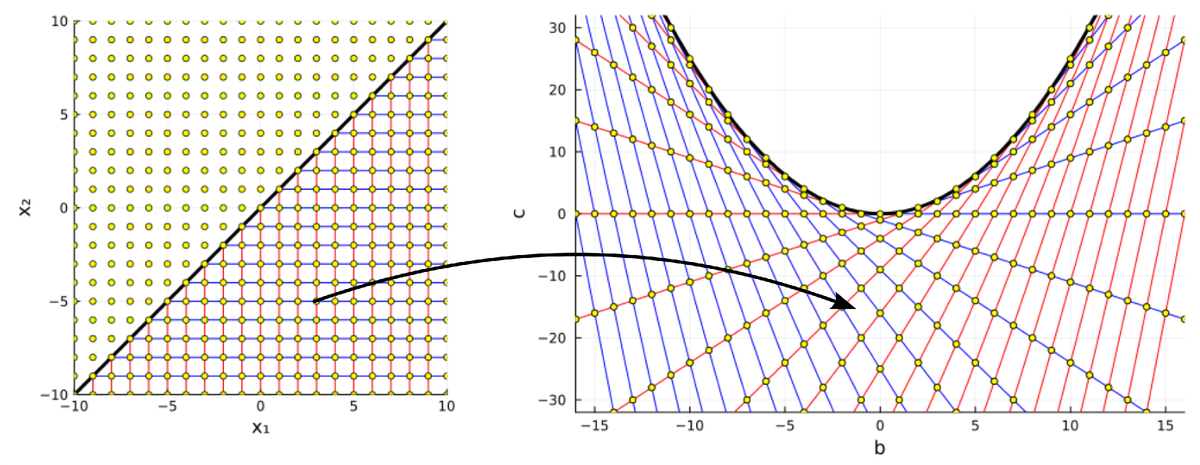
В поиске ответа нам опять поможет теорема Виета. Она определяет преобразование координат, отображающее пространство решений в пространство коэффициентов:

Назовём это преобразование именем Виета. Все пары целочисленных решений образуют равномерную решётку в пространстве всех действительных решений.

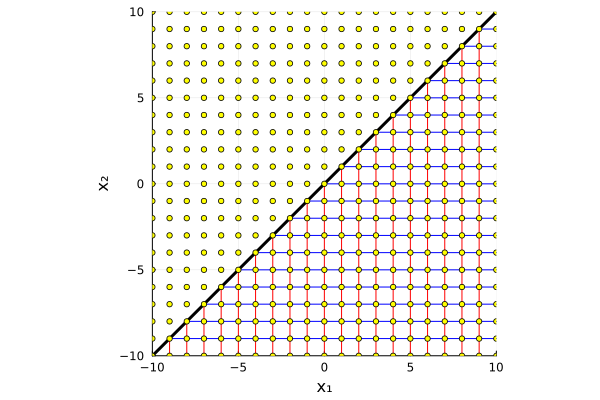
На этой решётке выделяется линия , которая соответствует нулевому дискриминанту и кратным корням. Эта линия является осью симметрии всего пространства решений. Действительно, одному уравнению соответствует две пары решений и , которые расположены симметрично относительно линии кратных корней. Так что достаточно рассмотреть как отображается в пространство коэффициентов только подпространство уникальных решений, например, нижняя полуплоскость.

Горизонтальные и вертикальные прямые линии, соответствующие уравнениям  и (красные и синие линии на диаграммах) преобразование Виета снова превращает в прямые:

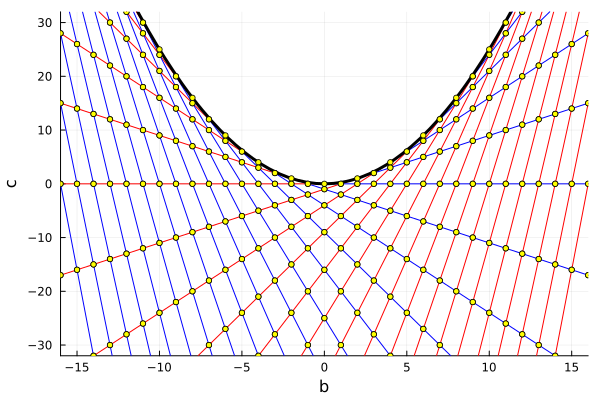
Какая красивая картинка! Линия кратных решений окаймляет "мёртвую область", в которой оказываются коэффициенты уравнений, не имеющих вещественных решений. К ней по касательной подходят линии, вдоль которых располагаются пары решений с одинаковым первым или одинаковым вторым элементом.

Линии, касательные параболе образуют прямолинейную, но непрямоугольную сетку. У неё есть интересное свойство: расстояния между всеми точками пересечений любой отдельно взятой касательной со всеми другими всегда одинаково. Нам оно потребуется, но мы позволим себе принять это эмпирическое наблюдение за факт без доказательства.

В отличие от доли нерешаемых уравнений, доля тех, что имеют целочисленные решения, будет сильно зависеть от диапазона, в котором выбираются коэффициенты. По мере его увеличения, число вариантов будет расти квадратично, как площадь в пространстве коэффициентов. В то же время, коэффициенты, дающие целочисленные решения будут располагаться на касательных к линии кратных корней, и их число будет расти линейно с увеличением диапазона, из-за того, что на касательных они располагаются на равном удалении друг от друга. Так что можно ожидать, что доля целочисленных решений будет падать пропорционально , если  и . Численный эксперимент показывает, что на очень больших сказывается отличие от обратной пропорциональности, но это уже такие тонкости, в которых возиться большого смысла нет.

Это значит, что уравнения с небольшими по модулю целыми коэффициентами с большей вероятностью будут иметь целочисленные корни, чем уравнения с большими коэффициентами.

И последнее замечание. В плоскости область нерешаемых уравнений ограничена параболой, тогда как в пространстве эта область представляет собой конус. В этом нет противоречия, плоскость сечёт конус параллельно образующей конуса, а такое коническое сечение является параболой.

Истинный облик квадратных уравнений

А куда деваются корни квадратного уравнения, когда оно не имеет действительных решений и откуда берутся комплексные корни? Как выглядят квадратные уравнения "на самом деле"? Сегодня мы увидим скрытый от вещественного мира облик привычных со школы квадратных уравнений.

Грамотные маткружковцы знают про существование комплексных корней квадратного уравнения, и даже знают, как правильно ставить ударение в слове "комплéксный". А как и откуда эти комплексные корни появляются по мере исчезновении вещественных? Где они располагаются и какой имеют геометрический смысл, применительно к параболе ?

Для того, чтобы порассуждать об этом, надо выйти за пределы вещественной числовой оси и увидеть уравнение таким, каким оно предстаёт в своём мире: в чудесном поле комплексных чисел, в которых любые алгебраические уравнения имеют решения.

Подставим в уравнение вместо переменной x комплексное число в форме :

Теперь раскроем все скобки и приведём подобные слагаемые относительно , не забывая, что

Равенство будет верным, если одновременно и вещественная и мнимая части левой половины равенства обратятся в ноль. Таким образом, мы свели одно уравнение в комплексных числах к системе вещественных уравнений на  и :

Второе уравнение при этом распадается на два: либо , либо .

Можно изобразить геометрические места точек, удовлетворяющих всем трём уравнениям в плоскости и увидеть, что происходит с корнями. Первое уравнение описывает гиперболы с асимптотами, пересекающимися в точке и симметрично расходящимися под наклоном . Ветви гиперболы могут проходить двумя разными способами, в зависимости от знака дискриминанта, либо пересекая ось абсцисс, либо нет. А второе и третье уравнения — это прямые линии, горизонтальная и вертикальная, соответственно.

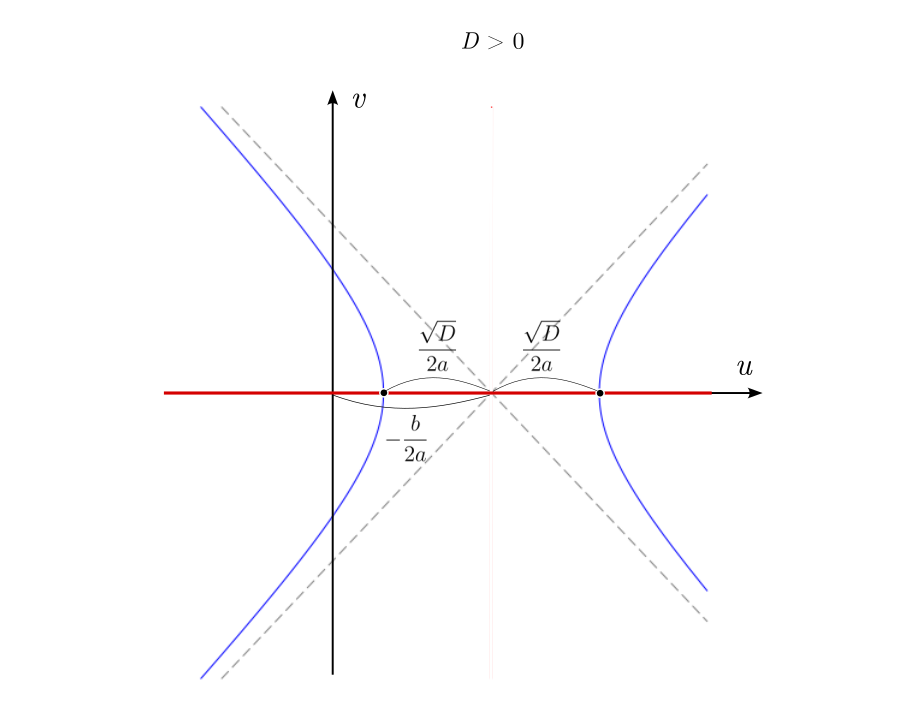
При положительном дискриминанте гиперболы пересекают вещественную ось, и точки пересечения соответствуют двум вещественным числам. Симметрия гипербол в точности согласуется с симметрией параболы, о которой мы говорили в самом начале.

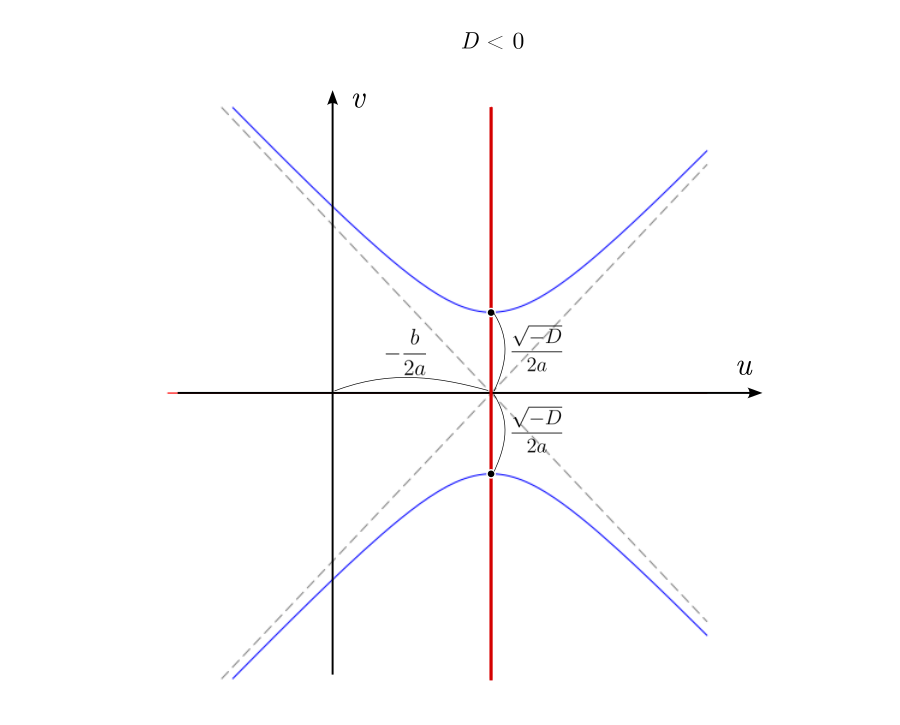
Когда дискриминант отрицателен, ветви гиперболы проходят выше и ниже вещественной оси и пересекают вертикальную линию в двух точках. Это и есть два комплексных корня с вещественной частью равной , и мнимой частью, отличающейся от нуля на величину

Нулевому дискриминанту соответствует вырожденная гипербола, совпадающая с асимптотами. Корень при этом кратный, и равен

Но откуда же взялись гиперболы? Квадратное уравнение — это же про параболы?

Истинное лицо квадратного уравнения

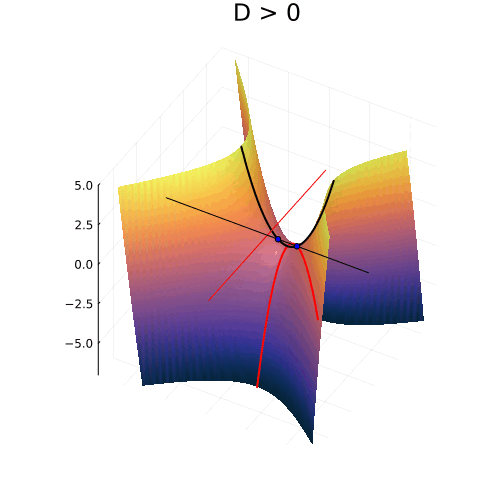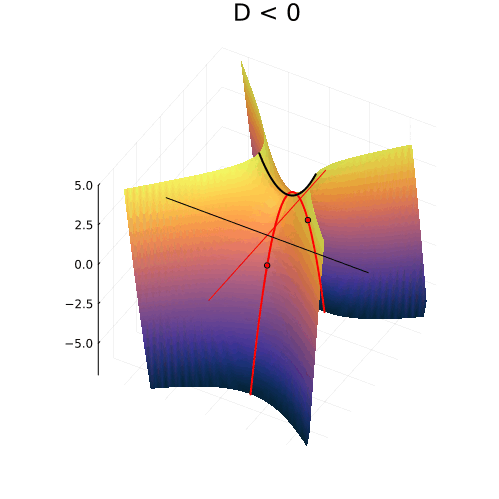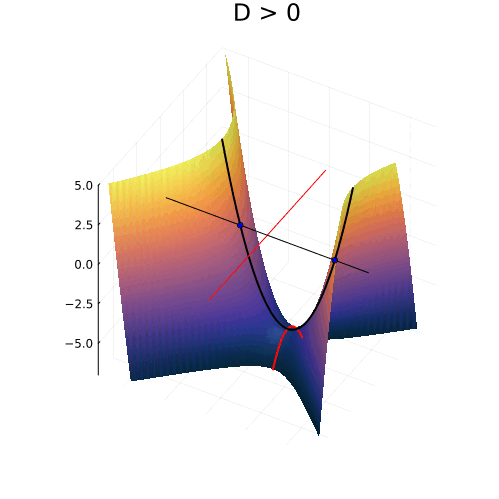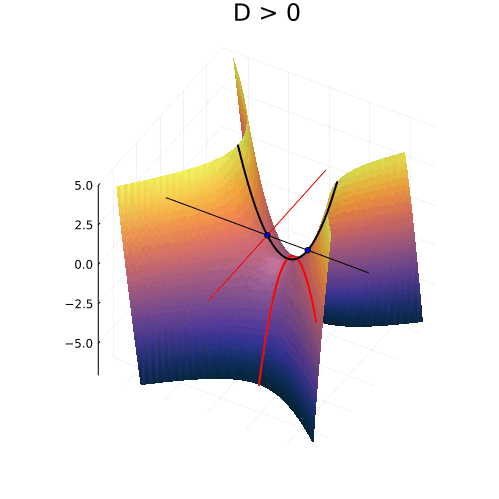
На самом деле, вещественная часть уравнения в комплексных числах описывает гиперболический параболоид. Вот как он выглядит:

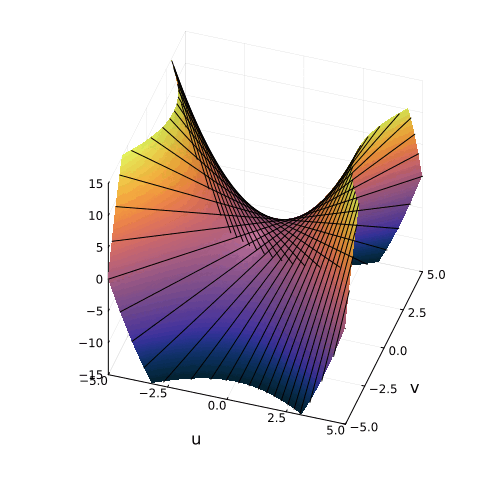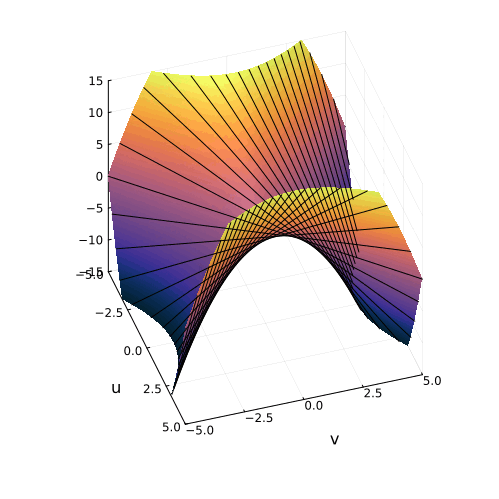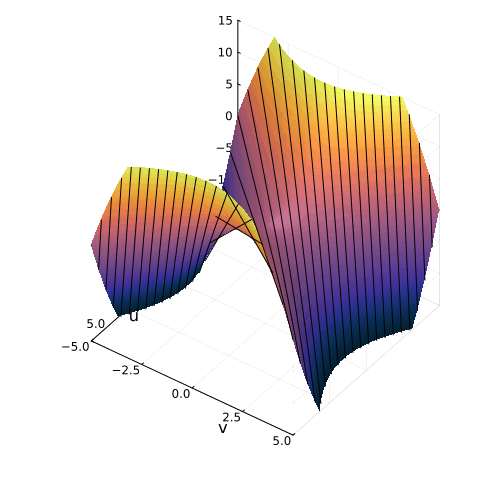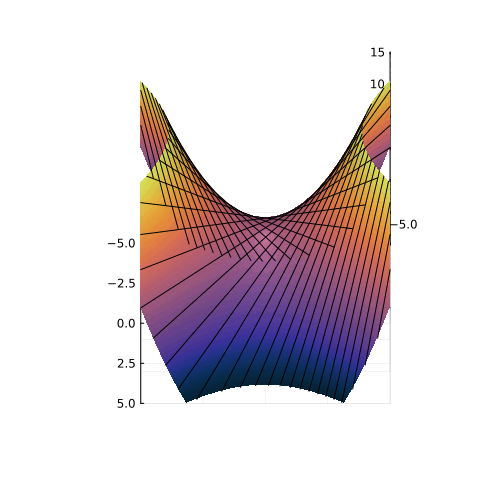
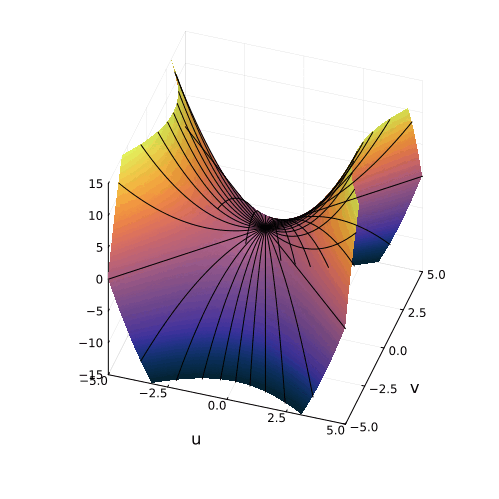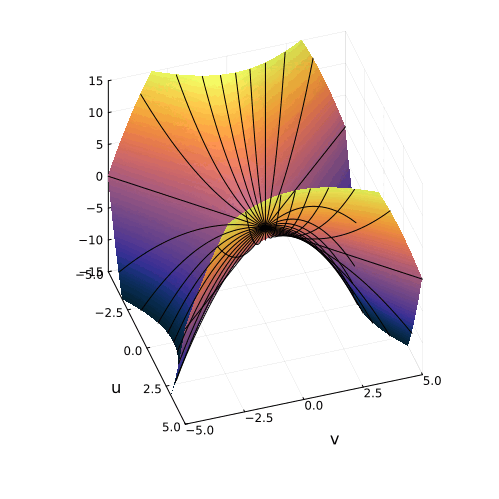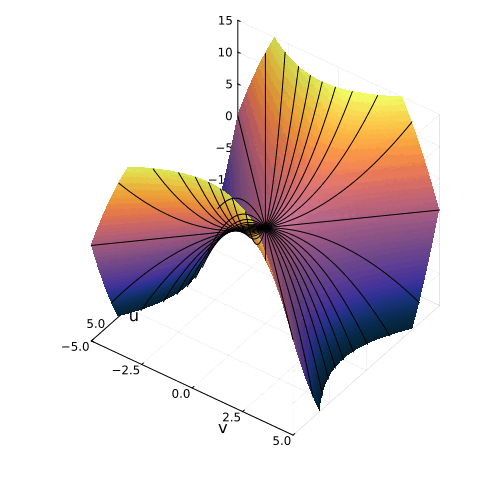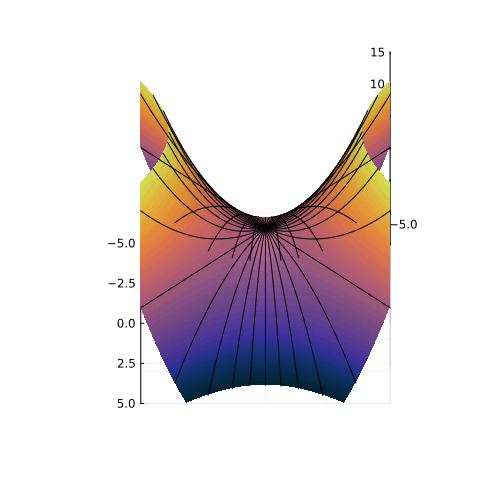
Эта поверхность замечательна во многих отношениях. Её можно построить с помощью движения прямой или параболы, либо представить, как поверхность, порождённую многообразием парабол, проходящих через одну точку, которая называется седловой, или многообразием гипербол, лежащих в параллельных плоскостях. Наконец, именно такую форму имеют картофельные чипсы известной марки. Прекрасный иллюстрированный рассказ об этом можно найти здесь.

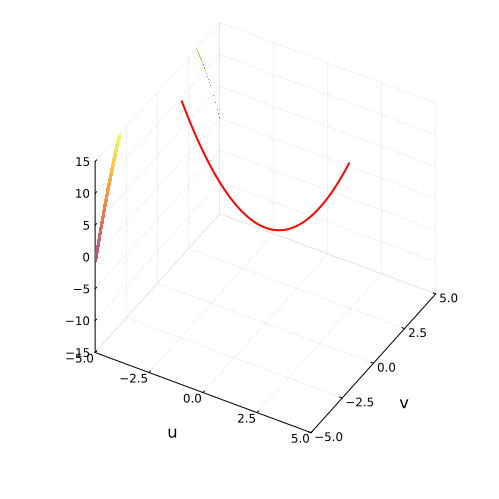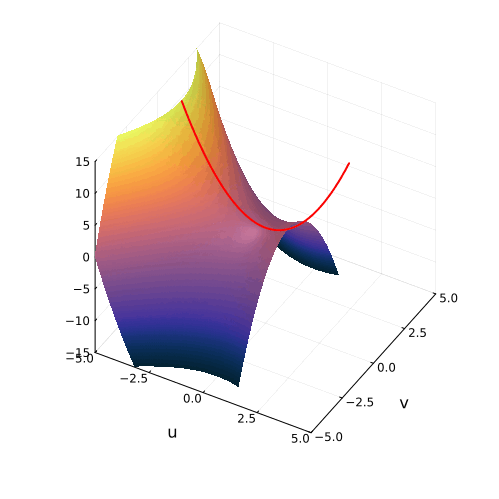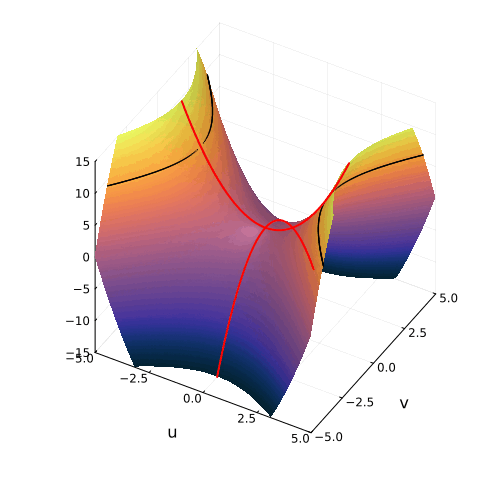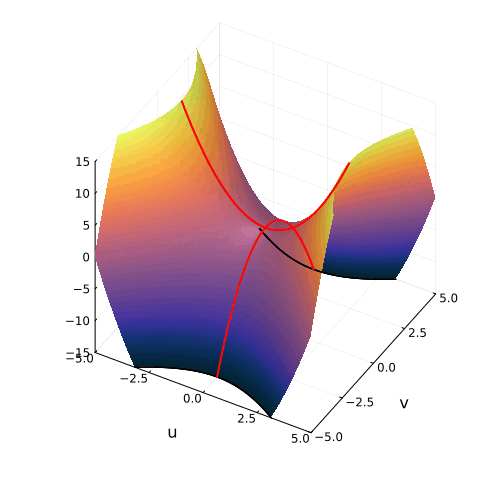
Линии пересечения параболоида с плоскостью это и есть знакомые нам гиперболы — горизонтальные сечения гиперболического параболоида. Теперь на корни квадратного уравнения мы можем взглянуть, увидев их во всей полноте. Плоскости  и , пересекая параболический гиперболоид в вертикально, образуют две параболы, касающиеся друг друга в седловой точке и расположенные во взаимно перпендикулярных плоскостях. Эти две параболы представляют собой многообразия всех корней квадратного уравнения.

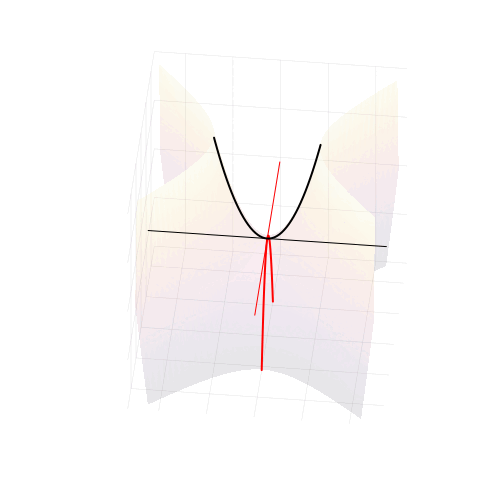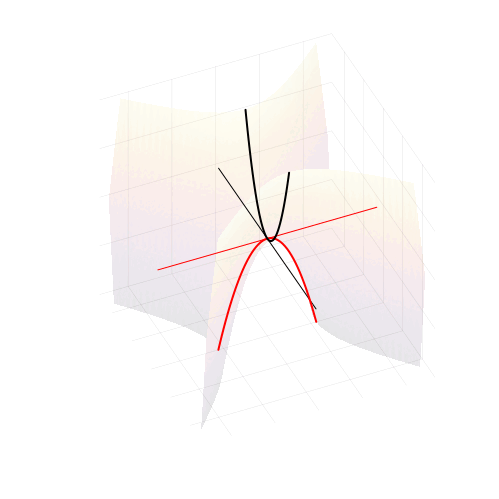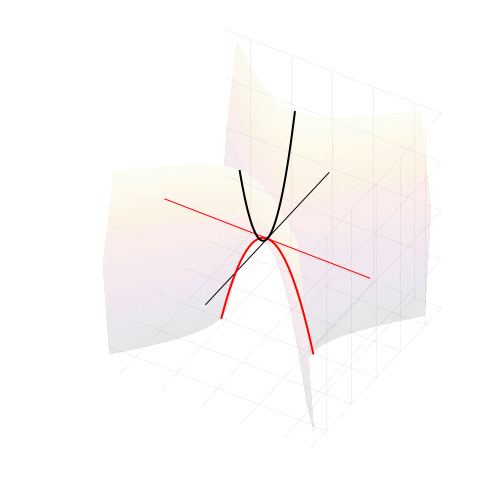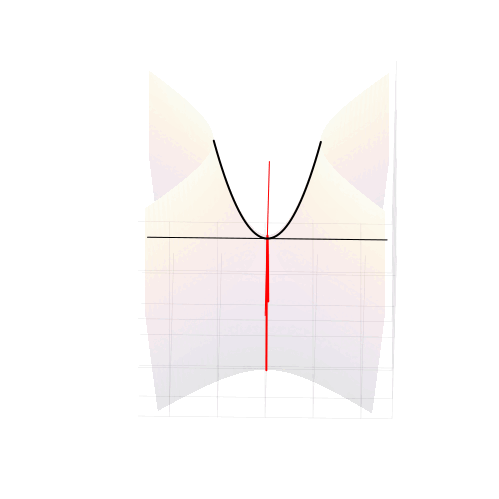
Положение седловой точки гиперболического параболоида это знакомое нам число Посмотрите, что происходит с поверхностью, при изменении знака дискриминанта. Если мы станем изменять коэффициенты квадратного уравнения, то параболоид станет перемещаться в пространстве пересечение многообразий корней уравнения с плоскостью рождает пару чисел, либо вещественных, либо комплексных

Теперь мы с уверенностью можем сказать, что видим, куда деваются вещественные корни уравнения и откуда берутся комплексные!

Параболоид в пространстве квадратных уравнений

Очертания гиперболического параболоида можно разглядеть и в сетке, образованной линиями равных решений в пространстве коэффициентов квадратных уравнений, которую мы построили в предыдущей части. И это, конечно же, не случайно. Мы рассмотрели преобразование Виета, которое строит найти отображение из пространства решений в пространство коэффициентов:

Где же здесь прячется параболоид? Уравнение гиперболического параболоида имеет два канонических вида:

которые переходят друг в друга при линейном преобразовании координат Это преобразование поворачивает и двое уменьшает все фигуры, не меняя их формы. Отсюда следует, что в сердце преобразования между вещественными корнями уравнения и коэффициентами тоже лежит гиперболический параболоид. Вот как выглядит это преобразование геометрически:

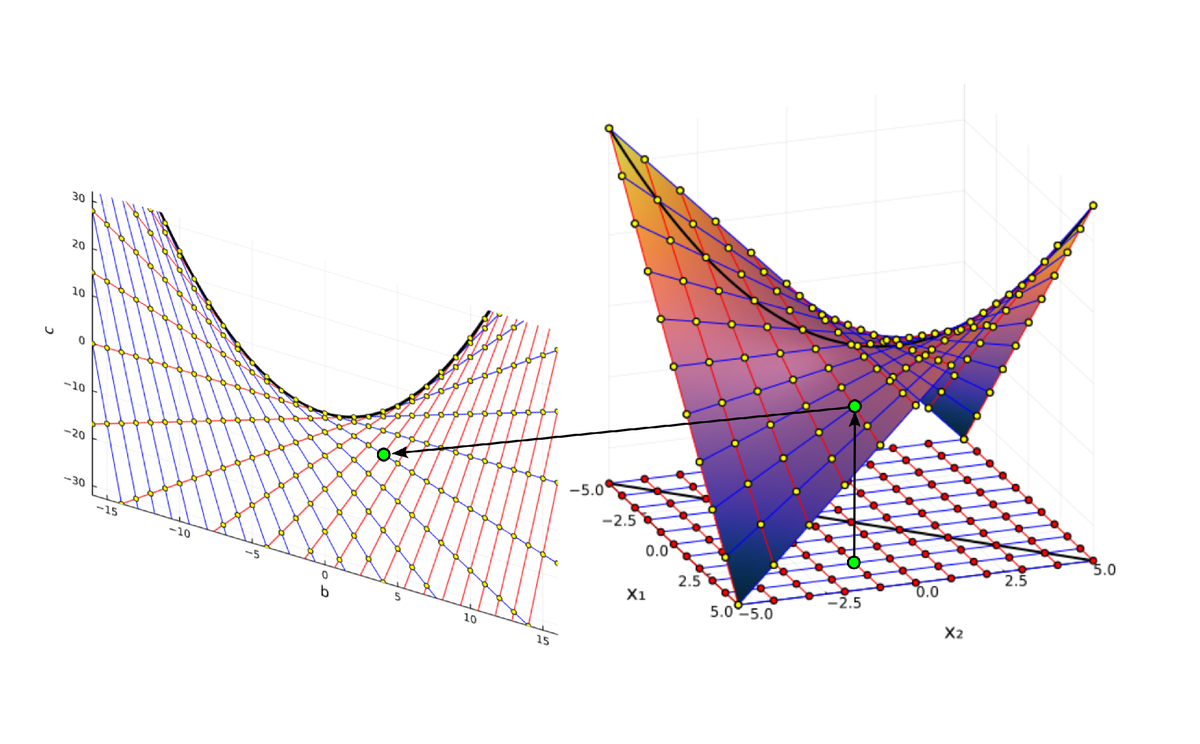
Вертикальная ось на этом графике соответствует свободному коэффициенту  в уравнении. Коэффициент при линейном члене , это сумма корней, так что плоскость представляет собой вертикальную плоскость, параллельную линии кратных корней. Проекцию параболоида на эту плоскость мы и видим, как преобразование Виета.

Параболоид в преобразовании Виета и параболоид, образуемый вещественной частью квадратного уравнения в комплексных числах, это разные фигуры, не связанные друг с другом. Но квадратные уравнения настолько пронизаны параболами, что не удивительно встретить параболоиды в разных частях их теории.

Можно бы завершить рассказ сакраментальной фразой: "Теперь мы знаем о квадратных уравнениях всё". Но, конечно же, главное, это разобраться а зачем нам вообще знать что-то про квадратные уравнения?