09.11.2020 20:48
pallada92 25 8400 Источник
В предыдущих выпусках:
1. Трехмерный движок на формулах Excel для чайников
2. Трехмерный движок внутри запроса SQL





Эта статья началась с шуточного ответа коллеги на мой вопрос о том, на какой популярный язык разметки портировать трехмерный движок в очередной раз.

Вообще, меня всегда интересовало, на что может быть похоже программирование внутриклеточных процессов. Как выглядят переменные, условия и циклы? Как вообще можно управлять молекулами, которые просто свободно перемещаются в цитоплазме?

Ответ довольно неожиданный — lingua franca для моделирования сложных процессов в клетках является реакции вида
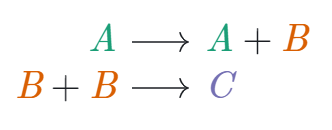
Эти реакции моделируются при помощи закона действующих масс, который одинаково работает и в химии, и в молекулярной биологии.

— Неужели при помощи этих примитивных реакций можно что-то программировать?
— Да, а то, что написано выше, вычисляет $B = \sqrt{A}$.

В этом пошаговом туториале мы вместе взорвем себе мозг, чтобы получить 10 таких реакций, которые производят рендер трехмерного куба.

Потом я расскажу, как полученные реакции скомпилировать в код ДНК, который можно синтезировать в лаборатории и (если очень повезет) получить трехмерный куб из двумерного массива пробирок.

Как обычно, я сделал веб-приложение с эмулятором таких реакций, в котором можно поупражняться в «реактивном» программировании. Вы сможете удивлять химиков способностью вычисления конечных концентраций в сложных системах реакций методом пристального взгляда.

Для понимания статьи никаких предварительных знаний не требуется, необходимые сведения из школьной программы по биологии мы повторим в начале статьи. Также мы разберем типичные паттерны, которые использует эволюция для достижения сложного поведения в живых клетках.


Дисклеймеры


  • Я никак не связан с биологией. Это просто пятничная будничная статья программиста для программистов о малознакомом предмете.
  • В этой статье точно есть куча фактических ошибок и терминологических косяков. Например, я только недавно узнал, что молекулярная биология и биохимия — не одно и то же. Если вы нашли что-то подобное — буду безумно рад комментариям в личку.
  • Весь материал был непозволительно упрощен, чтобы не грузить читателя лишними подробностями. Я старался избегать специфических терминов, где это возможно (например, «шагающие белки» вместо «кинезины»). Многие примеры взяты вперемешку от бактерий и многоклеточных организмов и могут никогда не встречаться вместе.
  • У любого утверждения обязательно будет множество исключений. Любое перечисление неполное. Примеры нерепрезентативные.


Статья будет состоять из трех частей, как если бы биологу, математику и программному инженеру дали исследовать одну и ту же задачу.


Часть I: Биология сложного поведения клеток


Эта часть посвящена краткому обзору примеров механизмов, которые позволяют клеткам управлять своими процессами подобно скриптам bash у системных администраторов.

Содержимое этой части не требуется для понимания последующих. Ее цель — дать примерное представление о том, что может скрываться за буками $A, B, C$ и т.д. в реакциях, которые будут рассматриваться далее, а также заинтересовать читателя, чтобы он захотел прочесть статьи в википедии про описываемые сюжеты.

Сразу предупрежу, что обзор не полный и не самый корректный. Если я пишу что-то про то, почему эволюция выбрала конкретное решение — воспринимайте это как полную спекуляцию.


1.1 Вспоминаем основы


Из чего состоит клетка:

  • ДНК — двухцепочечная спираль, состоящая из последовательности 4 нуклеотидов: A, C, G, T.
  • РНК — одноцепочечная спираль, которая может переносить копии участков ДНК (но не только, об этом подробнее в соответствующей главе).
  • Белки
    • Являются цепочками, которые составлены из 20 аминокислот.
    • Удивительной особенностью является то, что эти цепочки самопроизвольно складываются в сложные стабильные структуры.
    • Способны выполнять практически любые функции в клетке: строительный материал, катализаторы реакций, транспортировка веществ, передача сигналов и т. д.
  • Остальные молекулы — например, глюкоза или клетчатка.

Белки и ДНК созданы друг для друга как Paint и BMP.

  • В ДНК может кодироваться только информация о белках.
  • Принцип кодирования простой: тройки нуклеотидов кодируют одну аминокислоту.
  • Участок ДНК, кодирующий белок, называется ген.
  • Начало и конец гена обозначены специальными “метками”: промотор, терминатор, старт-кодон, стоп-кодон. Это довольно большая тема, в которую мы не будем углубляться в этой статье.
  • Между этими участками располагается некодирующая ДНК, которую некоторые пренебрежительно называют “мусорной”.


Белки получаются из ДНК в два этапа:Иллюстрация с сайта atdbio.com

  • Транскрипция: РНК-полимераза прикрепляется к ДНК и делает копию одного из её генов в виде РНК.
  • Трансляция: РНК попадает в рибосому, которая синтезирует последовательность аминокислот. После синтеза эта цепочка под действием химических связей сворачивается в белок нужной формы.



1.2 Белки — объекты первого класса в клетках


Подобно конструктору Лего, белки:

  • состоят из небольшого числа стандартных элементов (аминокислот),
  • легко собираются и разбираются,
  • не такие прочные, как обычные объекты, хотя если грамотно продумать их структуру, могут быть достаточно прочными,
  • идеально совместимы между собой,
  • при этом без проблем способны взаимодействовать и с объектами внешнего мира.

В бытовом понимании, белки представляются таким «строительным материалом» для мышц, в котором не ожидаешь найти сложного поведения. В биологии же они имеют репутацию нано-роботов, которые способны выполнять нетривиальные задачи в клетке.

Рекомендую посмотреть это видео, чтобы получить представление о том, как это выглядит на молекулярном уровне

Приведем несколько примеров белков со сложным поведением:



  • Пожалуй, самый крутой белок в клетке и один из самых сложных — рибосома. По сути это принтер, в который на вход подается РНК, а на выходе печатается белок, который в ней закодирован.
  • Если мы можем синтезировать белки, то нужно их и утилизировать, точнее разбирать обратно на аминокислоты. Для этого есть “сборщик мусора” из мира белков - протеасома.
    • Как протеасома понимает, какие белки разбирать? Достаточно пометить любой белок специальной белковой меткой - убиквитином.
    • По какому принципу ставятся эти метки? Этим занимаются белки, называемые убиквитинлигазами.
  • Для меня было неожиданно узнать, что для получения энергии важную роль играет белок АТФ-синтазы, который содержит вращающиеся части и работает подобно ветряной мельнице: ссылка на видео.



1.3 Паттерны проектирования белков


Белки, подобные перечисленным в предыдущей главе, являются достижением длительной эволюции и используются только для задач сопоставимой сложности и важности. Если же нужно быстро добавить новую функциональность, эволюция предпочитает декомпозировать задачу на несколько белков, составленных по стандартным паттернам.

Рассмотрим несколько примеров паттернов.

  • Allosteric regulation - способность белков распознавать молекулы определенного вида и захватывать их.
  • DNA-binding domain - часть белка, которая позволяет белку проверить участок ДНК на соответствие короткому регулярному выражению и закрепиться на нем. В отличие от CRISPR, этот механизм не подразумевает возможность редактировать этот участок.
  • Фосфорилирование - возможность пометить белок “флагом общего назначения” в виде остатка фосфорной кислоты. Чаще всего этот флаг имеет семантику временного отключения активности белка.

Хорошая новость: паттерны могут комбинироваться. Например:
  • «Если удалось захватить молекулу триптофана, то активировать поиск ДНК по регулярному выражению и закрепиться на нем»

Это настоящий белок, называемый “триптофановый репрессор”.

3d-модель с сайта www.rcsb.org/3d-view/1TRO/1

На картинке выше он показан закрепленным на молекуле ДНК. Красным показаны молекулы триптофана.

Точное значение регулярного выражения в привычном для программистов смысле я не нашел (это где-то в этой работе), но судя по комментариям к 3d-модели, последовательность TGTACTAGTTAACTAGTAC под него должна подходить.

Также белки позволяют производить внутри себя операцию логического отрицания:
  • «Если молекулы аллолактозы НЕТ, то активировать поиск ДНК по регулярному выражению и закрепиться на нем»

Это настоящий белок, называемый “лактозный репрессор”.

Хочу пояснить, что эти оба белка встречаются только у бактерий кишечной палочки, однако их механизм был открыт одним из первых, поэтому их часто приводят в пример в учебниках биологии.


1.4 Плохие новости


Трагедия с белками состоит в том, что ученые могут всех подробностях изучать механизмы взаимодействия белков и знать исходные последовательности аминокислот, но с невероятным трудом могут создавать новые белки с заданными свойствами.

Более того, даже «элементарная» на первый взгляд задача определения структуры белка является недостижимой по сложности на данном этапе развития вычислительной техники. Только вдумайтесь: известно, что цепочка из аминокислот единственным образом сворачивается в некоторую пространственную структуру из любого своего начального положения и мы практически бессильны в том, чтобы повторить этот процесс.

Порядок цифр такой: год работы суперкомпьютера позволяет моделировать первые 3 наносекунды процесса сворачивания белка. Есть замечательная игра Foldit, где люди могут соревноваться в способности сворачивать белки и иногда они получают решения не хуже полученных другими методами.

Таким образом, мы можем сколько угодно фантазировать на тему, как мы могли бы добавить в наши клетки белки с определенными свойствами, чтобы «пофиксить» какой-нибудь процесс, но будем бесконечно далеки от того, чтобы получить заветную последовательность ДНК.

Как же мы тогда собираемся портировать трехмерный движок в код ДНК? Для этого мы воспользуемся читом и будем использовать ДНК не совсем по прямому назначению. Но не будем забегать вперед.


1.5 Как белки узнают, куда им нужно двигаться?


При изучении процессов в клетке может сложиться впечатление о белках как о таких «юнитах» из компьютерных игр, которые знают, куда им нужно двигаться и с чем взаимодействовать. Или клетка может представляться как завод с конвейерными лентами, которые доставляют строительные материалы туда, где они нужны.

На самом деле аналогия с конвейерными лентами действительно имеет место быть — это называется микротрубочками. По ним перемещаются удивительные «шагающие белки», которые потребляют АТФ в качестве топлива (вы наверняка видели эти видео).

Но большинство процессов в клетке происходит без участия микротрубочек. Белки (как любые молекулы) просто перемещаются в цитоплазме случайным образом. Таким образом триптофановый репрессор будет пытаться присоединиться абсолютно ко всему, что есть в клетке, пока не наткнется на последовательность TGTACTAGTTAACTAGTAC. К счастью, геном кишечной палочки состоит всего лишь из 4 млн. пар нуклеотидов — в 1000 раз меньше, чем у людей.

По степени безумия для программиста эта идея сравнима с сортировкой массива случайными перестановками, пока массив не будет отсортирован целиком. Это даже хуже, чем полный перебор!


Эта идея покажется не такой плохой, если учесть факторы, которые нам трудно представить в макромире:

  • Даже в простых клетках находится много белков: >40 млн.
  • При этом различных видов белков не так много, например 1800 у кишечной палочки.
  • Эти белки двигаются хоть и случайно, но очень и очень быстро в масштабах клетки.
  • К тому же это движение происходит в трехмерном пространстве, про которое наша интуиция случайных блужданий работает хуже.



1.6 Сферическая клетка в вакууме


Если рассматривать клетку бактерии, у которой нет ядра и эндоплазматического ретикулума, а также не учитывать микротрубочки, получается следующая картина.

Внутри клетки находится равномерно распределенный суп из разнообразных белков, молекул, ДНК и РНК, которые случайным образом друг с другом сталкиваются и иногда взаимодействуют.

Где-то внутри этого супа происходит процесс биосинтеза белков: РНК-полимераза присоединяется к случайным участкам ДНК, пока не найдет метку начала гена. Она делает копию этого гена в виде РНК, которая спустя какое-то время попадает в рибосому. Рибосома синтезирует закодированный белок.

Каким-то магическим образом (мы это рассмотрим чуть позже) белки точно с такой же скоростью уничтожаются, чтобы клетка не “лопнула”.

Тут необходимо сделать важное пояснение, что если взять любую не бактериальную клетку, то в ней будет множество «отсеков» (органелл), которые более-менее изолированы друг от друга. Это довольно существенная деталь, которая позволяет значительно усложнить поведение клетки. В частности, вероятно, бактерии не способны образовывать многоклеточные организмы в том числе потому, что у них органеллы практически отсутствуют. Но чтобы не усложнять повествование, мы далее везде будем рассуждать про клетку без органелл, хотя будем обсуждать и механизмы типа альтернативного сплайсинга, которых нет у бактерий.

Если рассмотреть клетку, которая ничего не делает и которой не нужно делиться, то ее основную функцию можно сформулировать как поддержание постоянства концентраций белков в своем составе.

Даже поддержание постоянства своего состава не такой элементарный процесс.

  • Белки непрерывно самопроизвольно деградируют и их нужно постоянно пополнять с правильной скоростью.
  • Для синтеза необходимо обеспечивать достаточное количество строительных материалов.
  • Также нужно учитывать, что какие-то вещества из тех, которые синтезируются в клетке, могут уходить вовне или приходить извне.
  • Поэтому клетке нужно иметь какую-то обратную связь, чтобы переставать или начинать их синтезировать в зависимости от ситуации.

Мы пришли к тому, что даже самой простой клетке жизненно необходимо контролировать скорость синтеза своих белков в зависимости от внешних факторов. Но если внимательно посмотреть на процесс синтеза, то мы увидим, что хоть он и случайный, но на него пока не влияют никакие внешние факторы.


1.7 Как одни белки могут влиять на синтез других белков


Итак, нам нужен какой-нибудь способ влиять на активность синтеза определенных белков. Правильно это называется “регуляция экспрессии генов”.

Я бы провел аналогию с ядерным реактором, в котором управление происходит путем опускания и поднимания стержней. Так же и для управления процессами в клетке достаточно контролировать уровни экспрессии отдельных генов.

Идея состоит в том, чтобы вставить “костыль” в какое-нибудь место механизма синтеза белков, чтобы мешать ему это сделать. Если их нет - уровень экспрессии максимальный.

Картинка с Википедии

Один из типичных примеров - это знакомый нам триптофановый репрессор.

  • Он способен крепиться к ДНК, мешая РНК-полимеразе делать копию соответствующих генов, тем самым подавляя их экспрессию.
  • При этом его механизм крепления к ДНК активируется только если обнаруживается молекула триптофана.
  • Получается, что если триптофан есть, то гены “включены”, если нет - выключены.

Обратите внимание, что этот механизм может использоваться для получения логических конструкций: если перед каким-то геном есть несколько способов вставить «костыль», то ген будет экспрессироваться только если ни один костыль не сработал. Таким образом мы получаем возможность реализации отрицания ИЛИ.


1.8 РНК - когда данные имеют структуру в прямом смысле


Рибонуклеиновая кислота, вероятно, является самой важной технологией в истории жизни на Земле. Потому что без РНК невозможен синтез белков и репликация ДНК, при этом РНК способна выполнять и функции белков, и ДНК. Собственно, в этом и состоит идея гипотезы мира РНК.

На первый взгляд, в РНК нет ничего интересного — это та же ДНК, только без дублирования информации.

Еще хуже, в РНК во всей своей красе проявляется принцип комплементарности. То есть нуклеотиды A и U, а также G и C постоянно стремятся соединиться в пару. Единичные такие связи не очень прочные, однако если нашлись два длинных комплементарных участка, то они склеятся почти намертво. С учетом теории вероятностей, практически невозможно придумать такую длинную цепочку РНК, которая не могла бы сама с собой как-нибудь склеиться.

После такой склейки, РНК вполне может стать нечитаемым. При попадании такой «петли» (биологи их называют "шпильками") в рибосому, она либо застрянет, либо отвалится, не закончив задание печати.

Казалось бы, это просто катастрофа с точки зрения передачи информации. Однако, это открывает и новые возможности:

  • Мы можем делать разные прочные конструкции из РНК и использовать их для тех же целей, что и белки. Нередко белки имеют внутри себя каркасные вставки из РНК.
  • Эти петли можно использовать как еще один механизм вставки «костылей» в процесс биосинтеза белков.



Наверное, это уникальный случай, когда физический носитель, на котором записан код, взаимодействует с объектами, которыми этот код манипулирует.


1.9 Это просто шедевр применения плохих практик


Сейчас мы рассмотрим второй механизм контроля экспрессии группы генов, связанных с синтезом триптофана (первый механизм использует триптофановый репрессор, чтобы помешать РНК-полимеразе сделать копию соответствующей группы генов).

Итак, задача состоит в том, чтобы при недостатке триптофана включить экспрессию группы генов, связанных с его синтезом. При этом триптофан это не случайная молекула, это — аминокислота, то есть она используется рибосомой для синтеза белков.

То есть нам нужно как-то помешать рибосоме синтезировать участок РНК, если триптофан есть в достаточном количестве.

  • Первая идея: давайте попробуем поставить много кодонов, кодирующих триптофан подряд. Если триптофана мало, то рибосома приостановится т.к. рядом не будет необходимых «строительных материалов». Но таким образом мы получили обратное поведение: при отсутствии триптофана последующие гены будут экспрессироваться меньше.
  • Вторая идея: оказывается, можно сделать такой набор «шпилек» из РНК, который будет работать по принципу «лежачего полицейского». То есть если рибосома движется медленно, то она спокойно проходит сквозь шпильки, если двигается быстро — то застревает и отваливается.

Комбинируя эти две идеи мы получаем желаемое поведение.





Попытаюсь перефразировать в офисных терминах. Представьте, что вам нужно заставить принтер печатать заявку на закупку красного тонера, если он подходит к концу. Для этого вы разрабатываете такую бумагу, которая вызывает замятие, если много страниц печатаются подряд. Затем вы посылаете на принтер много заданий по принципу: пять страниц красных рисунков и одно черно-белое заявление на покупку красного тонера.

  • Если красной краски достаточно, то принтер будет печатать красные страницы подряд, что вызовет замятие. Заявление напечатано не будет.
  • Если краски мало, то он будет печатать медленно и без замятия в конце концов дойдет до последней страницы и распечатает заявление.



1.10 Don't repeat yourself в коде ДНК


Эта глава и вставка в следующей частично основаны на лекции Михаила Гельфанда, которую он читал для студентов факультета компьютерных наук ВШЭ. Рекомендую посмотреть ее целиком.

Удивительно, что эволюция способна приходить и к хорошим практикам там, где это критично для выживания. Например:

  • В иммунной системе необходимо вырабатывать пары антител и B-лимфоцитов с одинаковыми рецепторами.
  • Если лимфоцит распознает какой-то антиген, то начинают вырабатываться антитела, которые распознают и нейтрализуют этот же антиген.
  • То есть два разных гена должны содержать два абсолютно одинаковых участка, иначе будут большие проблемы с иммунной системой.
  • При этом мутации поощряются, главное — чтобы они происходили одновременно в двух белках.

Для решения подобных задач у эукариот имеется альтернативный сплайсинг — это полноценные директивы препроцессора в коде ДНК. Его обеспечивает еще один супер-наноробот из белков и РНК, называемый сплайсосомой.

Сплайсосома работает с РНК и ищет в ней специальные маркеры начала и конца на любом расстоянии друг от друга, после чего удаляет все, что находится между ними.

Этот механизм позволяет решать разнообразный спектр задач:

  • Можно просто закомментировать любой участок ДНК. Предполагается, что альтернативный сплайсинг появился, чтобы как-то спастись от вирусов, которые научились повсюду встраивать копии своего кода.
  • Обеспечить одинаковые копии одного участка ДНК в разных белках.
  • Условная конструкция, в которой в белок попадает один из двух альтернативных участков.
  • Можно компактно закодировать большое разнообразие белков, которые состоят из множества альтернативных частей и избежать комбинаторного взрыва длины кода.

Картинка из книги «WormBook: The Online Review of C. elegans Biology»

Вы только представьте, какой потенциал для сложного поведения открывает альтернативный сплайсинг в комбинации с РНК-шпильками! И это мы только затронули малую часть из изученных механизмов.


1.11 Почему клетки отличаются друг от друга


Я плохо учил биологию в школе, поэтому мне до недавнего времени не давал покоя следующий вопрос: если все клетки содержат одинаковую ДНК, почему тогда клетки отличаются друг от друга?

Если начать над ним думать, то попутно возникает второй вопрос: зачем вообще клеткам иметь одинаковый ДНК? Почему нельзя, например, аккуратно закомментировать какой-нибудь участок, который нужно отключить у данной конкретной клетки, а потом перед копированием его аккуратно раскомментировать?

Почему клетки стараются не менять свой ДНК без крайней необходимости
Это связано с тем, что целостность ДНК является критическим условием существования клетки:

  • Если обнаруживается проблема в коде ДНК, клетка пытается исправить ее всеми имеющимися способами, например:
    • если произошла вставка лишнего нуклеотида, либо потеря существующего, это определяется по комплементарной паре и исправляется,
    • если произошел разрыв, попытаться “сшить” его на месте,
    • найти резервную копию этого участка в парной хромосоме от второго родителя и скопировать ее оттуда.
  • Если неконсистентность не удается устранить, то с клеткой могут начать происходить самые нехорошие вещи, которые в лучшем случае в какой-то момент будут замечены и клетка самоликвидируется.
  • По этим причинам чаще всего эволюционные эксперименты с редактированием ДНК длятся недолго.

Эволюция нашла элегантное с точки зрения архитектуры решение проблемы иммутабельности ДНК: метилирование. Это дополнительный битовый слой метаданных, который позволяет отключать участки ДНК, не меняя их. Чаще всего метилирование используется для постоянного отключения ненужных клетке участков генома, в момент, когда она приобретает специализацию.

Хорошо, с персистентностью настроек разобрались, а как клетка определяет свою специализацию? Для этого необходимо затронуть тему межклеточного взаимодействия.

Клеточная мембрана подобно файерволлу позволяет определять довольно сложные политики того, какие белки и молекулы могут поступать извне или уходить вовне. В частности, клетки постоянно обмениваются сигналами (белки и другие молекулы), которые координируют поведение клеток.

Отдельная большая тема, выходящая за рамки данной статьи — как организовать правила обмена сигналами между клетками, чтобы они могли скоординироваться и определить, какая из них будет головой, руками и т.д. Уверен, те, кто имел дело с распределенными системами или клеточными автоматами, без проблем смогут придумать такой протокол.


1.12 Итог: откуда берется сложность в живых клетках?


На первый взгляд, клетке для поддержания жизнедеятельности не требуется особо сложной логики. Она должна просто следить за постоянным уровнем элементов, участвующих в метаболизме, контролировать получение и расход энергии, а также обеспечивать вывод токсинов.

С другой стороны, чтобы доставить человека на Луну тоже не требуется сложной логики. Нужно просто следить чтобы реактивный двигатель работал с нужной интенсивностью, уровень кислорода в кабине был постоянным, а углекислый газ не накапливался.

Это мы еще не затронули процесс копирования клетки, на который приходится большая часть сложности клеточных механизмов.

Если провести не очень корректное сравнение с обычным софтом (например, для управления заводом), то я бы осторожно предположил, что один белок соответствует одной строке кода из нескольких арифметических и логических операций.

Поэтому тот факт, что в клетке человека насчитывается порядка нескольких десятков тысяч видов белков, даже немного удивляет — как-то мало для управления такой сложной системой.


Если пофантазировать, что когда-то будут «программисты» клеточных процессов, то они скорее будут вести проектирование в масштабе графов взаимодействий абстрактных частиц («сигнальных путей»), чем на уровне структуры отдельных белков.

А это значит, что если мы хотим реализовать трехмерный движок, то нужно перейти к математике!


Часть II: Математика вычислений при помощи реакций


В первой части мы поняли, что многие процессы в клетке можно представить в виде модели системы частиц, которые равномерно перемешаны в некотором ограниченном пространстве и взаимодействуют друг с другом при «столкновении».

Безусловно, современные биологические модели опираются на гораздо более сложную математику. Однако многие их части можно приблизить законом действующих масс и, если мы разберемся с ним, то у нас появится базовая интуиция для понимания многих процессов в клетке.

Вероятно, системы реакций на законе действующих масс — одна из самых минималистичных архитектур, на которых можно реализовывать более-менее сложные вычисления. При этом это не какая-то абстрактная вычислительная машина, а модель, которая в некотором приближении работает во всех живых клетках.

Например, вот полное описание алгоритма рендера трехмерного куба в виде системы реакций, от начала и до конца:
Вы можете проверить эту систему в симуляторе, она обозначена там как «minimalist 3d engine».


2.1 Чему равно A + B


Чтобы понять закон действующих масс, достаточно разобраться, как работает следующая реакция:

$A + B \rightarrow C$

У нас есть абстрактные частицы $A$, $B$ и $C$ одинакового размера. Когда $A$ и $B$ сталкиваются, получается $C$.

Допустим, в пространстве объёма 1 равномерно размешано $a$, $b$ и $c$ штук этих молекул. Как будет меняться их количество со временем?

Если молекулы являются точками, то вероятность их столкновения всегда равна нулю независимо от количества. Поэтому модель должна учитывать их размер. К тому же, если частицы двигаются быстро, то столкновения будут происходить чаще. То есть скорость также надо учитывать. Но вместо того, чтобы учитывать все эти параметры по отдельности, в законе действующих масс есть одна константа $k$ — частота столкновения двух частиц в объеме 1. Если она не равна единице, то записывается над стрелкой:

$A + B \xrightarrow{k} C$

Таким образом, если $a=1$, $b=1$, то частота столкновений $A$ и $B$ будет равна $k$. Заметим, при увеличении $a$ с сохранением $b=1$ частота будет увеличиваться линейно (это вредно строго при условии, что молекулы не взаимодействует друг с другом и не сталкиваются, а проходят насквозь). Из аналогичных соображений частота столкновений пропорциональна $b$, поэтому для нашей реакции будет следующий ответ: $a\cdot b\cdot k$ столкновений $A$ и $B$ в единицу времени.

Но мы пока не учитывали, что $A$ и $B$ превращаются в $C$ и числа $a, b, c$ постоянно изменяются. Давайте возьмём маленький отрезок времени $dt$ и посчитаем изменение этих переменных. Всего произойдёт $l = dt\cdot a\cdot b\cdot k$ столкновений. Тогда $a$ и $b$ уменьшатся на $l$, а $c$ — увеличится на $l$.

Вот и все описание реакции. Далее эту частоту столкновений в единицу времени $l$ мы будем называть скоростью реакции.

Реакции с несколькими видами частиц справа (они называются продуктами реакции)

$A + B \xrightarrow{k} C + D + E + \cdots$

моделируются точно так же, просто тогда концентрации всех молекул в правой части увеличиваются на $l = dt\cdot a\cdot b\cdot k$.

В принципе вот и вся модель, на которую бы собираемся портировать трехмерный движок!

Такие модели применяют в химии, физике и биологии. В принципе ей можно моделировать и распределение вирусов в толпе людей или динамику популяций животных.


2.2 Моделирование реакций


Вы можете моделировать реакции при помощи интерактивного ObservableHQ-ноутбука.

Самая важная вещь, которую нужно понимать, что есть два вида графиков, которые показывают, что происходит с реакцией. Верхний показывает изменение концентраций частиц во времени, а нижний — предельные концентрации в зависимости от разных начальных значений одной из частиц.

То есть, если попытаться изобразить связь между ними, получится как-то так:



2.3 Примеры простых реакций


На первый взгляд, все реакции выглядят одинаково. Однако спустя некоторые время вы научитесь различать множество их видов.
$A + A \rightarrow B$ При столкновении двух частиц $A$, они «слипаются» в $B$
$A + A \rightarrow A$ Частица-каннибал
$A \rightarrow B$ Частицы $A$ самопроизвольно превращаются в $B$.
Это не требует столкновения с какой-либо частицей.
$A \rightarrow B + C$ Распад
$A \rightarrow \varnothing $ Исчезающий вид частиц (справа пусто)
$A \rightarrow A + B$ Фабрика
$A \rightarrow A + A$ Цепная реакция
$A + B \rightarrow A + C$ $A$ катализирует превращение $B$ в $C$.
С частицей $A$ ничего не происходит т.к. она есть слева и справа от реакции.
$A + B \rightarrow A + B + C$ При столкновении $A$ и $B$ возникает $C$.
С частицами $A$ и $B$ при этом ничего не происходит.



Часть III: Программная инженерия кода ДНК

$-\ \text{Talk is cheap. Show me the code (Linus Torvalds)}$




3.1 Алгоритм трехмерного движка


Итак, перед нами стоит задача придумать самый простой из возможных алгоритмов, который производит рендер чего-то трехмерного. Сначала нужно определиться с объектом:

  • Сфера — это просто круг с пятном, который можно нарисовать и без реализации движка.
  • Куб гораздо лучше подходит для этой роли. В принципе и куб можно нарисовать без движка как 3 четырехугольника с фиксированными координатами, но я считаю это не спортивным. Мы будем писать простой, но настоящий трехмерный движок!
  • В идеале хотелось бы что-то посложнее, например, куб с вырезанной сферой. Но с учетом того, что используемый нами компилятор ДНК еще в альфа-версии, лучше начать с чего-то простого.

В качестве алгоритма будем использовать уже знакомый из прошлых статей ray marching. Я подробно описал принцип его работы в статье про Excel. В кратком изложении он выглядит так:

  • Вход: координаты пикселя, выход: яркость пикселя.
  • По координатам текущего пикселя определить соответствующий трехмерный луч, выходящий из камеры.
  • Получить нормированный вектор направления этого луча.
  • Положить $v=0$. Сделать много итераций:
    • Получить точку на расстоянии $v$ от камеры на этом луче.
    • Вычислить значение функции SDF в этой точке.
    • Инкрементировать $v$ на значение функции SDF.
  • Вернуть яркость пикселя как $v$.



«Ядром» алгоритма ray marching является signed distance function (SDF). Она описывает объект, рендер которого будет происходить: она должна приближать расстояние до ближайшей точки объекта и быть отрицательной внутри него.

Для куба со стороной $2a$ эта функция очень простая:

$\text{cubeSDF}(x, y, z) = \max(|x|, |y|, |z|) - a,$

С учетом того, что координаты камеры будут фиксированными, многие константы в алгоритме можно вычислить заранее. Я вынес все эти расчеты в отдельный observableHQ-ноутбук, где при желании можно проследить за тригонометрическими и матричными преобразованиями.

Давайте посмотрим реализацию этого алгоритма на языке JavaScript:



Мы видим, что вначале идут линейные преобразования. потом неприятное взятие нормы, потом в цикле снова линейные операции с неприятным нормированием и приятная кусочно-линейная функция sdf куба.


3.2 Идея 1: Меняем метрику


Эх, если бы можно было что-то сделать с этим евклидовым расстоянием, то мы бы сэкономили немало драгоценных реакций… А так нам нужно сначала три раза возводить в квадрат, брать квадратный корень, а потом еще три раза делить!

Вообще, алгоритм ray marching опирается на то, что расстояние, откладываемое от камеры вдоль вектора, и то расстояние, которое возвращает sdf, должны соотноситься друг с другом. Однако он сильно не привязывается к тому, что расстояние именно евклидово.

Это значит, что мы можем попытать удачу, попробовав другие способы считать расстояние между векторами. Не всякая формула для этого подходит: для нее, например, должно выполняться неравенство треугольника. Поэтому мы возьмем параметрическое расстояние Минковского — обобщение евклидовой нормы, швейцарский нож из арсенала прикладных математиков. По ней длина вектора считается следующим образом:

$\text{norm}_p(x, y, z)=\sqrt[p]{|x|^p+|y|^p+|z|^p}$

Нужно только подобрать желаемый параметр $p$. Переход в другую метрику имеет некоторые побочные эффекты, например, сферы могут стать похожими на кубы. Но нашему кубу ничего не грозит т.к. его sdf не зависит от метрики.

imageкартинка с Википедии

Так как мы хотим избежать возведений в степень, логично попробовать $p=1$:

$\text{norm}_1(x, y, z)=|x|+|y|+|z|$

Эта метрика называется расстоянием городских кварталов или «манхэттенской метрикой». Хотя, если быть точнее, в нашем случае кварталы будут трехмерными.

Пробуем новую метрику в коде… вроде работает! Таким образом нам удалось сократить несколько реакций.

Но что если попробовать избавиться и от взятия модуля от координат? Эта метрика применяется к векторам, выпущенным из камеры в сторону объекта. Получается, если поставить камеру снизу сзади от куба, то все лучи из нее будут иметь только положительные координаты. Тогда при выполнении этих ограничений на положение камеры, норму вектора можно и вовсе заменить на

$\text{norm}(x, y, z)=x+y+z$

Самое интересное, что умножение на реакциях внутри себя делит вектор на сумму его координат. То есть использование такой нормы будет компактнее, чем реализация без нормы вообще!


3.3 Пробуем реализовать алгоритм при помощи CRN++


Язык программирования CRN++ был описан в научной статье Марко Васика и Дэвида Соловейчика в 2018 году и выложен на GitHub.

Это модуль Wolfram Mathematica, который позволяет конвертировать basic-подобные программы в системы реакций.

Проблема, которую решает этот язык, следующая. Реакции сами по себе происходят параллельно и непрерывно. Но большинство привычных нам алгоритмов требуют пошагового выполнения на основе дискретных условий.

Канонический пример, который сложно реализовать на реакциях — алгоритм Евклида. В нем нужно сначала определить, что больше: $a$ или $b$, а потом вычесть из большего меньшее и оставить меньшее. Эти два процесса нужно выполнять поочередно, иначе никак не получится получить наибольший общий делитель в конце.

Пример реализации алгоритма Евклида из статьи. Слева показан псевдокод алгоритма Евклида, справа — код на языке CRN++ до компиляции в систему реакций.

Для решения этой проблемы язык CRN++ использует «тактовый генератор» в виде осциллятора. В зависимости от номера текущего такта и результата сравнения, выполняется только часть реакций, обеспечивая требуемую семантику пошагового выполнения.

«Стандартная библиотека» языка включает в себя 7 функций: присваивание, сложение, вычитание, умножение, деление, квадратный корень и сравнение. Она не такая большая, потому что создатели определили жесткий критерий: реакции должны быть такими, чтобы точность вычислений увеличивалась экспоненциально со временем. Это требование позволяет гарантировать, что точность вычислений получающихся программ будет также увеличиваться экспоненциально с увеличением продолжительности такта.

Недостатком языка на данный момент является довольно большое количество реакций на выходе: даже hello world в виде счетчика требует 30 реакций.

Ну что, давайте попробуем написать трехмерный движок на этом языке.

Первая проблема заключается в том, что язык не предлагает решения для работы с отрицательными числами: значения переменных должны быть неотрицательными. Поэтому нам потребуется разбить некоторые переменные на две по принципу

$a = \texttt{aPositive} - \texttt{aNegative}$

Вторая проблема связана с тем, что функций max и abs нет в стандартной библиотеке. Однако их несложно реализовать через функцию вычитания. Особенность реализации вычитания в этом языке состоит в том, что возвращается нуль, если результат отрицательный:

$\text{sub}(a, b) = \max(0, a - b)$

Поэтому

$\max(a, b) = \text{sub}(a, b) + b$

$|a - b| = \text{sub}(a, b) + \text{sub}(b, a)$

Назначения переменных:

  • v — расстояние от камеры текущей позиции на луче.
  • dirX, dirY, dirZ — вектор луча из камеры для данного пикселя. Как мы обсудили в предыдущей главе, эти числа являются неотрицательными благодаря выбору подходящего расположения и направления камеры.
  • xPositive, xNegative, yPositive, yNegative, zPositive, zNegative — трехмерные координаты точки на расстоянии v от камеры вдоль луча. Уже могут быть отрицательными, поэтому требуется в два раза больше переменных.
  • xAbsolute, yAbsolute, zAbsolute — абсолютные значения от текущих $x, y, z$, которые можно увидеть в sdf куба.
  • xa1, xa2, ya1, ya2, za1, za2 — вспомогательные переменные при вычислении абсолютных значений из предыдущего пункта. Они хранят отдельные слагаемые с функциями sub, через которые мы реализовали abs.
  • maxXY, maxXYZ, maxXYTemp, maxXYZTemp — переменные для вычисления максимума из формулы sdf куба по формуле

    $\max(x, y, z) = \overbrace{\max(\underbrace{\max(x, y)}_{\texttt{maxXY}}, z)}^{\texttt{maxXYZ}} = \\ = \overbrace{\text{sub}(\max(x, y), z)}^{\texttt{maxXYZTemp}} + z = \text{sub}(\underbrace{\text{sub}(x, y)}_{\texttt{maxXYTemp}} + y, z) + z$

  • sdf — значение sdf куба, ради которого происходили все предыдущие вычисления.
  • nextV — вспомогательная переменная, которая хранит значение v для следующей итерации.

Основной цикл будет состоять из двух чередующихся тактов:

  • На четных тактах: nextV = v + sdf.
  • На нечетных: v = nextV.

Все остальные вычисления будут производиться непрерывно в «фоновом режиме» т.к. так получится гораздо меньше реакций на выходе. В итоге получается следующий код:


После «компиляции» из этого кода получается следующая система реакций. Обратите внимание, что переменная, в которую «записывается» результат, идет последним аргументом у функций.



Симуляция такой системы-монстра из 70 реакций и 68 видов частиц с приемлемой точностью занимает около минуты для одного пикселя. Численные эксперименты показали, что результат этой системы довольно неустойчивый и эффект от накопления ошибки дает от 5% до 50% расхождения с правильным ответом.

В принципе, мы бы могли на этом остановиться и сказать, что движок готов. Правда, у него будут нулевые шансы быть осуществленным на практике:

  1. Компилятор кода ДНК где-то часов за 12 может и выдаст несколько сотен заветных последовательностей ДНК, но они точно не будут вести себя в пробирке так, как описывались во входной системе. У этого компилятора и для пяти реакций эксперименты расходятся с требуемым поведением.
  2. Даже если все проблемы с компилятором будут решены, один такой эксперимент будет стоить очень больших денег. А он скорее всего с первого раза не сработает и нужно будет делать много отладочных запусков.
  3. С учетом сложности системы, ее отладка даже на компьютере занимает многие часы, не говоря уже о пробирке. А с учетом того, что система реакций сама по себе неустойчивая, любая ошибка вызовет трудно отслеживаемый каскад расхождений.



3.4 Заменяем «тактовый генератор» на «пропорциональный контроллер»


Обычно поиск пересечения луча из камеры с объектом в ray marching реализуют в виде чередования двух шагов в цикле:

  1. Посчитать расстояние до ближайшей точки фигуры (функция sdf) для некоторой точки на луче.
  2. Сдвинуть точку на это расстояние вперед.

Таким образом, с каждой итерацией точка становится все ближе к пересечению луча из камеры с объектом.


Этот алгоритм хорошо работает на наших процессорах так как семантика их выполнения — пошаговая. Когда же нам надо сделать симуляцию процессов, описываемых дифференциальными уравнениями, мы все равно пытаемся их приблизить при помощи алгоритмов, которые выполняются пошагово.

Но что если мы хотим реализовать ray marching в такой архитектуре, в которой пошаговое выполнение невероятно сложное, а дифференциальные уравнения определенного вида решаются легко?

Смотрите, если обозначить $\text{ray}(v)$ — точку на луче на расстоянии $v$ от камеры, то для одного пикселя алгоритм ray marching записывается в следующей форме:

$v_{i+1} = v_i + \text{sdf}(\text{ray}(v_i)),$

где $v_0, v_1, v_2, \ldots$ — значения $v$ на каждой итерации цикла. Если через $\Delta v_i$ обозначить $v_{i+1} - v_i$, то получим более компактную запись

$\Delta v_i = \text{sdf}(\text{ray}(v_i)).$

А в мире дифференциальных уравнений:

  • вместо последовательности $v_i$ у нас будет функция $v(t)$, непрерывно зависящие от времени,
  • вместо разностей соседних элементов $\Delta v_i$ у нас будет производная $v'(t)$.

Чисто механически мы можем попробовать переписать ray marching в таком виде:

$v'(t) = \text{sdf}(\text{ray}(v(t)))$

Таким образом, у нас теперь точка движется к объекту со скоростью, пропорциональной расстоянию до этого объекта. Если же точка случайно попадет внутрь объекта, то она начнет двигаться назад. Тогда по логике в пределе точка должна оказаться в точности на границе объекта.

Делаем быстрый прототип, чтобы проверить предположение.

Вроде работает!

Те, кто занимается программированием контроллеров, распознают тут пропорциональный регулятор — простейший из возможных ПИД-регуляторов. В этих терминах функция $\text{sdf}(\text{ray}(v))$ возвращает разницу между текущим значением $v$ и желаемым. Если условиться, что мы управляем значением $v$ не напрямую, а через задание ее скорости, то идея пропорционального регулятора состоит в том, чтобы сделать эту скорость пропорциональной разности текущего и желаемого значения.

Такое сравнение с контроллерами дает нам довольно полезную в дальнейшем идею: имеет смысл добавить коэффициент $k$ перед производной, чтобы в случае проблем можно было его уменьшить и обеспечить лучшую сходимость нашего алгоритма:

$v'(t) = k\cdot\text{sdf}(\text{ray}(v(t)))$

В итоге диаграмма «потоков данных» приобретает следующий вид:



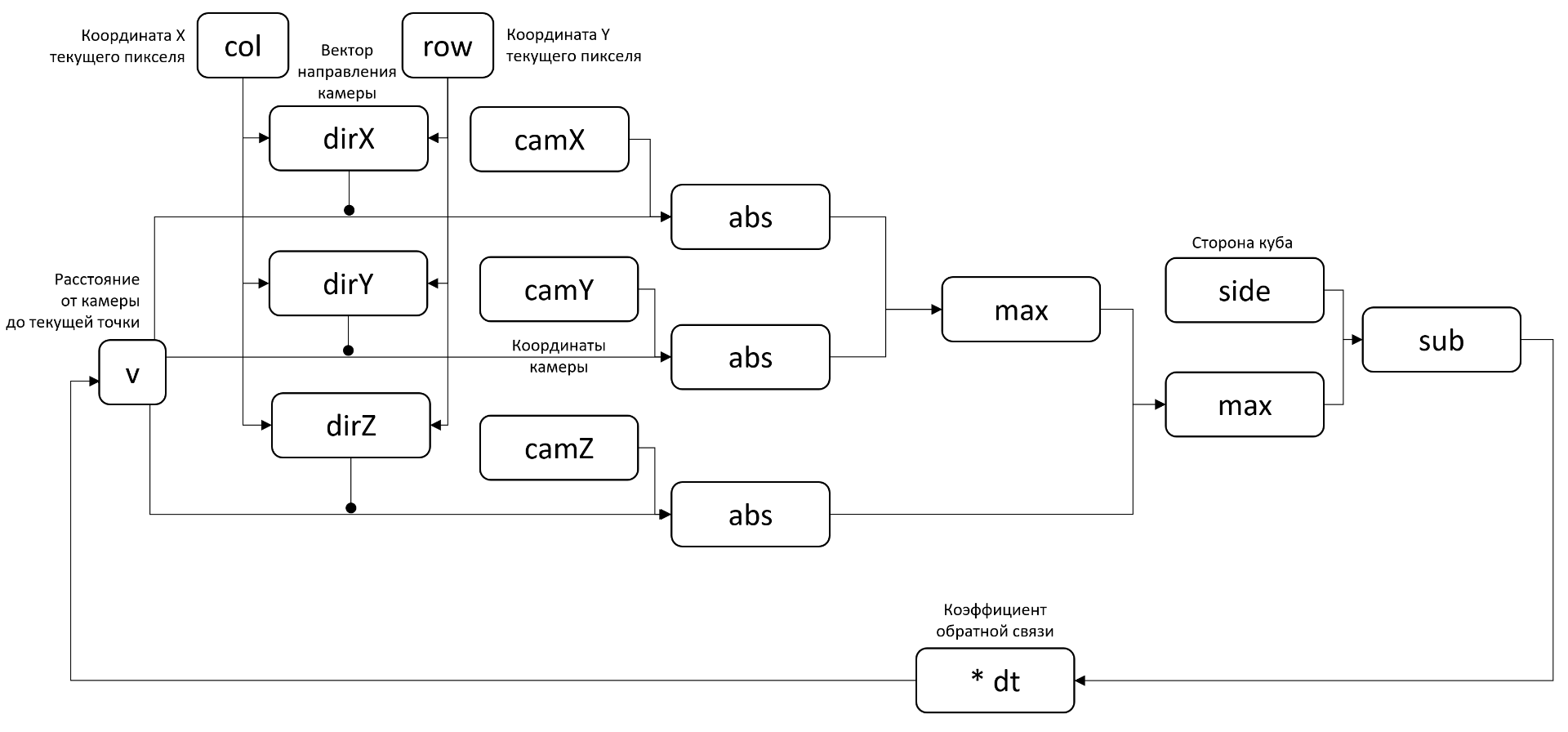
После записи в новой форме, нашему движку больше не нужна семантика пошагового выполнения, а следовательно и язык CRN++ нет необходимости использовать. К тому же, в CRN++ получаются довольно громоздкие реализации нужных нам функций: max и abs.


3.5 Нам нужен свой фреймворк


Как стало очевидно из предыдущей главы, язык CRN++ удобен для решения самых разнообразных задач, однако он также обладает рядом фатальных недостатков, которые проявляются при программировании алгоритмов наподобие нашего трехмерного движка.

Итак, позвольте представить первый реактивный фреймворк программирования реакций RxCRN!
CRN++ RxCRN
Парадигма структурное программирование граф вычислений с обменом сообщений между узлами
Синтаксис похожий на basic надмножество синтаксиса определения реакций с макросами
Средний размер результата около 30 реакций для самых простых примеров до 7 раз меньше на специально подобранных мною примерах
Точность вычислений падает экспоненциально с увеличением длины такта вычисления максимально точны (насколько это возможно на частицах)
Поддерживаемые функции ld, add, sub, mul, div, sqrt, am, cmp add, sub, mul, max, min, abs
Политика включения в «стандартную библиотеку» ошибка падает экспоненциально скорость протекания реакций падает до нуля
Runtime осциллятор для управления тактами отсутствует: это «исчезающий» фреймворк
Поддержка условных конструкций есть нет
Поддержка циклов один цикл с фиксированным числом шагов нет
Иммутабельность по умолчанию есть нет
Область применения разнообразные арифметические алгоритмы, работающие с неотрицательными числами только трехмерные движки и, по всей видимости, только для кубов
Как можно видеть из таблицы, если вы собрались реализовывать трехмерный движок для куба, то выбор очевиден.

Если отбросить шутки, то я не претендую на что-то новое: в научных статьях второй подход прекрасно известен и хорошо изучен теоретически под понятиями «rate-independent reactions», «dual-rail representation», «continuous Petri networks».


3.6 Реализация функции max через метафору «обмена сообщениями»


Перед тем, как перейти к движку, давайте посмотрим как реализована функция $R=\max(X, Y)$:

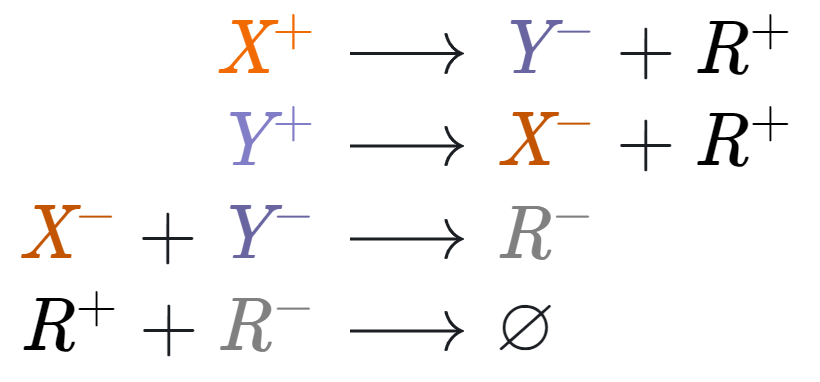
В принципе, даже школьник начальных классов сможет понять, как она работает: для этого не нужно решать дифференциальные уравнения. Те, кто работал с сетями Петри, вероятно, уже все поняли, а для остальных постараюсь объяснить происходящее в более привычных терминах.

Давайте представим, что у нас есть четыре агента: X, Y, R и max, которые обмениваются почтовыми сообщениями.



  • Агенты X, Y и R хранят у себя в памяти свои значения, которые являются целыми числами.
  • Агент R хочет, чтобы его число равнялось максимуму из чисел A и B.
  • Изначально числа всех агентов равны нулю.
  • Проблема состоит в том, что числа X и Y постоянно меняются и R хочет, чтобы его число также всегда было актуально. Поэтому они договорились посылать друг другу письма по почте об изменении своих чисел. Есть два типа писем: об увеличении значения на 1 и об уменьшении на 1.
  • R попросил своего друга max обрабатывать письма от X и Y и посылать R только уведомления о том, что число R увеличилось или уменьшилось.
  • Проблема состоит в том, что max обладает плохой памятью, но зато хорошо исполняет правила, которые мы можем написать ему в инструкции.

Задача выглядит очень простой и мы сразу можем написать первые два правила:

$\begin{align} X^+ + Y^+ &\rightarrow R^+\\ X^- + Y^- &\rightarrow R^- \end{align}$

Все присылаемые от X и Y письма складываются на стол к max и лежат, пока он не найдет правило, по которым он может с ними что-то сделать. Таким образом правила выше говорят R, что, если он находит пару писем о том, что X и Y одновременно увеличились или уменьшились, то он может смело информировать R о соответственном увеличении или уменьшении своего числа. Сами входящие письма он при этом выкидывает.

Вроде бы задача решена? Хотя нет, мы не учли случай, например, когда письма приходят только от X. Тогда мы не найдем пару писем из предыдущих правил, но число R при этом нужно будет все равно изменить.

При этом max должен учитывать два случая:

  1. Если число X сейчас максимальное, то письма об изменении X должны превращаться в письма об изменении R.
  2. Если число X сейчас не максимальное, то никак не реагировать на письма об его изменении.

Только вот незадача, у max нет памяти даже для того, чтобы запомнить, какое из чисел X или Y сейчас максимальное!

Если немного подумать над этой задачей, то вскоре станет ясно, что такой набор правил для max невозможно составить. Так как же тогда работает решение, которые было приведено в начале?

Просто для решения этой задачи нужно мыслить «out of the box»: давайте заставим max подделывать письма от X и Y!

Можете не переживать, проблем с законом у max не будет: он не будет посылать поддельные письма, а будет их просто складывать себе на стол. Правила подделки следующие:

$\begin{align} X^+ &\rightarrow Y^- + R^+\\ Y^+ &\rightarrow X^- + R^+ \end{align}$

То есть при получении письма об увеличении X, он должен его заменить на письмо об уменьшении Y и сказать R, что его число увеличилось. Звучит крайне нелогично… Неужели эти правила работают? Разве max не рискует таким образом уйти в бесконечный цикл и заспамить R?

Вы можете попробовать применять эти правила сами и вскоре придете к пониманию, как это устроено. Идея состоит в том, что, если max будет следовать этим правилам, то содержимое его стола будет предсказуемым:

  1. Если число X сейчас максимальное, то на столе будут только письма об уменьшении Y. При этом их количество равно разности X – Y.
  2. Если X и Y равны, то стол пустой.
  3. Если число Y сейчас максимальное, то на столе будут только письма об уменьшении X. При этом их количество равно разности Y – X.

Например, если X сейчас максимальное (то есть на столе находятся только письма $Y^-$), то поступление $Y^+$ приведет к следующему «каскаду» событий на столе max:

$\begin{align} Y^+ &\rightarrow X^- + R^+\\ X^- + Y^- &\rightarrow R^-\\ R^- + R^+ &\rightarrow \varnothing \end{align}$

В итоге на столе окажутся два противоположных письма для $R$, которые в зависимости от порядка применения правил либо «аннигилируют», либо будут отправлены оба. В любом случае R не изменится, как и требовалось.

Предлагаю читателю разобрать все остальные случаи в качестве упражнения.

Из этого примера можно вынести некоторые общие наблюдения:

  • Если смотреть на все письма, которые есть у X, Y и R в конкретный момент времени, то по ним не очевидно, как определять значения X и Y. Единственный способ состоит в том, чтобы по состоянию стола max восстановить, какое из чисел максимальное, а также разность с минимальным. Но для этого нужно математически анализировать все возможные состояния.
  • Тем не менее, мы можем рассуждать о значениях X, Y и R и написать, что $R = \max(X, Y)$, хотя эти числа не легко восстановить из текущего состояния системы. В каком-то приближении $X=X^+-X^-$, где $X^+$ и $X^-$ означают количества когда-либо отправленных писем каждого типа, но без учета «поддельных» писем.
  • Благодаря такому подходу с отрицательными частицами мы «бесплатно» получили поддержку отрицательных чисел. Но в обратную сторону это не работает: если отрицательные числа нам не нужны, мы не можем убрать отрицательные частицы т.к. иначе не сможем кодировать сообщения об уменьшении значений.



3.7 Реализуем движок


Итак, в этой главе мы применим все полученные знания, чтобы реализовать трехмерный движок в виде системы реакций закона действующих масс.

Сначала перечислим виды используемых частиц
$N_X, N_Y, N_Z$ Вектор направления камеры. Постоянный для текущего пикселя. Не нормирован. Так как камера направлена в положительную сторону, эти числа не имеют парных отрицательных.
$V$ Расстояние от камеры до текущей точки.
$C_X^+, C_Y^+, C_Z^+\\C_X^-, C_Y^-, C_Z^-$ Координаты текущей точки. Начальные концентрации кодируют координаты камеры.
$A_X^+, A_Y^+, A_Z^+\\A_X^-, A_Y^-, A_Z^-$ Абсолютные значения координат текущей точки. Отрицательные частицы нужны, чтобы кодировать информацию об уменьшении значений.
$T_X^+, T_Y^+, T_Z^+\\T_X^-, T_Y^-, T_Z^-$ Вспомогательные частицы для вычисления абсолютных значений из предыдущей строки.
$M_{XY}^+, M_{XY}^-$ $\max(A_X, A_Y)$
$M_{XYZ}^+, M_{XYZ}^-$ $\max(A_X, A_Y, A_Z) - 0.3$.
Вычисляет функцию sdf куба.
Начальная концентрация $M_{XYZ}^-$ должна равняться стороне куба 0.3.
$R$ Результат — яркость текущего «пикселя» в диапазоне $1.8\ldots 3.2$
Первые три реакции отвечают за определение координат текущей точки на расстоянии $V$ от камеры:

$\begin{align} N_X + V &\rightarrow N_X + C_X^+\\ N_Y + V &\rightarrow N_Y + C_Y^+\\ N_Z + V &\rightarrow N_Z + C_Z^+ \end{align}$

Это новая для нас конструкция, внутри которой происходит умножение на нормированный вектор. Обратите внимание, что с частицами $N_X, N_Y, N_Z$ ничего не происходит — они есть и слева и справа от стрелки и выступают как «катализаторы». А частица $V$ превращается в частицы $C_X^+, C_Y^+, C_Z^+$ с сохранением «массы», то есть

$V = C_X^+ + C_Y^+ + C_Z^+$

С учетом того, что все три реакции конкурируют друг с другом за получение частицы $V$, она распределится между ними в некоторой пропорции. Оказалось, что эта пропорция совпадает с пропорцией соответствующих «катализаторов». В итоге получается следующее распределение:

$(C_X^+, C_Y^+, C_Z^+) = \frac{(N_X, N_Y, N_Z)}{N_X+N_Y+N_Z}\cdot V$

Обратите внимание, что вектор $(N_X, N_Y, N_Z)$ естественным образом нормируется делением на сумму своих компонент, хотя мы специально ничего с ним не делали. А это ровно та нормализация по «манхэттенскому расстоянию», которая нам нужна в этом месте алгоритма. (см. главу 3.2). Получается, если бы нормирования не было вовсе, то нам бы пришлось добавлять дополнительные реакции, чтобы его избежать!

Хорошо, двигаемся дальше. Следующие три реакции

$\begin{align} C_X^+ &\rightarrow T_X^+ + A_X^+\\ C_X^- &\rightarrow T_X^- + A_X^+\\ T_X^+ + T_X^- &\rightarrow 2A_X^- \end{align}$

обеспечивают, чтобы $A_X$ хранил абсолютное значение от $C_X$. Тут происходит такая же история, что и с реализацией функции max, когда агенты C, T и A обмениваются почтовыми сообщениями. Статья и так уже получается приличная по объему, поэтому оставляю читателю в качестве упражнения разобраться в точном механизме работе этой системы реакций.

Далее идет то же самое, но для $A_Y = |C_Y|$:

$\begin{align} C_Y^+ &\rightarrow T_Y^+ + A_Y^+\\ C_Y^- &\rightarrow T_Y^- + A_Y^+\\ T_Y^+ + T_Y^- &\rightarrow 2A_Y^- \end{align}$

и, наконец, для $A_Z = |C_Z|$:

$\begin{align} C_Z^+ &\rightarrow T_Z^+ + A_Z^+\\ C_Z^- &\rightarrow T_Z^- + A_Z^+\\ T_Z^+ + T_Z^- &\rightarrow 2A_Z^- \end{align}$

Далее идет знакомая нам из предыдущей главы реализация $M_{XY} = \max(A_X, A_Y)$:

$\begin{align} A_X^- + A_Y^- &\rightarrow M_{XY}^-\\ A_X^+ &\rightarrow A_Y^- + M_{XY}^+\\ A_Y^+ &\rightarrow A_X^- + M_{XY}^+ \end{align}$

И, наконец, финальная функция максимума $M_{XYZ} = \max(M_{XY}, A_Z)$:

$\begin{align} M_{XY}^- + A_Z^- &\rightarrow M_{XYZ}^-\\ M_{XY}^+ &\rightarrow A_Z^- + M_{XYZ}^+\\ A_Z^+ &\rightarrow M_{XY}^- + M_{XYZ}^+ \end{align}$

Еще одним преимуществом выбора такого подхода является экономия на вычитании констант — достаточно просто обеспечить начальную концентрацию $M_{XYZ}^-$ равную $0.3$ и тогда $M_{XYZ}$ будет поддерживать свое значение, равным $\max(M_{XY}, A_Z) - 0.3$.

Наконец, предпоследняя реакция отвечает за «аннигиляцию» положительной и отрицательной частиц $M_{XYZ}$:

$\begin{align} M_{XYZ}^+ + M_{XYZ}^-&\rightarrow \varnothing \end{align}$

Чтобы движок заработал, необходимо замкнуть всю эту цепь на себя:

$\begin{align} M_{XYZ}^+ &\rightarrow M_{XYZ}^+ + V + R \end{align}$

Это простая реакция, но она требует ряда пояснений

  • С частицей $M_{XYZ}^+$ ничего не происходит — она есть по обе стороны реакции. Она только определяет скорость реакции.
  • Частицы $V$ и $R$ генерируются пропорционально $M_{XYZ}^+$. Напомню, что концентрация $M_{XYZ}^+$ соответствует текущему значению функции sdf. То есть это та самая «петля обратной связи» от пропорционального регулятора.
  • Частица $R$ не участвует больше ни в одной реакции — так и должно быть. Она просто «интегрирует» суммарное значение $V$.
  • Частица $V$ генерируется точно в таком же количестве, что и $R$, но, в отличие от последней, тут же конвертируется дальше в $C_X, C_Y, C_Z$ при помощи первых трех реакций.




3.8 We need to go deeper


Мы, наконец, получили 20 заветных реакций. Настал момент истины: либо эти реакции «нарисуют» трехмерный куб, либо весь наш «фреймворк» отправится в мусорную корзину!

Только есть небольшая чисто техническая проблема. Симуляция этой системы реакций обычным методом для одного пикселя требует порядка 3-10 секунд в зависимости от выбранного шага времени. Получается, что для одного «отладочного рендера» картинки 100x100 пикселей потребуется порядка 12 часов. Так что нам придется пока что ограничится несколькими выборочными пикселями.

К сожалению, в наших реакциях $R$ уходит в бесконечность на всех пикселях, которые были выбраны для проверки. Вообще, концентрация $R$ должна уходить в бесконечность (на практике, очевидно, она просто достигнет некоторого максимума) только там, где луч из камеры не пересекает куб, а на остальных пикселях стабилизироваться в концентрации, равной расстоянию до камеры в диапазоне $1.8\ldots 3.2$.

Отлаживать такие системы реакций не самое простое занятие. Тем более эта система замкнута на себя и состоит не из дискретных шагов (которые можно сравнить с итерациями аналогичной реализации на JS), а из узлов, которые непрерывно «уточняют» свое значение и пересылают «корректирующие» сообщения друг другу. При этом вычисления разных узлов происходят с некоторым запаздыванием, которое вполне может стать неустранимой причиной наших проблем.

В итоге оказалось, что проблема состоит в том, что «скорость» изменения $v$ очень большая и она «проскакивает» сквозь куб. Одно из решений могло состоять в том, чтобы добавить 6 реакций, которые обеспечивают $v$ «обратный ход» в этом случае. Но на самом деле достаточно просто регулировать коэффициент $k$, который мы обсуждали в главе 3.4 про пропорциональный контроллер.

Таким образом, если последней реакции уменьшить константу скорости до

$\begin{align} M_{XYZ}^+ &\xrightarrow{0.01} M_{XYZ}^+ + V + R, \end{align}$

то система стабилизируется.

Осталось разобраться, как получить саму картинку за приемлемое время. Я сначала перепробовал разные методы решения ОДУ первого порядка из конспектов курса численных методов: метод Эйлера с матрицей и без, метод средней точки, метод Рунге-Кутты, двухшаговый метод Адамса — Башфорта. Также пробовал использовать Wolfram Mathematica, но существенного ускорения не удалось получить. В итоге решил пойти с другого конца и использовать метод сэмплинга случайных пикселей для постепенного построения диаграммы Вороного. Спустя некоторое время получилась такая картинка:

А что, если использовать графическую карту для ускорения вычислений? Вычисления для пикселей не зависят друг от друга и не требуют входных параметров кроме координат. А на выходе нам нужен только цвет пикселя. Фрагментный шейдер идеально подходит для решения этой задачи. Однако есть проблемы с передачей структуры данных с описанием реакций в общем виде, поэтому придется генерировать код шейдера для каждой системы реакций.

Код шейдера WebGL для симуляции нашей системы реакций 
precision highp float;

void main() {

    float X = gl_FragCoord.x / 100.0;
    float Y = gl_FragCoord.y / 100.0;

    float cur_V = 0.0;
    float cur_T_Z_P = 0.0;
    float cur_T_Z_M = 0.0;
    float cur_T_Y_P = 0.0;
    float cur_T_Y_M = 0.0;
    float cur_T_X_P = 0.0;
    float cur_T_X_M = 0.0;
    float cur_R = 0.0;
    float cur_M_XY_P = 0.0;
    float cur_M_XY_M = 0.0;
    float cur_M_XYZ_P = 0.0;
    float cur_C_Z_P = 0.0;
    float cur_C_Y_P = 0.0;
    float cur_C_X_P = 0.0;
    float cur_A_Z_P = 0.0;
    float cur_A_Z_M = 0.0;
    float cur_A_Y_P = 0.0;
    float cur_A_Y_M = 0.0;
    float cur_A_X_P = 0.0;
    float cur_A_X_M = 0.0;
    float cur_X = 1.0 * X;
    float cur_Y = 1.0 * Y;
    float cur_C_X_M = 0.606;
    float cur_C_Y_M = 0.898;
    float cur_C_Z_M = 1.243;
    float cur_M_XYZ_M = 0.3;
    float cur_N_X = 0.036 + 0.555 * X + 0.147 * Y;
    float cur_N_Y = 0.853 + -0.517 * Y;
    float cur_N_Z = 0.737 + -0.27 * X + 0.302 * Y;

    for (int i=0; i<100000; i++) {

        float r0 = cur_N_X * cur_V * 0.1;
        float r1 = cur_N_Y * cur_V * 0.1;
        float r2 = cur_N_Z * cur_V * 0.1;
        float r3 = cur_C_X_P * 0.1;
        float r4 = cur_C_X_M * 0.1;
        float r5 = cur_T_X_M * cur_T_X_P * 0.1;
        float r6 = cur_C_Y_P * 0.1;
        float r7 = cur_C_Y_M * 0.1;
        float r8 = cur_T_Y_M * cur_T_Y_P * 0.1;
        float r9 = cur_C_Z_P * 0.1;
        float r10 = cur_C_Z_M * 0.1;
        float r11 = cur_T_Z_M * cur_T_Z_P * 0.1;
        float r12 = cur_A_X_M * cur_A_Y_M * 0.1;
        float r13 = cur_A_X_P * 0.1;
        float r14 = cur_A_Y_P * 0.1;
        float r15 = cur_A_Z_M * cur_M_XY_M * 0.1;
        float r16 = cur_M_XY_P * 0.1;
        float r17 = cur_A_Z_P * 0.1;
        float r18 = cur_M_XYZ_M * cur_M_XYZ_P * 0.1;
        float r19 = cur_M_XYZ_P * 0.001;

        cur_V = max(0.0, cur_V - r0 - r1 - r2 + r19);
        cur_T_Z_P = max(0.0, cur_T_Z_P + r9 - r11);
        cur_T_Z_M = max(0.0, cur_T_Z_M + r10 - r11);
        cur_T_Y_P = max(0.0, cur_T_Y_P + r6 - r8);
        cur_T_Y_M = max(0.0, cur_T_Y_M + r7 - r8);
        cur_T_X_P = max(0.0, cur_T_X_P + r3 - r5);
        cur_T_X_M = max(0.0, cur_T_X_M + r4 - r5);
        cur_R = max(0.0, cur_R + r19);
        cur_M_XY_P = max(0.0, cur_M_XY_P + r13 + r14 - r16);
        cur_M_XY_M = max(0.0, cur_M_XY_M + r12 - r15 + r17);
        cur_M_XYZ_P = max(0.0, cur_M_XYZ_P + r16 + r17 - r18);
        cur_C_Z_P = max(0.0, cur_C_Z_P + r2 - r9);
        cur_C_Y_P = max(0.0, cur_C_Y_P + r1 - r6);
        cur_C_X_P = max(0.0, cur_C_X_P + r0 - r3);
        cur_A_Z_P = max(0.0, cur_A_Z_P + r9 + r10 - r17);
        cur_A_Z_M = max(0.0, cur_A_Z_M + 2.0 * r11 - r15 + r16);
        cur_A_Y_P = max(0.0, cur_A_Y_P + r6 + r7 - r14);
        cur_A_Y_M = max(0.0, cur_A_Y_M + 2.0 * r8 - r12 + r13);
        cur_A_X_P = max(0.0, cur_A_X_P + r3 + r4 - r13);
        cur_A_X_M = max(0.0, cur_A_X_M + 2.0 * r5 - r12 + r14);
        cur_C_X_M = max(0.0, cur_C_X_M - r4);
        cur_C_Y_M = max(0.0, cur_C_Y_M - r7);
        cur_C_Z_M = max(0.0, cur_C_Z_M - r10);
        cur_M_XYZ_M = max(0.0, cur_M_XYZ_M + r15 - r18);
    }

    float res = (cur_R - 1.8) / 1.4;
    float intensity = (res >= 0.01 && res <= 1.0) ? clamp(res, 0.0, 1.0) : 1.0;

    // gamma correction
    float gray_out = pow(intensity, 1.0 / 2.2);

    gl_FragColor = vec4(gray_out, gray_out, gray_out, 1.0);
}

Запускаем шейдер и меньше чем через секунду получаем картинку:


Запустили шейдер на графической карте и получили трехмерный куб. Вроде бы вполне рядовое событие… Только не в этом случае: я хочу, чтобы вы осознали всю степень ненормальности программирования, которое тут происходит. Графическая карта используется для симуляции дифференциальных уравнений, которые используются для симуляции простой графической карты!

В главе 3.10 нас ждет следующий уровень, котором нити ДНК будут с трудом пытаться эмулировать реакции закона действующих масс.


3.9 Минификатор реакций


Нельзя ли еще уменьшить число реакций? Например, что если попробовать переписать пару реакций

$\begin{align} A &\rightarrow B + C\\ C &\rightarrow D + E \end{align}$

в одну реакцию

$\begin{align} A &\rightarrow B + D + E \end{align}$

Вообще, такое переписывание сильно изменит динамику реакций и результат. Однако, если реакции были составлены при помощи метафоры «отправки сообщений», то они не опираются на точные детали того, как реакции будут протекать во времени. В научных статьях это свойство называется «rate independent reactions».

Также нужно учесть, что, если у частицы $C$ была некоторая начальная концентрация, теперь на нее нужно увеличить начальные концентрации $D$ и $E$.

Чтобы прототипировать такие оптимизации, мне кажется, идеально подходит Wolfram Mathematica, которая построена вокруг парадигмы «символьных манипуляций». К тому же язык CRN++ также реализован на ней.

Код минификатора на Wolfram Mathematica 
SetDirectory[NotebookDirectory[]];
<< CRNSimulator.m
p[s_] := Symbol[SymbolName[s] <> "p"];
m[s_] := Symbol[SymbolName[s] <> "m"];
i[s_] := Symbol[SymbolName[s] <> "i"];
pmconc[var_, c_] := If[c > 0, conc[p@var, c], conc[m@var, -c]];
pm[var_] := p@var - m@var;
eqCnt[eqs_] := Length[Select[eqs, Head[#] === rxn &]];
leftLen[r_] := Length[r[[1]]];
On[Assert];
rxnReplace[r2_, r1_] := (
   Assert[Length[r1[[1]]] == 0];
   If[
    Length[r2[[2]]] > 0,
    Assert[Length[r2[[1]]] == 2];
    Assert[Length[r2[[2]]] > 1];
    Assert[! MemberQ[r2[[1]], r1[[1]]]];
    rxn[Evaluate[r2[[1]]], 
     Evaluate[r2[[2]] /. r1[[1]] -> Sequence @@ r1[[2]]], 
     Evaluate[r2[[3]]]],
    r2
    ]
   );
concReplace[c_, r1_] := (
   Assert[Length[r1[[1]]] == 0];
   If[c[[1]] === r1[[1]],
    Sequence @@ (conc[#, c[[2]]] & /@ r1[[2]]),
    c
    ]
   );
rxnOptimize[eqs_, headCount_] := Module[{
   eqs1 = Select[eqs, Head[#] === rxn && leftLen[#] == 0 &],
   eqs2 = Select[eqs, Head[#] === rxn && leftLen[#] == 2 &],
   concs = Select[eqs, Head[#] === conc &]
   },
  Do[
   concs = concReplace[#, eq1] & /@ concs;
   eqs2 = (rxnReplace[#, eq1] & /@ eqs2),
   {eq1, eqs1[[1 ;; headCount]]}
   ];
  Join[concs, eqs2, eqs1[[headCount + 1 ;;]]]
  ]

Полный код самой программы вместе с макросами для функций min, max, abs до минификации выглядит так:
Синтаксис p@x и m@x используется как сокращенная форма записи $X^+$ и $X^-$.

На выходе мы получаем 10 реакций 19 видов частиц с некоторыми начальными условиями:
Начальные концентрации частиц $N_X, N_Y, N_Z$ зависят от координат текущего пикселя $X$ и $Y$. Об этом подробнее в главе 3.11 про план гипотетического эксперимента.

Вы можете поиграться с этими реакциями в ObservableHQ-симуляторе. Эта система реакций в нем обозначена как «3d engine». Чтобы получить «рендер» самого куба, нужно нажать на кнопку «Recalculate» в подразделе «GPU-accelerated 2d plot».

Можно также попробовать нарисовать «граф потоков данных» данной системы реакций (он также тесно связан с сетью Петри):




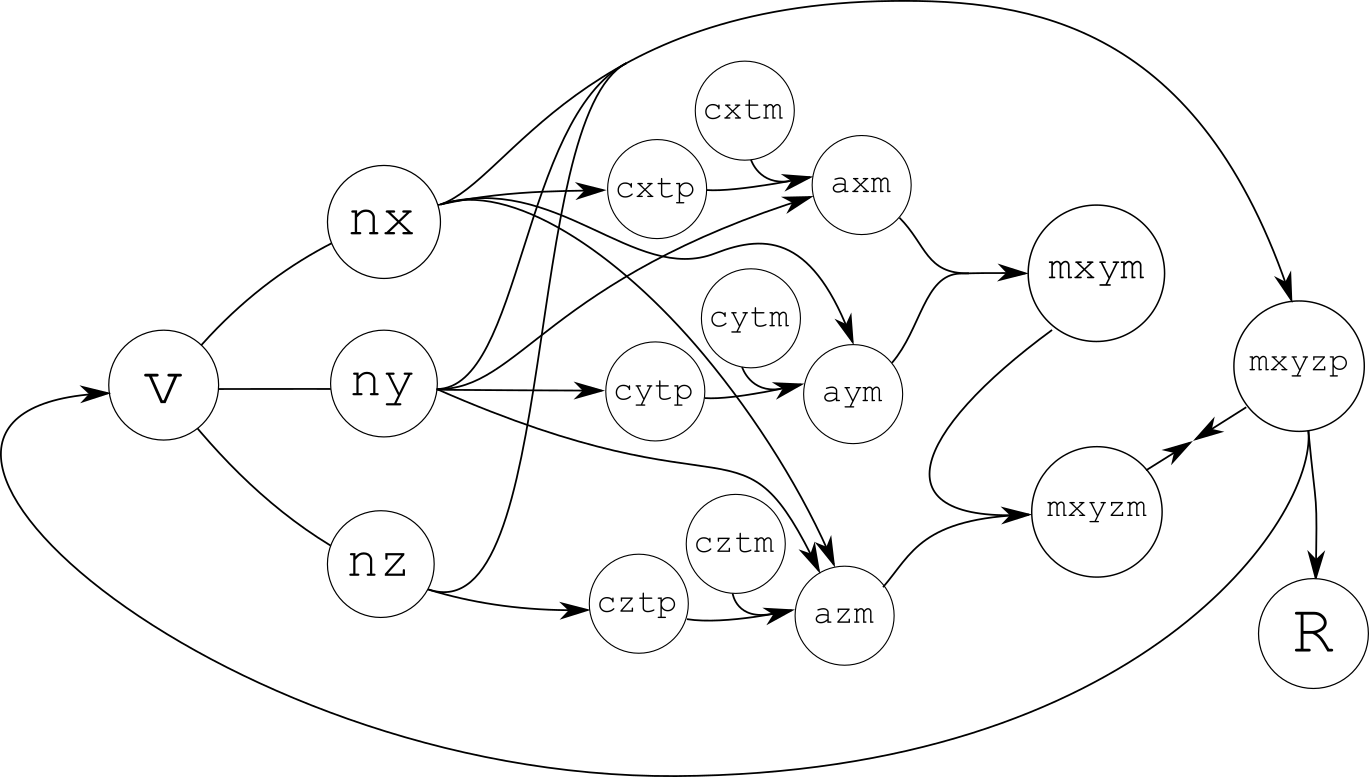
3.10 Получаем код ДНК


В этой главе мы реализуем нашу систему реакций в коде ДНК при помощи метода, описанного в статье Дэвида Соловейчика 2010 года.

Если смотреть глобально, то нужные нам последовательности ДНК получить не так уж сложно. Сначала нужно выбрать более-менее произвольные последовательности ДНК для каждой из частиц:


Для частицы $E$ они должны состоять из четырех частей длиной 15, 7, 15, 7 соответственно, которые будут дальше обозначаться $h_E, f_E, m_E, s_E$.

Далее, для каждой из реакции $R$ вида $A + B\rightarrow C$, нужно обеспечить присутствие трех видов комплексов: React, Produce и Helper. Их ДНК будет составлен из кода участвующих в реакции частиц, а также из двух уникальных для данной реакции последовательностей длины 15: $h_R$ и $h'_R$, которые также выбираются произвольно.



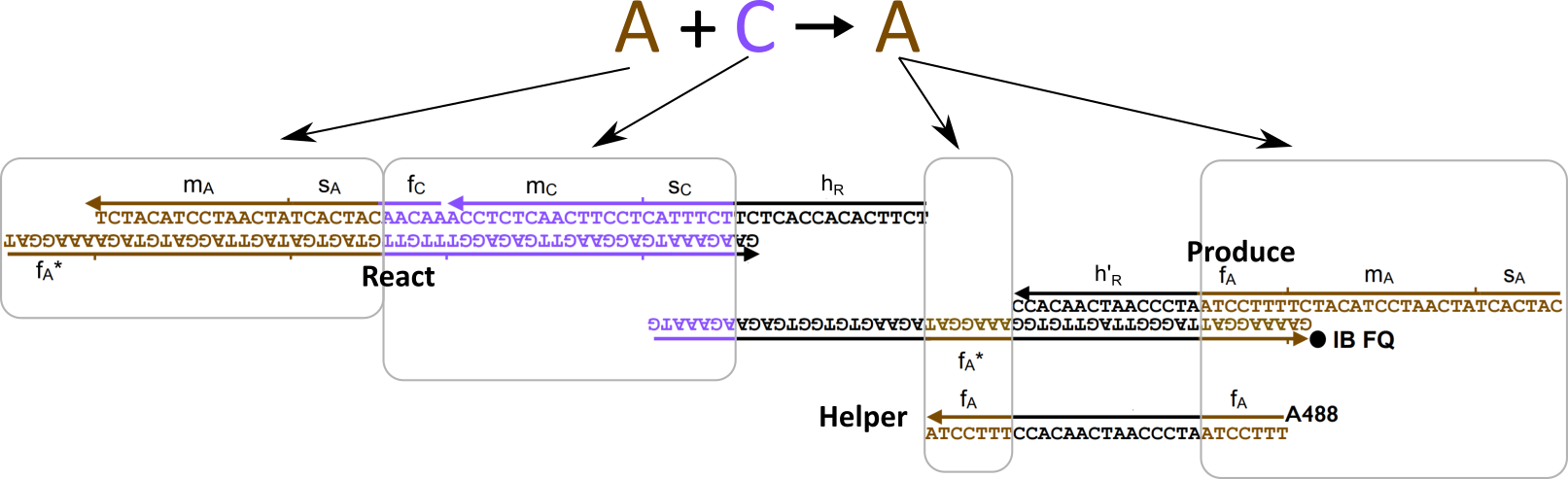
Обратите внимание, что комплексы состоят из «порванных» участков ДНК, в которых верхняя и нижняя часть не полностью совпадает. Именно благодаря этому свойству они могут активно взаимодействовать друг с другом и проводить нужные нам «вычисления».


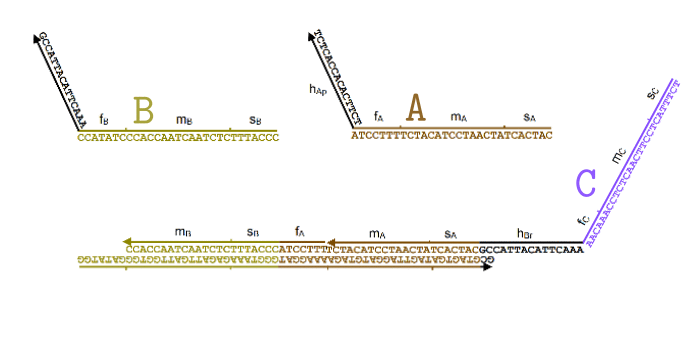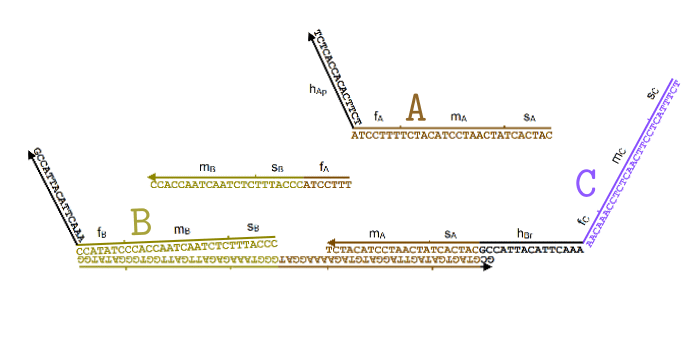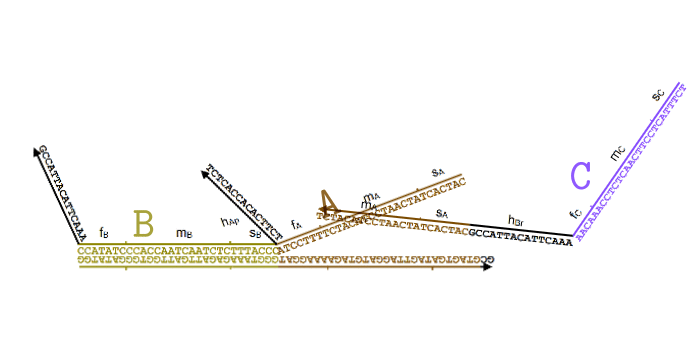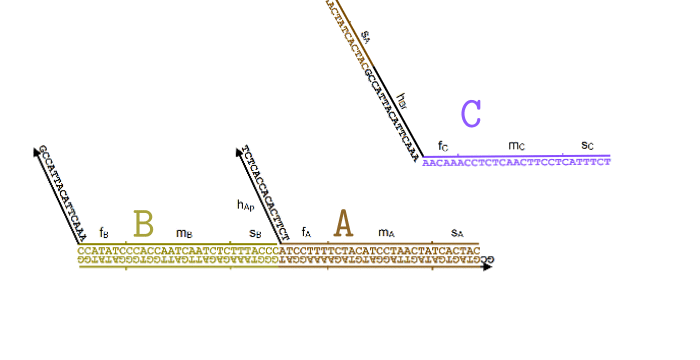
Я немного упростил процесс в этой анимации (убрал Produce и Helper), чтобы был наглядно виден принцип. В пробирке свободно перемещаются одноцепочечные нити ДНК, которые соответствуют частицам $A$ и $B$. Мы хотим, чтобы, встречаясь друг с другом, они исчезали и как бы превращались в частицу $C$.

Для этого появляется комплекс-монстр (в нижней части анимации), который сначала «съедает» частицу $B$, после чего у него «разблокируется» вторая ловушка для частицы $A$. Когда и частица $A$ попадет в эту ловушку, этот комплекс «выпустит» наружу частицу $C$, которая все время была у него «в заложниках».

Все эти процессы происходят благодаря тому, что неполные нити ДНК стремятся найти себе как можно более комплементарную пару. При этом если рядом оказывается лучший кандидат, они могут отказываются от текущего в пользу более комплементарного. Это описание выглядит как какая-то магия, но на самом деле просто является следствием «закона больших чисел» для стохастических процессов, в которых нити случайно связываются и разрываются друг с другом, но в среднем у более комплементарных оказывается большая вероятность оказаться связанными.

Мы немного отвлеклись, наша задача сейчас — получить код.

Думаю, читателю не составит труда написать небольшой скрипт, который выдаст нужные нам последовательности. Формально его содержание можно записать следующим образом, если через $a\,||\,b$ обозначать конкатенацию последовательностей ДНК, а через $a^*$ обозначить комплементарную последовательность:

$\begin{align} \text{Particle}(A) &= \begin{cases} \text{top}\colon & h_A\,||\,f_A\,||\,m_A\,||\,s_A\\ \text{bot}\colon & \varnothing \end{cases}\\ \text{React}(R\colon A+B\rightarrow C) &= \begin{cases} \text{top}\colon & m_A\,||\,s_A\,||\,f_C\,||\,m_C\,||\,s_C\,||\,h_R\\ \text{bot}\colon & f^*_A\,||\, s^*_A \,||\, f^*_C \,||\, m^*_C \,||\, s^*_C \end{cases}\\ \text{Produce}(R\colon A+B\rightarrow C) &= \begin{cases} \text{top}\colon & h'_R\,||\,f_A\,||\,m_A\,||\,s_A\\ \text{bot}\colon & s^*_C \,||\, h^*_R \,||\, f^*_A \,||\, h'^*_R \,||\, f^*_A \end{cases}\\ \text{Helper}(R\colon A+B\rightarrow C) &= \begin{cases} \text{top}\colon & f_A\,||\,h'_R\,||\,f_A\\ \text{bot}\colon & \varnothing \end{cases}\\ \end{align}$

Эти цепочки можно будет синтезировать в лаборатории и размешать в пробирке. Они будут как-то друг с другом взаимодействовать и даже иногда превращаться друг в друга, как планировалось. Однако они также будут иногда «склеиваться» друг с другом незапланированным образом. При этом некоторые реакции будут происходить активно, а другие — редко. Все эти эффекты будут следствием того, что базовые последовательности ДНК были сгенерированы случайно, а это значит, что некоторые из них будут чуть более комплементарные, а некоторое — менее.

Поэтому нам нужны не просто случайные последовательности, а еще и такие, которые не будут случайно друг с другом склеиваться. Точнее, степень их попарной комплементарности будет одинаковой и небольшой. Это не простая задача и для ее решения можно использовать open source утилиту stickydesign — от DNA and Natural Algorithms Group Калифорнийского технологического института.

Но мы совсем ленивы и поэтому будем сразу использовать утилиту piperine от этой же лаборатории, которая принимает на вход список реакций и на выходе возвращает готовый список последовательностей ДНК.

Если вы запутались во всей этой экосистеме трансляторов и компиляторов, вот картинка, как они примерно соотносятся друг с другом:


У меня не получилось установить piperine с первого раза, поэтому я создал докер-файл

Dockerfile 
FROM python:3.7-buster

RUN apt-get update
RUN apt-get install -y build-essential

RUN pip install --upgrade pip
RUN pip install numpy
RUN pip install scipy
RUN pip install git+https://github.com/DNA-and-Natural-Algorithms-Group/stickydesign.git
RUN pip install git+https://github.com/DNA-and-Natural-Algorithms-Group/peppercompiler.git


WORKDIR /home
COPY nupack3.0.6.tar.gz .
RUN tar -xvzf nupack3.0.6.tar.gz

RUN apt-get install -y cmake

WORKDIR /home/nupack3.0.6
ENV NUPACKHOME=/home/nupack3.0.6
RUN mkdir build

# WORKDIR /home/nupack3.0.6/build

# RUN cmake ../
RUN make
# RUN make install

RUN pip install git+https://github.com/DNA-and-Natural-Algorithms-Group/piperine.git

WORKDIR /home/data

# RUN piperine-design my.crn -n 3 --energy 7.5 --deviation 0.5 --maxspurious 0.5

Обратите внимание, что вам в любом случае потребуется зарегистрироваться и скачать архив с nupack3.0.6, который необходим для работы piperine.

Утилита запускается следующей командой:

piperine-design all.crn -n 1 --energy 7.7 --deviation 0.5 --maxspurious 0.765

  • Параметр n задает число раз, которые процесс компиляции ДНК будет повторяться, чтобы из них выбрать лучший вариант. Если вы не собираетесь проводить реальный эксперимент, то лучше поставить значение 1.
  • Параметр energy задает целевое значение энергии для генерируемых цепочек. Обычно значение 7.5-7.7 подходит, иначе утилита даст подсказку.
  • Параметр deviation задает приемлемое относительное отклонение от целевого значения. Значение 0.5 вполне подходит по умолчанию.
  • Параметр maxspurious требует fine-tuning со стороны пользователя. Если он будет меньше оптимального значения — то утилита выдаст сообщение об ошибке, а если чуть больше — то просто будет бесконечно считать результат. Рекомендую пробовать значения с шагом 0.01 начиная с где-то с 0.5.

Входной файл содержит систему реакции в таком же синтаксисе, в котором работает веб-симулятор. Есть два ограничения: число продуктов реакции справа от > не может быть больше 2, а также нельзя задавать константы скоростей у реакций справа от вертикальной черты. Поэтому систему реакций для куба придется немного откорректировать:

Файл cube.crn для piperine 
N_Y + N_Y_M ->
N_Z + N_Z_M -> 
D + N_X -> TX1 + TX2
TX1 -> A_Y_M + A_Z_M
TX2 -> C_X_P + TX3
TX3 -> M_XYZ_P + N_X
D + N_Y -> TY1 + TY2
TY1 -> A_X_M + A_Z_M
TY2 -> C_Y_P + TY3
TY3 -> M_XYZ_P + N_Y
D + N_Z -> TZ1 + TZ2
TZ1 -> C_Z_P + M_XY_M
TZ2 -> M_XYZ_P + N_Z
C_X_M + C_X_P -> 2 A_X_M
C_Y_M + C_Y_P -> 2 A_Y_M
C_Z_M + C_Z_P -> 2 A_Z_M
A_X_M + A_Y_M -> M_XY_M
M_XY_M + A_Z_M -> M_XYZ_M
M_XYZ_P + M_XYZ_M ->
2 M_XYZ_P -> T1 + T2
T1 -> R + D
T2 -> 2 M_XYZ_P

Рекомендую его запускать командой piperine-design all.crn -n 1 --maxspurious 0.765. Процесс компиляции займет около часа. В итоге вы получите множество файлов, самые интересные из которых будут cube0.seqs и cube0_strands.txt. Их содержимое будет выглядеть примерно так:

Signal strands
Strand N_Y0 : CATCTTTACAATACTATCCCTCACTCTTTCCCTAATTTCTACCT
Strand N_Y_M0 : CATTCTTCCATACCATCATTACTCAACTT
Strand Fuel0c0 : TTCACTTTTTATCAAACCAATCTCCATTTCACTCAACCCTTACA
Strand Fuel0d0 : CTCATTTTCAATACATAATCTCCTTCATTCCTTTCCTCTTCTCA
Strand N_Z0 : TCATCTCTTATCTCCAACCCACACTTCTTCCCTTAACAATTACA
Strand N_Z_M0 : ATCTCTCACCCATTCTATCCACATCCTTT
...



3.11 План гипотетического эксперимента


Честно признаюсь, я очень мало изучал материалов касательно того, как производятся подобные эксперименты, поэтому могу упускать что-то существенное. Надеюсь, на Хабре найдутся биологи, которые объяснят, насколько описываемое в этой главе оторвано от реальности.

Итак, мы должны каким-то образом синтезировать все неполные нити ДНК и их комплексы, описанные в предыдущей главе, смешать их в правильных пропорциях и залить в большую емкость с названием Base.

Нужно расставить «экран» из большого числа маленьких пробирок, каждая из которых будет работать как отдельный пиксель, и залить в них одинаковое количество Base.

Также мы должны подготовить две дополнительные смести с названиями Row и Col, благодаря которым в пробирки будет передана информация об их расположении на «экране».



Принцип кодирования простой — в пробирку нужно залить столько капель Row, какой у нее порядковый номер строки, и столько капель Col, какой у нее номер столбца.

Далее нужно будет подождать некоторое время, пока процесс «вычисления» стабилизируется. Если все будет хорошо, концентрация цепочек ДНК, соответствующих частице $R$, будет соответствовать яркости соответствующего пикселя рендера куба.

Чтобы убедиться, что вычисления прошли корректно, мы заранее прикрепим флюорофор (например, Alexa Fluor 647), который будет активироваться при освобождении частицы $R$. Если на такой флюорофор направить свет определенной частоты волны, он начнет светиться определенным цветом



Технология синтезирования нужных нам обрывков ДНК и «помечания» их флюорофорами вполне рутинная и вроде как в Москве можно заказать онлайн-доставку нужных олигонуклеотидов.

Насколько я понимаю, «узким местом» этого эксперимента будет его бюджет. Речь идет о сотнях разных видов олигонуклеотидов, при том, что минимальный объем для заказа одного вида во много раз превосходит требуемый для эксперимента.




Итог


Вот так, при помощи нехитрых приспособлений мы смогли создать себе монитор с нескучными обоями, один только отладочный запуск которого обойдется в семизначную сумму (хотя есть способы сэкономить).

На Хабре часто появляются заголовки новостей про прорывы в биотехнологиях, однако в них обычно дается мало деталей того, как это все реализовано. В этой статье мы очень поверхностно познакомились с одним из довольно экзотических подходов реализации вычислений при помощи ДНК. Однако, я надеюсь, мне удалось хоть чуть-чуть ответить на главный вопрос молекулярной биологии, который возникает у читателей Хабра: «черт побери, да как вообще можно что-то программировать при помощи этих молекул?».


Спасибо Cerberuser, ikle и dbalabanov за сообщения о найденных ошибках в тексте статьи.