13.04.2022 19:17
yurixi 1 5100 Источник


Воображение при математических рассуждениях работает в двух направлениях: с одной стороны, всё представляется в наглядных графиках. Чтобы ощутить как выглядят взаимосвязи варьируются параметры. А второе направление — результат отношения к формуле как к значкам, у которых для сохранением верности при изменениях есть очень чёткие правила. Используя и образное понимание и формальность одновременно можно сильно продвинуться в том чтобы разобраться в интересующих вопросах. Потом всё перепроверить, и узнать больше о самом вопросе, и себе. Так что, включайте рабочий инструмент и приступим.

Я расскажу о константе $\gamma$, не менее важной, чем $e$ или $\pi$.

Сумму

$\sum_{n=1}^{\infty}\left[\frac{1}{n}-\frac{1}{n+1}\right]=1$

Легко подсчитать. В развёрнутом виде левое слагаемое второго элемента сокращается с правой частью первого элемента, и так происходит с каждой парой элементов суммы. И в результате останется левая часть первого элемента, и правая часть последнего. Правая часть последнего стремится к нулю. Значит, сумма будет равна левой части первого элемента, единице.

Получилась «цепочка», которая сложена так, что для результата бóльшую важность имеют её концы. Сделаем ещё одну цепочку, только вместо обращения числа поставим его логарифм.

Натуральный логарифм, кроме того, что это операция обратная возведению в степень, это интеграл дроби $1/x$:

$ \int\limits_{0}^{k}\frac{1}{x^s}\,dx=\frac{k^{r}}{r}\qquad r = 1-s\qquad B(x)=\frac{x}{e^x-1} $

$ \int\limits_{1}^{k}\frac{1}{x^s}\,dx=\lim_{a \to s}\frac{k^{1-a}-1}{1-a}=\frac{\ln(k)}{B(\ln(k^r))} \qquad B(0)=1 $

$\int\limits_{b}^{k}\frac{1}{x^s}\,dx=\frac{k^{1-s}-b^{1-s}}{1-s}= \frac{(k/b)^{r}-1}{r/b^r}=\frac{e^{r\ln(k/b)}-1}{r/b^r}=\\=\frac{b^r\ln(k/b)}{B(r\ln(k/b))}=\frac{\ln\left(\frac{k^b}{b^b}\right)/b^{s}}{B\left(\ln\left(\frac{k\,\,b^s}{k^sb\,}\right)\right)}$

Разница двух логарифмов может быть представлена как логарифм от дроби. Индекс программисты привыкли вести с нуля, и часто это удобнее. Так что, если мы запишем сумму, которую планировали, то, с учётом, что логарифм от нуля не определён, и надо добавить величину $m$, получится:

$ \sum_{n=0}^{k-1}\ln\left(\frac{n+m+1}{n+m}\right)=\ln(k+m)-\ln(m) $

И тогда будет верно такое соотношение:

$ \ln(k+m)-\sum_{n=0}^{k-1}\ln\left(\frac{n+m+1}{n+m}\right)=\ln(m) $

В котором первый логарифм можно превратить в интеграл.

$ \int \limits_{1}^{k_1} \frac{1}{x}\,dx-\sum_{n=0}^{k_2-1}\ln\left(\frac{n+m+1}{n+m}\right)=\ln(m) $

$ k_1=k_2+m $

Интеграл можно представить как сумму, с добавлением числа $\gamma$, компенсирующее их расхождение, включая различие верхних границ.

$ \sum_{n=1}^{k}\frac{1}{n}-\gamma_{km}-\sum_{n=0}^{k-1}\ln\left(\frac{n+m+1}{n+m}\right)=\ln(m) $

И тогда две суммы можно объединить

$ \sum_{n=1}^{k}\left[\frac{1}{n}+\ln\left(1-\frac{1}{n+m}\right)\right]=\gamma_{km}+\ln(m)$

В пределе $k\to\infty$ обе стороны сойдутся. Величина $\gamma$ уже не будет зависеть от $m$.

Так получилась постоянная Эйлера $\gamma=0.57721566490\dots$.

Сумму можно перевести в произведение, как сумму степеней.

$ \prod_{n=1}^{\infty}e^{\frac{1}{n}}\left(\frac{an+1-a}{an+1}\right)=e^{\gamma}/a\qquad a=1/m$

$a e^{-\gamma} \prod_{n=1}^{\infty}e^{\frac{1}{n}}\left(\frac{an+1-a}{an+1}\right)=1 $

Выглядит как произведение-аналог первой суммы.

Как было замечено в статье «Скучные числа», отношение этого выражения для двух разных параметров имеет разложение, в котором вдруг появляется число пи:

$e^{-\gamma} \prod_{n=1}^{\infty}e^{\frac{1}{n}}\left(\frac{n}{n+1}\right)=1 \qquad 2 e^{-\gamma} \prod_{n=1}^{\infty}e^{\frac{1}{n}}\left(\frac{2n-1}{2n+1}\right)=1 $

$1=\frac{e^{-\gamma}}{2e^{-\gamma}}\prod_{n=1}^{\infty}\frac{e^{1/n}}{e^{1/n}}\cdot\frac{\quad \,\,n\,\quad(n +1/2)}{(n+1)(n-1/2)}= $

$={1\over2}\prod_{n=1}^{\infty}\frac{\quad \,n\,\,\quad(n)(n+1/2)(n +1/2)}{(n+1)(n)(n+1/2)(n-1/2)} $

$={1\over2}\prod_{n=1}^{\infty}\frac{n^2}{n^2-1/4}\cdot\frac{(n+1/2)^2}{n^2+n}=\frac{1}{2}\cdot\frac{\pi}{2}\cdot\frac{4}{\pi}$

Внутри произведения обе дроби одинаковы, за исключением смещения $n$ на $1/2$. Как будто взаимодействие дробей происходит уже на половине шага.

Если переписать выражение для целого шага, получится:

$ \prod_{n=2}^{\infty}\frac{(n/2)^2}{(n/2)^2-(1/2)^2}=2 $

Интересное разложение двойки. Это тоже цепочка, результат зависит от начального индекса.

$ \prod_{n=k+1}^{\infty}\frac{n^2}{n^2-1}=\frac{k^2-1}{k^2}\prod_{n=k}^{\infty}\frac{n^2}{n^2-1} =\left(\frac{k}{k-1}\right)^{-1}\left(\frac{(k+1)}{(k+1)-1}\right)\prod_{n=k}^{\infty}\frac{n^2}{n^2-1} $

$ \prod_{n=k}^{\infty}\frac{n^2}{n^2-1}=\frac{k}{k-1} $

Это была разминка. Теперь разбираемся глубже.

Постоянная Эйлера-Маскерони, $\gamma$, так же как $e$ и $\pi$, вычисляется через предел. Здесь это предел различия суммы и интеграла от $1/x$. Сразу добавим в соотношение суммы и интеграла параметр дискретизации $\beta$, при увеличении которого разница суммы и интеграла приближается к нулю.

$\sum_{n=0}^{k-1}\left(\frac{\beta}{n+\beta}\right)^s -\gamma_{k\beta}(s)= \beta\int\limits_{1}^{k/\beta+1}\frac{1}{x^s}\,dx=\beta\frac{(k/\beta+1)^{1-s}-1}{1-s} $

Крайняя левая дробь похожа на определение дзета-функции, но отражает закономерность расчёта для случая, когда $(\beta-1)$ первых членов в сумме не учитывается. Верхний предел интеграла обозначим $h=k/\beta+1$.

Получается, дзета-функция Римана это сумма простенького интеграла и числа $\gamma$, которое уже с учётом степени $s$ становится функцией.

$\beta^{-s}\cdot \sum_{n=0}^{\infty}\left(\frac{\beta}{n+\beta}\right)^s=\zeta(s)- \sum_{n=1}^{\beta-1}\frac{1}{n^s}=\frac{1}{\beta^{s-1}(s-1)} +\frac{\gamma_{\beta}(s)}{\beta^{s}} $

Ориентировочное различие этих двух частей в том, что для интеграла, превращающегося в дробь, соотношение первых членов суммы дзеты не важнó, он отражает общее свойство всей остающейся суммы.

А теперь пора вспомнить, что при вычислении дзета-функции $s$ — это комплексная величина. Реальная часть может быть единичной, при этом сам аргумент не равен единице, в этой области расположена граница сходимости. Интегральная часть с учетом верхнего предела интегрирования выражается как

$\operatorname{I}(s)=\frac{1-\frac{1}{h^{s-1}}}{\beta^{s-1}(s-1)} $

Если задать $s=1+w\,i,\,\beta=1$, то

$\operatorname{I}(1+w\,i)=\frac{i}{w}e^{-(\ln(k+1)w)\,i}-\frac{i}{w} $

Можно заметить, что присутствует слагаемое, которое определяется как колебания в зависимости не только от мнимой части аргумента, но и от логарифма единицы плюс количества слагаемых суммы дзеты. Получается, процесс схождения не зависит от количества слагаемых, а значение во время суммирования крутится вокруг предполагаемого результата. Поэтому эту колебательную часть для улучшения сходимости проще убрать, вычесть.

На иллюстрации ниже представлены значения, полученные на линии аргументов $s=0.5+x i$.



Синяя линия — результат суммирования тридцати слагаемых.
Красная линия — колебательная часть интеграла с аналогичным параметром.
Жёлтая линия — дзета-функция.
Зелёная линия — результат вычитания из прогрессивной суммы колебательной части интеграла.

Видно, что результат вычитания достаточно приближен к дзета-функции, осталось небольшое равномерное колебание.

Мы уже заступили за линию единичной реальной части аргумента. Внутри интегральной части

$\operatorname{I}(\sigma+w\,i)=\frac{1-\frac{1}{h^{\sigma-1+w\,i}}}{\sigma-1+w\,i}=\frac{h^{(1-\sigma)-w\,i}-1}{(1-\sigma)-w\,i} $

Можно заметить элемент $h^{1-\sigma}$, модуль которого с ростом $h$ при $\sigma<1$ только увеличивается. То есть, в этой области при сложении ряда для дзета-функции — результат, как и колебательная часть интеграла, всё сильнее отходит от значения дзета-функции, полученного аналитическим продолжением.

Колебательная часть интеграла компенсирует расхождение суммы. Можно предположить, что компенсацию можно улучшить, изменив верхний предел интегрирования у интегральной части. В этом случае интеграл как бы заберёт у гаммы часть дзеты на себя, дополнительно уточняя прогрессирующую сумму. Осталось определить, от чего зависит полезная величина сдвига.

График зависимости модуля различия от добавки к параметру $k$ в верхнем пределе интеграла немного озадачивает.


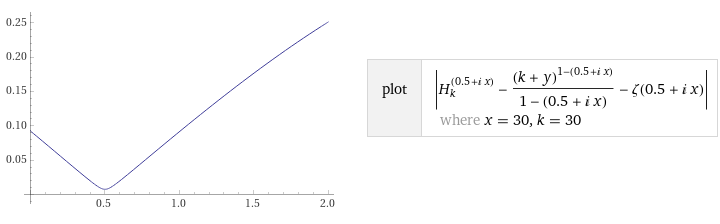
Судя по нему, минимум модуля различия находится около места, в которой верхний предел интеграла уменьшается ровно на половину отсчёта. Конечно, для разных аргументов положение минимума отличается, но при возрастании количества слагаемых оно остаётся $0.5$, со всё большей точностью.

Так как изменение предела идёт в меньшeю сторону, то получается, что передача происходит в обратном направлении, интеграл отдаёт часть гамме и этим приближает свою колебательную часть к той, которая не важна для получения аналитического значения дзеты.

$\sum_{n=1}^{k}\frac{1}{n^s}=\underbrace{\gamma_k(s)-(I_{h}-I_{h-1/2})}_{\gamma(s)}+I_{h}-I_1 $

$\zeta(s) \quad\sim\quad \sum_{n=1}^{k}\frac{1}{n^s}-I_{h-1/2}=\gamma_k(s)-I_1$

Здесь все $I$ — это составляющие интеграла, вклад от различных пределов.
  • $I_1=1/(1-s)=1/r$ — вклад нижнего предела, в виде значения первообразной.
  • $I_h$ — вклад верхнего предела.
  • $I_{h-1/2}$ — вклад пониженного верхнего предела.
  • $\gamma(s)$ — гамма, в первом приближении является разницей между дзетой и интегралом. Зависит от $k$ по своему определению — это различие суммы и интеграла для данного $k.$
  • $\gamma_k(s)$ — гамма, которая после включения в себя интеграла половины отсчёта изменила свою зависимость от $k$. Является результатом второго шага приближения. В пределе $k\to\infty$ обе гаммы совпадают.

Два приближения $\gamma(1-r)$

$ P_1(k)=\sum_{n=1}^{k}\frac{n^r}{n}-\frac{(k+1)^{r}-1}{r} \qquad P_2(k)=\sum_{n=1}^{k}\frac{n^r}{n}-\frac{(k+1/2)^{r}-1}{r} $

Можно рассмотреть в виде начального значения и изменения на каждое слагаемое.

$P_1(0)=0\qquad P_1(k)-P_1(k-1)=\frac{k^r}{k}-\frac{(k+1)^{r}-k^{r}}{r} $

$P_2(0)=\frac{1-(1/2)^r}{r}\qquad P_2(k)-P_2(k-1)=\frac{k^r}{k}-\frac{(k+1/2)^{r}-(k-1/2)^{r}}{r}$

$P_3(0)=\frac{1}{r}\qquad P_3(k)-P_3(k-1)=\frac{k^r}{k}-\frac{k^{r}-(k-1)^{r}}{r}$

Первое приближение убирает расходящуюся часть. Второе убирает расходящуюся часть, но не всю — та часть, которая быстрее приближает к конечному значению, остаётся. То, что эта часть равна половине отсчёта может быть связано с тем что без последнего отсчёта, точно происходит нехватка, а с последним отсчётом точно перебор. И с увеличением количества отсчётов величины недобора и перебора сближаются.

При превышении реальной части $r$ единицы, или при отрицательной реальной части $s$, оба приближения опять расходятся. А нам хорошо бы узнать $\gamma(1-r)$ для всех $r$. Для этого надо рассказать ещё об одной функции.

У функции $x^s/e^x$ есть такое свойство, что интеграл этой функции, поделённой на $x$, будет равен интегралу этой функции, поделённому на $s$.

$ \Gamma(s)= \int\limits_{0}^{\infty}\frac {1}{x}\cdot \frac{x^{s}}{e^x} \, dx = \int\limits_{0}^{\infty} \frac {1}{s} \cdot \frac{x^{s}}{e^x} \, dx \\\operatorname{Re}(s)>0\quad s\Gamma(s)=\Gamma(s+1) $

Этот интеграл называется Гамма-функцией. Но чтобы не путать с функцией-обобщением постоянной Эйлера, обозначенной строчной гаммой, буду использовать функцию $D(s)=1/\Gamma(s+1)$. Я называю это «откатная» функция, так как умножение на аргумент заменяет уменьшение аргумента на единицу. Из других преимуществ — то что она никогда не уходит в бесконечность, а в целых числах обратна факториалу числа.

$ sD(s)=D(s-1) \\\frac{1}{D(s)}=\int\limits_{0}^{\infty}\frac{x^s}{e^x} \, dx $

Через интеграл эта функция определена только при $\operatorname{Re}(s)>-1$.

Так как у функции умножение на аргумент сдвигает график вправо, то её нулевое значение в минус единице отражено дальше, на все отрицательные целые числа, и из-за этих нулей можно предположить, что функция является произведением всех функций вида $f_n(s)=(s+n)$, с натуральным числом в параметре. Чтобы учесть, что в нуле она должна быть равна единице, добавляется коэффициент.

$ D(s)\quad\sim \quad \lim_{k\to\infty}d_k\prod_{n=1}^{k}(n+s) $

Этот коэффициент в нуле должен повторять произведение всех $n$, значит, можно попробовать $d=1/(k!)$ Но это всё равно что внутреннюю часть произведения переписать в виде дроби с $n$ в знаменателе.

$\sim\prod_{n=1}^{k}\frac{n+s}{n} $

Это для $s = 1$ превратит произведение в цепочку, и результат будет $k+1$. Второй конец цепочки при любом $k$ продолжает влиять на результат.

Коэффициент должен зависеть от $s$, сохраняя свойства функции. При этом надо убрать зависимость от $k$. Существует решение, добавить ещё пару множителей, чтобы при $s=1$ единица сохранялась.

$ D(s)=\lim_{k\to\infty}\exp\left({{\sum_{n=1}^{k}\left[\ln\left(\frac{n+s}{n}\right)\right]-s\ln(k+1)}}\right) =\\=\lim_{k\to\infty}\exp\left({{\sum_{n=1}^{k}\left[\ln\left(\frac{n+s}{n}\right)\right]-s\int\limits_1^{k+1} \frac{dx}{x}}}\right) =\\= \lim_{k\to\infty} e^{\gamma s} \prod_{n=1}^{k}\frac{n+s\,}{n\,e^{s/n}}=e^{\gamma s} \prod_{n=1}^{\infty}\frac{1+\frac{s}{n}}{e^{s/n}} $

Без $\gamma$ не обошлось. Хотя, если сразу знать, что от аргумента у коэффициента только степенная зависимость, то можно определить коэффициент по-другому.

$D(s)=\prod_{n=0}^{\infty}\frac{1+\frac{s}{n}}{\left(1+\frac{1}{n}\right)^s} $

Но предыдущее выражение имеет своё преимущество: видно, какую производную имеет эта функция в нулевой точке. Отдельно произведение имеет единичную производную, а всё выражение целиком — $\gamma$.

В завершение — о точном значении $\gamma(s)$ для всех $s$.

У дзета-функции есть симметрия относительно линии $\operatorname{Re}(s)=1/2$:

$ \frac{\zeta(s)}{\zeta(r)}=\frac{ s\cdot D\left(\frac{s}{2}\right){\pi^{\frac{s}{2}}}}{r\cdot D\left(\frac{r}{2}\right){\pi^{\frac{r}{2}}}} $

Она показывает, что для разворота функции по оси достаточно через умножение переставить полюс и тривиальные нули, пересчитать экспоненциальный множитель — оставшаяся функция-множитель уже симметрична.

Исходя из этого у функции $\gamma(s)$ симметрия будет такая:

$ \frac{\gamma(s)\cdot (1-s)-1}{s\cdot\gamma(1-s)-1}=\frac{D\left(\frac{s}{2}\right)}{D\left(\frac{1-s}{2}\right)}\pi^{s-1/2} $

И значит, точно определить значение функция можно и для $\operatorname{Re}(s)<0$.

Но есть ощущение, что кроме точного значения в этом числе заложено что-то ещё, что-то большее.

Комментарии (1)


  1. sashagil
    16.04.2022 09:46
    #24269233

    Оставляю терминологический комментарий: приём, с которого вы начинаете заметку, и который вы назваете "цепочкой", общепринято называется "телескопическая сумма", "телескопический ряд" (https://ru.wikipedia.org/wiki/Телескопический_ряд) - калька с telescoping sum. Имеется в виду физическая аналогия в виде старинного телескопа или складной подзорной трубы из входящих друг в друга трубок.