О спинорах человеческим языком / forpes.ru

02.05.2023 22:02

flx0 13 5500 Источник

$\newcommand{\e}{\mathcal{\mathbf{e}}}\newcommand{\x}{\mathcal{\mathbf{x}}}\newcommand{\y}{\mathcal{\mathbf{y}}}\newcommand{\z}{\mathcal{\mathbf{z}}}\newcommand{\u}{\mathcal{\mathbf{u}}}\newcommand{\v}{\mathcal{\mathbf{v}}}\newcommand{\w}{\mathcal{\mathbf{w}}}\newcommand{\scalar}[2]{\left<#1|#2\right>}\newcommand{\spinup}{\left| \uparrow \right>}\newcommand{\spindown}{\left| \downarrow \right>}$

Одной из самых больших сложностей в осознании квантовой механики для меня стали спиноры. Действительно, откройте любое популярное изложение, и вам навешают лапшу на уши о то что "спинор - это такой объект, который при повороте на 360 градусов превращается в свою противоположность". Полезное определение? Кажется не очень.

Ну хорошо, черт с ними с популярными изложениями. Откроем учебник физики. Представление векторов как матриц (почему, откуда?), их разложения по столбцам и строкам, какие-то стрелочки $\left| \uparrow \right>$ , $\left| \downarrow \right>$ , матрицы Паули, Гамма-матрицы, вся эта дичь вроде работает и ее можно использовать для решения уравнения Дирака, но выглядит ли это разумным человеческим языком?

Дело в том, что матрицы очень хорошо выполняют одну роль - роль представления разнообразных геометрических структур. Линейные операторы? Пожалуйста. Элементы алгебры Ли? Вот вам матрицы! Графы - матрицы смежности! Веса соединений нейросетей, и так далее, тысячи применений им! Однако же, глядя на матрицу вы ровным счетом ничего не можете сказать о той структуре, которую она представляет. И именно поэтому изложение спиноров в подавляющем большинстве литературы для меня выглядело какой-то взятой с потолка чепухой.

В этой статье я решительно отказываюсь использовать матрицы - язык машин, и вместо этого предлагаю вашему внимание описание спиноров на языке людей - языке геометрической алгебры.

Введение в геометрическую алгебру

Если вы встретили название "геометрическая алгебра" впервые, я рекомендую начать знакомство с ней с этого видео. Для остальных, напомню основные положения.

Начнем с рассмотрения линейного векторного пространства , снабженного операцией скалярного произведения $\scalar{\cdot}{\cdot}$ .

Дополнительно введем операцию внешнего произведения векторов $\u\wedge\v$ . Эта формальная операция ставит в соответствие каждой паре векторов бивектор. Если вектор - это "направление + длина", то бивектор - это "направление + площадь". Домножая на новые векторы можно получать 3-векторы ("направление + объем"), и, в общем случае, k-векторы.

Пример внешнего произведения векторов с образованием бивектора

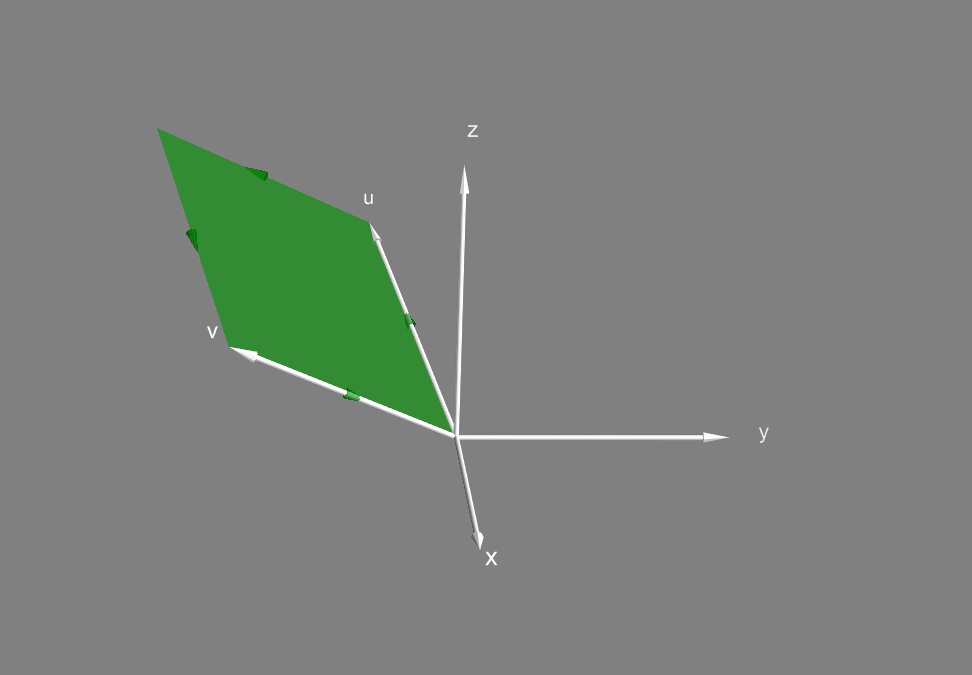
Для бивектора неважна форма, только направление и площадь. Этот же бивектор можно изобразить, к примеру, так:

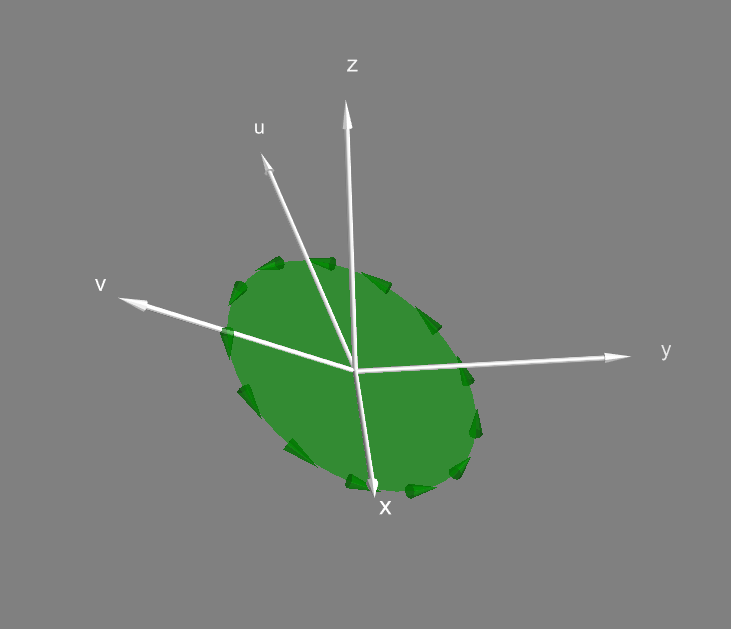
При перемножении в обратном порядке $\v\wedge\u$ , направление бивектора сменится на противоположное, то есть операция внешнего произведения антикоммутативна:

$\u\wedge\v = - \v\wedge\u$

Из антикоммутативности также следует что $\forall\u:\u\wedge\u = 0$ .

Это приводит к тому, что в n-мерном пространстве не может существовать k-вектора у которого . Внешнее произведение отлично от нуля тогда и только тогда когда все входящие в него векторы линейно независимы. n-вектор наибольшей возможной степени также называется псевдоскаляром. Дело в том что как и скаляр, он имеет всего одну степень свободы, но в отличие от скаляра псевдоскаляр изменяет знак при отражении.

Геометрическое произведение двух векторов определено следующим образом:

$\u\v = \scalar{\u}{\v} + \u\wedge\v$

В случае если векторы параллельны друг другу, $\u\wedge\v=0$ , а значит геометрическое произведение сводится к скалярному (а значит для паралльных векторов произведение коммутативно), а в случае когда они ортогональны, геометрическое произведение сводится к антикоммутативному внешнему. В общем случае, геометрическое произведение двух векторов предствляет собой сумму скаляра и бивектора.

Векторное пространство, снабженное операцией геометрического произведения образует алгебру Клиффорда, или, как ее называл сам Клиффорд, геометрическую алгебру.

Элементы алгебры Клиффорда называются мультивекторами. Любой мультивектор можно представить как формальную сумму k-векторов для $0 \le k \le n$ .

В этой статье я буду рассматривать только положительно определенные алгебры Клиффорда, то есть такие, в которых скалярное произведение любых векторов неотрицательное, и $\v^2 = 0 \Leftrightarrow \v=0$ . Положительно определенная алгебра Клиффорда над $\mathbb{R}^n$ обозначается .

Роторы

Рассмотрим такое выражение, где $\w$ - произвольный вектор, $\u$ - единичный вектор ( $\u^2 = 1$ ):

$\u\w\u = \u\left(\w_{\parallel} + \w_{\perp}\right)\u= \u \w_{\parallel} \u + \u \w_{\perp} \u= \u \u \w_{\parallel} - \u \u \w_{\perp}= \w_{\parallel} - \w_{\perp}$

Часть вектора $\w$ , параллельная $\u$ , коммутирует с $\u$ , а ортогональная часть - антикоммутирует. Благодяря этому, операция сопряжения $\u\w\u$ отражает вектор $\w$ относительно вектора $\u$ .

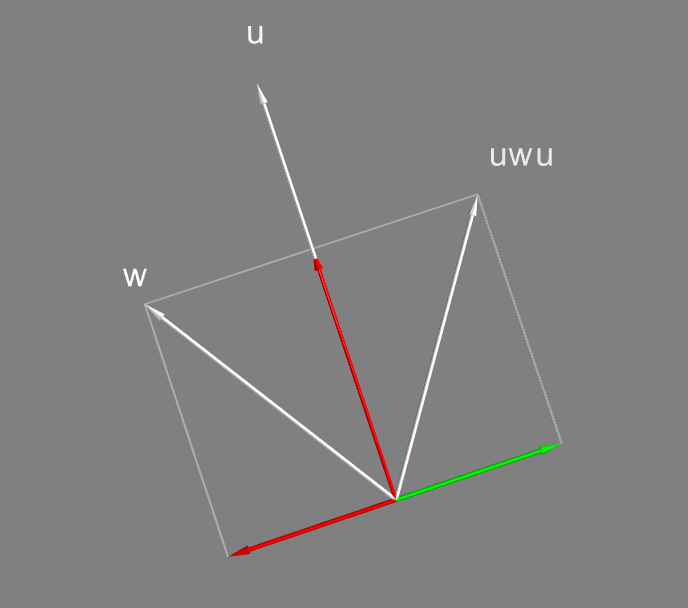
Два отражения можно скомбинировать. Выражение

$\v\u\w\u\v$

сначала отражает вектор $\w$ относительно $\u$ , потом отражает получившийся вектор относительно $\v$ . Такое двойное отражение оказывается эквивалентно повороту на удвоенный угол между $\u$ и $\v$ !

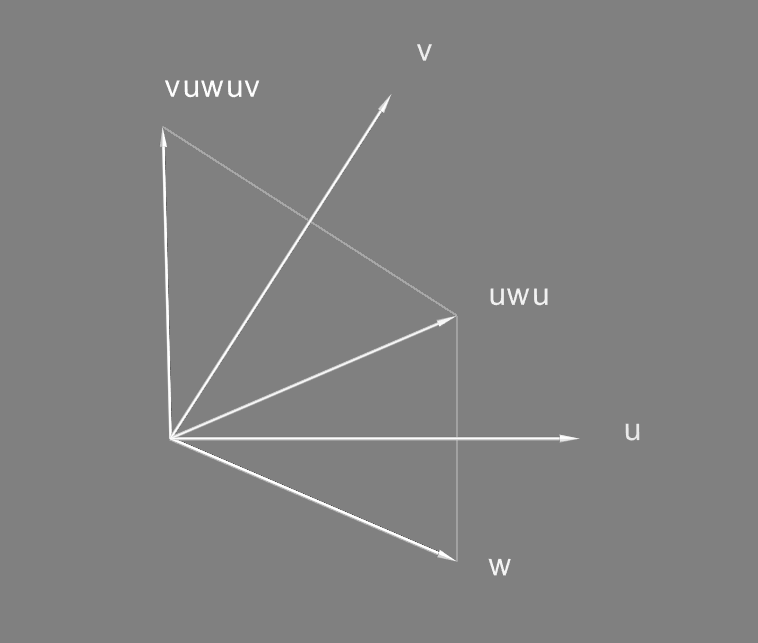
(Для двух измерений эквивалентность двух отражений повороту на удвоенный угол между $\u$ и $\v$ видна по построению, ну а доказательство для трех и более я предлагаю в качестве упражнения читателю)

Поэтому, геометрическое произведение двух единичных векторов также называется ротором. Напомню, что геометрическое произведение это

$\u\v = \scalar{\u}{\v} + \u\wedge\v$

При этом, скалярное произведение двух единичных векторов равняется косинусу угла $\phi$ между ними, а внешнее произведение - это площадь паралелограмма (равная синусу $\phi$ ) и плоскость, в которой он лежит. То есть, этот ротор можно представить так:

$\u\v = \cos\phi + \sin\phi \cdot \bar{\bar{b}}$

где $\bar{\bar{b}}$ - это единичный бивектор (т.е. $\bar{\bar{b}}^2 = -1$ ), находящийся в той же плоскости, что и $\u\wedge\v$ .
Напомню, что такой ротор поворачивает вектор на удвоенный угол. То есть, для поворота на угол $\phi$ следует воспользоваться ротором

$\cos\frac{\phi}{2} + \sin\frac{\phi}{2} \cdot \bar{\bar{b}}$

Стоит отметить, что при сопряжении порядок векторов слева и справа противоположный. Можно переписать наше исходное выражения с использованием операции обращения порядка:

$\v\u\w\u\v = \left(\u\v\right)^\dagger\w\left(\u\v\right)$

Как следует из названия, операция обращения порядка действует на k-векторы следующим образом:

$\left(\e_1 \wedge \e_2 \wedge ... \wedge \e_k \right)^\dagger = \e_k \wedge ... \wedge \e_2 \wedge \e_1$

Как нетрудно видеть, обращение не меняет скаляры и векторы, но изменяет знак бивекторов и тривекторов на противоположный. Обращение является антиавтоморфизмом, то есть оно сохраняет операцию произведения, изменяя порядок операндов. $\forall A,B$ :

$\left(AB\right)^\dagger = B^\dagger A^\dagger$

Отсюда,

$\left(\u\v\right)^\dagger = \v\u = \cos{\phi} - \sin{\phi} \cdot \bar{\bar{b}}$

Итого, поворот вектора $\w$ на угол $\theta$ в плоскости единичного бивектора $\bar{\bar{b}}$ задается следующим выражением:

$R^\dagger \w R=\left( \cos\frac{\theta}{2} - \sin\frac{\theta}{2} \cdot \bar{\bar{b}} \right)\w\left( \cos\frac{\theta}{2} + \sin\frac{\theta}{2} \cdot \bar{\bar{b}} \right)$

Это можно записать и через экспоненты:

$R^\dagger \w R =\exp\left(- \frac{\theta}{2} \cdot \bar{\bar{b}}\right) \cdot \w \cdot \exp\left(\frac{\theta}{2} \cdot \bar{\bar{b}}\right)$

но на вопрос почему так, я предлагаю читателю ответить самостоятельно.

Spin(n)

Вращения можно комбинировать. Так, на вектор $\v$ можно сначала подействовать ротором , а после этого ротором :

$\u = Q^\dagger R^\dagger \v R Q = \left(RQ\right)^\dagger \v \left( R Q \right)$

Альтернативно, можно считать это действием ротора на ротор , с образованием нового ротора , который уже в свою очередь действует на $\v$ . Однако, если на векторы роторы действуют сопряжением (с двух сторон), то друг на друга они действуют умножением с одной стороны.

Иными словами, роторы образуют группу. На первый взгляд могло бы показаться, что эта группа - группа вращений в n-мерном пространстве, также известная как , однако при ближайшем рассмотрении оказывается, что действие ротора на вектор неотличимо от действия ротора , хотя это разные элементы группы. Действительно,

$(-R)^\dagger \v (-R) = R^\dagger \v R$

То есть получается из группы всех роторов путем "забывания" разницы между и . Говорят, что группа роторов образует двойное покрытие группы всех вращений. Группа роторов в носит название .

В связи с этим возникает вопрос: а нельзя ли из вектора извлечь что-то типа квадратного корня, так чтобы роторы действовали на этот корень умножением вместо сопряжения? Как-то так:

$R^\dagger \v R = R^\dagger s^\dagger s R$

Или, если не получится извлечь такой корень, то хотя бы представить вектор в виде суммы из нескольких "квадратов":

$\v = \sum_i s_i^\dagger s_i$

Тогда и действие ротора на него будет выглядеть так:

$R^\dagger \v R= \sum_i R^\dagger s_i^\dagger s_i R= \sum_i \left(s_i R \right)^\dagger \left(s_i R \right)$

С одной стороны, мы точно знаем, что такие составляющие разложения вектора не лежат в . Так как роторы - элементы четной алгебры, и скомбинировать из них элемент нечетной алгебры невозможно.

С другой стороны, сделав предположение что такое разложение существует в нашей алгебре, придумаем для мультивекторов и $s_i^\dagger$ новое название - спиноры.

Осталось только найти мультивекторы, подходящие под это название.

Проекторы и идеалы

Проекторы

Рассмотрим мультивектор $p = \frac{1}{2}\left(1 + \v \right)$ , где $\v^2 = 1$ . Возведем его в квадрат

$p^2 = \frac{1}{4}\left(1 + \v \right)^2= \frac{1}{4}\left(1 + 2 \v + \v^2 \right)= \frac{1}{4}\left(1 + 2 \v + 1 \right)= \frac{1}{2}\left(1 + \v \right)= p$

Квадрат объекта равняется ему самому. Необычно. Назовем такой объект для которого проектором.

Это название происходит от того факта, что действие проектора умножением на произвольный мультивектор преобразует его в "проекцию" , такую, что любое последующее действие проектора ее не изменяет: $\left(A p\right) p = A p$ .

"Проекции" обладают крайне интересным с точки зрения алгебры свойством: если проектор при умножении стоит справа (или слева), его нельзя оттуда просто убрать. Поясню эту мысль: произвольные мультивекторы A и B можно переставлять местами с использованием их коммутатора :

Однако, в силу того что любая степень проектора равняется ему самому, такая перестановка просто дублилует , всегда оставляя справа его копию:

(и даже если на выписать эту копию явно, как я сделал выше, призрачная копия справа никуда не исчезнет).

Благодаря этому свойству, произведение любого элемента алгебры на проекцию также является проекцией. Подалгебра, обладающая таким свойством, называется идеалом. Мы будем говорить, что проектор порождает в алгебре левый идеал $Cl(n) \cdot p$ (т.е. все мультивекторы вида $Ap, \forall A\in Cl(n)$ ) и правый идеал $p \cdot Cl(n)$ (мультивекторы вида $pA, \forall A\in Cl(n)$ ).

Ортогональные пары

Если - проектор, то и $\left(1 - p\right)$ - тоже проектор. Действительно,

$\left(1 - p\right)^2 = 1 - 2p + p^2 = 1 - 2p + p = 1 - p$

Более того, и $\left(1 - p\right)$ - ортогональны:

$p\left(1 - p\right) = p - p^2 = p - p = 0$

Такие ортогональные пары проекторов часто обозначают как и $p_{-}$ .

Используя ортогональные пары проекторов, любой мультивектор можно представить как сумму его проекций $A = A p_{+} + A p_{-}$ (т.к. $p_{+} + p_{-} = 1$ ).

В частности, для проектора, образованного из единичного вектора $\v$ ,

$\displaylines{ p_{+} = \frac{1}{2}\left(1 + \v \right) \\ p_{-} = \frac{1}{2}\left(1 - \v \right) \\ \v = p_{+} - p_{-}}$

Заметили?

$\v = p_{+} - p_{-} = p_{+}^2 - p_{-}^2 = p_{+}^\dagger p_{+} - p_{-}^\dagger p_{-}$

Это же именно такое разложение, какое мы искали! Почти. Перед вторым слагаемым вылез минус, но мы пока этот факт проигнорируем.

Тогда, при повороте вектора $\v$ ротором имеем:

$\u = R^\dagger \v R= R^\dagger \left( p_{+}^\dagger p_{+} - p_{-}^\dagger p_{-} \right) R= R^\dagger p_{+}^\dagger p_+ R - R^\dagger p_{-}^\dagger p_- R= \left(p_+ R\right)^\dagger \left(p_+ R\right) - \left(p_- R\right)^\dagger \left(p_- R\right)$

Компоненты разложения (то есть - спиноры) $q_\pm^\dagger =R^\dagger p_\pm^\dagger$ повернутого вектора $\u$ лежат в левых идеалах, образованных и $p_{-}$ , а компоненты $q_\pm =p_\pm R$ - в правых.

Таким образом, с точки зрения геометрической алгебры, спинор - это элемент идеала, образованного некоторым проектором.

Я отмечу и еще одно интересное свойство проекторов:

$\frac{1}{2}\left(1 + \v \right)\v= \frac{1}{2}\left(\v + \v^2 \right)= \frac{1}{2}\left(1 + \v \right)$

Проектор, полученный из единичного вектора, умеет поглощать в себя этот вектор. Или наоборот, - производить в любых нужных количествах.

А что там у физиков?

А у физиков своя атмосфера. Они любят странные значки. Проектор $\frac{1}{2}\left(1 + \z\right)$ в алгебре с базисными векторами $\x,\y,\z$ обозначается так:

$\frac{1}{2}\left(1 + \z\right) = \spinup$

Подействуем на него ротором $\cos\frac{\pi}{2} + \x\z\sin\frac{\pi}{2} = \x\z$ , который повернул бы вектор на 180 градусов:

$\frac{1}{2}\left(1 + \z\right)\x\z = -\frac{1}{2}\left(1 + \z\right)\x = \spindown$

Логично, стрелочка перевернулась на 180 градусов.
Повторное действие ожидаемо дает $-\spinup$ :

$\frac{1}{2}\left(1 + \z\right)\x\z \x\z = -\frac{1}{2}\left(1 + \z\right)\x\x\z\z = -\spinup$

Умножение стрелочек на псевдоскаляр $i = \x\y\z$ (для , , и $\forall A:iA = Ai$ ) дает и остальные элементы базиса идеала, образованного проектором $\frac{1}{2}\left(1 + \z\right)$ :

$i \left| \uparrow \right>= \left| \uparrow \right> i= \frac{1}{2}\left(1 + \z\right) i= \frac{1}{2}\left(1 + \z\right) \x\y\z= \frac{1}{2}\left(1 + \z\right) \x\y$

Аналогично:

$i \left| \downarrow \right>= \left| \downarrow \right> i= \frac{1}{2}\left(1 + \z\right) \x\z i= \frac{1}{2}\left(1 + \z\right) \x\z\x\y\z= \frac{1}{2}\left(1 + \z\right) \x\x\y\z\z= \frac{1}{2}\left(1 + \z\right) \y$

Выпишем еще раз, просто чтобы иметь все в одном месте:

$\begin{array}{ll}\frac{1}{2}\left(1 + \z\right) = \left| \uparrow \right> \\\frac{1}{2}\left(1 + \z\right)\x\y = i \left| \uparrow \right> \\-\frac{1}{2}\left(1 + \z\right)\x = \left| \downarrow \right> \\\frac{1}{2}\left(1 + \z\right)\y = i \left| \downarrow \right> \\\end{array}$

Как нетрудно видеть, эти 4 элемента образуют базис в правом идеале, порожденном $\frac{1}{2}\left(1 + \z\right)$ . Ну а псевдоскаляр ведет себя точно так же как обыкновенная мнимая единица. Поэтому любой элемент идеала представим в виде

$\left(\alpha + i\beta\right) \spinup + \left(\gamma + i\delta\right) \spindown$

Нормированные элементы (т.е. такие что $\alpha^2 + \beta^2 + \gamma^2 + \delta^2 = 1$ ) являются проекциями роторов.

Здесь самое время вспомнить о самой первой картинке в этой статье.

Одно из возможных представлений спина "вверх"

$\left(\alpha + i\beta\right) \spinup= \frac{1}{2}\left(1 + \z\right)\left(\alpha + \beta \x\y\z \right)= \frac{1}{2}\left(1 + \z\right)\left(\alpha\z + \beta \x\y \right)$

Именно правая часть $\left(\alpha\z + \beta \x\y \right)$ на ней и изображена, причем здесь $\alpha$ и $\beta$ пробегают всю единичную окружность (физически, частота пробегания определяется массой частицы, но это уже совсем за рамками этой статьи). Состояния вида $\left(\gamma + i\delta\right)\spindown$ при таком подходе выглядят чуть менее интересно:

Одно из возможных представлений спина "вниз"

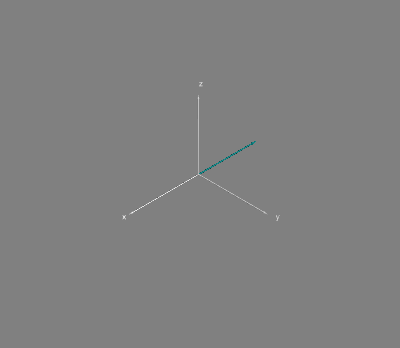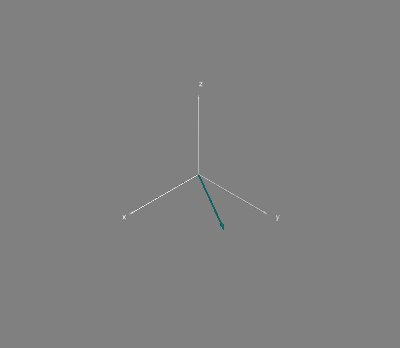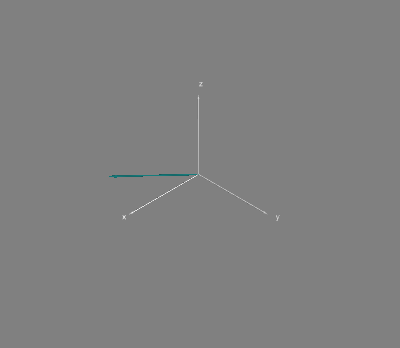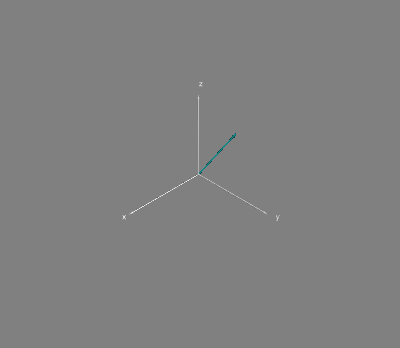
Ну а в общем случае $\left(\frac{1}{2}\left(1 + \z\right)\left(\alpha\z + \beta \x\y - \gamma \x + \delta \y \right)\right)$ состояние частицы может выглядеть как-то так:

Одно из решений уравнения Дирака для стационарной частицы в однородной компактной вселенной

Или, в другом представлении $\left(\frac{1}{2}\left(1 + \z\right)\left(\alpha\z + \beta \x\y - \gamma \z\x + \delta \z\y \right)\right)$ , что абсолютно то же самое благодаря порождению вектора $\z$ проектором, так:

То же самое, альтернативная визуализация

Можно, кстати, провернуть еще один финт ушами, и посмотреть что будет если скоммутировать проектор с ротором:

$\begin{array}{ll}\spinup = \frac{1}{2}\left(1 + \z\right) \\i \spinup = \frac{1}{2}\left(1 + \z\right)\x\y = \x\y \frac{1}{2}\left(1 + \z\right) \\\spindown = -\frac{1}{2}\left(1 + \z\right)\x = -\x\frac{1}{2}\left(1 - \z\right) \\i \spindown = \frac{1}{2}\left(1 + \z\right)\y = \y \frac{1}{2}\left(1 - \z\right)\end{array}$

Оказывается, что в базисные элементы правого идеала, отмеченные стрелочкой $\spinup$ одновременно лежат в левом идеале, образованном $\frac{1}{2}\left(1 + \z\right)$ , а элементы, отмеченные стрелочкой $\spindown$ лежат левом идеале ортогонального ему проектора $\frac{1}{2}\left(1 - \z\right)$ . Насколько я понимаю, именно это различие и получается наблюдать экспериментально, и именно из этого наблюдения происходит сама нотация в виде стрелочек.

Дальше физики говорят, что есть дуальные спиноры, типа $\spinup^\dagger$ . Но, мы с вами уже знаем что это такое. Просто операция обращения, переход между правым и левым идеалами.

Кроме того, у них есть 2-спиноры. Помните разложение $\v = p_{+}^\dagger p_{+} - p_{-}^\dagger p_{-}$ ?
Его можно записать и с помощью (вот черт, не получилось совсем без них!) матриц:

$\v = \begin{bmatrix}p_+^\dagger & -p_-^\dagger\end{bmatrix}\begin{bmatrix}p_+ \\p_-\end{bmatrix}$

Левый множитель здесь - дуальный 2-спинор, правая - обычный. Подумать о том как действуют роторы (а также перестановка множителей, умножение на константы и т.д.) на такую штуку я оставляю читателю.

И даже 4-спиноры. Но сюда я уже влезать не буду, поскольку рассмотрение алгебр, в которых квадрат вектора может быть отрицательным (привет метрике Минковского), выходит за рамки этой статьи. Может быть, в следующий раз.

О спинорах человеческим языком +20