02.07.2023 08:51
xyli0o 24 7100 Источник

Иногда хочется решить задачу просто потому что решение легко проверить, прям сразу для множество вариантов. Взяли список из 25 элементов, отсортировали его, и применили искомую функцию 25 раз, профит. Плюс задачка напоминает обложку тетрадки по арифметике за пятый класс, там где табличка произведений, ну та где находим пятый столбец и седьмой ряд и на пересечений их будет произведение. Там же в табличке видно что 6x6 - это квадрат, а 9x4 это совсем не квадрат (скорее ближе к прямоугольнику) хотя площадь у них равная. Так вот, "литкод" хочет чтобы мы нашли n-ый элемент в данной табличке по возрастанию.

Одно из возможных решений - собрать элементы в список, отсортировать его, взять n-ый элемент, профит (на всякий случай не забываем про алгоритм select_nth_unstable в расте). К сожалению, элементов в табличке очень много, поэтому интереснее собрать только часть элементов. Помедитировав немного над табличкой (https://ru.wikipedia.org/wiki/Таблица_умножения) лучше ее разбить на группы (как показано ниже) и только после собрать и выбрать элемент. Критерий группы - все элементы меньше или равны крайнему правому (см. плиз на рисунке ниже).

1 2 3 4 5
2 4 * * *
3 * * * *
4 * * * *
5 * * * *

-  - - -  -
-  - 6 8 10
-  6 9 * *
-  8 * * *
- 10 * * *

- -  -  -  -
- -  -  -  -
- -  - 12 15
- - 12  * *
- - 15  * *

- - -  -  -
- - -  -  -
- - -  -  -
- - - 16 20
- - - 20 *

- - - -  -
- - - -  -
- - - -  -
- - - -  -
- - - - 25

Принцип разбиения на группы вроде как напоминает https://ru.wikipedia.org/wiki/Гармонический_ряд, что вроде неплохой знак :) Так, теперь само разбиение: первый ряд из таблички берем целиком, от второго ряда первую половину, третьего - первую треть и т.д. Для второй итерации - вторую половину второго ряда, далее вторую треть третьего, вторую четверть и т.д. То есть если табличка 10x10, для третьего ряда разбиение есть 3,3,4 по элементам для первой, второй и третьей итерации; для четвертого ряда 2,3,2,3 - для четырех итераций соответственно. Еще момент, для каждой итерации кол-во элементов в группе различно. Например для таблички из рисунка выше в первой итерации 5+2+1+1+1=10 элементов, для второй итерации 3+2+1+1=7.

Чтобы найти 20-й элемент в табличке 5x5, мы берем третью группу, так как в первой группе 10 элементов, во второй - 7, третьей - 4; то есть мы складываем дельты, пока сумма не превысит искомый индекс. Звучит OK, но работает медленно - потому что дельта разная и, как следствие, линейный поиск.

Для бинарного поиска неплохо бы перейти от дельт 10,7,4,3,1 к полусуммам 10, 17, 21, 24, 25. Каждый ряд таблички участвует в нескольких группах, например третий ряд - в первых трех группах, четвертый - в четырех группах. Для третьго ряда разбиение 1,2,2 по кол-ву элементов, для четвертого 1,1,1,2. Немного детальнее - для таблички 5x5 и третьего ряда мы пять делим на три и остаток от деления переносим на следующий шаг. Чтобы перейти к полусуммам, на каждый шаг деления на три давайте пять умножим на i (номер шага), то есть получим (5/3, 10/3, 15/3 -> 1,3,5 то есть наши полусуммы. Еще раз для сравнения было->стало: (5/3, {5+r}/3, {5+r2}/3) или 1,2,2 -> (5/3, 10/3, 15/3) или 1,3,5. Собираем полусуммы рядов в группу, профит. Остальное - детали реализации.

Наверно, основной поинт статьи в переходе от линейного к бинарному поиску. На всякий случай, для миллиарда элементов binary search делает 30 проверок, linear search примерно 2**30. Спасибо за внимание.

Комментарии (24)


  1. nronnie
    02.07.2023 10:08
    #25709600
    +17

    Так а в чем исходная задача-то? Из вашего потока сознания вообще непонятно.


    1. just-a-dev
      02.07.2023 10:08
      #25709612
      +1

      Я отреверсинжинирил из его потока сознания так: дана матрица KxM заполненная числами по правилам таблицы умножения. Нужно найти N е число в матрице в порядке возрастания


      1. nronnie
        02.07.2023 10:08
        #25709670
        +1

        Всё еще непонятно. Что значит "по правилам таблицы умножения"? M[k, m] = k * m? Мне правда интересно, потому сам задачи на алгоритмы люблю.


        1. just-a-dev
          02.07.2023 10:08
          #25709786

          Ну скорее M(k, m)=(k+1)*(m+1), если индексация с 0


      1. nronnie
        02.07.2023 10:08
        #25709700

        Если речь идет о том, чтобы найти N-е в массиве чисел, то её без сортировки можно решить за линейное время O(размер массива).


        1. Alexandroppolus
          02.07.2023 10:08
          #25709828

          Ну здесь-то определенная сортировка присутствует, и можно намного быстрее. Автор, кажется, поставил амбициозную планку O(ln N), а взял ли её - пока не совсем понятно.


    1. xyli0o Автор
      02.07.2023 10:08
      #25709848
      +1

      https://leetcode.com/problems/kth-smallest-number-in-multiplication-table/


      1. nronnie
        02.07.2023 10:08
        #25709854

        Ну вот, достаточно было ссылку дать, и сразу стало все понятно. Ок, интересно, подумаю сам на досуге.


  1. pfemidi
    02.07.2023 10:08
    #25709686
    +9

    Я вообще ничего не понял. Где задача? Какая задача? Кроме непонятного набора потока слов я тут вообще ничего не увидел.


  1. ioncorpse
    02.07.2023 10:08
    #25710300

    Вопрос "не как?", вопрос "зачем?".


  1. vadimr
    02.07.2023 10:08
    #25710402
    +2

    Очевидно, что, если не учитывать повторений чисел в списке, то позиция k-го числа в бесконечной таблице умножения равна k. Пока не будем рассматривать ограничения, вызванные тем, что m < k и n < k, а обратим внимание, что количество повторений каждого числа в таблице равно количеству его двучленных факторизаций, то есть разбиений на множители (не обязательно простые). В огромной (m >= k и n >= k) таблице умножения для решения нашей задачи надо искать сумму ряда S(z) = F(1)+F(2)+...F(z), где F(x) – количество двучленных факторизаций натурального числа x, а z – минимальное натуральное число, для которого S(z) >= k. Двучленные факторизации, в свою очередь, являются подмножеством всех возможных факторизаций.

    Известно, что для поиска факторизаций перебор делителей не является наиболее эффективным алгоритмом. Поэтому, если поставлена задача найти наиболее эффективный алгоритм (а точные требования к решению непонятны даже из постановки на литкоде, не то, что из статьи на хабре), то надо копать в сторону именно продвинутой факторизации, а это достаточно серьёзная математика – алгоритм Полларда, вот это всё. Тут вообще не нужен поиск в массиве, а нужен грамотный перебор факторизаций (с учётом добавочных граничных условий по m и n и с учётом двучленности). Лишние значения, среди которых надо было бы искать, при переборе просто не будут образовываться.

    Сложность перебора делителей составляет O(sqrt(N)*log(N)^2), в то время как сложность алгоритма Полларда составляет O(N^(1/4)). Различие для больших N грандиозно, поэтому предложенный автором алгоритм в любом случае очень неэффективен.

    Решение легко проверить в смысле найденной величины, но нифига не легко проверить в смысле эффективности. Навскидку, построение наиболее эффективного алгоритма – это не решённая математическая проблема. А даже приблизительно эффективный алгоритм вспотеешь программировать. По сложности и бессмысленности задачи, думаю, это уровень международной олимпиады по программированию. На литкоде не зря стоит уровень Hard.

    Поверхностный взгляд на решения на литкоде показывает, что там вроде бы как никто даже и не пытался думать в эту сторону, и предлагаются простые неэффективные решения с бинарным поиском среди перебора делителей.


    1. vadimr
      02.07.2023 10:08
      #25710500

      Фактически, наивный поиск k методом перебора делителей имеет факториальную сложность. Действительно, если число z раскладывается на p простых делителей, то в таблице умножения оно встретится в количестве (p-1)!/2 раз. Для решения задачи нам совершенно не нужно вычислять и просматривать все эти (p-1)!/2разбиений. Достаточно того, что мы знаем их количество.


  1. Didntread
    02.07.2023 10:08
    #25710518

    правильно ли я понимаю, что эта задача, но с бесконечной таблицей, решается за O(1): надо из k вычесть максимальную сумму арифметической прогрессии, чтобы узнать диагональ. Неужели с конечной такие сложности нужны?


    1. vadimr
      02.07.2023 10:08
      #25710578

      Знание диагонали нам не поможет.


      1. Didntread
        02.07.2023 10:08
        #25710656

        k=(1+n)n/2

        допустим k=16, тогда n=5.18

        округляем n к меньшему, (1+n)n/2=15 Получаем, что наше число первое (16-15) на 6й диагонали, т.е. 6


        1. vadimr
          02.07.2023 10:08
          #25710668

          Я не понял, как Вы считаете, но для k=16 ответ 7:

          1 2 2 3 3 4 4 4 5 5 6 6 6 6 7 7

          Из общих соображений, тут так просто не разрулить, потому что повторитель числа зависит от его простоты. Число повторяется 2 раза тогда и только тогда, когда оно простое, а это вычислительно сложно проверяется.


          1. Didntread
            02.07.2023 10:08
            #25710672

            у вас таблица сдвинута, по ссылке на литкод 12233...


            1. vadimr
              02.07.2023 10:08
              #25710678

              Да, поправил, но это в данном случае неважно, следующая тоже 7.

              В связи с этим и 1 - единственное простое, которое повторяется 1 раз.


              1. Didntread
                02.07.2023 10:08
                #25710706

                чтобы узнать позицию по диагонал: если разница между k и суммой прогрессии четное, то верхняя часть, если не четная то нижняя. Так мы узнаем x и y, перемножив получим ответ.


                1. vadimr
                  02.07.2023 10:08
                  #25710718

                  Число же может разлагаться на два множителя сколь угодно большим количеством способов, не обязательно только на x и y. Это яснее на больших числах.


              1. Didntread
                02.07.2023 10:08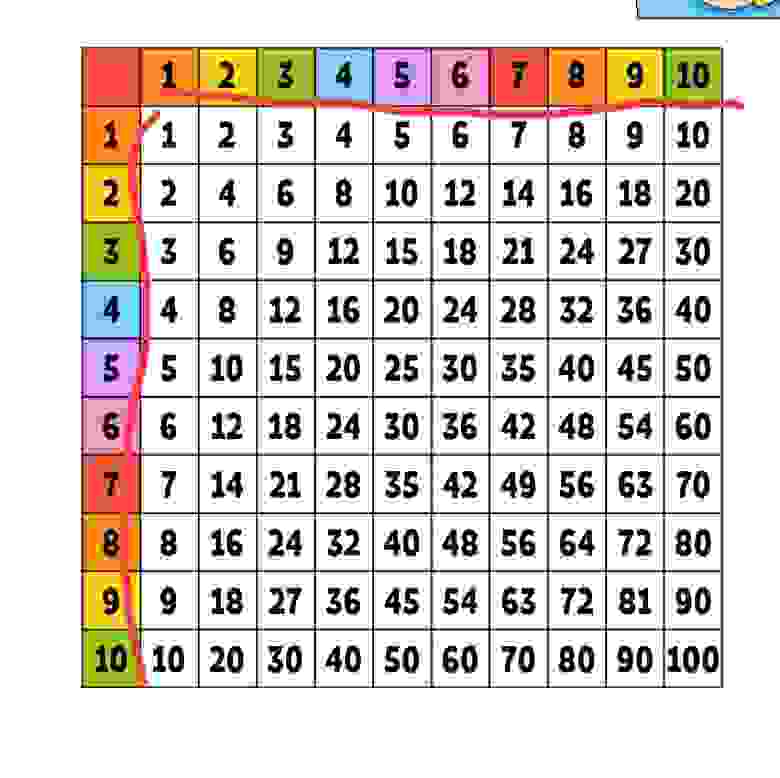
                #25710720


                1. vadimr
                  02.07.2023 10:08
                  #25710742

                  Большие различия, которые вы не подобьёте округлением, начинают появляться с числа 30, являющемся минимальным произведением 4 простых. А для него надо рисовать таблицу умножения до 30x30.


                1. gybson_63
                  02.07.2023 10:08
                  #25717446

                  Если из каждого ряда взять 1/n первых элементов (n номер ряда), то они будут меньше всех остальных в таблице. Если взять за сумму ряда порядковый номер нужного элемента K, то можно посчитать множитель из первого ряда, взяв который сумма ряда будет K (он может оказаться и больше, чем в таблице). Но в целых числах это всё считается не прям сразу и погрешность большая на малых числах.

                  Но как отправная точка может сгодится кому. Как асимптоматика в принципе вообще очень хорошо должно быть


      1. Didntread
        02.07.2023 10:08
        #25710784

        да, похоже вы правы.