В этой статье мы узнаем как выглядит матрица, как ее задать в Python и базовые операции с ними.

Для начала запишем систему уравнений в общем виде:

Коэффициенты при неизвестных составляют прямоугольную таблицу:

называемую матрицей из m строк и n столбцов.

Небольшая справка по определениям:

1) Если система уравнений не имеет ни одного решения, то она называется несовместной.

2) Если система обладает решениями, то она является совместной.

3) Если система имеет единственное решение, то она является определенной и неопределенной, если решений больше, чем одно.

Создание матриц на Python

Для более удобной работы с матрицами лучше всего использовать Jupyter Notebook, который вы можете использовать, скачав Anaconda. Jupyter имеет несколько основных преимуществ: 1) Многие библиотеки уже установлены, 2) Блочный код, т.е. вы можете проверить его по частям, 3) Довольно простое создание и использование собственных библиотек.

Если вам не понравиться Jyputer, вы можете перейти на Google Colab.

Способы создания матриц:

Для работы с матрицами в Python в основном используется 2 библиотеки: Sympy и Nympy.

Рассмотрим базовые методы для Sympy:

Дана матрица:

from sympy import *
А = Matrix([[-3, 9, 2,4,0], [1,4,-1,3,-1], [0,2,-2,4,2], [3,1,0,-2,3]])

Чтобы узнать размерность матрицы воспользуемся методом shape() (т.е. узнаем сколько столбцов и строчек в этой матрице)

shape(A)

Также можно взять отдельную строчку или столбец(нумерация работает также, как индексы в Python):

A.row(0)
A.col(-1)

Также вы можете удалять строчки или столбцы с помощью команд row_del() и col_del()

A.col_del(0)
A.row_del(1)

Можно еще и добавлять строки и столбцы, указывая на какое место вы бы хотели их поставить по индексу

M = Matrix([[1, 2], [-2, 0]])
M = M.row_insert(1, Matrix([[0, 4]]))
M = M.col_insert(0, Matrix([1, -2, 3]))

Также в Sympy есть отдельные методы для некоторых типов матриц:

1) Нулевая матрица

zeros(3,2)

2) Матрица, состоящая из единиц

ones(3,2)

3) Единичная матрица(квадратичная матрица, у которой на главной диагонали единицы, а остальные нули)

eye(4)

Также можно задать матрицу по главной диагонали:

diag(1,2,3)

Для продвинутых ребят можно сделать такие прикольные штуки

diag(-1, ones(2,2), Matrix([5,7,5]))l

Рассмотрим задание матрицы в Numpy

import numpy as np

C = np.array([[1,2,3], [4,5,6], [7,8,9]])
M = np.matrix([[1,2,3], [4,5,6], [7,8, 9]])

Ну и совсем странный способ

H = np.matrix('1,2,3;4,5,6;7,8,9')

В Numpy методы для быстрого создания матрицы практически такие же

1) Матрица из нулей

np.zeros((2,3))

2) Матрица из единиц

np.ones((2,3))

3) Единичная матрица

np.eye(3)

И создание матрицы через главную диагональ

np.diag([1,2,3])

Также в этой статья я хочу рассмотреть основные математические операции с матрицами(сложение, вычитание, умножение)

Сложение

Складывать и вычитать матрицы можно только одинаковой размерности - т.е. матрицы, у которых совпадает кол-во строк и строчек

На Sympy:

A = Matrix([[1,2,3], [4,5,6], [7,8,9]])
B = Matrix([[1,2,3], [4,5,6], [7,8,9]])
print(A+B)

На Numpy:

A = np.array([[1,2,3], [4,5,6], [7,8,9]])
B = np.array([[1,2,3], [4,5,6], [7,8,9]])
print(A+B)

Свойства сложения матриц

1) A+B=B+A(коммутативность)

2) A+(B+C) = (A+B)+C(ассоциативность)

3) Для любой матрицы A существует противоположная ей (-A), такая что их сумма является нулевой матрицей

Вычитание работает в Python по тем же правилам.

Умножение матрицы на число происходит самым интуитивно понятным образом: каждый элемент матрицы домножается на число

А вот перемножение матриц является более сложной операцией

Примечание:

Перемножить можно только те матрицы, если число столбцов матрицы A равно числу строк матрицы B. Если матрица A имеет размер (m*n), а матрица B имеет размер(k*n), то полученная матрица будет (m*n).

Пример

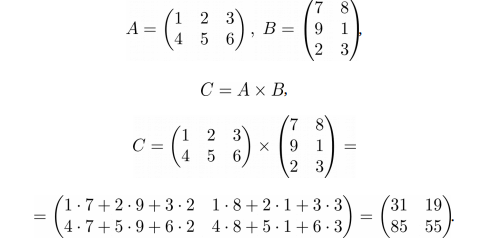
В Sympy это делается через простую операцию умножения

A = Matrix([[1,2,3], [4,5,6]])
B = Matrix([[7,8], [9, 1], [2,3]])
C = A*B

B Numpy это делается череp операцию dot():

A = np.array([[1,2,3], [4,5,6]])
B = np.array([[7,8], [9, 1], [2,3]])
C = A.dot(B)
print(C)

На этом сегодня все. В следующей статье рассмотрим решение систем линейных уравнений, методы Гаусса и Жордана, построение через разложение и нахождение определителя матрицы. Пишите, что еще хотите узнать в моем разборе. Для личного общения со мной: https://t.me/Nikotineaddiction