Теорема о четырех цветах — это математический вопрос, который возник еще в 19 веке. Он заключается в том, можно ли раскрасить любую карту, используя только четыре цвета, таким образом, чтобы ни одна из двух соседних областей не имела одинакового цвета. В этом материале мы расскажем, у кого впервые возник этот вопрос, причем тут теория графов, кто и как пытался доказать эту теорему и что из этого вышло.

Появление теоремы о четырех цветах и ее суть

Первоначально вопросом четырех цветов заинтересовался студент Фредерик Гатри, который изучал карту графств Англии. Гатри заметил, что для того, чтобы два соседних графства были разных цветов, необходимо всего четыре цвета. Это наблюдение заставило его задаться вопросом, возможно ли применить этот принцип к любой карте, будь то весь мир, страна или группа островов.

На первый взгляд это может показаться простым вопросом. Однако эта проблема вызвала многочисленные математические исследования и дискуссии, которые продолжаются уже более века. Ее решение потребовало математического творчества и вычислительных возможностей современных компьютеров и стало одним из важнейших в теории графов.

Теория графов в контексте теоремы о четырех цветах 

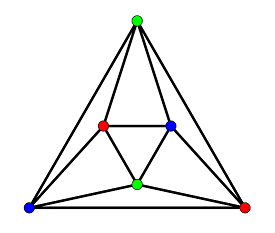
Граф — это набор точек (вершины) и линий (ребра), которые соединяют их. Теория графов — это раздел математики, который изучает графы, их свойства и следующие вопросы:

• сколько ребер нужно, чтобы соединить все вершины;

• существует ли способ путешествовать по ребрам и посещать каждую вершину только один раз;

• какой кратчайший путь от одной вершины к другой.

В контексте теоремы о четырех цветах каждый регион карты представляется как вершина графа, а между вершинами проводятся ребра, которые представляют регионы, у которых есть общая граница.

Таким образом, задача раскраски карты превращается в задачу раскраски графа: нужно раскрасить вершины так, чтобы соседние регионы были разных цветов. Хроматическим числом графа называют минимальное число цветов, которыми можно правильно раскрасить вершины графа.

Графы, полученные на картах, просты, так как в них нет ребер, которые начинаются и заканчиваются в одной и той же вершине (петли), и каждая пара вершин может быть соединена только одним ребром. Граф является планарным, если его возможно нарисовать так, чтобы ни одно ребро не пересекалось.

Доказательства теоремы о четырех цветах

Первая попытка доказать теорему о четырех цветах была предпринята юристом Альфредом Кемпе в 1879 году. Ниже мы подготовили его набросок аргументации, которая изложена в современных терминах с использованием графов вместо карт.

Альфред заметил, что для графа с одной вершиной необходим только один цвет. Затем он использовал аргумент, что для графа с двумя вершинами можно использовать не более четырех цветов, затем с тремя вершинами и так далее.

Предположим, что можно раскрасить все простые планарные графы с n вершинами не более чем четырьмя цветами — это тривиально для n меньше 5. Теперь рассмотрим граф с n+1 вершинами. Как показать, что и она будет раскрашиваться не более чем в четыре цвета?

С помощью тщательного подсчета Кемпе показал, что каждый простой планарный граф должен содержать хотя бы одну вершину с не более чем пятью соседями. С учетом всех вариантов это означает, что каждый возможный граф, построенный на основе карты, содержит одну из шести специальных конфигураций вершин.

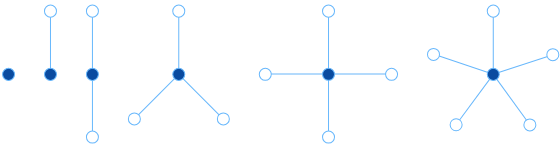
Теперь посмотрим на вершины, соседние с удаленной. Если они имеют три или менее цветов, то мы можем раскрасить удаленную вершину одним из оставшихся цветов.

Мы только что показали, что граф с n+1 вершинами может быть раскрашен четырьмя цветами. Если соседние вершины включают все четыре цвета, то Кемпе придумал  метод перекраски некоторых вершин, чтобы освободить цвет для удаленной вершины, и снова доказал, что для графа с n+1 вершиной требуется всего четыре цвета.

В 1890 году математик Перси Хоуд выявил случай, в котором метод Кемпе не сработал. Несмотря на неудачу, работа Хоуда доказала, что любая карта может быть раскрашена пятью или меньшим количеством цветов. Он также расширил задачу на карты, нарисованные на более сложных поверхностях, и доказал, что для карты на пончике с g отверстиями может потребоваться 12(7+√1+48g) цветов.

Но даже когда была доказана теорема Хивуда для общих поверхностей, проблема четырех красок осталась нерешенной.

Компьютерные вычисления и консерватизм математического сообщества

В 1976 году Вольфганг Хакен и Кеннет Аппель при содействии Джона Коха сообщили о доказательстве теоремы. Их подход заключался в разбиении шести частных случаев Кемпе на 1936 подслучаев, каждый из которых проверял компьютер.

На конференции в 1976 году, через 124 года после постановки проблемы четырех цветов, реакция в зале была неоднозначной. «Я ожидал, что аудитория разразится бурными овациями, но вместо этого они ответили вежливыми аплодисментами», — написал Дон Альберс, который присутствовал на выступлении. Возможно, это произошло потому, что вместо того, чтобы приводить аргументы на бумаге, команда в большей степени опиралась на вычисления компьютера.

Математическое сообщество с неохотой приняло результаты. Ученые не были готовы отдать логические рассуждения машине и считали, что доказательство должно быть понятным и проверяемым исключительно человеком. Консерватизм и нежелание принимать достижения, которые позволяют экономить время, не были чем-то новым.

В 17 веке аналогичное возмущение вызвало использование математиками новых алгебраических методов для решения задач геометрии. Аналогичная ситуация может повториться и с машинным обучением. Сейчас не ясно, примут ли математики теорему, открытую и доказанную непрозрачным алгоритмом.

Доказательство четырехцветной задачи было только началом компьютерной революции в математике. В 1998 году Томас Хейлз с помощью компьютера доказал  гипотезу Иоганна Кеплера. В ней говорилось, что наиболее эффективный способ укладки сфер — тот, который обычно используют для укладки апельсинов в продуктовом магазине.

В июле 2010 года исследователям с помощью компьютера удалось найти «алгоритм Бога». Оказалось, что максимальное количество поворотов, которое необходимо для решения кубика Рубика — это 20 поворотов граней или 26, если половину поворотов считать за два.

Вопросы цветности непланарных графов

Работа Хоуда с поверхностями показала возможность исследования хроматичности непланарных графов. Действительно, хроматическое число конкретного графа не зависит от поверхности, на которой нарисована соответствующая карта.

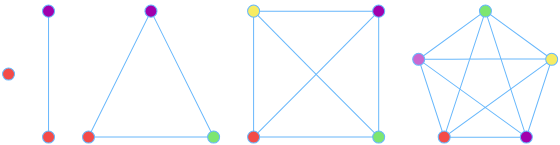
Например, граф, в котором каждая вершина соединена с каждой другой вершиной, называется полным графом, а хроматическое число полного графа с n вершинами равно n. Таким образом, если большой граф содержит полный граф с n вершинами, то известно, что хроматическое число большого графа не меньше n.

Применение теории графов в других областях

Помимо картографии, теорию графов используют и в других областях. Например, в информатике Интернет можно представить как граф, сайты — как вершины, а ссылки — как ребра. В биологии графы могут представлять собой сети взаимодействующих генов или белков. В социальных науках графы — это сети друзей или профессиональных связей.

Судоку — это замаскированная проблема раскраски графов. Каждую клетку можно рассмотреть как вершину, а девять цифр — как цвета.

Доказать оригинальную теорему пока никому не удалось

Несмотря на попытки математиков доказать оригинальную теорему четырех цветов без помощи компьютера, сделать это до сих пор никому не удалось. Даже сегодня ученые продолжают предлагать новые доказательства, но обычно, как и работа Кемпе, они содержат ошибки.