Описан алгоритм построения кусочно-постоянной зависимости переменной от взвешенной суммы
, минимизирующей сумму квадратов отклонений
от средних значений на диапазонах изменения величины
.
Мотивация
Задача восстановления зависимости некоторой величины от ряда признаков распространена в анализе данных. Кусочно-постоянная регрессия будет полезна, если требуется выделить характерные диапазоны изменения интегрального признака (взвешенной суммы признаков), чтобы рассмотреть отдельно точки, принадлежащие этим диапазонам. Таким образом, получив информацию о распределении точек внутри каждого из них и исследовав зависимость от прочих факторов, можно сделать выводы о сегментированных данных.
Формальная постановка
Входные данные - множество точек и количество диапазонов
.
Определим целевую функцию
зависящую от диапазонов изменения величины , где в
-й диапазон попадают точки с индексами из множества
, и
- это среднее арифметическое значений
, где
.
Требуется оптимальным образом разбить точки
на диапазоны и найти такое разбиение, при котором
минимально.
Требуется найти такие весовые коэффициенты
, при которых указанный минимум, найденный при заданных
, будет наименьшим.
Алгоритм
Первая задача решается методом динамического программирования. Упорядочим точки по возрастанию координаты
. Выделим подзадачи с параметрами
- разбить точки с индексами от
до
на
диапазонов. Зная решение подзадачи
, пытаемся улучшить решение подзадач
для
, заполняя матрицы
- минимум целевой функции,
- размер последнего диапазона в оптимальном разбиении. Окончательно
будет равно минимуму целевой функции, а само разбиение можно будет восстановить по значениям
.
Вторая задача является дискретной, и поскольку значение целевой функции зависит только от порядка следования точек , то в зависимости от аргументов
целевая функция носит кусочно-постоянный характер, поэтому стандартные нелинейные оптимизаторы здесь неприменимы.
Для подбора коэффициентов предлагается следующий итерационный метод. В качестве начального приближения выбираются коэффициенты
, вычисленные из множественной линейной регрессии. Затем на каждой итерации алгоритма будем вычислять оптимальное разбиение при найденных весовых коэффициентах, после чего зафиксируем размеры диапазонов разбиения и оптимизируем весовые коэффициенты при заданных размерах диапазонов.
Таким образом, приходим к следующей подзадаче:
Требуется найти коэффициенты
, при которых целевая функция будет минимальна среди всех разбиений на диапазоны, имеющих заданный размер.
Эту задачу предлагается решать наискорейшим покоординатным спуском по каждой переменной . Итак, определим функции
. Требуется найти такое
, при котором значение целевой функции
(при заданных размерах диапазонов), вычисленный для точек
, окажется наименьшим.
Последняя задача относится к вычислительной геометрии и может быть решена по-разному. Наивный метод состоит в переборе всех точек пересечения графиков функций и
и вычислении для каждой точки значения целевой функции
с последующим выбором наилучшего
. Сложность алгоритма составит
.
Другой способ похож на алгоритм заворачивания подарка для выпуклой оболочки. Этот метод строит графики порядковых статистик множеств по нарастанию
. Нас интересует всё множество событий, когда при постепенном увеличении
содержимое диапазонов изменится вследствие перестановки точки на границе диапазонов с точкой из соседнего диапазона. Поскольку таких событий не более
, то сложность алгоритма составит
.
И наконец, можно, как в алгоритме Грэхема, упорядочить все точки по возрастанию координаты и добавлять точки по одной, обновляя каждый раз решение подзадачи построения графиков порядковых статистик в зависимости от
для уже рассмотренных точек. Поскольку
порядковых статистик можно построить за время
, то нахождение минимума целевой функции займет такое же время.
Таким образом, чтобы оптимизировать значение целевой функции при заданных размерах диапазонов по коэффициентам
, будем оптимизировать по очереди коэффициент в каждом слагаемом в наборе точек
, беря остальные слагаемые в этой сумме в качестве свободного члена
.
Комментарии (8)

spidersarecute
01.09.2023 21:09+1Не понял постановку задачи...
Описан алгоритм построения кусочно-постоянной зависимости переменной
от взвешенной суммы
Может быть, в формуле должно быть y = w1 x1 + w2 x2 ... ? И непонятно, что такое p.
Требуется найти такие весовые коэффициенты
, при которых указанный минимум, найденный при заданных
, будет наименьшим.
Здесь тоже не понял. У вас в формулу для J коэффициенты wk никак не входят.

lapkin25 Автор
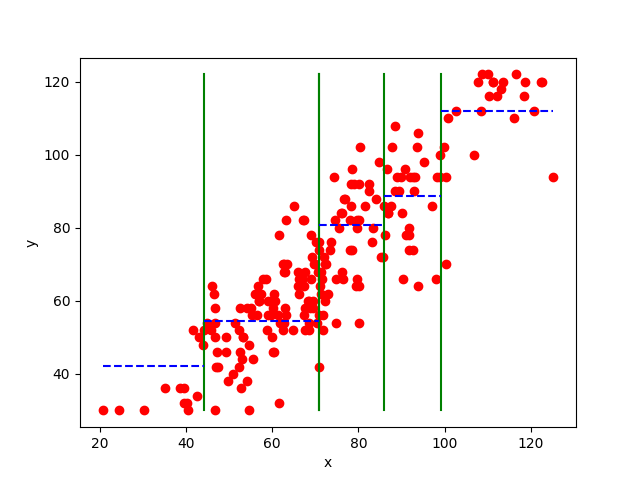
01.09.2023 21:09p - это число признаков (независимых переменных), через x обозначена взвешенная сумма координат x_k. На рисунке по горизонтальной оси отложена взвешенная сумма, по вертикальной - зависимая переменная. Ищем зависимость вида y = f(x), для этого промежуток изменения величины x разбивается на интервалы. Далее можно анализировать распределение точек внутри каждого интервала в отдельности - например, как точки каждого интервала зависят от дополнительных факторов z1, z2, ... В формулу для J коэффициенты w_k входят за счет того, что I_k - это диапазон - возможность объединения значений x в диапазоны зависит от их порядка, а порядок следования взвешенных сумм координат каждой точки зависит от коэффициентов w_k.

spidersarecute
01.09.2023 21:09+1Ищем зависимость вида y = f(x), для этого промежуток изменения величины x разбивается на интервалы
А, то есть мы сначала для каждой точки вычисляем x, а потом уже на основании этого x делим на интервалы... А вы не рассматривали использование деревьев решений? То есть, деревьями разбить входные точки на группы.

lapkin25 Автор
01.09.2023 21:09Как я понимаю, деревья могут применяться для многомерных данных. Здесь мы исходим из интегрального показателя, который вычисляется как взвешенная сумма. Признаков больше 30, и выборка не слишком большая, чтобы пытаться объяснять зависимость слишком громоздкой моделью. Тут идея анализа в том, чтобы сгруппировать данные по какому-то критерию. В дереве этих критериев будет множество, и, хотя оно может подстроиться под нашу выборку, содержательную информацию, которую дают обычные статистики типа среднего, дисперсии, взятые отдельно по каждой группе, будет получить затруднительно.

120gramm
01.09.2023 21:09Юлий, какое практическое применение данной регрессии?

lapkin25 Автор
01.09.2023 21:09Такое же, как и у любой другой обобщенной линейной модели. Здесь каждый диапазон изменения интегрального признака (взвешенной суммы) - это своего рода кластер. А точки, относящиеся к каждому кластеру, можно изучать по отдельности.

mikko_kukkanen
Почему кусочно-постоянная, а не, например, кусочно-линейная? Или "криволинейная" типа кривых безье?
lapkin25 Автор
Да, кусочно-линейная тоже рассматривается часто. Но если взять для примера данные, представленные на рисунке, то видно, что параметр наклона внутри каждого диапазона несущественен за счет разброса точек по игреку.