Привет, уважаемые читатели!

Одной из ключевых задач при работе с данными является уменьшение размерности данных, чтобы улучшить их интерпретируемость, ускорить алгоритмы обучения машин и, в конечном итоге, повысить качество решений. Сегодня мы поговорим о методе, который считается одним из наиболее мощных инструментов в арсенале данных разработчиков — методе главных компонент, или PCA (Principal Component Analysis).

PCA — это статистический метод, который позволяет сократить размерность данных, сохраняя при этом наибольшее количество информации. Он основан на линейной алгебре и математической статистике, и представляет собой мощный инструмент для анализа многомерных данных. Главная идея PCA заключается в том, чтобы найти новые признаки, называемые главными компонентами, которые максимально коррелируют с исходными данными.

На практике, PCA может использоваться для различных целей, включая снижение размерности для визуализации данных, удаление шума из данных, улучшение производительности моделей машинного обучения и многое другое.

Несколько причин, почему PCA стоит внимания:

1. Улучшение визуализации данных: Снижение размерности позволяет отобразить данные в двумерном или трехмерном пространстве, что облегчает визуальное исследование и анализ данных.

2. Сокращение вычислительной сложности: Уменьшение размерности может значительно сократить количество признаков, что приводит к ускорению обучения моделей машинного обучения и снижению потребления ресурсов.

3. Улучшение качества моделей: Многие алгоритмы машинного обучения могут страдать от проклятия размерности. PCA может помочь уменьшить размерность данных, сохраняя при этом важные характеристики, что приводит к лучшей производительности моделей.

4. Поиск скрытых закономерностей: PCA может помочь выявить скрытые зависимости между признаками и их влияние на данные.

Принцип работы метода главных компонент (PCA)

В основе PCA лежит идея нахождения новых признаков, называемых главными компонентами, которые максимально коррелируют с исходными данными и при этом ортогональны друг другу. Эти главные компоненты формируют новый базис в пространстве признаков, исключая лишнюю информацию и снижая размерность.

Представим, что у нас есть матрица данных X, где каждая строка представляет собой наблюдение, а каждый столбец — признак. Наша цель — найти такие новые признаки (главные компоненты), которые наилучшим образом описывают изменчивость данных. Главные компоненты вычисляются как собственные векторы ковариационной матрицы данных.

Ковариационная матрица позволяет нам измерить, как признаки взаимосвязаны друг с другом. Ковариация между двумя признаками показывает, насколько они меняются вместе. Если ковариация положительна, это означает, что признаки увеличиваются вместе, в то время как отрицательная ковариация указывает на обратное изменение. Ковариационная матрица X обычно вычисляется следующим образом:

где:

• C - ковариационная матрица.

• X - матрица данных.

• u - вектор средних значений признаков.

• n - количество наблюдений.

Основные шаги алгоритма PCA:

1. Стандартизация данных: Прежде чем приступить к вычислению главных компонент, важно стандартизировать данные, приводя их к нулевому среднему и единичной дисперсии. Это важно, потому что признаки с разными масштабами могут исказить результаты PCA.

   from sklearn.preprocessing import StandardScaler
   scaler = StandardScaler()
   X_scaled = scaler.fit_transform(X)

2. Вычисление ковариационной матрицы: После стандартизации данных мы вычисляем ковариационную матрицу C.

   cov_matrix = np.cov(X_scaled, rowvar=False)

3. Вычисление собственных векторов и собственных значений: Следующим шагом является вычисление собственных векторов и собственных значений ковариационной матрицы. Это можно сделать с использованием различных библиотек, таких как NumPy.

   eigenvalues, eigenvectors = np.linalg.eig(cov_matrix)

4. Сортировка главных компонент: Главные компоненты сортируются в порядке убывания собственных значений. Это позволяет нам выбрать наиболее информативные компоненты.

5. Проекция данных на главные компоненты: Наконец, мы проецируем исходные данные на новый базис, образованный главными компонентами. Это позволяет нам снизить размерность данных.

   projected_data = X_scaled.dot(eigenvectors[:, :k])

Главные компоненты, полученные на последнем шаге, представляют собой новые признаки, которые можно использовать для анализа или обучения моделей машинного обучения.

Реализация PCA

Пример 1: Улучшение классификации с PCA

В этом примере мы используем библиотеку scikit-learn для применения PCA к набору данных Iris и улучшения классификации с использованием метода опорных векторов (SVM).

from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC

# Загрузка данных
data = load_iris()
X, y = data.data, data.target

# Разделение данных на обучающий и тестовый наборы
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Применение PCA
pca = PCA(n_components=2)
X_train_pca = pca.fit_transform(X_train)
X_test_pca = pca.transform(X_test)

# Обучение SVM на данных после PCA
svm = SVC()
svm.fit(X_train_pca, y_train)

# Оценка производительности модели
accuracy = svm.score(X_test_pca, y_test)
print(f'Accuracy after PCA: {accuracy:.2f}')

Результат:

Accuracy after PCA: 1.00

Пример 2: Ускорение обучения на больших данных

PCA также может быть полезен для ускорения обучения моделей на больших наборах данных. В этом примере мы используем библиотеку TensorFlow и PCA для уменьшения размерности данных перед обучением нейронной сети.

import tensorflow as tf
from sklearn.decomposition import PCA

# Загрузка большого набора данных
(X_train, y_train), (X_test, y_test) = tf.keras.datasets.mnist.load_data()

# Преобразование изображений в векторы
X_train = X_train.reshape(-1, 28 * 28)
X_test = X_test.reshape(-1, 28 * 28)

# Применение PCA
pca = PCA(n_components=50)
X_train_pca = pca.fit_transform(X_train)
X_test_pca = pca.transform(X_test)

# Здесь мы могли бы обучить нейронную сеть на данных X_train_pca

Пример 3: Улучшение кластеризации

PCA также может быть использован для улучшения кластеризации данных. В следующем примере мы используем библиотеку K-means для кластеризации данных и сравниваем результаты до и после применения PCA.

from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt

# Создание синтетических данных
X, y = make_blobs(n_samples=300, centers=4, random_state=42)

# Кластеризация без PCA
kmeans = KMeans(n_clusters=4)
y_pred = kmeans.fit_predict(X)

# Кластеризация после применения PCA
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)
kmeans_pca = KMeans(n_clusters=4)
y_pred_pca = kmeans_pca.fit_predict(X_pca)

# Визуализация результатов
plt.figure(figsize=(12, 6))
plt.subplot(121)
plt.scatter(X[:, 0], X[:, 1], c=y_pred, cmap='viridis')
plt.title("Кластеризация без PCA")
plt.subplot(122)
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y_pred_pca, cmap='viridis')
plt.title("Кластеризация после PCA")
plt.show()

Визуализация данных

Пример 1: Визуализация данных Iris

Мы используем набор данных Iris и применяем PCA для сокращения размерности до 2 компонентов и визуализации данных в двумерном пространстве.

from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt

# Загрузка данных
data = load_iris()
X, y = data.data, data.target

# Применение PCA для сокращения размерности
pca = PCA(n_components=2)
X_reduced = pca.fit_transform(X)

# Визуализация данных
plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=y, cmap='viridis')
plt.title("Визуализация данных Iris с PCA")
plt.xlabel("Главная компонента 1")
plt.ylabel("Главная компонента 2")
plt.show()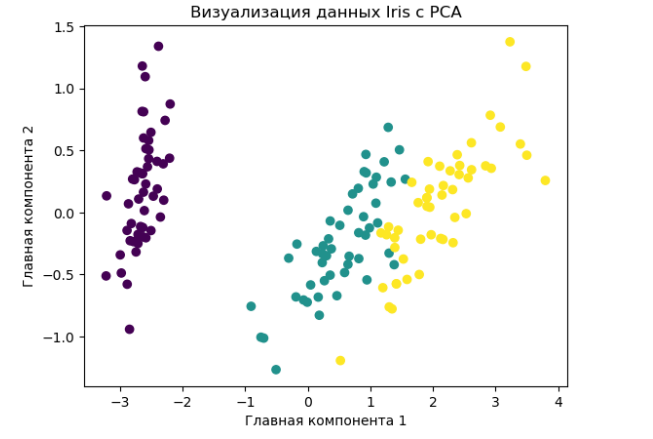

Оценка и интерпретация результатов PCA

При применении PCA одним из важных вопросов является выбор оптимального числа главных компонент. Выбор неправильного числа компонент может привести к потере информации или избыточной сложности модели. Существует несколько методов для оценки оптимального числа компонент, включая метод локтя и метод объясненной дисперсии.

Метод локтя: Этот метод заключается в анализе доли объясненной дисперсии в зависимости от числа компонент. Мы строим график, где по оси X отложено число компонент, а по оси Y - доля объясненной дисперсии. График будет иметь форму локтя, и точка, где снижение доли объясненной дисперсии замедляется, будет указывать на оптимальное число компонент.

Пример кода для метода локтя:

from sklearn.decomposition import PCA
import matplotlib.pyplot as plt

# Создаем экземпляр PCA
pca = PCA()

# Обучаем PCA на данный X
pca.fit(X)

# Строим график объясненной дисперсии
explained_variance_ratio = pca.explained_variance_ratio_
plt.plot(range(1, len(explained_variance_ratio) + 1), explained_variance_ratio, marker='o')
plt.xlabel("Число компонент")
plt.ylabel("Доля объясненной дисперсии")
plt.title("Метод локтя для выбора числа компонент")
plt.show()

Метод объясненной дисперсии: Этот метод заключается в выборе числа компонент так, чтобы доля объясненной дисперсии достигла заданного порога (например, 95% или 99%). Это позволяет сохранить большую часть информации при снижении размерности.

Пример кода для метода объясненной дисперсии:

from sklearn.decomposition import PCA

# Создаем экземпляр PCA с заданным порогом
pca = PCA(0.95)  # сохраняем 95% доли объясненной дисперсии

# Обучаем PCA на данный X
X_reduced = pca.fit_transform(X)

Анализ объясненной дисперсии

После выбора оптимального числа компонент и преобразования данных, важно проанализировать объясненную дисперсию. Это позволяет нам понять, как много информации мы сохранили после снижения размерности.

Пример кода для анализа объясненной дисперсии:

explained_variance_ratio = pca.explained_variance_ratio_
cumulative_variance = explained_variance_ratio.cumsum()

# Визуализация объясненной дисперсии
plt.plot(range(1, len(cumulative_variance) + 1), cumulative_variance, marker='o')
plt.xlabel("Число компонент")
plt.ylabel("Накопленная доля объясненной дисперсии")
plt.title("Анализ объясненной дисперсии")
plt.show()

Интерпретация главных компонент

После снижения размерности и выбора оптимального числа компонент, становится важным понять, что представляют собой эти компоненты. Интерпретация главных компонент может помочь в понимании того, какие признаки они кодируют и какие зависимости между признаками они выделяют.

Для интерпретации главных компонент можно анализировать их веса (собственные векторы) и связанные с ними признаки. Например, в случае анализа изображений, можно выяснить, что первая главная компонента может быть связана с освещенностью изображений, а вторая - с ориентацией объектов.

Пример кода для анализа главных компонент:

# Получение собственных векторов (весов) главных компонент
eigen_vectors = pca.components_

# Визуализация весов для первых нескольких компонент
plt.figure(figsize=(10, 5))
for i in range(5):
    plt.subplot(1, 5, i + 1)
    plt.imshow(eigen_vectors[i].reshape(имя_изображения), cmap='viridis')
    plt.title(f"Главная компонента {i + 1}")
    plt.axis('off')
plt.show()

Интерпретация главных компонент зависит от конкретной задачи и данных, над которыми вы работаете. Это может потребовать дополнительного анализа и доменных знаний для полного понимания значения главных компонент.

Еще примеры использования PCA

Пример 1: Уменьшение размерности медицинских изображений

В медицинской области, особенно в снимках МРТ или КТ, размерность данных может быть огромной, что затрудняет анализ:

# Генерация медицинского датасета
from sklearn.datasets import make_blobs
X, _ = make_blobs(n_samples=300, n_features=3000, random_state=42)

# Применение PCA
from sklearn.decomposition import PCA
pca = PCA(n_components=50)
X_reduced = pca.fit_transform(X)

Пример 2: Улучшение анализа текстовых данных

В анализе текста, особенно при работе с большими корпусами, можно использовать PCA для уменьшения размерности и выделения наиболее важных признаков:

# Генерация текстового датасета
from sklearn.feature_extraction.text import TfidfVectorizer
corpus = ["Это первый документ.", "Это второй документ.", "А это третий документ."]
vectorizer = TfidfVectorizer()
X = vectorizer.fit_transform(corpus)

# Применение PCA
pca = PCA(n_components=2)
X_reduced = pca.fit_transform(X.toarray())

Пример 3: Визуализация данных в больших временных рядах

При работе с временными рядами, PCA может помочь визуализировать изменения в данных, что может быть полезно при анализе финансовых рынков или мониторинге производственных процессов:

# Генерация временного ряда
import numpy as np
time = np.linspace(0, 10, 1000)
signal = np.sin(time) + np.random.normal(0, 0.1, 1000)

# Применение PCA для визуализации
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
X_reduced = pca.fit_transform(signal.reshape(-1, 1))

Пример 4: Улучшение анализа спектральных данных

В анализе спектральных данных, таких как спектрограммы, PCA может помочь выделить важные частоты и уменьшить размерность данных:

# Генерация спектрального датасета
import numpy as np
freqs = np.array([10, 20, 30, 40, 50])
data = np.array([np.sin(2 * np.pi * f * np.linspace(0, 1, 1000)) for f in freqs])

# Применение PCA
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
X_reduced = pca.fit_transform(data.T)

Пример 5: Улучшение обработки геоданных

При работе с геоданными, такими как координаты GPS, PCA может быть использован для уменьшения размерности и выделения наиболее важных факторов:

# Генерация геодатасета
import numpy as np
latitude = np.linspace(37.7749, 37.8049, 1000)
longitude = np.linspace(-122.4194, -122.3894, 1000)
coordinates = np.column_stack((latitude, longitude))

# Применение PCA
from sklearn.decomposition import PCA
pca = PCA(n_components=1)
X_reduced = pca.fit_transform(coordinates)

Заключение

PCA позволяет улучшить анализ данных, сократить вычислительные затраты и выделить наиболее информативные признаки. Важно помнить, что правильный выбор числа компонент и грамотная интерпретация результатов играют ключевую роль в успешном применении PCA в проектах

Статья подготовлена в рамках набора на онлайн-курс «Системный аналитик. Advanced». Чтобы узнать, достаточно ли ваших знаний для прохождения программы курса, пройдите вступительное тестирование.