Аналит, линейка, линал — эти слова ассоциируются скорее с фразой «сдать и забыть», а не с тем, для чего на самом деле нужен замечательный раздел математики под названием линейная алгебра. Давайте попробуем посмотреть на него с разных сторон и разберемся, что же в нем хорошего и почему он так полезен в приложениях.
Часто первое знакомство с линейной алгеброй выглядит как-то так:
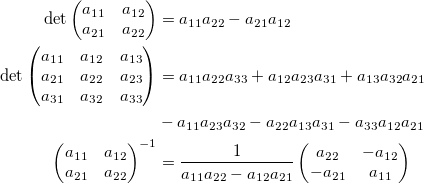
Не очень вдохновляет, правда? Сразу возникает два вопроса: откуда это все взялось и зачем оно нужно.
Начнем с практики
Когда я занимался вычислительной гидродинамикой (CFD), один из коллег говорил: «Мы не решаем уравнения Навье-Стокса. Мы обращаем матрицы.» И действительно, линейная алгебра — «рабочая лошадка» вычислительной математики:

Попробую проиллюстрировать эту связь на более простом примере, чем гидродинамика.
Пусть у нас есть тонкий металлический стержень с закрепленными концами, температура которых поддерживается равной нулю. Начнем греть стержень с помощью распределенного источника тепла, выделяющего q(x) Джоулей в секунду на единицу длины стержня в окрестности точки x. Какая температура t=t(x) установится? Сделаем очень грубый набросок модели. Когда установится равновесие, для каждого отрезка [x-h, x+h] нашего стержня приток тепла от источника должен быть равен сумме потоков тепла через границы отрезка. Если h достаточно мало, то с точностью до констант (в которые войдет h, да простят мне это читатели) это равенство можно записать так:
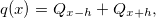
где Qx-h — поток тепла через левую границу, а Qx+h — через правую. Согласно закону Фурье тепловой поток пропорционален разности температур (ведь если нырнуть в бассейн, то в первые секунды будет холоднее всего). Поэтому (с точностью до констант, содержащих h)

Пусть h=1/N. Рассмотрим точки вида xi = i · h, где i=0, 1, 2, ..., N. Они называются сеткой. Тогда переменные ti=t(xi) будут удовлетворять уравнениям
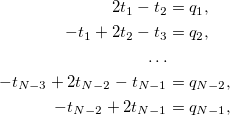
где мы уже учли граничные условия, а qi=q(xi). Ну вот мы и получили систему линейных уравнений:
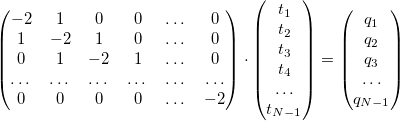
Конкретно эту систему можно решить «в лоб» так называемым методом прогонки, но в настоящих моделях системы становятся сложнее. Тут и приходит на помощь линейная алгебра, которая позволяет
- записать систему в короткой форме A · y = b (вот откуда взялось умножение матриц!);
- понять, имеет ли она решение и единственно ли оно;
- (в данном примере) найти его с помощью простой формулы y = A-1 b, как будто A — число;
- (перетекая в вычислительную математику) построить эффективные численные методы решения систем линейных уравнений.
И это — лишь взгляд на линейную алгебру с точки зрения математического моделирования. А еще есть квантовая механика, статистика и многое другое.
В качестве еще одного примера приведу известную задачу о ссылочном ранжировании страниц одного сайта (или интернета в целом).
Есть N страниц, каждая из которых может содержать ссылки на другие страницы. Требуется определить, какие страницы являются наиболее важными. Как именно измерять «важность» — часть задачи. Мы будем представлять ее количественно в виде неотрицательного числа (веса). Начнем с естественного предположения: чем больше ссылок на данную страницу, тем больше ее вес. В этом подходе есть следующий недостаток: мы не учитываем вес ссылающихся страниц. Логично, что ссылка со страницы, имеющий больший вес, должна иметь большее значение. Эти рассуждения приводят нас к такой модели:
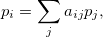
где aij — количество ссылок на i-ую страницу с j-ой, разделенное на общее количество ссылок с j-й страницы. Эту формулу можно читать так: вес i-й страницы равен сумме произведений веса j-й страницы на долю ссылок с j-й страницы на i-ую. Таким образом, мы свели нашу задачу к системе линейных уравнений. Более того, вектор весов p оказывается собственным вектором матрицы A, отвечающим собственному значению 1:
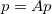
Существование этого вектора (строго говоря, для немного модифицированной матрицы A) гарантируется теоремой Фробениуса-Перрона. А найти его можно методом простых итераций.
Итак, линейная алгебра — это очень универсальный набор идей и инструментов, которые можно применять в самых разных областях. Но бесплатен только сыр в мышеловке, и за универсальность приходится платить: некоторые определения и теоремы могут показаться излишне абстрактными и запутанными. Но это не так: на самом деле, многие абстракции призваны упрощать жизнь, а не усложнять ее. «Если это выглядит как утка, плавает как утка и крякает как утка, то, вероятно, это утка» — по сути абстракция, причем весьма удобная, если к ней привыкнуть. То же самое с линейной алгеброй. Чтобы проиллюстрировать этот момент немного конкретнее, давайте дополним наш «внешний осмотр» кратким обсуждением того, что внутри.
Теперь немного теории
Линейная алгебра изучает векторные пространства и функции, которые отображают одно векторное пространство в другое. В основном рассматриваются линейные функции (удовлетворяющие соотношению f(? · x + ? · y) = ? · f(x) + ? · f(y) для любых чисел ? и ? и любых векторов x и y). Бывают и нелинейные (например, квадратичные формы). Но прежде всего нужно понимать что такое вектор (и векторное пространство). И это не так тривиально, как могло бы показаться.
В учебниках и курсах обычно приводится абстрактное определение из 8 пунктов. Еще иногда говорят, что векторное пространство — это аддитивно записанная абелева группа в которой определено умножение на скаляры, удовлетворяющее 4 аксиомам. Но тем, кто впервые изучает линейную алгебру, это вряд ли поможет разобраться. Гораздо проще рассмотреть несколько конкретных примеров, и увидеть в них аналогию. А определение из 8 пунктов — всего лишь формализация этой аналогии. Поэтому перейдем сразу к примерам.
Знакомые всем со школы направленные отрезки конечно же являются векторами. Множество направленных отрезков — пример векторного пространства. Теперь рассмотрим многочлены. Их можно складывать друг с другом и умножать на числа. Обратите внимание: с точки зрения алгебры эти операции сложения многочленов и умножения многочлена на число работают точно по тем же правилам, что и для направленных отрезков. Например, равенство x+y = y+x (коммутативность) выполняется как для направленных отрезков, так и для многочленов. Поэтому множество многочленов является векторным пространством, а многочлены — векторами.
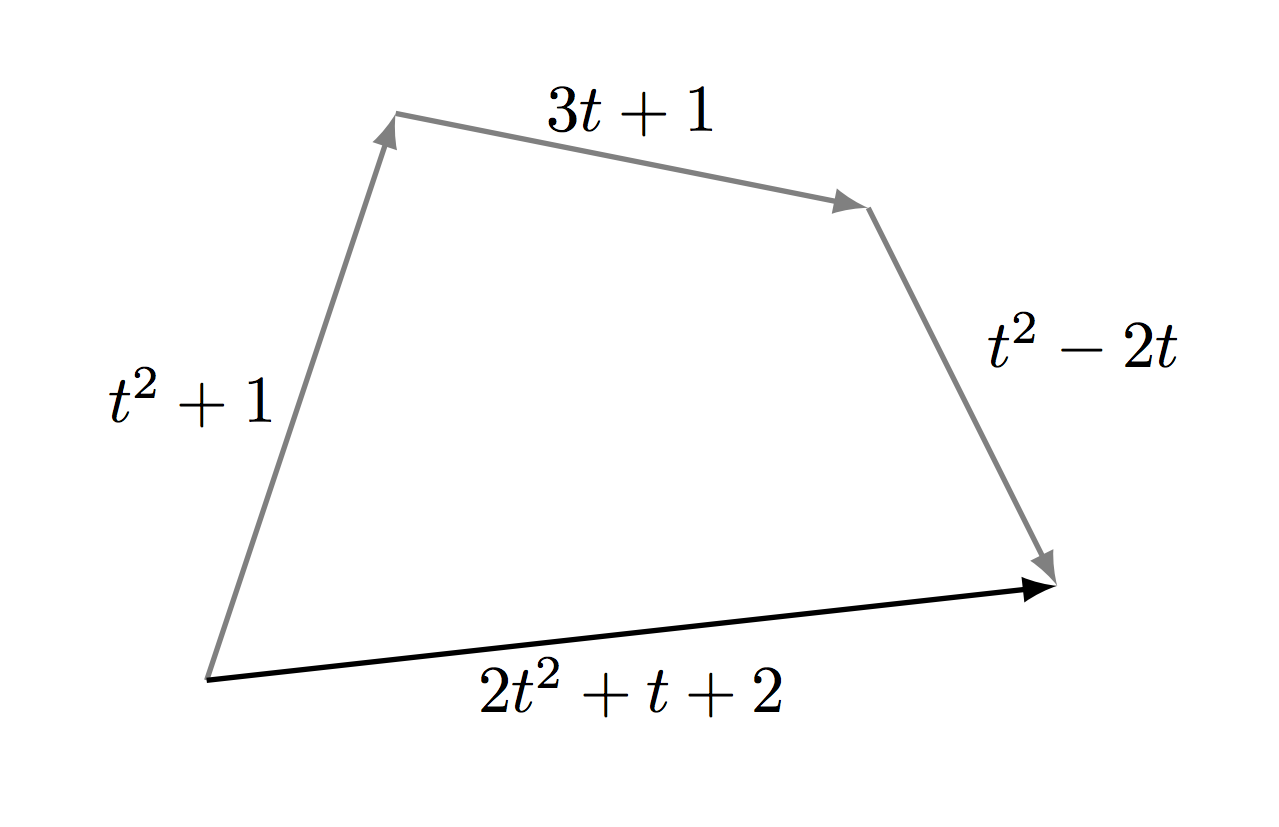
Раз многочлены похожи на направленные отрезки, то у них тоже должны быть координаты. Но как их искать и сколько координат у многочлена? Всем хорошо известно что на плоскости каждый вектор имеет ровно две координаты, а в пространстве — три. Почему это так? И что такое размерность вообще? Линейная алгебра дает ответ на данный вопрос: размерность — это максимальное число линейно независимых векторов. Что значит линейно независимых? Векторы x1, x2, ..., xn называются линейно зависимыми если найдутся числа ?1, ?2, ..., ?n, хотя бы одно из которых отлично от нуля, такие что
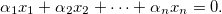
Если векторы не являются линейно зависимыми, то они называются линейно независимыми. (Понятие линейной зависимости обобщает понятия параллельных и компланарных векторов: два вектора линейно зависимы тогда и только тогда, когда они параллельны. Три вектора линейно зависимы тогда и только тогда, когда они компланарны.)
Размерность пространства может быть как конечной (пространство многочленов степени не выше N), так и бесконечной (пространство всех многочленов). Оба случая встречаются на практике, но давайте ограничимся конечномерными. Пусть векторы x1, x2, ..., xn линейно независимы и n — размерность пространства. Тогда любой другой вектор x можно записать в виде линейной комбинации x1, x2, ..., xn, причем единственным образом. Коэффициенты соответствующей линейной комбинации и называются координатами.
Теперь у нас есть строгое определение координат. Но смысл не только в этом: по пути мы столкнулись с более фундаментальными (и менее заметными) понятиями линейной комбинации и линейной зависимости. А еще мы узнали что в n-мерном линейном пространстве не может быть больше, чем n линейно независимых векторов. Этот факт — один из краеугольных камней линейной алгебры.
Казалось бы, мы все еще знаем слишком мало, чтобы извлечь из этого хоть какую-то пользу. Однако уже сейчас мы можем решать задачи, на первый взгляд не имеющие отношения к линейной алгебре. Например, такую: даны многочлены p и q; существует ли многочлен от двух переменных R=R(x,y) такой, что R(p(t), q(t))=0 при всех t?
Тем временем наш «пробный заезд» подходит к концу. Но остается еще коротко обсудить различные способы изучения линейной алгебры. Ограничусь здесь небольшим обзором своего собственного опыта и попробую дать на основе него пару советов.
Википедия Книга — лучший источник знаний
Мое знакомство с линейной алгеброй началось с самостоятельного изучения книги О.В. Мантурова и Н.М. Матвеева «Курс высшей математики», когда я учился в школе. Эта книга — далеко не лучший (но и не худший) источник знаний в данной области. Просто она стала первым учебником по высшей математике, попавшим в мои руки, и ее содержание показалась мне более интересным, чем школьная программа. Хотя сейчас можно с уверенностью сказать: есть куча других книг, которые школьникам стоит (и будет не менее интересно) изучить в первую очередь. Например, «Как решают нестандартные задачи» (Канель-Белов А.Я., Ковальджи А.К.) или «Ленинградские математические кружки» (Генкин С.А., Итенберг И.В., Фомин Д.В.). Если же Вы возьметесь изучать линейную алгебру по книгам, то стоит запастись терпением: для достижения желаемого результата может потребоваться больше времени, чем кажется.
Своими основными знаниями линейной алгебры (и многих других разделов математики) я все же обязан Л.И. Коваленко — легендарному преподавателю МФТИ, семинары и консультации которой всегда собирали аншлаг. Сложно переоценить то внимание, которое она оказывала каждому студенту, до позднего вечера принимая задания и так называемые «карточки» — индивидуальные задачи. А еще во время этих сдач мы активно общались друг с другом. Все это позволяло не только быстрее освоить то, что написано в учебниках, но и то, чего там нет — интуицию, хитрые приемы и прочее.
Живое общение студентов с преподавателями (и друг с другом) ничто не заменит, и в этом преимущество традиционных курсов. Но когда я сам работал ассистентом и вел семинары, часто возникало желание некоторые вещи автоматизировать, чтобы на содержательное общение оставалось больше времени. Нужно ли студенту ждать встречи с преподавателем, чтобы получить стандартный ответ на стандартный вопрос? Или узнать правильно ли решена такая-то стандартная задача? Впрочем, не нужно недооценивать студентов: по большей части, они сами хорошо чувствуют когда делают «почти бессмысленную работу», и их это тоже демотивирует. Проверка доказательства или метода решения — это одно, но вот, скажем, проверку решения системы линейных уравнений можно практически полностью доверить компьютеру. Более того, во многих случаях можно автоматизировать не только проверку ответа, но и часть самого решения — например, элементарные преобразования матриц.
Итак,
- идеи и методы линейной алгебры проще всего понять решая интересные задачи (в том числе из других областей: это позволит лучше разобраться в абстрактных понятиях);
- лучше всего делать это не в одиночку, а вместе с друзьями и хорошим преподавателем (еще очень полезны различные форумы);
- если вас демотивируют рутинные действия — пользуйтесь онлайн-курсами и другими способами автоматизации (здесь нужно иметь чувство меры. Например, перед тем как обращать матрицы в Wolfram Alpha, стоит научиться это делать с помощью ручки и бумаги);
- книги позволяют двигаться вглубь, но не забывайте следить за временем;
- основные понятия и теоремы линейной алгебры не появились на пустом месте. Полезно стремиться понять мотивировки, внутреннюю логику и развивать свое интуитивное видение предмета. Ведь наверняка Крамеру, Гауссу, Пеано и многим другим было интересно открывать (прежде всего для себя) эти основы; почему же тем, кто изучает линейную алгебру сейчас, должно быть скучно это делать?
Комментарии (14)

Redwan
21.04.2015 23:03Хорошая статья на ту же тему betterexplained.com/articles/linear-algebra-guide

agarus
22.04.2015 08:16Что-то я не понял задачу про стержень. Если источник распределенный то почему он греет в окрестностях точки? Мы заменили его на N точечных? Можно уточнить где t0 и tN? — их отсутствие связано с температурой концов поддерживаемых на нуле? и что такое qi? если это поток тепла через хi, то не должно ли быть учтено q0 и qN? И как он рассчитывается?
Большое спасибо за ссылку на вычислительную гидродинамику. Можно покопаться где еще используется линейная геометрия кроме компьютерной графики.
gsk Автор
23.04.2015 16:23Да, отсутствие t0 и tN связано с (нулевыми) граничными условиями. Источник — распределенный: в любом отрезке стержня достаточно малой длины ℓ с центром в x выделяется q(x) · ℓ тепла в единицу времени. Теперь давайте строить модель немного аккуратнее: разрежем стержень в точках xi + h/2. Примерно вот так:
По краям получатся отрезки длины h/2, а остальные будут иметь длину h. Будем считать что на каждом из отрезков температура постоянна (но у двух соседних отрезков температуры могут отличаться). А дальше — обычный закон сохранения энергии: тепло, выделившееся на каждом отрезке длины h должно передаваться соседям через границы (пунктирные линии на рисунке).
Теперь насчет маленьких отрезков по краям: раз температура на концах стержня постоянна, то выделившееся в них тепло должно благополучно куда-то уходить (иначе температура не будет постоянной).

Gumanoid
А можете объяснить «на пальцах» что такое собственные вектора/значения? Никак не могу понять их физический смысл…
gsk Автор
Если преобразование «растягивает» вектор x в ? раз, то этот вектор называется собственным. А число ? называется собственным значением, соответствующим x. При этом вектор x должен быть отличен от нуля (это — часть определения, просто для удобства). А физический смысл может быть разным. Например, если наше преобразование — это вращение твердого тела, то ось, вокруг которой мы поворачиваем, — будет, по существу, собственным вектором. Если угол поворота кратен 90 градусам, то будут еще собственные векторы в перпендикулярной плоскости.
Mrrl
Если 90 градусов — не будут. Дополнительные собственные вектора (с собственным значением -1) появляются только при повороте на 180 гр.
gsk Автор
Да, с 90 градусами я погорячился. Еще при повороте на 360 градусов будут векторы с собственным значением 1.
ReRayne
Вставлю свои 5 копеек.
Как слышу про собственный вектор и собственное значение, сразу вспоминаю курс Introduction to Robotics.
Вот например рассказ зачем нужны собственные вектора и значения.
www.robots.ox.ac.uk/~sjrob/Teaching/EngComp/ecl4.pdf
Кстати, автору привет с физтеха. 2 года назад перевелась туда именно ради отличных курсов по фундаменталке. Спасибо вам за подобные рассказы, они очень нужны многим студентам, которые приходят на 1-е пары в технические ВУЗы и спрашивают: «Зачем мне математика? Я же на программиста пришел!»
gsk Автор
Да, пример про шарики на пружинках (по Вашей ссылке) — тоже хороший. А если учитывать и массы пружинок, то он объясняет еще и зачем одновременно приводить пару квадратичных форм к диагональному виду.
mihalicyn
Задачи, связанные с отысканием собственных значений и векторов возникают настолько часто в различных физических задачах, что сформулировать общую идею крайне трудно.
С наиболее общей точки зрения (математической) — они эффективны потому, что в базисе из таких векторов оператор выглядит наиболее просто, если конечно их хватает, чтобы базис образовать (а зачастую «правильные» операторы из физических задач как раз такие, что собственный базис у них будет — например, самосопряженные). «Простота» обусловлена тем, что функции от оператора в собственном базисе вычислять очень легко — это будет оператор, с собственными значениями равными функции от собственных значений исходного. Из этого, на первый взгляд, чисто технического момента вытекает куча красоты — выписываются явные разложения в ряды по собственным функциям (читай — векторам :-) ) для решений различных краевых задач (уравнение теплопроводности, например). В квантовой механике спектр (читай — набор собственных чисел, хотя это не совсем так. Строго говоря, нужно смотреть на резольвенту оператора) это возможные значения физической величины (в квантовой механике физические величины могут принимать не все значения). Ну и так далее. :) Приложений куча!
gsk Автор
Еще можно сказать что собственный вектор линейного оператора и одномерное инвариантное подпространство — это почти одно и то же.
ivlis
В теории колебаний собственные числа это частоты колебаний системы при свободном движении, а собственные значения это «траектории» (молы). В Гамильтоновой динамике это энергии уровней невозмущённой системы.
Ostrie_Brevna
Если грубо и для частного случая (конечномерных пространств), то собственный вектор линейного оператора (линейный оператор в данном частном случае задаётся матрицей) — это такой вектор, который остаётся неизменным под воздействием своего оператора. В базисе из собственных векторов, если такой удаётся получить, в некоторых случаях «жизнь становится проще» (например, матрица самого оператора оказывается диагональной). В Википедии, в статье про собственные векторы есть хорошая иллюстрация, где на примере известной картины Леонардо да Винчи показывается воздействие линейного оператора а также то, что происходит в этом случае с собственными векторами.