В первой части было рассказано об алгебре множеств, рассматриваемой в качестве оснований классической логики и показано, как можно обосновать без аксиом законы алгебры множеств, которые полностью соответствуют законам классической логики.

В Части 2 будут показаны недостатки и некорректности силлогистики, а также рассмотрена новая, основанная на законах алгебры множеств, математическая модель полисиллогистики, в которую добавлены новые методы логического анализа, включающие распознавание ошибок в рассуждении и методы получения абдуктивных заключений.

Математическая модель полисиллогистики

Задачи полисиллогистики

Сначала обратимся к истории логики. В основе силлогистики, созданной Аристотелем, лежат 4 типа суждений:
: Все есть , пример: «Все крокодилы рептилии».
: Некоторые есть , пример: «Некоторые студенты спортсмены».
: Все не есть , пример: «Все жирафы не земноводные».
: Некоторые не есть , пример: «В заданном множестве целых чисел некоторые четные числа не делятся на 5».

и – общепринятые обозначения типов суждений, при этом типы и называются общими суждениями, а типы и – частными.

О недостатках и ошибках силлогистики подробно рассказано в статье «Почему в учебниках логики содержатся логические ошибки?». Ниже эти недостатки перечислены, а так же предлагаются способы их устранения.

• Недостаток 1: В силлогизме предусмотрено только 2 посылки и одно заключение. Предлагается одним методом анализировать системы с любым числом посылок, для которых возможны более одного следствия. Тем самым мы переходим к анализу полисиллогистики.

• Недостаток 2: В правилах силлогистики большое значение имеют деление терминов на меньший (), средний () и больший (P). Причем, если со средним термином все ясно – это тот, который присутствует в посылках и отсутствует в заключении, то с терминами S и P возникает путаница. В общих суждениях термин S находится на первом месте и соответствует субъекту, а термин P – на втором и соответствует предикату суждения. В частных суждениях статус терминов в основном определяется в соответствии с порядком слов в формулировке суждения на естественном языке. Например, в суждении «Некоторые студенты спортсмены» термин «студенты» считается субъектом, хотя по смыслу термин «студенты» в этом предложении не является ни субъектом и ни предикатом по отношению к термину «спортсмены». Такое «неравноправие» терминов в частных суждениях приводит к путанице в правилах вывода заключений, в результате чего некоторые правильные рассуждения в силлогистике распознаются как неправильные. В предлагаемой модели «равноправие» терминов в частных суждениях восстановлено.

• Недостаток 3: В силлогистике все основные термины (в приведенных примерах и ) не должны быть равны пустому множеству. Этот запрет существенно ограничивает возможности анализа, так как не позволяет проверить существование анализируемых объектов (с точки зрения математики множество не существует, если для данных посылок доказано его равенство пустому множеству). Предлагается не запрещать равенства терминов рассуждения пустому множеству, но при этом предусмотреть для некоторых терминов запрет равенства пустому множеству, если это входит в условия задачи.

• Недостаток 4: В основном варианте силлогистики не разрешается термин с отрицанием размещать в начале суждения (например, суждение "Некоторые не есть " считается неправильным). Результатом этого запрета является то, что в силлогистике некоторые правильные рассуждения распознаются как неправильные. В предлагаемой системе этот запрет не имеет смысла.

• Недостаток 5: В силлогистике при изменении порядка посылок часто образуются неправильные модусы силлогизма, в силу чего изменение порядка посылок в силлогистике запрещено. В предлагаемой системе этот запрет не имеет смысла.

Рассмотрим, как можно на основе законов алгебры множеств построить систему логического вывода с учетом предложенных исправлений. Аристотелевы типы суждений можно выразить в соотношениях алгебры множеств. Пусть термины и в примерах суждений соответствуют некоторым одноименным множествам. Тогда

: : : :

Тогда для моделирования полисиллогистики предлагается следующая математическая модель.

Пусть в универсуме задана система множеств без перечисления их элементов, при этом допускается возможность равенства этих множеств пустому множеству или универсуму. Не исключается также, что некоторые из этих множеств окажутся равными друг другу. Для этой системы заданы посылки логического вывода двух типов:

• общие суждения заданы как соотношения включения между некоторыми из заданных множеств (например, ) и

• частные суждения, выражающие истинность непустого пересечения некоторых пар множеств (например, ).

Также в этой системе можно установить следующие два вида ограничений:

• Ограничения подмены термина выражаются как недопустимость равенства некоторых пар множеств (например, ).

• Ограничения пустоты выражаются как недопустимость равенства пустому множеству некоторых из заданных множеств (например, ).

Кроме того в этой модели в качестве одного из условий можно предусмотреть

• Предполагаемое следствие, которое выражено в виде общего суждения.

Тогда для этой модели рассуждений можно решать следующие задачи:

• Задача 1: Найти следствия в виде соотношений включения между не заданными в условиях задачи парами множеств (тем самым выводятся следствия в виде новых общих суждений).

• Задача 2: Проверить, нарушаются ли в данной системе ограничения подмены термина.

• Задача 3: Если задано предполагаемое следствие, то проверить, выводится ли это следствие из заданных посылок. В случае отрицательного результата формируются варианты посылок, добавление которых в модель рассуждений, позволяет превратить предполагаемое не выводимое следствие, в обычное следствие. Формируемые варианты таких посылок являются абдуктивными заключениями.

• Задача 4: Проверить, нарушаются ли в данной системе ограничения пустоты (проверяется отсутствие или наличие парадоксов в рассуждении).

• Задача 5: Найти новые пары множеств, для которых доказывается непустое пересечение (тем самым выводятся заключения в виде новых частных суждений).

• Задача 6: Установить, для каких множеств, помимо тех, что заданы в ограничениях пустоты, доказывается их безусловное неравенство пустому множеству.

В силлогистике с большими трудностями и не без ошибок решаются только Задачи 1 и 5. Решения задач 1 – 5 можно найти в книге «Логика и математика». Предлагаемая здесь математическая модель несколько отличается от той, что изложена в этой книге. Далее мы рассмотрим методы решения всех шести задач. Для решения некоторых из этих задач потребовалось сформулировать и обосновать ранее неизвестные законы алгебры множеств.

Логический анализ на основе известных законов алгебры множеств

Решение всех задач полисиллогистики удобно начать с построения графа включений. Тогда их решение существенно упрощается.

• Литералом назовем обозначение множества или его дополнения, при этом ясно, что, например, и – это разные литералы.

• Графом включений назовем рисунок, на котором литералы представлены точками (они называются вершинами графа), а отношение включения между множествами изображаются в виде линий со стрелками (они называются дугами графа). Если, например, , то на графе включений стрелка направлена от литерала к литералу ().

Для упрощения мы не будем на рисунках изображать точки – просто будем рисовать стрелки от литерала к литералу.

Порядок действий при решении всех задач начинается одинаково:

1. рисуем граф включений для всех посылок (как изображать на графе частные суждения, будет показано далее при решении Задачи 5);

2. применяем закон контрапозиции ко всем посылкам и дорисовываем граф включений.

Полученный граф включений можно теперь использовать для анализа и решения всех задач полисиллогистики.

• Решение Задачи 1

Для решения Задачи 1 (вывод общих суждений) используются в качестве правил вывода следующие известные законы алгебры множеств:

• Правило вывода 1 (закон контрапозиции): эквивалентно ;

• Правило вывода 2 (закон инволюции дополнения): ;

• Правило вывода 3 (закон транзитивности): если и , то .

Пример 1. Данный, немного измененный мной, пример из книги «История с узелками» придуман известным писателем, логиком и математиком Ч. Л. Доджсоном (литературный псевдоним – Льюис Кэрролл). Он приведен здесь потому, что в нем демонстрируется неожиданность вывода из данных посылок и ситуация, когда абсурд не обусловлен ошибками в доказательствах, а незаметно присутствует в посылках.

1. Те, кто нарушает свои обещания, не заслуживают доверия.

2. Любители выпить очень общительны.

3. Человек, выполняющий свои обещания, честен.

4. Ни один трезвенник не мошенник.

5. Тому, кто очень общителен, всегда можно верить.

Необходимо вычислить основное следствие из этих посылок.

Сформулируем посылки полисиллогизма в виде соотношений между следующими множествами: – люди; – нарушающие обещания; – заслуживающие доверия; – любители выпить; – очень общительные; – честные; – мошенники.

Тогда суждения Примера 1 можно выразить в виде следующих соотношений.

Теперь построим граф включений

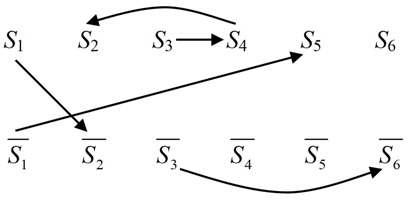
Граф включений лучше изображать таким способом: в верхней строке пусть будут расположены все позитивные литералы, в нижней – все негативные. Так мы не пропустим ни одного литерала и к тому же на такой схеме, в которой противоположные литералы расположены по вертикали, легко строить контрапозиции исходных суждений.

Применим правило контрапозиции к исходным посылкам.
6)
7)
8)
9)
10)

Построим граф включений для посылок и их контрапозиций (изображены пунктирными линиями).

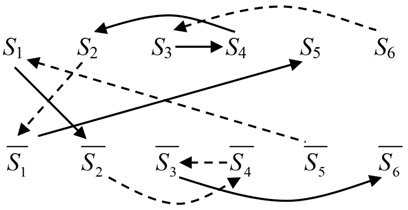
Из рисунка видно, что контрапозиции исходных суждений можно легко построить, используя два простых правила.

• Правило 1: Если исходное суждение соединяет литералы в одной строке, то его контрапозиция соединяет противоположные литералы в другой строке, при этом направление стрелки меняется на обратное.

• Правило 2: Если исходное суждение соединяет литерала в разных строках, то его контрапозиция соединяет противоположные литералы, при этом направление стрелки (вверх или вниз) не изменяется.

Теперь легко находится решение задачи. Выберем на графе литералы, в которые не входит ни одна стрелка (начальные литералы) и «прогуляемся» из них по направлению стрелок. В результате получим такой путь на графе:

.

Правило транзитивности позволяет нам утверждать, что если имеется путь от одного литерала к другому, то множество, соответствующее начальному литералу, включено в множество, соответствующее конечному литералу. Отсюда ясно, что

• : Все мошенники честные.

• Решение Задачи 2

Для решения Задачи 2 (проверка ограничения подмены терминов) используется еще один известный закон алгебры множеств:

• закон эквивалентности: если и то .

Отсюда еще одно правило вывода:

• Правило вывода 4 (закон эквивалентности): если и то

• Пример 2. Задано множество целых положительных чисел с разными признаками делимости. Между некоторыми классами чисел этого множества заданы следующие соотношения:

1. Все четные числа не делятся на 3.

2. Все числа, не делящиеся на 5, делятся на 3.

3. Все числа, делящиеся на 5, четные.

Проверить, соблюдается ли отношение равенства между некоторыми классами чисел.

Обозначим: – четные числа, – числа, кратные 3-м, – числа, делящиеся на 5.
Тогда посылки Примера 2 можно выразить в виде следующих соотношений между множествами:

Как и в предыдущем примере, построим граф включений, дополненный контрапозициями исходных посылок

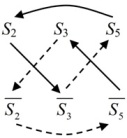
В этом графе нет начальных вершин, поэтому выбираем любую вершину и прослеживаем путь из нее:

Видно, что круг замкнулся. Ясно, что новые суждения в этой цепочке не появятся. Теперь в качестве начала для другой цепочки выберем какой-нибудь литерал из оставшихся литералов, например, . Тогда получим другой замкнутый круг

Полученная ситуация с замкнутыми кругами названа коллизией цикла. Для получения решения при коллизии цикла можно использовать два известных закона алгебры множеств – закон транзитивности и закон эквивалентности. Тогда несложно доказать, что все литералы, содержащиеся в одном цикле, представляют эквивалентные друг другу множества. В данном примере это означает, что в одном множестве чисел совмещены разные свойства. Например, в одном множестве все четные числа не делятся на 3 и кратны 5-ти.

И если в ограничениях подмены термина задана невозможность равенства каких-либо пар множеств, содержащихся в цикле, то придется признать это рассуждение некорректным.

• Решение Задачи 3

Для решения задачи 3 (поиск абдуктивных заключений) можно воспользоваться известными законами алгебры множеств.

• Пример 3. Рассмотрим шуточную задачу. Найдите пропущенную посылку в рассуждении: Титулованные особы не закладывают за воротник, поскольку все, кто не носит цилиндров, не являются титулованными особами, и к тому же любой, кто закладывает за воротник, сморкается в галстук.

Обозначим – титулованные особы, – те, кто закладывает за воротник, – те, кто носят цилиндр, – те, кто сморкается в галстук.

Сформулируем посылки:

Предполагаемое следствие здесь .

Построим граф включений для посылок и их контрапозиций. На рисунке также изображено красной стрелкой предполагаемое следствие.

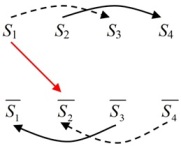
На рисунке видно, что путь между литералами и отсутствует, но его можно восстановить, если соединить стрелкой литералы и . Тем самым мы получим абдуктивное заключение: Те, кто носят цилиндр, не сморкаются в галстук.

В общем, метод поиска абдуктивных заключений в модели полисиллогистики понятен: надо в графе включений соединить разорванный путь, начало которого – это первый литерал предполагаемого следствия, а конец – второй литерал.

Логический анализ на основе ранее неизвестных законов алгебры множеств

Для решения Задач 4, 5, 6 необходимо использовать законы, формулировки которых не встречаются в соответствующих публикациях по алгебре множеств. Для них предложены соответствующие названия и на их основе сформулированы правила решения задач. Поскольку для этих правил не найдено соответствия с правилами логического вывода в математической логике, они названы не правилами вывода, а правилами логического анализа.

• Решение Задачи 4 (Распознавание и анализ парадоксов)

Рассмотрим решение Задачи 4. Эта задача решается так: после вывода всех следствий проверяется наличие (или отсутствие) следствий типа . Если такие следствия есть, то полученная ситуация называется коллизией парадокса. В этом случае возможны 2 варианта решения. Если для множества не задано ограничение
, то из коллизии парадокса следует, что . В противном случае рассуждение можно считать содержащим ошибку.

Для решения коллизии парадокса используются следующий закон алгебры множеств

• Закон парадокса: если доказано, что , то .

В публикациях по алгебре множеств этот закон не встречается. Поэтому целесообразно привести его доказательство.

• Доказательство закона парадокса. По определению операции дополнения в множестве содержатся те и только те элементы универсума , которые не являются элементами . Предположим, что имеется элемент такой, что . В то же время из условия следует, что элемент содержится в , т.е. . Полученное противоречие можно разрешить единственным способом: .

К закону парадокса приводит ситуация, когда некоторый объект обладает свойством и в то же время не обладает им. Выразим эту ситуацию в виде соотношения между множествами:

1. ;

2. .

Вычислим контрапозиции этих суждений:
3) ;
4) .
Из суждений и по закону транзитивности следует . Таким образом, данная ситуация равносильна закону парадокса. Теперь можно сформулировать еще одно правило.

• Правило логического анализа 5 (закон парадокса): если , то .

Из закона парадокса, в частности, следует, что некоторые парадоксы теории множеств, которые якобы свидетельствуют о противоречивости понятия «множество», на самом деле говорят о том, что множеств, у которых в соответствии с заданными определениями выводятся несовместимые свойства, просто не существует.

В общем случае, если с помощью Правила 5 найдены безусловно пустые множества, и этот результат не нарушает ограничений, то пустые множества и множества, которые включены в них, можно удалить из состава всех множеств системы, после чего в системе можно решать другие задачи.

• Пример 4. Данный пример взят из книги Кэрролла «История с узелками» (раздел «Символическая логика»), но в него добавлена еще одна посылка. Даны посылки:

1. Все члены палаты общин находятся в полном рассудке.

2. Ни один член парламента, носящий титул пэра, не станет участвовать в скачках на мулах.

3. Все члены палаты лордов носят титул пэра.

4. Все, кто не принимает участия в скачках на мулах, в полном рассудке

Нужно распознать в этом рассуждении коллизию парадокса.

Обозначим – члены парламента, – члены палаты общин (тогда – члены палаты лордов), – те, кто в полном рассудке, – те, кто носят титул пэра, – те, кто принимает участие в скачках на мулах.

Сформулируем на языке алгебры множеств посылки

1. ;

2. ;

3. ;

4. .

Построим граф включений с контрапозициями

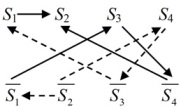
На этом графе можно найти только один начальный литерал – . Из него идут 2 пути, и оба приводят к литералу , то есть к коллизии парадокса . Отсюда ясно, что все члены парламента в полном рассудке.

В общем случае, если коллизия парадокса обнаружена и не нарушает ограничения пустоты, то литералы, соответствующие пустым множествам, рекомендуется удалить из условий задачи и из графа включений вместе с исходящими из них дугами. Это необходимо для правильного решения следующих Задач.

• Решение Задачи 5 (вывод заключений в виде частных суждений)

Рассмотрим, как изображаются на графе включений исходные частные суждения, которые выражаются в виде неравенства (например, ). Предложенная модель полисиллогистики не предназначена для работы с такими выражениями, но можно использовать другой вариант формулировки частных суждений. Пусть заданы некие вспомогательные (т.е. не связанные с основными терминами рассуждения) непустые множества, которые мы обозначим . Тогда каждое частное суждение можно выразить в виде двух суждений, в которых используется одно из вспомогательных множеств. Например, суждение можно выразить как два суждения и .

При этом надо соблюдать обязательное правило: в разных посылках, выражающих частные суждения, вспомогательные множества должны быть разными. Иначе можно получить в процессе анализа такие соотношения, которые в некоторых частных случаях могут нарушаться. Тогда для решения задачи 5 можно использовать следующий закон алгебры множеств.

• Закон непустого пересечения: если , и , то .

Доказательство этого закона элементарное. Однако его формулировка мне не встречалась в работах по дискретной математике. Возможно, это обусловлено тем, что связь алгебры множеств с логическим анализом не рассматривалась.

На основе этого закона сформулируем правило.

• Правило логического анализа 6 (закон непустого пересечения): если , и , то .

Рассмотрим пример использования этого правила.

• Пример 5. Даны посылки.

1. Мастер Афоня сможет выполнить некоторые работы Заказа 1.

2. Ни одна работа Заказа 2 не входит в состав работ Заказа 1. Спрашивается, входят ли в состав Заказа 2 все работы, которые может выполнить мастер Афоня?

Обозначим – множество работ, выполняемых Афоней, – множество работ Заказа 1, – множество работ Заказа 2. Тогда условия задачи можно сформулировать в виде следующих посылок:

1. ;

2. ;

3. .

Построим граф включений, добавив в него контрапозиции исходных суждений.

На рисунке видно, что из идут пути в и . По Правилу 5 это означает, что . Отсюда ясно, что часть работ, которые может выполнять мастер Афоня, не входят в состав работ Заказа 2. Поэтому ответ на вопрос задачи отрицательный.

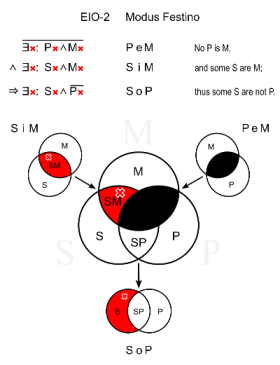
Интересно отметить, что данное рассуждение не является правильным в традиционной силлогистике. Однако, если на первое место поставить общее суждение , то мы получим правильный силлогизм (модус (Festino) второй фигуры силлогизма). Для сравнения посмотрите, как обосновывается этот модус в традиционной силлогистике с помощью диаграмм Венна. Рисунок взят из статьи Syllogism.

Общее правило решения задачи 5 будет сформулировано ниже после решения Задачи 6.

• Решение Задачи 6 (Распознавание безусловно непустых множеств)

После того, как построен граф включений заданного примера, проверены ограничения и удалены пустые множества, можно приступить к решению Задачи 6. Для ее решения необходим довольно простой закон алгебры множеств, формулировку которого мне не удалось найти в публикациях.

• Закон существования множества: если и , то .

Доказательство этого закона весьма просто. Поскольку , то существует элемент такой, что . Поскольку , то . Следовательно, .

Этот закон интересен тем, что он по форме соответствует давно известному в логике правилу вывода modus ponens: если выводимы формулы и , то выводима формула ( – обозначение логической связки импликации).

Рассмотренный закон лежит в основе еще одного правила.

• Правило логического анализа 7 (закон существования множества): если и , то .

Для общего решения Задачи 6, можно воспользоваться графом включений, откорректированным после проверки ограничений. В этом случае можно применить следующий алгоритм.

• Алгоритм распознавания всех безусловно непустых множеств

1. Отметить в графе включений литералы, которые являются непустыми по условиям задачи. К ним относятся вспомогательные литералы (), введенные при формулировке частных суждений (Задача 5) и литералы, перечисленные в ограничениях пустоты (Задача 4).

2. Отметить на графе включений все литералы, содержащиеся в путях, исходящих из отмеченных вершин. Отмеченные на данном шаге литералы являются не заданными в условиях задачи безусловно непустыми множествами.

3. Конец алгоритма.

После выявления в графе включений всех безусловно непустых множеств (отмеченные литералы на графе включений в приведенном выше алгоритме) можно сформулировать общее правило для распознавания пар множеств, имеющих непустое пересечение, т.е. общее решение Задачи 5. Для этого среди всех литералов, представляющих безусловно непустые множества, выделим литералы из которых на графе включений исходят две или более ветви. Назовем эти литералы узлами. Тогда в соответствии с Законом непустого пресечения будет верным следующее правило.

• Общее правило решения Задачи 5: Если литералы и находятся в разных ветвях, исходящих из одного узла, то множества, представленные этими литералами, имеют непустое пересечение, т. е. .

Разумеется, непустое пересечение будет и у пар множеств, находящихся на одной ветке, исходящей из безусловно непустого множества. Но для таких множеств имеется более сильная связь: они оба непустые и одно из них включено в другое.

Спасибо за то, что прочитали статью до конца. И все же, если не трудно, задайте себе (а может быть, и собеседнику) следующий вопрос, который никак не умаляет величайший вклад Аристотеля в развитие логики: Не пора ли отказаться от преподавания методов логического анализа на основе традиционной силлогистики?

Дизайн баннера выполнен Анной Горской