27.04.2024 13:51
carbon2409 82 25000 Источник

Всем привет! Я реализовал, похоже, собственный алгоритм поиска кратчайшего пути с отрицательными ребрами графа.

Почему собственный? Я искал подобное решение, но не нашел, возможно, оно уже было реализовано, просто плохо поискал. Жду Нобелевскую премию =)

Додумался я до него путем модификации классического Дейкстры. Прошу адекватно отнестись к содержимому, ибо это моя первая статья, и, возможно, я ничего не придумывал и, вообще, этот алгоритм не работает вовсе (но по моим тестам он работает правильно).

Повторюсь, алгоритм работает с отрицательными ребрами графа (но не с циклическими отрицательными). Чем этот алгоритм отличается от известного Беллмана-Форда?

Сложностью! У известного алгоритма сложность составляет O(n3). У "моего" алгоритма по моим расчетам сложность не превышает оригинальной сложности алгоритма Дейкстры, а именно O(n2). Если это не так, поправьте, пожалуйста, после ознакомления с реализацией на языке Python

Реализация

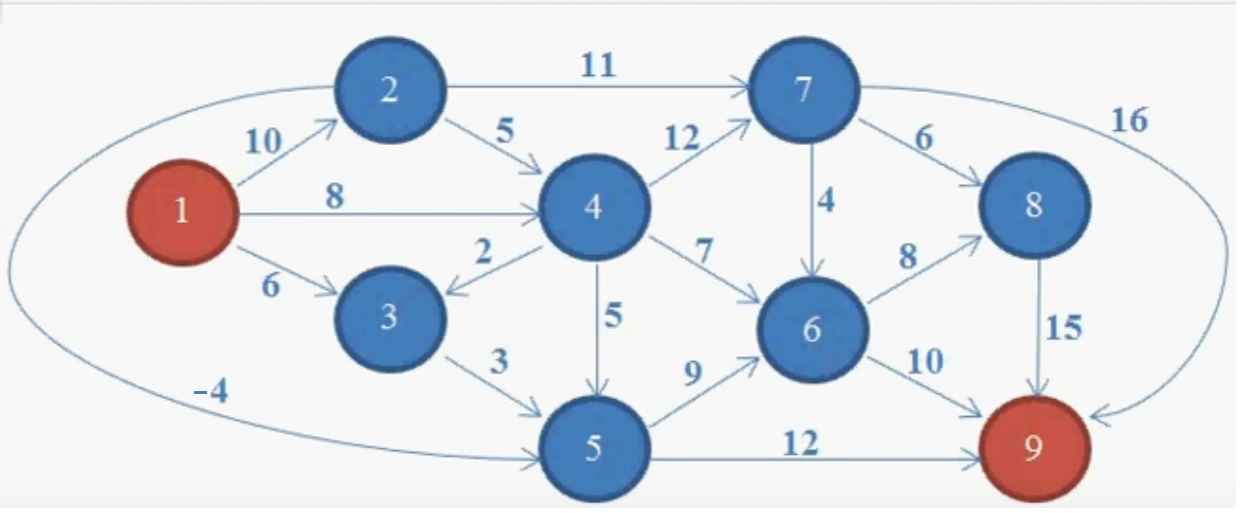
Пример графа с отрицательным ребром
Пример графа с отрицательным ребром

Итак, у нас есть граф с отрицательным ребром между 2-м и 5-м узлом. Наша задача - найти кратчайший путь от источника (1-го узла) до 9-го узла.

Граф будет храниться в виде хэш таблицы, где:

graph = {
нода_1_(источник): {сосед_1: вес до него, сосед_2: вес до него, ...},
нода_2: {сосед_1: вес до него, сосед_2: вес до него, ...},
...
}

graph = {
    1: {2: 10, 3: 6, 4: 8},
    2: {7: 11, 4: 5, 5: -4},
    3: {5: 3},
    4: {7: 12, 3: 2, 5: 5, 6: 7},
    5: {6: 9, 9: 12},
    6: {8: 8, 9: 10},
    7: {6: 4, 8: 6, 9: 16},
    8: {9: 15},
    9: {}
}

Важно! Нужно писать узлы графа в порядке их отдаленности от источника. Т.е. сперва описываем первых соседей источника. После того, как описали их, приступаем к следующим соседям соседей. Т.е. описываем поуровнево, будто это не взвешенный граф, а обыкновенное дерево, где реализовываем поиск в ширину. В Python словари являются упорядоченными (начиная с версии 3.6), поэтому нам не стоит прибегать к другим структурам данных, типа Ordered dict из модуля collections.
Можно описать граф матрицей смежностей, но мне так проще.

P.S. Тот, кто задается подобным вопросом:

Определение графа знаете? Набор вершин и дуг, в котором дуги являются парами связных вершин, плюсом веса для дуг в нашем случаи. Никакого порядка там в принципе не предусмотрено.

Заранее отвечаю.

Хорошо, буду от вашей структуры отталкиваться. У нас какая задача? Найти кратчайший путь из точки А в точку В. Находим в вашем представлении графа точку А и смотрим на его соседей. Потом находим этих соседей и смотрим их соседей и т.д. Вот это "находим" в вашей беспорядочной структуре будет за N выполняться N раз. Это будет в том случае, если ноды у вас просто беспорядочно расположены в массиве (если вы используете эту структуру данных для хранения). Обычно в программе номер ноды совпадает с номером ячейки в массиве, что позволяет получить к этой ноде доступ за константу. В алгоритме Дейкстры (не я придумал его) как раз таки задача решается именно таким представлением графа, где номер ноды (или буква в лексиграфическом порядке) совпадает с номером ячейки в массиве. То, как вы пытаетесь представить граф - это по сути выстрел себе в ногу. Если отталкиваться от реальной жизни, нужно еще реализовать построение такой структуры графа. Условно ты находишься на перекрестке 1, мне надо в перекресток 10. А дай ка гляну, какие там дороги исходят из перекрестка 7 и запишу. Хотя можно было на второе место записать дороги перекрестка 2. В общем, замечание ваше понятно, но это всё общепринятая условность представления данных графа, я это не придумывал.
Поиск в ширину же выполнится за линейное время, поэтому он никак не увеличивает сложность алгоритма.

Так же нам понадобится еще 2 хэш таблицы.
Минимальные веса от источника до этой ноды в виде:
costs = {
нода_1_(источник): 0,
нода_2: infinity,
нода_3: infinity,
...
}
Заполнять и обновлять мы ее будем по мере прохождения по "детям" узлов.

costs = {}  # Минимальный вес для перехода к этой ноде (кратчайшие длины пути до ноды от начального узла)

Таблица родителей нод, от которых проходит кратчайший путь до этой ноды:

parents = {}  # {Нода: его родитель}

Ее так же будем заполнять и обновлять по мере прохождения по детям узлов.

Как и в алгоритме Дейкстры, будем отмечать еще неизвестные до узлов расстояния бесконечностью. Инициализируем эту переменную:

infinity = float('inf')  # Бесконечность (когда минимальный вес до ноды еще неизвестен)

Далее создаем пустое множество. Там будут храниться обработанные узлы (что значит "обработанные", поясню далее, а пока просто создаем множество)

processed = set()  # Множество обработанных нод

Приступим к самому алгоритму!

  1. Начинаем с источника (первого узла). Смотрим на веса всех его соседей в таблице costs. Путь до них бесконечный, а любое число уже меньше бесконечности, поэтому обновляем веса. Так же вносим родителей всех узлов, т.к. мы обнаружили путь до ноды короче. Когда посмотрели всех соседей, вносим наш рассматриваемый узел в множество обработанных узлов processed (этот узел мы не будем обрабатывать в дальнейшем).

  2. Здесь важный момент и отличие от алгоритма Дейкстры. Мы будем смотреть не минимальный по весу необработанный узел, а смотреть вообще ВСЕХ соседей поочередно. Т.е. у нас есть соседи после первого этапа алгоритма.
    Мы поочередно так же будем искать уже их соседей и обновлять минимальные веса. Если же достижимый вес окажется меньше, чем внесенный в таблицу, то мы его заменяем. Так же заменяем его родителя в таблице parents.
    Когда посмотрели всех соседей, вносим узел в множество обработанных. Т.е. множество обработанных - это те узлы, у которых мы рассмотрели всех его соседей!

  3. И так повторяем поуровнево (не приступаем к соседям соседей, пока не обработаем первых соседей), пока не будут обработаны все узлы.

    Код:

graph = {
    1: {2: 10, 3: 6, 4: 8},
    2: {7: 11, 4: 5, 5: -4},
    3: {5: 3},
    4: {7: 12, 3: 2, 5: 5, 6: 7},
    5: {6: 9, 9: 12},
    6: {8: 8, 9: 10},
    7: {6: 4, 8: 6, 9: 16},
    8: {9: 15},
    9: {}
}

parents = {}  # {Нода: его родитель}
costs = {}  # Минимальный вес для перехода к этой ноде (кратчайшие длины пути до ноды от начального узла)
infinity = float('inf')  # Бесконечность (когда минимальный вес до ноды еще неизвестен)

processed = set()  # Множество обработанных нод
for node in graph.keys():
    if node not in processed:  # Если нода уже обработана не будем ее заново смотреть (иначе м.б. беск. цикл)
        for child, cost in graph[node].items():  # Проходимся по всем детям
            new_cost = cost + costs.get(node,
                                        0)  # Путь до ребенка = путь родителя + вес до ребенка (если родителя нет, то путь до него = 0)
            min_cost = costs.get(child,
                                 infinity)  # Смотрим на минимальный путь до ребенка (если его до этого не было, то он беск.)
            if new_cost < min_cost:  # Если новый путь будет меньше минимального пути до этого,
                costs[child] = new_cost  # то заменяем минимальный путь на вычисленный
                parents[child] = node  # Так же заменяем родителя, от которого достигается мин путь
        processed.add(node)  # Когда все дети (ребра графа) обработаны, вносим ноду в множество обработанных

print(f'Минимальные стоимости от источника до ноды: {costs}')
print(f'Родители нод, от которых исходит кратчайший путь до этой ноды: {parents}')

# -> Минимальные стоимости от источника до ноды: {2: 10, 3: 6, 4: 8, 7: 20, 5: 6, 6: 15, 9: 18, 8: 23}
# -> Родители нод, от которых исходит кратчайший путь до этой ноды: {2: 1, 3: 1, 4: 1, 7: 4, 5: 2, 6: 4, 9: 5, 8: 6}

Мы получили кратчайшие расстояния от источника до каждого достижимого узла в графе, а так же родителей этих узлов. Как же нам построить цепочку интересующего нас пути от источника до 9-ой ноды (либо до любой другой достижимой)? Ответ в коде ниже:

def get_shortest_path(start, end):
    '''
    Проходится по родителям, начиная с конечного пути,
    т.е. ищет родителя конечного пути, потом родителя родителя и т.д. пока не дойдет до начального пути.
    Тем самым мы строим обратную цепочку нод, которую мы инвертируем в конце, чтобы получить
    истинный кратчайший путь
    '''
    parent = parents[end]
    result = [end]
    while parent != start:
        result.append(parent)
        parent = parents[parent]
    result.append(start)
    result.reverse()
    shortest_distance = 0
    for i in range(len(result)-1):  # Узнаем кратчайшее расстояние
        node_1 = result[i]
        node_2 = result[i + 1]
        shortest_distance += graph[node_1][node_2]
    result = map(str, result)  # В случае если имена нод будут числами, а не строками (для дальнейшего join)
    print(f'Кратчайший путь от {start} до {end}:  {shortest_distance}')
    return result


shortest_path = get_shortest_path(start=1, end=9)
print('-->'.join(shortest_path))

# -> Кратчайший путь от 1 до 9:  18
# -> 1-->2-->5-->9

Итак, мы нашли кратчайший путь до 9 узла, и обратите внимание, он проходит через ребро с отрицательным весом! Т.е. нас теперь не пугает наличие такого ребра, в отличие от оригинальной Дейкстры.

Сложность

В оригинальном алгоритме Дейкстры сложность в худшем случае складывается из

  1. Прохода по всем узлам графа (n)

  2. В этот цикл вложен еще один - поиск минимального не посещенного узла. Он работает за O(n), но можно сделать и за O(Elogn) путем реализации кучи (heapq)

  3. Прохождение по соседям узла. Занимает O(E), где Е - количество ребер в графе. Т.к. это константа, то ее опускают.

Итого алгоритм занимает O(n2+E), а с реализацией кучи, скорость возрастает до O(Elogn) (на самом деле это будет не всегда так, но в большинстве случаев)

Что касается "моего" алгоритма, то если где-то не ошибаюсь:

  1. Проход по всем узлам графа O(n)

  2. Проход по всем соседям O(n)

  3. Обновление весов O(1)

Итого O(n2). Not bad! Что по памяти? costs - O(n), parents - O(n), processed - O(n)
Считаю, неплохо для такого рода алгоритма.

Еще деталь такая. При реализации классической Дейкстры, в случае, когда поиск МИНИМАЛЬНОГО по весу узла совпадет с нашим конечным целевым узлом,
то мы можем прервать дальнейшую обработку, т.к. мы уже нашли кратчайший путь до интересующего узла. В "моем" же алгоритме мы все равно будем обрабатывать все узлы.

Выводы

В случае, если нам могут встретится отрицательные ребра в графе, можно пользоваться данным алгоритмом. Можно воспользоваться и известным Беллмана-Форда, кому как нравится, но мне показался он более сложным в понимании.
В случае, если нам известно, что граф не содержит отрицательных весов, тогда можно смело пользоваться Дейкстрой.

ЕЩЕ РАЗ ПОДЧЕРКИВАЮ!

Я не знаю, был ли этот алгоритм до этого или нет. Может он вообще работает некорректно, но я тестировал его с разными данными, и он работал правильно.

Если будут какие-то поправки или замечания, жду обратную связь. Может быть, реализация вообще работает только с определенными графами, возможно, есть и такие, которые все сломают :)

Всем спасибо, жду Ваше мнение по поводу этой статьи!

Update_1:

Все-таки алгоритм не работает с определенными графами :(

Приведу пример, подсказанный с комментариев (спасибо большое за него):

Хотим попасть с источника 1 до конечной ноды 5.

graph = {    
    1: {2: 1, 3: 20, 5: 10},
    2: {4: 1},
    3: {5: 1},
    5: {},
    4: {3: 1},
}

# OUT
"""
Минимальные стоимости от источника до ноды: {2: 1, 3: 3, 5: 10, 4: 2}
Родители нод, от которых исходит кратчайший путь до этой ноды: {2: 1, 3: 4, 5: 1, 4: 2}
Кратчайший путь от 1 до 5:  10
1-->5
"""
# Правильный ответ - 4
# 1-->2-->4-->3-->5

Происходит это, потому что мы обновляем веса уже обработанных нод, но не обновляем в свою очередь их соседей (по идее веса соседей с учетом обновления веса родителя могут быть короче).

Чтобы все работало, нужно заново обрабатывать этого родителя, что в свою очередь приводит к росту сложности. Я даже уже не знаю, в какую, по-моему кубическую, что по сути уже бесполезно использовать, т.к. есть уже известный алгоритм Беллмана-Форда с такой же ассимптотикой. Возможно, можно как-то и оптимизировать хитрым способом, но пока в голову ничего не пришло. Если есть какие-то мысли по этому поводу, какие-то идеи - welcome! Присылайте идеи в комментариях.

Всем спасибо за помощь и фидбэк! Я добился своей цели - ответил себе на вопрос, корректный ли алгоритм или нет. Спасибо людям за это, я получил опыт и закрепил знания, а это уже победа!

Update_2:

Ситуация немного изменилась. Как мне объяснили в комментариях более подготовленные люди, сложность алгоритма была не O(n2), а O(n+E), где n - количество узлов, E - количество ребер в графе. Т.е. алгоритм был быстрее мной предполагаемой сложности. Соответственно, у меня появилась мысль: "а почему бы не обработать тот случай, который ломал алгоритм? Сложность возрастет, ну и пусть, она явно не будет выше квадратичной".

Каждая вершина обрабатывается во внутреннем цикле ровно один раз. Учитывая, что граф обрабатывается списками смежности, то суммарное количество итераций внутреннего цикла -- в точности количество ребер. Если быть более точным, то оценка O(N+E).

Что ж, я попробовал это сделать. Мы немного изменим код и введем новую структуру данных - список очередности обработки узлов графа. Что за список, как он работает?

lst = [key for key in graph.keys()]  # Формируем очередность прохождения узлов графа

Он будет служить нашей итерабельной последовательностью первого цикла. Зачем? Если вдруг у ноды соседом будет уже обработанная нода (т.е. будет проблема, описанная ранее), то мы эту ноду снова будем обрабатывать. Код:

graph = {
    1: {2: 1, 3: 20, 5: 10},
    2: {4: 1},
    3: {5: 1},
    5: {},
    4: {3: 1},
}
lst = [key for key in graph.keys()]  # Формируем очередность прохождения узлов графа
parents = {}  # {Нода: его родитель}
costs = {}  # Минимальный вес для перехода к этой ноде (кратчайшие длины пути до ноды от начального узла)
infinity = float('inf')  # Бесконечность (когда минимальный вес до ноды еще неизвестен)

processed = set()  # Множество обработанных нод
for node in lst:
    if node not in processed:  # Если нода уже обработана не будем ее заново смотреть (иначе м.б. беск. цикл)
        for child, cost in graph[node].items():  # Проходимся по всем детям
            new_cost = cost + costs.get(node,
                                        0)  # Путь до ребенка = путь родителя + вес до ребенка (если родителя нет, то путь до него = 0)
            min_cost = costs.get(child,
                                 infinity)  # Смотрим на минимальный путь до ребенка (если его до этого не было, то он беск.)
            if new_cost < min_cost:  # Если новый путь будет меньше минимального пути до этого,
                costs[child] = new_cost  # то заменяем минимальный путь на вычисленный
                parents[child] = node  # Так же заменяем родителя, от которого достигается мин путь
                if child in processed:  # UPDATE: если ребенок был в числе обработанных
                    lst.append(child)  # Вновь добавляем эту ноду в список для того, чтобы обработать его заново
                    processed.remove(child) # Удаляем из обработанных
        processed.add(node)  # Когда все дети (ребра графа) обработаны, вносим ноду в множество обработанных

print(f'Минимальные стоимости от источника до ноды: {costs}')
print(f'Родители нод, от которых исходит кратчайший путь до этой ноды: {parents}')


def get_shortest_path(start, end):
    '''
    Проходится по родителям, начиная с конечного пути,
    т.е. ищет родителя конечного пути, потом родителя родителя и т.д. пока не дойдет до начального пути.
    Тем самым мы строим обратную цепочку нод, которую мы инвертируем в конце, чтобы получить
    истинный кратчайший путь
    '''
    parent = parents[end]
    result = [end]
    while parent != start:
        result.append(parent)
        parent = parents[parent]
    result.append(start)
    result.reverse()
    shortest_distance = 0
    for i in range(len(result)-1):  # Узнаем кратчайшее расстояние
        node_1 = result[i]
        node_2 = result[i + 1]
        shortest_distance += graph[node_1][node_2]
    result = map(str, result)  # В случае если имена нод будут числами, а не строками (для дальнейшего join)
    print(f'Кратчайший путь от {start} до {end}:  {shortest_distance}')
    return result


shortest_path = get_shortest_path(start=1, end=5)
print('-->'.join(shortest_path))

# -> Кратчайший путь от 1 до 5:  4
# -> 1-->2-->4-->3-->5

По предложенным мне графам проводил тесты, все работает корректно. Пытался сам сломать алгоритм, но не получалось. Я сам не силен в тестировании, поэтому я и прошу помощи на этой площадке, чтобы более компетентные люди попробовали меня опровергнуть. Я все равно считаю на 99.99%, что этот алгоритм не рабочий. Но никак не могу себе это доказать и понять :) Быть может, у Вас, дорогие друзья, получится сломать алгоритм? Если получилось, пришлите мне, пожалуйста, пример графа. Если у Вас есть опровержение, то тоже интересно будет на него взглянуть.

P.S. Что в итоге после некоторых рассуждений?

  1. Алгоритм, похоже, рабочий :)

  2. Ошибся со сложностью Беллмана-Форда. Его сложность составляет O(N*E).

Что касается сложности данного алгоритма, то в наихудшем случае она будет такая же O(N*E). Но я так и не нашел наихудший случай. Во всех случаях, которые я тестировал, он работал быстрее Беллмана-Форда. Давайте рассуждать.

Смоделируем ситуацию "в лоб". Посчитаем количество операций на наихудшем графе, который мне прислали, где алгоритм чувствуте себя несколько хуже, чем на других примерах. Пример графа (извиняюсь за ручной рисунок)

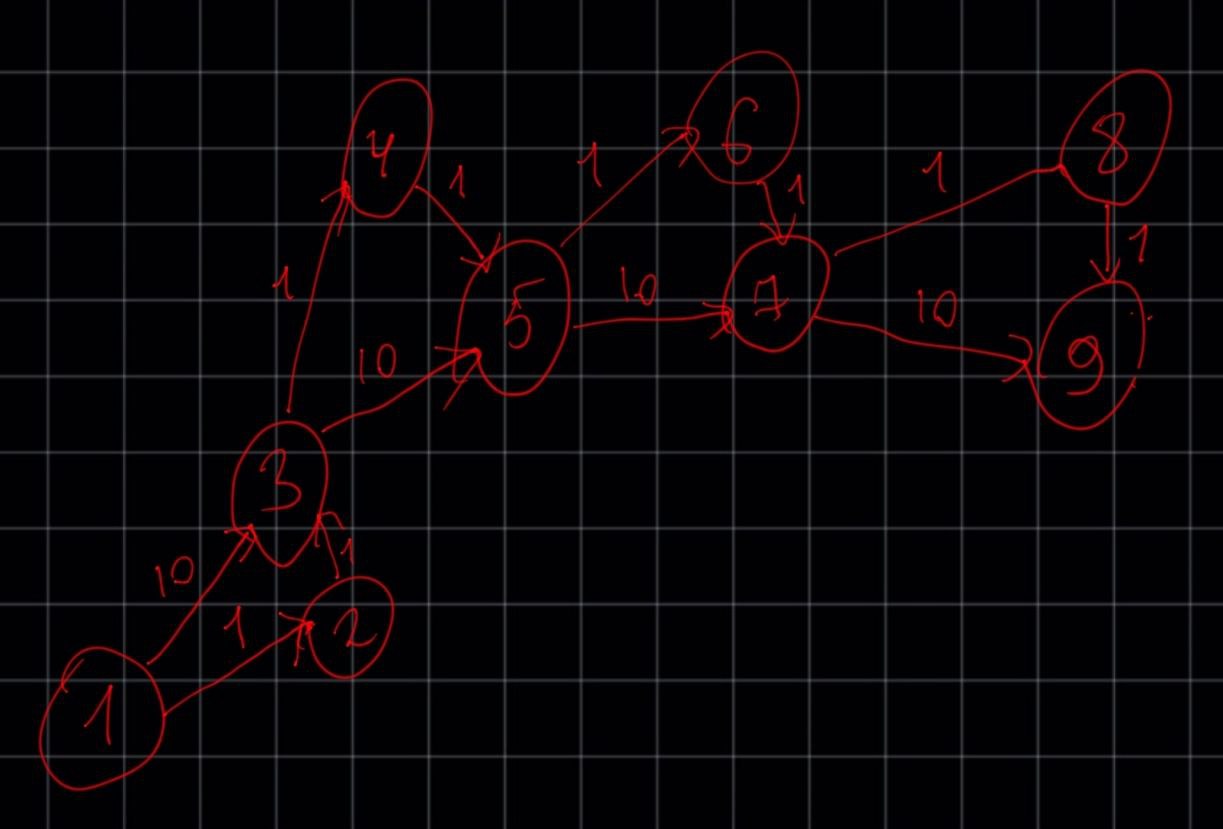
graph = {
  1: {3:10, 2:1}, 

  3: {5:10, 4:1 }, 
  2: {3:1}, 

  5: {7:10, 6:1 }, 
  4: {5:1}, 

  7: {9:10, 8:1}, 
  6: {7:1}, 

  9: {},
  8: {9:1}, 
}

cycle_count = 0
processed = set()  # Множество обработанных нод
for node in lst:
    if node not in processed:  # Если нода уже обработана не будем ее заново смотреть (иначе м.б. беск. цикл)
        for child, cost in graph[node].items():  # Проходимся по всем детям
            cycle_count += 1
            new_cost = cost + costs.get(node,
                                        0)  # Путь до ребенка = путь родителя + вес до ребенка (если родителя нет, то путь до него = 0)
            min_cost = costs.get(child,
                                 infinity)  # Смотрим на минимальный путь до ребенка (если его до этого не было, то он беск.)
            if new_cost < min_cost:  # Если новый путь будет меньше минимального пути до этого,
                costs[child] = new_cost  # то заменяем минимальный путь на вычисленный
                parents[child] = node  # Так же заменяем родителя, от которого достигается мин путь
                if child in processed:  # UPDATE: если ребенок был в числе обработанных
                    lst.append(child)  # Вновь добавляем эту ноду в список для того, чтобы обработать его заново
                    processed.remove(child) # Удаляем из обработанных
        processed.add(node)  # Когда все дети (ребра графа) обработаны, вносим ноду в множество обработанных
        
print(f'Количество операций: {cycle_count}')
# -> Количество операций: 30
# По Беллману-Форду было бы: 9*12=108 судя по формуле

По Беллману-Форду количество операций, судя по формуле, превышает более чем в 3 раза!

Вы можете сказать: "да это просто граф такой попался". Что-ж рассмотрим граф, который является 100% наихудшим случаем для Беллмана-Форда, судя по информации из открытых источников.

Представим такого вида линейный граф: 1-->2-->3-->4-->5. Где каждое ребро имеет вес 1. По Беллману-Форду кол-во операций свелось бы как раз к его формуле (наихудшему случаю), а именно 5*4=20. В моем алгоритме: 

graph = {
    1: {2:1},
    2: {3:1},
    3: {4:1},
    4: {5:1},
    5: {},
}
# -> Количество операций: 4

Т.е. по сути за линию выполнил.

Если я что-то неправильно сделал, может быть, глупость совершил, что в "лоб" посчитал количество операций, то с радостью выслушаю, в чем мой "косяк". Но вроде как взял наихудшие случаи.

Таким образом имеем отличный по ассимптотике алгоритм поиска кратчайших путей с отрицательными весами. Быстрее стандартного алгоритма Беллмана-Форда! Спасибо за пояснения и уточнения, если, вдруг, снова нашли какой-то случай уникальный, то, повторюсь, присылайте такой случай. Всем спасибо!

Комментарии (82)


  1. purplesyringa
    27.04.2024 14:26
    #26769351
    +12

    Насколько вы уверены в том, что Ваш алгоритм работает?

    graph = {
    1: {2: 1, 3: 10},
    2: {4: 1},
    3: {5: 1},
    4: {3: 1},
    5: {}
}

    Вот на таком графе он выдает расстояние от 1 до 5, равное 11, при этом существует путь 1->2->4->3->5 длины 4. Условие из пункта "Важно!" вроде как выполнено.


    1. mk2
      27.04.2024 14:26
      #26769647
      +4

      Если ребро ведёт из "нижней вершины" в "верхнюю" и обновляет путь до "верхней" вершины, все пути из "верхней" тоже нужно пересчитывать. Представленный алгоритм это не делает.

      Алгоритм Дейкстры этого не делает, потому что он обходит вершины в порядке наименьшей дистанции до исходной, и благодаря отсутствию отрицательных рёбер имеет строгую математическую гарантию, что обновить путь не придётся.

      У автора порядок обхода вершин задаётся на входе и если он "правильный" - вершины сразу отсортированы по дистанции от начальной - всё будет работать как надо. Если "неправильный" - как видно по этому тесткейсу, работать не будет.


      1. 1CHer
        27.04.2024 14:26
        #26769907
        +1

        Да, повеселили конечно у автора первое условие, по сути отсортируйте сначала а потом уже я найду. В этом условии и есть решение. Так ведь?


        1. carbon2409 Автор
          27.04.2024 14:26
          #26770023
          +1

          Исправил код, посмотрите, пожалуйста, еще раз на реализацию


    1. carbon2409 Автор
      27.04.2024 14:26
      #26770015
      +1

      Спасибо, что привели пример такого вида графа. Я протестировал этот граф, саму цепочку нод он правильно посчитал, но вот с расстоянием да, ошибся. Как вариант, модифицировал код, чтобы он просто проходил по цепочке и обновлял расстояние. Посмотрите еще раз на функцию "get_shortest_path". Костыль, но работает :)


      1. Ababaj
        27.04.2024 14:26
        #26770225
        +9

        Это математическая задача теории графов - не самой сложной математики и не Pythоn-ом ее решают, а головой!


        1. carbon2409 Автор
          27.04.2024 14:26
          #26770253

          Так пожалуйста, решайте головой! Берите карту местности вместо смартфона c навигатором и на листочке считайте, как быстрее всего доехать из условной Москвы до Сочи. Уверен, занятие Вам будет по душе :)


          1. carbon2409 Автор
            27.04.2024 14:26
            #26770575

            Странно, что меня минусуют, ведь я воспринял комментарий так: "Ты питонист, ты не математик! Все питонисты - не математики! Так что не лезь в нашу нишу, программист!" Я и ответил соответствующе, м.б, если обидел, извини, конечно, но и ты меня задел, на самом деле.


            1. randomsimplenumber
              27.04.2024 14:26
              #26770779
              +13

              Математические задачи решаются головой, на питоне кодятся. Сначала - доказательство, что алгоритм корректный, потом - его реализация. Ну, или тестами обмазывать.


              1. carbon2409 Автор
                27.04.2024 14:26
                #26771483
                +2

                Я не математик, я вообще даже в техническом ВУЗе не учился. А учился я на биолога-химика. В IT сферу ушел, потому что мне с детства нравилась эта тема, но родители хотели, чтобы я был медиком :) В итоге математический бэкграунд у меня хромает. Поэтому и пишу здесь, в надежде найти людей компетентнее. Спасибо!


                1. Katasonov
                  27.04.2024 14:26
                  #26774447
                  +2

                  "Я реализовал, похоже, собственный алгоритм поиска кратчайшего пути". Вот прям прочитав начало статьи сразу стало понятно что образование у вас не профильное. Это не в обиду сказано, просто рекомендация потратить много месяцев на базу.


              1. Ababaj
                27.04.2024 14:26
                #26776735

                Позвольте дополнить: математическая задача решается одним из методов ее решения с доказательством; каждый метод генерирует десятки алгоритмов, может сотни; каждый алгоритм может быть запрограммирован тысячами способов, пионтстами, бейсикистами, СИ-иистами, и т.д. В примитивных задачах, часто, метод=алгоритму!


          1. Ababaj
            27.04.2024 14:26
            #26776147

            Вы спутали голову с задницей!

            А следующий ваш ответ-жалоба ниже лишён логики, что означает: вам не понять алгоритмы! Так что даже, если начнёте с нуля, матрицы и их умножения, а это 9 клас советской школы - бесполезно! Лучше подайте в суд на Российское образование, что утерян ещё один пытливый ум!


  1. CorwinH
    27.04.2024 14:26
    #26769353
    +7

    Прохождение по соседям узла. Занимает O(E), где Е - количество ребер в графе. Т.к. это константа, то ее опускают.

    Это не константа. Максимальное число рёбер зависит от количества узлов. Вы не можете утверждать, чт для любого количества узлов N у графа будет "не более Е рёбер", где Е - константа.

    И далее в формуле Вы пишете O(n^2 + E), как будто Вы обходите соседей только для одного, а не для всех узлов.


    1. middle
      27.04.2024 14:26
      #26770541
      +1

      Более того, максимальное количество рёбер в графе квадратично от количества вершин.


      1. Tiriet
        27.04.2024 14:26
        #26771697
        +1

        А минимальное количество ребер в связном графе- линейно от количества вершин E>=N-1.


    1. carbon2409 Автор
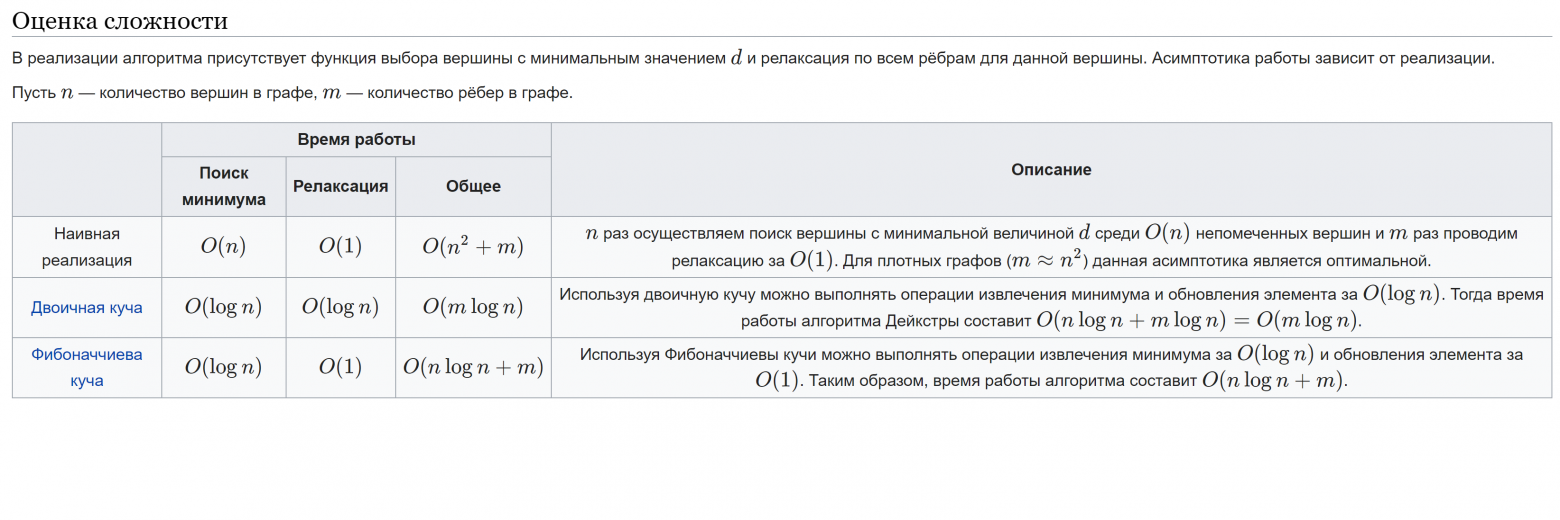
      27.04.2024 14:26
      #26770621

      Я описал сложность оригинальной Дейкстры, не совсем понял Вашего исправления. Пояснения в картинке. Источник


      1. anonymous
        27.04.2024 14:26
        #26771615

        НЛО прилетело и опубликовало эту надпись здесь


      1. CorwinH
        27.04.2024 14:26
        #26771763
        +1

        Я описал сложность оригинальной Дейкстры, не совсем понял Вашего исправления.

        1) В описании сложности алгоритма Дейкстры нигде не написано, что E - это константа и её можно опустить.

        2) В оригинальном алгоритме Дейкстры каждое ребро встретится во внутреннем цикле только один раз (для неориентированного графа - 2 раза). Написанное Вами "Мы будем смотреть не минимальный по весу необработанный узел, а смотреть вообще ВСЕХ соседей поочередно" я понял так, что у Вас одно ребро может рассматриваться более одного раза.


  1. Rsa97
    27.04.2024 14:26
    #26769409
    +3

    IMHO, так гораздо проще:

    Для всех узлов записываем длину пути (бесконечность), путь в узел (пусто) и количество родительских узлов.
Создаём очередь узлов для обработки. Помещаем туда стартовый узел,
Пока не дошли до конца очереди.
  Выбираем следующий узел из очереди.
  Для каждого его дочернего узла.
    Если стоимость пути через родительский узел меньше сохранённой, то запоминаем новую стоимость и новый путь.
    Уменьшаем счётчик родительских узлов. Если он равен нулю, то добавляем дочерний узел в очередь для обработки.
Восстанавливаем обратный путь из финального узла.


    1. carbon2409 Автор
      27.04.2024 14:26
      #26770037

      Спасибо за упрощение объяснения! Надеюсь, кому-то оно позволит понять мысль лучше.


      1. Rsa97
        27.04.2024 14:26
        #26770187
        +2

        Это не упрощение вашего объяснения, а несколько другой алгоритм.


  1. vode_an
    27.04.2024 14:26
    #26769497
    +15

    Когда кажется - юнит тесты писать нужно


  1. malkovsky
    27.04.2024 14:26
    #26769615
    +36

    Поставил минус. Статья выглядит примерно так: "мне понравилось изучать алгоритмы, я много интересовался задачей о кратчайших путях и думаю, что мне удалось придумать что-то новое, но в моём окружении нет достаточно компетентных людей, которые бы молги объяснить получилось или нет и почему. Поэтому я напишу статью на хабре и может там мне подскажут". Рвение похвально, но хабр не место для таких статей, для этого есть например stackoverflow.

    По существу:
    * Ваш алгоритм работает за O(E)
    * Ваш алгоритм НЕ выдаёт корректные кратчайшие пути

    Пример уже писали выше, поделюсь своим

    Hidden text

    graph = { 1: {2: 20, 3: 30, 4: 10}, 3: {2: 1}, 4: {3: 1} }

    --> Минимальные стоимости от источника до ноды: {2: 20, 3: 11, 4: 10}

    Если поменять местами описание 3 и 4, то расстояния будут корректными

    За алгоритм поиска кратчайших путей, который работает O(E) нобелевскую премию не дадут, а вот премью Тьюринга вполне возможно, правда над этим после Дейкстры/Данцига бьются уже 60 лет, есть почти за O(E), но не совсем (надеюсь коллеги поправят если что).

    По уровню материала кажется, что Вам следует разобраться с доказательствами корректности и сложности Дейкстры, Форда-Белламна и Флойда-Уоршела. Если после этого не отпадет желание изучать CS, то вот отличная обзорная презентация от Гольдберга по кратчайшим путям.

    Искренне желаю удачи, молодым талантам надо помогать, но и не позволять филонить!


    1. carbon2409 Автор
      27.04.2024 14:26
      #26769963
      +23

      "мне понравилось изучать алгоритмы, я много интересовался задачей о кратчайших путях и думаю, что мне удалось придумать что-то новое, но в моём окружении нет достаточно компетентных людей, которые бы молги объяснить получилось или нет и почему. Поэтому я напишу статью на хабре и может там мне подскажут"

      Вы абсолютно правы, я самоучка, у меня нет в окружении ни преподавателей, ни знакомых, кто этим интересуется.

      Рвение похвально, но хабр не место для таких статей

      А теперь приведу текст политики самого хабра

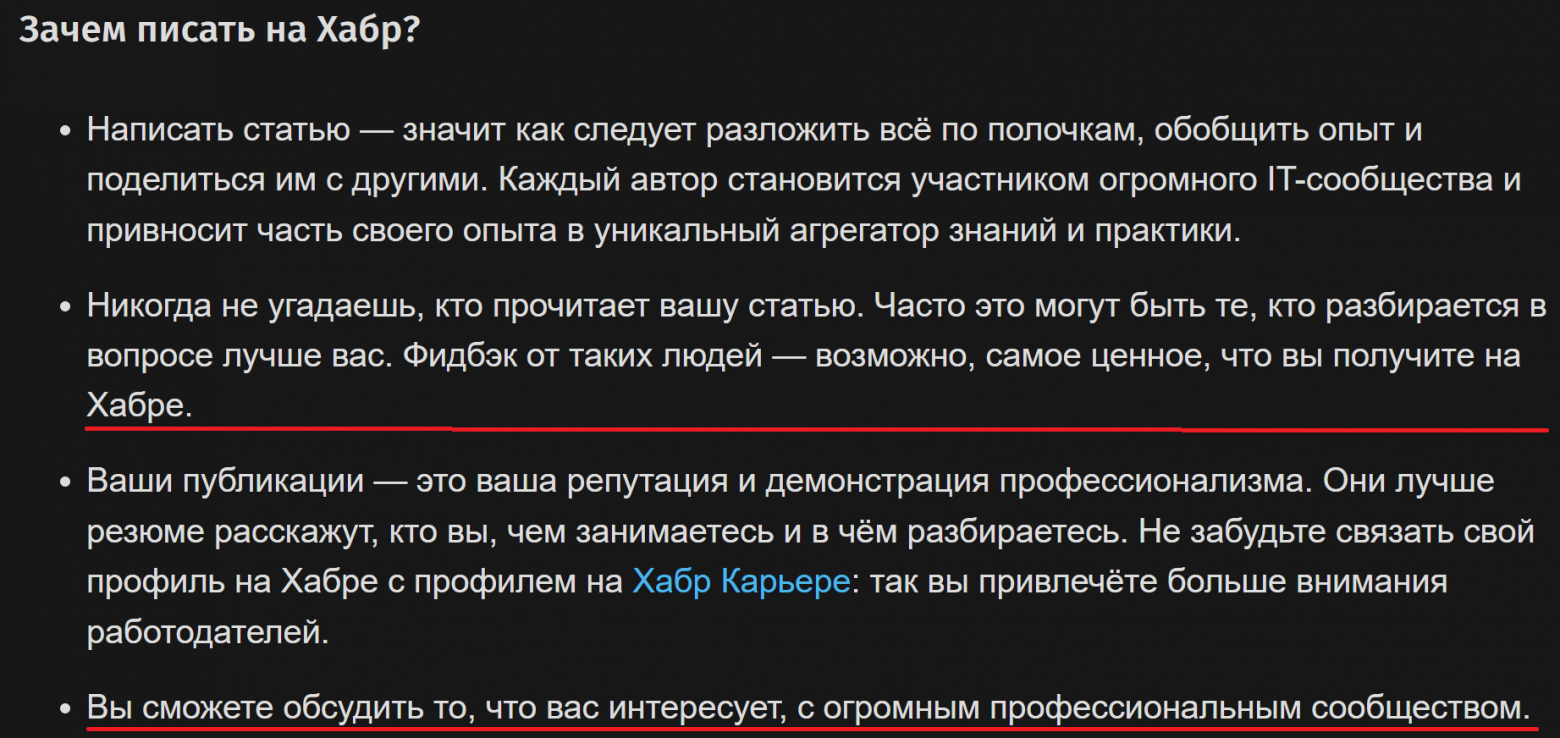
      Считаю, что ставить минус и "хейтить" за то, чем пользуешься по правилам и следуя философии площадки наравне с "моргать дальним и сигналить впереди едущему автомобилю, который едет по ПДД", мол я тут уже не первый год "за рулем", знаю как тут все устроено... В общем, суть уловили, я думаю.

      нобелевскую премию не дадут

      Здесь, очевидно, была шутка, но если и Вы шутили, то ок

      Пример уже писали выше, поделюсь своим

      graph = { 1: {2: 20, 3: 30, 4: 10}, 3: {2: 1}, 4: {3: 1} }

      --> Минимальные стоимости от источника до ноды: {2: 20, 3: 11, 4: 10}

      Если поменять местами описание 3 и 4, то расстояния будут корректными

      Не совсем понял, что не так с этим примером? Вы откуда и куда хотите попасть? Если с 1 до 4 ноды, то будет 10, т.е. все правильно.

      * Ваш алгоритм работает за O(E)

      Вот тут очень спорно, на самом деле, но я не силен в оценивании ассимптотики, поэтому, думаю, коллеги смогут что-то сказать по этому поводу.

      Спасибо за фидбэк!


      1. malkovsky
        27.04.2024 14:26
        #26770663

        Считаю, что ставить минус и "хейтить"

        Я не очень понимаю значения глагола "хейтить", но полагаю, что оно было бы более применимо, если бы я например просто молча поставил минус.

        Здесь, очевидно, была шутка, но если и Вы шутили, то ок

        Постирония на тему того, что если бы Ваш алгоритм действительно работал, то шутка про нобелевскую премию была бы не такой уж и шуткой.

        Не совсем понял, что не так с этим примером? Вы откуда и куда хотите попасть? Если с 1 до 4 ноды, то будет 10, т.е. все правильно.

        Расстояние от 1 до 2 это 12 (1->4->3->2), а алгоритм посчитал 20

        Вот тут очень спорно

        Каждая вершина обрабатывается во внутреннем цикле ровно один раз. Учитывая, что граф обрабатывается списками смежности, то суммарное количество итераций внутреннего цикла -- в точности количество ребер. Если быть более точным, то оценка O(V+E).


        1. carbon2409 Автор
          27.04.2024 14:26
          #26771129
          +1

          Я не очень понимаю значения глагола "хейтить", но полагаю, что оно было бы более применимо, если бы я например просто молча поставил минус.

          Согласен, вы хотя бы рассказали, что не так, высказали ваше мнение, спасибо, учту.

          Расстояние от 1 до 2 это 12 (1->4->3->2), а алгоритм посчитал 20

          Я исправляю эту ситуацию. Подробнее ниже описал. Следим за ситуацией, как говорится :)

          Каждая вершина обрабатывается во внутреннем цикле ровно один раз. Учитывая, что граф обрабатывается списками смежности, то суммарное количество итераций внутреннего цикла -- в точности количество ребер. Если быть более точным, то оценка O(V+E).

          Слушайте, если это действительно так, т.е. пока что неработающий алгоритм работает за линейное время, то можно обработать ту проблему, которая ломает алгоритм и тогда сложность будет, если не ошибаюсь, составлять O(n^2). Сейчас есть исправленный код, я его тестирую, если все работает нормально, дополню статью. Становится еще интереснее!


    1. KvanTTT
      27.04.2024 14:26
      #26770049
      +48

      Рвение похвально, но хабр не место для таких статей, для этого есть например stackoverflow.

      Хабр - место в том числе и для таких статей, не нужно тут элитарность вводить.


    1. edogs
      27.04.2024 14:26
      #26770107
      +55

      Поставил минус. Рвение похвально, но хабр не место для таких статей, для этого есть например stackoverflow.

      Во-первых, эта статья более техническая и качественная чем 80% статей которые мы видели за последние полгода. Работающий код. Рассуждения. Обоснование. Огромные перспективы на развитие еще боле грамотной дискуссии в комментах.
      Во-вторых, стэковерфлоу сейчас настолько токсичный (уж насколько мы не любим это слово, но тут только оно) междуусобойчик для олдов, что новичку там появляться страшно. Найти решение там - гуд, задавать вопросы или публиковаться - ну на фиг.
      Автора и статью яростно плюсуем:)


      1. carbon2409 Автор
        27.04.2024 14:26
        #26770197
        +1

        Спасибо за добрую оценку!


      1. Lodinn
        27.04.2024 14:26
        #26770649
        +6

        Ironic.

        Буквально на днях с коллегами спорил, слышал от них ровно обратное - что на stackoverflow соваться не страшно: там помогут не создавая ощущения, что ты - тварь ничтожная, а вот от хабра или тем более ЛОРа такое ощущение есть. По тону статьи хорошо заметно, что автору хочется фидбека, но он боится разгрома в комментах и/или минусов в карму. Это вполне можно рассматривать как признак не очень здоровой среды. А можно и не рассматривать.

        Рискну предположить, что дело в индивидуальной чувствительности и предпочтениях в обучении. Ну и, конечно, совсем разный формат.


        1. ImagineTables
          27.04.2024 14:26
          #26772023

          там помогут не создавая ощущения, что ты - тварь ничтожная

          Если спросить в стопицотый раз, как отцентрировать див внутри дива, то помогут: вопрос закроют, а тебе дадут ссылку на предыдущий, раз сам искать не умеешь.

          А спроси, как писать оптимальные по производительности селекторы и стили, так сразу «ненастоящий вопрос».

          А ещё как-то я постил вопрос про CSS, сопроводив его для иллюстрации разметкой на кастомном языке (диалект HTML, абсолютно очевидный), которую тупо скопировал из проекта. И хотя вопрос касался строго CSS, а разметка была приведена для пущей понятности, ни одна тварь не ответила про CSS, зато около десяти тварей сочло своим долгом написать, что я не умею в HTML. После пояснений, что это код не для браузера, вопрос закрыли как ненастоящий (!!!).

          Это нормально и абсолютно предсказуемо, потому что приход таков, каков поп, а основатели, в первую очередь дядя Джоэл, показали себя, введя изменения правил спустя годы после открытия проекта, и удалив дохренищща полезного контента, который висел у меня в закладках. Надо быть настоящим говнюком, чтобы придавать законам обратную силу без очень веских причин.


        1. MyraJKee
          27.04.2024 14:26
          #26776515

          Согласен с вашими коллегами.


    1. Weron2
      27.04.2024 14:26
      #26770171
      +11

      Я тоже заступлюсь за автора. Среди множества последних статей, к этой статье меньше всего вопросов что она делает на хабре. Более того как уже поясняли, хабр это то место где можно получить хорошую обратную связь (я сам этим пользуюсь и буду пользоваться), и поэтому я считаю что нужно таких статей еще больше. поэтому статье и автору плюс однозначный. И вам плюс за за то что делаете хабр тоже лучше) В отличие от других минусаторов, вы хотя бы даете обратную связь, аргументируете, даете полезные советы.


      1. carbon2409 Автор
        27.04.2024 14:26
        #26770257
        +1

        Спасибо большое, как начинающему автору, очень приятно!


    1. Fen1kz
      27.04.2024 14:26
      #26770463
      +14

      Поставил вам минус за элитарность. Из-за вас хабр и превратился в помойку с "новостями"


      1. malkovsky
        27.04.2024 14:26
        #26771503
        +4

        А каким образом? Я изредко пишу технические статьи в области где хорошо разбираюсь, дал развернутый комментарий автору по поводу фундаментальных технических проблем статьи.

        Вы пришли и сказали, что я хам, поэтому поставите мне минус, не дав при этом ни автору, ни комьюнити никакой полезной информации по теме.

        А точно из-за меня хабр помойкой с новостями?


    1. APh
      27.04.2024 14:26
      #26770501
      +9

      Мне кажется, что одна из крупных и давних проблем Хабра -- снобизм. О чём автор и написал.

      Ещё одна -- двойные стандарты. Когда похают Россию -- норм. Если только отпустишь сарказм про США, то карму занизят, что даже и лайки не работают. ))

      Демократия... ))

      Мне, лично, кажется, что не стоит самодельным авторам так бить по рукам.

      Пусть пишут. Рейтинг статьи сам по себе должен регулировать этот вопрос: показы, рейтинг автора, в конечном итоге и пр.

      Иначе, получится, как в Википедии, где, вроде, как народное голосование по всем вопросам, но...

      Если добавляешь данные о применении кассетного минирования жилых кварталов на востоке самостийной, то бан. А если рассказать без ссылок и доказательств про Бучу, то медали выдают.

      Надо тоньше работать. И давать дорогу молодым.


      1. IvanPetrof
        27.04.2024 14:26
        #26770643
        +2

        Карму и за сарказм про Россию сливают. Но комменты плюсуют. Я регулярно это проверяю))


  1. thevlad
    27.04.2024 14:26
    #26770025
    +2

    У вас в статье собственно три основные проблемы:

    1. "Нужно писать узлы графа в порядке их отдаленности от источника. Т.е.
      сперва описываем первых соседей источника. После того, как описали их,
      приступаем к следующим соседям соседей."

    Таким образом вы решаете не известную задачу, а какую-то другую. Соответственно, чтобы получить честные оценки асимптотики, нужно добавить этот этап препроцессинга

    1. Сложность Дейкстры при нормальной реализации, это "Dijkstra's algorithm with Fibonacci heap O ( E + V log ⁡ V )", или "Dijkstra's algorithm with binary heap O ( ( E + V ) log ⁡ V)" https://en.wikipedia.org/wiki/Shortest_path_problem (то есть фактически близко к линейному)

    2. Ваш алгоритм не работоспособен для негативных и положительных весов в общем случаи, то есть не является аналогом Bellman–Ford.


    1. carbon2409 Автор
      27.04.2024 14:26
      #26770069

      1. А каким образом Вы представляете граф во входную точку программы? Произвольные ноды и описание их соседей? Насколько помню, даже та же матрица смежностей реализует представление графа "по порядку". Даже возьмем ту же карту и текущую геопозицию. На вход программе уже будет произведен поиск в ширину и все будет по порядку. Не представляю, как можно подать на вход описание нод в разнобой, м.б. имеет место быть где-то, но это можно обработать в коде, поэтому, возможно Вы и правы насчет сложности.

      2. Я об этом написал вообще-то, что сложность с реализацией приоритетной очереди будет такая, но она не всегда будет такой, в редких случаях "быстрее будет медленный алгоритм", как бы тавтологически не звучало.

      3. Аргументируйте, пожалуйста. Приведите пример графа и разберемся вместе. По существу, это пальцем в небо тыкнули.


      1. thevlad
        27.04.2024 14:26
        #26770201
        +6

        1. Не надо пожалуйста издеваться над здравым смыслом. Определение графа знаете? Набор вершин и дуг, в котором дуги являются парами связных вершин, плюсом веса для дуг в нашем случаи. Никакого порядка там в принципе не предусмотрено. Не говоря уже о различных представлениях в виде матриц смежности.

        3. Замените половину весов на отрицательные и посмотрите, что там посчитается.


        1. carbon2409 Автор
          27.04.2024 14:26
          #26771437
          +1

          Определение графа знаете? Набор вершин и дуг, в котором дуги являются парами связных вершин, плюсом веса для дуг в нашем случаи. Никакого порядка там в принципе не предусмотрено.

          Хорошо, буду от вашей структуры отталкиваться. У нас какая задача? Найти кратчайший путь из точки А в точку В. Находим в вашем представлении графа точку А и смотрим на его соседей. Потом находим этих соседей и смотрим их соседей и т.д. Вот это "находим" в вашей беспорядочной структуре будет за N выполняться N раз. Это будет в том случае, если ноды у вас просто беспорядочно расположены в массиве (если вы используете эту структуру данных для хранения). Обычно в программе номер ноды совпадает с номером ячейки в массиве, что позволяет получить к этой ноде доступ за константу. В алгоритме Дейкстры (не я придумал его) как раз таки задача решается именно таким представлением графа, где номер ноды (или буква в лексиграфическом порядке) совпадает с номером ячейки в массиве. То, как вы пытаетесь представить граф - это по сути выстрел себе в ногу. Если отталкиваться от реальной жизни, нужно еще реализовать построение такой структуры графа. Условно ты находишься на перекрестке 1, мне надо в перекресток 10. А дай ка гляну, какие там дороги исходят из перекрестка 7 и запишу. Хотя можно было на второе место записать дороги перекрестка 2. В общем, замечание ваше понятно, но это все общепринятая условность представления данных графа, я это не придумывал.

          Замените половину весов на отрицательные и посмотрите, что там посчитается.

          И все будет работать, в чем подвох? Если вы хотите сделать отрицательный вес графу, который направлен обратно, то это будет отрицательный цикл, а я писал о том, что на таких графах алгоритм не работает (он уйдет в беск. минимизацию веса). На таком графе и дефолтный Беллмана-Форда не будет работать, в чем тогда Ваша претензия. Спасибо!


      1. Lodinn
        27.04.2024 14:26
        #26770681
        +4

        Если что, есть три классических представления графа - списки вершин и рёбер, матрица смежности, список смежности. Нигде не гарантируется упорядоченность. Это часть задачи.

        Пользуясь примером с картой, пусть на входе есть список городов в алфавитном порядке. В том же порядке даны соответствующие рёбра графа. Где-то в самом начале "пути" от Владивостока до Хабаровска встретятся Владикавказ, Воркута и Выборг. Решением задачи мы, собственно, пытаемся навести порядок в структуре, сотворённой без учёта взаимного расположения городов и доступности транспорта. Так понятнее?

        "На входе будет произведён поиск в ширину" - тогда включайте в алгоритм. Тоже путь.


        1. carbon2409 Автор
          27.04.2024 14:26
          #26771455

          тогда включайте в алгоритм

          Хорошо, допустим, включу, но от этого общая сложность не изменится. Поиск в ширину за линейное время выполняется, если граф представлен в корректной структуре данных. Поправьте, если не прав. Спасибо!


          1. Lodinn
            27.04.2024 14:26
            #26772627

            Всё так, но именно поэтому этому утверждению самое место в исходном обосновании ;) Так сразу можно сказать, что если кто не по фэншую принёс данные, то ещё E log E набежит на сортировку рёбер графа, например.

            Да, и ещё - сложность для обхода графов обычно выражают как функцию количества рёбер и количества вершин, не пренебрегая ни одной из компонент. А то вдруг решите натравить алгоритм на полные графы, и тут-то выяснится, что O(E) - это O(N^2). А может быть, ближе к O(N). В общем, в таком представлении полезнее выходит.


  1. NoobodyKms
    27.04.2024 14:26
    #26770157
    +2

    Хорошая статья, делай еще! Идея неплохая!


  1. insecto
    27.04.2024 14:26
    #26770405
    +3

    Чёт я не понял зачем новый алгоритм. Разве нельзя ко всем весам прибавить 4 и свести задачу к неотрицательным весам?


    1. KvanTTT
      27.04.2024 14:26
      #26770469
      +1

      Тоже такое первое приходит в голову, когда вижу граф с отрицательными весами.


    1. Rsa97
      27.04.2024 14:26
      #26770477
      +11

      Нельзя.
      Возьмём граф (AB: -2, BC: 2, AС: 1). Очевидно, что путь ABC со стоимостью 0 выгоднее, чем AC со стоимостью 1.
      Теперь добавим 2 ко всем рёбрам, чтобы избавиться от отрицательной стоимости. Получим граф (AB: 0, BC: 4, AC: 3). Путь ABC теперь имеет стоимость 4, а путь AC стоимость 3, что явно не соответствует исходному графу.
      В общем, ваша "добавка" будет входить в путь столько раз, сколько рёбер на этом пути.
      И, соответственно, чем больше рёбер имеет путь, тем большая стоимость к нему добавится.


      1. FF_hunter
        27.04.2024 14:26
        #26770563

        Если бы всё было так просто, то можно было бы в конце расчетов вычесть эту добавку столько раз, сколько ребер в итоговом пути получилось. Подозреваю, что при этом сломается динамическое программирование при обходе вершин.


        1. Rsa97
          27.04.2024 14:26
          #26771413

          Обязательно сломается.
          Классический алгоритм Дейкстры это модификация волнового алгоритма. Если представить, что волна распространяется по графу с фиксированной скоростью, а веса рёбер - это длины пути, то фактически минимальная стоимость пути до определённого узла - это время прихода в него волны. Отрицательные стоимости рёбер, как и вычитание добавки, отправляют волну в прошлое и она может прийти в уже обработанный алгоритмом узел, а повторная обработка узлов алгоритмом Дейкстры не предусмотрена.


    1. qazzar
      27.04.2024 14:26
      #26770525

      Контрпример, пользуясь терминологией автора:

      graph = {
    1: {2: -4, 3: 7}
    2: {3: 10}
    3: {}
}

      Проблема в том, что прибавляемая сумма зависит от длины пути.

      1 -> 2 -> 3 (два ребра)

      1 -> 3 (одно ребро)


  1. kirillgrachoff
    27.04.2024 14:26
    #26770519
    +2

    Возможно, автору понравится алгоритм Джонсона и алгоритм Дейкстра с Фибоначчиевой кучей. Можно посмотреть лекции МФТИ авторства Филиппа Руховича. Там есть довольно интересные алгоритмы, сложность которых довольно неплохая, если выполнены некоторые хитрые соотношения на V и E.

    https://neerc.ifmo.ru/wiki/index.php?title=Алгоритм_Джонсона
    https://neerc.ifmo.ru/wiki/index.php?title=Фибоначчиева_куча
    https://youtu.be/zeB-DgV53d0?si=ZjF1oBvWHoQlsqjw


  1. psi_lion
    27.04.2024 14:26
    #26770521
    +2

    Если дать этой программе на вход вершины в том порядке, в котором они идут в искомом кратчайшем пути -- то она вероятно его найдёт. Проблема в том, что у порядка обхода в ширину такого свойства нет, так что вы просто спрятали сложность алгоритма в этот препроцессинг. Выше уже приводили несколько контрпримеров, даже без отрицательных весов, я приведу версию, в которой parents тоже считается некорректно:

    Hidden text
    graph = {    
    1: {2: 1, 3: 20, 5: 10},
    2: {4: 1},
    3: {5: 1},
    5: {},
    4: {3: 1},
}
#   1 ---
#  / \   \
# 2   3 - 5
# | /
# 4

# outputs:
costs = {2: 1, 3: 3, 5: 10, 4: 2}
parents = {2: 1, 3: 4, 5: 1, 4: 2}
# на самом деле должно быть parents[5] == 3 и costs[5] == 4 
# (1 -> 2 -> 4 -> 3 -> 5)

    Вся программа работает за O(V + E) (если доступ ко всем использованным питоновским структурам данных работает за (амортизационное) O(1), но это вроде правда), так как внутренний цикл проходится по всем рёбрам по 1 разу, а внешний -- по всем вершинам, и это оптимальное время, за которое можно из правильно отсортированного списка вершин получить кратчайшие расстояния, но сама сортировка займёт больше времени.

    Ещё не совсем понял, зачем вам нужен processed , как будто бы в него просто переписываются все пройденные вершины, которые и так обрабатываются ровно 1 раз, поскольку внешний цикл проходится по ним ровно 1 раз


  1. krammnic
    27.04.2024 14:26
    #26770523

    1. Не очень полезно с существованием SPFA

    2. Необходимо более строгое доказательство и оценки/проверки на случайных графах, например модели Эрдеша-Реньи


  1. kuzinat0r
    27.04.2024 14:26
    #26770549
    +3

    Привет! Не хочу расстраивать, но у вас не получилось создать собственный алгоритм) И даже модификации Дейкстры не вышло.

    Первое - проверка processed ничего не делает. Вы никогда не попытаетесь повторно обработать узел, если у вас не будет дубликатов ключей в хэш-таблице.

    Второе - это не Дейкстра, а всего лишь один проход Беллмана-Форда. То, что у вас граф задан матрицей смежности, а не списком рёбер, ничего не меняет. Посмотрите сами - для каждого узла вы рассматриваете все исходящие из него рёбра. После обработки каждого узла вы просмотрите всё рёбра в графе - что и делает Беллман-Форд. Но! - вы это делаете всего один раз, поэтому ваш алгоритм заведомо некорректен.


  1. qazzar
    27.04.2024 14:26
    #26770597
    +4

    Недопонимание основано на том, что автор ищет путь в ориентированном графе, что является тривиальным алгоритмом. В свою очередь, алгоритмы Дейкстры и Форда-Беллмана без проблем работают на неориентированных графах.

    Если рассмотреть работу данного алгоритма на неориентированном графе, то сразу возникнут проблемы:

    Проблема 1. Неправильная ориентация ребра на этапе препроцессинга (этап, который автор решил опустить в посте).

    Фраза "Нужно писать узлы графа в порядке их отдаленности от источника" крайне расплывчата и, если я правильно понял, может привести, например, к такому:

    Дано: Неориентированный граф с 5-ю вершинами

    Ребра: (1, 2), (1, 3), (2, 5), (2, 6), (3, 4), (4, 5)

    Найти кратчайший путь от 1 до 6

    Порядок "отдалености" от начальной вершины может быть таким, что ребра ориентируются так:

    1 -> 2, 1 -> 3, 2 -> 5, 2 -> 6, 3 -> 4, 4 -> 5

    Как видно, в изначальном неориентированном графе есть путь 1 -> 3 -> 4 -> 5 -> 2 -> 6. В измененном ориентированном графе такого пути нет (нет ребра 5 -> 2). Если этот путь самый короткий, то алгоритм его не найдет.

    Проблема 2. Проблема возникает только если закрыть глаза на первую проблему и остальные шероховатости алгоритма, которые разобраны в других комментариях, но всё же я опишу и её.

    Можно подвесить неориентированный граф за начальную вершину так, чтобы проблемы 1 не возникло. Но в таком случае алгоритм находит (не без доработок) расстояние (и путь) только от одной конкретно заданной вершины до другой конкретно заданной вершины. Напомню, что, например, Дейкстра находит от одной до всех остальных.

    Дабы не быть голословным:

    Дано: Неориентированный граф с 4-мя вершинами

    Ребра: (1, 2), (1, 3), (2, 4), (3, 4)

    Веса: (1, 2) -> 10, остальные по 1

    Найти кратчайший путь от 1 до 4

    Ориентируем граф: 1 -> 2, 1 -> 3, 2 -> 4, 3 -> 4 (учли все возможные пути из вершины 1 в вершину 4)

    Кратчайший путь найден: 1 -> 3 -> 4 (вес: 2)

    Какой же за кратчайший путь от вершины 1 до вершины 2? Согласно алгоритму 1 -> 2 (вес: 10). Верный же ответ: 1 -> 3 -> 4 -> 2 (вес: 3)

    P.S. Автору шлю лучи поддержки! Посту поставил плюс, ведь главное разобраться, а не устраивать срач.


    1. mk2
      27.04.2024 14:26
      #26770669
      +3

      > автор ищет путь в ориентированном графе, что является тривиальным алгоритмом

      Неориентированный граф - частный случай ориентированного, проблема не в этом. Проблема в том, что автор ищет путь в ациклическом графе.

      И ациклический граф мы действительно можем топологически отсортировать и рассчитать расстояния от одной вершины до всех за O(N+E)

      А вообще, как заметили выше, это практически действительно один шаг Форда-Беллмана. Но вершины ациклического графа как раз можно обрабатывать в порядке топологической сортировки, и при этом одного шага достаточно.


      1. qazzar
        27.04.2024 14:26
        #26772125

        Полностью соглашаюсь с вышесказанным. Извините, ошибся.

        Действительно неориентированный граф можно представить как ориентированный циклический. Тогда проблема с топологической сортировкой вершин возникает не только в неориентированных (как я написал), но и во всех циклических графах.


  1. Dmitri-D
    27.04.2024 14:26
    #26770723
    +1

    это не справедливо требовать предупорядоченности графа под исходную точку, и не учитывать сложность предупорядочивания. Обычно граф задан заранее. Например - граф дорог. Ширина дорог, наличие поворотов, светофоров, переходов и пр. учитваются в виде весов. Сейчас нужно посчитать лучший машрут из точки А в Z, а через секунду для другого пользователя из K в G. И значит надо постоянно предупорядочивать чтобы ваш алгоритм работал. Я правильно понимаю суть важных ограничений?


  1. TimID
    27.04.2024 14:26
    #26770819
    +2

    Самообман в оценке сложности алгоритма виден невооруженным взглядом. Она связана с непониманием вычислительной сложности используемых программных конструктов (и показывает, почему Python не считается приемлемым для обучения базовым методам программирования) - очень многие действия кажутся "бесплатными". Например, использование множеств и самосортирующихся списков - да-да, это всё тоже считается в оценке сложности.
    А в остальном алгоритм - просто немного кривая реализация Дейкстры, но не в варианте "оптимально растущей границы" (традиционный метод), а комбинация поиска в ширину с поиском в глубину. Причем с апостериорной оценкой удаленности узлов. За счет ... хм, "бесплатного" множества, которое, как бы "сразу знает", а не перебирает всё, что в него накидано, при каждом запросе.
    И вот что ещё важно. Реальный граф, по которому ищется путь - это тысячи узлов и, часто, намного больше. В таких ситуациях любое "оптимизация" вроде сортировок всех узлов - огромная вычислительная нагрузка.


    1. carbon2409 Автор
      27.04.2024 14:26
      #26771821
      +2

      использование множеств и самосортирующихся списков - да-да, это всё тоже считается в оценке сложности

      Какие "самосортирующиеся списки" вы имеете в виду, поясните, пожалуйста.

      За счет ... хм, "бесплатного" множества, которое, как бы "сразу знает", а не перебирает всё, что в него накидано, при каждом запросе

      В алгоритме операция с множеством осуществляется за константное время, там ничего не перебирается, а лишь проверяется наличие элемента в этом множестве. Напомню, множество в Python реализовано хэш таблицей.

      Python не считается приемлемым для обучения базовым методам программирования

      Здесь мне сказать нечего, очень и очень спорное выражение, пожалуй, не буду его развивать.

      И вот что ещё важно. Реальный граф, по которому ищется путь - это тысячи узлов и, часто, намного больше. В таких ситуациях любое "оптимизация" вроде сортировок всех узлов - огромная вычислительная нагрузка.

      Про это я уже написал, прочтите, пожалуйста, выше.

      Благодарю!


  1. guliverza
    27.04.2024 14:26
    #26771627

    1


  1. malkovsky
    27.04.2024 14:26
    #26771743
    +5

    Комментарий по алгоритму в update 2.

    Я не готов ручаться за мелкие баги, но в целом ваш алгоритм должен работать, так как Вы переизобрели алгоритм Форда-Беллмана с реализацией на очереди, можно про это почитать вот тут

    https://acm.math.spbu.ru/~sk1/courses/1718s_au/conspect/conspect.pdf
    https://algs4.cs.princeton.edu/44sp/

    Также стоит отметить, что по форме алгоритм очень схож со scanning method (его кстати тоже Форд придумал), который является общим видом для большинства известных алгоритмов поиска кратчайшего пути, различающихся лишь тем как выбирать очередную вершину из lst. При выборе наименьшей по расстоянию получается Дейкстра, при выборе в порядке обычной очереди получается Форд-Беллман. Про этот метод можно прочитать в том числе в презентации Гольдберга, ссылку на которую я уже присылал

    http://forskning.diku.dk/PATH05/GoldbergSlides.pdf


    1. carbon2409 Автор
      27.04.2024 14:26
      #26771799

      Здравствуйте! Вижу, Вы подкреплены в теме. Сейчас, к сожалению, нет возможности просмотреть и изучить вами присланный материал. Можете, пожалуйста, сказать, правильно ли я оценил сложность (N^2) и какова сложность уже известного алгоритма, о котором Вы упоминаете? Насколько помню, у Беллмана-Форда кубическая сложность, про модификацию его алгоритма я не слышал. Спасибо!


      1. malkovsky
        27.04.2024 14:26
        #26771845
        +2

        @wataruв соседней ветке написал, что сложность у Форда-Беллмана O(VE) и пример хороший привел где, к сожалению, отдельные оптимизации его асимптотически не ускоряют (т.е. оптимизации работают, алгоритм отрабатывает быстрее, но это все еще O(VE) с меньшей константой).

        Сейчас, к сожалению, нет возможности просмотреть и изучить вами присланный материал.

        Ну .... Вы сами сделали выбор попробовать допилить алгоритм вместо того, чтобы изучить материал ;)


  1. wataru
    27.04.2024 14:26
    #26771797
    +2

    Вообще, что касается алгоритмов, то тут по умолчанию надо считать, что он не работает, пока не доказано обратное. Надо математически доказать, что найдутся кратчайшие пути. Ввести какие-то инварианты, вроде "до вершин в обработанном множестве найдены кратчайшие пути". Показать, почему он поддерживается.

    Главная проблема вашего алгоритма - он работает по слоям. Однако кратчайший путь может состоять из огромного количества коротких ребер и идти задом-на-перед по слоям. Сама идея этого расслоения графа принципиально не работает.

    Что касается заплатки в upd2, то у вас там получился в итоге форд беллман, только сильно накрученный. По крайней мере, сложность точно такая же: O(VE). Ибо каждая вершина может быть в очереди на обработку до O(V) раз.

    Вот тест:

    graph = {
  1: {3:10, 2:1}, 

  3: {5:10, 4:1 }, 
  2: {3:1}, 

  5: {7:10, 6:1 }, 
  4: {5:1}, 

  7: {9:10, 8:1}, 
  6: {7:1}, 

  9: {},
  8: {9:1}, 
}

    Это линия из треугольников, где выгоднее брать два ребра вместо одного. Если подсчитать, сколько раз вершины будут обработаны и вывести - там будет номер треугольника +-1. Так что в среднем будет O(n) на каждую вершину. Тут ребер не много, но можно граф усложнить.


    1. carbon2409 Автор
      27.04.2024 14:26
      #26771991

      Надо математически доказать, что найдутся кратчайшие пути. Ввести какие-то инварианты, вроде "до вершин в обработанном множестве найдены кратчайшие пути". Показать, почему он поддерживается.

      С этим беда у меня, я не сильный математик, чтобы доказать что-то, поэтому и пишу здесь. Знаю, что обычно доказывают по индукции или "от противного".

      Если подсчитать, сколько раз вершины будут обработаны и вывести

      Я ради интереса сделал это. Просто вставил счетчик операций в мой цикл и посмотрел на вашем примере графа. Кстати, спасибо за пример, алгоритм чувствует себя похуже других графов. Результат ниже:

      graph = {
  1: {3:10, 2:1},

  3: {5:10, 4:1 },
  2: {3:1},

  5: {7:10, 6:1 },
  4: {5:1},

  7: {9:10, 8:1},
  6: {7:1},

  9: {10: 1, 11: 10},
  8: {9:1},
  10: {11:1},
  11: {}
}

cycle_count = 0
processed = set()  # Множество обработанных нод
for node in lst:
    if node not in processed:  # Если нода уже обработана не будем ее заново смотреть (иначе м.б. беск. цикл)
        for child, cost in graph[node].items():  # Проходимся по всем детям
            cycle_count += 1
            new_cost = cost + costs.get(node,
                                        0)  # Путь до ребенка = путь родителя + вес до ребенка (если родителя нет, то путь до него = 0)
            min_cost = costs.get(child,
                                 infinity)  # Смотрим на минимальный путь до ребенка (если его до этого не было, то он беск.)
            if new_cost < min_cost:  # Если новый путь будет меньше минимального пути до этого,
                costs[child] = new_cost  # то заменяем минимальный путь на вычисленный
                parents[child] = node  # Так же заменяем родителя, от которого достигается мин путь
                if child in processed:  # UPDATE: если ребенок был в числе обработанных
                    lst.append(child)  # Вновь добавляем эту ноду в список для того, чтобы обработать его заново
                    processed.remove(child) # Удаляем из обработанных
        processed.add(node)  # Когда все дети (ребра графа) обработаны, вносим ноду в множество обработанных
        
print(f'Количество операций: {cycle_count}')
# -> Количество операций: 45
# По Беллману-Форду было бы: 9*8=72 судя по формуле

      В нашем графе мы бы совершили 45 операций, вместо 72 (если судить по формуле).

      Кроме того, нашел информацию, что Беллман-Форд имеет наихудшую сложность, которая предполагает ему формула, при линейном графе. Что имею в виду? Представим такого вида линейный граф: 1-->2-->3-->4-->5. Где каждое ребро имеет вес 1. По Беллману-Форду кол-во операций свелось бы как раз к его формуле, а именно 5*4=20. В моем алгоритме:

      graph = {
    1: {2:1},
    2: {3:1},
    3: {4:1},
    4: {5:1},
    5: {},
}
# -> Количество операций: 4

      Т.е. по сути за линию выполнил.

      Если я что-то неправильно сделал, может быть, глупость совершил, что в "лоб" посчитал количество операций, то с радостью выслушаю, в чем мой "косяк". Но вроде как взял наихудшие случаи.

      Спасибо за пояснения Вам!


      1. wataru
        27.04.2024 14:26
        #26771997
        +1

        Как вам уже написали, это практически известный алгоритм "форд-беллман с очередью". Это оптимизация и в некоторых случаях он работает быстрее форда-беллмана. Но худший случай остается таким же. Ну, в пару раз быстрее получается, но это не принципиально.


  1. aryk38
    27.04.2024 14:26
    #26773369
    +2

    "Важно! Нужно писать узлы графа в порядке их отдаленности от источника. "

    скажите - мне одному смешно или кто то ещо хихикает с такого "поиска" кратчайшего пути


    1. carbon2409 Автор
      27.04.2024 14:26
      #26775345

      А что, собственно, не так? Я пояснил этот момент, он никак не влияет на оценку сложности. Или вам смешно от того, что не знакомы с поиском в ширину? Какие злые люди, лишь бы вставить свои 5 грязных копеек. Судя по вашему профилю, вы эти копеечки пытаетесь вставить всюду. Будьте добрее!


    1. mbait
      27.04.2024 14:26
      #26778079
      +1

      Тебе одному. Существует достаточное количество алгоритмов, которым требуется предобработка данных. Полистай КМП для примеров.


  1. kuzinat0r
    27.04.2024 14:26
    #26773473
    +2

    Попробуйте сдать эту задачу - https://cses.fi/problemset/task/1671/. Ваша текущая реализация и неправильные ответы выдает, и вываливается за ограничения по времени. Вот когда система засчитает вам задачу - тогда с алгоритмом и приходите)


    1. carbon2409 Автор
      27.04.2024 14:26
      #26775203

      Здравствуйте! Спасибо за задачу. Прежде чем обсудить ее, напишу сразу - задачу я решил с моим алгоритмом, но есть нюансы. А теперь к самим нюансам:

      1. После ознакомления с условием задачи я обратил внимание на их тест-кейс:

      В их тест-графах присутствуют узлы, у которых 2 разных по весу ребра направлены на один и тот же узел. Т.е. в схеме это выглядит вот так:

      От первого узла к третьему 2 ребра разных весов. Я не специалист по графам, поэтому не могу сказать корректен ли этот пример. По моей логике не совсем, но если этому имеет место быть, то ок.

      1. Из первого нюанса следует то, что мне пришлось обрабатывать такие случаи, т.к. в моем алгоритме не предусмотрены такие структуры графов. Мне приходилось записывать в мою структуру графа меньшую из ребер, а поиск меньшего занимало определенное количество ресурсов.

      2. Я пробовал кидать решение на CPython и PyPy. Обратил внимание на то, что там присутствуют тесты с 10^5 узлов и 10^6 ребер. Ограничение 1 сек. Для стандартного питона это ну ооочень тяжко. Для PyPy уже полегче (практически в 2 раза быстрее). Результаты отправки:

      CPython
      CPython
      PyPy
      PyPy

      Обратите внимание! Ложные ответы отсутствуют (там 23 теста, но у них так же Time Limit). Причем если посмотреть на результаты времени тестов, то можно заметить, что PyPy быстрее примерно в 2 раза. Смотрим на 11 тест. У нас ограничение в 1 сек. Наш тест занял примерно пол секунды на PyPy с верным ответом. А в CPython он вышел за пределы времени (0.5*2=1). Причем код один и тот же. Получается, алгоритм не выдает неверные решения, как вы сказали, а просто выходит за пределы времени. Это не означает что алгоритм не рабочий! Если этот же алгоритм написать на C++, то он скорее всего не выйдет за time limit (но я не знаю этот язык). Плюс ко всему эту задачу нужно решать обычной Дейкстрой (который в любом случае быстрее моего алгоритма), там в условиях отсутствуют ребра с отрицательным весом.

      Таким образом, я делаю вывод, что алгоритм работает, но нюансы языка и спорная особенность задачи не позволяют ее сдать в эту систему. Добра Вам!

      Hidden text
      from collections import deque
n, m = map(int, input().split())
arr = [[] for _ in range(n+1)]
graph = {}

for _ in range(m):
    a, b, c = map(int, input().split())
    arr[a].append((b, c))


queue = deque()
graph[1] = {}
for i in arr[1]:
    neighbor = i[0]
    is_include_before = graph[1].get(neighbor, False)
    if not is_include_before:
        graph[1][neighbor] = i[1]
        queue.append(neighbor)
    else:
        graph[1][neighbor] = min(is_include_before, i[1])


while queue:
    current = queue.popleft()
    if current not in graph:
        graph[current] = {}
    for i in arr[current]:
        if i[0] not in graph:
            graph[i[0]] = {}
        neighbor = i[0]
        is_include_before = graph[current].get(neighbor, False)
        if not is_include_before:
            graph[current][neighbor] = i[1]
            queue.append(neighbor)
        else:
            graph[current][neighbor] = min(is_include_before, i[1])



lst = [key for key in graph.keys()]  # Формируем очередность прохождения узлов графа
parents = {}  # {Нода: его родитель}
costs = {}  # Минимальный вес для перехода к этой ноде (кратчайшие длины пути до ноды от начального узла)
infinity = float('inf')  # Бесконечность (когда минимальный вес до ноды еще неизвестен)

cycle_count = 0
processed = set()  # Множество обработанных нод
for node in lst:
    if node not in processed:  # Если нода уже обработана не будем ее заново смотреть (иначе м.б. беск. цикл)
        for child, cost in graph[node].items():  # Проходимся по всем детям
            cycle_count += 1
            new_cost = cost + costs.get(node,
                                        0)  # Путь до ребенка = путь родителя + вес до ребенка (если родителя нет, то путь до него = 0)
            min_cost = costs.get(child,
                                 infinity)  # Смотрим на минимальный путь до ребенка (если его до этого не было, то он беск.)
            if new_cost < min_cost:  # Если новый путь будет меньше минимального пути до этого,
                costs[child] = new_cost  # то заменяем минимальный путь на вычисленный
                parents[child] = node  # Так же заменяем родителя, от которого достигается мин путь
                if child in processed:  # UPDATE: если ребенок был в числе обработанных
                    lst.append(child)  # Вновь добавляем эту ноду в список для того, чтобы обработать его заново
                    processed.remove(child) # Удаляем из обработанных
        processed.add(node)  # Когда все дети (ребра графа) обработаны, вносим ноду в множество обработанных


def get_shortest_path(start, end):
    '''
    Проходится по родителям, начиная с конечного пути,
    т.е. ищет родителя конечного пути, потом родителя родителя и т.д. пока не дойдет до начального пути.
    Тем самым мы строим обратную цепочку нод, которую мы инвертируем в конце, чтобы получить
    истинный кратчайший путь
    '''
    parent = parents[end]
    result = [end]
    while parent != start:
        result.append(parent)
        parent = parents[parent]
    result.append(start)
    result.reverse()
    shortest_distance = 0
    for i in range(len(result)-1):  # Узнаем кратчайшее расстояние
        node_1 = result[i]
        node_2 = result[i + 1]
        shortest_distance += graph[node_1][node_2]
    return shortest_distance


print(0, end=' ')
for i in range(2, n+1):
    print(get_shortest_path(1, i), end=' ')


      1. wataru
        27.04.2024 14:26
        #26775325

        Проблема не только в языке. Ваш метод работает за O(VE), когда как дейкстара работает за O(V+E). Ваш метод даже на С++ не зайдет по ограничению времени (10^(5+6) - 100 миллиардов операций вы в 1 сек ну никак не запихнете). Правда, ваш метод работает и с отрицательными ребрами, когда как в этой задаче их нет, поэтому она рассчитана на более простой и быстрый алгоритм.


        1. carbon2409 Автор
          27.04.2024 14:26
          #26775393

          когда как дейкстара работает за O(V+E)

          Тут немножко поправлю Вас, Дейкстра с кучей работает за O(ElogV)

          Правда, ваш метод работает и с отрицательными ребрами, когда как в этой задаче их нет, поэтому она рассчитана на более простой и быстрый алгоритм.

          Полностью согласен, для этой задачи не нужно использовать этот алгоритм.


          1. wataru
            27.04.2024 14:26
            #26775419

            ут немножко поправлю Вас, Дейкстра с кучей работает за O(ElogV)

            Да. и у меня там квадрат потерялся. O(V^2+E) или O((V+E)logV). В этой задаче нужна дейкстра с кучей, ибо вершин много, а ребер мало.


      1. kuzinat0r
        27.04.2024 14:26
        #26775471

        Здравствуйте.

        Из первого нюанса следует то, что мне пришлось обрабатывать такие случаи - но это ваша проблема) Не стоит заявлять, что в тесткейсах графы какие-то неправильные. Ну и да - в задаче о минимальном пути можно удалить ребра, не потеряв важную инфу. Но в общем случае модифицировать граф не выйдет.

        Ложные ответы отсутствуют - а вот это утерждение надо бы подтвердить) там же можно скачать файл с входными данными - запустите локально и посмотрите, что он выдаёт. Наверное, выход лучше писать в файл и сравнивать программно. Если все тесткейсы пройдут - вот тогда можете утверждать, что алгоритм работает верно. Именно поэтому их так много - там как раз задаются разные хитрые графы, которые ломают некорректные алгоритмы, которые "выглядят рабочими". Или рабочие, но слишком медленные) Заодно можете засечь, сколько времени занимает обработка.

        Если этот же алгоритм написать на C++, то он скорее всего не выйдет за time limit - выйдет. Ассимптотика не изменится. Поверьте, если ваш алгоритм вылезает за временные ограничения - 99.9% вероятность в том, что ваш алгоритм имеет неправильную ассимптотику. Только в олимпиадах высокого уровня временные ограничения задаются так, чтобы максимально быстрый алгоритм еле-еле влезал в них. Вот там да, бывают ситуации, когда код на С++ влезет, а его аналог на питоне - нет. Но это не ваш случай.

        Плюс ко всему эту задачу нужно решать обычной Дейкстрой (который в любом случае быстрее моего алгоритма) - но ведь изначально посыл поста был в том, что вы изобрели новый алгоритм, который лучше Дейкстры :) А выходит, что нет. Вы молодец, что попытались самостоятельно улучшить алгоритм. Но вы не молодец, потому что продолжаете обвинять кого угодно (нюансы языка, спорные особенности задачи...) в том, что ваше решение не проходит. А что надо сделать, так это вывод о том, какой на самом деле алгоритм у вас получился, и чем он лучше существующих(и отличется ли от них вообще)


  1. SAIIIYK
    27.04.2024 14:26
    #26774801

    Подкину пару идей.

    1) Метод наименьшего сопротивления (электрический). Проводится измерение суммы расстояний начального и конечного пути, и затем подбирается трассировка.

    2) нейросетевой метод. Обучается нейросеть на куче примеров. Полученную функцию используем для аппроксимации кратчайшему пути. Можно использовать нейросеть Кохонена для кластеризации и картографирования 2д путей... Но метод может не подойти.

    Любой из методов подразумевает перебор позиций. Тут уже сугубо машинная проблематика, упирающаяся в несколько-поточный процессор. Могу сказать что если перебор брать на нейросетевом методе на ядре cuda по скорости вычислений может превзойти классические методы благодаря кратному превосходству в многопоточности.


    1. Spyman
      27.04.2024 14:26
      #26777147

      По методу 1 - вы предполагаете строить каждый граф в виде физической модели? Или как ещё можно измерить сумму расстояний предварительно не построив путь о.О

      По методу 2 - как вы докажете что ваша обученная нейросеть обладает 100% точность решения задачи как любой математически доказанный алгоритм?

      Ну и по комментарию про сугубо машинную проблематику - это не самом деле сверхмасштабная и дорогая ошибка. Если с таким подходом заходить в реальные проекты где алгоритмы важны, очень скоро выяснится что алгоритм с квадратичной сложностью от алгоритма с линейной может отличаться огромными переплатами за машиночасы. Легко может оказаться что вместо 1 nvidia tesla вам потребуется их 1000


  1. BronzeSeal
    27.04.2024 14:26
    #26778189

    А чем обычный алгоритм Дейкстры плох?

    Находим самый маленький вес ребра и увеличиваем на него все веса. Путь при этом не изменится.