13.04.2016 12:20
wataru 87 21100 Источник

Всем известно, что если посадить обезьяну за печатную машинку и заставить ее вечно случайно стучать по клавишам, то, рано или поздно, она напечатает «Войну и мир», собрание трудов Пифагора и даже статью, которую вы сейчас читаете.



Потрясающий факт, но еще интереснее попытаться понять, сколько же времени ей понадобится для набора конкретного текста. Чтобы не водить лишний параметр — скорость набора обезьяной — будем искать ответ на вопрос: сколько нажатий на клавиши ей потребуется в среднем. А вам очевидно, что строку «abc» набирать гораздо легче чем «aaa»? Решению этой задачи и посвящен этот пост. Попутно объясняется префикс функция и ее свойства.


Понятно, что время, потраченное обезьяной на набор конкретного текста — это некоторая случайная величина. Поэтому логично спросить про ее математическое ожидание.


Формальная постановка задачи


Дана строка s, состоящая из прописных латинских букв („a“-„z“). Нужно найти мат. ожидание количества случайных нажатий на клавиши до того, как будет набрана вся строка s, если все символы набираются равновероятно (с вероятностью 1/26).


Код решения

Чтобы понять, почему это работает и что это за функция Pi() нужно прочитать всю статью :(.


string s; //строка, которую набирает обезьяна
int n = s.length();
vector<int> p = Pi(s);
vector<long double> pow(n+1);
pow[0] = 1;
int i;
for (i = 1; i <= n; i++) {
  pow[i] = pow[i-1]*26;
}
long double ans = 0;
for (i = n; i>0; i = p[i-1]) {
  ans += pow[i];
}
cout << ans;

Префикс функция


Именно эта функция поможет нам решить поставленную задачу. Префикс функция была введена Д. Кнутом и М. Праттом (и параллельно Д. Моррисом) для их знаменитого алгоритма поиска подстроки в строке (алгоритм КМП). Префикс функция для строки s возвращает длину самого длинного собственного префикса строки, который также является ее суффиксом.


Префиксы и суффиксы

Префикс — это просто начало строки, если отбросить сколько-то символов с конца. Так у строки "aba" есть 4 префикса: "" (пустая строка), "a", "ab" и "aba". Суффикс — тоже самое, но символы удаляются с начала. При этом некоторые суффиксы и префиксы могут совпасть. Для строки "aba" есть 3 таких префикса-суффикса: "","a" и "aba" (четвертый суффикс "ba" не совпадает с префиксом "ab"). Суффикс или префикс называется собственным, если он короче всей строки.


Формально говоря: \pi(s) = max\{ k \,|\, 0\le k &lt; |s|,\, pref_k(s) = suf_k(s)\}


Где prefk (s) — это префикс длины k строки s, а sufk(s) — это суффикс длины k строки s.


Как в алгоритме КМП, так и в других применениях, гораздо полезнее рассматривать префикс функцию сразу для всех префиксов данной строки. Да, звучит страшно — для каждого префикса нужно найти наибольший собственный префикс, который совпадает с суффиксом префикса. Но на самом деле все просто:


\pi_s(k) = \pi(pref_k(s)),\, 1\le k \le |s|


Такая расширенная префикс функция полезна прежде всего тем, что ее проще вычислять, чем просто \pi(s). Ниже показаны значения \pi_s(k) для s=«ababac».


   k: 1 2 3 4 5 6
   s: a b a b a c
P(i): 0 0 1 2 3 0

Вычисление префикс функции


Код вычисления
vector<int> Pi(string s) {
  int n = s.length();
  vector<int> p(n);
  p[0] = 0;
  for (int i = 1; i < n; i++) {
    int j = p[i-1]; 
    while (j > 0 && s[i] != s[j]) { 
      j = p[j];
    }
    if (s[i] == s[j]) j++;
    p[i] = j;
  } 
  return p;
}

Быстрое, за O(N), вычисление префикс функции основано на двух простых наблюдениях.


(1) Чтобы получить префикс-суффикс для позиции k надо взять какой-то префикс-суффикс для позиции k-1 и дописать к нему в конец символ на позиции k.


(2) Все префиксы-суффиксы строки s длины n можно получить как \pi_s(n),\, \pi_s(\pi_s(n)),\, \pi_s(\pi_s(\pi_s(n))) и так далее, пока очередное значение не станет равным 0. Это свойство можно проверить на строке «abacaba». Тут \pi_s(7)=3,\, \pi_s(3)=1,\, \pi_s(1)=0, что соответствует всем префиксам-суффиксам («aba», «a» и «»). Так получается потому, что максимальный префикс-суффикс имеет длину \pi_s(n). Следующий по длине префикс-суффикс будет короче. Но поскольку первый префикс-суффикс встречается как в начале, так и на конце строки s, то следующий префифкс-суффикс будет длиннейшим префиксом-суффиксом в первом префиксе-суффиксе.


Поэтому для построения префикс функции для позиции i достаточно проитерироваться начиная со значения префикс функции в предыдущей позиции пока продолжение суффикса новым символом не будет также и префиксом (для этого надо проверить только один новый символ). Такой алгоритм выполняется за линейное время, потому что значение префикс функции каждый раз увеличивается максимум на 1, поэтому оно не может уменьшится более чем n раз, а значит, вложенный цикл суммарно выполнится не более чем n раз.


Конечный автомат KMP


Следующий математический объект, необходимый в решении поставленной задачи — это конечный автомат, принимающий строки, заканчивающиеся на заданную строку s. Этот автомат используется в другой, менее известной модификации алгоритма Кнута-Морисса-Пратта. В этой версии алгоритма строится конечный автомат, который принимает все строки, которые заканчиваются на заданную строку (шаблон). Затем автомату передается строка-текст. Каждый раз, когда автомат принимает переданный ему текст, найдено очередное вхождение шаблона. Именно этот автомат и поможет нам решить задачу об обезьяне за печатоной машинкой.


Что такое конечный автомат

Конечный автомат — это математический объект который проще всего представить себе как некоторую коробку у которой есть какое-то внутреннее состояние. Изначально коробка находится в начальном состоянии. В коробку можно вводить строки, по одному символу за раз. После каждого символа коробка меняет свое состояние, при чем в зависимости от текущего состояния и введенного символа. Так же некоторые состояния являются хорошими (математический термин — конечные состояния). Говорят, что автомат принимает строку, если после скармливания ему этой строки символ-за-символом, автомат находится в хорошем состоянии.


Для определения КА нужно определить начальное состояние, хорошие состояния и функцию перехода — для каждого состояния и символа нужно указать новое состояние, в которое автомат перейдет. Удобно рисовать автомат как полный ориентированный граф, где вершины — это стостояния, а на каждом ребре написан ровно один символ. Из каждой вершины должно быть ровно одно ребро с каждым символом. Тогда для обработки какой-то строки надо просто перейти по ребрам с символами из этой строки. Если путь закончился в конечном состоянии, то автомат такую строку принимает.


Для построения этого автомата мы будем использовать уже известную нам префикс функцию.
В автомате будет n+1 состояние, пронумерованные от 0 до n. Состояние k соответствует совпадению последних k набранных символов с префиксом шаблона длины k (Если мы ищем строку «abac» то нам от текущего текста интересно только что там на конце: «abac», «aba», «ab», «a» или что-то друге. Этой информации достаточно чтоб получить такуюже после дописывания одного символа). Состояние 0 будет начальным, а состояние n — конечным. Иногда может быть неразбериха: например, для сроки «ababccc» при скормленой автамату строке «zzzabab» можно выбрать как состояние 2, так и 4. Но, чтобы не терять нужную информацию о набранном тексте, мы всегда будем выбирать наибольшее состояние.


пример конечного автомата KMP

Вот автомат для строки "ababac". Для примера алфавит состоит только из символов 'a'-'c'. Параллельные ребра объединены для наглядности. На самом деле каждому ребру соответствует только один символ. Начальное состояние — 0, конечное — 6.


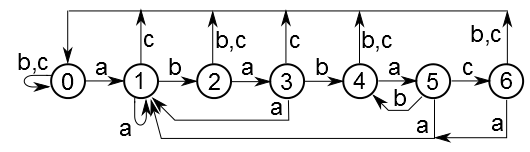
Несложно убедиться, что любой путь из состояния 0 в состояние 6, каким бы сложным он не был, обязательно кончается на строку "ababac". И наоборот, любой такой путь обязательно закончится в состоянии 6.


Код построения конечного автомата
string s; //исходная строка.
int n = s.length();
vector< vector<int> > nxt(n+1, vector<int>(256)); 
// функция перехода nxt[состояние][символ] == новое состояние
vector<int> p = Pi(s); // Префикс функция. См. код выше
nxt[0][s[0]] = 1; //единственный переход из состояния 0 не в 0.
for (int i = 1; i <= n; i++) {
  for (int c = 0; c < 256; c++)
    nxt[i][c] = nxt[p[i-1]][c]; //p[] индексируется с нуля, поэтому нужно -1
  if (i < n) nxt[i][s[i]] = i+1;
}

Обратите внимание, как строятся переходы. Для расчета переходов из состояния i мы рассматриваем 2 варианта. Если новый символ — это s[i] — то переход будет в состояние i+1. Тут все очевидно: если было совпадение в i символов — то добавив следующий символ из строки s мы увеличим длину совпадения на 1. Если же символ не совпал, то мы просто копируем переходы из состояния \pi_s(i). Почему? Переход в этом случае будет точно в состояние с номером ?i. Значит после перехода мы забудем часть информации о набранном тексте. Можно сделать это перед переходом. Самый минимум, что мы можем стереть, это притвориться что на самом деле сейчас состояние не i, а \pi_s(i). Это как в том примере выше, можно было считать что текст кончается на «abab» или «ab». Если из «abab» никаких переходов нет — можно использовать переходы из «ab».


Решение


Теперь мы готовы решить поставленную задачу.
Построим для строки s автомат KMP. Поскольку все символы набираются обезьяной случайно, нам не важны сами символы, а только ребра в графе переходов. Задачу можно переформулировать так: найти мат. ожидание количества переходов в случайном блуждании из состояния 0 пока не достигнуто состояние n.


Логично в такой постановке ввести переменные: Ek, 0?k?n — матожидание количества переходов до достижения состояния n. E0 будет ответом к исходной задаче. Пусть Z — это множество допустимых символов (алфавит). Можно составить систему уравнений:


E_n = 0


E_k = 1 + \frac{1}{|Z|}\sum_{c \in Z}{E_{nxt[k][c]}}, k=0..n-1


Уравнение (1) означает, что достигнув состояния n случайное блуждание останавливается.
Для любого другого состояния будет сделан какой-то переход, поэтому в уравнении (2) присутствует слагаемое 1. Второе слагаемое — это сумма по всем возможным вариантам, умноженным на вероятность этих вариантов. Все вероятности одинаковы — поэтому она вынесена за знак суммы.


Вот уже есть решение задачи за O(n^3): построенную систему линейных уравнений можно решить методом Гаусса. Но если немного посмотреть на эту систему и вспомнить, что есть префикс функция, то есть решение гораздо проще и быстрее.


Вспомним построение конечного автомата. (Для простоты далее вместо \pi_s я буду использовать просто \pi). Переходы из состояния k почти полностью совпадают с переходами из состояния \pi(k). Отличие в переходе только по символу s[k-1]. Поэтому правые части уравнений (2) для состояний k и \pi(k) отличаются только одним слагаемым. В уравнении для \pi(k) стоит E_{nxt[\pi(k)][s[k-1]]} вместо E_{nxt[k][s[k-1]]} в уравнении для k. При чем nxt[k][s[k-1]]=k+1. Используя этот факт можно переписать уравнения (2):


E_k = E_{\pi(k)} + \frac{1}{|Z|}(E_{k+1}-E_{nxt[\pi(k)][s[k-1]]})


Теперь нужно сделать еще одно наблюдение. Оказывается


nxt[\pi(k)[s[k-1]] = \pi(k+1)


Т.е. чтобы найти префикс функцию для какого-то состояния, надо взять префикс функцию от предыдущего состояния и перейти оттуда по символу, ведущему в следующее состояние.
Действительно, если рассмотреть состояние \pi(k), то оно соответствует строке, заканчивающейся на символ s[k-1]. Значит туда есть переходы по этому символу. Рассмотрим самое большое состояние, из которого такой переход есть, но которое имеет номер < k. Если после перехода по символу s[k-1] мы получили какой-то суффикс pref_k(s), то до перехода это был суффикс pref_{k-1}(s). Поскольку это было самое правое такое состояние, то оно соответствует максимальному префиксу-суффиксу pref_{k-1}(s), а значит оно имеет номер \pi(k-1). Вот мы и получили этот удивительный и полезный факт.


Тогда (3) преобразуется в:


E_k = E_{\pi(k)} + \frac{1}{|Z|}(E_{k+1}-E_{\pi(k+1)})


Или по-другому:


|Z| (E_k - E_{\pi(k)}) =(E_{k+1}-E_{\pi(k+1)})


С обеих сторон от знака равенства тут отрицательные числа (логично, что чем больше k, тем меньше Ek). Умножим обе части на -1.


|Z| (E_{\pi(k)}-E_k) =E_{\pi(k+1)}-E_{k+1}


Но (4) справедливо только для k>0. Для k=0 можно явно выписать уравнение (2), ведь только один из |Z| переходов ведет в состояние 1, а все остальные возвращаются в состояние 0:


E_0 = 1 + \frac{1}{|Z|}E_1 + \frac{|Z|-1}{|Z|}E_0


Теперь соберем все переменные слева, домножим уравнение на |Z| и заменим 0=\pi(1) (префикс функция для одного символа всегда равна 0, т.к. непустых собственных префиксов у одного символа нет):


E_{\pi(1)} - E_1 = |Z|


Я позволю себе повторить уравнения (1), (4) и (5), так как они составляют систему, которую мы теперь решим аналитически:


E_{\pi(1)} - E_1 = |Z| \|Z| (E_{\pi(k)}-E_k) =E_{\pi(k+1)}-E_{k+1},\, k=1..n-1 \ E_n = 0


Подставляя первое уравнение в левую часть второго при k=1, затем при k=2 и т.д. получаем:


E_{\pi(k)} - E_k = |Z|^k ,\, k=1..n


Вот уже решение почти готово: теперь рассмотрим (6) при k=n и вспомним, что E_n = 0, получаем:


E_{\pi(n)} = |Z|^n


Подставляем это значение в (6) при k = \pi(n) — получаем:


E_{\pi(\pi(n))} = |Z|^n + |Z|^{\pi(n)}


Аналогично, получаем:


E_{\pi(\pi(\pi(n)))} = |Z|^n + |Z|^{\pi(n)} + |Z|^{\pi(\pi(n))}


И так можно продолжать то тех пор, пока не получим выражение для E_0, что, кстати, и является ответом к задаче. Обозначим \pi^k примененную k раз подряд функцию \pi, тогда:


E_0 = \sum_{k:\pi^k(n) &gt; 0}|Z|^k


Таким образом, мы получили решение задачи за O(n): построить префикс функцию к строке s и итерироваться по ней начиная с n пока не достигнем 0, попутно складывая степени |Z| равные текущей длине префикса. Это и есть то самое решение, приведенное в начале статьи.


Глядя на (*) становится понятно, почему строку «aaa» набрать сложнее чем «abc», ведь в у «aaa» только третья итерация \pi равна нулю, а у второй строки вообще нет непустых префиксов равным суффиксам и \pi сразу дает ноль.


Замечания


Префикс функция и автомат КМП очень полезные инструменты для работы со строками. Если у уважаемых читателей есть интерес, то я могу разобрать решения других задач. О любых опечатках прошу сообщать в личку, спасибо.


Update:


Во-первых, спасибо огромное parpalak за его замечательный сервис для подготовке статьей с формулами на Хабре (https://habrahabr.ru/post/264709/). Без него этой статьи бы не было. Очень стыдно, что забыл сразу об этом написать.


Во-вторых, очень многих комментаторов путает их интуиция. В теорвере это часто случается. Да, вероятности набрать тексты одинаковой длины с первого раза одинаковы. Да, частота вхождения одинаковых по длине текстов одинакова в бесконечном случайном тексте. Все это верно, но из этих фактов не следует, что мат.ожидания количества символов до первого вхождения строк будут одинаковыми. И наоборот, из того, что строка «чч» в бесконечном тексте встретится позже, чем строка «чк» никак не следует, что в казино надо после черного ставить на красное.


Давайте на пальцах посчитаем матожидания до выпадания двух строк «чч» и «чк». Матожидание — это сумма по всем i: вероятности набрать строку за i символов в первый раз умноженной на i. Фраза выделенная жирным означает что, во-первых, последние набранные символы совпадают с искомыми (эта вероятность одинакова для обеих строк), и, во-вторых, среди первых i-2 символов искомая строка не встречается. Этот второй множитель и отличается для разных строк. Вероятность не найти строку — это просто количество всех текстов, в которых этой строки нет, деленное на количество всех текстов такой длины.


Теперь важное: строк длины k не содержащих строку «чк» всего k+1: «к…к», «к…кч», «к…кчч», «к…ккччч», …, «кч…ч» и «ч…ч». Это потому, что после символа «ч» может быть только «ч».


Сток же длины k не содержащих строку «чч» будет гораздо больше, а именно Fk+1 — число Фиббоначи под номером k+1 (это числа 1, 1, 2, 3, 5, 8, 13,… — каждое следующее есть сумма двух предыдущих). Например, для k=2 3 строки будут «кк», «кч», «чк». Эти числа очень быстро растут и поэтому все слагаемые для мат ожидания для строки «кк» будут больше, так как там вероятность больше.


Обратите внимание, все из-за того, что вероятности напечатать текст в первый раз за сколько-то нажатий зависят от вероятности не напечатать текст ни разу в начале и середине текста. Эта вероятность прямо пропорциональна количеству строк не содержащих заданную строку, а оно для разных шаблонов разное.


Еще раз, это не я придумал, это известный факт, хоть и крайне неинтуитивный. Посмотрите, например, на эту статью (ищите там задачу про Алису и Боба — 4 абзац): https://habrahabr.ru/post/279337/

Комментарии (87)


  1. Invision70
    13.04.2016 16:00
    #8851875
    +8

    Спасибо, интересная статья!
    … теперь я знаю как у меня получалось писать код все это время…


  1. WayMax
    13.04.2016 16:01
    #8851879
    +25

    Но вы так и не ответили на главный вопрос статьи :(


    1. wataru
      13.04.2016 16:03
      #8851883
      -14

      В смысле? Приведен алгоритм и формула (с выводом). Применять по своему усмотрению для любого конкретного текста.


      1. ganqqwerty
        13.04.2016 16:28
        #8851945
        +13

        не, вы напишите время в секундах/веках


        1. wataru
          13.04.2016 17:46
          #8852093
          +1

          Да, наверно, это неточность в статье. Если не задавать с какой скоростью обезьяна печатает, вопрос о времени в секундах не имеет смысла.


          1. deniskreshikhin
            14.04.2016 01:37
            #8852653
            +4

            Те обезъяны что умеют печатать, обычно печатают со скоростью 200 символов в секунду, рекорд около 700 символов.
            Так что можете произвести оценку.


            1. mapron
              14.04.2016 04:53
              #8852681
              +1

              В секунду? Может, в минуту? Я не уверен, что механика печатной машинки справится с такими скоростями.


              1. deniskreshikhin
                14.04.2016 07:55
                #8852715

                Хех, да в минуту.


  1. GarryC
    13.04.2016 17:03
    #8852025

    Прошу прощения за придирку, но Ваша программа действительно не отвечает на вопрос о времеени, которое потребуется обезьяне, поскольку Вы подсчитываете среднее количество символов, и необходимо еще задать количество вводимых символов в единицу времени для преобразования, а так статья интересная.
    Хорошо было бы добавить среднее количество символов для строки «ааа» и «авс», чтобы увидеть, насколько проще набрать первую из них.


    1. napa3um
      13.04.2016 17:47
      #8852097
      -4

      Вероятности встретить подстроки 'aaa' и 'abc' в бесконечном случайном потоке равновероятных символов строго одинаковы и зависят только от длины подстроки. Чего-то автор перемудрил, мне кажется.


      1. wataru
        13.04.2016 17:51
        #8852103
        +2

        Да, вероятность встретить в бесконечном тексте одинакова. Но нас-то интересует время до первого набора заданной строки.


        1. napa3um
          13.04.2016 17:56
          #8852119

          Я, видимо, не понимаю, почему мат-ожидания встретить одну или другую подстроку с одинаковыми длинами (которые появляются в потоке с одинаковыми вероятностями) будут разными.


          1. wataru
            13.04.2016 18:00
            #8852125
            +2

            тут дело в том, что для строки «aaa», когда набрано 2 первых символа при следующем символе «a» текст соберется, а для оставшихся 26-ти символов будет откат в 0 правильно набранных символов. Т.е. с вероятностью 1/26 набор закончится а с вероятностью 25/26 надо будет начинать набор с нуля. Для строки «abc» же, после корректного нажатия двух первых символов: с вероятностью 1/26 текст наберется, с вероятностью 1/26 будет снова набран первый символ «a» и останется набирать только 2, и с вероятностью 24/26 надо будет начинать с нуля. Именно из за этого перекоса в вероятностях сложнее закончить собирать первую строку.


            1. napa3um
              13.04.2016 18:01
              #8852129
              -1

              Всё ещё не понимаю. Как добавить условие «начать с нуля», например, вот в такую симуляцию: http://pastebin.com/T7jjNtkH (за 10 минут на node.js так и не разошлись количества подстрок, постоянно обгоняя друг друга).
              Или я вообще не правильно понял условия?


              1. wataru
                13.04.2016 18:08
                #8852145
                +2

                Похоже что вы не так поняли условие. В задаче просится мат. ожидание нажатий до ПЕРВОЙ встречи строки. Вы там считаете среднее количество вхождений и оно, действительно одинаково. Если бы обезьяна продолжала печатать после корректного набора и мы потом считали сколько раз она напечатала нужный нам текст, то было бы то, что вы сейчас считаете. Мы же после корректного набора обезьяну выгоняем.


                1. napa3um
                  13.04.2016 18:12
                  #8852153
                  -1

                  Вычисление мат-ожидания до первой встречи подстрок я заменяю на вычисление вероятностей этих подстрок. Разве это не однозначно определяемые друг через друга величины?


              1. wataru
                13.04.2016 18:14
                #8852157
                +1

                Я понял в чем проблема — вам кажется, что матожидание до первой встречи обратно пропорционально частоте встречи в бесконечной случайной строке. Это похоже на правду для точек на прямой. Средняя длина отрезка между двумя точками обратно пропорциональна их частоте. Но со строками это не так. Строку «aaa» можно наложить на другое ее вхождение, а строку «abc» — нельзя. При наложении двух строк связь матожидания расстояния между ними и частоты нарушается.


                1. napa3um
                  13.04.2016 18:22
                  #8852171

                  Вы сами придумали решение (и условия)? Или это уже кто-то придумал до вас? Погуглил, везде эта задача решается через длину искомой строки, содержимое (повторяемость букв) в ней не имеет значения.

                  (Позже попробую перечитать ещё раз, с учётом того, что вы там что-то исправили в статье. Я, признаюсь, не вникал в ваши формулы и код.)


                  1. wataru
                    13.04.2016 19:11
                    #8852223
                    +1

                    Задача была на какой-то олимпиаде лет 10 назад. Тогда я ее именно таким образом и решил. И это было правильное решение.

                    Единственное изменение в статье — это замечание в самом начале о том. что считать будем нажатия по клавишам а не время в секундах.


                    1. napa3um
                      13.04.2016 19:18
                      #8852233

                      https://ru.wikipedia.org/wiki/Теорема_о_бесконечных_обезьянах
                      В Википедии, получается, неверно интерпретируется независимость вероятностей символов в потоке?


                      1. wataru
                        13.04.2016 19:23
                        #8852247
                        +1

                        В википедии нет ничего про время набора. А вероятность там указана набрать текст правильно с первого раза. Тут действительно нет никакой разницы, как устроена строка.


                        1. napa3um
                          13.04.2016 19:29
                          #8852261

                          Время набора текста зависит от мат-ожидания совпадения потока с текстом, которое зависит от вероятности набрать текст. Разве нет?


            1. Source
              14.04.2016 01:06
              #8852631

              Строго говоря, для набора текста вероятности гораздо сложнее… в частности, обезьяна вероятнее будет лупить некоторое время в одну область клавиатуры, а не распределять нажатия равномерно по всей её поверхности. Так что задачу надо про роботов формулировать, а не про обезьян, чтобы удобнее считать было.


      1. LoadRunner
        13.04.2016 18:41
        #8852187
        +2

        Вам должны помочь понять комментарии из этой ветки.
        Или лучше сразу этот комментарий прочитать.


        1. napa3um
          13.04.2016 18:53
          #8852199

          Мне пока не ясны условия задачи, приводящие к её такому усложнению. А то, что префиксные штуки круты и полезны — не сомневаюсь. И то, что в указанной вами задаче с Алисой и Бобом вероятности не равные — я тоже понимаю почему. Но вот в постановке задачи про обезьян (как я её всегда знал) такие ухищрения не были нужны. (Перечитаю позже статью внимательнее.)


          1. LoadRunner
            13.04.2016 18:57
            #8852203
            +1

            Вы просто замените бесконечный ряд монет на бесконечный ряд символов. И паттерн «abc» встретите раньше, чем паттерн «aaa».


            1. napa3um
              13.04.2016 19:03
              #8852213
              -1

              http://pastebin.com/T7jjNtkH
              Вот бесконечный поток символов, в котором я считаю количество вхождений подстрок, что однозначно определяет вероятности вхождения подстрок, что однозначно определяет мат-ожидание встретить ту или иную строку. И эти величины для любых подстрок одинаковой длины равны.

              (Всё ещё без перечитывания статьи отвечаю, возможно, у автора введены дополнительные ограничения, меняющие решение, которые я не уловил. Я условия задачи принимаю «классические», как, например, в https://ru.wikipedia.org/wiki/Теорема_о_бесконечных_обезьянах .)


              1. LoadRunner
                13.04.2016 19:05
                #8852219
                +1

                В классических условиях мы не считаем количество подстрок, мы ждём самого первого выпадения искомой подстроки в бесконечном ряду символов, а дальше хоть трава не расти.


                1. napa3um
                  13.04.2016 19:12
                  #8852227
                  -2

                  Это называется математическим ожиданием появления подстроки, однозначно выводимым из вероятности появления этой подстроки, которая, в свою очередь, однозначно выводится из количества встреченных подстрок и длины потока символов. При этом длина потока символов устремлена в бесконечность. Т.е., всё как в классических условиях, и всё ещё нет причин вводить префиксы.


                  1. mihaild
                    15.04.2016 12:08
                    #8854559

                    Нет, вероятность события «первый раз строка встретилась в позиции N» не выводится однозначно из «вероятность того, что строка встретилась в позиции i».
                    Хотя бы элементарно P(строка встретилась первый раз в позиции 2) = P(строка не встретилась в позиции 1) * P(строка не встретилась в позиции 2 | строка не встретилась в позиции 1) — и второй множитель в общем случае не равен P(строка не встретилась в позиции 2).

                    Например, если нам гарантируется, что на одной монетке орел и решка при бросках чередуются, а вторая — честно случайная, то вероятность того, что на 1й орел выпадет раньше, чем на второй, равна 1/4 [при первом броске на 1й орел, на 2й решка] + 1/8 [при первом броске на 1й орел, на 2й орел; при втором броске на 2й решка] = 3/8, а вероятность того, что на 2й орел выпадет раньше 1/4 [при первом броске на 1й решка, на 2й орел] — т.е. вероятности отличаются, хотя вероятность получить орла в каждой позиции одинакова.


              1. wataru
                13.04.2016 19:16
                #8852229
                +1

                Проблема в вашем бесконечном потоке в том, что строка «aaaa» посчитается Вами как 2 вхождения строки «aaa». Но между этими вхождениями -2 (минус два) символа! Или, в другой интерпретации, вам надо набрать всего один дополнительный символ, чтобы получить из первого вхождения второе. Для строки «abc» таких ситуаций никогда не бывает.

                Эти лишние невозможные отрезки нельзя учитывать. Потому что обезьяна никогда не сможет напечатать строку из трех символов всего одним нажатием. Если такие пары исключить, то в бесконечной строке получается меньше отрезков (которые можно учитывать) между двумя подряд идущими включениями подстроки, а значит матожидание будет больше.


                1. napa3um
                  13.04.2016 19:24
                  #8852251

                  Я считаю вероятность, а она считается именно через количество вхождений (с учётом длины потока, устремлённой в бесконечность), даже если строки будут накладываться друг на друга. В задаче про обезьян вероятности нажатия кнопок одинаковы и независимы, значит, нет никаких причин вычленять из потока уже «сыгравшие» подстроки при подсчёте вероятности. А мат-ожидание уже само по себе — величина ожидаемости _первого_ «выстрела».

                  (Допускаю, что ошибаюсь, не понимая дополнительных условий в вашей задаче и опираясь на решение в Википедии. Я всё ещё не перечитал вашу статью, так что не тратьте на меня время пока.)


                  1. wataru
                    13.04.2016 19:34
                    #8852275
                    +2

                    Ну вот приводили пример с монетками. Пусть наши строки будут "aaa" и "baa", а алфавит только {a,b}. Тогда, только если "aaa" в потоке встречается не на первом месте, то перед ним будет буква "b", а значит "baa" встречается почти всегда раньше, чем "aaa" в любом потоке. Так как мы считаем до первого вхождения — то мат. ожидание меньше.


                    Еще раз, ваша ошибка в том, что вы заменяете мат. ожидание до первого события на обратную величину к частоте события. Это верно только для Пуассоновских потоков. Поток в нашей задаче таким не является. Потому что для строки "aaa" событие может произойти 2 раза подряд, а для строки "abc" — не может никогда.


                    1. napa3um
                      13.04.2016 19:39
                      #8852305

                      Всё, теперь понял, спасибо за терпение. Действительно, теперь получается похоже на задачу про Алису и Боба.


                    1. sebres
                      13.04.2016 20:32
                      #8852379
                      -2

                      А ничего что вы при этом ввели новое условие — "а алфавит только {a,b}."
                      Ничего подобного в вашем примере нет. По мне это как сравнивать булево и десятичное сложения (т.е. одно из них как бы становится "умножением"))).


                      И да, я знаю что такое мат-ожидание… И на абсолютно случайных последовательерстях вероятность встретить паттерн «abc» раньше, чем паттерн «aaa» на самом деле равна 0, честно-честно (при этом естественно не считая «aaaa» за 2 вхождения строки «aaa»).
                      Хотя может объясните мне, почему вы все же считаете «abcd» за 2 разных вхождения — строки «abc» и строки «bcd» — потому что вы это на самом деле делаете… Но два раза «aaa» никак низя… :)


                      1. wataru
                        13.04.2016 20:49
                        #8852391
                        +1

                        Маленький алфавит — это для наглядности. Но это условие нисколько не влияет на то, что строки "aaa" и "baa" точно так же равновероятны. Но в этом примере очевидно, что "baa" встречается раньше.


                        Точно так же, но это менее очевидно "abc" для всего алфавита всречается раньше "aaa". Интуиция тут такая — когда набрана первая буква "a" из "abc" можно или набрать вторую букву, или снова набрать "a" или набрать какой-то нерелевантный мусор. Для строки "aaa" можно только набрать вторую букву или какой-то мусор. Варианта остаться с одной набранной буквой — нет. Тут любая ошибка делает так, что на конце текущей последовательности вообще нет правильно набранного текста. Для "abc" есть вариант сделать не серьезную ошибку, которого для "aaa" нет.


                        Вот вам — поэкспериментируйте. https://jsfiddle.net/zwnfft73/4/
                        В alf задается сколько букв в алфавите, в iter — сколько итераций делать. Для "aaa" ответ всегда больше чем для "abc".


                        1. sebres
                          13.04.2016 21:45
                          #8852475
                          -3

                          вы не правы в том смысле что если вероятностно (а не интуитивно) посмотреть на "a" и какой-то мусор, и "b" и какой-то мусор, то оно в профиль одинаково (и тут размер алфавита важен, только по стольку поскольку он не равен двум).
                          Остальные вопросы вы (и комментаторы ниже, судя по смыслу) решили проигнорировать… Ну да ладно, я к сожалению вышку на уровне профессора не знаю, чтобы вам по полочкам разложить, типа нутром понимаю, но как собак — ни скажу)))


                          1. wataru
                            13.04.2016 21:55
                            #8852483

                            Простите, дискуссия вышла из под контроля. Если вы продублируете вопросы, я на них с удовольствием отвечу.


                            Да, это противоречит интуиции, но все приведенные тут в комментариях симуляции показывают одно и то же. Мат. ожидание для разных строк не одинаково, как и выведено в посте математически.


                            1. sebres
                              13.04.2016 22:16
                              #8852511

                              вы вероятно не про-то, я говорил не про статью, а лишь про способ притянуть в качестве объяснение пример с булевым алфавитом. И только...


                              1. wataru
                                13.04.2016 22:26
                                #8852517

                                Пример с булевым алфавитом разрушает довод "строки встречаются в бесконечном потоке равновероятно => первое вхождение на одинаковом расстоянии". Для больших алфавитов нет такого простого и очевидного примера, к сожалению. Но даже для всех 26 символов получается вот что (для строк "aaa" и "baa"): Перед первой строкой "aaa" почти в одном их 26 случаев идет символ "b", а значит вторая строка встречается раньше в 1/26 всех потоков. Обратного эффекта нет, поэтому появляется перекос.


                                1. sebres
                                  14.04.2016 01:19
                                  #8852645

                                  Пример с булевым алфавитом разрушает довод "строки встречаются в бесконечном потоке равновероятно => первое вхождение на одинаковом расстоянии".

                                  для строк "aaa" и "baa" — т.е. вы сознательно совершаете ту же ошибку снова применяя булевы значения (уже не на булевом алфавите). Хотя размер алфавита в общем-то вы совершенно правильно связали с эффектом названым вами "перекосом".


                                  Что например для строк "aaa" и "baz"? Т.е. во первых не используя чисто булев алфавит, а во вторых исключив (помоему важнейший здесь) другой параметер — одна из строк начинается или оканчивается подстрокой другого паттерна.
                                  Что здесь где перед чем чаще будет встречаться?


                                  Вот выше в ветке вы сами предложили не путать теплое с мягким (я про ваше "неверно посчитается как 2 вхождения строки", потому как интересно только первое вхождение), здесь же, думается мне, вы делаете это сами (я про теплое с мягким).
                                  Попытаюсь объяснить: дело в том, что вы здесь путаете частотные и вероятностные характеристики. Потому как "первое вхождение на одинаковом расстоянии" у них действительно равновероятно находится на том же самом месте.
                                  У вас проблема в чем: например вы генерируете грубо говоря 26 * N последовательностей и говорите, что частный случай где "baa" находится чаще раньше чем "aaa" — есть факт.


                                  При этом делая две ошибки (даже три на самом деле):


                                  • во первых, грубо говоря "обезьяна печатает 1 раз" т.е. тупо случайная последовательность символов одна единственная (а не 26 и не 26*N); соответственно и вероятности что нахождения первой "aaa" в сравнении с первой "baa" (что наоборот) одинаковы.
                                  • во вторых, ваш подход к объяснению с коротким алфавитом как бы не совсем "честен", ибо используете вы частный случай, где одна подстрока содержится в другой, но главное на самом деле практически исключаете здесь бесконечную последовательность случайных величин (ряда) с достаточной плотностью распределения;
                                  • ну и в третьих, последовательности для поиска просто настолько коротки, что при частотном анализе все это и вырождается в частный случай...

                                  Еще раз, это не про сабж конкретно, т.к. сама статья имхо замечательная, и насколько осилил мат-часть, даже (наверно) правильно все доказано (по теме мат-ожидания уже лет двадцать ничего не делал, да и мозг плавится после тяжелого трудового дня))).
                                  Я вам только про "неправильность" что ли вашего примера и некоторые ваши замечания и выкладки про вероятности и смешивания последней с мат-ожиданием. И ни за что другое :)))


                      1. LoadRunner
                        13.04.2016 21:02
                        #8852407

                        Мне кажется, что не равна нулю, а стремится к нему, но лидерство у последовательности из неповторяющихся символов.


                      1. napa3um
                        13.04.2016 21:07
                        #8852417

                        Я на node.js тоже проверил: http://pastebin.com/BKivbrWS
                        Примерно в 1.16 раз быстрее обнаруживается строка 'abc', чем 'aaa' на потоке случайно распределённых символов 'abcdefg', действительно.


    1. wataru
      13.04.2016 17:54
      #8852113
      +1

      Вы правы, стоило более четко формулировать задачу. Я добавил замечание про количество нажатий в статью, спасибо.

      Согласно формуле, для строки «aaa» нужно 18278 нажатий в среднем, а для «abc» — 17576. Разница будет еще заметнее, если ограничится алфавитом только из трех букв (39 против 27).


      1. loginsin
        13.04.2016 19:00
        #8852205

        Пару глупых проверок «в одну строку» на баше:

        Для 'AAA' (с алфавитом 'ABC'):

        alxr@loginsin ~ $ avr=0 ; for((cnt=0;cnt<500;++cnt)) ; do I=0 ; S="" ; while(true) ; do CHR="\x"`printf "%x" $[(RANDOM%3) + 65]`; CC=`printf $CHR` ; S="${S}${CC}" ; if [ "${S}" == "A" -o "${S}" == "AA" -o "${S}" == "AAA" ] ; then if [ "${S}" == "AAA" ] ; then break ; fi ; else S="" ; fi ; I=$[I+1] ; done ; avr=$[avr+I] ; echo "$cnt: $I" ; done ; echo $[avr/500]
...
37



        alxr@loginsin ~ $ avr=0 ; for((cnt=0;cnt<500;++cnt)) ; do I=0 ; S="" ; while(true) ; do CHR="\x"`printf "%x" $[(RANDOM%3) + 65]`; CC=`printf $CHR` ; S="${S}${CC}" ; if [ "${S}" == "A" -o "${S}" == "AB" -o "${S}" == "ABC" ] ; then if [ "${S}" == "ABC" ] ; then break ; fi ; else S="" ; fi ; I=$[I+1] ; done ; avr=$[avr+I] ; echo "$cnt: $I" ; done ; echo $[avr/500]
...
37


        При перепроверках числа примерно одинаковые. Можно и упростить, но хотелось увидеть сами строчки из буковок :)

        Если сделать так:
        alxr@loginsin ~ $ avr=0 ; for((cnt=0;cnt<50;++cnt)) ; do I=0 ; S="" ; while(true) ; do CHR="\x"`printf "%x" $[(RANDOM%26) + 65]`; CC=`printf $CHR` ; S="${S}${CC}" ; if [ "${S}" == "A" -o "${S}" == "AB" -o "${S}" == "ABC" ] ; then if [ "${S}" == "ABC" ] ; then break ; fi ; else S="" ; fi ; I=$[I+1] ; done ; avr=$[avr+I] ; echo "$cnt: $I" ; done ; echo $[avr/500]

        То алфавит будет 'A...Z'. Ждать придется подольше, но числа действительно где-то рядом с обозначенными:
        Для 'AAA'
        0: 11896
1: 20309
2: 74986
3: 2185
^C


        Для 'ABC'
        0: 15595
1: 13412
2: 11241
3: 2308
^C


        В случае с алфавитом 'A..Z' строка 'AAA' действительно появляется значительно реже


      1. ARad
        13.04.2016 19:40
        #8852311
        -4

        Не верю. Автор ошибается! Вероятность одинаковая и соответственно нужно одинаковое количество нажатий.


        1. wataru
          13.04.2016 19:41
          #8852317
          +1

          Автор трижды перепроверил свои выкладки =)


          https://habrahabr.ru/post/200834/#comment_8852275


          1. ARad
            13.04.2016 22:51
            #8852533

            Это равнозначно тому что при алфавите { к, ч } комбинации (к, ч) или (ч к) встрятся раньше комбинаций (к к) или (ч ч). Т.е. можно спокойно идти в казино и после красного ставить на черное а после черного ставить на красное. Сотни лет это не работает, а тут у автора заработало? Ну пусть сходит поиграет, я посмотрю как он без штанов вернется!


            1. Phaker
              14.04.2016 02:34
              #8852667
              +1

              Из утверждения


              среднее время до первого появления строки 'abc' меньше среднего времени до первого появления строки 'aaa'

              не следует утверждение


              строка 'abc' в среднем появляется раньше строки 'aaa'.

              Автор доказывает совершенно корректно первое утверждение. Второе же, безусловно, является неверным. Если вы делаете ставку на то, какая строка появится первой, то ваши шансы строго 50 на 50. Но если вы платите за каждое появление символа по одной монете, то ставить надо на строку 'abc'. Ждать её в среднем придётся меньше.


              Чтобы прочувствовать разницу между этими утверждениями, вот вам ещё пара условных примеров из жизни. Представьте остановку, на которую приходят по определённому расписанию маршрутка и автобус.


              Ситуация 1
              И автобус, и маршрутка ходят с одинаковыми интервалами, но маршрутка едет всегда непосредственно перед автобусом. Тогда среднее время ожидания автобуса и среднее время ожидания маршрутки равны, но когда бы вы ни пришли на остановку, первой появится маршрутка.


              Ситуация 2
              Пусть теперь автобус ходит вдвое реже, но появляется непосредственно перед каждой второй маршруткой. Шансы увидеть первым автобус или маршрутку уравнялись, но среднее время ожидания автобуса вдвое больше.


              1. ARad
                14.04.2016 07:33
                #8852709

                Вы издеваетесь? Автор пишет что для набора 'abc' в среднем потребуется меньше нажатий клавиш чем для 'ааа'. Про время автор вообще ничего не пишет!
                Это все равно что после черного надо ставить на красное, а после красного на черное, потому что такие комбинации встретятся раньше чем «черное черное» или «красное красное».
                Тысячи людей так думали и проигрывали в казино огромные деньги. А ТУТ автор взял и изобрел денежную машину! Ну удачи ему!
                Это все равно что изобрести вечный двигатель. ХИТРЫХ формул и механизмов вечных двигателей тысячи, только не один так и не заработал!


                1. pftbest
                  14.04.2016 10:15
                  #8852837

                  Есть разница. В казино ваш выйгрыш в текущем раунде никак не зависит от того выйграли ли вы прошлый раунд, и было ли там красное. А тут пространство событий совершенно другое.


                  1. ARad
                    14.04.2016 10:30
                    #8852861

                    Все при случайном наборе и в рулетке совершенно одинаковое, так как и тут и там, события независимы друг от друга и алфавит можно оставить всего из двух букв К и Ч.


                    1. wataru
                      14.04.2016 10:34
                      #8852875
                      +1

                      Почти. Вот если бы вы при каждом новом броске платили 1$, а как-только последние 2 броска совпали с вашей комбинацией, вы получаете 10$ — тогда да — выгоднее ставить на "чк" а не на "чч".


                1. wataru
                  14.04.2016 10:16
                  #8852839

                  Почитайте апдейт к статье.


  1. grechnik
    13.04.2016 18:18
    #8852165

    И в качестве упражнения на закрепление материала: https://projecteuler.net/problem=316.


  1. sobakinilya
    13.04.2016 19:37
    #8852293

    Бесконечность…


  1. ivanish
    13.04.2016 19:38
    #8852295

    Да почти что никогда не получится это. 26 букв, знаки, заглавные, пробелы. Причем все тома буква в букву.


    1. wataru
      13.04.2016 19:39
      #8852307
      +8

      Вы недооцениваете Бесконечность.


      1. ivanish
        13.04.2016 21:28
        #8852439
        -4

        Вы переоцениваете Бесконечность.


        1. ooprizrakoo
          14.04.2016 01:37
          #8852651
          +4

          «почти что» в масштабах бесконечности означает «совершенно точно».


  1. sovaz1997
    13.04.2016 19:39
    #8852309
    -3

    Я на эту статью посмотрел немного с другой стороны: давайте найдем вероятность появление живого существа… Не, вероятность появления мира, в котором мы живем. Тогда мы сможем на 99 % предсказать минимальный размер вселенной. Если же она бесконечна, то этот комментарий я пишу не один)). Хотя, я не верю, что вселенная бесконечна: адресного пространства не хватит :D


  1. iKBAHT
    13.04.2016 21:05
    #8852409

    вот реализация вавилонской библиотеки https://www.youtube.com/watch?v=Gw6sBRKz7cM


    1. Semenar
      14.04.2016 18:25
      #8853563

      Ссылка на неё: libraryofbabel.info


  1. gena_glot
    13.04.2016 21:25
    #8852437

    Модель крутая. Но видна ошибка «Поскольку все символы набираются обезьяной случайно». Такие дела, не напишет, короче. Именно поэтому.


    1. wataru
      13.04.2016 22:03
      #8852495
      +1

      В чем здесь ошибка? После того как автомат построен случайное блуждание никак не зависит от назначенных ребрам символов. Или вы тоже сомневаетесь в правдивости первого утверждения в статье? Его доказательство хорошо расписано в Википедии (https://ru.wikipedia.org/wiki/Теорема_о_бесконечных_обезьянах).


      1. napa3um
        13.04.2016 22:14
        #8852509
        +1

        Имеется ввиду, наверное, что реальные мартышки не могут выступать случайными оракулами даже с ненормальным распределением. Вполне может оказаться, что буквы в каких-то сочетаниях они точно никогда не наберут (в силу анатомических/моторных/когнитивных особенностей). Подобная неслучайность «случайного» выбора человека рассматривается в модели «гадалка Шеннона».

        Конечно, в задаче об обезьянах всеми этими особенностями пренебрегают, т.к. это лишь «лирическое» описание мат-модели, есть в ней и покруче расхождения с реальностью (вечная жизнь мартышек, вечный ресурс печатных машинок, вечный интерес печатать, вечный надсмотрщик, проверяющий текст на совпадения и т.д.)


  1. Wesha
    13.04.2016 22:37
    #8852527

    На импровизированной полке расположились в ряд шесть стопок отпечатанного текста, каждая около фута толщиной. Бэйнбридж не без усилия поднял одну из стопок и положил её перед профессором Мэллардом.
    — Результат деятельности шимпанзе А, которого мы зовем Биллом, — сказал он просто.
    "Оливер Твист, сочинение Чарлза Диккенса," — увидел профессор Мэллард. Он прочитал первую страницу рукописи. Потом вторую. Потом лихорадочно перелистал всю рукопись до конца.
    — Вы хотите сказать, — спросил он, — что этот шимпанзе написал…
    — Слово в слово и запятая в запятую, — ответил Бэйнбридж. — Янг, мой дворецкий, и я сверили её с изданием, которое есть в моей библиотеке. Как только Билл кончил, он сразу начал печатать социологические труды итальянца Вильфредо Парето. Если он и дальше будет работать в таком темпе, к концу месяца закончит и это.
    — И все шимпанзе… — с трудом произнес побледневший профессор Мэллард. — И все они…
    — О да, все они пишут книги, которые, по моим расчетам, должны быть в Британском музее. Проза Джона Донна, кое-что из Анатоля Франса, Копан Дойль, Гален, избранные пьесы Сомерсета Моэма, Марсель Пруст, мемуары покойной Марри Румынской и еще монография какого-то доктора Вилея о болотных травах Мэна и Массачусетса. Я могу подвести итог, Мэллард: с тех пор как четыре недели назад я начал этот эксперимент, ни один из шимпанзе не испортил буквально ни одного листа бумаги.

    — Мэлони Рассел. Несокрушимая логика


  1. FSA
    14.04.2016 07:00
    #8852707
    +1

    > напечатает «Войну и мир»

    > все символы набираются равновероятно (с вероятностью 1/26).

    Что-то тут не так. Даже если взять русский алфавит, то уже будет 33 буквы, а если тот, что был до революции, то 35. Ну и вставки на французском языке ещё нужно добавить, а это ещё 26 букв. Плюс знаки препинания и прочее.


  1. ARad
    14.04.2016 11:26
    #8852911

    Что не так с такой программой?

    var str1 = «чч»;
    var str2 = «чк»;
    var c1 = 0;
    var c2 = 0;
    var rnd = new Random();
    for (var i = 1; i < 100000; i++)
    {
    var str = "";
    while (str.IndexOf(str1) < 0 && str.IndexOf(str2) < 0)
    {
    if (rnd.Next(2) == 0)
    str += 'к';
    else
    str += 'ч';
    }
    if (str.IndexOf(str1) >= 0)
    c1++;
    if (str.IndexOf(str2) >= 0)
    c2++;
    }
    Console.WriteLine("{0} {1}", c1, c2);

    http://csharppad.com/gist/d29770ed3b4179d1ee7691a592b2c99a


    1. ARad
      14.04.2016 11:35
      #8852919

      Немного усовершенствовал программу. Результат тот же. С автором не совпадает!!!

      var str1 = «чч»;
      var str2 = «чк»;
      var c1 = 0;
      var c2 = 0;
      var n1 = 0;
      var n2 = 0;
      var rnd = new Random();
      for (var i = 1; i < 100000; i++)
      {
      var str = "";
      while (str.IndexOf(str1) < 0 && str.IndexOf(str2) < 0)
      {
      if (rnd.Next(2) == 0)
      str += 'к';
      else
      str += 'ч';
      }
      if (str.IndexOf(str1) >= 0)
      {
      c1++;
      n1 += str.Length;
      }
      if (str.IndexOf(str2) >= 0)
      {
      c2++;
      n2 += str.Length;
      }
      }
      Console.WriteLine("{0} {1}", c1, n1);
      Console.WriteLine("{0} {1}", c2, n2);

      http://csharppad.com/gist/b5b51c377ff9ab0101d93470aceb3542


      1. wataru
        14.04.2016 12:07
        #8852953
        +1

        Проблема в том, что вы считаете количество нажатий до первой встречи строки str1 при том что строка str2 ни разу не встретилась (и наоборот для второй строки). Это совсем другие величины. Можно этот пример довести до абсурда и считать сразу для всех четырех возможных строчек. Тогда цикл while у вас всегда завершится на второй итерации, что, согласитесь, странно. И вы подсчитаете для каждой строки сумму из двоек. Более того у вас при этом ответ не сойдется с текущей вашей программой.


        Надо или разделить на 2 параллельных цикла отдельно для str1 и str2, или гнать цикл while пока не встретятся ОБЕ строки, запоминая где первый раз каждая из них попалась.


        1. ARad
          14.04.2016 12:42
          #8852983

          Автор говорит что легче набрать ЧК чем ЧЧ. Программа говорит что одинаково.
          Если посадить сто тысячь обезьян то примерно половина из них сначала наберет ЧК, а вторая половина ЧЧ. При этом они наберут примерно одинаковое количество букв. В чем проблема в моей программе?


          1. wataru
            14.04.2016 12:55
            #8853031
            +1

            Проблема в том, что вы проводите другой эксперимент. Вы выгоняете обезьян из-за машинки когда они напечатали или одно или другое. В исходной же задаче обезьяна печатает пока не наберет только одну заданную строку. Этот эксперимент для двух разных строк дает разные результаты.


            Да, вероятности встретить сначала "чч" или "чк" одинаковы.
            Я не говорил нигде про вероятность получить сначала одно или другое. Я считал среднее количество нажатий.
            Кстати, из того, что матожидание одной величины больше матожидания второй величины никак не следует, что первая окажется больше второй в более чем половине случаев.


            1. ARad
              14.04.2016 13:23
              #8853075

              Я не выгоняю их из-за машинки. Но я действительно провожу другой эксперимент. Если обезьяна уже набрала ЧЧ, я не считаю сколько ей еще надо нажать клавиш чтобы в той же строке набрать ЧК. А вы как раз ЭТО считаете. И тогда действительно получается ваше мат ожидание. Где ЧК набрать быстрее, но в жизни вы один и у вас любая комбинация потребует примерно одного и того же количества СЛУЧАЙНЫХ нажатий.


              1. wataru
                14.04.2016 13:35
                #8853091
                +1

                Если обезьяна уже набрала ЧЧ, я не считаю сколько ей еще надо нажать клавиш чтобы в той же строке набрать ЧК. А вы как раз ЭТО считаете.

                А именно это и надо считать.


                Измените ваш код для работы только с ОДНОЙ строкой. Мы же считаем как тяжело получить одну строку, именно ту, которую выбрали? Потом запустите этот код для разных строк "чч" и "чк" и вы получите разные результаты.


                Вот вы никак не понимаете разницу между вопросами:
                1) из двух строк выберете ту, которая встретится раньше в случайном тексте (правильный ответ — неважно)
                2) выберете строку так, чтоб для ее печати потребовалось в среднем меньше символов (ответ — "чк" лучше "чч")


                На первый взгляд кажется, что если в среднем требуется меньше символов, то и встречаться первый раз строка должна раньше других. Но это не так.


          1. wataru
            14.04.2016 12:57
            #8853039
            +1

            Да из 100 тысяч обезьян примерно половина напечатает сначала "чч" а примерно половина "чк" (если выгонять их когда случится одно из двух). Но если первые 50 тысяч заставить печатать пока они не наберут "чч", а вторые 50 тысяч — пока они не наберут "чк", то первые обезьяны напечатают более длинные тексты.


            1. ARad
              14.04.2016 13:32
              #8853089

              Я их не выгоняю, я просто не рассматриваю что они там дальше написали и есть ли там другая строка тоже и как она далеко.


              1. wataru
                14.04.2016 13:35
                #8853095
                +1

                То же самое, что и выгнать. Вы отбрасываете что бы она дальше ни напечатала.


            1. Wesha
              14.04.2016 19:24
              #8853631

              Да из 100 тысяч обезьян

              Моя литературная память не может промолчать...


              Я молчу. Это мой общий ключ. Теперь придется переупаковывать все базы данных. Тёмный Дайвер подносит трубку к Чингизу. Тот почему-то смотрит на меня почти с таким же негодованием, как и на Тёмного Дайвера. Но голос сохраняет спокойным:
              — Открыл первый шифр? Хорошо. Теперь набирай ключ… он простой… ламерский…
              Вот оно в чем дело!
              — Это фраза, первая буква строчная, все остальные прописные. Пробелы значимы. В конце должна стоять точка. Набирай… и повторяй по буквам.
              Чего он тянет…
              Чингиз выдыхает и ледяным голосом произносит:
              — Сорок тысяч обезьян в жопу сунули банан.

              — Сергей Лукьяненко. "Фальшивые зеркала"


      1. vitesse
        14.04.2016 13:36
        #8853099
        +1

        Так как интуитивно мне тоже казалось, что строки «abc» и «aaa» равнозначны и верить автору никак не хотелось, то я написал свой вариант проверки на C# dotnetfiddle.net/Ice8sV (желательно запускать с большим количеством итераций на локальном компьютере). Прогонял несколько раз и практически всегда стока «abc» собирается чаще чем «aaa» — с теор.вером. сложно спорить. Спасибо автору за интересную головоломку!


        1. ARad
          14.04.2016 15:14
          #8853229

          Как раз ваша программа постоянно показывает примерно равные значения! Я ее переделал для алфавита из двух символов. https://dotnetfiddle.net/bqtYr5
          По автору AB будет на 1.5 раза легче набрать чем AA (при алфавите из 2 символов). Это было бы сразу заметно.


          1. ARad
            14.04.2016 15:40
            #8853273

            Тут разница в подходах подсчета.
            Автор считает мат. ожидание в НАБОРЕ строк и из этого делает вывод что АБ набрать быстрее.
            А мы набираем всего ОДНУ строку и потом смотрим что встретилось раньше. И тут мат ожидание будет равным.


            1. wataru
              14.04.2016 16:13
              #8853341
              +1

              Я считаю матожидание количества символов для одной, заранее заданной строки. А вы считает вероятность того, что одна строка будет раньше другой или частоту вхождения строки в бесконечный поток. И то и другое не является матожиданием количества символов.


          1. wataru
            14.04.2016 16:12
            #8853337
            +1

            Эта программа считает не то — количество вхождений. Оно будет одинаковым.
            Вот программа, которая считает то, про что в задаче и спрашивается — https://jsfiddle.net/zwnfft73/4/
            Поиграйтесь прямо в браузере — результаты разные.


  1. GWhiskas
    14.04.2016 14:05
    #8853127

    Спасибо за статью.
    У меня ранее возникал вопрос, только в другой интерпретации, а именно: когда программа «Антиплагиат», в любом из институтов, потеряет свою целесообразность. Ведь при написании диплома, мало кто пишет на какую-нибудь новую тему, или исследует предметную область, ранее неизвестную человеку. Большинство использует книги, статьи интернета, лекции преподавателей (многие из этих лекции, были лекциями предыдущих преподавателей). И как скоро возникнет ситуация, что уже все предметные области расписаны на столько, что уже просто нечего будет написать.


    1. ARad
      14.04.2016 15:19
      #8853237

      Зачем писать на тему по которой уже нечего написать? Это уже НЕ научная работа получается, вас же просили толочь воду в ступе! Дипломная работа не обязана вносить что то новое, а вот кандидатская и докторская обязана.


  1. KasperGreen
    17.04.2016 14:43
    #8856975
    +1

    Это же пример обыкновенного брутфорса. Притом с такой энтропией, что обезьяне проще быстренько (на фоне затрачиваемого времени на брутфорс) эволюционировать до Льва Толстого (всего то пару десятков миллионов лет), чем перебирать все возможные комбинации. Даже если обезьяна будет сверхактивно стучать по дымящейся клавиатуре, это займёт гугол миллиардов лет — минимум.