Компьютеры проникли в большинство сфер жизни человека и продолжают развиваться. Автопилот, банковская сфера, машинный перевод, медицина, финансовые рынки, полеты в космос — все это возможно благодаря одной простой идее.
В этой статье я предлагаю заглянуть за границы возможностей компьютеров и рассмотреть чего же они не могут. И почему. Алан Тьюринг еще в 30-е годы обозначил невозможные для компьютера задачи.
Машина Тьюринга
Если быть предельно точным, то та самая публикация Тьюринга, которая положила начало компьютерным наукам[1], была именно о вычислимых функциях, что подчеркивает существование границы, которую не может перешагнуть машина Тьюринга.
Машина Тьюринга(МТ) — это абстрактная вычислительная машина, тесно связанная с понятием алгоритма[10]. Это самый простой компьютер.
Также стоит помнить, что любая функция, которая может быть вычислена физическим устройством, может быть вычислена машиной Тьюринга[2]. Это ведет к тому, что все выводы касающиеся абстрактной машины Тьюринга, полностью применимы к любым компьютерам на любой архитектуре.
Невычислимые функции и проблема остановки
Проблему остановки[3] можно сформулировать как: не существует общего алгоритма, который бы мог определить, остановится ли программа, по ее описанию и входным данным.
Т.е. функция определения остановки невычислима. Доказательства можно найти в Википедии.
На практике это выглядит так — сам компьютер никогда не сможет определить точно, зависнет ли его очередная программа в бесконечном потоке инструкций или нет. А ведь написанные человеком программы ой как несовершенны.
Одна известная попытка решить эту задачу возникла в недрах Майкрософт под названием Microsoft Terminator[4]. В Microsoft хотели уменьшить количество забагованных драйверов к железу путем построение автоматической системы проверки их на корректность. Они пытались построить инструмент доказательства корректности математической модели программы. О положительных результатах мне не известно, но, думаю, частично повысить стабильность драйверов им удалось.
Busy Beaver Game
Эту задачу в 1962 году обозначил венгерский математик Tiber Rado, в статье "On non-computable functions"[5]. При помощи аналогии с бобром, он объяснял машину Тьюринга, но название закрепилось. Еще в этой статье было упомянуто самое большое число, известное на то время.
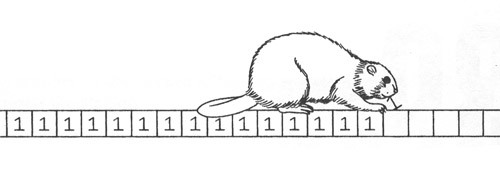
Если ограничить машину Тьюринга(MT) N состояниями, то можно создать конечное число машин.
При росте количества состояний N, количество возможных машин Тьюринга растет быстрее чем экспоненциально: (4(n+1))^2n.
Среди оставшихся МТ будут два типа — те, что останавливаются и нет.
Rado задался одним вопросом в двух формулировках:
- Какое максимальное количество операций может совершить МТ с N состояниями до своего завершения. Это и называют числом Busy Beaver, обозначается как BB(n) или S(n).
- Какое максимально количество единиц может напечатать МТ с N на пустой ленте до завершения. Обозначается как ?(n).
Очевидно, что это число существует. И посчитав его, можно было бы проверить, завершается ли выполнение МТ за это число шагов. Если нет — очевидно, что она будет работать вечно, так как максимальный порог пройден.
The Busy Beaver Game предлагает найти программу для машины Тьюринга с N состояниями, которая работает максимально долго и потом завершается.
В качестве входных данных, лента машины Тьюринга заполнена нулями.
Необходимо составить программу, которая заполнит ее максимальным числом единиц и завершится, перейдя в состояние HALT.
Вот так выглядят правила для машины Тьюринга с двумя состояниями (N=2). Этот же пример является решением Busy Beaver для N=2.
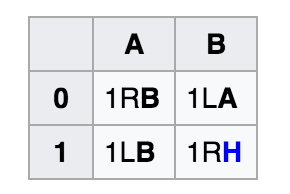
Выполнение программы происходит примерно так:
- Вся лента заполнена нулями в качестве входных данных.
- Начальное состояние — A.
- Считываем текущий бит — если это 1, то выполняем код A1, иначе — A0.
- Инструкции 1RB означают — записать на летну 1, перейти вправо, перейти в состояние B.
- Работа программы продолжается пока не наступит переход на состояние HALT(H)
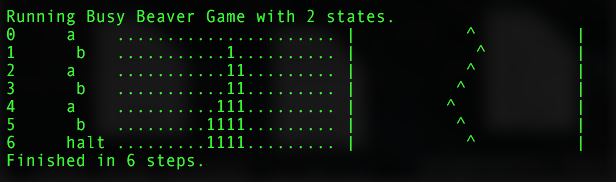
Рисунок 1. Визуализация пошаговой работы MT при N=2. Первая колонка — это номер шага. Вторая колонка показывает как меняются состояния МТ по мере выполнения. Третья колонка — состояния ленты, где видно очередность появления единиц на ней. Четвертая — траектория перемещения указателя по ленте.
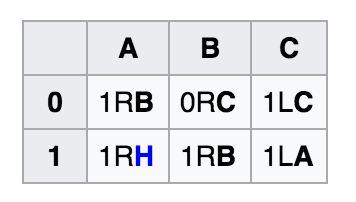
Рисунок 2. Решение Busy Beaver для задачи N=3
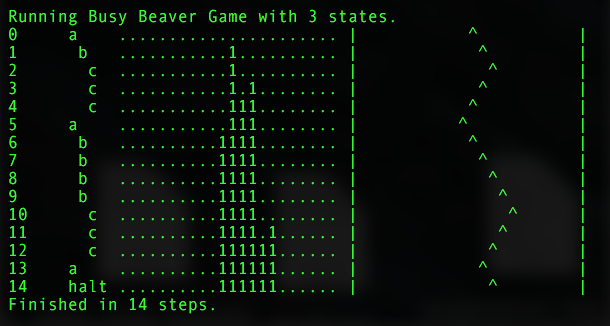
Рисунок 3. Визуализация пошаговой работы MT при N=3.
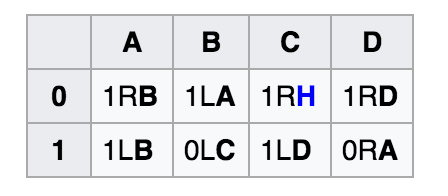
Рисунок 4. Решение Busy Beaver для задачи N=4
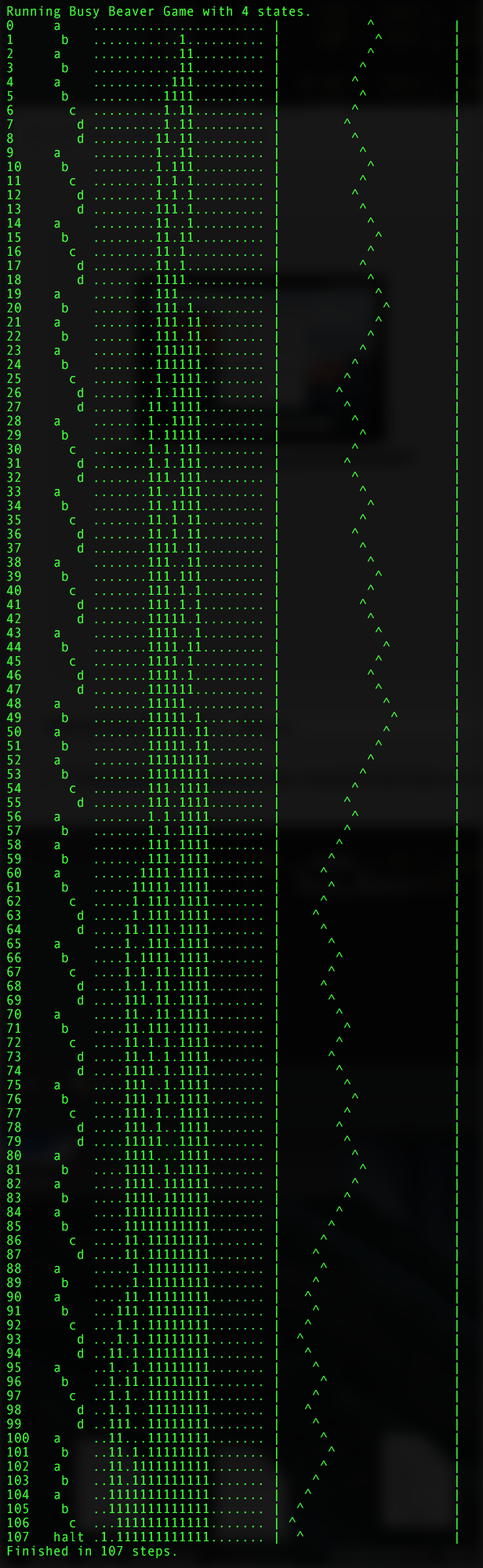
Рисунок 5. Визуализация пошаговой работы MT при N=4. Вот такая елка, с Наступающим!
Для отображения такого графа N=5 нам бы потребовалось 47,176,870 шагов минимум.
При N=6, максимальное найденное на сегодня число Бобра S(6) = 7.4 ? 10^36534.
Для N=7 есть только предварительная оценка S(7) > ?(7) > 10^10^10^10^18705352[6]
На сегодняшний день есть мнение, что люди могут найти S(6) и предоставить доказательства что оно максимальное. S(7) же абсолютно недоступно[8].
Существуют различные вариации: на ленту можно записывать 3,4,5,6 символов, вместо {0,1}. При этом числа только растут.
Как решают эту задачу?
Общий подход к решению выглядит как разделение всех возможных машин Тьюринга на следующие классы:
- Tree-normalized: эти машины исключены из пространства поиска, потому что доказанно, что они эквивалентны другим МТ или их поведение очевидно[8]
- Candidate-halter: Машины, которые гарантированно останаливаются — это кандидаты на звание чемпионов Busy Beaver Game.
- Non-candidate-halter: останавливаюстя, но не удовлетворяют определенным требованиям.
- Non-halter: множество мелких классов для каждого из которых проявляет специфическое поведение связанное с не остановкой.
- Holdouts: все что осталось, при том не ясно останавливаются или нет эти машины. Когда этот класс окажется пустым, можно считать задачу Busy Beaver решенной.
При помощи нормализации по дереву(tree normalization) можно значительно сократить количество МТ.
- Примером метода tree normalization может служить удаление половины МТ, где первый шаг делается влево. Потому как существует аналогичная зеркальная машина, которая начинает движение вправо[8].*
Сверхтьюринговые вычисления
Если бы удалось построить машину для расчета BB(n), это была бы уже сверхтьюринговая машина.
Сверхтьюринговые вычисления — это такие вычисление, которые не могут быть проделаны на машине Тьюринга[9]. Но можно ли построить физический сверхтьюринговый компьютер[7]?
Важный вопрос для создания Сильного Искусственного Интеллекта — оперирует ли разум человека только тьюринговыми вычислениями?
Заключение
Зачем пытаться решить нерешаемую задачу? Может потому, что пограничные случаи в математике открывают всю полноту исходной теории.
The Busy Beaver Game тесно связана с теорией вычислимости, проблемой остановки и теорией сложности.
Еще эта задача заставила меня задуматься — что же такого может вычислить машина Тьюринга на протяжении чуть менее чем бесконечность?
Ссылки
[1] On Computable Numbers
[2] Тезис Черча-Тьюринга
[3] Проблема остановки
[4] Microsoft Terminator
[5] On non-computable functions
[6] Good bound for S(7)
[7] Hypercomputation: Hype or Computation?
[8] The complex behavior of simple machines. Rona Machilin
[9] Сверхтьюринговые вычисления
[10] Машина Тьюринга
[11] Python and C++ sources by by Peteris Krumins
Комментарии (12)
WinPooh73
21.12.2016 14:21Впервые прочитал про эту задачу в 80-х в журнале «Scientific American» (русский вариант выходил под названием «В мире науки»). Кому любопытно взглянуть — статья в рубрике «Занимательный компьютер», посвящённая «охоте на бобра-работягу» в номере 1984-10, читательские отклики в номере 1985-05.
marcor
21.12.2016 14:24+1Как пример машин вне Тьюринга мне припоминаются нейронные сети. Вроде, даже слышал, что на них проблема самоостанова решается, но утверждать не берусь.
Кстати, а квантовый ассемблер относится к таким?
snowman647
21.12.2016 14:39+2Нейронными сетями для постройки супертьюринговых машин занимается Hava Siegelmann. Вот одна из ее публикаций The Super-Turing Computational Power of plastic Recurrent Neural Networks, но на практике еще никому не удалось создать машины для гипервычислений. Квантовые модели тоже не позволяют этого сделать.
Randl
21.12.2016 14:41+1Так NN же вычислимы на машине Тюринга? Если NN будет супертьюринговой, то и сама машина будет супертьюринговой, разве нет?
snowman647
21.12.2016 14:44Идея в том, чтобы построить не мат. модель, а отдельное физическое устройство, обладающее неким свойством, что позволит ему вычислять с бесконечной точность. Но это только теория.
Sergey_Kovalenko
22.12.2016 00:15А вот вам еще одна головоломка про машину Тьюринга:
Не для всех программ, реализующих функции из натуральных в множество {0,1}, есть способ выяснить, останавливаются ли они на каждом аргументе или нет. Однако для некоторых таких программ существуют доказательства того, что они останавливаются. Процесс же поиска всех таких доказательств, как, наверное, известно читателям, всегда можно переложить на некоторую МТ, а значит множество программ, реализующих упомянутые функции и имеющих доказательство своей всюду определенности, алгоритмически перечислимо. Давайте построим МТ, перечисляющую для них пары (текст алгоритма, доказательство), и определим новую функцию G(n): она равна на n-том аргументе 1, если n-тая функция равна на нем 0 и наоборот. Читатель должен видеть, что задающий эту функцию алгоритм, не только всюду определен, но и имеет доказательство своей всюду определенности и конечно же не может совпадать ни с одним из имеющихся в списке!
Есть ли решение у этого парадокса?snowman647
23.12.2016 02:20Думаю, слабое место этого парадокса в том, что не удастся создать такую аксиоматическую теорию, которая сможет доказать останавливаемость всех программ, из множества тех, что останавливаются.
А доказательство остановки G(n) лежит в плоскости другой аксиоматики, отличной от той, что используется изначально.
PDivision
22.12.2016 17:48+1Sergey_Kovalenko
22.12.2016 23:29Хорошо, попытаюсь объяснить.
Вся математика с начала прошлого века попыталась стать формальной. С этого времени доказательства проводятся в формальных аксиоматических системах, которые суть
1. некоторый способ составлять слова и предложения из печатных символов, этот способ задает язык теории, причем проверка, является ли некоторая цепочка символов словом или предложением, должна быть выполнима всегда завершающимся алгоритмом, одним для всех цепочек.
2. формальных правил вывода, позволяющим из всякого семейства предложений, взятых в качестве первоначальных, выводить (продуцировать) другие предложения. На процесс продуцирования налагается то же требование алгоритмичности, что и в пункте 1.
3. Некоторого начального семейства формул, называемых аксиомами. Это семейство не обязательно должно быть конечным, однако должен быть предъявлен алгоритм, позволяющий для всякого предложения языка эффективно выяснить, является оно аксиомой или нет.
Формула языка называется доказанной, если она аксиома либо получена из аксиом и уже доказанных формул.
Основной прием предыдущего парадокса состоит в том, что все программы МТ, для которых существует доказательство конечности времени выполнения на каждом натуральном числе, можно выписать на листке бумаги в ряд (алгоритмически перечислить). Для этого будем перебирать все цепочки из букв и пробелов и алгоритмически проверять не является ли каждая из них доказательством конечности выполнения некоторой программы МТ на всех натуральных числах. Как только вы обнаружили очередное доказательство, проверьте нет ли указанной в нем программы в вашем списке, если нет — добавьте в него программу и найденное доказательство. Утверждается, что если программа имеет доказательство конечности своего выполнения на каждом натуральном числе, то рано или поздно вы на него наткнетесь и она таким образом попадет в список.
Конечно «существуют» программы, которые завершаются на любом натуральном числе, но этот факт никак нельзя доказать, однако для приведенного парадокса этот факт не имеет значения.
snowman647
23.12.2016 02:09Спасибо за пояснения, посидел с листочком и ручкой, парадокс осознал, по большей части. Отвечу в предыдущий пост.
Sergey_Kovalenko
23.12.2016 14:12Я очень рад, что вам удалось решить этот парадокс, и мне хотелось бы по этому поводу указать на некоторые его следствия и добавить пару комментариев к решению.
На сегодняшний день в математике не используются языки, объектами высказываний которых были бы значения предложений самих этих языков, поэтому, как вы правильно заметили, доказательство всюду определенности G(n) не может быть проведено внутри никакой из современных теорий, если та использовалась для построения участвующего в парадоксе списка. Однако, математики никогда не ограничивали себя одной какой-либо теорией и не гнушаются на ходу придумать одну-другую, лишь бы с их помощью решалась стоящая перед ними на тот момент задача. Скорее, у каждого из них имеется некоторый запас доказательных методов и неформальных «истин», в которые они верят. В таком свете, приведенный парадокс показывает, что если вы имеете некоторый набор самоочевидных для вас доказательных методов, то все равно этот набор не включает достаточно самоочевидного относительно этого набора диагонального метода, участвующего в парадоксе.
Второе замечание — а собственно чем так плохи языки, способные высказываться о значении своих предложений и как решается парадокс в этом случае? Вы можете шаг за шагом попытаться представить в этом случае алгоритм действий, описанный в парадоксе. Скажем, вы уже нашли первые сто программ с доказательствами их всюду определенности и вот теперь смотрите на предложение, которое описывает диагональную конструкцию. Задает ли оно функцию и является ли тогда доказательством ее всюду определенности? Если предположить, что «да», то поставив его на сто первое место в списке, вы тут же придете к противоречию, если же вы решите «нет» и не поместите его в список, то с этого самого момента оно начнет задавать всюду определенную функцию и быть доказательством ее всюду определенности.
Все это было бы простой забавой и ненужным софизмом, если бы человечество остро не нуждалось в языках, способных высказываться о собственном значении в связи с задачами восприятия и мышления (описывая что-то, вы всегда можете описать и ваш язык описания, а размышляя над чем-то, размышлять над ходом мыслей). Но пока революция в основаниях математики только зреет.
Randl
Еще хороший пример — проблема соответствий Поста. На гитхабе есть её решалка даже.