10.08.2017 05:51
PatientZero 41 26700 Источник
«Я экспериментировал с задачами кубического представления в стиле предыдущей работы Эндрю и Ричарда Гая. Численные результаты были потрясающими…» (комментарий на MathOverflow)
Вот так ушедший на покой математик Аллан Маклауд наткнулся на это уравнение несколько лет назад. И оно действительно очень интересно. Честно говоря, это одно из лучших диофантовых уравнений, которое я когда-либо видел, но видел я их не очень много.

Я нашёл его, когда оно начало распространяться как выцепляющая в сети нердов картинка-псевдомем, придуманная чьим-то безжалостным умом (Сридхар, это был ты?). Я не понял сразу, что это такое. Картинка выглядела так:


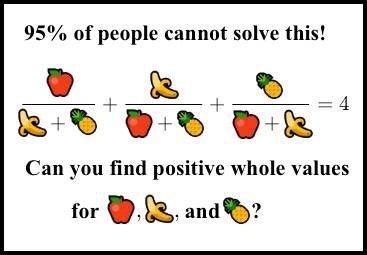
«95% людей не решат эту загадку. Сможете найти положительные целочисленные значения?»

Вы наверно уже видели похожие картинки-мемы. Это всегда чистейший мусор, кликбэйты: «95% выпускников МТИ не решат её!». «Она» — это какая-нибудь глупая или плохо сформулированная задачка, или же тривиальная разминка для мозга.

Но эта картинка совсем другая. Этот мем — умная или злобная шутка. Примерно у 99,999995% людей нет ни малейших шансов её решить, в том числе и у доброй части математиков из ведущих университетов, не занимающихся теорией чисел. Да, она решаема, но при этом по-настоящему сложна. (Кстати, её не придумал Сридхар, точнее, не он полностью. См. историю в этом комментарии).

Вы можете подумать, что если ничего другое не помогает, то можно просто заставить компьютер решать её. Очень просто написать компьютерную программу для поиска решений этого кажущегося простым уравнения. Разумеется, компьютер рано или поздно найдёт их, если они существуют. Большая ошибка. Здесь метод простого перебора компьютером будет бесполезен.

Не знаю, удастся ли уместить полное решение в статью, если не принять, что все уже знают всё необходимое об эллиптических кривых. Я могу привести здесь только краткий обзор. Основной справочный источник — это чудесная, относительно недавняя работа Бремнера и Маклауда под названием «An unusual cubic representation problem» («Необычная проблема кубического представления»), опубликованная в 2014 году в Annales Mathematicae et Informaticae.

Итак, приступим.


Мы ищем положительные целочисленные решения уравнения

$\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}=4 \tag 1$


(я заменил обозначения переменных теми, которые используются в работе).

Первое, что нужно сделать, исследуя любое уравнение — попробовать поместить его в нужный контекст. Надо задать вопрос: что это за уравнение? Так, нас просят найти целочисленные решения, то есть это задача теории чисел. В текущей формулировке в уравнении используются рациональные функции (многочлены, делящиеся на другие многочлены), но очевидно, что мы можем домножить на общее кратное знаменателей, чтобы подчистить уравнение и получить только многочлены, то есть привести его к виду диофантова уравнения. Требование «положительности» довольно необычно, и, как мы увидим, усложняет всё.

Итак, сколько же у нас тут переменных? Вопрос кажется глупым: очевидно, что три, а именно $a$, $b$ и $c$. Но не торопитесь. Опытный исследователь теории чисел мгновенно заметит, что уравнение однородное. Это значит, что если $(a,b,c)$ является одним из решений уравнения, то решением является и $(7a,7b,7c)$. Понимаете, почему? Умножив каждую переменную на какую-нибудь постоянную ($7$ — это просто пример), мы ничего не изменим, потому что константа в каждой из частей сокращается.

$\frac{ta}{tb+tc}=\frac{ta}{t(b+c)}=\frac{a}{b+c}$


Это значит, что уравнение только притворяется трёхмерным. На самом деле оно двухмерно. В геометрическом представлении у нас есть поверхность (одно уравнение с тремя переменными в общем случае задаёт двухмерную поверхность. В целом, $k$ уравнений с $n$ переменными задают $d$-мерное многообразие, где $d=n-k$). Но эта поверхность на самом деле ограничена линией, колеблющейся и проходящей через начало координат. Получившуюся поверхность можно понять, разобравшись в том, как она рассекает единичную плоскость. Это проективная кривая.

Проще всего объянить это сведение можно так: мы можем разделить решения, какими бы они ни были, на те, при которых $c=0$, и те, при которых $c\neq 0$. В первом случае у нас остаётся всего две переменные, $a$ и $b$, а во втором мы просто можем разделить на $c$ и получить решение при $c=1$. Поэтому мы можем просто искать рациональные решения в $a$ и $b$ для случая $c=1$, умножать их на общий делитель и получать целочисленное решение в $a$, $b$ и $c$. В сущности, целочисленные решения однородных уравнений соответствуют рациональным решениям неоднородной версии, которая на одну размерность меньше.

Продолжим: какова степень нашего уравнения? Степень уравнения — это максимальная степень, любого появляющаяся в уравнении одночлена, где «одночлен» — это произведение нескольких переменных, чья «степень» является количеством перемножаемых одночленов. Например, $a^2bc^4$ будет одночленом степени $7=2+1+4$.

Поведение диофантовых уравнений сильно зависит от их степени. В целом:

  • Со степенью $1$ всё просто.
  • Степень $2$ полностью проанализирована и может быть решена довольно элементарными способами.
  • Степень $3$ — это обширный океан глубокой теории и миллион нерешённых проблем.
  • Степень $4$ и выше… Очень, очень сложны.

Мы имеем степень $3$. Почему? Мы просто умножаем на делители:

$a(a+b)(a+c)+b(b+a)(b+c)+c(c+a)(c+b)=4(a+b)(a+c)(b+c)$


Даже без раскрывания скобок можно увидеть, что степень равна $3$: мы никогда не перемножаем более трёх переменных за раз. У нас получатся части типа $a^3$, $b^2c$ и $abc$, но никогда не будет чего-то больше трёх множителей. Если провести преобразования, то уравнение будет иметь вид

$a^3+b^3+c^3-3(a^2b+ab^2+a^2c+ac^2+b^2c+bc^2)-5abc=0$


Вы можете возразить, что умножение на делители невозможно, если какие-то из них оказываются равны $0$. Это верно — действительно, наше новое уравнение имеет несколько решений, не соответствующих исходному уравнению. Но на самом деле это хорошо. Версия с многочленами добавляет к оригиналу несколько «заплаток» и с ним становится проще работать. Нам просто нужно будет проверять, не исчезают ли исходные делители при каждом конкретном решении.

На самом деле уравнение с многочленами легко решить, например, $a=-1$, $b=1$, $c=0$. Это хорошо: у нас есть рациональное решение (рациональная точка). Это значит, что наше кубическое уравнение (степень = 3) на самом деле является эллиптической кривой.

Когда обнаруживаешь, что уравнение представляет собой эллиптическую кривую, то а) радуешься и б) отчаиваешься, потому что предстоит ещё много чего изучить. Это уравнение — прекрасный пример того, как мощную теорию эллиптических кривых можно применить к нахождению безумно сложно определяемых решений.


Первое, что обычно делают эллиптической кривой — приводят её в вейерштрассову форму. Это уравнение, которое выглядит как

$y^2 = x^3 + ax + b$


а иногда как

$y^2 = x^3 + ax^2+bx+c$


(это называется развёрнутой вейерштрассовой формой. Она необязательна, но иногда более удобна).

Обычно любую эллиптическую кривую можно привести к такому виду (если вы только не работаете над полями с малыми характеристиками, но здесь нам не нужно о них волноваться). Объяснять способ поиска правильного преобразования было бы слишком долго, поэтому просто знайте, что это абсолютно механический процесс (критически важно в нём то, чтобы была хотя бы одна рациональная точка, которая у нас есть). Существуют разные пакеты вычислительной алгебры, которые сделают всё за вас.

Но даже если вы не знаете. как найти преобразование, проверить его очень просто, по крайней мере, это выполняется чисто механически. Необходимое преобразование в нашем случае задаётся страшно выглядящими формулами

$x = \frac{-28(a+b+2c)}{6a+6b-c}$


$y = \frac{364(a-b)}{6a+6b-c}$


Я знаю, что они похожи на неизвестно откуда взявшуюся магию вуду, но поверьте, это не так. Получив эти преобразования, с помощью монотонных, но довольно простых алгебраических расчётов мы покажем, что

$y^2 = x^3+109x^2+224x \tag 2$


Это уравнение, хоть и выглядит совсем по-другому, на самом деле является достоверной моделью исходного. Графически оно выглядит так — типичная эллиптическая кривая с двумя вещественными частями:



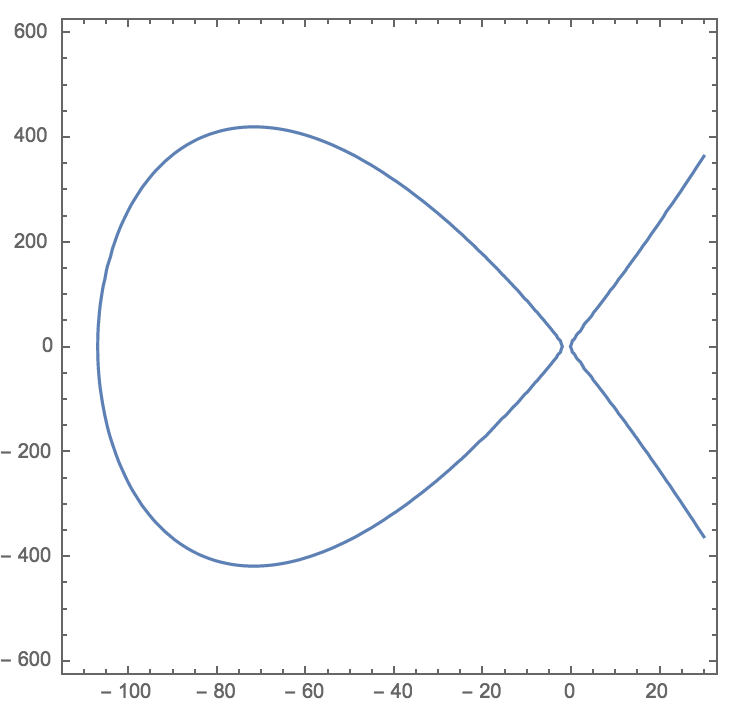
«Рыбий хвост» справа растёт «в бесконечность и дальше». Овальная фигура слева является замкнутой и оказывается для нас довольно интересной.

Имея любое решение $(x,y)$ этого уравнения, мы можем восстановить необходимые значения $a$, $b$, $c$ с помощью уравнений

$a = \frac{56-x+y}{56-14x}$


$b = \frac{56-x-y}{56-14x}$


$c = \frac{-28-6x}{28-7x}$


(Помните, что триплет $(a:b:c)$ нужно воспринимать проективно – какие бы значения вы ни получили с помощью этих уравнений, их всегда можно умножить на любую константу).

Два показанных нами отображения, из $a$, $b$, $c$ в $x$, $y$ и наоборот, показывают, что эти два уравнения «одинаковы» с точки зрения теории чисел: рациональные решения одного дают рациональные решения другого. Технически это называется бирациональной эквивалентностью, а она является фундаментальным понятием алгебраической геометрии. Как мы уже заметили, могут существовать точки-исключения, которые не отображаются правильно. Это случаи, когда $a+b$, $a+c$ или $b+c$ оказываются равны $0$. Это привычная расплата в случае бирациональной эквивалентности, и она не должна вызывать никаких волнений.


Давайте рассмотрим пример.

На эллиптической кривой (2) есть хорошая рациональная точка:

$x=-100$, $y=260$. Возможно, её не так просто найти, но очень просто проверить: просто вставьте эти значения и вы увидите, что две половины одинаковы (я выбирал эту точку не случайным образом, но пока это неважно). Можно просто проверить, какие значения $a$, $b$, $c$ она нам даёт. Мы получаем $a = 2/7$, $b=-1/14$, $c=11/14$, и поскольку мы можем умножить на общий делитель, то результаты преобразуются в $a = 4$, $b=-1$, $c=11$.

И в самом деле,

$\frac{4}{-1+11}+\frac{-1}{4+11}+\frac{11}{4-1}=4$


как можно с лёгкостью убедиться. Это простое решение нашего исходного уравнения в целых числах, но, увы, не в положительных целых. Это решение непросто вывести вручную, но и несложно получить без всей этой рассматриваемой здесь махины, приложив немного терпения. Самая сложность заключается в положительных решениях.

Теперь, получив рациональную точку на эллиптической кривой, например, $P=(-100,260)$ на нашей кривой (2), можно начать генерировать другие с помощью техники хорд и касательных, рассмотренной в предыдущей статье на Quora.



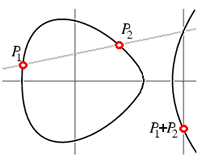
Для начала прибавим нашу точку $P$ к ней самой, найдя касательную к кривой в точке $P$ и определив, где она снова встречается с кривой. Результат будет немного пугающим:

$P+P=2P=(8836/25, -950716/125)$


и снова эта новая точка соответствует значениям $a$, $b$, $c$, являющимся решением исходного уравнения

$(a,b,c)=(9499, -8784, 5165)$


Это решение определённо непросто найти вручную, но оно всё ещё под силу компьютеру. Однако оно по-прежнему неположительно.

Не пугаясь неудач, мы продолжаем вычислять $3P=2P+P$, что можно определить соединением прямой линией $P$ и $2P$ и нахождением третьей точки пересечения с кривой. И снова мы вычисляем $a$, $b$, $c$, и снова результат неположителен. То же самое будет и с $4P$, и с $5P$, и так далее… пока мы не наткнёмся на $9P$.

9P=(-66202368404229585264842409883878874707453676645038225/13514400292716288512070907945002943352692578000406921,
58800835157308083307376751727347181330085672850296730351871748713307988700611210/1571068668597978434556364707291896268838086945430031322196754390420280407346469)

Его определённо непросто найти, но с помощью нашей машинерии нам достаточно повторить девять раз простую геометрическую процедуру. Соответствующие значения $a$, $b$, $c$ потрясающи:

a=154476802108746166441951315019919837485664325669565431700026634898253202035277999,
b=36875131794129999827197811565225474825492979968971970996283137471637224634055579,
c=4373612677928697257861252602371390152816537558161613618621437993378423467772036

Это 80-разрядные числа! Вы никак не смогли бы найти 80-разрядные числа на компьютере с помощью простого перебора. Выглядит невероятным, но вставив эти огромные числа в простое выражение $a/(b+c)+b/(a+c)+c/(a+b)$, мы действительно получим ровно $4$.

Фактически, они являются наименьшими решениями задачи. Если мы продолжим прибавлять к самой себе точку $P$, то при этом просто будут расти делители. Непросто это доказать, потому что всегда есть вероятность сокращения, но теория высот для эллиптической кривой позволяет нам показать, что эти астрономические числа на самом деле являются простейшим решением уравнения.




Вернёмся к теории. Эллиптическая кривая над рациональными значениями имеет ранг, который является количеством точек, необходимых, чтобы использовать для метод хорд и касательных и быть уверенным, что мы рано или поздно найдём все рациональные точки на кривой. Наша эллиптическая кривая (2) имеет ранг 1. Это значит, что у неё есть бесконечное количество рациональных точек, но все они получаются из единственной, которая является ничем иным, как нашей точкой $P=(-100, 260)$. Алгоритмы вычисления ранга и нахождения такого генератора далеки от тривиальных, но SageMath (теперь имеющий название CoCalc) выполняет их меньше чем за секунду всего в нескольких строках кода. Мой код можно посмотреть здесь. Он воспроизводит всё решение с нуля, но, конечно же, использует встроенные методы Sage для работы с эллиптическими кривыми.

В нашем случае точка $P$ лежит на овальной части кривой, как и точки $mP$ для любого положительного целого $m$. Они «кружатся» по овалу и постепенно довольно равномерно по нему распределяются. Это очень удачно, потому что только небольшая часть этого овала даёт положительные решения в отношении $a$, $b$, $c$: это выделенная жирным часть графика ниже, взятого из работы Бремнера и Маклауда.



Точки $P$, $2P$, и так далее, не лежат на выделенной части, а $9P$ — лежит, именно так мы и получили наши 80-разрядные положительные решения.

Бремнер и Маклауд изучили, что происходит, если мы заменяем $4$ чем-то другим. Если вы думаете, что решения будут большими, то подождите, пока не увидите, какими окажутся решения при результате $178$. Вместо 80 разрядов нам понадобится 398 605 460 разрядов. Да, это только количество разрядов решения. Если заменить результат на $896$, то решение будет содержать триллионы разрядов. Триллионы. Для этого невинно выглядящего уравнения:

$a/(b+c)+b/(a+c)+c/(a+b)=896$



Поразительный пример того, как диофантовы уравнения с небольшими коэффициентами могут иметь огромные решения. Это внушает не просто трепет, а ощущение бездонности. Отрицательное решение десятой проблемы Гильберта означает, что рост решений при увеличении коэффициентов — это невычислимая функция, потому что если бы она была вычисляемой, то у нас был бы простой алгоритм решения диофантовых уравнений, а его не существует (ни простого, ни сложного). Соответствие $4 \to$ 80-разрядные числа, $178 \to$ числа из сотен миллионов разрядов и $896 \to$ триллионы разрядов даёт нам небольшое представление о первых, небольших шагах этой чудовищной невычислимой функции. Немного измените числа в уравнении, и решения запросто превзойдут всё, что может вместиться в нашу жалкую, крошечную Вселенную.

Вот такое удивительно хитрое небольшое уравнение.

Благодарю пользователя MrShoor, приславшего мне ссылку на эту интересную статью.

Комментарии (41)


  1. vesper-bot
    10.08.2017 09:41
    #10353102

    Теперь понятно, откуда сложности в вычислениях всяких там ECDHE. ЕМНИП в нем требуется, чтобы кривая имела ранг 1.


  1. karellen
    10.08.2017 12:16
    #10353634
    -9

    Отлично! Надо построить на этом новую криптовалюту, обогатиться и уехать жить на Бали.


    1. khim
      10.08.2017 19:08
      #10354802
      +5

      Всё уже украдено до нас: большинство криптовалют и так на этом и построено…


  1. InstaHeat
    10.08.2017 12:17
    #10353640
    -8

    Попробовал почитать и попробовал решить.
    Сразу скажу, что я филолог и к этой теме не имею отношения. Может быть хотя бы кто-то посмеется над тем, как филологи размышляют.

    У меня была другая логика. Если правая часть равна сумме элементов левой, то по идее 1 левый элемент в этом случае должен равняться 1,33333333333
    Соль в том, что во всех 3 элементах одни и те же переменные. Поэтому мы можем считать, что 4=любая переменная, деленная на сумму двух других.
    Теперь остается только проблема понять как относятся все 3 переменные между собой. То, как переменные располагались в элементах левой части, дает выводы (которые нужно подтверждать или опровергать):
    — одна из них равна нулю
    — одна из них равна 1
    — они все равны
    — одна больше двух других, при этом 2 другие равны между собой
    Дальше мне знания уже не позволяют делать какие-то уверенные ходы. Но в принципе перебором можно было бы отсечь некоторые выводы. Мне до сих пор представляется что последние 2 из моих вариантов наиболее реалистичны


    1. zedroid
      10.08.2017 12:54
      #10353762

      По моим ощущениям хитрость именно в том, что уравнение однородное. А порядки такие возникают из-за того, что мы ищем не приближенное решение с ошибкой меньше заданной, а точное и рациональное. Например приближенное нерациональное навскидку лежит между (3.7 1 1) и (3.8 1 1)


    1. InstaHeat
      11.08.2017 09:14
      #10355582
      -3

      Недоумение
      Не пойму, к чему все так активно минусят. Я сразу предупредил что ни разу не математик и просто пробую построить какую-то логику
      Вместо того, чтобы указать на ошибки или выразить свое мнение словами народ активно минусует по инерции, наверняка даже не прочитав и половину текста.
      Просто так принято — докинуть сверху. Замечательно, а, главное, разумно


      1. michael_vostrikov
        11.08.2017 11:06
        #10355866
        +3

        Может потому что вы не спросили, в чем у вас ошибка, а просто считаете ваше решение верным? По крайней мере 2 из ваших вариантов. Даже после прочтения статьи.
        И да, логика у вас неправильная, вернее ее нет. Например, по какой идее 1 элемент из суммы 3 чисел должен равняться 1,33333333333? Может это "1.3+1.3+1.4". Или как из одних и тех же переменных следует, что 4=любая переменная, деленная на сумму двух других? Тем более что "переменная, деленная на сумму двух других" это описание 3 слагаемых, которые только в сумме дают 4.


        1. InstaHeat
          11.08.2017 11:13
          #10355890
          -5

          Может потому что вы не спросили, в чем у вас ошибка, а просто считаете ваше решение верным?

          Да неужели? А начальный текст для чего? Может быть просто у нас большие проблемы с культурой чтения, или лень вчитываться?
          Я расписал как мыслил, не более того. Может быть люди считать и умеют, но вот с восприятием текста, очевидно, проблемы.


          1. khim
            11.08.2017 12:20
            #10356112
            +1

            А начальный текст для чего?
            Не знаю для чего начальный текст. Там было обещание показать какую-то логику. Логик, как известно, существует много — но у них у всех есть общее свойство: мы сначала постулируем, что собираемся использовать какие-то правила игры, а потом им следуем. А главное, что все логики объединяет — это то, что нельзя выдумывать «из пальца» постулаты, они всегда должны на что-то опираться. У вас же, что ни фраза — то шедевр.

            Если правая часть равна сумме элементов левой, то по идее 1 левый элемент в этом случае должен равняться 1,33333333333
            С какого перепугу? Откуда эта безумная (и неверная, кстати) «идея»?

            Cоль в том, что во всех 3 элементах одни и те же переменные.
            А что они, вообщем-то, там в разных позициях стоят — нас не волнует?

            Поэтому мы можем считать, что 4=любая переменная, деленная на сумму двух других.
            Это-то откуда следует?

            То, как переменные располагались в элементах левой части, дает выводы (которые нужно подтверждать или опровергать):
            — одна из них равна нулю
            — одна из них равна 1
            — они все равны
            — одна больше двух других, при этом 2 другие равны между собой
            А единственный возможный в реальности вариант (они все три разные) — мы выкинули из рассмотрения… на основании чего? И вообще — что это за варианты такие, один другого бессмысленнее?

            Мне до сих пор представляется что последние 2 из моих вариантов наиболее реалистичны
            На основании чего, о чём мы вообще говорим?

            Вы попросили — указать вам на ошибки «в логике», но обычно такой вопрос предполагает, что вы, в общем, всё делаете правильно, но где-то что-то «немного» перепутали. Если же ваше рассуждение выглядит как поток никак не связанных с друг другом фраз… то о чём тут можно говорить?


            1. InstaHeat
              11.08.2017 12:39
              #10356152
              -6

              Вам всем не пришлось бы так долго занудствовать, если бы вы определили главное предложение в комментарии: Сразу скажу, что я филолог и к этой теме не имею отношения
              Все удивительным образом становится понятно, не правда ли? Человек пытается рассказать как он пробовал мыслить, показывает шаги (заранее предполагая, что они будут нелепыми).
              И логика в этом контексте явно не в понятии «наука, дисциплина».

              тут страшная тайна
              Касательно изложения текста тоже различают различные подходы, и это тоже называют логикой. А еще можно посмотреть в толковом словаре значение слова логика, там их минимум 4, где 2 значения — то, о чем шла речь в моем первом комментарии.


              1. mayorovp
                11.08.2017 13:05
                #10356224
                +3

                Ну и нафига филолог лезет решать математическую задачу, которую редкий математик способен решить? И почему филолог думает, что его попытки кому-то интересны?


                Конечно, если бы вы все-таки решили задачу — никто бы не посмотрел что вы филолог; решения математических задач можно проверить. Но решения-то у вас нет! Только заведомо тупиковое предложение.


                1. InstaHeat
                  11.08.2017 13:13
                  #10356252
                  -3

                  Потому что имею все свободы чтобы это сделать? Потому что было такое желание? Потому что интересно было попробовать? Можно выбрать что угодно или додумать самому.

                  Никто не спорит что это может быть неинтересно, однако тут реакция на «неинтересно» сильно приближается к реакции «казнить», что тупо нелогично


                  1. mayorovp
                    11.08.2017 13:15
                    #10356262
                    +3

                    Если вас есть свобода писать глупые комментарии — то нас есть свобода ставить им минусы.


                    1. InstaHeat
                      11.08.2017 13:23
                      #10356276
                      -6

                      Весь юмор в том, что оценивается комментарий как глупый как раз из-за неспособности понять другого человека, и из-за предубеждений. Мне интересно только в этой моральной болезни разобраться, я и так знаю что математик из меня никакой.
                      Самое явление куда более проблематично. Знаменитый возглас «А судьи кто?» не на пустом месте родился. Это болезнь общества, и болезнь давняя. Сейчас это просто интересной формы метастазы


                      1. khim
                        11.08.2017 14:10
                        #10356380
                        +5

                        Весь юмор в том, что оценивается комментарий как глупый как раз из-за неспособности понять другого человека, и из-за предубеждений.
                        Да-да, классика жанра: Сливши дискуссию с технарём, ГСМ, однако, тут же убеждает себя, что на самом деле выиграл спор, заставив оппонента продемонстрировать узколобость и неспособность к абстрактному мышлению.

                        Мне интересно только в этой моральной болезни разобраться
                        Почему вы считаете это болезнью? Это, в общем-то, всего-навсего прагматизм. Как вам уже неоднократно говорили: если бы вы все-таки решили задачу — никто бы не посмотрел что вы филолог; решения математических задач можно проверить.

                        Это болезнь общества, и болезнь давняя.
                        Болезнь общества — это как раз то, что некоторые личности доживают до глубоких седин, сохраняя, в общем-то, детсадовское мышление. Демонстрируют свои неудачные попытки что-то сделать и считают, что их должны ценить только за то что «они пытались». А на резонное замечение что даже в школе уже ценятся не «попытки», а результат — вызывают обвинения в том, что весь мир сговорился против них.

                        Но наш мир, на самом деле, весьма терпим к подобного рода личностям. Чесслово — в Интернете есть много сайтов, где ваши рассуждения будут приняты «на ура», независимо от того, насколько в них присуствует логика (в любом смысле). Но Хабр — не один из них.


          1. michael_vostrikov
            11.08.2017 14:23
            #10356406
            +4

            Мне до сих пор представляется что последние 2 из моих вариантов наиболее реалистичны
            Вместо того, чтобы указать на ошибки

            Начальный текст заканчивается тем, что вы считаете правильными 2 своих варианта. Никаких вопросов типа "что я не учитываю?" или "почему не сходится с ответом из статьи?" там нет. Почему вам кто-то должен указывать на ошибки? Тем более что ошибка одна — неверные рассуждения.


            Весь юмор в том, что оценивается комментарий как глупый как раз из-за неспособности понять другого человека, и из-за предубеждений.

            Комментарий оценивается как глупый именно потому что его поняли и соотнесли с ситуацией. Наверно это из-за предубеждений ни одна дробь из статьи не равна 1,33333333333. А остальные комментарии минусуют потому что вы не желаете понять причины и обвиняете всех вокруг.


      1. Vitter
        12.08.2017 00:41
        #10357510
        +4

        Хоть я не минусил, но вот почему минусят.
        Я вот тоже не математик, хотя и не филолог.

        Естественно, не хочу решать в лоб, поэтому пытаемся применить логику: схитрить и упростить:

        1) a = b = c = 0
        НЕТ, так как получается 0/0 + 0/0 + 0/0 = 4
        И хоть 0/0 — это неопределённость и грубо говоря решение верное, но и неверное одновременно

        2) a = b = 0
        Так как уравнение симметрично, нам не важно, какие переменные равны
        0 + 0 + с/0 = 4
        НЕТ

        3) a = 0
        0 + b/c + c/b = 4
        По скольку числа натуральные, уже можно предположить, что будет сумма дробей с разным делителем, либо сума с целом и дробным, то есть НЕТ
        Но можно посомневаться и досчитать:
        b + c = 4bc
        Сумма натуральных чисел почти всегда (кроме малых чисел) меньше их произведения, и уж точно всегда меньше произведения умноженного на 4

        Итак, нельзя избавиться ни от одной переменной
        Но, может, они равны?

        4) a = b = c
        НЕТ, так как 1/2 + 1/2 + 1/2 = 4

        5) a = c
        a/b+a + b/2a + a/a+b = 4
        b/2a + 2a/a+b = 4
        b(a+b) + 4a^ = 4*2a(a+b)
        b^ + ab + 4a^ = 8a^ + 8ab
        b^ — 7ab — 4a^ = 0
        Такое я не могу решить, спрашиваю у Вольфрама:
        Он даёт ответ:
        y = 1/2 (+-7x -+v65)
        НЕТ Никак иррациональное число не сделать целым

        Итак, мало того, что все переменные ненулевые, нет ни одного одинакового значения

        6) 1 + 1 + 2 = 4
        a/b+c = 1; b/a+c = 1; c/a+b = 2
        a = b + c; b = a +c; c = 2a + 2b
        a = (a + c) + c
        НЕТ, c = 0

        7) В отчаянии пытаемся тупо подобрать разные числа, например (1,2,3), (1,2,4),…

        8) Начинаем решать в лоб по полному решению ((((


        1. Vitter
          12.08.2017 00:45
          #10357516
          +2

          Уточнение:
          y = 1/2 (+-7x -+xv65)


        1. MrShoor
          12.08.2017 07:46
          #10357700
          +3

          Только в третьем пункте не b + c = 4bc, а b^2+c^2 = 4bc. Вы потеряли степень после умножения на bc


    1. id_potassium_chloride
      13.08.2017 11:56
      #10358706
      +2

      Удачи в поиске решения такими способами :)


  1. dmagin
    10.08.2017 13:12
    #10353788
    +2

    Какая крутая статья! Спасибо )


  1. vesper-bot
    10.08.2017 14:02
    #10353914
    +2

    Кстати, вот это немного неверно:


    В нашем случае точка P лежит на овальной части кривой, как и точки mP для любого положительного целого m.

    Точка 2P, исходя из её координат, лежит на "рыбьем хвосте", потому что её Х больше нуля. Я так понимаю, что m должно быть нечетным, чтобы точка была на овале, но так как считать в лоб mP нельзя, а надо P+(P+(P+(P+.....+P)))...), то считать точки 2P и далее все равно придется. Т.е. процесс можно оптимизировать немного, если прибавлять сразу 2Р, вычисляя по порядку P, 2P, 3P, 5P,… (2m+1)P.


  1. pda0
    10.08.2017 14:06
    #10353934
    +6

    Хорошо, что вовремя перестал решать сам и начал читать статью. Только 80-разрядных чисел мне в обед не хватало! :)


    1. Aivendil
      10.08.2017 15:51
      #10354318

      И не говорите! Автор, стоит ставить предупреждение в начало, ато ведь я машинально хотел сначала сам порешать перед тем как готовое решение читать. Теперь боюсь представить сколько времени мог убить впустую:)


    1. vak0
      13.08.2017 11:56
      #10358708
      +1

      Я тоже начал было с ручкой и бумагой решать, понял, что не знаю, как подступиться, ну, думаю, ща я его в excel-е перебором… Не может же быть, что в детской на вид задачке решения будут больше 100 :-) Нашел (7, 14, 29), обрадовался было, а там оказалось 3.99996 при проверке. Хорошо, что на этом остановился, куда уж тут с excel-ем-то лезть в калашный ряд :-).
      Автору спасибо большое за статью, я далеко не математик, но прочел на одном дыхании!


  1. grokinn
    10.08.2017 15:11
    #10354190
    +3

    Думал что вольфрам альфа мне тут же выдаст ответ, но он выдал что то ещё более сложное чем эта статья.


    1. 32bit_me
      10.08.2017 16:52
      #10354486
      +4

      А вы написали просто уравнение a/(b + c) + b/(a + c) + c / (a + b) = 4 или уточнили, что решение должно быть целым и положительным?
      Если не уточнили, то вольфрам написал просто решения в вещественных числах.


  1. bogolt
    10.08.2017 15:25
    #10354254
    +2

    Про эти уровнения даже рассказ есть Юровицкий Владимир — Диофантов кинжал


    1. Quarc
      13.08.2017 11:56
      #10358710

      Спасибо за наводку, потрясающий рассказ!


  1. AC130
    10.08.2017 19:10
    #10354806
    +4

    Я думаю, стоит также упомянуть ещё один результат из оригинальной статьи: решения в целых положительных числах для нечётных N (в примере N = 4) не существует. Что автоматически открывает новые просторы для троллинга.


  1. yury-dymov
    11.08.2017 08:45
    #10355560
    +8

    <сарказм>Теперь будет что на собеседованиях спрашивать!</сарказм>


  1. FUNNYDMAN
    11.08.2017 18:06
    #10356894
    +2

    Интересная и познавательная статья. Спасибо.


  1. Gigo
    13.08.2017 11:56
    #10358714
    +1

    Спасибо за пост — поразминал мозги — было веселео.
    Зашел к задаче чуть с другой стороны не смотря на текущее решение
    В начале в экселе набросал формлу1
    image
    Увидел закономерность
    a=b=c=0.5
    Если 7a=b=c=3.75 Следуя логике определить влияние каждой переменной на % увеличения/уменьшения значения можно, но там или дробные части или целые мнозначные.
    На этом этапе эксель закончился
    Включил пхп)) решив что если приблизительное решение и есть то в пределах 1000 — методом перебора 1000*1000*1000 итераций офисный ноут отказался решать)
    сократил его мучения к диапазону -100..100
    Получилось как то так

    for($a=-100;$a<=100;$a++){
	for($b=-100;$b<=100;$b++){
		for($c=-100;$c<=100;$c++){
			@$x = ($a/($b+$c)) + ($b/($a+$c)) + ($c/($a+$b));
			if($x==4){
				echo $a.'*'.$b.'*'.$c."<br>";
				//exit();
			}
		}
	}
}

    Ответов нашел 144 (с отрицательными результатами)
    С положительными ничего не получилось (правда старался уже не очень и посмотрел решение)
    автор нашел первые числа 4 / -1 / 11
    Учитывая что в перелелах -100..100 есть 144 комбинации где и положительные числа меньше (теже -1 / 4 / 11) могу предположить что есть решение с значительно меньшими числами, но заниматься этим вопросом дальше как то недосуг
    Может кому будет интересно все решения:
    -99*-81*45
    -99*45*-81
    -88*-72*40
    -88*40*-72
    -81*-99*45
    -81*45*-99
    -77*-63*35
    -77*35*-63
    -72*-88*40
    -72*40*-88
    -66*-54*30
    -66*30*-54
    -63*-77*35
    -63*35*-77
    -55*-45*25
    -55*25*-45
    -54*-66*30
    -54*30*-66
    -45*-55*25
    -45*25*-55
    -45*81*99
    -45*99*81
    -44*-36*20
    -44*20*-36
    -40*72*88
    -40*88*72
    -36*-44*20
    -36*9*-99
    -36*20*-44
    -35*63*77
    -35*77*63
    -33*-27*15
    -33*15*-27
    -32*8*-88
    -30*54*66
    -30*66*54
    -28*7*-77
    -27*-33*15
    -27*15*-33
    -25*45*55
    -25*55*45
    -24*6*-66
    -22*-18*10
    -22*10*-18
    -20*5*-55
    -20*36*44
    -20*44*36
    -18*-22*10
    -18*10*-22
    -16*4*-44
    -15*27*33
    -15*33*27
    -12*3*-33
    -11*-9*5
    -11*5*-9
    -10*18*22
    -10*22*18
    -9*-11*5
    -9*5*-11
    -9*36*99
    -8*2*-22
    -8*32*88
    -7*28*77
    -6*24*66
    -5*9*11
    -5*11*9
    -5*20*55
    -4*1*-11
    -4*16*44
    -3*12*33
    -2*8*22
    -1*4*11
    1*-4*-11
    2*-8*-22
    3*-12*-33
    4*-16*-44
    4*-1*11
    5*-20*-55
    5*-11*-9
    5*-9*-11
    6*-24*-66
    7*-28*-77
    8*-32*-88
    8*-2*22
    9*-36*-99
    9*-5*11
    9*11*-5
    10*-22*-18
    10*-18*-22
    11*-5*9
    11*9*-5
    12*-3*33
    15*-33*-27
    15*-27*-33
    16*-4*44
    18*-10*22
    18*22*-10
    20*-44*-36
    20*-36*-44
    20*-5*55
    22*-10*18
    22*18*-10
    24*-6*66
    25*-55*-45
    25*-45*-55
    27*-15*33
    27*33*-15
    28*-7*77
    30*-66*-54
    30*-54*-66
    32*-8*88
    33*-15*27
    33*27*-15
    35*-77*-63
    35*-63*-77
    36*-20*44
    36*-9*99
    36*44*-20
    40*-88*-72
    40*-72*-88
    44*-20*36
    44*36*-20
    45*-99*-81
    45*-81*-99
    45*-25*55
    45*55*-25
    54*-30*66
    54*66*-30
    55*-25*45
    55*45*-25
    63*-35*77
    63*77*-35
    66*-30*54
    66*54*-30
    72*-40*88
    72*88*-40
    77*-35*63
    77*63*-35
    81*-45*99
    81*99*-45
    88*-40*72
    88*72*-40
    99*-45*81
    99*81*-45


    1. MrShoor
      13.08.2017 19:51
      #10359036

      Ваш перебор не эффективный. Надо:

      for($a=-100;$a<=100;$a++){
	for($b=a;$b<=100;$b++){
		for($c=b;$c<=100;$c++){


  1. 3dcryx
    13.08.2017 11:56
    #10358716
    +1

    У меня в детстве была древняя книжка по математике, там предлогали поискать рациональные решения уравнения x^3+y^3=3 и я даже искал до тех пор пока в ответы не заглянул....