15.06.2018 17:03
R3EQ 9 3000 Источник

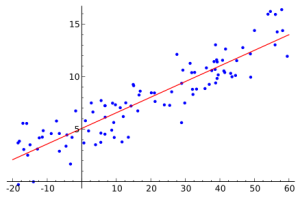
Выражаясь простым языком, модель регрессии в математической статистике строится на основе известных данных, в роли которых выступают пары чисел. Количество таких пар заранее определено. Если представить себе, что первое число в паре – это значение координаты $x$, а второе – $y$, то множество таких пар чисел можно представить на плоскости в декартовой системе координат в виде множества точек. Данные пары чисел берутся не случайно. На практике, как правило, второе число зависит от первого. Построить регрессию – это значит подобрать такую линию (точнее, функцию), которая как можно точнее приближает к себе (аппроксимирует) множество вышесказанных точек.




Для чего это всё нужно? Прежде всего, это нужно для составления т.н. прогнозов. Часто нужно узнать $y$, зная только $x$, если он отличается от тех иксов, на основе которых строилась регрессия. Приведу простой пример. Имеется статистика зависимости роста человека от его возраста на основе 100 исследованных разных человек. Таким образом, мы имеем 100 пар чисел {возраст; рост}. При этом «рост» – зависимая величина, а «возраст» — независимая. Грамотно построив модель регрессии, мы можем с определённой достоверностью «предсказать» рост по любому значению возраста.

На практике, в зависимости от ситуации, в построении моделей регрессии используют линейные, параболические, степенные и другие типы функций. В курсе математической статистики чаще всего рассматривается линейная модель регрессии. Иногда затрагивают случай посложнее – параболическую модель. Делая обобщение, несложно догадаться, что линейная и параболическая модели являются частными случаями более сложной модели – полиномиальной. Построить модель регрессии – это значит найти параметры той функции, которая будет в ней фигурировать. Для линейной регрессии – два параметра: коэффициент и свободный член.


Полиномиальная регрессия может применяться в математической статистике при моделировании трендовых составляющих временных рядов. Временной ряд — это, по сути, ряд чисел, которые зависят от времени. Например, средние значения температуры воздуха по дням за прошедший год, или доход предприятия по месяцам. Порядок моделируемого полинома оценивается специальными методами, например, критерием серий. Цель построения модели полиномиальной регрессии в области временных рядов всё та же – прогнозирование.


Для начала рассмотрим задачу полиномиальной регрессии в общем виде. Все рассуждения основаны на обобщении рассуждений в задачах линейной и параболической регрессии. После этих рассуждений я перейду к частному случаю — рассмотрению данной модели для временных рядов.


Пусть даны два ряда наблюдений $x_i$ (независимая переменная) и $y_i$ (зависимая переменная), $i=\overline{1,n}$. Уравнение полинома имеет вид

$y=\sum\limits_{j=0}^k b_jx^j,\ \ \ \ \ (1)$


где $b_j$ — параметры данного полинома, $j=\overline{0,k}$. Среди них $b_0$ — свободный член. Найдём по методу наименьших квадратов (МНК) параметры $b_j$ данной регрессии.

По аналогии с линейной регрессией, МНК также основан на минимизации следующего выражения:

$S=\sum\limits_{i=1}^n\left(\hat y_i-y_i\right)^2\to\min\ \ \ \ \ (2)$



Здесь $\hat y_i$ — теоретические значения, являющиеся значениями полинома (1) в точках $x_i$. Подставляя (1) в (2), получаем

$S=\sum\limits_{i=1}^n\left(\sum_{j=0}^kb_jx_i^j-y_i\right)^2\to\min.$



На основании необходимого условия экстремума функции $(k+1)$ переменных $S=S(b_0, b_1,\dots,b_k)$ приравняем к нулю её частные производные, т.е.

$S'_{b_p}=2\sum\limits_{i=1}^nx_i^p\left(\sum\limits_{j=0}^kb_jx_i^j-y_i\right)=0,\ \ \ p=\overline{0,k}.$


Поделив левую и правую часть каждого равенства на 2, раскроем вторую сумму:

$\sum\limits_{i=1}^nx_i^p\left(b_0+b_1x_i+b_2x_i^2+\dots+b_kx_i^k\right)-\sum\limits_{i=1}^nx_i^py_i=0,\ \ \ p=\overline{0,k}.$


Раскрывая скобки, перенесём в каждом $p$-ом выражении последнее слагаемое с $y_i$ вправо и поделим обе части на $n$. В результате у нас получилось $(k+1)$ выражений, образующие систему линейных нормальных уравнений относительно $b_p$. Она имеет следующий вид:

$\left\{ \begin{array}{l} b_0+b_1\overline x+b_2\overline{x^2}+\dots+b_k\overline{x^k}=\overline y\\ b_0\overline x+b_1\overline{x^2}+b_2\overline{x^3}+\dots+b_k\overline{x^{k+1}}=\overline{xy}\\ b_0\overline{x^2}+b_1\overline{x^3}+b_2\overline{x^4}+\dots+b_k\overline{x^{k+2}}=\overline{x^2y}\\ \ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\\ b_0\overline{x^k}+b_1\overline{x^{k+1}}+b_2\overline{x^{k+2}}+\dots+b_k\overline{x^{2k}}=\overline{x^ky} \end{array} \right.\ \ \ \ \ (3)$


Можно переписать систему (3) в матричном виде: $AB=C$, где


$A=\left( \begin{array}{ccccc} 1 & \overline x & \overline{x^2} & \ldots & \overline{x^k}\\ \overline x & \overline{x^2} & \overline{x^3} & \ldots & \overline{x^{k+1}}\\ \overline{x^2} & \overline{x^3} & \overline{x^4} & \ldots & \overline{x^{k+2}}\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ \overline{x^k} & \overline{x^{k+1}} & \overline{x^{k+2}} & \ldots & \overline{x^{2k}} \end{array} \right),\ \ B=\left(\begin{array}{c} b_0\\b_1\\b_2\\\vdots\\b_k \end{array} \right),\ \ C=\left(\begin{array}{c} \overline y\\\overline{xy}\\\overline{x^2y}\\\vdots\\\overline{x^ky} \end{array} \right).$


Теперь перейдём к применению вышеизложенных фактов в случае с временными рядами. Пусть дан временной ряд $x_t$, где $t=\overline{1,n}$. Требуется построить полиномиальный тренд порядка $k$, который аппроксимирует данный временной ряд как можно точнее. В качестве независимой переменной $x$ будем брать $t$, исходя из определения временного ряда. Эти иксы представляют собой ряд натуральных чисел, обозначающие период времени. В качестве $y$ берутся значения временного ряда $x_t$. При этом видно, что значения элементов $a_{ij}$ матрицы системы $A$ не зависят от $x_t$. Так как в общем случае, очевидно,

$a_{ij}=\overline{x^{i+j-2}}=\frac1n\sum\limits_{r=1}^nx_r^{i+j-2},$


то в случае с временными рядами

$a_{ij}=\frac1n\sum\limits_{r=1}^nr^{i+j-2},$


где $i,j=\overline{1,(k+1)}.$

Элементы $c_j$ матрицы-вектора свободных членов $C$ в общем случае получаются, как

$c_j=\overline{x^{j-1}y}=\frac1n\sum\limits_{r=1}^nx_r^{j-1}y_r.$


А в случае с временными рядами

$c_j=\frac1n\sum\limits_{r=1}^nr^{j-1}x_r,$


где $j=\overline{1,(k+1)}.$

Таким образом, решив систему (3), мы сможем найти искомые параметры полиномиального тренда $b_0,\dots,b_k.$


Для заполнения матриц системы и для её решения можно применять один из численных методов при моделировании тренда на компьютере. При этом результат вычисления будет достаточно точным.


В результате трендовая составляющая примет вид:

$T_t=\sum\limits_{i=0}^kb_it^i,\ \ \ t=0,1,2,\dots.$


Стоит также отметить, что смоделированная трендовая составляющая $T_t$, определена не только на текущие периоды $[1;n]$, но и на будущие периоды $t>n$.

Сразу отмечу, что полиномиальная регрессия моделирует только трендовую составляющую временного ряда. Полная модель временного ряда подразумевает ещё и другие составляющие, что выходит за рамки данной статьи.


На практике мне лично не встречались временные ряды с порядком полиномиального тренда более, чем 2. Этим и объясняется распространённость моделей линейной и праболической регрессии, как частных случаев полиномиальной.

Комментарии (9)


  1. mwambanatanga
    15.06.2018 20:19
    #18779913

    Построить регрессию – это значит подобрать такую линию (точнее, функцию), которая как можно точнее приближает к себе (аппроксимирует) множество вышесказанных точек.
    Это точно? И если я подберу функцию, которая пройдёт через все точки (для n точек это будет полином степени n-1), то будет ли это означать, что я нашёл оптимальные параметры регрессии? Или всё же чего-то не хватает в опредлении?


    1. edd_k
      15.06.2018 20:43
      #18779961
      +2

      Или же что-то лишнее. Фраза «как можно точнее» не к месту.

      P.S.: Да и в целом хотелось бы спросить автора о смысле статьи, в которой он описывает (слегка добавив своих слов, искажающих суть/определения) то, что множество раз описано более точно во множестве учебников


      1. R3EQ Автор
        15.06.2018 20:58
        #18780031

        Лично я не встречал подробного описания полиномиальной регрессии в учебниках, по аналогии с линейной регрессией. Много раз описана именно линейная регрессия, реже — параболическая.


    1. R3EQ Автор
      15.06.2018 20:55
      #18780017

      В теории да, но на практике получается, что порядок полинома гораздо меньше числа наблюдений. Он выбирается исходя из того или иного критерия.


      1. mwambanatanga
        16.06.2018 18:06
        #18782445

        В теории да, но на практике получается, что порядок полинома гораздо меньше числа наблюдений.
        Имеет место непонимание проблемы. Оно не просто «получается». Чем меньше степень полинома, тем больше ошибка («зазор» между исходными данными и функцией регрессии). И тем не менее, на практике никто и никогда не использует полиномиальную функцию, которая идеально проходит через все точки. Интересно, почему?
        Он выбирается исходя из того или иного критерия.
        Как-то не очень информативно.

        Ладно, хватит ходить кругами. Цель регрессии — не «найти функцию». Форма функции определяется теоретической моделью описываемого процесса. А регрессия всего лишь подбирает оптимальные параметры (коэффициэнты) для нашей функции. Такие параметры, при которых функция проходит как можно ближе к точкам.


    1. mkm565
      15.06.2018 22:18
      #18780241

      Трудно сказать, для чего переписывать главу про полиномиальную регрессию из учебника без упонимания о том, что полученная матрица Вандермонда обладает отвратительной обусловленностью, что делает эту регрессию намного хуже на практике, чем ортогональние полиномы, например.
      Была (и есть) очень старая книга, которая во времена исторического материализма явлалась для многих (включая меня) настольной кногой про практической статистике.
      Худсон Д. Статистика для физиков. PDF- во многих местах в Инете.
      Там регрессия была расписана очень подробно, включая один из самих важних моментов — оценивание ошибок и выбор количества аппроксимирующих функций.
      Вратце. Оценка ошибки измерений (нормальное распределение, и т.д.) по данним регрессии:


      sigma=R/(n-m-1)


      sigma — оценка дисперсии.
      R — остаточана сумма квадратов
      n — число точек измерений
      m — число полиномов


      Понятно, что ежели, увеличить число полиномон до n-1, до мы проведем интерполяцию и никакой оценки ошибки измерений дать не сможем. Поетому надо минимизировать sigma.
      В той же главе рассматривается практический способ контроля числа полиномов с использованием критерия Фишера.


      Всегда использовал. Не подводила никогда.


      1. R3EQ Автор
        15.06.2018 23:22
        #18780381

        В данной статье я просто рассмотрел МНК на случай полиномиальной регрессии и применение данной модели в моделировании трендовой составляющей временных рядов. Всё! Я не ставил для себя цель исследования качества данной модели, проверки гипотез и т.д. И причём здесь нормальное распределение случ. величин, если речь шла о временных рядах? И кстати, здесь нет никаких матриц Вандермонда, которая как раз-таки и возникает в задаче интерполяции многочленами.


        1. mwambanatanga
          16.06.2018 18:19
          #18782479

          И причём здесь нормальное распределение случ. величин, если речь шла о временных рядах?
          Дык разница между теоретическим значением и реальными данными и есть случайная ошибка модели. Всё крутится именно вокруг минимизации этой ошибки. И методом наименьших квадратов (LS) вы минимизирует именно эту случайную величину. И теоретическое обоснование оптимальности результата LS (или GMM, или ML) основывается на свойствах этой случайной величины (т.е. на её фукнции распреленения).


          1. R3EQ Автор
            16.06.2018 18:27
            #18782507

            Описываемый мной метод применяется для моделирования трендовой составляющей временных рядов. Кроме трендовой составляющей в нём присутствуют другие компоненты, в том числе и случайная, и сезонная. Все исследования оптимальности результата, о которых вы говорите, проводятся при полном моделировании временного ряда, они естественно необходимы.