В этой публикации описаны простейшие методы вычисления интегралов функций от одной переменной на отрезке, также называемые квадратурными формулами. Обычно эти методы реализованы в стандартных математических библиотеках, таких как GNU Scientific Library для C, SciPy для Python и других. Публикация имеет целью продемонстрировать, как эти методы работают "под капотом", и обратить внимание на некоторые вопросы точности и производительности алгоритмов. Также хотелось бы отметить связь квадратурных формул и методов численного интегрирования обыкновенных дифференциальных уравнений, о которых хочу написать ещё одну публикацию.
Определение интеграла
Интегралом (по Риману) от функции на отрезке называется следующий предел:
где — мелкость разбиения, , , — произвольное число на отрезке .
Если интеграл от функции существует, то значение предела одно и то же вне зависимости от разбиения, лишь бы оно было достаточно мелким.
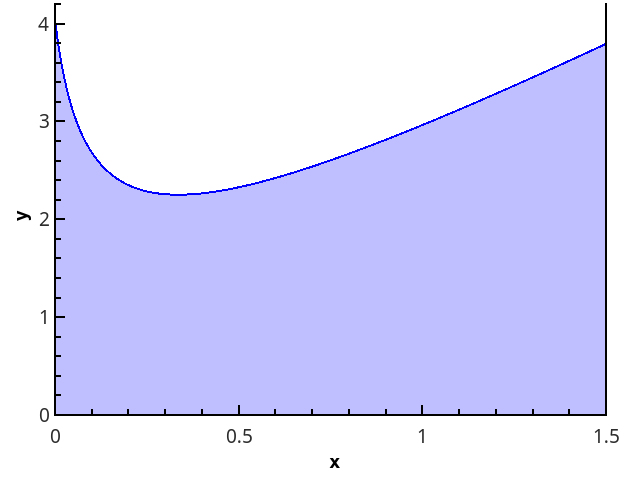
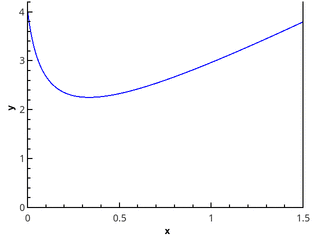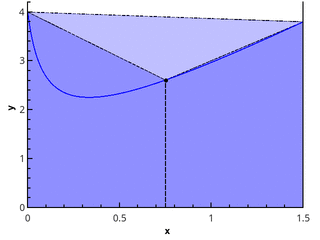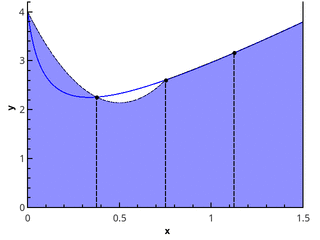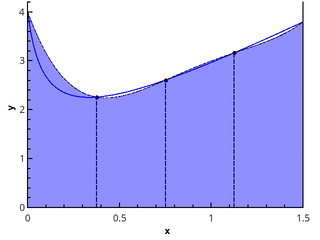
Более наглядно геометрическое определение — интеграл равен площади криволинейной трапеции, ограниченной осью 0x, графиком функции и прямыми x = a и x = b (закрашенная область на рисунке).
Квадратурные формулы
Определение интеграла (1) можно переписать в виде
где — весовые коэффициенты, сумма которых должна быть равна 1, а сами коэффициенты — стремиться к нулю при увеличении числа точек, в которых вычисляется функция.
Выражение (2) — основа всех квадратурных формул (т.е. формул для приближенного вычисления интеграла). Задача состоит в том, чтобы выбрать точки и веса таким образом, чтобы сумма в правой части приближала требуемый интеграл как можно точнее.
Вычислительная задача
Задана функция , для которой есть алгоритм вычисления значений в любой точке отрезка (имеются в виду точки, представимые числом с плавающей точкой — никаких там функций Дирихле!).
Требуется найти приближённое значение интеграла .
Решения будут реализованы на языке Python 3.6.
Для проверки методов используется интеграл .
Кусочно-постоянная аппроксимация
Идейно простейшие квадратурные формулы возникают из применения выражения (1) "в лоб":
Т.к. от метода разбиения отрезка точками и выбора точек значение предела не зависит, то выберем их так, чтобы они удобно вычислялись — например, разбиение возьмём равномерным, а для точек вычисления функции рассмотрим варианты: 1) ; 2) ; 3) .
Получаем методы левых прямоугольников, правых прямоугольников и прямоугольников со средней точкой, соответственно.
def _rectangle_rule(func, a, b, nseg, frac):
"""Обобщённое правило прямоугольников."""
dx = 1.0 * (b - a) / nseg
sum = 0.0
xstart = a + frac * dx # 0 <= frac <= 1 задаёт долю смещения точки,
# в которой вычисляется функция,
# от левого края отрезка dx
for i in range(npoints):
sum += func(xstart + i * dx)
return sum * dx
def left_rectangle_rule(func, a, b, nseg):
"""Правило левых прямоугольников"""
return _rectangle_rule(func, a, b, nseg, 0.0)
def right_rectangle_rule(func, a, b, nseg):
"""Правило правых прямоугольников"""
return _rectangle_rule(func, a, b, npoints, 1.0)
def midpoint_rectangle_rule(func, a, b, nseg):
"""Правило прямоугольников со средней точкой"""
return _rectangle_rule(func, a, b, nseg, 0.5)Для анализа производительности квадратурных формул построим график погрешности в координатах "число точек — отличие численного результата от точного".
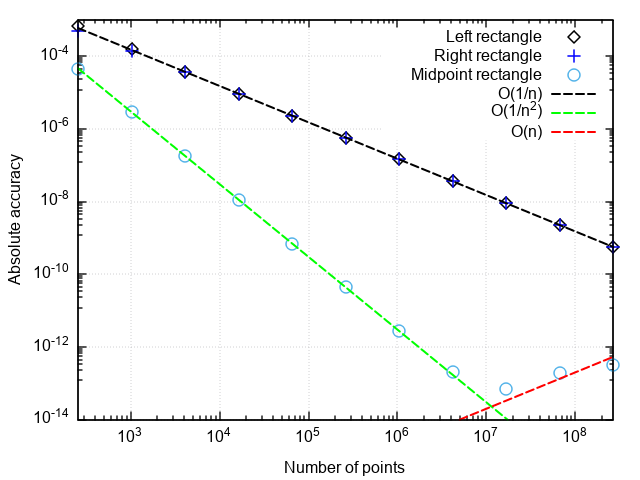
Что можно заметить:
- Формула со средней точкой гораздо точнее, чем с правой или левой точками
- Погрешность формулы со средней точкой падает быстрее, чем у двух остальных
- При очень мелком разбиении погрешность формулы со средней точкой начинает возрастать
Первые два пункта связаны с тем, что формула прямоугольников со средней точкой имеет второй порядок аппроксимации, т.е. , а формулы правых и левых прямоугольников — первый порядок, т.е. .
Возрастание погрешности при измельчении шага интегрирования связано с нарастанием погрешности округления при суммировании большого числа слагаемых. Эта ошибка растёт как , что не даёт при интегрировании достигнуть машинной точности.
Вывод: методы прямоугольников с правой и левой точками имеют низкую точность, которая к тому же медленно растёт с измельчением разбиения. Поэтому они имеют смысл разве что в демонстрационных целях. Метод прямоугольников со средней точкой имеет более высокий порядок аппроксимации, что даёт ему шансы на использование в реальных приложениях (об этом чуть ниже).
Кусочно-линейная аппроксимация
Следующий логический шаг — аппроксимировать интегрируемую функцию на каждом из подотрезков линейной функцией, что даёт квадратурную формулу трапеций:
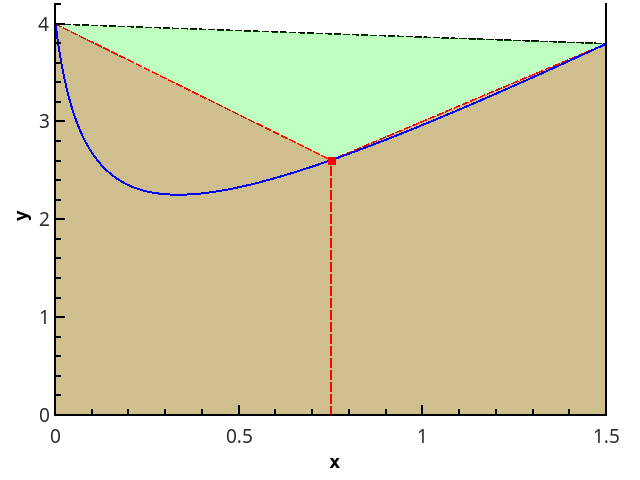
Иллюстрация метода трапеций для n=1 и n=2.
В случае равномерной сетки длины всех отрезков разбиения равны, и формула имеет вид
def trapezoid_rule(func, a, b, nseg):
"""Правило трапеций
nseg - число отрезков, на которые разбивается [a;b]"""
dx = 1.0 * (b - a) / nseg
sum = 0.5 * (func(a) + func(b))
for i in range(1, nseg):
sum += func(a + i * dx)
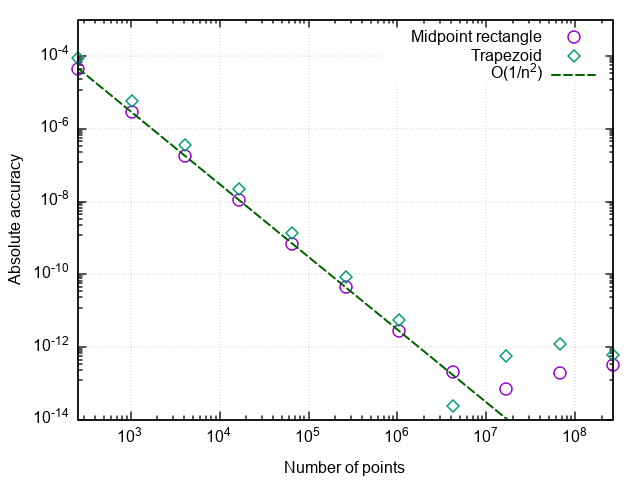
return sum * dxПостроив график ошибки от числа точек разбиения, убеждаемся, что метод трапеций тоже имеет второй порядок аппроксимации и вообще даёт результаты, слабо отличающиеся от метода прямоугольников со средней точкой (в дальнейшем — просто метод прямоугольников).
Контроль точности вычисления
Задание в качестве входного параметра числа точек разбиения не слишком практично, поскольку обычно требуется вычислить интеграл не с заданной плотностью разбиения, а с заданной погрешностью. Если подынтегральная функция известна наперёд, то можно оценить погрешность заранее и выбрать такой шаг интегрирования, чтобы заданная точность заведомо достигалась. Но так редко бывает на практике (и вообще, не проще ли при известной наперёд функции и сам интеграл протабулировать наперёд?), поэтому необходима процедура автоматической подстройки шага под заданную погрешность.
Как это реализовать? Один из простых методов оценки погрешности — правило Рунге — разность значений интегралов, рассчитанных по n и 2n точкам, даёт оценку погрешности: . Метод трапеций удобнее для удвоения мелкости разбиения, чем метод прямоугольников с центральной точкой. При расчёте методом трапеций для удвоения числа точек нужны новые значения функции только в серединах отрезков предыдущего разбиения, т.е. предыдущее приближение интеграла можно использовать для вычисления следующего.
Метод прямоугольников не требует вычислять значения функции на концах отрезка. Это означает, что его можно использовать для функций, имеющих на краях отрезка интегрируемые особенности (например, sinx/x или x-1/2 от 0 до 1). Поэтому показанный далее метод экстраполяции будет работать точно так же и для метода прямоугольников. Отличие от метода трапеций лишь в том, что при уменьшении шага вдвое отбрасывается результат предыдущих вычислений, однако можно утроить число точек, и тогда предыдущее значение интеграла также можно использовать для вычисления нового. Формулы для экстраполяции в этом случае необходимо скорректировать на другое соотношение шагов интегрирования.
Отсюда получаем следующий код для метода трапеций с контролем точности:
def trapezoid_rule(func, a, b, rtol = 1e-8, nseg0 = 1):
"""Правило трапеций
rtol - желаемая относительная точность вычислений
nseg0 - начальное число отрезков разбиения"""
nseg = nseg0
old_ans = 0.0
dx = 1.0 * (b - a) / nseg
ans = 0.5 * (func(a) + func(b))
for i in range(1, nseg):
ans += func(a + i * dx)
ans *= dx
err_est = max(1, abs(ans))
while (err_est > abs(rtol * ans)):
old_ans = ans
ans = 0.5 * (ans + midpoint_rectangle_rule(func, a, b, nseg)) # новые точки для уточнения интеграла
# добавляются ровно в середины предыдущих отрезков
nseg *= 2
err_est = abs(ans - old_ans)
return ansС таким подходом подынтегральная функция не будет вычисляться по нескольку раз в одной точке, и все вычисленные значения используются для окончательного результата.
Но нельзя ли при том же количестве вычислений функции добиться более высокой точности? Оказывается, что можно, есть формулы, работающие точнее метода трапеций на той же самой сетке.
Кусочно-параболическая аппроксимация
Следующим шагом аппроксимируем функцию элементами парабол. Для этого требуется, чтобы число отрезков разбиения было чётным, тогда параболы могут быть проведены через тройки точек с абсциссами {(x0=a, x1, x2), (x2, x3, x4), ..., (xn-2, xn-1, xn=b)}.
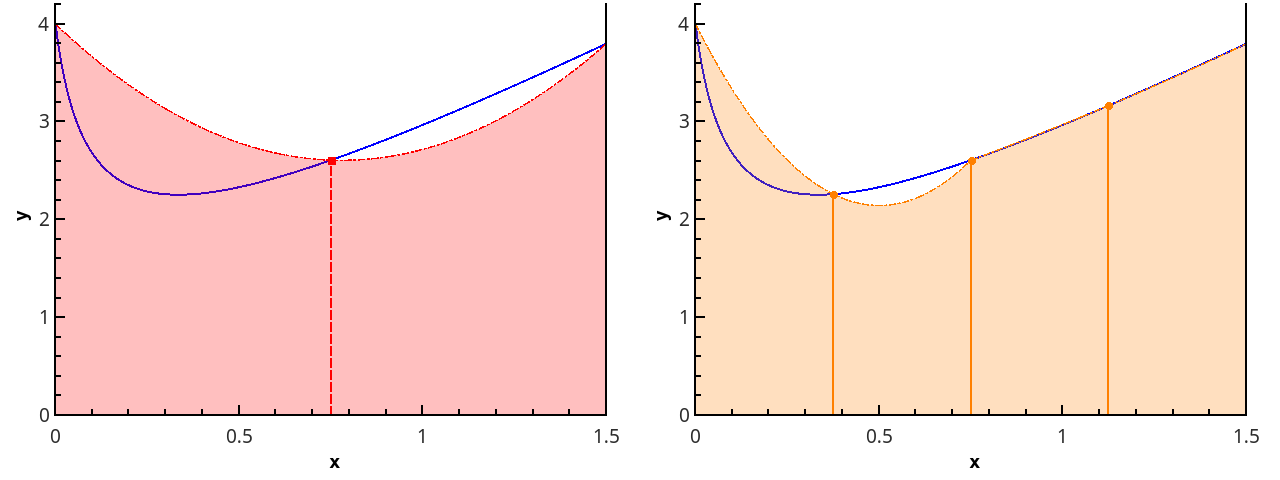
Иллюстрация кусочно-параболического приближения на 3 и 5 точках (n=2 и n=3).
Приближая интеграл от функции на каждом из отрезков [xk;xk+2] интегралом от параболической аппроксимации на этом отрезке и считая точки равномерно распределенными (xk+1=xk+h), получаем формулу Симпсона:
Из формулы (4) напрямую получается "наивная" реализация метода Симпсона:
def simpson_rule(func, a, b, nseg):
"""Правило трапеций
nseg - число отрезков, на которые разбивается [a;b]"""
if nseg%2 = 1:
nseg += 1
dx = 1.0 * (b - a) / nseg
sum = (func(a) + 4 * func(a + dx) + func(b))
for i in range(1, nseg / 2):
sum += 2 * func(a + (2 * i) * dx) + 4 * func(a + (2 * i + 1) * dx)
return sum * dx / 3Для оценки погрешности можно использовать точно так же вычисление интеграла с шагами h и h/2 — но вот незадача, при вычислении интеграла с более мелким шагом результат предыдущего вычисления придётся отбросить, хотя половина новых вычислений функции будет в тех же точках, что и раньше.
Бесполезной траты машинного времени, к счастью, можно избежать, если реализовать метод Симпсона более хитроумным образом. Присмотревшись повнимательнее, заметим, что интеграл по формуле Симпсона может быть представлен через два интеграла по формуле трапеций с разными шагами. Яснее всего это видно на базовом случае аппроксимации интеграла по трём точкам :
Таким образом, если реализовать процедуру уменьшения шага вдвое и хранить два последних вычисления методом трапеций, метод Симпсона с контролем точности реализуется более эффективно.
class Quadrature:
"""Базовые определения для квадратурных формул"""
__sum = 0.0
__nseg = 1 # число отрезков разбиения
__ncalls = 0 # считает число вызовов интегрируемой функции
def __restart(func, x0, x1, nseg0, reset_calls = True):
"""Обнуление всех счётчиков и аккумуляторов.
Возвращает интеграл методом трапеций на начальном разбиении"""
if reset_calls:
Quadrature.__ncalls = 0
Quadrature.__nseg = nseg0
# вычисление суммы для метода трапеций с начальным числом отрезков разбиения nseg0
Quadrature.__sum = 0.5 * (func(x0) + func(x1))
dx = 1.0 * (x1 - x0) / nseg0
for i in range(1, nseg0):
Quadrature.__sum += func(x0 + i * dx)
Quadrature.__ncalls += 1 + nseg0
return Quadrature.__sum * dx
def __double_nseg(func, x0, x1):
"""Вдвое измельчает разбиение.
Возвращает интеграл методом трапеций на новом разбиении"""
nseg = Quadrature.__nseg
dx = (x1 - x0) / nseg
x = x0 + 0.5 * dx
i = 0
AddedSum = 0.0
for i in range(nseg):
AddedSum += func(x + i * dx)
Quadrature.__sum += AddedSum
Quadrature.__nseg *= 2
Quadrature.__ncalls += nseg
return Quadrature.__sum * 0.5 * dx
def trapezoid(func, x0, x1, rtol = 1e-10, nseg0 = 1):
"""Интегрирование методом трапеций с заданной точностью.
rtol - относительная точность,
nseg0 - число отрезков начального разбиения"""
ans = Quadrature.__restart(func, x0, x1, nseg0)
old_ans = 0.0
err_est = max(1, abs(ans))
while (err_est > abs(rtol * ans)):
old_ans = ans
ans = Quadrature.__double_nseg(func, x0, x1)
err_est = abs(old_ans - ans)
print("Total function calls: " + str(Quadrature.__ncalls))
return ans
def simpson(func, x0, x1, rtol = 1.0e-10, nseg0 = 1):
"""Интегрирование методом парабол с заданной точностью.
rtol - относительная точность,
nseg0 - число отрезков начального разбиения"""
old_trapez_sum = Quadrature.__restart(func, x0, x1, nseg0)
new_trapez_sum = Quadrature.__double_nseg(func, x0, x1)
ans = (4 * new_trapez_sum - old_trapez_sum) / 3
old_ans = 0.0
err_est = max(1, abs(ans))
while (err_est > abs(rtol * ans)):
old_ans = ans
old_trapez_sum = new_trapez_sum
new_trapez_sum = Quadrature.__double_nseg(func, x0, x1)
ans = (4 * new_trapez_sum - old_trapez_sum) / 3
err_est = abs(old_ans - ans)
print("Total function calls: " + str(Quadrature.__ncalls))
return ansСравним эффективность метода трапеций и парабол:
>>> import math
>>> Quadrature.trapezoid(lambda x: 2 * x + 1 / math.sqrt(x + 1 / 16), 0, 1.5, rtol=1e-9)
Total function calls: 65537
4.250000001385811
>>> Quadrature.simpson(lambda x: 2 * x + 1 / math.sqrt(x + 1 / 16), 0, 1.5, rtol=1e-9)
Total function calls: 2049
4.2500000000490985Как видим, обоими методами ответ можно получть с достаточно высокой точностью, но количество вызовов подынтегральной функции разительно отличается — метод более высокого порядка эффективнее в 32 раза!
Построив график погрешности интегрирования от числа шагов, можно убедиться, что порядок аппроксимации формулы Симпсона равен четырём, т.е. ошибка численного интегрирования (а интегралы от кубических многочленов с помощью этой формулы вычисляются с точностью до ошибок округления при любом чётном n>0!).
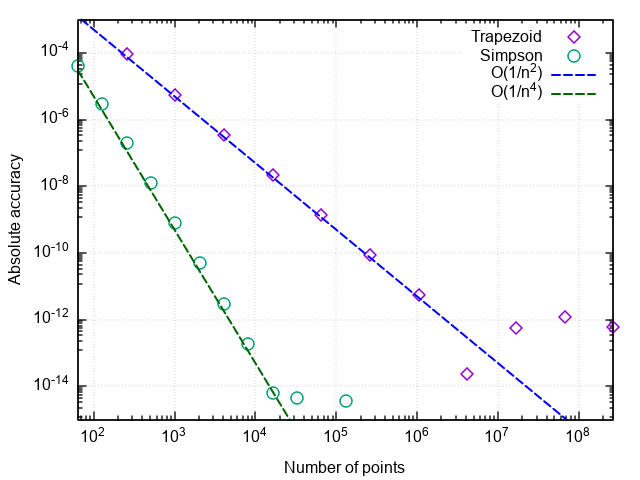
Отсюда и возникает такой рост эффективности по сравнению с простой формулой трапеций.
Что дальше?
Дальнейшая логика повышения точности квадратурных формул, в целом, понятна — если функцию продолжать приближать многочленами всё более высокой степени, то и интеграл от этих многочленов будет всё точнее приближать интеграл от исходной функции. Этот подход называется построением квадратурных формул Ньютона-Котеса. Известны формулы вплоть до 8 порядка аппроксимации, но выше среди весовых коэффициентов wi в (2) появляются знакопеременные члены, и формулы при вычислениях теряют устойчивость.
Попробуем пойти другим путём. Ошибка квадратурной формулы представляется в виде ряда по степеням шага интегрирования h. Замечательное свойство метода трапеций (и прямоугольников со средней точкой!) в том, что для неё этот ряд состоит только из чётных степеней:
На нахождении последовательных приближений к этому разложению основана экстраполяция Ричардсона: вместо того, чтобы приближать подынтегральную функцию многочленом, по рассчитанным приближениям интеграла строится полиномиальная аппроксимация, которая при h=0 должна давать наилучшее приближение к истинному значению интеграла.
Разложение ошибки интегрирования по чётным степеням шага разбиения резко ускоряет сходимость экстраполяции, т.к. для аппроксимации порядка 2n нужно всего n значений интеграла методом трапеций.
Если считать, что каждое последующее слагаемое меньше предыдущего, то можно последовательно исключать степени h, имея приближения интеграла, рассчитанные с разными шагами. Поскольку приведённая реализация легко позволяет дробить разбиение вдвое, удобно рассматривать формулы для шагов h и h/2.
Легко показать, что исключение старшего члена погрешности формулы трапеций в точности даст формулу Симпсона:
Повторяя аналогичную процедуру для формулы Симпсона, получаем:
Если продолжить, вырисовывается такая таблица:
| 2 порядок | 4 порядок | 6 порядок | ... |
|---|---|---|---|
| I0,0 | |||
| I1,0 | I1,1 | ||
| I2,0 | I2,1 | I2,2 | |
| ... | ... | ... |
В первом столбце стоят интегралы, вычисленные методом трапеций. При переходе от верхней строки вниз разбиение отрезка становится вдвое мельче, а при переходе от левого столбца вправо повышается порядок аппроксимации интеграла (т.е. во втором столбце находятся интегралы по методу Симпсона и т.д.).
Элементы таблицы, как можно вывести из разложения (5), связаны рекуррентным соотношением:
Погрешность приближения интеграла можно оценить по разности формул разных порядков в одной строке, т.е.
Применение экстраполяции Ричардсона вместе с интегрированием методом трапеций называется методом Ромберга. Если метод Симпсона учитывает два предыдущих значения по методу трапеций, то метод Ромберга использует все ранее вычисленные методом трапеций значения для получения более точной оценки интеграла.
Дополнительный метод добавляется в класс Quadrature
class Quadrature:
"""Базовые определения для квадратурных формул"""
__sum = 0.0
__nseg = 1 # число отрезков разбиения
__ncalls = 0 # считает число вызовов интегрируемой функции
def __restart(func, x0, x1, nseg0, reset_calls = True):
"""Обнуление всех счётчиков и аккумуляторов.
Возвращает интеграл методом трапеций на начальном разбиении"""
if reset_calls:
Quadrature.__ncalls = 0
Quadrature.__nseg = nseg0
# вычисление суммы для метода трапеций с начальным разбиением на nseg0 отрезков
Quadrature.__sum = 0.5 * (func(x0) + func(x1))
dx = 1.0 * (x1 - x0) / nseg0
for i in range(1, nseg0):
Quadrature.__sum += func(x0 + i * dx)
Quadrature.__ncalls += 1 + nseg0
return Quadrature.__sum * dx
def __double_nseg(func, x0, x1):
"""Вдвое измельчает разбиение.
Возвращает интеграл методом трапеций на новом разбиении"""
nseg = Quadrature.__nseg
dx = (x1 - x0) / nseg
x = x0 + 0.5 * dx
i = 0
AddedSum = 0.0
for i in range(nseg):
AddedSum += func(x + i * dx)
Quadrature.__sum += AddedSum
Quadrature.__nseg *= 2
Quadrature.__ncalls += nseg
return Quadrature.__sum * 0.5 * dx
def romberg(func, x0, x1, rtol = 1e-10, nseg0 = 1, maxcol = 5, reset_calls = True):
"""Интегрирование методом Ромберга
nseg0 - начальное число отрезков разбиения
maxcol - максимальный столбец таблицы"""
# инициализация таблицы
Itable = [[Quadrature.__restart(func, x0, x1, nseg0, reset_calls)]]
i = 0
maxcol = max(0, maxcol)
ans = Itable[i][i]
error_est = max(1, abs(ans))
while (error_est > abs(rtol * ans)):
old_ans = ans
i += 1
d = 4.0
ans_col = min(i, maxcol)
Itable.append([Quadrature.__double_nseg(func, x0, x1)] * (ans_col + 1))
for j in range(0, ans_col):
diff = Itable[i][j] - Itable[i - 1][j]
Itable[i][j + 1] = Itable[i][j] + diff / (d - 1.0)
d *= 4.0
ans = Itable[i][ans_col]
if (maxcol <= 1): # методы трапеций и парабол обрабатываются отдельно
error_est = abs(ans - Itable[i - 1][-1])
elif (i > maxcol):
error_est = abs(ans - Itable[i][min(i - maxcol - 1, maxcol - 1)])
else:
error_est = abs(ans - Itable[i - 1][i - 1])
print("Total function calls: " + str(Quadrature.__ncalls))
return ansПроверим, как работает аппроксимация высокого порядка:
>>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 0) # трапеции
Total function calls: 65537
4.250000001385811
>>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 1) # параболы
Total function calls: 2049
4.2500000000490985
>>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 4)
Total function calls: 257
4.250000001644076Убеждаемся, что, по сравнению с методом парабол, число вызовов подынтегральной функции снизилось ещё в 8 раз. При дальнейшем увеличении требуемой точности преимущества метода Ромберга проявляются ещё заметнее:
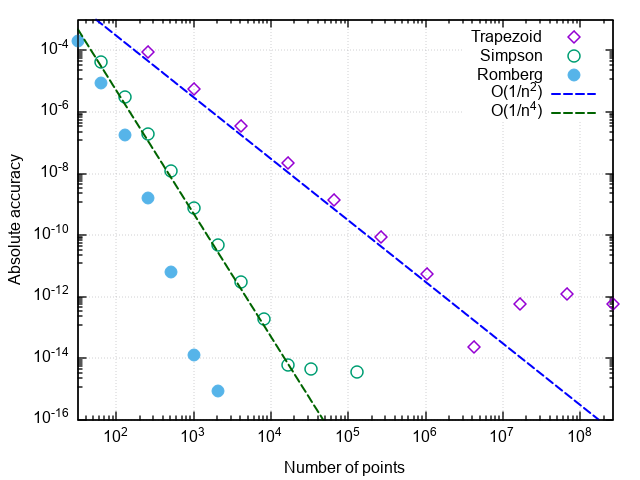
Некоторые замечания
Замечание 1. Количество вызовов функции в этих задачах характеризует число суммирований при вычислении интеграла. Уменьшение числа вычислений подынтегрального выражения не только экономит вычислительные ресурсы (хотя при более оптимизированной реализации и это тоже), но и уменьшает влияние погрешностей округления на результат. Так, при попытке вычислить интеграл тестовой функции метод трапеций зависает при попытке достигнуть относительной точности 5?10-15, метод парабол — при желаемой точности 2?10-16(что является пределом для чисел в двойной точности), а метод Ромберга справляется с вычислением тестового интеграла вплоть до машинной точности (с ошибкой в младшем бите). То есть, повышается не только точность интегрирования при заданном числе вызовов функции, но и предельно достижимая точность вычисления интеграла.
Замечание 2. Если метод сходится при задании некоторой точности, это не означает, что вычисленное значение интеграла имеет ту же самую точность. В первую очередь, это относится к случаям, когда задаваемая погрешность близка к машинной точности.
Замечание 3. Хотя метод Ромберга для ряда функций работает почти магическим образом, он предполагает наличие у подынтегральной функции ограниченных производных высоких порядков. Это значит, что для функций с изломами или разрывами он может оказаться хуже простых методов. Например, проинтегрируем f(x)=|x|:
>>> Quadrature.trapezoid(abs, -1, 3, rtol=1e-5)
Total function calls: 9
5.0
>>> Quadrature.simpson(abs, -1, 3, rtol=1e-5)
Total function calls: 17
5.0
>>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 2)
Total function calls: 17
5.0
>>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 3)
Total function calls: 33
5.0
>>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 4)
Total function calls: 33
5.000001383269357Замечание 4. Может показаться, что чем выше порядок аппроксимации, тем лучше. На самом деле, лучше ограничить число столбцов таблицы Ромберга на уровне 4-6. Чтобы понять это, посмотрим на формулу (6). Второе слагаемое представляет собой разность двух последовательных элементов j-1-го столбца, поделенную на примерно 4j. Т.к. в j-1-м столбце находятся аппроксимации интеграла порядка 2j, то сама разность имеет порядок (1/ni)2j ~ 4-ij. C учётом деления получается ~4-(i+1)j ~ 4-j2. Т.е. при j~7 второе слагаемое в (6) теряет точность после приведения порядков при сложении чисел с плавающей точкой, и повышение порядка аппроксимации может вести к накоплению ошибки округления.
Замечание 5. Желающие могут ради интереса применить описанные методы для нахождения интеграла и эквивалентного ему . Как говорится, почувствуйте разницу.
Заключение
Представлено описание и реализация базовых методов численного интегрирования функций на равномерной сетке. Продемонстрировано, как с помощью несложной модификации получить на базе метода трапеций класс квадратурных формул по методу Ромберга, что значительно ускоряет сходимость численного интегрирования. Метод хорошо работает для интегрирования "обычных" функций, т.е. слабо меняющихся на отрезке интегрирования, не имеющих особенностей на краях отрезка (см. Замечание 5), быстрых осцилляций и т.д.
Продвинутые методы численного интегрирования для более сложных случаев можно найти в книгах из списка литературы (в [3] — с примерами реализации на C++).
Литература
- А.А. Самарский, А.В. Гулин. Численные методы. М.: Наука. 1989.
- J. Stoer, R. Bulirsch. Introduction to Numerical Analysis: Second Edition. Springer-Verlag New York. 1993.
- W.H. Press, S.A. Teukolsky, W.T. Vetterling, B.P. Flannery. Numerical Recipes: Third Edition. Cambridge University Press. 2007.
Комментарии (31)

Itanium_Next
24.08.2018 17:28Вы рассмотрели методы, которые хороши на равномерной сетке. Но, во-первых, не всегда имеется равномерная сетка, но интергал посчитать хочется, а во-вторых, существуют методы, которые дают безумно хороший результат при малом числе узлов (квадратура Гаусса, например)

Pand5461 Автор
24.08.2018 18:37+1Слова «базовые алгоритмы» в название вынесены не просто так. Я так и написал, что всё относится к интегрированию функций, которые можем вычислить по требованию, и на равномерной сетке.
Что значит «не всегда имеется равномерная сетка» — не понял, в этом контексте. Если функция табулированная, то без дополнительных предположений о существовании и ограниченности высших производных методы высоких порядков лучше и не применять, поэтому будет достаточно интерполировать функцию сплайном и его уже проинтегрировать (аналитически, конечно). Если вы о том, что для каких-то функций равномерная сетка — не лучший выбор, — то, я думаю, у кого эти функции часто встречаются, знают, какой заменой переменных интеграл можно привести к более удобному для вычисления виду.
Квадратуры Гаусса штука хорошая, но если их давать не в виде чёрного ящика «считайте функцию вот в этих точках с вот такими весами, и будет счастье», то математическое обоснование выходит за рамки «ресурса для широких кругов программистов и сочувствующих». К тому же, в книге Штёра-Булирша обращается внимание на невозможность априорной оценки нужного порядка формулы Гаусса, т.е. приходится перебирать порядки до сходимости (а предыдущие точки использовать для следующего порядка нельзя), из-за чего привлекательность по сравнению с методом Ромберга уже теряется. Итого, тоже специфическая тема, про которую те, кому она актуальна, и так должны знать из других источников.
В книгах из списка литературы можно прочитать и про гауссовы квадратуры, и про преобразование несобственных интегралов, и даже про автоматическую замену переменных для устранения особенностей на краях отрезка. Но это всё-таки продвинутые и специфические темы.

SmartyTimmi
24.08.2018 22:15+1Давно ждал подобной статьи) И как статья хороша, и как шпаргалка, чтобы объяснять. Очень жду подобное на неравномерных сетках и multigrid`ах, в идеале бы еще реализации на numpy с его особенностями, было бы прекрасно)

nkozhevnikov
А я где-то слышал, что высшая математика программисту не нужна.
maxzhurkin
Вообще говоря, это то, что входит в понятие прикладной математики, но без высшей, конечно, тоже не обходится
ArbeitMachtFrei
А я вот нигде про высшую математику не слышал. Математический анализ — слышал, численные методы — слышал, всякие там дифференциальные уравнения — и про них слышал, а «высшая математика» — что за зверь такой?
nkozhevnikov
Вот как раз математический анализ, дифференциальные уравнения и тому подобное попадают под термин «высшая математика».
Вообще, так сложилось, что под это определение относят всю математику, изучаемую в ВУЗах.
ArbeitMachtFrei
> всю математику, изучаемую в ВУЗах
В заборостроительных, что ли? Ну да, откуда выпускнику заборостроительного знать о существовании какой-то еще математики, помимо «изучаемой в ВУЗах».
Zenitchik
Не всю. У нас была кафедра элементарной математики.
ArbeitMachtFrei
Ума нет — иди в пед.
maxzhurkin
Грубо
djinninia
Я часто слашала, как студенты экономисты, психологи итд (абсолютно не хочу их обидеть) с многозначительностью называли свой курс высшей математики «вышка».
У меня же на радиофизическом факультете сей предмет называли МатАн.
GlukKazan
Ну вообще говоря в «вышку» помимо матана много чего входит. Та же «линейка», которой вы пользуетесь, у примеру. Я тоже, к сожалению, пользуюсь математикой не так много, как хотелось бы, да и так себе я математик, если честно. Но есть области где математика используется активно. САПР например или тот же геймдев. Ну и одной «вышкой» математика тоже не ограничивается.
djinninia
Честно говоря, многим программистам математика, пардон, не нужна. К примеру возьмём Web-разработчиков (да простят они меня, если я их нечаянно обидела).
Я, как инженер-программист, пользуюсь математикой, к сожалению, не так много, как хотелось бы (линейная алгебра в основном).
Но поскольку мне всю сознательную жизнь внушали, что математика важна — я продолжаю в это верить.
Вопрос: чем сейчас занимаются все эти монстры (в самом хорошем смысле это слова), преодолевшие огромные проходной бал на специальность «Прикладная математика», «МатМех», «МехМат»? Уверенна, что чем-то полезным.
Хотелось бы, конечно, увидеть статью «Я — математик-пограммист и математику применяю так-то». Может и есть, честно — не искала.
dom1n1k
Граница водораздела очень проста.
Программисты (а скорее кодеры), которые в своей работе используют кирпичи из готовых библиотек/фреймворков и склеивают их тонким слоем собственного кода-раствора — в математике действительно не нуждаются.
Как только вам нужно сделать что-то новое и залезть в те области, которые до того были под капотом — математика вылазит из всех щелей, даже тех, откуда казалось бы не ждали. Даже в вебе.
Я например, писал внешне несложную визуализацию данных — считал двойные итегралы для корректного учета интенсивности цветов, ну а про матрицы вы и сами в курсе.
Free_ze
Выглядит как сравнение теплого с мягким, а не «граница водораздела», кмк.
Где-то влоб можно встретить злую математику в полный рост (криптография та же, моделирование физических процессов), а где-то хватит «вышмата» с гуманитарного факультета (дизайн с интегралами). На том же прикладном уровне «новизны».
dom1n1k
Абсолютно вписывается и крипотография, и все остальное. Одно дело, если я пишу что-то в духе import std/crypto… hash(password)… encrypt(message)… — мне достаточно знания терминологии и поверхностного понимания что куда подставлять. И совсем другое, если нужно нечто новое и/или нестандартное — когда лезешь под капот, сразу понимаешь, как всё непросто на самом деле.
Lexicon
Мне, как и djinninia(полагаю) интересны реальные истории реальных разработчиков, сталкивающихся с действительно сложными задачами, где сияют именно эти самые люди-математики.
А вы погружаетесь в холивар, скажем, интегралы и реализация графиков концептуально элементарны, в большинстве случаев нет никакой нужды реализовать нечто подобное самостоятельно, даже если из кирпичей давно делают кирпичи же и кирпичами погоняют.
Pand5461 Автор
Надо сказать, математические библиотеки — это специфические такие кирпичи, с характером.
Там, можно сказать, общее правило — какой функцией ни пользуешься, на уровне алгоритма принцип работы нужно знать. Иначе на каких-нибудь входных данных она сломается, а ты даже не будешь понимать почему.
А иногда вообще лучше свой велосипед написать от греха подальше, чем пользоваться этими библиотеками.
Пример бага из мода Principia для Kerbal Space Program (это пишет автор, который в курсе тонкостей реализации, а для пользователя это «что происходит, всё зависло»):
Да, это не продакшен, а хобби-проект. Но, по-моему, хорошая иллюстрация того, что если уж коснулся применения численных методов, то их теорию знать надо — иначе возьмёшь библиотечную функцию, а она даёт ошибку в один бит, а для задачи это критично.
Или посмотреть форумы Intel, где регулярно появляются посты о том, какие функции сломаны в обновлённом MKL.
BratSinot
Математика (в купе с решением задач и доказательством теорем / лемм), в первую очередь, приводит мыслительные процессы в порядок, что приводит к развитию дедуктивного, аналитического, следственного и т.д. мышлений.
Даже web-разработчикам она пригодится, может и косвенно, но пригодится.
djinninia
Полностью соглашусь.
Меня, честно говоря, расстраивает, когда с каких-нибудь медиа звучит: «ах, зачем эта математика, кому нужны все эти формулы» (про школьную программму)
Слышала, для развития логического мышления есть альтернатива математике — изучение древних сложных языков. Также встречала людей, изучавших иврит, например, которые с лёгкостью воспринимали математику.
BratSinot
Ну так если изучать не по принципу «заучить словарь», а с точки зрения структуры языка, каких-то связей, то математики там не меньше. Математика это же не про формулы, а про структуры, объекты и отношения между ними. Даже прикладная математика далеко не всегда про формулы.
Keyten
Ну школьная программа действительно, как правило, сводится к заучиванию формул, и потому и правда не нужна в таком виде, в котором она сейчас существует.
Pand5461 Автор
Сужу по физтеху: большинство программирующих математиков и физиков не считает себя программистами. Поэтому они, скорее, скажут "я учёный, и программирование мне нужно тут-то и там-то, почти на каждом шагу".
BratSinot
Потому-что они больше расчетами занимаются, а не программированием как таковым.
Pand5461 Автор
Вы могли бы пояснить, что именно хотели донести этой фразой?
Keyten
А нужна ли физика программисту? А если он пишет физический движок? А химия нужна или биология? А если он пишет эмуляцию эволюции в биологических целях?
Нужно понимать, что математика точно так же относится к этому списку. Она нужна программисту только если она ему нужна. Если ты пишешь физический движок — тебе нужна физика (и некоторая математика заодно, но не вся). Если ты пишешь рендер четырёхмерной геометрии, тебе опять нужна некоторая математика (но опять не вся). Если ты пишешь параллакс на сайте, наконец, тебе нужна некоторая математика. Если ты пишешь, ну например, админку, в которой получение данных с сервера, какая-то их обработка, mvc, вот это всё, тебе математика скорее не нужна.
Словом, есть задачи, в которых она нужна, и есть в которых нет. Но математика совершенно точно не является необходимым или достаточным условием быть программистом.
Maxim_Andreev
Я думаю, здесь скорее обратный принцип: если ты владеешь математическим аппаратом, то скорее всего, ты в конце концов найдёшь себя на позиции, где математика нужна. Аналогично с физикой. Если же ты в процессе обучения осваивал только лишь написание кода по тьюториалам, разумеется, никто тебя за разработку физического движка или рендеринг четырёхмерной геометрии не посадит, и математика с физикой тебе никогда в жизни не пригодятся.
Таким образом, отметая для себя при обучении в ВУЗе матан и физику, вы существенно ограничиваете область применения своих знаний и скорее всего будете претендовать на те же позиции, что и выпускники колледжей.
Keyten
Вы правы, да. Но хочется добавить, что при желании этому всему можно спокойно научиться и без вуза, самому.
Maxim_Andreev
Вопрос только — за чей счёт? Чудес не бывает: на то, чтобы стать специалистом в какой-то теме, нужно по меньшей мере нескольких тысяч часов, которые одними свободными от работы вечерами не нагнать.
Потом, обучение гораздо быстрее проходит при плотном общении со специалистами в соответствующей области. ВУЗ как сообщество специалистов — наиболее комфортная среда для обучения чему бы то ни было. Конечно, можно самому создать себе препятствие в виде отказа от получения образования, а потом героически его преодолеть… но зачем?
Само собой, это не отменяет необходимость постоянно самостоятельно обучаться в процессе работы, но эффективнее делать это, когда есть какая-то база. Скажем, я без проблем возьмусь на работе за программирование метода Ньютона, хотя на лекциях по численным методам мало чего о нём понял, но даже близко не подойду к криптографии, потому что на то, чтобы вникнуть в одни только основы, нужно несколько месяцев усердного обучения.
cyberzx23
Это очень спорное утверждение. Я программист и работаю в геймдеве. За свою карьеру я несколько раз писал модули интегрирования ОДУ и мне приходилось досконально вникать в различные методы численного интегрирования и проводить собственные исследования. Про линейную алгебру и матричное исчисление даже говорить не буду, без этих навыков в геймдеве делать нечего.