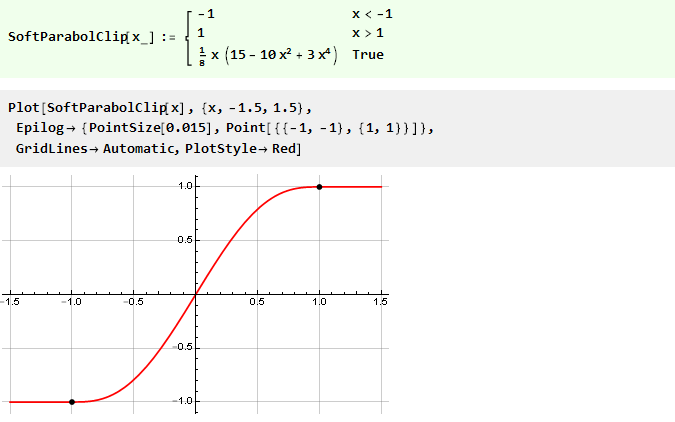
Самая простая реализация ограничения — это принудительная установка в некоторое значение при превышении определённого уровня. Например, для синусоиды с возрастающей амплитудой это будет выглядеть так:

В роли ограничителя здесь выступает функция Clip, в качестве аргумента которой передаётся входной сигнал и параметры ограничения, а результатом функции является выходной сигнал.
Посмотрим на график функции Clip отдельно:
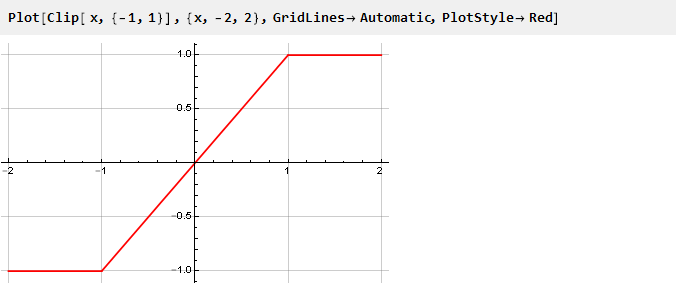
Из него видно, что пока мы не превышаем пределы ограничения, выходное значение равно входному и сигнал не меняется; при превышении же выходное значение от входного уже никак не зависит и остаётся на одном и том же уровне. По сути, мы имеем кусочно-непрерывную функцию, составленную из трёх других: y=-1, y=x и y=1, выбираемых в зависимости от аргумента, и эквивалентную следующей записи:

Переход между функциями происходит довольно резко; и выглядит заманчивым сделать его более плавным. Математически эта резкость обусловлена тем, что производные функций в точках стыковки не совпадают. Это легко увидеть, построив график производной функции Clip:
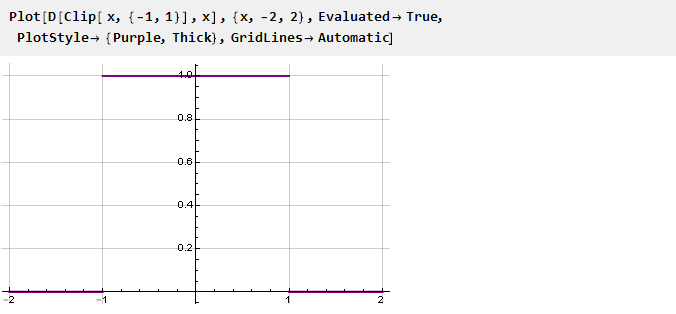
Таким образом, чтобы обеспечить гладкость функции ограничения, необходимо обеспечить равенство производных в точках стыковки. А поскольку крайние функции у нас константы, производные от которых равны нулю, то и производные функции ограничения в точках стыковки тоже должны быть равны нулю. Далее будут рассмотрены несколько таких функций, обеспечивающих гладкую стыковку.
Синус
Самое простое — это использовать функцию sin на интервале от -pi/2 до pi/2, на границах которого значения производной равны нулю по определению:
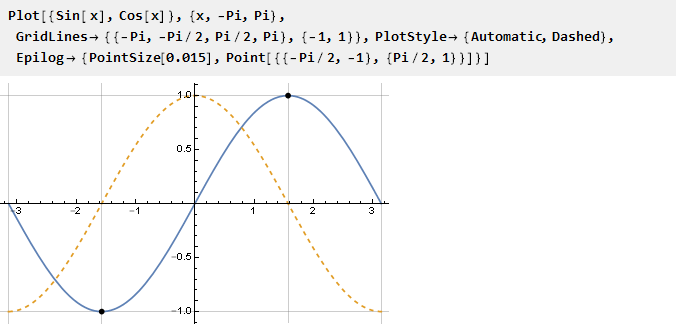
Нужно только масштабировать аргументы, чтобы единица проецировалась на Pi/2. Теперь мы можем определить собственно ограничивающую функцию:

И построить её график:
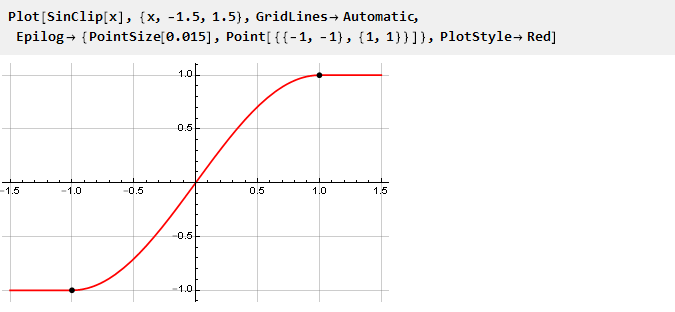
Так как пределы ограничения у нас жёстко определены, то ограничение задаётся через масштабирование входного сигнала с последующим (при необходимости) обратном масштабировании.
Здесь также уже нет ситуации, при которой входной сигнал передаётся на выход без искажений — чем меньше уровень усиления, тем меньше уровень искажений вследствие ограничения — но сигнал искажается в любом случае.
Влияние параметра усиления на искажение сигнала можно посмотреть и в динамике:

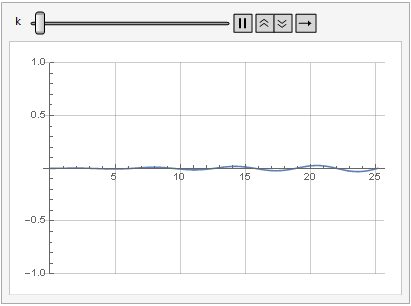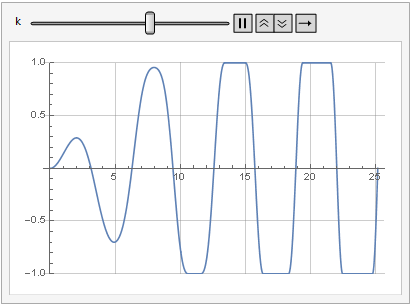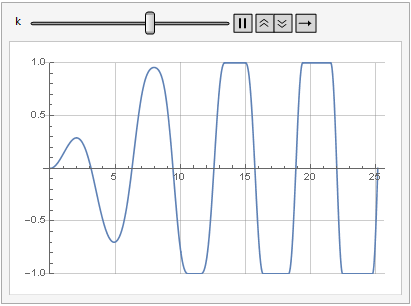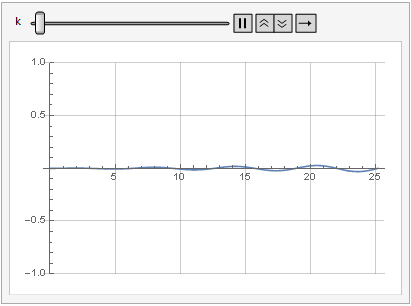
Больше гладкости
Посмотрим на производную нашей функции:
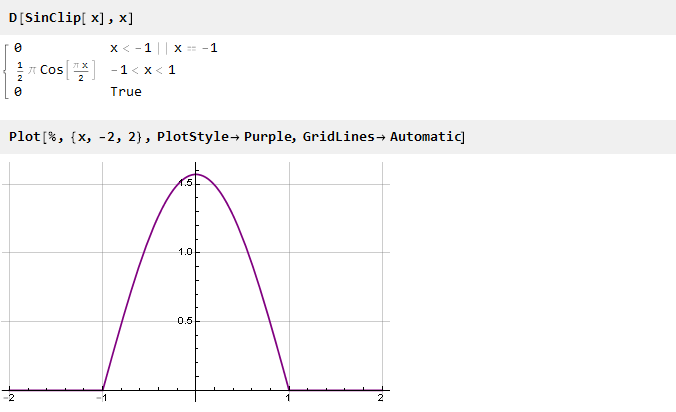
В ней уже нет разрывов в значениях, но есть разрывы в производной (второй, если считать от изначальной функции). Для того, чтобы её устранить, можно пойти обратным путём — сначала сформировать гладкую производную, а затем её проинтегрировать для получения искомой функции.
Самый простой способ обнулить производную точках -1 и 1 — это просто возвести функцию в квадрат — все отрицательные значения функции станут положительными и, соответственно, возникнут перегибы в точках пересечения функции с нулём.
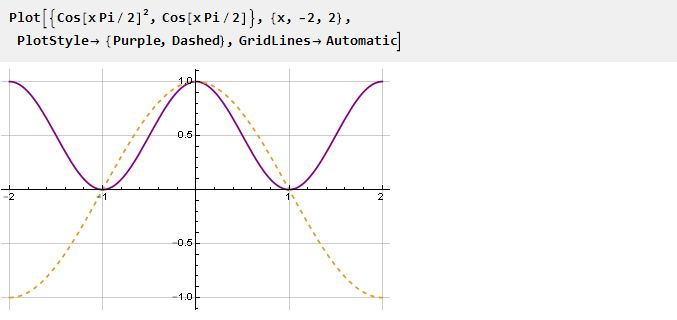
Находим первообразную:
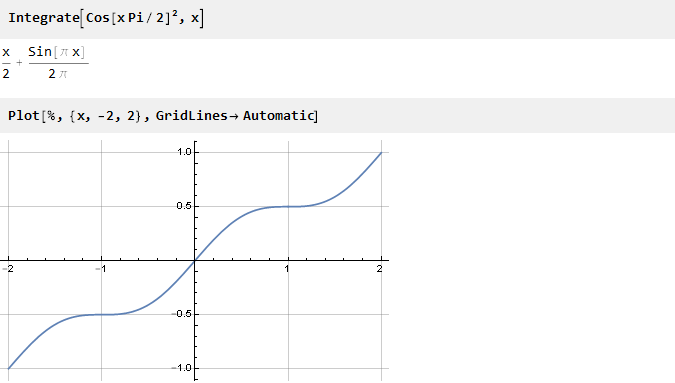
Теперь осталось масштабировать её по оси ординат. Для этого найдём её значение в точке 1:

И поделим на неё (да, конкретно здесь это элементарное умножение на 2, но далеко не всегда так бывает):

Таким образом, итоговая функция ограничения примет вид:
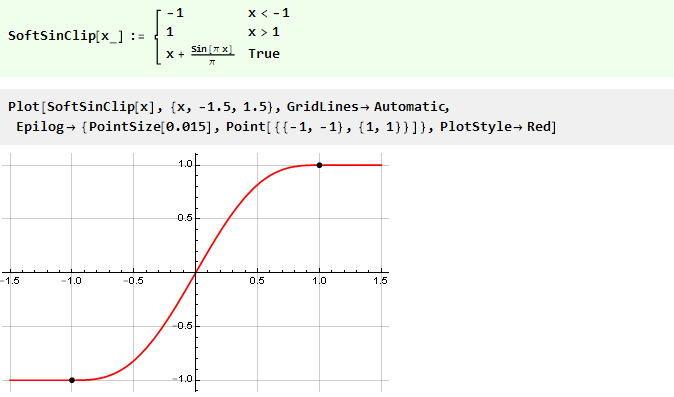
Переходим на полиномы
Использование тригонометрический функций в некоторых случаях может оказаться несколько расточительным. Поэтому попробуем построить необходимую нам функцию, оставаясь в рамках элементарных математических операций.
Рассмотрим параболу:
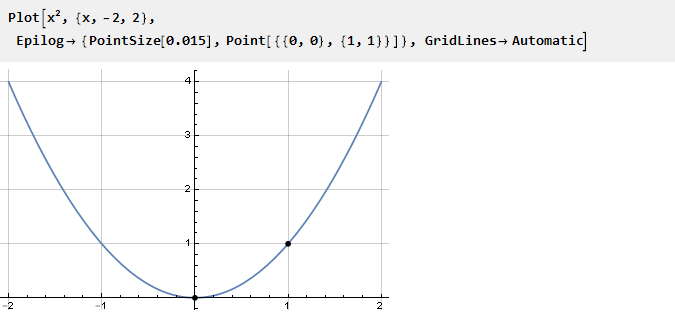
Так как у неё уже есть перегиб в точке ноль, мы можем использовать одну и ту же часть на интервале {0,1} для для стыковки с константами. Для отрицательных значений её нужно сместить вниз и влево:

а для положительных — отразить по вертикали и горизонтали:

И наша функция с параболой примет вид:
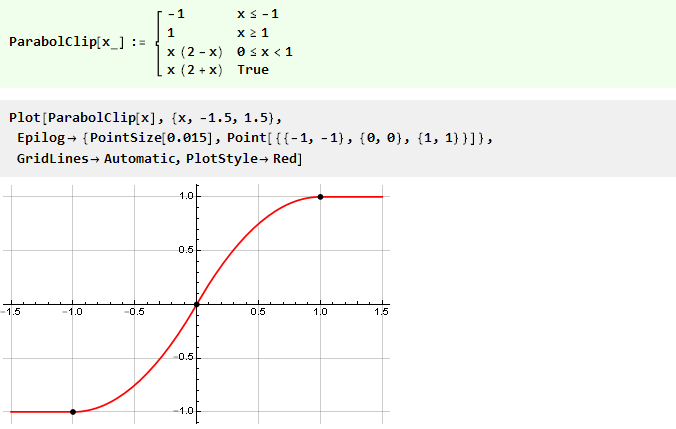
Немного усложним
Вернёмся к нашей параболе, перевернём её и сместим на единицу вверх:
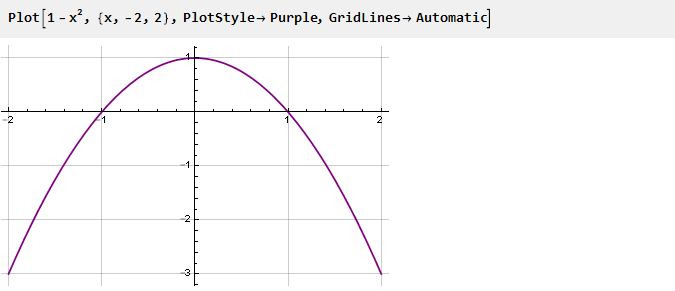
Это будет производная нашей функции. Чтобы сделать её более гладкой в точках стыковки, возведём в квадрат, обнулив таким образом вторую производную:
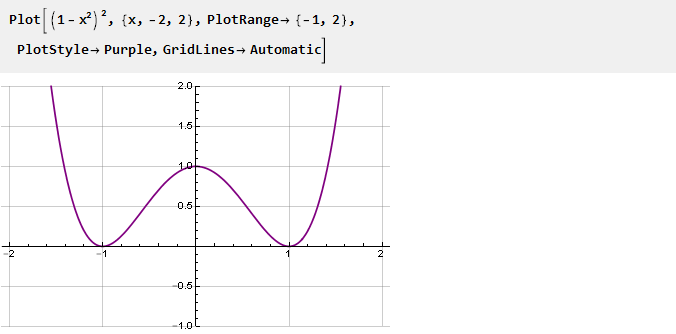
Интегрируем и масштабируем:

Получаем ещё более гладкую функцию:
Больше гладкости богу гладкости
Здесь мы попробуем добиться гладкости в точках стыковки на ещё более высших производных. Для этого для начала определим функцию как полином с неизвестными коэффициентами, а сами коэффициенты попробуем найти через решение системы уравнений.
Начнём со 1-й производной:

2-я:

3-я:

Все эти коэффициенты выглядит так, как будто в них есть какая-то логика. Выпишем множители, помножив их на значение степени при х; а чтобы не писать каждый раз одно и тоже, автоматизируем процесс нахождения коэффициентов:

Похоже на биномиальные коэффициенты. Сделаем смелое предположение, что это они и есть, и исходя из этого, запишем обобщённую формулу:

Проверим:
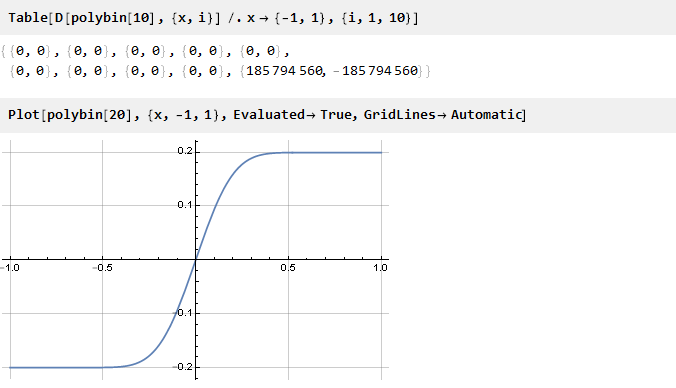
Похоже на правду [1]. Осталось только посчитать масштабный коэффициент, чтобы привести края к единице:

А после масштабирования и упрощения мы обнаружим, что наши познания в математике несколько устарели [2]:
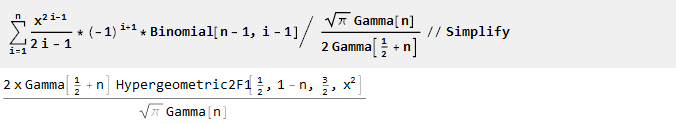
Таким образом, мы получили производящую функцию порядка n, в которой n-1 первых производных будут равны нулю:

Посмотрим, что получилось:
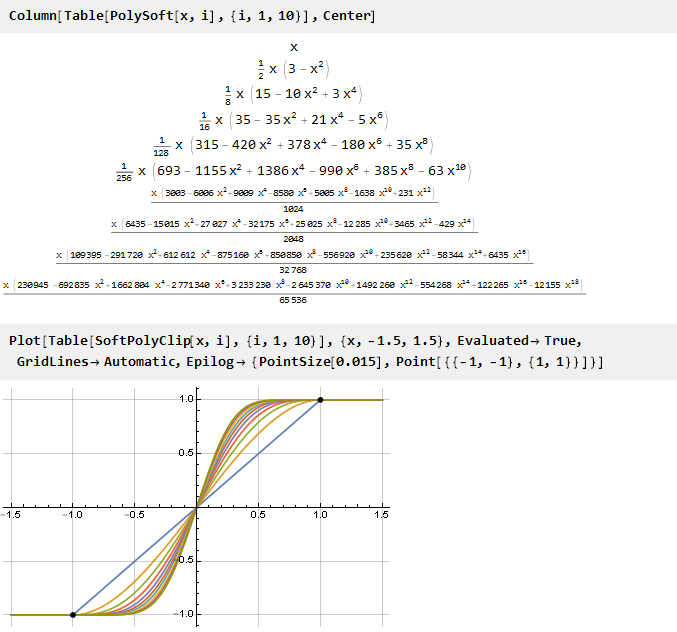
И поскольку наша обобщённая формула получилась непрерывной, при желании можно использовать и нецелые значения параметров:
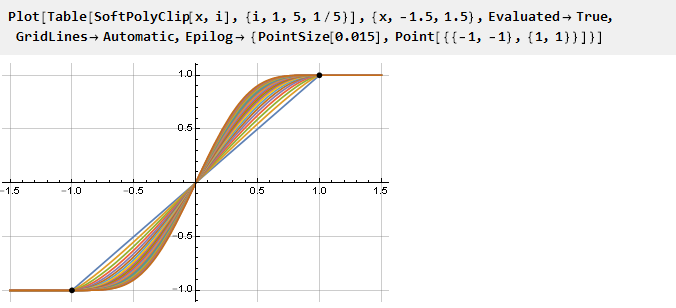
Также можно построить графики производных, приведённых к одному масштабу:
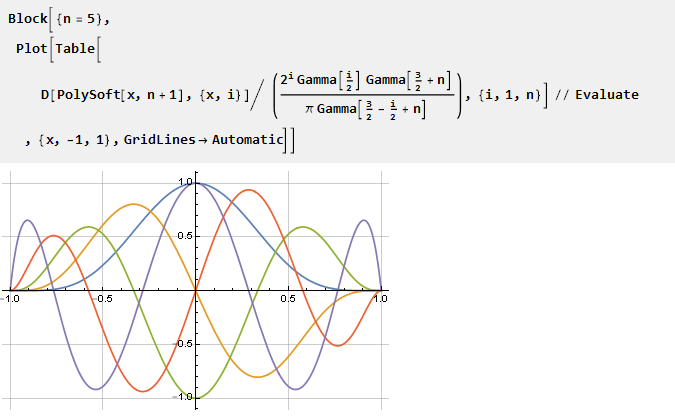
Добавляем жёсткости
Было бы заманчиво, иметь возможность регулировать и степень «жёсткости» ограничения.
Вернёмся к нашей перевёрнутой параболе и добавим коэффициент при степени x:

Чем больше n, тем больше наша производная «квадратная», а её первообразная — соответственно, резкая:
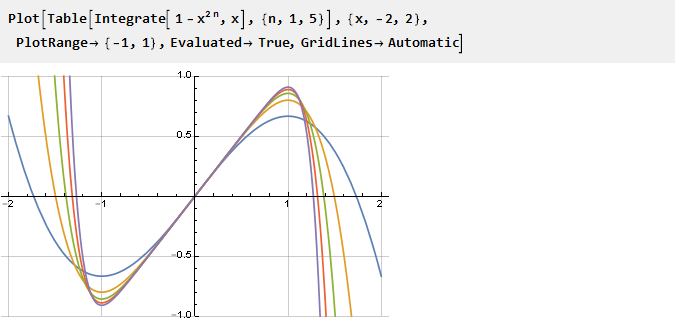
Посчитаем первообразную и скорректируем масштаб:

Попробуем теперь задать дробный шаг для параметра:
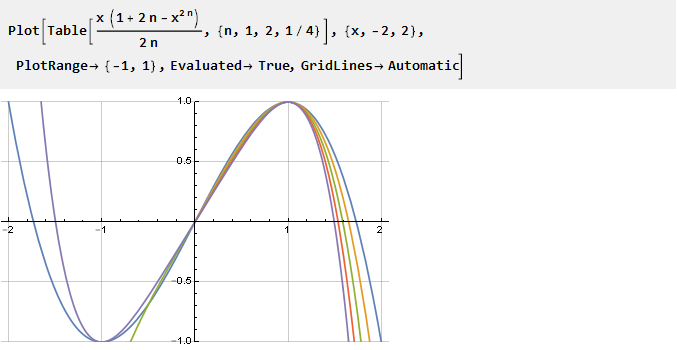
Как видим, в отрицательной части не для всех n имеется корректное решение, но в правой (положительной) части необходимые нам условия по-прежнему соблюдаются — поэтому для отрицательных значений мы можем просто использовать её в перевёрнутом виде с реверсированным аргументом. И поскольку область определения параметра уже не ограничена только положительными целыми числами, то можно упростить формулу, заменив 2n на n:

А заменив n на n-1, можно сделать формулу чуть более красивой:
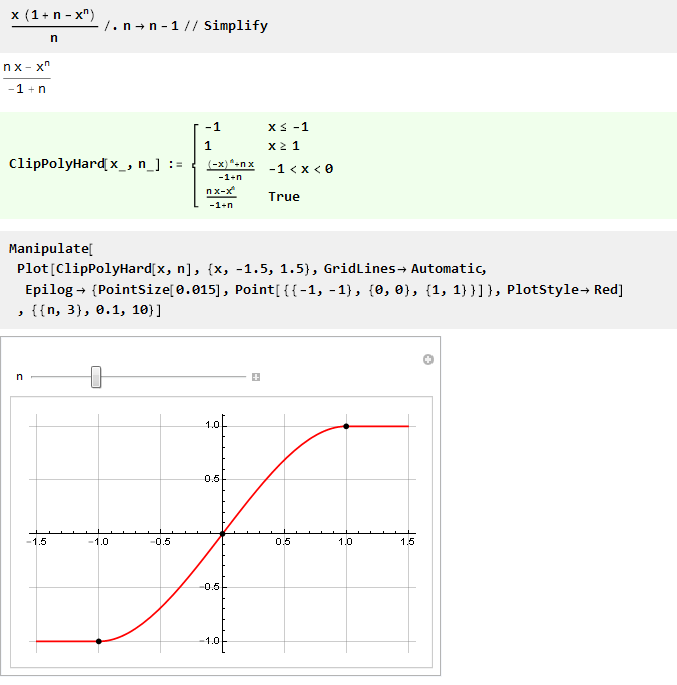
Поскольку при n равным единице мы получаем деление на ноль, то попробуем найти предел:

Предел находится, а значит, теперь можно доопределить [3] функцию для n равным 1 и рассматривать её для всех n больших нуля:
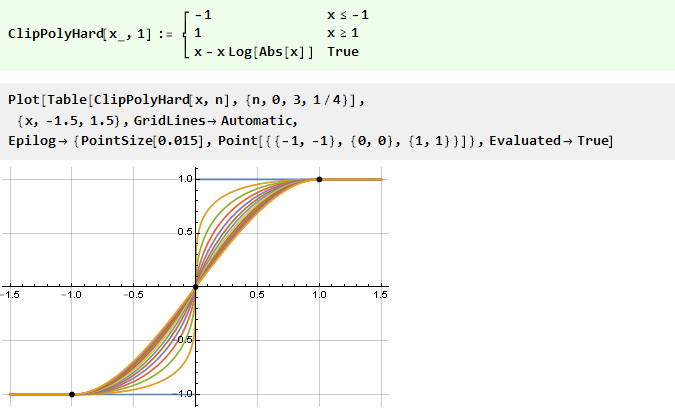
Если же мы изначально возведём нашу перевёрнутую параболу в квадрат, то получим ещё более гладкую функцию:
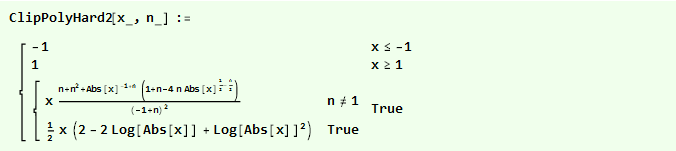
И можем сравнить их на одном графике:
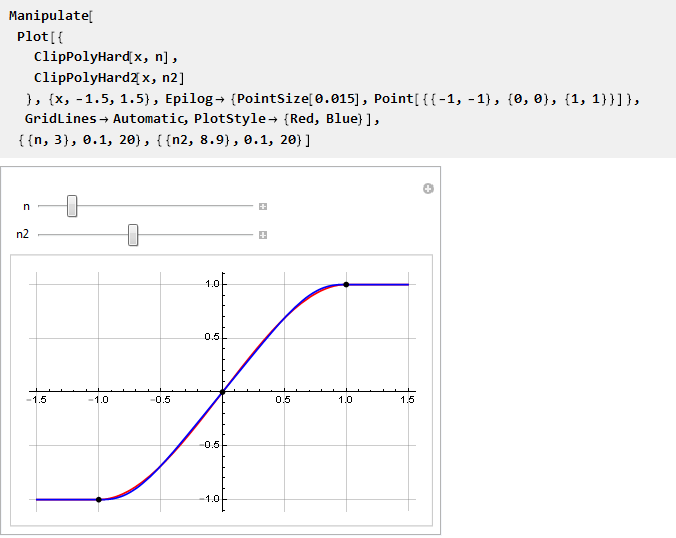
Рационализируй это
Посмотрим на следующую функцию:
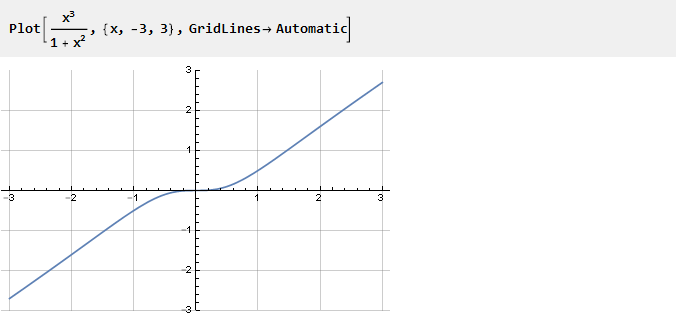
Появилась она не случайно.
Если убрать из неё единицу, x2 сократится и останется просто x, т.е наклонная прямая. Таким образом, чем меньше значение x, тем большее влияние оказывает единица в знаменателе, создавая необходимое нам искривление. А рассматривая эту функцию в разных масштабах, можно контролировать степень этого искривления:

Таким образом, мы можем переписать предыдущую функцию с контролем жёсткости, используя только рациональный полином 3-порядка:
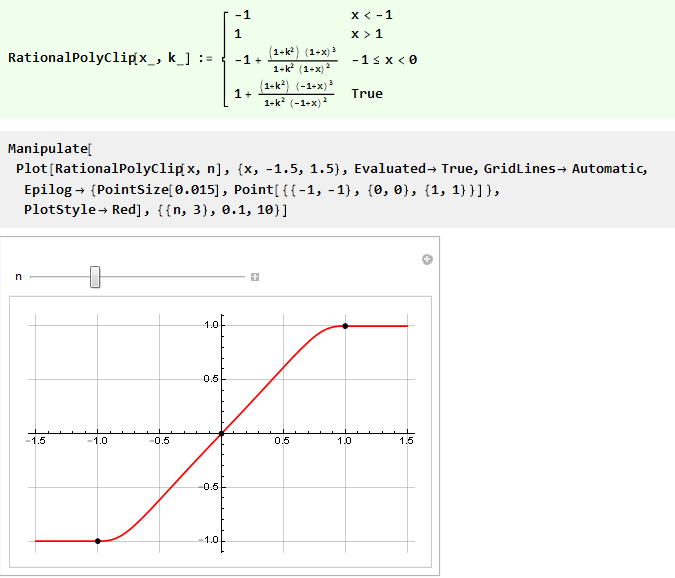
Автоматизируй это
Чтобы не задавать каждый раз кусочно-непрерывные функции, мы можем определить вспомогательную функцию, которая сделает это самостоятельно, принимая на вход донорскую функцию в качестве аргумента.
Если наша функция уже обладает диагональной симметрией и выровнена по центру координат (как синусоида), то можно сделать просто
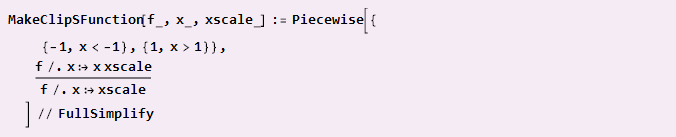
Пример использования:

Если же нужно собирать из кусочков, как в случае с параболой, и центр координат определяет точки стыковки, то формула слегка усложнится:
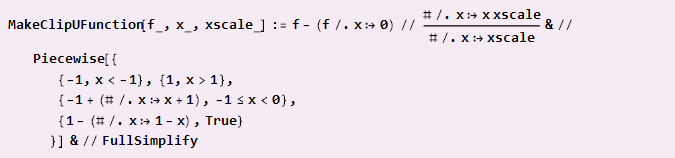
Пример использования:

Перейдём на экспоненту
Совершенно любая функция может быть донором для решения этой задачи, нужно лишь только обеспечить ей точки перегиба. Возьмём, например, сдвинутую вниз на единицу экспоненту:
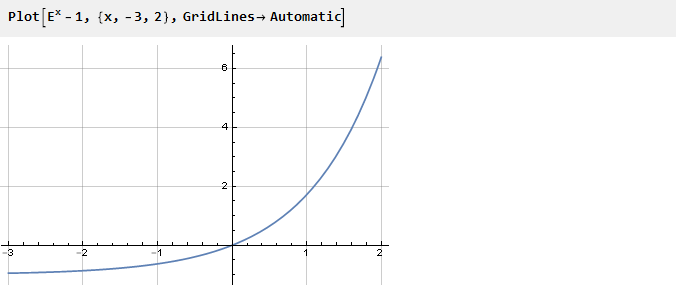
Ранее, для обеспечения необходимого перегиба в точке ноль, мы возводили функцию в квадрат. Но можно пойти и другим путём — например, суммировать с другой функцией, производная которой в точке ноль противоположна по знаку с производной экспоненты. Например, -x:
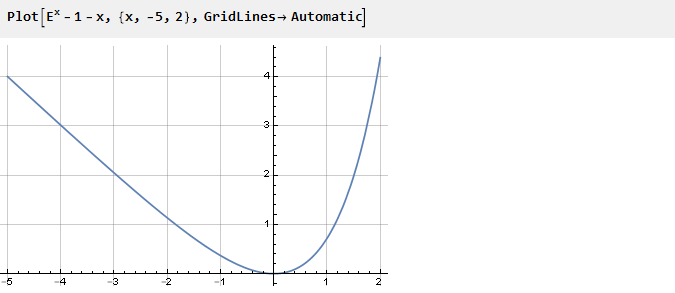
В зависимости от того, с какой стороны мы будем брать кривую, будет и зависеть итоговый вид функции. Теперь, воспользовавшись ранее определённой вспомогательной функцией и выбрав одну из сторон, получим:

Либо

И теперь можем сравнить их на одном графике:
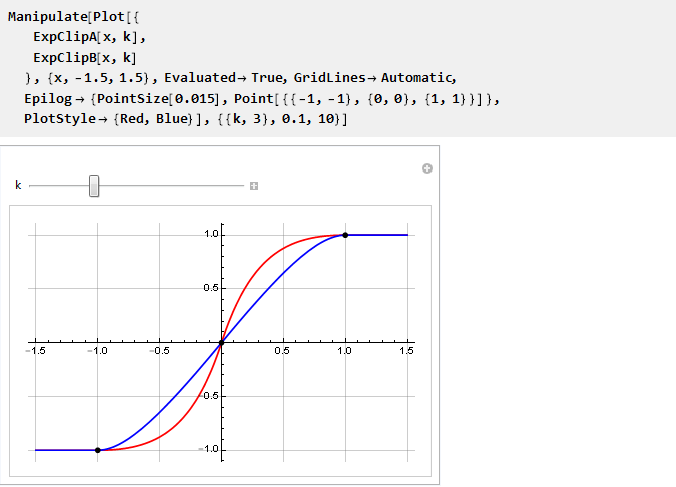
Видно, что при k>0 они стремятся к совпадению; и так как напрямую посчитать их значения мы не можем, поскольку получим деление на ноль, то воспользуемся пределом:

И получили уже известную нам кусочную функцию из параболы.
Нарушая симметрию
Пока что мы рассматривали исключительно симметричные функции. Однако бывают случаи, когда симметрия нам не нужна — например, для имитации искажений при звучании ламповых усилителей.
Возьмём экспоненту и умножим её на перевёрнутую параболу в квадрате — чтобы получить пересечение с осью абсцисс в точках -1 и 1, а заодно и обеспечить гладкость второй производной; параметризацию же осуществим через масштабирование аргумента экспоненты:
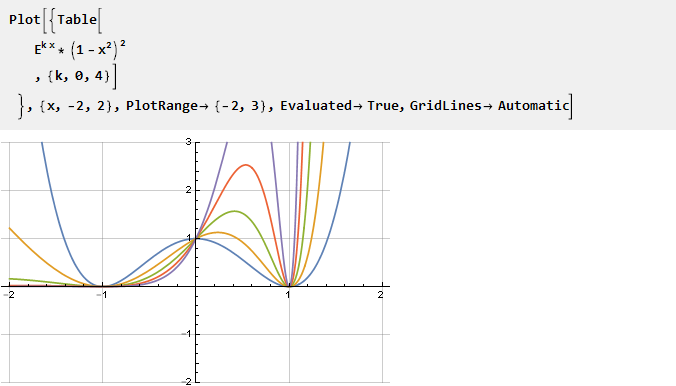
Найдём первообразную и масштабируем её:
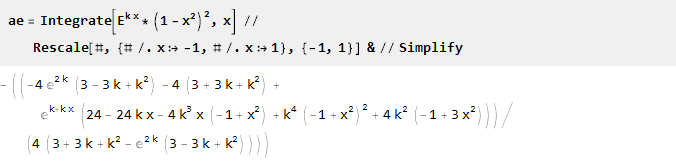
Так как при k=0 получим деление на ноль:

То дополнительно найдём предел,

который представляет из себя уже известный нам гладкий полином 3-го порядка. Соединив всё в одну функцию, получим
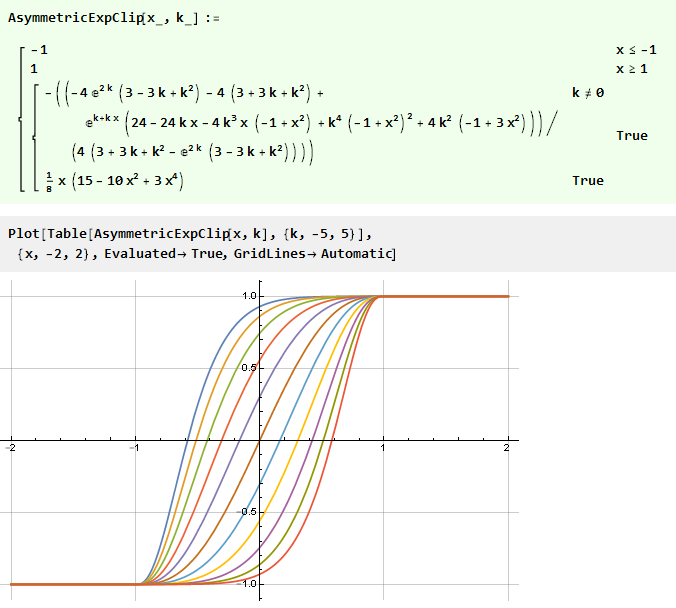
Вместо того, чтобы изначально проектировать асимметричную функцию, можно пойти и другим путём — использовать готовую симметричную, но «искривлять» значение этой функции с помощью дополнительной функции кривой, определённой на промежутке {-1,1}.
Рассмотрим, например, гиперболу:
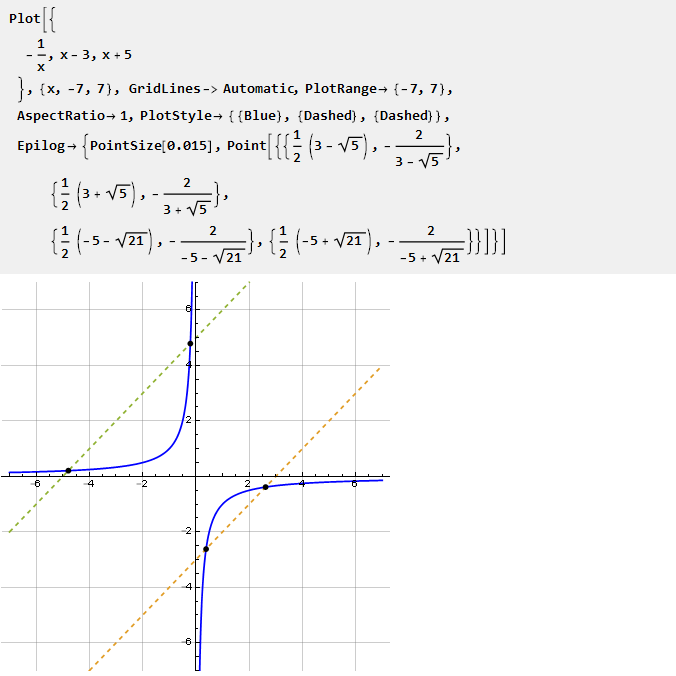
Рассматривая её отрезок в разных масштабах, можно регулировать степень искривления в обе стороны. Как же найти этот отрезок? Исходя из графика, можно было бы искать пересечения гиперболы с прямой. Однако, поскольку такое пересечение существует не всегда, это создаёт некоторые сложности. Поэтому мы пойдём другим путём.
Для начала добавим в гиперболу масштабирующие коэффициенты:

затем составим систему уравнений, задающих условия прохождения гиперболы через заданные точки — и её решение даст интересующие нас коэффициенты:

Теперь подставим решение в исходную формулу и упростим:

Посмотрим, что у нас получилось в зависимости от параметра k:
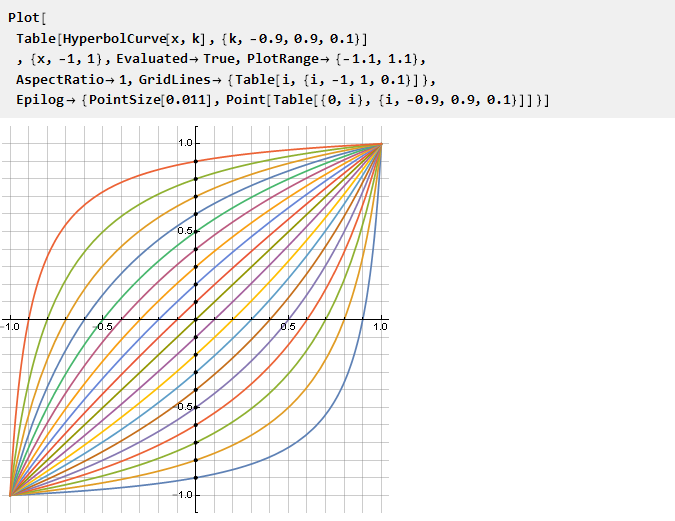
Примечательно, что при k=0 формула естественным образом схлопывается в x и никаких особых ситуаций не происходит — хотя применительно к исходной гиперболе это равносильно отрезку нулевой длины, причём двум сразу. Не менее примечательно, что обратной к ней функцией является она же самая, но с отрицательным параметром k:

Теперь мы можем использовать её для модификации произвольной функции ограничения, а параметр k таким образом будет задавать точку пересечения с осью ординат:
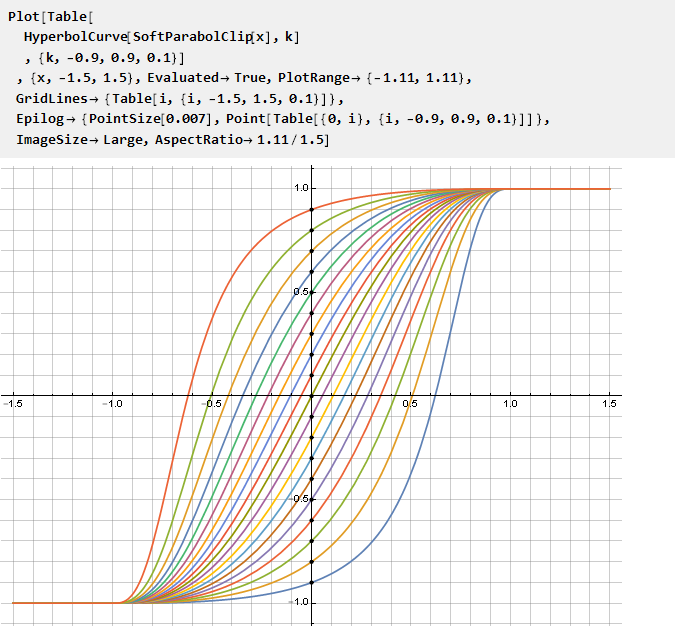
Аналогичным образом можно строить кривые и из других функций, например, степенной с переменным основанием:
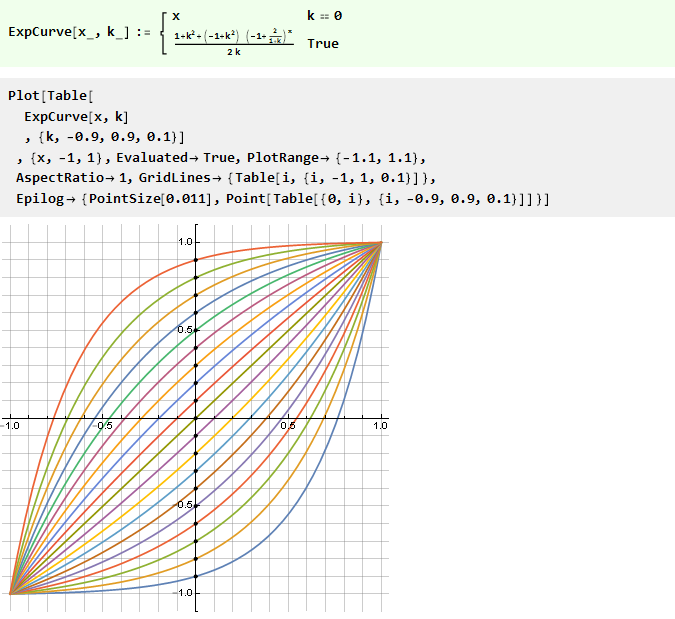
Или обратной к ней логарифмической:
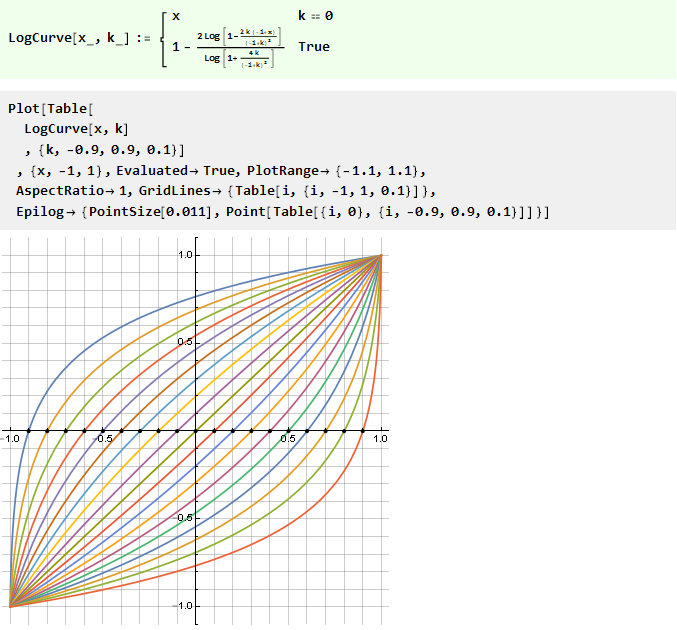
Нужно больше точности
Мы можем захотеть иметь гарантированно линейный промежуток у функции на некотором интервале. Это логично организовать введением прямой линии в кусочно-непрерывную функцию,
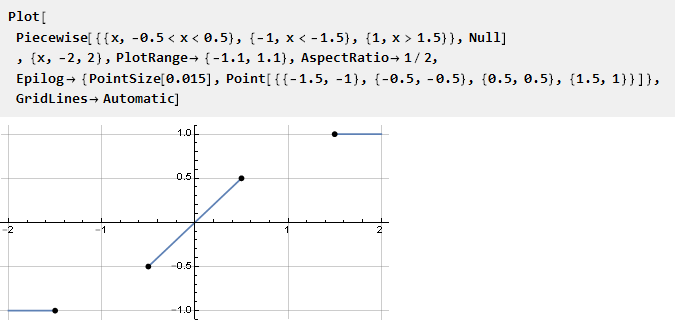
пустые места в которой необходимо заполнить какой-нибудь функцией. Очевидно, что для гладкой стыковки с линейным участком её первая производная должна быть равна единице; а все последующие (по возможности) нулю. Чтобы не не выводить такую функцию заново, мы можем взять уже готовую и адаптировать под эту задачу. Также можно заметить, что крайние точки отстоят чуть дальше единицы — это необходимо, чтобы сохранить наклон линейного участка.
Возьмём выведенную ранее функцию PolySoft и сместим её так, чтобы в центре координат получить единицу:
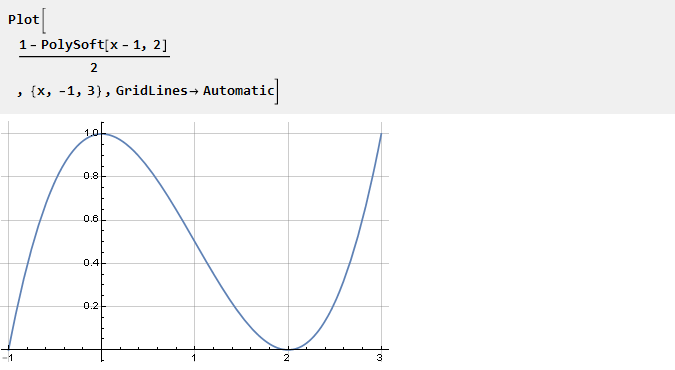
Из её свойств следует, что n-1 последующих производных в точках 0 и 2 будут равны нулю:
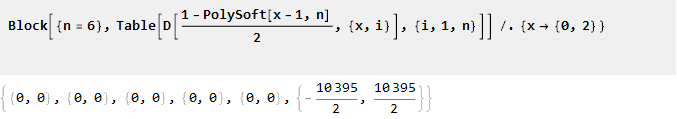
Теперь проинтегрируем её:
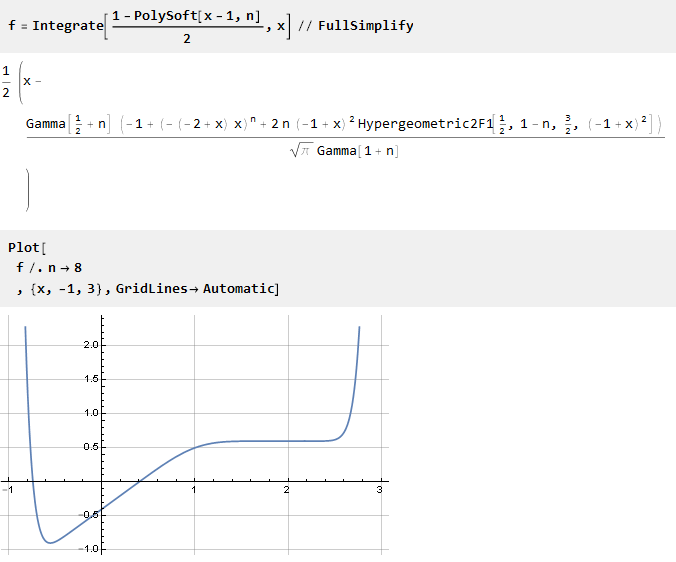
Функция оказалась сдвинутой вниз относительно оси абсцисс. Поэтому необходимо добавить константу (равную значению функции в точке 0), чтобы совместить центры координат:

Здесь у нас появился ноль в степени n. Он не сократился, так как значение ноль в степени ноль не определено; мы можем его удалить вручную, а можем при упрощении явно указать, что n у нас больше нуля:

Проверим на всякий случай. Значение в точках 0 и 2 для всех n:

Производные на краях интервала (для полинома порядка 5):

Как видим функция получилась довольно громоздкой. Чтобы не таскать её и не переусложнять вычисления, дальше будем манипулировать уже с конкретным полиномом, например 4-го порядка:

И вот теперь ею можно заполнить свободное пространство:

Проверим:
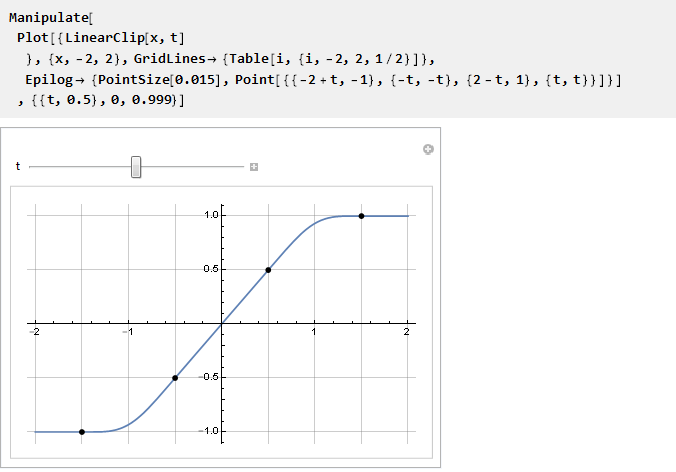
Уходим в бесконечность
Иногда может оказаться потребность в функциях, которые стремятся к единице, но не достигают её. Википедия подсказывает несколько известных решений:
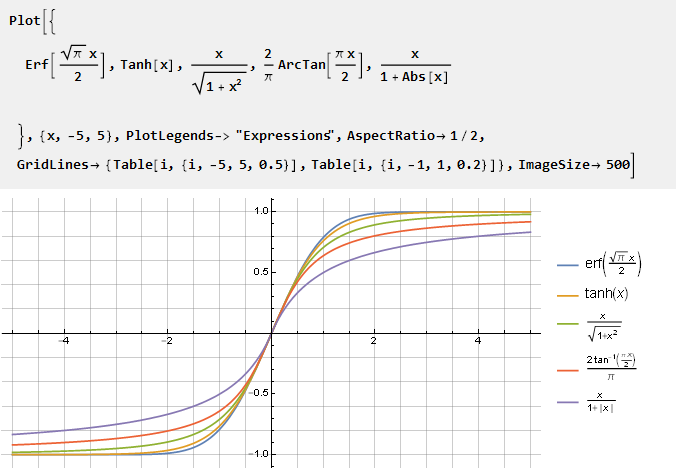
Так как эти функции единицы не достигают, их удобнее нормировать по производной в центре координат.
Мы можем модифицировать форму таких функции через их аргумент с помощью какой-нибудь диагонально-симметричной функции, например:
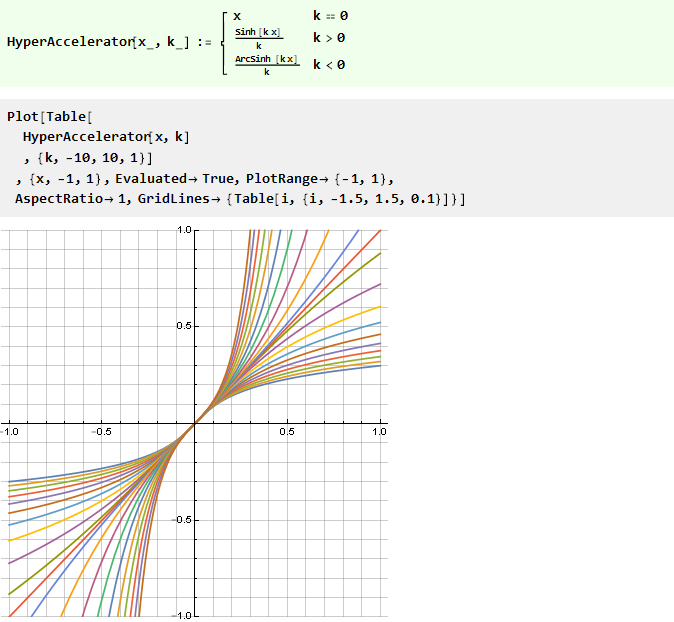
Эта функция, к слову, также является обратной самой к себе, т.е.
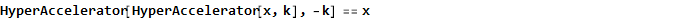
И, применительно к арктангенсу в качестве примера, получим
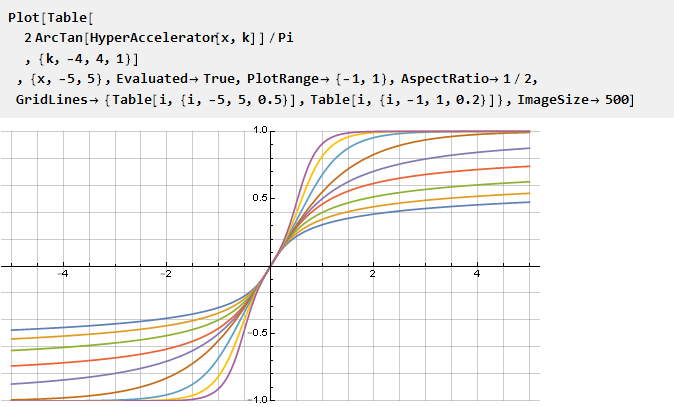
что, в частности, с параметром k=1 даст нам функцию Гудермана.
Как видим, при таком подходе можно получить нежелательные перегибы, поэтому более предпочтительно контролировать жёсткость ограничения непосредственно через свойство самой функции. Рассмотрим несколько таких функций с параметром, вывод которых для краткости опустим.
Из степенной функции:
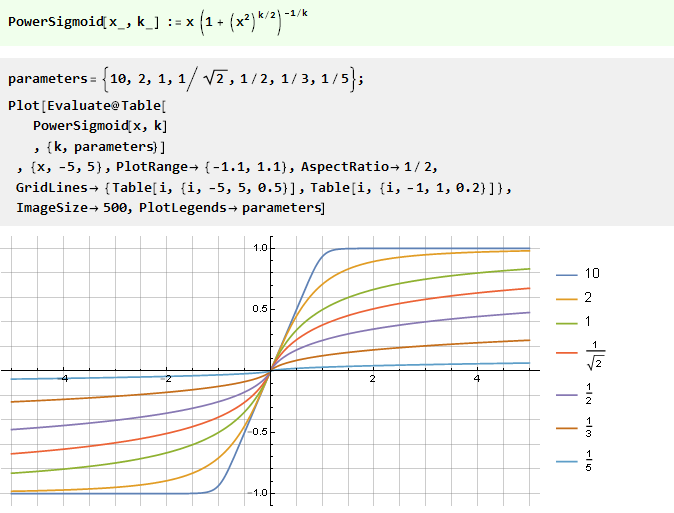
Из суммы двух v-образных функций со смещением:
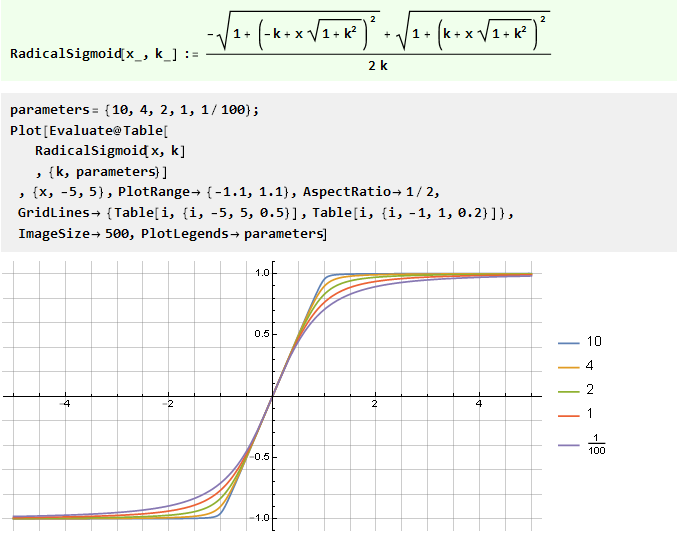
Из обобщённой функции ошибок:
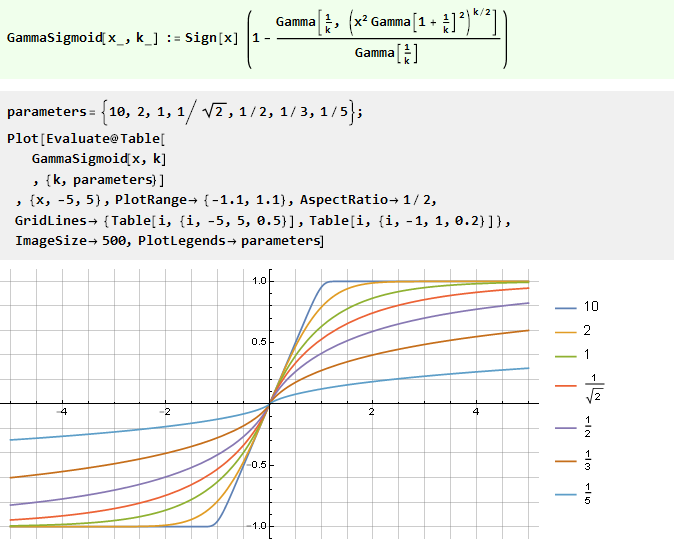
Интегрированием рационального полинома:
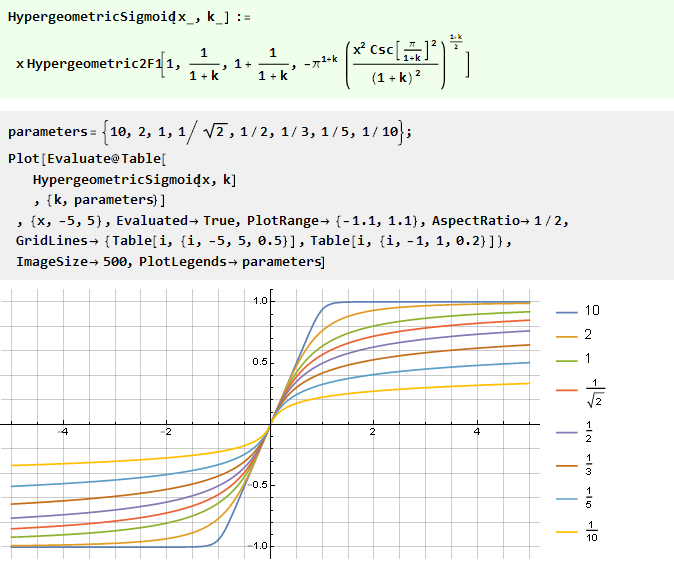
Интересно, что её частным случаем является арктангенс:

Заключение
Построение подобного рода функций может быть увлекательным занятием, в ходе которого будут получаться как простые, так и сложные, как красивые, так и не очень, формулы. Может показаться, что все они сильно друг на друга похожи и надобности в подобном разнообразии нет. Это не обязательно так.
Разница может быть сильнее видна в других масштабах — например, логарифмическом. Кроме того, помимо обозначенных в заголовке задач, подобные функции могут использоваться и в других задачах — смешивании сигналов, когда плавное затухание одного сигнала сочетается с плавным нарастанием другого, или построении акустических фильтров — и тогда разница будет восприниматься на слух, или же для построения градиентов — и тогда разница будет восприниматься на глаз. Кроме того, они также могут использоваться в качестве доноров для других, более сложных функций — например, оконных.
В завершение стоит уточнить ещё несколько моментов.
Все функции здесь были определены в диапазоне от -1 до 1. В случае, если нужен другой диапазон (например, от 0 до 1), его легко можно пересчитать либо вручную:
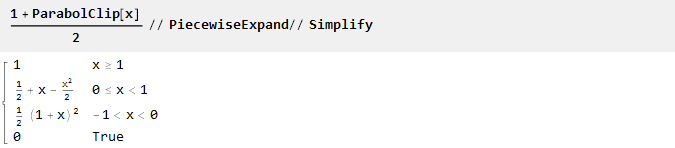
Либо используя встроенную функцию масштабирования:

А для облегчения экспорта полученных формул в программный код может пригодиться функция CForm:
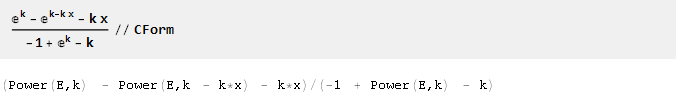
Исходный документ Mathematica можно скачать здесь.
Примечания:
[1] настоящий математик наверняка сможет строго доказать (или опровергнуть) это утверждение.
[2] в стандартном курсе мат.анализа гипергеометрические функции не рассматриваются.
[3] эта перегрузка определена только для символьной единицы; единица в формате с плавающей точкой (например, при построении графика) распознана не будет.
Комментарии (20)

Daddy_Cool
28.09.2018 01:40Вау! Я впечатлен! Спасибо!
Иногда нужны такие функции — попробую задействовать при случае.

galaxy
28.09.2018 02:26Точка перегиба — это не совсем то, что вы думаете.
Кстати, можно сделать и бесконечно дифференцируемую подобную функцию
Refridgerator Автор
28.09.2018 06:04Тоже думал о бесконечно дифференцируемой функции, но не смог её самостоятельно вывести.
Кстати, ту формулу по ссылку можно упростить, если привести аргумент и значения функции к диапазону от -1 до 1 — и тогда получается Tanh[2x / (1-x2)]. Возможно, вместо гиперболического тангенса подойдут и другие сигмоиды, если должным образом масштабировать аргумент.

Refridgerator Автор
28.09.2018 17:05Варианты типа Erf[(3*x)/(1-2*x4+x6)] или Tanh[Tan[x*Pi/2]] тоже подходят. Но возникла сложность: мне (точнее Вольфраму) не удалось их проинтегрировать, чтобы использовать в кусочной функции с линейным участком.

mayorovp
28.09.2018 09:36Какой смысл в функции ограничения сигнала если она искажает его? Хотя бы для малых x должно выполняться
f(x) ? x. Для чего требуется чтобы былоf'(0) = 1. А у вас вместо этогоSinClip'(0) = ?/2,SoftSinClip'(0) = 2,ParabolClip'(0) = 2,SoftParabolClip'(0) = 15/8.
А вот соблюдаемые вами ограничения
f(1) = 1иf(-1) = -1, напротив, не требуются: кого интересует поведение сигнала вблизи границ, когда было решено ограничить и сгладить его?
Refridgerator Автор
28.09.2018 10:04Какой смысл в функции ограничения сигнала если она искажает его?
В начале статьи об этом говорится прямым текстом: когда искажение требуется исходя из поставленной задачи — например при реализации эффекта "overdrive". Хаб «Звук» включен в статью не случайно.
А вот соблюдаемые вами ограничения f(1) = 1 и f(-1) = -1, напротив, не требуются
Они требуются исходя из постановки задачи — ограничение и соблюдение непрерывности.
кого интересует поведение сигнала вблизи границ, когда было решено ограничить и сгладить его?
Кого не интересует, тот решает свои задачи как-то по другому.
mayorovp
28.09.2018 10:18Хорошо, рассмотрим звук и эффект "overdrive". Зачем он меняет уровень громкости звука?
Они требуются исходя из постановки задачи — ограничение и соблюдение непрерывности.
Непрерывность этого не требует. А ограничение и монотонность требуют f(+?) = 1 и f(-?) = -1. Так откуда взялись требования на f(1) и f(-1)?

Refridgerator Автор
28.09.2018 10:58Хорошо, рассмотрим звук и эффект «overdrive». Зачем он меняет уровень громкости звука?
Громкость звука обычно меняют, чтобы тихие звуки сделать громче (или наоборот). «Оverdrive» делает это с той же целью — чтобы сделать громкость струны на протяжении её звучания более равномерным. Но это — скорее побочный эффект, поскольку основная задача овердрайва — придать звуку гитары характерное звучание, что обеспечивается насыщением сигнала верхними гармониками, полученными вследствие ограничения. Это легко увидеть, если сделать преобразование Фурье от ограниченной по амплитуде синусоиды.
Непрерывность этого не требует.
Не буду спорить — похоже, мы изучали разную математику, ну или это я чего-то не понимаю. В моём понимании непрерывность — это отсутствие точек разрыва.
mayorovp
28.09.2018 11:00Зачем делать Оverdrive с побочным эффектом если можно сделать его без побочного эффекта?
В моём понимании непрерывность — это отсутствие точек разрыва.
В моем понимании это слово означает то же самое. Но все-таки, откуда появилось требование f(1) = 1?

Refridgerator Автор
28.09.2018 11:12Зачем делать Оverdrive с побочным эффектом если можно сделать его без побочного эффекта?
Побочный эффект потому и называется «побочным», что является следствием чего-то другого. Но в данном случае этот эффект — положительный. Устройство, в котором этот эффект является целеобразующим — называется «компрессор», и вот уже в нём искажение сигнала является негативным побочным эффектом, который невозможно исключить.
Но все-таки, откуда появилось требование f(1) = 1?
Если вы считаете это требование избыточным — продемонстрируйте свой вариант решения на формулах и графиках.
mayorovp
28.09.2018 12:01Какой же он положительный когда меняется громкость тихих звуков?
Если вы считаете это требование избыточным — продемонстрируйте свой вариант решения на формулах и графиках.
Вот мое решение:
SoftSinClipNorm(x) = SoftSinClip(x/2) = x/2 + sin (?x/2) / ?, -2 < x < 2 -1, x < -2 1, x > 2
График рисуйте как-нибудь сами.

Refridgerator Автор
28.09.2018 12:17Вот мое решение
Это та же функция, только в другом масштабе. Масштабирование вид функции не меняет. О том, что рассмотренные в статье функции нормированы к единице и их масштаб можно менять в зависимости от конкретной задачи — сказано в заключении. О нормировании производных упоминается в двух последних главах.
mayorovp
28.09.2018 12:30В заключении вы меняете диапазон выходных значений. И, к слову, тоже делаете это неправильно: для функции Clip диапазоны рабочих входных и выходных значений должны соответствовать друг другу, там нужно две операции Rescale вместо одной.
А я вам пишу про то, что в рамках исходной задачи — аккуратно обрезать у сигнала все что выходит за пределы (-1, 1) — вы составили неправильно работающую функцию. Которая не только обрезает сигнал, но и зачем-то меняет его громкость.
Refridgerator Автор
28.09.2018 13:17А я вам пишу про то, что в рамках исходной задачи — аккуратно обрезать у сигнала все что выходит за пределы (-1, 1)
Исходная задача — это не только обрезание, но и множество других — о чём сказано и в заголовке, и введении, и в заключении.
вы составили неправильно работающую функцию. Которая не только обрезает сигнал, но и зачем-то меняет его громкость.
Это взаимосвязанные параметры. Невозможно обрезать сигнал без изменения его громкости, даже если нормируете ограничиваю функцию по производной в точке ноль.
Если вы увеличиваете яркость картинки в 2 раза, то максимальная яркость пикселя после этого — 510 — не помещается в диапазон 0..255, и её нужно как-то в этот диапазон уместить, что без ограничения никак не получится. Если же наоборот ограничивать картинку по уровню, скажем, 127 — это также неизбежно повлечёт за собой снижение яркости.
И в этих случаях нормирование аргумента к единице имеет больше смысла, чем нормирование производной.

Refridgerator Автор
29.09.2018 10:20-1В заключении вы меняете диапазон выходных значений. И, к слову, тоже делаете это неправильно: для функции Clip диапазоны рабочих входных и выходных значений должны соответствовать друг другу, там нужно две операции Rescale вместо одной.
Не должны, симметричность масштаба лишь один из возможных сценариев. Я уже неоднократно говорил, что ограничение сигнала — лишь один из вариантов применения таких функций, наиболее понятный, и служит лишь в качестве затравки для статьи. Сам я их использую для других целей, описанных в заключении (и для их подробного описания нужны отдельные статьи), и там масштабирование не симметричное.

Refridgerator Автор
28.09.2018 10:13Хотя бы для малых x должно выполняться f(x) ? x.
Вы, похоже, пропустили целую главу, в которой этот вопрос подробно рассматривается.
Refridgerator Автор
29.09.2018 10:24-1В которой, кстати, присутствует анимация, наглядно демонстрирующая, как длина линейного участка влияет на координаты точек стыковки.

toivo61
28.09.2018 15:47Сжатие динамического диапазона в реальном мире (физике), это немного больше, чем рассмотренный здесь клиппиг и софт-клиппинг.
Компрессоры (АРУ) работают, все таки, не моментальными значениями.
Refridgerator Автор
28.09.2018 17:13Компрессоры (АРУ) работают, все таки, не моментальными значениями.
Само собой. Компрессор работает с усреднённым значением амплитуды. А вот чтобы он на тихом сигнале не пытался увеличить громкость в 100000 раз — и нужно ограничение.

basilbasilbasil
Годнота! Спасибо!