Итак, очередная статья из цикла «математика на пальцах». Сегодня мы продолжим разговор о методах наименьших квадратов, но на сей раз с точки зрения программиста. Это очередная статья в серии, но она стоит особняком, так как вообще не требует никаких знаний математики. Статья задумывалась как введение в теорию, поэтому из базовых навыков она требует умения включить компьютер и написать пять строк кода. Разумеется, на этой статье я не остановлюсь, и в ближайшее же время опубликую продолжение. Если сумею найти достаточно времени, то напишу книгу из этого материала. Целевая публика — программисты, так что хабр подходящее место для обкатки. Я в целом не люблю писать формулы, и я очень люблю учиться на примерах, мне кажется, что это очень важно — не просто смотреть на закорючки на школьной доске, но всё пробовать на зуб.
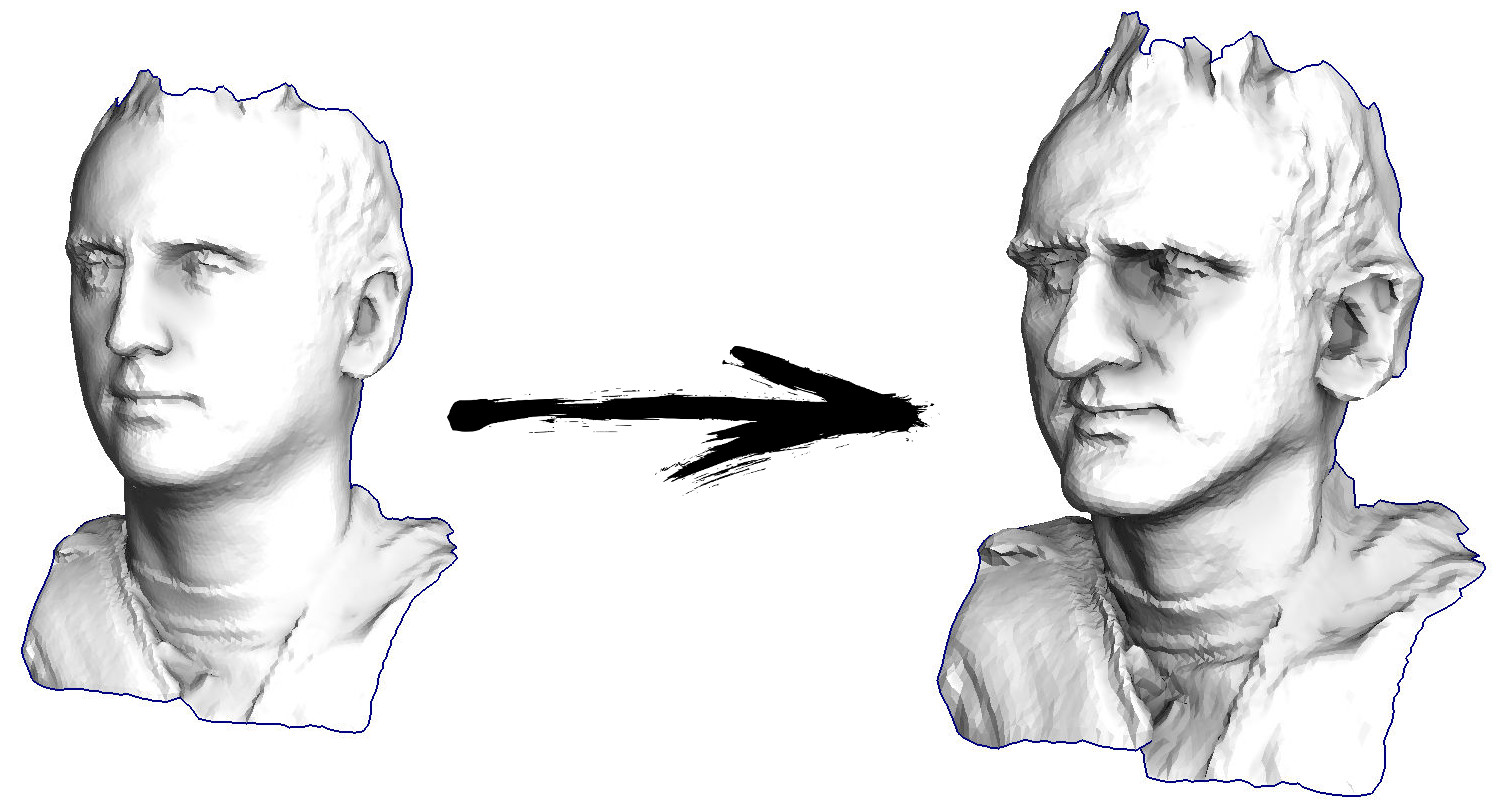
Итак, начнём. Давайте представим, что у меня есть триангулированная поверхность со сканом моего лица (на картинке слева). Что мне нужно сделать, чтобы усилить характерные черты, превратив эту поверхность в гротескную маску?
В данном конкретном случае я решаю эллиптическое дифференциальное уравнение, носящее имя Симеона Деми Пуассона. Товарищи программисты, давайте сыграем в игру: прикиньте, сколько строк в C++ коде, его решающем? Сторонние библиотеки вызывать нельзя, у нас в распоряжении только голый компилятор. Ответ под катом.
На самом деле, двадцати строк кода достаточно для солвера. Если считать со всем-всем, включая парсер файла 3Д модели, то в двести строк уложиться — раз плюнуть.
Давайте расскажу, как это работает. Начнём издалека, представьте, что у нас есть обычный массив f, например, из 32 элементов, инициализированный следующим образом:

А затем мы тысячу раз выполним следующую процедуру: для каждой ячейки f[i] мы запишем в неё среднее значение соседних ячеек: f[i] = ( f[i-1] + f[i+1] )/2. Чтобы было понятнее, вот полный код:
Каждая итерация будет сглаживать данные нашего массива, и через тысячу итераций мы получим постоянное значение во всех ячейках. Вот анимация первых ста пятидесяти итераций:
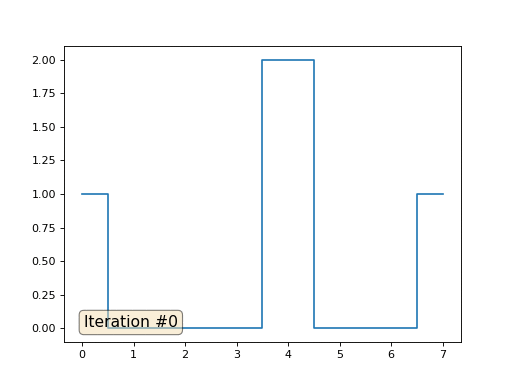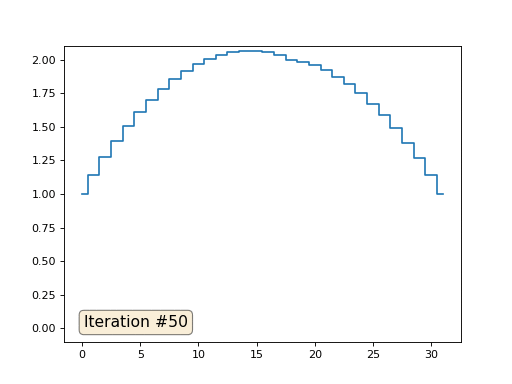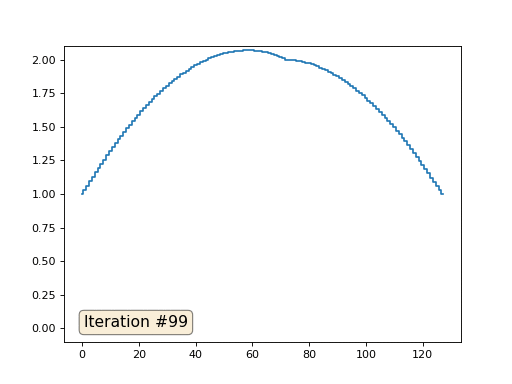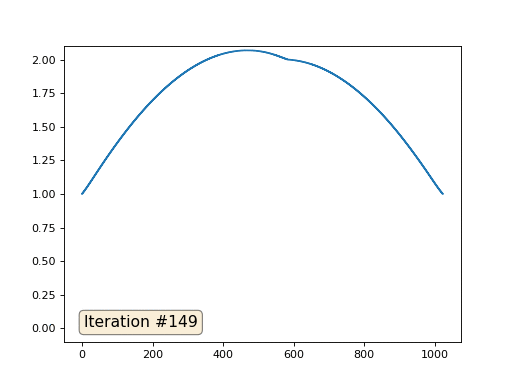
Если вам неясно, почему происходит сглаживание, прямо сейчас остановитесь, возьмите ручку и попробуйте порисовать примеры, иначе дальше читать не имеет смысла. Триангулированная поверхность ничем принципиально от этого примера не отличается. Представьте, что для каждой вершины мы найдём соседние с ней, посчитаем их центр масс, и передвинем нашу вершину в этот центр масс, и так десять раз. Результат будет вот таким:

Разумеется, если не остановиться на десяти итерациях, то через некоторое время вся поверхность сожмётся в одну точку ровно так же, как и в предыдущем примере весь массив стал заполнен одним и тем же значением.
Полный код доступен на гитхабе, а здесь я приведу самую важную часть, опустив лишь чтение и запись 3Д моделей. Итак, триангулированная модель у меня представлена двумя массивами: verts и faces. Массив verts — это просто набор трёхмерных точек, они же вершины полигональной сетки. Массив faces — это набор треугольников (количество треугольников равно faces.size()), для каждого треугольника в массиве хранятся индексы из массива вершин. Формат данных и работу с ним я подробно описывал в своём курсе лекций по компьютерной графике. Есть ещё третий массив, который я пересчитываю из первых двух (точнее, только из массива faces) — vvadj. Это массив, который для каждой вершины (первый индекс двумерного массива) хранит индексы соседних с ней вершин (второй индекс).
Первое, что я делаю, это для каждой вершины моей поверхности считаю вектор кривизны. Давайте проиллюстрируем: для текущей вершины v я перебираю всех её соседей n1-n4; затем я считаю их центр масс b = (n1+n2+n3+n4)/4. Ну и финальный вектор кривизны может быть посчитан как c=v-b, это не что иное, как обычные конечные разности для второй производной.

Непосредственно в коде это выглядит следующим образом:
Ну а дальше мы много раз делаем следующую вещь (смотрите предыдущую картинку): мы вершину v двигаем v := b + const * c. Обратите внимание, что если константа равна единице, то наша вершина никуда не сдвинется! Если константа равна нулю, то вершина заменяется на центр масс соседних вершин, что будет сглаживать нашу поверхность. Если константа больше единицы (заглавная картинка сделана при помощи const=2.1), то вершина будет сдвигаться в направлении вектора кривизны поверхности, усиливая детали. Вот так это выглядит в коде:
Кстати, если меньше единицы, то детали будут наоборот ослабляться (const=0.5), но это не будет эквивалентно простому сглаживанию, «контраст картинки» останется:

Обратите внимание, что мой код генерирует файл 3Д модели в формате Wavefront .obj, рендерил я в сторонней программе. Посмотреть получившуюся модель можно, например, в онлайн-вьюере. Если вам интересны именно методы отрисовки, а не генерирование модели, то читайте мой курс лекций по компьютерной графике.
Давайте вернёмся к самому первому примеру, и сделаем ровно то же самое, но только не будем переписывать элементы массива под номерами 0, 18 и 31:
Остальные, «свободные» элементы массива я инициализировал нулями, и по-прежнему итеративно заменяю их на среднее значение соседних элементов. Вот так выглядит эволюция массива на первых ста пятидесяти итерациях:
Вполне очевидно, что на сей раз решение сойдётся не к постоянному элементу, заполняющему массив, а к двум линейным рампам. Кстати, действительно ли всем очевидно? Если нет, то экспериментируйте с этим кодом, я специально привожу примеры с очень коротким кодом, чтобы можно было досконально разобраться с происходящим.
Пусть нам дана обычная система линейных уравнений:

Её можно переписать, оставив в каждом из уравнений с одной стороны знака равенства x_i:
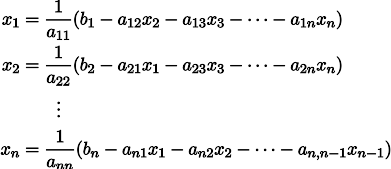
Пусть нам дан произвольный вектор , приближающий решение системы уравнений (например, нулевой).
, приближающий решение системы уравнений (например, нулевой).
Тогда, воткнув его в правую часть нашей системы, мы можем получить обновлённый вектор приближения решения .
.
Чтобы было понятнее, x1 получается из x0 следующим образом:
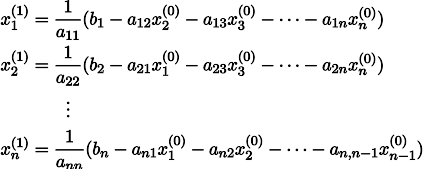
Повторив процесс k раз, решение будет приближено вектором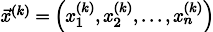
Давайте на всякий случай запишем рекурретную формулу:
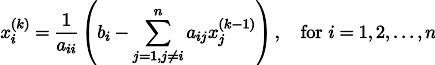
При некоторых предположениях о коэффициентах системы (например, вполне очевидно, что диагональные элементы не должны быть нулевыми, т.к. мы на них делим), данная процедура сходится к истинному решению. Эта гимнастика известна в литературе под названием метода Якоби. Конечно же, существуют и другие методы численного решения систем линейных уравнений, причём значительно более мощные, например, метод сопряжённых градиентов, но, пожалуй, метод Якоби является одним из самых простых.
А теперь давайте ещё раз внимательно посмотрим на основной цикл из примера 3:
Я стартовал с какого-то начального вектора x, и тысячу раз его обновляю, причём процедура обновления подозрительно похожа на метод Якоби! Давайте выпишем эту систему уравнений в явном виде:

Потратьте немного времени, убедитесь, что каждая итерация в моём питоновском коде — это строго одно обновление метода Якоби для этой системы уравнений. Значения x[0], x[18] и x[31] у меня зафиксированы, соответственно, в набор переменных они не входят, поэтому они перенесены в правую часть.
Итого, все уравнения в нашей системе выглядят как — x[i-1] + 2 x[i] — x[i+1] = 0. Это выражение не что иное, как обычные конечные разности для второй производной. То есть, наша система уравнений нам просто-напросто предписывает, что вторая производная должна быть везде равна нулю (ну, кроме как в точке x[18]). Помните, я говорил, что вполне очевидно, что итерации должны сойтись к линейным рампам? Так именно поэтому, у линейной функции вторая производная нулевая.
А вы знаете, что мы с вами только что решили задачу Дирихле для уравнения Лапласа?
Кстати, внимательный читатель должен был бы заметить, что, строго говоря, у меня в коде системы линейных уравнений решаются не методом Якоби, но методом Гаусса-Зейделя, который является своебразной оптимизацией метода Якоби:
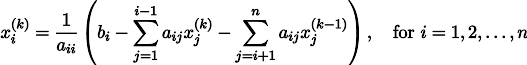
А давайте мы самую малость изменим третий пример: каждая ячейка помещается не просто в центр масс соседних ячеек, но в центр масс плюс некая (произвольная) константа:
В прошлом примере мы выяснили, что помещение в центр масс — это дискретизация оператора Лапласа (в нашем случае второй производной). То есть, теперь мы решаем систему уравнений, которая говорит, что наш сигнал должен иметь некую постоянную вторую производную. Вторая производная — это кривизна поверхности; таким образом, решением нашей системы должна стать кусочно-квадратичная функция. Проверим на дискретизации в 32 сэмпла:
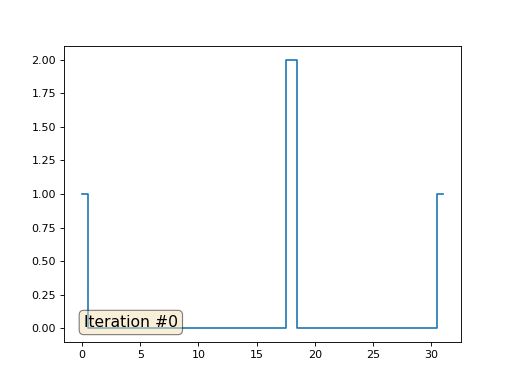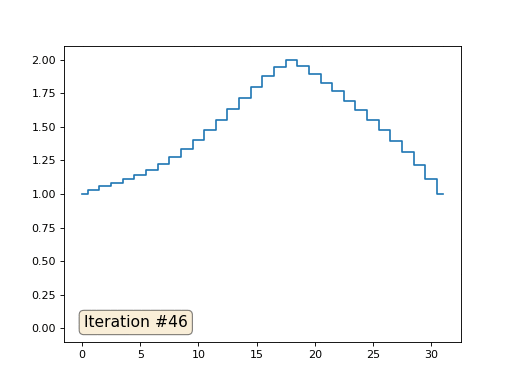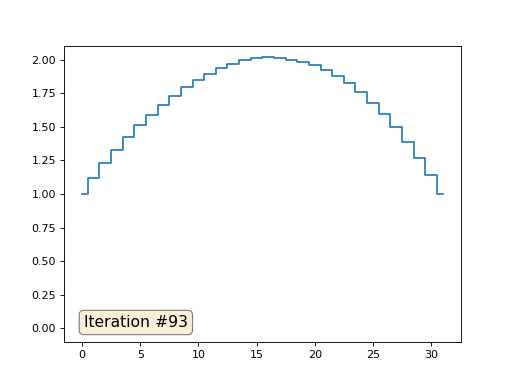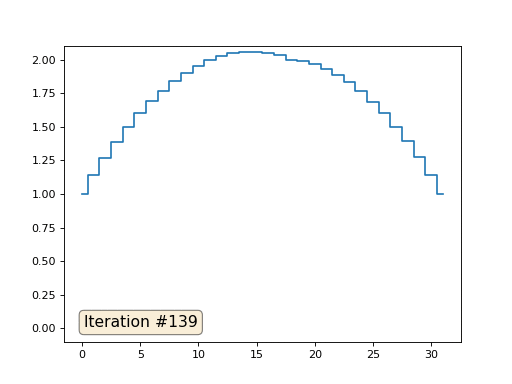
При длине массива в 32 элемента наша система сходится к решению за пару сотен итераций. А что будет, если мы попробуем массив в 128 элементов? Тут всё гораздо печальнее, количество итераций нужно уже исчислять тысячами:
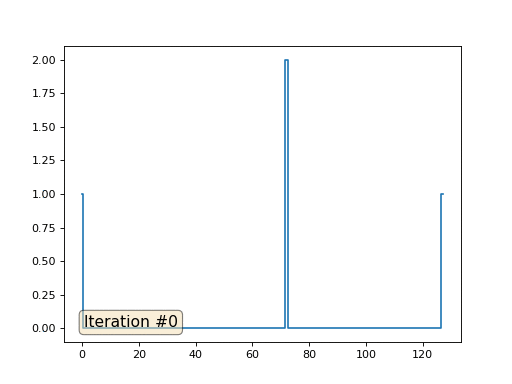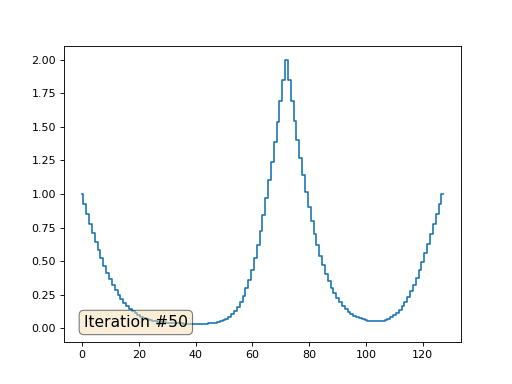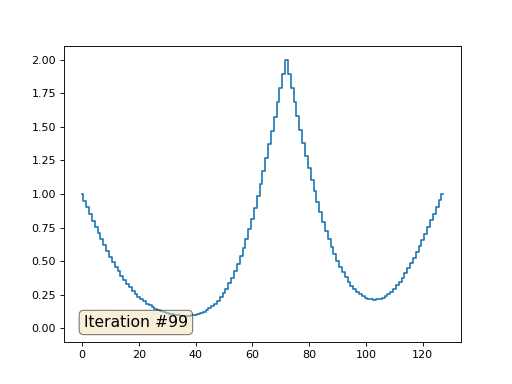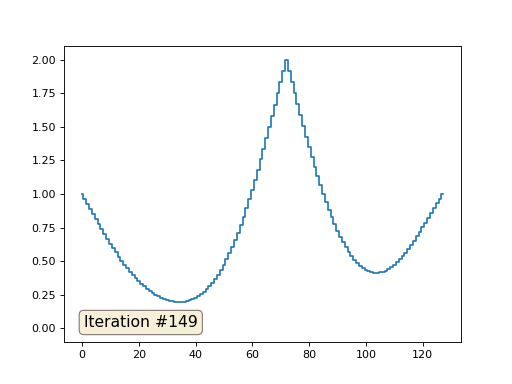
Метод Гаусса-Зейделя крайне прост в программировании, но малоприменим для больших систем уравнений. Можно попытаться его ускорить, применяя, например, многосеточные методы. На словах это может звучать громоздко, но идея крайне примитивная: если мы хотим решение с разрешением в тысячу элементов, то можно для начала решить с десятью элементами, получив грубую аппроксимацию, затем удвоить разрешение, решить ещё раз, и так далее, пока не достигнем нужного результата. На практике это выглядит следующим образом:
А можно не выпендриваться, и использовать настоящие солверы систем уравнений. Вот я решаю этот же пример, построив матрицу A и столбец b, затем решив матричное уравнение Ax=b:
А вот так выглядит результат работы этой программы, заметим, что решение получилось мгновенно:

Таким образом, действительно, наша функция кусочно-квадратичная (вторая производная равна константе). В первом примере мы задали нулевую вторую производную, в третьем ненулевую, но везде одинаковую. А что было во втором примере? Мы решили дискретное уравнение Пуассона, задав кривизну поверхности. Напоминаю, что произошло: мы посчитали кривизну входящей поверхности. Если мы решим задачу Пуассона, задав кривизну поверхности на выходе равной кривизне поверхности на входе (const=1), то ничего не изменится. Усиление характеристических черт лица происходит, когда мы просто увеличиваем кривизну (const=2.1). А если const<1, то кривизна результирующей поверхности уменьшается.
Развиваю идею, предложенную SquareRootOfZero, поиграйте с этим кодом:
Это результат по умолчанию, рыжий Ленин — это начальные данные, голубая кривая — это их эволюция, в бесконечности результат сойдётся в точку:
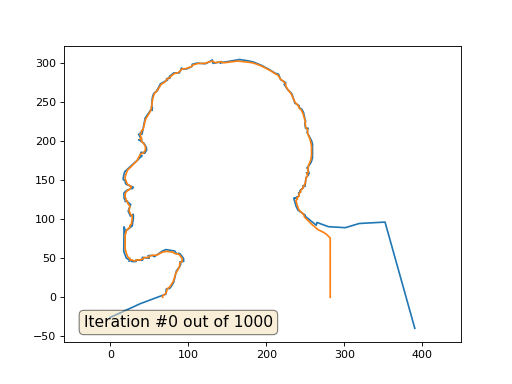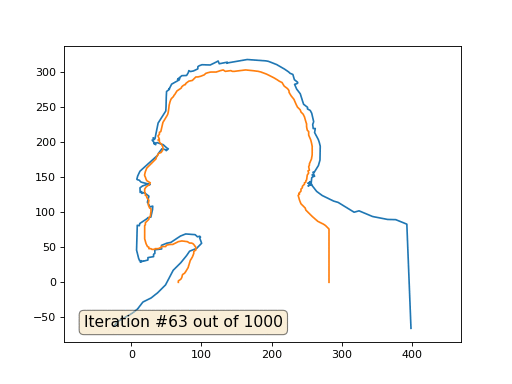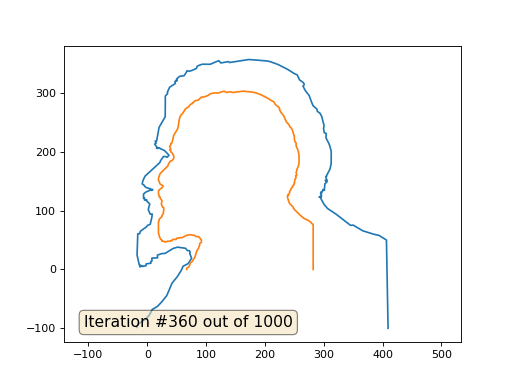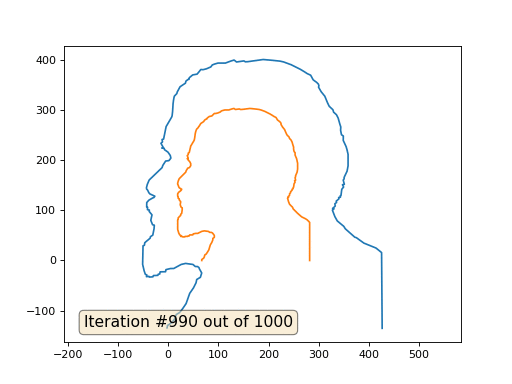
А вот результат с коэффицентом 2.:
Домашнее задание: почему во втором случае Ленин сначала превращается в Дзержинского, а затем снова сходится к Ленину же, но большего размера?
Очень много задач обработки данных, в частности, геометрии, могут формулироваться как решение системы линейных уравнений. В данной статье я не рассказал, как строить эти системы, моей целью было лишь показать, что это возможно. Темой следующей статьи будет уже не «почему», но «как», и какие солверы потом использовать.
Кстати, а ведь в названии статьи присутствуют наименьшие квадраты. Увидели ли вы их в тексте? Если нет, то это абсолютно не страшно, это именно ответ на вопрос «как?». Oставайтесь на линии, в следующей статье я покажу, где именно они прячутся, и как их модифицировать, чтобы получить доступ к крайне мощному инструменту обработки данных. Например, в десяток строк кода можно получить вот такое:

Stay tuned for more!
Итак, начнём. Давайте представим, что у меня есть триангулированная поверхность со сканом моего лица (на картинке слева). Что мне нужно сделать, чтобы усилить характерные черты, превратив эту поверхность в гротескную маску?

В данном конкретном случае я решаю эллиптическое дифференциальное уравнение, носящее имя Симеона Деми Пуассона. Товарищи программисты, давайте сыграем в игру: прикиньте, сколько строк в C++ коде, его решающем? Сторонние библиотеки вызывать нельзя, у нас в распоряжении только голый компилятор. Ответ под катом.
На самом деле, двадцати строк кода достаточно для солвера. Если считать со всем-всем, включая парсер файла 3Д модели, то в двести строк уложиться — раз плюнуть.
Пример 1: сглаживание данных
Давайте расскажу, как это работает. Начнём издалека, представьте, что у нас есть обычный массив f, например, из 32 элементов, инициализированный следующим образом:

А затем мы тысячу раз выполним следующую процедуру: для каждой ячейки f[i] мы запишем в неё среднее значение соседних ячеек: f[i] = ( f[i-1] + f[i+1] )/2. Чтобы было понятнее, вот полный код:
import matplotlib.pyplot as plt
f = [0.] * 32
f[0] = f[-1] = 1.
f[18] = 2.
plt.plot(f, drawstyle='steps-mid')
for iter in range(1000):
f[0] = f[1]
for i in range(1, len(f)-1):
f[i] = (f[i-1]+f[i+1])/2.
f[-1] = f[-2]
plt.plot(f, drawstyle='steps-mid')
plt.show()
Каждая итерация будет сглаживать данные нашего массива, и через тысячу итераций мы получим постоянное значение во всех ячейках. Вот анимация первых ста пятидесяти итераций:

Если вам неясно, почему происходит сглаживание, прямо сейчас остановитесь, возьмите ручку и попробуйте порисовать примеры, иначе дальше читать не имеет смысла. Триангулированная поверхность ничем принципиально от этого примера не отличается. Представьте, что для каждой вершины мы найдём соседние с ней, посчитаем их центр масс, и передвинем нашу вершину в этот центр масс, и так десять раз. Результат будет вот таким:

Разумеется, если не остановиться на десяти итерациях, то через некоторое время вся поверхность сожмётся в одну точку ровно так же, как и в предыдущем примере весь массив стал заполнен одним и тем же значением.
Пример 2: усиление/ослабление характеристических черт
Полный код доступен на гитхабе, а здесь я приведу самую важную часть, опустив лишь чтение и запись 3Д моделей. Итак, триангулированная модель у меня представлена двумя массивами: verts и faces. Массив verts — это просто набор трёхмерных точек, они же вершины полигональной сетки. Массив faces — это набор треугольников (количество треугольников равно faces.size()), для каждого треугольника в массиве хранятся индексы из массива вершин. Формат данных и работу с ним я подробно описывал в своём курсе лекций по компьютерной графике. Есть ещё третий массив, который я пересчитываю из первых двух (точнее, только из массива faces) — vvadj. Это массив, который для каждой вершины (первый индекс двумерного массива) хранит индексы соседних с ней вершин (второй индекс).
std::vector<Vec3f> verts;
std::vector<std::vector<int> > faces;
std::vector<std::vector<int> > vvadj;
Первое, что я делаю, это для каждой вершины моей поверхности считаю вектор кривизны. Давайте проиллюстрируем: для текущей вершины v я перебираю всех её соседей n1-n4; затем я считаю их центр масс b = (n1+n2+n3+n4)/4. Ну и финальный вектор кривизны может быть посчитан как c=v-b, это не что иное, как обычные конечные разности для второй производной.

Непосредственно в коде это выглядит следующим образом:
std::vector<Vec3f> curvature(verts.size(), Vec3f(0,0,0));
for (int i=0; i<(int)verts.size(); i++) {
for (int j=0; j<(int)vvadj[i].size(); j++) {
curvature[i] = curvature[i] - verts[vvadj[i][j]];
}
curvature[i] = verts[i] + curvature[i] / (float)vvadj[i].size();
}
Ну а дальше мы много раз делаем следующую вещь (смотрите предыдущую картинку): мы вершину v двигаем v := b + const * c. Обратите внимание, что если константа равна единице, то наша вершина никуда не сдвинется! Если константа равна нулю, то вершина заменяется на центр масс соседних вершин, что будет сглаживать нашу поверхность. Если константа больше единицы (заглавная картинка сделана при помощи const=2.1), то вершина будет сдвигаться в направлении вектора кривизны поверхности, усиливая детали. Вот так это выглядит в коде:
for (int it=0; it<100; it++) {
for (int i=0; i<(int)verts.size(); i++) {
Vec3f bary(0,0,0);
for (int j=0; j<(int)vvadj[i].size(); j++) {
bary = bary + verts[vvadj[i][j]];
}
bary = bary / (float)vvadj[i].size();
verts[i] = bary + curvature[i]*2.1; // play with the coeff here
}
}
Кстати, если меньше единицы, то детали будут наоборот ослабляться (const=0.5), но это не будет эквивалентно простому сглаживанию, «контраст картинки» останется:

Обратите внимание, что мой код генерирует файл 3Д модели в формате Wavefront .obj, рендерил я в сторонней программе. Посмотреть получившуюся модель можно, например, в онлайн-вьюере. Если вам интересны именно методы отрисовки, а не генерирование модели, то читайте мой курс лекций по компьютерной графике.
Пример 3: добавляем ограничения
Давайте вернёмся к самому первому примеру, и сделаем ровно то же самое, но только не будем переписывать элементы массива под номерами 0, 18 и 31:
import matplotlib.pyplot as plt
x = [0.] * 32
x[0] = x[31] = 1.
x[18] = 2.
plt.plot(x, drawstyle='steps-mid')
for iter in range(1000):
for i in range(len(x)):
if i in [0,18,31]: continue
x[i] = (x[i-1]+x[i+1])/2.
plt.plot(x, drawstyle='steps-mid')
plt.show()
Остальные, «свободные» элементы массива я инициализировал нулями, и по-прежнему итеративно заменяю их на среднее значение соседних элементов. Вот так выглядит эволюция массива на первых ста пятидесяти итерациях:

Вполне очевидно, что на сей раз решение сойдётся не к постоянному элементу, заполняющему массив, а к двум линейным рампам. Кстати, действительно ли всем очевидно? Если нет, то экспериментируйте с этим кодом, я специально привожу примеры с очень коротким кодом, чтобы можно было досконально разобраться с происходящим.
Лирическое отступление: численное решение систем линейных уравнений.
Пусть нам дана обычная система линейных уравнений:

Её можно переписать, оставив в каждом из уравнений с одной стороны знака равенства x_i:
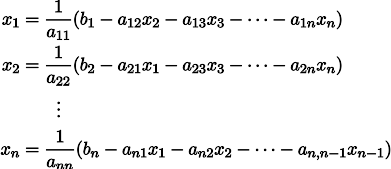
Пусть нам дан произвольный вектор
 , приближающий решение системы уравнений (например, нулевой).
, приближающий решение системы уравнений (например, нулевой).Тогда, воткнув его в правую часть нашей системы, мы можем получить обновлённый вектор приближения решения
 .
.Чтобы было понятнее, x1 получается из x0 следующим образом:
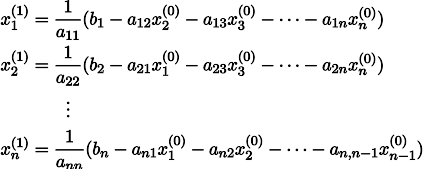
Повторив процесс k раз, решение будет приближено вектором
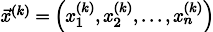
Давайте на всякий случай запишем рекурретную формулу:
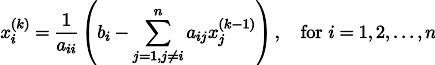
При некоторых предположениях о коэффициентах системы (например, вполне очевидно, что диагональные элементы не должны быть нулевыми, т.к. мы на них делим), данная процедура сходится к истинному решению. Эта гимнастика известна в литературе под названием метода Якоби. Конечно же, существуют и другие методы численного решения систем линейных уравнений, причём значительно более мощные, например, метод сопряжённых градиентов, но, пожалуй, метод Якоби является одним из самых простых.
Пример 3 ещё раз, но уже с другой стороны
А теперь давайте ещё раз внимательно посмотрим на основной цикл из примера 3:
for iter in range(1000):
for i in range(len(x)):
if i in [0,18,31]: continue
x[i] = (x[i-1]+x[i+1])/2.
Я стартовал с какого-то начального вектора x, и тысячу раз его обновляю, причём процедура обновления подозрительно похожа на метод Якоби! Давайте выпишем эту систему уравнений в явном виде:

Потратьте немного времени, убедитесь, что каждая итерация в моём питоновском коде — это строго одно обновление метода Якоби для этой системы уравнений. Значения x[0], x[18] и x[31] у меня зафиксированы, соответственно, в набор переменных они не входят, поэтому они перенесены в правую часть.
Итого, все уравнения в нашей системе выглядят как — x[i-1] + 2 x[i] — x[i+1] = 0. Это выражение не что иное, как обычные конечные разности для второй производной. То есть, наша система уравнений нам просто-напросто предписывает, что вторая производная должна быть везде равна нулю (ну, кроме как в точке x[18]). Помните, я говорил, что вполне очевидно, что итерации должны сойтись к линейным рампам? Так именно поэтому, у линейной функции вторая производная нулевая.
А вы знаете, что мы с вами только что решили задачу Дирихле для уравнения Лапласа?
Кстати, внимательный читатель должен был бы заметить, что, строго говоря, у меня в коде системы линейных уравнений решаются не методом Якоби, но методом Гаусса-Зейделя, который является своебразной оптимизацией метода Якоби:
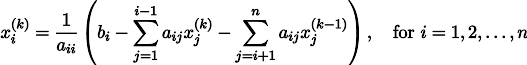
Пример 4: уравнение Пуассона
А давайте мы самую малость изменим третий пример: каждая ячейка помещается не просто в центр масс соседних ячеек, но в центр масс плюс некая (произвольная) константа:
import matplotlib.pyplot as plt
x = [0.] * 32
x[0] = x[31] = 1.
x[18] = 2.
plt.plot(x, drawstyle='steps-mid')
for iter in range(1000):
for i in range(len(x)):
if i in [0,18,31]: continue
x[i] = (x[i-1]+x[i+1] +11./32**2 )/2.
plt.plot(x, drawstyle='steps-mid')
plt.show()
В прошлом примере мы выяснили, что помещение в центр масс — это дискретизация оператора Лапласа (в нашем случае второй производной). То есть, теперь мы решаем систему уравнений, которая говорит, что наш сигнал должен иметь некую постоянную вторую производную. Вторая производная — это кривизна поверхности; таким образом, решением нашей системы должна стать кусочно-квадратичная функция. Проверим на дискретизации в 32 сэмпла:

При длине массива в 32 элемента наша система сходится к решению за пару сотен итераций. А что будет, если мы попробуем массив в 128 элементов? Тут всё гораздо печальнее, количество итераций нужно уже исчислять тысячами:

Метод Гаусса-Зейделя крайне прост в программировании, но малоприменим для больших систем уравнений. Можно попытаться его ускорить, применяя, например, многосеточные методы. На словах это может звучать громоздко, но идея крайне примитивная: если мы хотим решение с разрешением в тысячу элементов, то можно для начала решить с десятью элементами, получив грубую аппроксимацию, затем удвоить разрешение, решить ещё раз, и так далее, пока не достигнем нужного результата. На практике это выглядит следующим образом:

А можно не выпендриваться, и использовать настоящие солверы систем уравнений. Вот я решаю этот же пример, построив матрицу A и столбец b, затем решив матричное уравнение Ax=b:
import numpy as np
import matplotlib.pyplot as plt
n=1000
x = [0.] * n
x[0] = x[-1] = 1.
m = n*57//100
x[m] = 2.
A = np.matrix(np.zeros((n, n)))
for i in range(1,n-2):
A[i, i-1] = -1.
A[i, i] = 2.
A[i, i+1] = -1.
A = A[1:-2,1:-2]
A[m-2,m-1] = 0
A[m-1,m-2] = 0
b = np.matrix(np.zeros((n-3, 1)))
b[0,0] = x[0]
b[m-2,0] = x[m]
b[m-1,0] = x[m]
b[-1,0] = x[-1]
for i in range(n-3):
b[i,0] += 11./n**2
x2 = ((np.linalg.inv(A)*b).transpose().tolist()[0])
x2.insert(0, x[0])
x2.insert(m, x[m])
x2.append(x[-1])
plt.plot(x2, drawstyle='steps-mid')
plt.show()
А вот так выглядит результат работы этой программы, заметим, что решение получилось мгновенно:

Таким образом, действительно, наша функция кусочно-квадратичная (вторая производная равна константе). В первом примере мы задали нулевую вторую производную, в третьем ненулевую, но везде одинаковую. А что было во втором примере? Мы решили дискретное уравнение Пуассона, задав кривизну поверхности. Напоминаю, что произошло: мы посчитали кривизну входящей поверхности. Если мы решим задачу Пуассона, задав кривизну поверхности на выходе равной кривизне поверхности на входе (const=1), то ничего не изменится. Усиление характеристических черт лица происходит, когда мы просто увеличиваем кривизну (const=2.1). А если const<1, то кривизна результирующей поверхности уменьшается.
Update: ещё одна игрушка в качестве домашнего задания
Развиваю идею, предложенную SquareRootOfZero, поиграйте с этим кодом:
Скрытый текст
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
fig, ax = plt.subplots()
x = [282, 282, 277, 274, 266, 259, 258, 249, 248, 242, 240, 238, 240, 239, 242, 242, 244, 244, 247, 247, 249, 249, 250, 251, 253, 252, 254, 253, 254, 254, 257, 258, 258, 257, 256, 253, 253, 251, 250, 250, 249, 247, 245, 242, 241, 237, 235, 232, 228, 225, 225, 224, 222, 218, 215, 211, 208, 203, 199, 193, 185, 181, 173, 163, 147, 144, 142, 134, 131, 127, 121, 113, 109, 106, 104, 99, 95, 92, 90, 87, 82, 78, 77, 76, 73, 72, 71, 65, 62, 61, 60, 57, 56, 55, 54, 53, 52, 51, 45, 42, 40, 40, 38, 40, 38, 40, 40, 43, 45, 45, 45, 43, 42, 39, 36, 35, 22, 20, 19, 19, 20, 21, 22, 27, 26, 25, 21, 19, 19, 20, 20, 22, 22, 25, 24, 26, 28, 28, 27, 25, 25, 20, 20, 19, 19, 21, 22, 23, 25, 25, 28, 29, 33, 34, 39, 40, 42, 43, 49, 50, 55, 59, 67, 72, 80, 83, 86, 88, 89, 92, 92, 92, 89, 89, 87, 84, 81, 78, 76, 73, 72, 71, 70, 67, 67]
y = [0, 76, 81, 83, 87, 93, 94, 103, 106, 112, 117, 124, 126, 127, 130, 133, 135, 137, 140, 142, 143, 145, 146, 153, 156, 159, 160, 165, 167, 169, 176, 182, 194, 199, 203, 210, 215, 217, 222, 226, 229, 236, 240, 243, 246, 250, 254, 261, 266, 271, 273, 275, 277, 280, 285, 287, 289, 292, 294, 297, 300, 301, 302, 303, 301, 301, 302, 301, 303, 302, 300, 300, 299, 298, 296, 294, 293, 293, 291, 288, 287, 284, 282, 282, 280, 279, 277, 273, 268, 267, 265, 262, 260, 257, 253, 245, 240, 238, 228, 215, 214, 211, 209, 204, 203, 202, 200, 197, 193, 191, 189, 186, 185, 184, 179, 176, 163, 158, 154, 152, 150, 147, 145, 142, 140, 139, 136, 133, 128, 127, 124, 123, 121, 117, 111, 106, 105, 101, 94, 92, 90, 85, 82, 81, 62, 55, 53, 51, 50, 48, 48, 47, 47, 48, 48, 49, 49, 51, 51, 53, 54, 54, 58, 59, 58, 56, 56, 55, 54, 50, 48, 46, 44, 41, 36, 31, 21, 16, 13, 11, 7, 5, 4, 2, 0]
n = len(x)
cx = x[:]
cy = y[:]
for i in range(0,n):
bx = (x[(i-1+n)%n] + x[(i+1)%n] )/2.
by = (y[(i-1+n)%n] + y[(i+1)%n] )/2.
cx[i] = cx[i] - bx
cy[i] = cy[i] - by
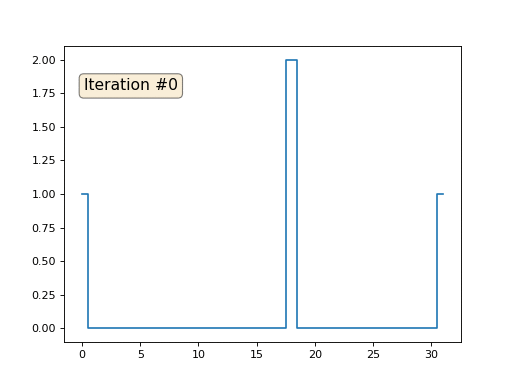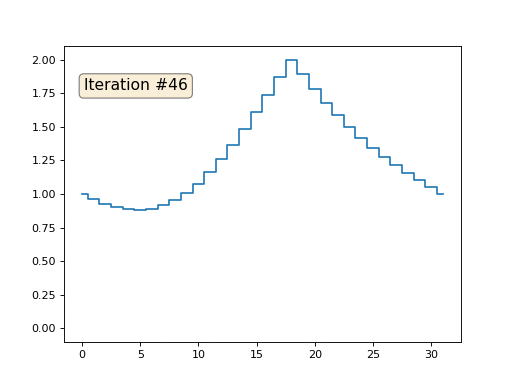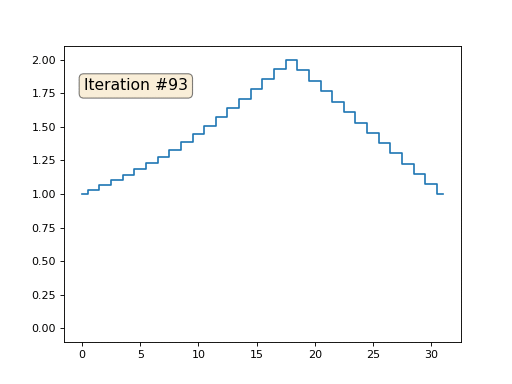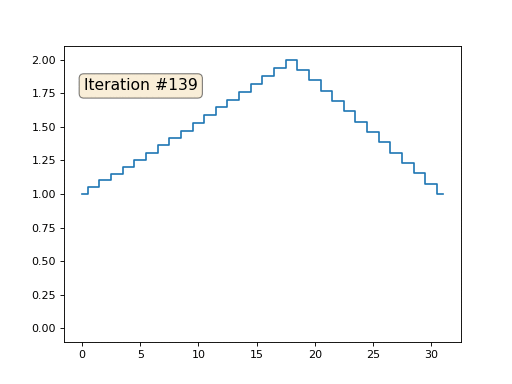
lines = [ax.plot(x, y)[0], ax.text(0.05, 0.05, "Iteration #0", transform=ax.transAxes, fontsize=14,bbox=dict(boxstyle='round', facecolor='wheat', alpha=0.5)), ax.plot(x, y)[0] ]
def animate(iteration):
global x, y
print(iteration)
for i in range(0,n):
x[i] = (x[(i-1+n)%n]+x[(i+1)%n])/2. + 0.*cx[i] # play with the coeff here, 0. by default
y[i] = (y[(i-1+n)%n]+y[(i+1)%n])/2. + 0.*cy[i]
lines[0].set_data(x, y) # update the data.
lines[1].set_text("Iteration #" + str(iteration))
plt.draw()
ax.relim()
ax.autoscale_view(False,True,True)
return lines
ani = animation.FuncAnimation(fig, animate, frames=np.arange(0, 100), interval=1, blit=False, save_count=50)
#ani.save('line.gif', dpi=80, writer='imagemagick')
plt.show()
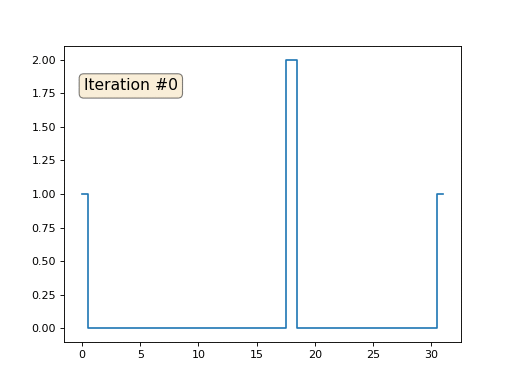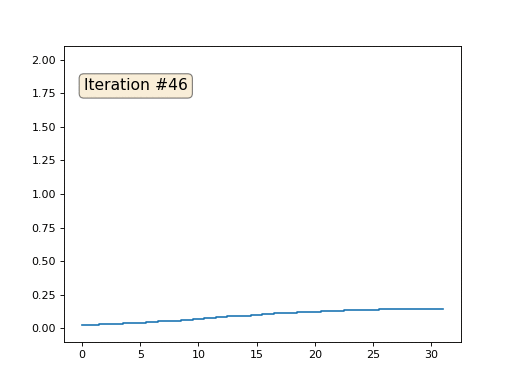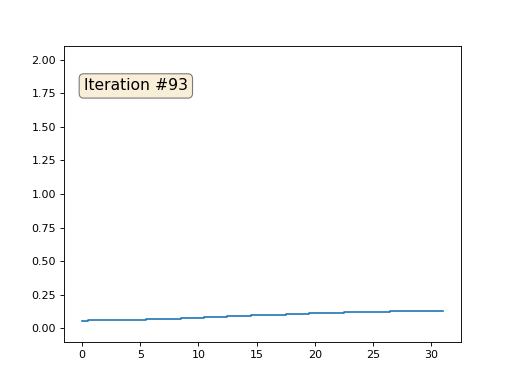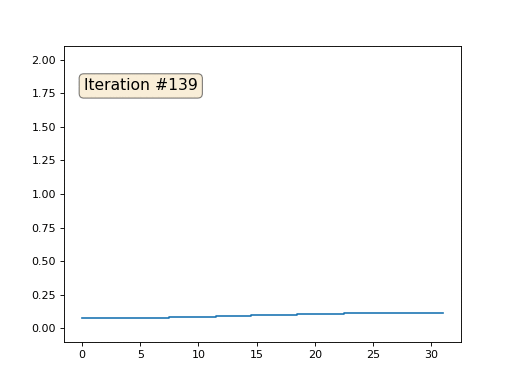
Это результат по умолчанию, рыжий Ленин — это начальные данные, голубая кривая — это их эволюция, в бесконечности результат сойдётся в точку:

А вот результат с коэффицентом 2.:

Домашнее задание: почему во втором случае Ленин сначала превращается в Дзержинского, а затем снова сходится к Ленину же, но большего размера?
Заключение
Очень много задач обработки данных, в частности, геометрии, могут формулироваться как решение системы линейных уравнений. В данной статье я не рассказал, как строить эти системы, моей целью было лишь показать, что это возможно. Темой следующей статьи будет уже не «почему», но «как», и какие солверы потом использовать.
Кстати, а ведь в названии статьи присутствуют наименьшие квадраты. Увидели ли вы их в тексте? Если нет, то это абсолютно не страшно, это именно ответ на вопрос «как?». Oставайтесь на линии, в следующей статье я покажу, где именно они прячутся, и как их модифицировать, чтобы получить доступ к крайне мощному инструменту обработки данных. Например, в десяток строк кода можно получить вот такое:

Stay tuned for more!

KhodeN
Эм… ну да, фигня, начальная школа.
Как же все относительно в мире.
haqreu Автор
Про начальную я не говорил; но вообще решение систем линейных уравнений — седьмой класс школы. Производные — десятый. Программирование на таком уровне — десятый. Что я упустил?
KhodeN
Статья безусловно классная. Формулы страшные. Ну вот чисто внешне пугают. Как у Хоккинга: «каждая новая формула сокращает число читателей вдвое».
Я довольно востребованный прикладной программист с большим опытом. Но без образования и знаний математики. И с этой точки зрения статья обманула мои ожидания фразой «вообще не требует знаний».
Возможно вы учились в очень классной школе. Но мне кажется, вы переоцениваете уровень седьмого и десятого классов.
haqreu Автор
Мне кажется, что вы путаете «не требует специальных знаний» и «читается с чашкой чая в одной руке, с мышкой в другой».
На всю статью вообще одна формула:
dfgwer
Математические формулы на первый взгляд совершенно непонятны. Трюк в том чтобы читать медленно, по слогам. Сначало смотрим, что означает каждая буква, находим эти буквы в формуле, найдя все смыслы всех букв и их места в формуле быстро проходимся еще разок отмечая все буквы и смыслы. Затем начинаем смотреть на преобразования, многократно перечитывая и сверяя куда каждая буква пошла. И так в конце концов дойдем до конца блока формул. Это займет значительно больше времени чем обычное чтение.
На лирическое отступление из этой статьи, нужно потратить минут 5.
haqreu Автор
Большое спасибо, именно так.
oleg-x2001
Программист не знающий самой элементарной математики скорее всего говнокодер (да, говнокодеры тоже могут востребованы), а не программист.
KhodeN
Подавляющее число задач не связаны с математикой вообще никак. CRUD и бизнес-логика редко требуют сложных вычислений. А вот знания 100500 библиотек на все случаи жизни, умение писать простой и понятный код (поддерживаемый), умение расставлять приоритеты, изучать постоянно что-то новое — нужно всегда.
Программисты решают задачи бизнеса. Если задача решается с приемлемым качеством и в приемлемый срок — он профи.
Если появится проблема, требующая знаний — получить эти знания или нанять человека, специализирующегося на них — не проблема.
Ставить ярлык "говнокодер" я бы не стал, если человек не умеет в диффуры.
haqreu Автор
Нанять человека — это не уже не программист, а к управляющий.
oleg-x2001
При чем здесь диффуры? Есть масса других, более универсальных вещей, которые называются «дискретная математика». Про теорию алгоритмов слышали? Сбалансированные деревья, алгоритмы на графах и все такое? Да, в чистом виде сбалансированные деревья реализовывать в «бизнес-логике» приложения надо нечасто, да и с графами работать тоже. А вот в менее явной форме вполне. Кто сказал что горе-программист, для которого система линейных уравнений (не говоря уже про логарифмы и прочие элементарные вещи начальной школы) это непостижимо сложная вещь, может написать простой, понятный и эффективнй код? Такой же программист-неуч? А может быть, на самом деле можно написать намного более эффективный код, практически не теряя в его читабельности?
И я все-таки не утверждаю что каждый программист-неуч обязательно говнокодер. Хороший программист не обязан обладать знаниями Д. Кнута чтобы быть действительно хорошим программистом. Скорее всего, примеры таких программистов все же есть. Но, повторяю, чтобы утверждать что код, написанный неучем, действительно хороший, нужно какая-то точка отсчета. И желательно, чтобы оценку качества проводили не такие же неучи.
fndrey357
Частная задача — 1-2-3 неизвестных — 7-8 класс.
Общая задача — N неизвестных чуть выше уровень…
haqreu Автор
Покажете мне восьмиклассника, который умеет решать систему с тремя неизвестными, но не сможет решить с четырьмя?
fndrey357
Сын мой :)
Они решают 2-3 неизвестных, без обобщений на n неизвестных. Так прописано в библии по подготовке к ЕГЭ. Им больше 3 и не надо…
Они в ступор встают, когда им пишешь что-то типа «а в степени n, где n=3»…
haqreu Автор
А вы можете попробовать ему дать следующую систему уравнений? Что он скажет?
{x1-x2 = 0
x2-x3 = 0
x3-x4 = 0
x4 = 2
fndrey357
Ну я ему потихоньку мозги вставляю. Сомневаюсь, что учителя это делают и остальные родители.
vassabi
как отец шестиклассницы скажу, что она решила эту систему «обученным в школе» способом (т.е. без обобщений) по цепочке снизу вверх.
pchelintsev_an
Пример вызова реализации МНК в пакете Maxima:
/* Задаём матрицу с данными */
M:matrix([-1, -0.5], [0, 0], [1, 0.5], [2, 0.9], [3, 1]);
/* Модель: U - переменная, A, B, C - неизвестные параметры */
f(U,A,B,C):=A*exp(B*U)+C*U^2;
/* Загружаем модуль пакета для МНК */
load(lsquares);
/* Вызываем реализацию МНК в пакете */
klist:lsquares_estimates(M, [U,I], I=f(U,A,B,C), [A,B,C]);
/* Подставляем найденные параметры в модель */
I(U):=float(ev(f(U,A,B,C), klist));
/* Определяем коэффициент детерминации R^2. Сначала найдём среднее значение */
mny:0;
for i:1 thru length(M) step 1 do mny:mny+M[i,2];
mny:mny/length(M);
/* Находим суммы квадратов */
sum1:0;
sum2:0;
for i:1 thru length(M) step 1 do (sum1:sum1+(M[i,2]-I(M[i,1]))^2, sum2:sum2+(M[i,2]-mny)^2);
/* Вычисляем до целой части коэффициент R^2 и выводим его */
Rsq:round((1-sum1/sum2)*100)$
printf(true, "R^2 = ~d%", Rsq)$
/* Сформируем из матрицы M список точек */
plist:create_list(M[k], k, 1, length(M));
/* Строим график */
plot2d([['discrete,plist], I(U)], [U, -1, 4], [style, [points, 2, 1, 1], lines], [color, red, blue]);
Я не так давно для одной модели использовал в Maxima не lsquares_estimates, а решал экстремальную задачу на минимум суммы квадратов остатков модели (модуль lbfgs — метод Бройдена-Флетчера-Гольдфарба-Шанно). lsquares_estimates умеет определять линейность модели относительно неизвестных параметров. Если линейность имеет место, получаемую нормальную систему линейных уравнений пакет решает аналитически (ответ в обыкновенных дробях выдаёт), иначе вызывает численное решение экстремальной задачи указанным методом. При этом не всегда удачно подбирает начальное приближение к решению. Надо как-нибудь сюда статью об этом написать.
haqreu Автор
Спасибо за пример! Буду им пользоваться в качестве шпаргалки для построения графиков в максиме. Жаль только, что он не имеет прямого отношения к рассмотренным в статье примерам. И скромная просьба прятать впредь длинный код под тег <spoiler>, иначе сильно загромождается страница комментариев. Ещё раз спасибо!
pchelintsev_an
Небольшое дополнение. Если пакет обламывается на plot2d в Windows, то, скорее всего, Вы работаете в системе под пользователем, в имени которого есть русские буквы. Дело в том, что пакет пытается создать временный текстовый файл для Gnuplot. Поэтому надо перенаправить директорию для временных файлов в другое место, например, в корень диска d:
maxima_tempdir:"d:\\";Если экспериментальных данных много, забивать их списком долго (например, переносить из Excel). В Maxima есть возможность чтения данных в матрицу из текстового файла:
M:read_matrix("d:\data.txt");Файл data.txt выглядит просто (без пустой строки в конце):
-1 -0.50 0
1 0.5
2 0.9
3 1
c0f04
Спасибо за интересную статью! Кажется, потребуется к ней несколько раз вернуться после Википедии, чтобы осознать, что же тут написано по части математики.
haqreu Автор
А что из математики вы не поняли без википедии? Все пассажи про эллиптические дифференциальные уравнения тут, мягко скажем, необязательные. А решение СЛАУ, вроде, должно быть достаточно прозрачным, нет?
c0f04
Если с математикой постоянно не работаешь, то математический язык очень сложно воспринимать. Могу без проблем преобразовать через матрицы систему координат, но когда лезу в Википедию что-либо подсмотреть, обычно хочется всё переписать с нуля после того, как пойму, что там написано.
Математика без пояснения на бытовых примерах очень сложна для восприятия большинству. И каждый пример должен быть подкреплён практическим использованием. В Вашем случае любопытные примеры получились.
SquareRootOfZero
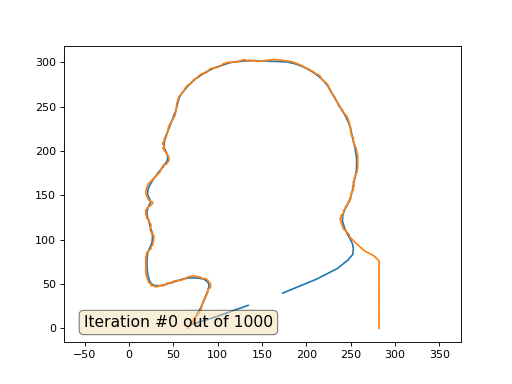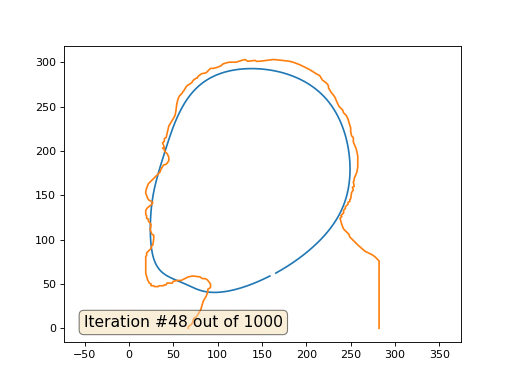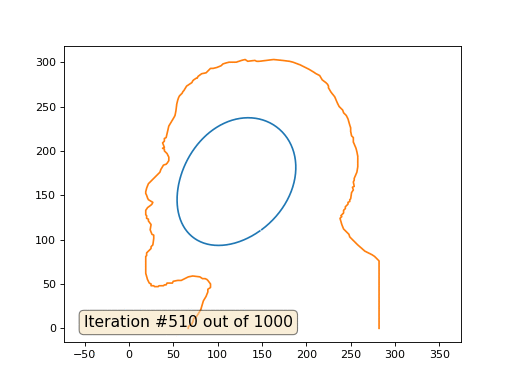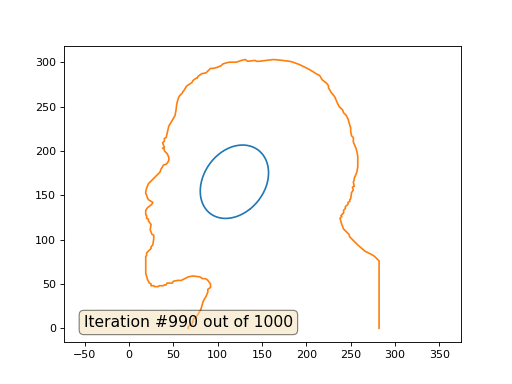
В целом, пост понравился, но несколько сбивают с толку резкие перескоки с 3D-сканов на график функции из двух ступенек. Почему бы как-то не свести иллюстративную базу воедино? К примеру, как-то так:
haqreu Автор
Отличный совет. Немного настораживает правая нижняя точка, но это мы починим, выкладывайте код с вождём!
SquareRootOfZero
Правую нижнюю точку специально зафиксировал (уже отпустил). Ну вроде так:
haqreu Автор
сделал апдейт, спасибо
DelphiCowboy
Реально круто! Это ведь и к любому рельефу и фактуре можно применить!
MajinSaha
Статью пробежал минуты за 2, всё это знакомо. Но меня всегда удивляло, как вы на Хабре так непринуждённо классные иллюстрации делаете к постам? Мне кажется, это самое сложное при подготовке материала. У каждого блогера свой велосипед или на Хабре есть какой-то единый крутой инструментарий?
haqreu Автор
У каждого свой велосипед. На картинки в этой статье я потратил несколько дней.
Спасибо на добром слове, приятно видеть, что они нравятся людям!
IGR2014
То чувство когда увидел пост в твиттере хабра, узнал лицо, понял что будет интересно и зашёл прочитать
Kyushu
Решение линейных систем довольно обширная тема. Методы делятся на прямые и итерационные, матрицы на плотные и разреженные. Для вычислительных задач число неизвестных достигает миллионов и есть множество открытых пакетов, которые решают линейные системы с использованием MPI, в разработку которых вложены сотни человеко-лет. Многосеточные методы хорошо работают только для определенных классов матриц.
"… данная процедура сходится к истинному решению" — подобная фраза просто находка для экзаменатора по математике.
haqreu Автор
Какие именно солверы использовать — это отдельная тема, в статью не входящая. А в целом вы что сказать-то хотели? Что я где-то глупость сморозил? Так отлично, поправьте её. Про находки: мне часто доводится экзаменовать студентов, но я не очень понимаю, о каких находках вы говорите.
Kyushu
"… данная процедура сходится к истинному решению" — так понятнее?
haqreu Автор
Нет.
Kyushu
Хорошо. Решение может быть точным, приближенным, единственным, неединственным… Но что такое истинное решение? Это скорее из области веры, чем вычислительной математики.
haqreu Автор
Я думал, вы про условия сходимости, а вы вовсе про русский язык. Давайте так:
47 миллионов результатов.
mayorovp
На самом деле это из области метрологии «просочился» термин.
Arastas
Что-то мне кажется, что это не очень хорошая находка для экзамена. Или хорошая находка для не очень хорошего экзаменатора.
Kyushu
Такое понятие вычислительной математики как «истинное решение» мне неизвестно. За всю математику не скажу, возможно, где-то оно и используется. Вот, например, откуда «истинное решение» появилось в данном, написанном вполне профессиональном языком, посте? Для экзаменатора — это возможность построить логическую беседу на тему — что такое решение, чем истинное решение отличается от неистинного решения.
haqreu Автор
Скажите, пожалуйста, что вы думаете по поводу следующей фразы:
Kyushu
Это утверждение неверно. А вы ожидали что-то другого? :)
haqreu Автор
Вообще да, ожидал. А почему оно неверно?
Kyushu
Так, не сочтите за труд, напишите, пожалуйста, чего вы ожидали.
haqreu Автор
Вы зря ёрничаете, я, вроде, ничего плохого вам не говорил.
Я лишь хотел вас подвести к мысли о том, что система сама по себе решений не имеет. Решают задачи, а не уравнения. А когда мы договоримся про то, какую задачу решали, тогда можно будет договариваться про прилагательные рядом со словом решение.
Kyushu
Так чего вы ожидали-то? И что делают с уравнениями? :)
Arastas
Скажите, вы когда-либо преподавали студентам? Вы считаете, что задача экзаменатора это "построить логическую беседу на тему"? Это, возможно, задача при проведении семинара, но вряд ли при проведении экзамена.
Kyushu
Задача экзамена выяснить какими знаниями обладает студент и как умеет пользоваться ими: решать задачи, объяснять решения и свои утверждения. Выясняется это, в частности, в виде беседы, в которой студенту задаются вопросы. Что непонятного? Студентам не преподавал, но экзамены иногда принимаю.
Arastas
Я не знаю, как вы себе это представляете, но у меня перед глазами встает такая картина. Экзамен. Студент, волнуясь, рассказывает про решение СЛАУ, и тут экзаменатор, который до этого слушал его с несколько скучающим видом, вскидывается и, едва пряча ехидную улыбку, спрашивает: так-так-так, голубчик! Вот вы говорите — истинное решение, да? Расскажите-ка, а почему же оно "истинное"? И какие такие не истинные бывают?
Жуткая картинка, на самом деле.
Kyushu
И не говорите…
Jeka178RUS
Спасибо было интересно, а матан реально простецкий!
olwi
Что-то сглаживание из первого примера выглядит как-то странно.
Формула
f[i] = (f[i-1] + f[i+1])/2вроде бы как предполагает локальное (зависящее лишь от ближайших соседей) и симметричное преобразование, но приведенный алгоритм реализует нечто другое.Если предположить, что в начале очередной итерации
f = [f0, f1, f2, ..., f31], то проделав несколько шагов итерации вручную, видно, что при этом происходят следующие замены:f0 -> f1
f1 -> (f0+f2)/2 == (f1+f2)/2
f2 -> (f1+f3)/2 == (f1+f2+2*f3)/4
f3 -> (f2+f4)/2 == (f1+f2+2*f3+4*f4)/8
f4 -> (f3+f5)/2 == (f1+f2+2*f3+4*f4+8*f5)/16
...
f30 -> (f29+f31)/2 == (f1+f2+2*f3+4*f4+...+(2**29)*f31)/(2**30)
f31 -> f30 == (f1+f2+2*f3+4*f4+...+(2**29)*f31)/(2**30)
Это преобразование 1) нелокальное (все значения зависят от f1, хоть и с экспоненциально убывающим коэффициентом); 2) асимметричное (значения с большими индексами зависят от всех значений с меньшими индексами, но обратное неверно); 3) от f0 вообще ничего не зависит.
Да, при этом некое «сглаживание» несомненно происходит (с каждой итерацией значения всё меньше отличаются), но то ли это сглаживание, которое имелось в виду?
AngReload
Ага, тут должно быть два буфера — на вход и выход, которые после каждого прохода меняются местами.
haqreu Автор
Ну вот вы и есть тот самый внимательный читатель :)
Сравните имплементации метода Якоби и метода Гаусса-Зейделя.
А вот так выглядит первая итерация обоих методов:
Гаусс-Зейдель:
leshabirukov
Надо образец сделать не сглаживанием одного лица, а усреднением по выборке лиц, вот тогда будет настоящий генератор карикатур.
haqreu Автор
Да, может получиться хороший проект, но тут есть технические сложности. Сосканировать много лиц несложно, но вот что с ними дальше делать, это уже интересный вопрос. Две поверхности легко «смешать», если они имеют одинаковую сетку треугольников. Даже если мы умеем смешивать разные сетки, нам нужно точно сопоставить нос одной модели с носом другой, глаза с глазами и т.п. Это всё решается, но задача нетривиальная.
leshabirukov
Можно попробовать построить для каждого лица карту высот от сглаженной версии, и совмещать разные карты поиском максимума корреляции. Максимумы и минимумы высот — характерные точки, из их координат формируем вектор признаков, по этому вектору усредняем. Как-то так.
haqreu Автор
Ну это один из вариантов, но лица имеют разные пропорции, и кросс-корреляция поможет весьма относительно. Без построения карт и корреляции можно обойтись совсем, использовав методы кросс-параметризации поверхностей. Но это уже довольно тяжёлая артиллерия, и явно выходит за пределы статьи с пометкой «обучающий материал».
Refridgerator