01.07.2019 13:36
Scorobey 9 4600 Источник

Введение


Одним из первых радиотелескоп построил американец Грот Рёбер в 1937 году. Радиотелескоп представлял собой жестяное зеркало диаметром 9.5 м, установленное на деревянной раме:



К 1944 году Рёбер составил первую карту распределения космических радиоволн в области Млечного пути.

Развитие радиоастрономии повлекло за собой ряд открытий: в 1946 г. было открыто радиоизлучение из созвездия Лебедь, в 1951 г. – внегалактическое излучение, в 1963 г. – квазары, в 1965 г. открыто реликтовое фоновое излучения на волне 7.5 см.

В 1963 был построен уникальный 300-метровый радиотелескоп в Аресибо (Пуэрто-Рико). Это неподвижная чаша, имеющая перемещающийся облучатель, построена в естественной расщелине местности.



Одиночные радиотелескопы имеют небольшое угловое разрешение, которое определяется формулой:
$\Theta=\frac{\lambda }{d}$
где $\lambda$ – длина волны, $d$ – диаметр радиотелескопа.

Очевидно, что для улучшения разрешения необходимо увеличивать диаметр антенны, что физически является трудно реализуемой задачей. Решить ее удалось с появлением радиоинтерферометров.



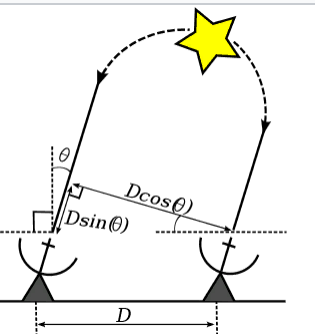
Фронт электромагнитной волны, излучённой далёкой звездой вблизи Земли, можно считать плоским. В случае самого простого интерферометра, состоящего из двух антенн, разность хода лучей, пришедших на эти две антенны, будет равна:
$\Delta =D\cdot sin(\Theta )$,
где:$\Delta $— разность хода лучей;$D $— расстояние между антеннами;$\Theta $— угол между направлением прихода лучей и нормалью к линии, на которой расположены антенны.

При $\Theta =0 $ волны, пришедшие на обе антенны, суммируются в фазе. В противофазе волны первый раз окажутся при:

$\Delta =\frac{\lambda }{2},\Theta =arcsin\frac{\lambda }{2D}$,
где: $\lambda$— длина волны.

Следующий максимум будет при $\Delta =\lambda, $ минимум при $\Delta =\frac{3\lambda}{2}$ и т. д. Получается многолепестковая диаграмма направленности (ДН), ширина главного лепестка которой при $\lambda<< D$ равна $\lambda/D $. Шириной главного лепестка определяется максимальное угловое разрешение радиоинтерферометра, оно приблизительно равно ширине лепестка.

Радиоинтерферометрия со сверхдлинными базами (РСДБ) — это вид интерферометрии, используемый в радиоастрономии, при котором приёмные элементы интерферометра (телескопы) располагаются не ближе, чем на континентальных расстояниях друг от друга.

Метод РСДБ позволяет объединять наблюдения, совершаемые несколькими телескопами, и тем самым имитировать телескоп, размеры которого равны максимальному расстоянию между исходными телескопами. Угловое разрешение РСДБ в десятки тысяч раз превышает разрешающую силу лучших оптических инструментов.

Современное состояние РСДБ — сетей


Сегодня космос слушают несколько РСДБ — сетей:

  • Европейская –EVN (European VLBI Network), состоящая более чем из 20-ти радиотелескопов;
  • Американская –VLBA (Very Long Baseline Array), включающая десять телескопов диаметром 25 метров каждый;
  • Японская — JVN (Japanese VLBI Network) состоит из десяти антенн, расположенных в Японии, включая четыре астрометрических антенны (проект VERA — VLBI Exploration of Radio Astrometry);
  • Австралийская – LBA (Long Baseline Array);
  • Китайская – CVN ( Chinese VLBI Network), состоящая из четырех антенн;
  • Южно Корейская – KVN (Korean VLBI Network), включающая в себя три 21- метровых радиотелескопа;
  • Российская — на основе постоянно действующего радиоинтерферометрического комплекса – «Квазар-КВО» с радиотелескопами диаметром зеркала 32 м, оснащенными высокочувствительными криорадиометрами в диапазоне волн от 1.35 см до 21 см. Длина баз – эффективный диаметр синтезированного «зеркала» – составляет около 4400 км в направлении восток-запад (см.рисунок).



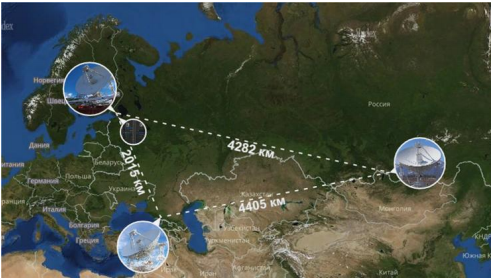
В РСДБ — комплексе «Квазар-КВО» в качестве источника опорной частоты для всех частотных преобразований применяются водородные стандарты, в которых используется переход между уровнями сверхтонкой структуры основного состояния атома водорода с частотой 1420.405 МГц, соответствующей в радиоастрономии линии 21 см.

Задачи, решаемые средствами РСДБ


  • Астрофизика. Выполняется построение радиоизображений естественных космических объектов (квазаров и других объектов) с разрешением десятые и сотые доли mas (миллисекунд дуги).
  • Астрометрические исследования. Построение координатновременных систем. Объектами исследований являются радиоисточники чрезвычайно малых угловых размеров, включая квазизвездные радиоисточники и ядра радиогалактик, которые из-за большой удаленности являются почти идеальными объектами для создания сети опорных неподвижных объектов.
  • Исследования по небесной механике и динамике солнечной системы, космической навигации. Установление радиомаяка на поверхностях планет и слежение за радиомаяками межпланетных автоматических станций позволяет использовать метод РСДБ для исследования таких параметров, как орбитальное движение планеты, направление осей вращения и их прецессию, динамику системы планета спутник. Для Луны решается также весьма важная задача определения физической либрации и определения динамики систем Луна — Земля.

Навигация в космосе средствами РСДБ


  • Контроль перемещений астронавтов по лунной поверхности в 1971 г. Передвигались они с помощью лунохода «Ровер». Точность определения его положения относительно лунного модуля достигала 20 см и зависела в основном от либрации луны (Либрация- периодические маятникообразные колебания Луны относительно ее центра масс);
  • Навигационное сопровождение доставки и сброса аэростатных зондов с пролетных аппаратов в атмосферу Венеры (проект ВЕГА). Расстояние до Венеры составляет более 100 млн. км, мощность передатчиков всего 1 Вт. Запуски аппаратов ВЕГА-1/2 состоялись в декабре 1984 г. Аэростаты были сброшены в атмосферу Венеры 11 и 15 июня 1985 г. Наблюдение велось в течение 46 часов.

Структурная схема упрощенной РСДБ — сети


На основе реальной РСДБ — сети, используя программные средства Python, промоделируем упрощенную систему РСДБ в виде отдельных моделей для каждого блока или процесса. Данной совокупности моделей будет достаточно для наблюдения основных процессов. Структурная схема упрощенной РСДБ — сети представлена на рисунке:



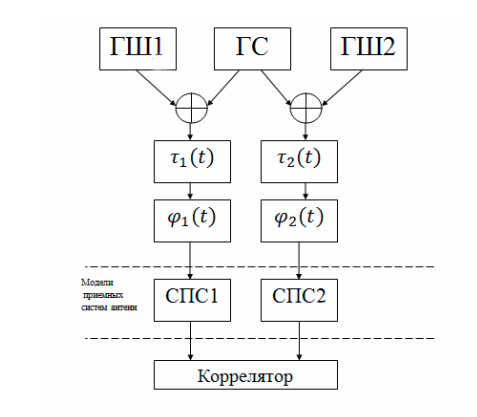
Система включает следующие компоненты:

  • генератор полезного фазомодулированного сигнала (ГС);
  • генераторы шума (ГШ1, ГШ2). В системе имеются два радиотелескопа (приемные антенны), которые имеют собственные шумы. Кроме того, существуют шумы атмосферы и других естественных и искусственных источников радиоизлучения;
  • блок задержки по времени, имитирующий линейно меняющуюся во времени задержку, обусловленную вращением Земли;
  • фазовращатель, моделирующий эффект Доплера;
  • система преобразования сигналов (СПС), состоящая из гетеродина, для переноса сигнала вниз по частоте, и полосового фильтра;
  • FX-коррелятор.

Схема коррелятора приведена на следующем рисунке:



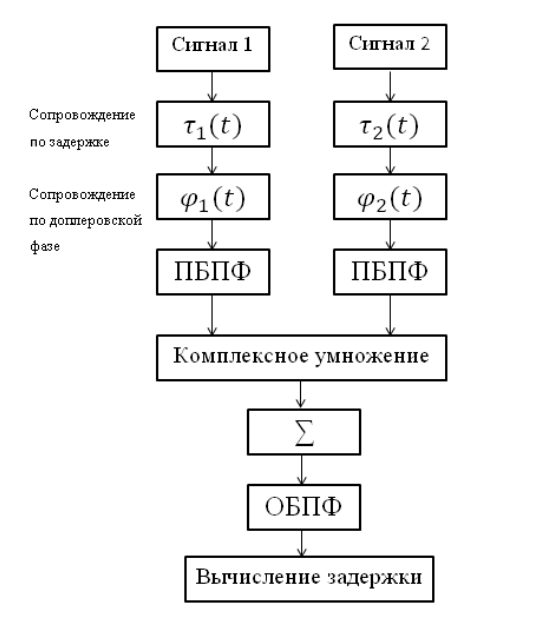
Приведенная схема коррелятора, который включает в себя следующие блоки:

  • прямого быстрого преобразования Фурье (ПБПФ) и обратного преобразования Фурье (ОБПФ);
  • компенсирующий ранее внесенную задержку;
  • компенсирующий эффект Доплера;
  • комплексного перемножения двух спектров;
  • суммирования накопленных реализаций.

Модель навигационных сигналов


Наиболее удобными для РСДБ- измерений являются навигационные сигналы космических аппаратов спутниковых навигационных систем, таких как GPS и ГЛОНАСС. К навигационным сигналам предъявляется ряд требований:

  • позволять хорошо определять псевдодальность;
  • передавать информацию о положении навигационной системы;
  • быть отличимым от сигналов других НС;
  • не создавать помех другим радиосистемам;
  • не требовать для приема и передачи сложной аппаратуры.

В достаточной мере им удовлетворяет сигнал с бинарной (двухпозиционной) фазовой модуляцией – BPSK (binary phase shift key), которая в русскоязычной литературе обозначается ФМ-2. Эта модуляция меняет фазу несущего колебания, на ?, что можно представить в виде:

$S(t)=A\cdot G(t)\cdot cos(2\pi ft),$

где G(t)– модулирующая функция.

Для реализации фазовой модуляции можно использовать два генератора, каждый из которых формирует одну и ту же частоту, но с различной начальной фазой. Модулирующая функция позволяет расширить спектр сигнала и точно измерить псевдодальность (расстояние между спутником и приемником, вычисленное по времени распространения сигнала без поправки за расхождение часов спутника и приемника).

Приведу листинг, поясняющий основные принципы BPSK:

Листинг
from scipy import*
from pylab import*
import numpy as np
import scaleogram as scg 
f = 2; #fчастота синусоиды
fs = 100; #период дискретизации синусоидальной волны
t = arange(0,1,1/fs) #разбить время на сегменты 1 / fs
#установка фазовых сдвигов для разных сигналов BPSK
p1 = 0;
p2 = pi;
#получить количество битов для модуляции
N =12#ведите количество битов для модуляции
#генерирование случайного сигнала
bit_stream=np.random.random_integers(0, 1, N+1)
#выделение динамических переменных
time =[];
digital_signal =[];
PSK =[];
carrier_signal =[];
#ПОЛУЧЕНИЕ СИГНАЛОВ
for ii in arange(1,N+1,1):
    #оригинальный цифровой сигнал
    if bit_stream [ii] == 0:
        bit = [0 for w in arange(1,len(t)+1,1)];
    else:
       bit = [1 for w in arange(1,len(t)+1,1)];
    digital_signal=hstack([digital_signal,bit ])
    #Генерация сигнала BPSK
    if bit_stream [ii] == 0:
        bit = sin (2*pi*f*t+p1);
    else:
        bit = sin (2*pi*f*t+p2);
    PSK=hstack([PSK,bit])
    #Генерация несущей волны
    carrier = sin (2*f*t*pi);
    carrier_signal = hstack([carrier_signal,carrier]) ;
    time = hstack([time ,t]);
    t=t+1
suptitle("Сигналы двоичной фазовой модуляции (BPSK)")   
subplot (3,1,1);
plot(time,digital_signal,'r');
grid();
subplot (3,1,2);
plot (time,PSK);
grid();
subplot (3,1,3);
plot (time,carrier_signal);
grid()
show()
figure()
title("Спектр сигнала двоичной фазовой модуляции (BPSK)")
n = len(PSK) 
k = np.arange(n)
T = n/fs
frq = k/T
frq = frq[np.arange(int(n/2))] 
Y = fft(PSK)/n 
Y = Y[range(n //2)] / max(Y[range(n // 2)])
plot(frq[75:150], abs(Y)[75:150], 'b')#Выбор окна Фурье преобразования
grid()
#Скалограмма вейвлет преобразования PSK  сигнала
scales = scg.periods2scales( arange(1, 40))
ax2 = scg.cws(PSK, scales=scales, figsize=(6.9,2.9));
show()


Получим:







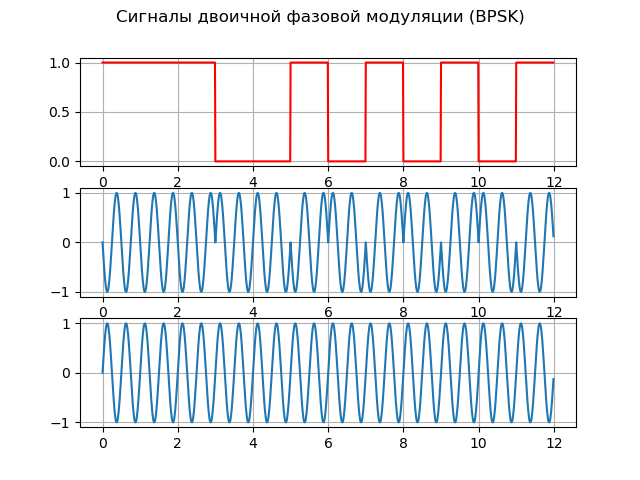
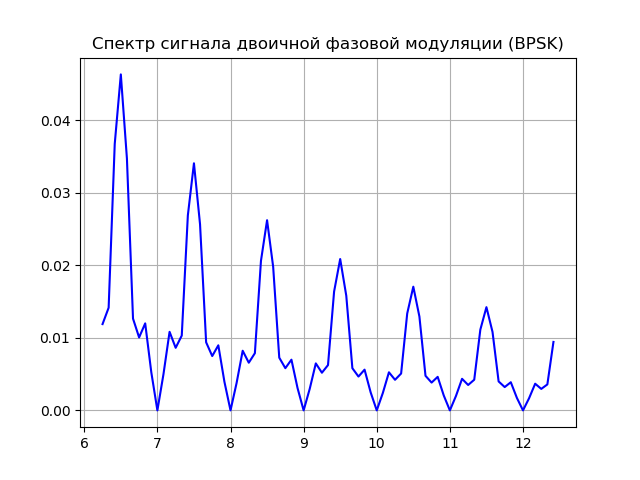
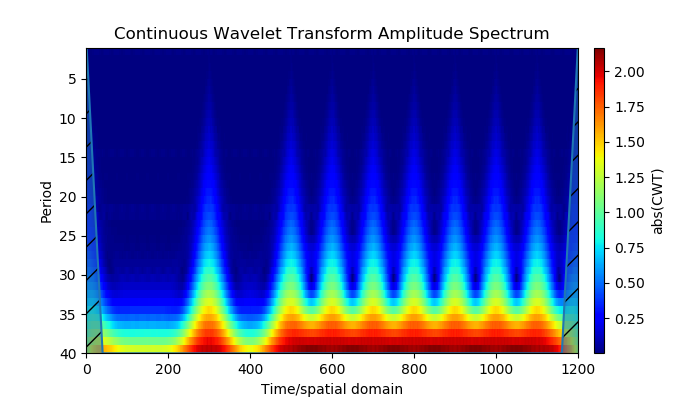
Модель источников сигналов


Навигационный фазомодулированный гармонический сигнал от спутника или космического аппарата имеет вид:

$x=a(2\pi f_{c}t+\sum s_{n} cos(2\pi f_{n}t)),$

где частота несущего колебания $f_{c}=8,4 $ ГГц.

У сигнала есть несколько управляемых параметров: амплитуда n-го модулирующего колебания
$s_{n}, $ его частота $f_{c}$ и амплитуда несущего колебания a.

Для получения корреляционной функции, в которой будут максимально подавлены её боковые лепестки и достигнут наиболее узкий корреляционный пик, мы будем варьировать значения частот, используя значения 2, 4, 8 и 16 МГц, и индекса модуляции в пределах от 0 до 2? с шагом ?. Приведу листинг программы для такого поиска параметров фазомодулированной функции для конечного результата:

Листинг
# coding: utf-8
from pylab import*
from scipy import signal
from scipy import *
T = 5e-7 #длительность одной реализации
N = 2**18 #кол-во отсчетов
delay =4 #задержка
t1 =linspace(0, T, N)
t2 = linspace(0 + delay, T + delay, N)
fs = (N - 1)/T #частота дискретизации
ax = 1e-3
bx = 2e-6
ay = 2e-3
by = 3e-6
aex = 1e-3 + 30e-9
bex = 2e-6 + 10e-12
aey = 2e-3 + 30e-9
bey = 3e-6 + 10e-12
taux = ax + bx*t1
tauy = ay + by*t2
tauex = aex + bex*t1
tauey = aey + bey*t2
#амплитуда шума
# print("амплитуда шума:")
No1 = No2 = 0
fc = 8.4e9 #частота сигнала
#амплитуды модулирующих колебаний
A1 = 2*pi
A2 = 0
A3 =2*pi
A4 = 4*pi
# модулирующие частоты
fm1 = 2e6
fm2 = 4e6
fm3 = 8e6
fm4 = 16e6
f = 20e6 # центральная частота на НЧ
ff = fc - f # частота гетеродина
fco = 16e6 #частота среза относительно центральной частоты
def korel(x,y):
    #эффект доплера
    def phase_shifter1(x, t, tau, b):
     L = linspace(0, N, N)
     fexp = ifftshift((L) - ceil((N - 1)/2))/T
     s = ((ifft(fft(x)*exp(-1j*2*pi*tau*fexp))).real)*exp(1j*2*pi*b*fc*t)
     return s
    #компенсация эффекта доплера
    def phase_shifter2(x, t, tau, b):
     L = linspace(0,N,N)
     fexp = ifftshift((L) - ceil((N - 1)/2))/T
     s =((ifft(fft(x)*exp(1j*2*pi*tau*fexp))).real)*exp(-1j*2*pi*b*fc*t)
     return s
    #гетеродинирование
    def heterodyning(x, t):
     return x*exp(-1j*2*pi*ff*t)
    #фильтрация
    def filt(S): 
     p = signal.convolve(S,h)
     y = p[int((n - 1)/2) : int(N+(n - 1)/2)]
     return y
    def corr(y1, y2):
     Y1 = fft(y1)
     Y2 = fft(y2)
     #свертка
     Z = Y1*Y2.conjugate()
     #ОПФ
     z = ifft(Z)/N
     return sqrt(z.real**2 + z.imag**2)
    #построение графика КФ
    def graf(c, t):
        c1=c[int(N/2):N]
        c2=c[0:int(N/2)]
        C = concatenate((c1, c2))
        xlabel('Время,с')
        ylabel('Амплитуда')
        title('Оптимальная корреляционная функция ')
        grid(True)
        plot(t*1e9 - 250, C, 'b',label=" Подавлены боковые лепестки \n и сужен главный лепесток")
        legend(loc='best')
        show()
    noise1 = random.uniform(-No1, No1, size = N) #шум первого сигнала
    noise2 =noise1 #шум второго сигнала   
    x1 = heterodyning(phase_shifter1(x + noise1, t1, taux, bx), t1)
    y1 = heterodyning(phase_shifter1(y + noise2, t2, tauy, by), t2)
    n = 100001 #порядок фильтра
    #ИХ фильтра
    h = signal.firwin(n, cutoff = [((f - fco) / (fs * 0.5)), ((f + fco) / (fs *0.5))], pass_zero = False)
    x2 = filt(x1)
    y2 = filt(y1)
    X2 = phase_shifter2(x2, t1, tauex, bex)
    Y2 = phase_shifter2(y2, t2, tauey, bey)
    Corr = corr(X2, Y2)
    graf(Corr, t1)
#Влияние одной компоненты модулирующего колебания
##for A1 in [pi/4,pi/2,pi]:   
##    x = cos(2*pi*fc*t1 + A1*cos(2*pi*fm1*t1))
##    y = cos(2*pi*fc*t2 + A1*cos(2*pi*fm1*t2))
##    korel(x,y)     
##for fm in [ fm2,fm3,fm4]:
##    A1=2*pi
##    x = cos(2*pi*fc*t1 + A1*cos(2*pi*fm*t1))
##    y = cos(2*pi*fc*t2 + A1*cos(2*pi*fm*t2))
##    korel(x,y)
#Влияние двух компонент модулирующего колебания
##for fm2 in [ fm1, fm2,fm3,fm4]:
##    A1=2*pi
##    A2=2*pi
##    fm1=2e6
##    x = cos(2*pi*fc*t1 + A1*cos(2*pi*fm1*t1)+A2*np.cos(2*pi*fm2*t1))
##    y =cos(2*pi*fc*t2 + A1*cos(2*pi*fm1*t2)+A2*np.cos(2*pi*fm2*t2))
##    korel(x,y)    
x = cos(2*pi*fc*t1 + A1*cos(2*pi*fm1*t1)+A2*np.cos(2*pi*fm2*t1)+A3*cos(2*pi*fm3*t1)+A4*cos(2*pi*fm4*t1))
y =  cos(2*pi*fc*t2 + A1*cos(2*pi*fm1*t2) +A2*cos(2*pi*fm2*t2) +A3*cos(2*pi*fm3*t2)+A4*cos(2*pi*fm4*t2))
korel(x,y)


Получим:



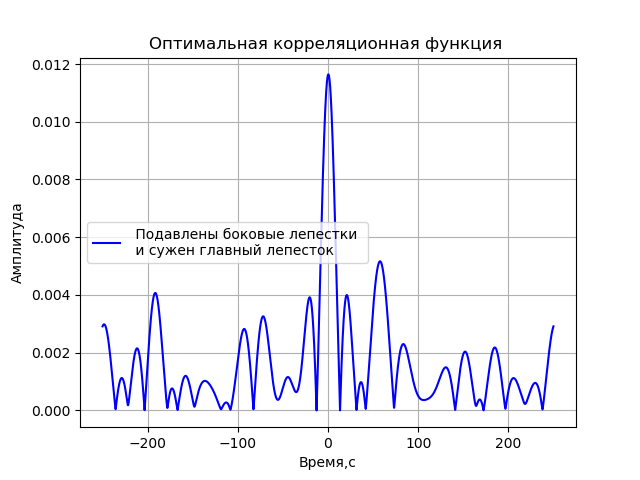
Полученная функция имеет вид:

$x=cos(2\pi f_{c}t+2\pi cos(2\pi 10^{6}t)+2\pi cos(2\pi 10^{8}t)+4\pi cos(2\pi 10^{16}t)). (1)$

Далее указанная функция будет использоваться для моделирования РСДБ.

Модель генератора шума, имитирующего помехи, принимаемые вместе с сигналом из космоса и из атмосферы Земли


Функция (1) фазомодулированного навигационного сигнала может быть применена к обоим каналам радиоинтерферометра, но при этом нужно учитывать задержку сигнала во втором канале и шум в обоих каналах как показано в следующем листинге:

Листинг
# coding: utf-8
from pylab import*
from scipy import signal
from scipy import *
T = 5e-7 #длительность одной реализации
N = 2**16 #кол-во отсчетов
delay =1e-7  #задержка
t1 =linspace(0, T, N)
t2 = linspace(0 + delay, T + delay, N)
fc = 8.4e9 #частота сигнала
# print("амплитуда шума:")
No1 = No2 = 0.5
noise1 = random.uniform(-No1, No1, size = N) #шум первого сигнала
noise2 =random.uniform(-No1, No1, size = N) #шум второго сигнала
x = cos(2*pi*fc*t1 + 2*pi*cos(2*pi*2*10**6*t1)+2*pi*cos(2*pi*8*10**6*t1)+4*pi*cos(2*pi*16*10**6*t1))
y = cos(2*pi*fc*t2 + 2*pi*cos(2*pi*2*10**6*t2)+2*pi*cos(2*pi*8*10**6*t2)+4*pi*cos(2*pi*16*10**6*t2))
title("Имитация равномерно распределённого шума \n в навигационных каналах РСДБ")
plot(t1,x,label=" Первый канал")
plot(t2,y,label="Второй канал c задержкой")
x=noise1;y=noise2 
plot(t1,x,label="Шум первого канала")
plot(t2,y,label="Шум второго канала")
legend(loc='best')
grid(True)
figure()
noise1_2 = np.random.uniform(-No1, No1, size = N) #шум первого и второго сигнала
sko=np.std(noise1_2)
mo= np.mean(noise1_2)
sko=round(sko,2)
mo=round(mo,2)
title("Гистограмма исследуемого шума. СКО:%s,МО:%s"%(sko,mo))
ylabel('Частота попадания в интервал')
xlabel('Интерваал возможных значений')
hist(noise1_2,bins='auto')
show()


Получим:



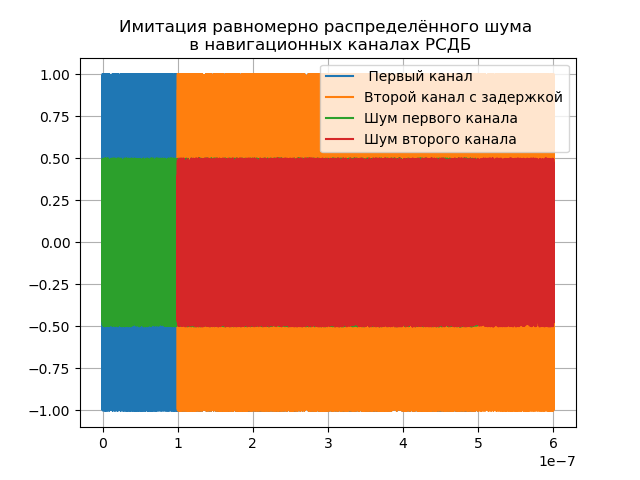
Задержка delay =1e-7 установлена для демонстрации, в реальности она зависит от базы и может достигать четырёх и более единиц.



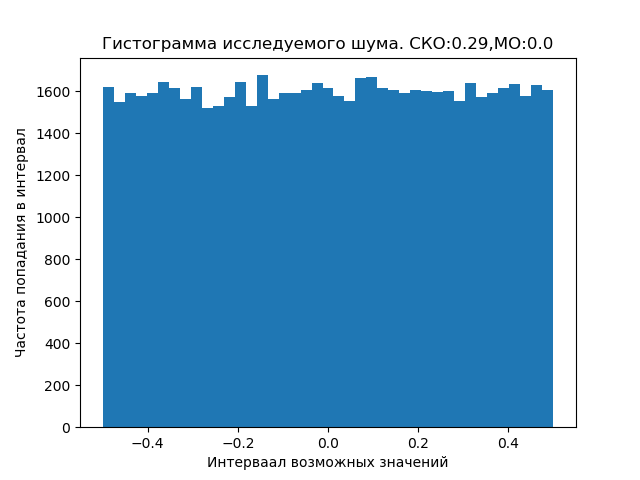
Шумы как космические, так и околоземные могут быть распределены по закону отличного от приведенного равномерного, что требует специальных исследований.

Моделирование эффекта Доплера


В связи с тем, что Земля имеет округлую форму и вращается вокруг своей оси, то сигналы из космоса поступают на антенны с разными задержками. По этой причине требуется сдвинуть сигналы по времени и учесть доплеровскую частоту. Приближено будем считать, что задержка меняется по линейному закону:

$\tau _{x}(t)=a_{x}+b_{x}t, (2)$

где $a_{x}=1..3\cdot 10^{-3}$ мс, а $b_{x}=1..3\cdot 10^{-6}$ мс. Доплеровская фаза находится, как производная от задержки:

$f_{dx}=\frac{d\tau(t)}{dt}=b_{x}, (3)$

Принимаемый сигнал должен иметь вид:

$\hat{x}=x(t-\tau _{x})e^{j2\pi f_{dx}t},$
где x( t) – излучаемый сигнал космического аппарата.

Демонстрация эффекта Доплера приведена в следующем листинге:

Листинг
# coding: utf-8
from pylab import*
from scipy import signal
from scipy import *
T = 5e-7#длительность одной реализации
N = 2**16 #кол-во отсчетов
t1 =linspace(0, T, N)
delay =4 #задержка
t2 = linspace(0 + delay, T + delay, N)
fc = 8.4e9#частота сигнала
def phase_shifter1(x, t, tau, b):
 L = linspace(0, N, N)
 fexp = ifftshift((L) - ceil((N - 1)/2))/T
 s = ((ifft(fft(x)*exp(-1j*2*pi*tau*fexp))).real)*exp(1j*2*pi*b*fc*t)
 return s.real
figure()
title("Эффект Доплера для первого канала")
ax = 3e-3
bx = 3e-6
taux = ax + bx*t1
x = cos(2*pi*fc*t1 + 2*pi*cos(2*pi*2*10**6*t1)+2*pi*cos(2*pi*8*10**6*t1)+4*pi*cos(2*pi*16*10**6*t1))
sx=phase_shifter1(x, t1, taux, bx )
plot(t1[0:150],x[0:150],label=" Сигнал первого канала без эффекта Доплера")
plot(t1[0:150],sx[0:150],label=" Сигнал первого канала с эффектом Доплера")
grid(True)
legend(loc='best')
figure()
title("Эффект Доплера для второго канала")
ay = 2e-3
by = 3e-6
tauy = ay + by*t2
y = cos(2*pi*fc*t2 + 2*pi*cos(2*pi*2*10**6*t2)+2*pi*cos(2*pi*8*10**6*t2)+4*pi*cos(2*pi*16*10**6*t2))
sy= phase_shifter1(y, t2, tauy, by)
plot(t2[0:150],y[0:150],label=" Сигнал  второго канала без эффекта Доплера")
plot(t2[0:150],sy[0:150],label=" Сигнал второго канала с эффектом Доплера")
grid(True)
legend(loc='best')
show()


Получим:





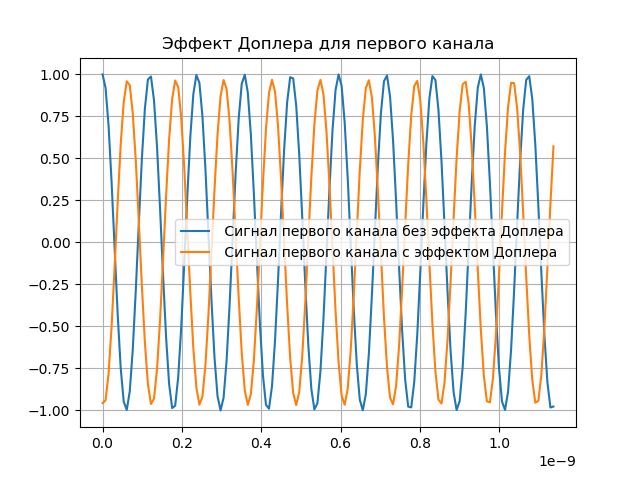
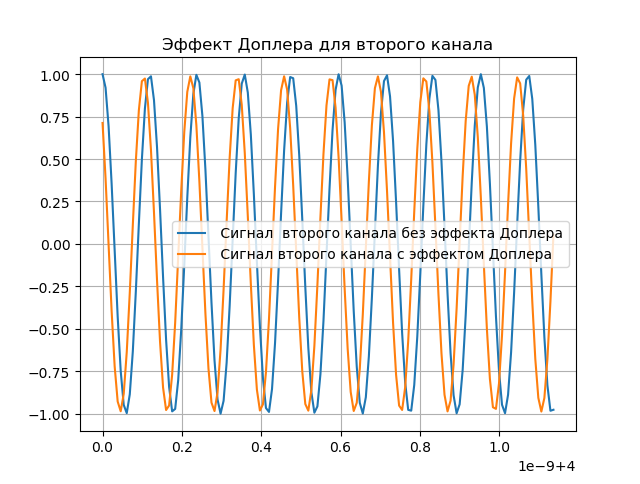
Моделирование компенсации эффекта Доплера


Очевидно, что внесенные в сигнал изменения должны быть компенсированы. Для этой цели в системе присутствует сопровождение по задержке и доплеровской фазе. После прохождения сигналом системы регистрации, вносится задержка:

$\tau _{ex}(t)=a_{x}+b_{ex}t, (4)$

Будет считать, что задержка рассчитывается с определенной точностью, такой что $\left | a_{ex}-a_{x} \right |< 30 $ нс $\left | b_{ex}-b_{x} \right |< 10 $ нс, т.е. она будет немного отличаться он внесенной ранее задержки. Понятно, что задержка вносится с противоположным знаком, чем внесенная ранее.

Полученный сигнал будет иметь вид:

$\hat{x}=\tilde{x}(t+\tau _{ex})e^{-j2\pi f_{de}t}. (5)$

Компенсация эффекта Доплера приведена в следующем листинге:

Листинг
# coding: utf-8
from pylab import*
from scipy import signal
from scipy import *
T = 5e-7#длительность одной реализации
N = 2**16 #кол-во отсчетов
t1 =linspace(0, T, N)
delay =4 #задержка
t2 = linspace(0 + delay, T + delay, N)
fc = 8.4e9#частота сигнала
def phase_shifter1(x, t, tau, b):
 L = linspace(0, N, N)
 fexp = ifftshift((L) - ceil((N - 1)/2))/T
 s = ((ifft(fft(x)*exp(-1j*2*pi*tau*fexp))).real)*exp(1j*2*pi*b*fc*t)
 return s.real
ax = 3e-3
bx = 3e-6
taux = ax + bx*t1
x = cos(2*pi*fc*t1 + 2*pi*cos(2*pi*2*10**6*t1)+2*pi*cos(2*pi*8*10**6*t1)+4*pi*cos(2*pi*16*10**6*t1))
sx=phase_shifter1(x, t1, taux, bx )
ay = 2e-3
by = 3e-6
tauy = ay + by*t2
y = cos(2*pi*fc*t2 + 2*pi*cos(2*pi*2*10**6*t2)+2*pi*cos(2*pi*8*10**6*t2)+4*pi*cos(2*pi*16*10**6*t2))
sy= phase_shifter1(y, t2, tauy, by)
def phase_shifter2(x, t, tau, b):
 L = linspace(0,N,N)
 fexp = ifftshift((L) - ceil((N - 1)/2))/T
 s =((ifft(fft(x)*exp(1j*2*pi*tau*fexp))).real)*exp(-1j*2*pi*b*fc*t)
 return s.real
figure()
title("Компенсация эффекта Доплера для первого канала")
aex = 1e-3 + 30e-9
bex = 2e-6 + 10e-12
tauex = aex + bex*t1
x1 = phase_shifter2(sx, t1, tauex, bex)
plot(t1[0:150],x1[0:150],label=" Сигнал первого канала без эффекта Доплера")
grid(True)
legend(loc='best')
figure()
title("Компенсация эффекта Доплера для  второго канала")
aey = 2e-3 + 30e-9
bey = 3e-6 + 10e-12
tauey = aey + bey*t2
y2 = phase_shifter2(sy, t2, tauey, bey)
plot(t2[0:150],y2[0:150],label=" Сигнал второго канала без эффекта Доплера")
grid(True)
legend(loc='best')
show()


Получим:





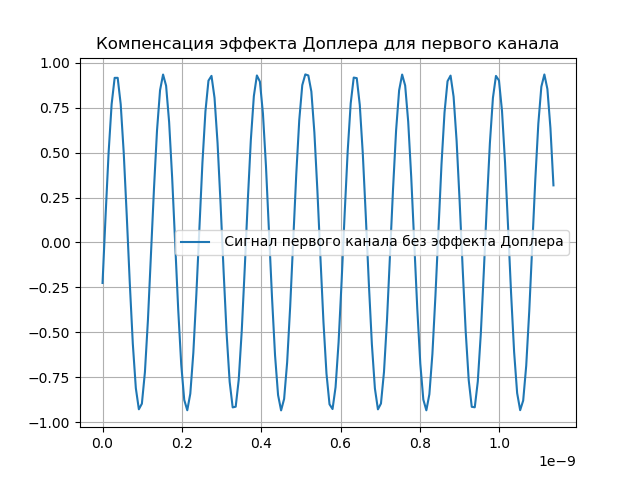
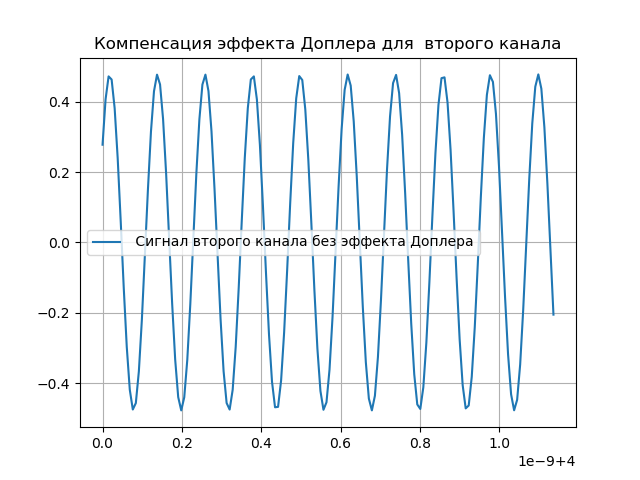
Моделирование гетеродинирования сигнала


После попадания сигнала в систему регистрации происходит преобразование частоты, которое так же называют гетеродинированием. Это нелинейное преобразование, при котором из сигналов двух различных частот $f_{1} $и $f_{2}$ выделяется сигнал разностной частоты — $f=\left | f_{1} -f_{2}\right .| $Частота сигнала гетеродина будет равна разности между частотой исследуемого сигнала и частотой, которую требуется получить после переноса. Осуществляется гетеродинирование с помощью вспомогательного генератора гармонических колебаний — гетеродина и нелинейного элемента. Математически гетеродинирование представляет собой умножение сигнала на экспоненту:

$x_{g}=\hat{x}e^{j2\pi f_{g}t},(6)$
где $f_{g}$ – сигнал гетеродина.

Программа для гетеродинирования:

Листинг
# coding: utf-8
from pylab import*
from scipy import signal
from scipy import *
T = 5e-7 #длительность одной реализации
N = 2**16 #кол-во отсчетов
t1 =linspace(0, T, N)
fs = (N - 1)/T #частота дискретизации
fc = 8.4e9 #частота сигнала
f = 20e6 # центральная частота на НЧ
ff = fc - f # частота гетеродина
def spectrum_wavelet(y,a,b,c,e,st):# построение спектра
    n = len(y)# длина сигнала
    k = arange(n)
    T = n / a
    frq = k / T  # двухсторонний частотный диапазон
    frq = frq[np.arange(int(n/2))]  # односторонний частотный диапазон
    Y = fft(y)/ n # FFT вычисления и нормализация
    Y = Y[arange(int(n/2))]/max(Y[arange(int(n/2))])
    plot(frq[b:c],abs(Y)[b:c],e,label=st) # построение спектра
    xlabel('Freq (Hz)')
    ylabel('|Y(freq)|')
    legend(loc='best')
    grid(True)  
x = cos(2*pi*fc*t1 + 2*pi*cos(2*pi*2*10**6*t1)+2*pi*cos(2*pi*8*10**6*t1)+4*pi*cos(2*pi*16*10**6*t1))
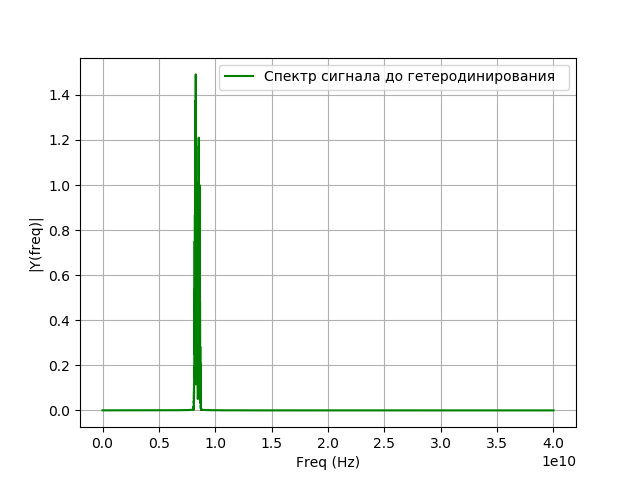
a=fs;b=0;c=20000;e='g'; st=' Спектр сигнала до гетеродинирования  '
spectrum_wavelet(x,a,b,c,e,st)
show()


Получим:





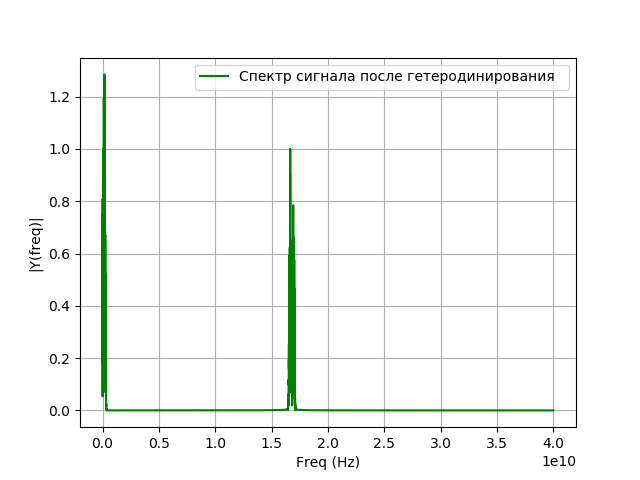
Моделирование фильтрации сигнала после гетеродинирования


После гетеродинирования сигнал поступает на полосовой фильтр. Полоса пропускания (ПП) фильтра $f_{pass}=32$ МГц. Импульсная характеристика (ИХ) фильтра рассчитывается оконным методом с помощью библиотечной функции signal.firwin. Для получения сигнала на выходе фильтра, производится свертка ИХ фильтра и сигнала во временной области. Интеграл свертки для нашего случая принимает вид:

$\check{x}(t)=\int_{-\infty }^{+\infty}x_{g}(t)h(t-{t}')dt,(7)$

где h(t) – импульсная характеристика фильтра.

Свертка находится с помощью библиотечной функции signal.convolve. Регистрируемый сигнал с учётом гетеродинирования и фильтрации представлен в виде формулы

$\check{x}(t)=(\hat{x}(t)e^{-j2\pi f_{g}t})*h$

где свертка обозначена знаком *.

Программа для моделирования фильтрации:

Листиннг
# coding: utf-8
from pylab import*
from scipy import signal
from scipy import *
T = 5e-7 #длительность одной реализации
N = 2**16 #кол-во отсчетов
t1 =linspace(0, T, N)
fs = (N - 1)/T #частота дискретизации
fc = 8.4e9 #частота сигнала
f = 20e6 # центральная частота на НЧ
ff = fc - f # частота гетеродина
def spectrum_wavelet(y,a,b,c,e,st):# построение спектра
    n = len(y)# длина сигнала
    k = arange(n)
    T = n / a
    frq = k / T  # двухсторонний частотный диапазон
    frq = frq[np.arange(int(n/2))]  # односторонний частотный диапазон
    Y = fft(y)/ n # FFT вычисления и нормализация
    Y = Y[arange(int(n/2))]/max(Y[arange(int(n/2))])
    plot(frq[b:c],abs(Y)[b:c],e,label=st) # построение спектра
    xlabel('Freq (Hz)')
    ylabel('|Y(freq)|')
    legend(loc='best')
    grid(True)  
x = cos(2*pi*fc*t1 + 2*pi*cos(2*pi*2*10**6*t1)+2*pi*cos(2*pi*8*10**6*t1)+4*pi*cos(2*pi*16*10**6*t1))
def heterodyning(x, t):
     return x*exp(-1j*2*pi*ff*t).real
z=heterodyning(x, t1)
fco = 16e6 #частота среза относительно центральной частоты
n = 100001 #порядок фильтра
h = signal.firwin(n, cutoff = [((f - fco) / (fs * 0.5)), ((f + fco) / (fs *0.5))], pass_zero = False)
def filt(S):    
 p = signal.convolve(S,h)
 y = p[int((n - 1)/2) : int(N+(n - 1)/2)]
 return y
q=filt(z)
a=fs;b=0;c=850;e='g'; st='Спектр сигнала после фильтра '
spectrum_wavelet(q,a,b,c,e,st)
show()


Получим:



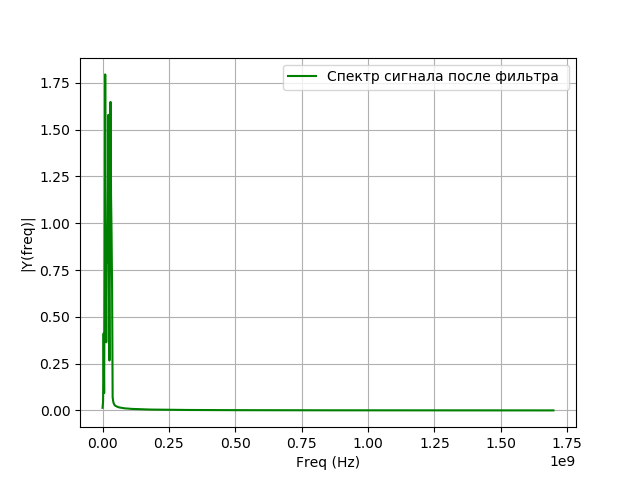
В цифровых преобразователях сигнала для РСДБ в основном используются фильтры с конечной импульсной характеристикой (КИХ), так как они имеют ряд преимуществ по сравнению с фильтрами с бесконечной импульсной характеристикой (БИХ):

  1. КИХ- фильтры могут иметь строго линейную фазовую характеристику в случае симметричности импульсной характеристики (ИХ). Это значит, что используя такой фильтр, можно избежать фазовых искажений, что особенно важно для радиоинтерферометрии. Фильтры с бесконечной импульсной характеристикой (БИХ) не обладают свойствами симметрии ИХ и не могут иметь линейную ФЧХ.
  2. КИХ- фильтры нерекурсивны, а значит — всегда устойчивы. Устойчивость же БИХ -фильтров не всегда можно гарантировать.
  3. Практические последствия того, что для реализации фильтров используется ограниченное число битов, значительно менее существенны для КИХ-фильтров.

В приведенном листинге реализована модель полосового КИХ- фильтра с помощью оконного метода, был подобран порядок фильтра такой, чтобы форма АЧХ фильтра была близка к прямоугольной. Количество коэффициентов смоделированного фильтра n=100001, то есть порядок фильтра P=100000.

Программа для построения АЧХ и ФЧХ полученного КИХ- фильтра:

Листинг
# coding: utf-8
from pylab import*
from scipy import signal
from scipy import *
T = 5e-7 #длительность одной реализации
N = 2**16 #кол-во отсчетов
t1 =linspace(0, T, N)
fs = (N - 1)/T #частота дискретизации
fc = 8.4e9 #частота сигнала
f = 20e6 # центральная частота на НЧ
ff = fc - f # частота гетеродина
fco = 16e6 #частота среза относительно центральной частоты
n = 100001 #порядок фильтра
h = signal.firwin(n, cutoff = [((f - fco) / (fs * 0.5)), ((f + fco) / (fs *0.5))], pass_zero = False)
#график ФЧХ
def AFC(A, n, f, deltf, min, max):
    plot((fftfreq (n, 1./fs)/1e9),
    10*log10(abs(fft(A))), 'k')
    axvline((f - fco)/1e9, color = 'red', label='Границы полосы пропускания')
    axvline((f + fco)/1e9, color = 'red')
    axhline(-3, color='green', linestyle='dashdot')
    text(8.381, -3, repr(round(-3, 9)))
    xlabel('Частота, ГГц')
    ylabel('Коэффициент передачи, дБ')
    title('АЧХ')
    grid(True)
    axis([(f - deltf)/1e9, (f + deltf)/1e9, min, max])
    grid(True)
    show()
#график ФЧХ
def PFC(A, n, f, deltf, min, max):
    plot(fftfreq(n, 1./fs)/1e9,
    np.unwrap(np.angle(fft(A))), 'k')
    axvline((f - fco)/1e9, color='red', label='Границы полосы пропускания')
    axvline((f + fco)/1e9, color='red')
    xlabel('Частота, ГГц')
    ylabel('Фаза,град')
    title('ФЧХ')
    axis([(f - deltf)/1e9, (f + deltf)/1e9, min, max]) #границы графика
    grid(True)
    legend(loc='best')
    show()
AFC(h, n, f, 20e6, -30, 1)
PFC(h, n, f, 20e6, -112, 0)


Получим:





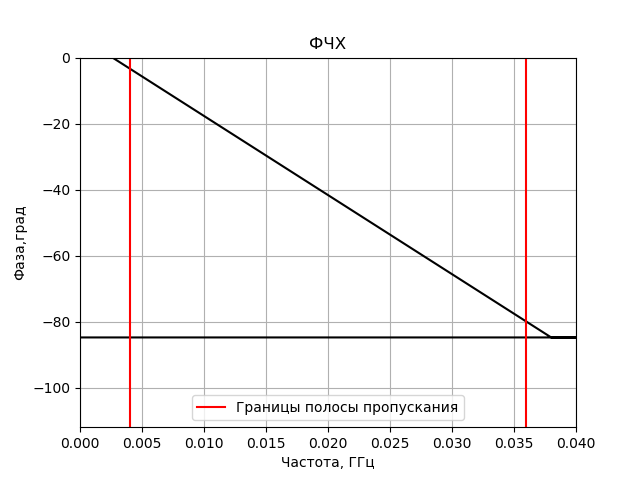
Модель FX-коррелятора


Далее каждый сигнал подвергается быстрому Фурье преобразованию(БПФ). БПФ реализуется с помощью библиотечной функции fft из scipy.fftpack. Полученные спектры комплексно- сопряжено умножаются:

$S(j\omega)=S_{1}(j\omega)*S_{2}(j\omega)=(a_{1}+jb_{1})*(a_{2}-jb_{2}) =a_{1}a_{2}+b_{1}b_{2}+j(b_{1}a_{2}-a_{1}b_{2})$

Последнее действие – обратное БПФ. Так как интерес представляет амплитуда корреляционной функции, то полученный сигнал необходимо преобразовать по формуле:

$A=\sqrt{re^{2}+im^{2}}$

Программа для корреляционной функции без учета искажений системы регистрации:

Листинг
# coding: utf-8
from pylab import*
from scipy import signal
from scipy import *
T = 5e-7#длительность одной реализации
N = 2**16 #кол-во отсчетов
t1 =linspace(0, T, N)
delay =4 #задержка
t2 = linspace(0 + delay, T + delay, N)
fc = 8.4e9#частота сигнала
def corr(y1, y2):
    Y1 = fft(y1)
    Y2 = fft(y2)
    #свертка
    Z = Y1*Y2.conjugate()
     #ОПФ
    z = ifft(Z)/N
    q=sqrt(z.real**2 + z.imag**2)
    c1=q[int(N/2):N]
    c2=q[0:int(N/2)]
    C = concatenate((c1, c2))
    xlabel('Время,с')
    ylabel('Амплитуда')
    title('Корреляционная функция ')
    grid(True)
    plot(t1*1e9 - 250, C, 'b')
    show()
x= cos(2*pi*fc*t1 + 2*pi*cos(2*pi*2*10**6*t1)+2*pi*cos(2*pi*8*10**6*t1)+4*pi*cos(2*pi*16*10**6*t1))
y = cos(2*pi*fc*t2 + 2*pi*cos(2*pi*2*10**6*t2)+2*pi*cos(2*pi*8*10**6*t2)+4*pi*cos(2*pi*16*10**6*t2))
corr(x, y)


Получим:



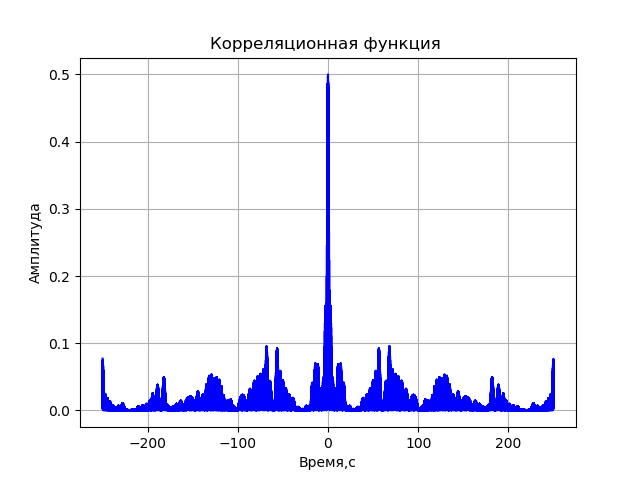
Полный листинг компьютерной модели РСДБ:


Листинг
# coding: utf-8
from pylab import*
from scipy import signal
from scipy import *
T = 5e-7 #длительность одной реализации
N = 2**18 #кол-во отсчетов
delay =4 #задержка
t1 =linspace(0, T, N)
t2 = linspace(0 + delay, T + delay, N)
fs = (N - 1)/T #частота дискретизации
ax = 1e-3
bx = 2e-6
ay = 2e-3
by = 3e-6
aex = 1e-3 + 30e-9
bex = 2e-6 + 10e-12
aey = 2e-3 + 30e-9
bey = 3e-6 + 10e-12
taux = ax + bx*t1
tauy = ay + by*t2
tauex = aex + bex*t1
tauey = aey + bey*t2
#амплитуда шума
# print("амплитуда шума:")
No1 = No2 = 0
# амплитуда несущего колебания
# print("амплитуда сигнала:")
fc = 8.4e9 #частота сигнала
f = 20e6 # центральная частота на НЧ
ff = fc - f # частота гетеродина
fco = 16e6 #частота среза относительно центральной частоты
#эффект Доплера
def phase_shifter1(x, t, tau, b):
 L = linspace(0, N, N)
 fexp = ifftshift((L) - ceil((N - 1)/2))/T
 s = ((ifft(fft(x)*exp(-1j*2*pi*tau*fexp))).real)*exp(1j*2*pi*b*fc*t)
 return s
#компенсация эффекта Доплера
def phase_shifter2(x, t, tau, b):
 L = linspace(0,N,N)
 fexp = ifftshift((L) - ceil((N - 1)/2))/T
 s =((ifft(fft(x)*exp(1j*2*pi*tau*fexp))).real)*exp(-1j*2*pi*b*fc*t)
 return s
#гетеродинирование
def heterodyning(x, t):
 return x*exp(-1j*2*pi*ff*t)
#фильтрация
def filt(S): 
 p = signal.convolve(S,h)
 y = p[int((n - 1)/2) : int(N+(n - 1)/2)]
 return y
def spectrum_wavelet(y,a,b,c,e,st):# построение спектра
    n = len(y)# длина сигнала
    k = arange(n)
    T = n / a
    frq = k / T  # двухсторонний частотный диапазон
    frq = frq[np.arange(int(n/2))]  # односторонний частотный диапазон
    Y = fft(y)/ n # FFT вычисления и нормализация
    Y = Y[arange(int(n/2))]/max(Y[arange(int(n/2))])
    plot(frq[b:c],abs(Y)[b:c],e,label=st) # построение спектра
    xlabel('Freq (Hz)')
    ylabel('|Y(freq)|')
    legend(loc='best')
    grid(True)    
def corr(y1, y2):
 Y1 = fft(y1)
 Y2 = fft(y2)
 #свертка
 Z = Y1*Y2.conjugate()
 #ОПФ
 z = ifft(Z)/N
 return sqrt(z.real**2 + z.imag**2)
#построение графика КФ
def graf(c, t):
    c1=c[int(N/2):N]
    c2=c[0:int(N/2)]
    C = concatenate((c1, c2))
    xlabel('Время, с')
    ylabel('Амплитуда')
    title('Корреляционная функция ')
    grid(True)
    plot(t*1e9 - 250, C, 'b')
    show()
noise1 = random.uniform(-No1, No1, size = N) #шум первого сигнала
noise2 =random.uniform(-No1, No1, size = N) #шум второго сигнала
def signal_0():
    x = cos(2*pi*fc*t1 + 2*pi*cos(2*pi*2*10**6*t1)+2*pi*cos(2*pi*8*10**6*t1)+4*pi*cos(2*pi*16*10**6*t1))
    y = cos(2*pi*fc*t2 + 2*pi*cos(2*pi*2*10**6*t2)+2*pi*cos(2*pi*8*10**6*t2)+4*pi*cos(2*pi*16*10**6*t2))
    return x,y
title("Сигналы + шум +эффект Доплера до фильтра")
x,y= signal_0()
x1 = heterodyning(phase_shifter1(x + noise1, t1, taux, bx), t1)
plot(x1.real,label=" Первый канал")
y1 = heterodyning(phase_shifter1(y + noise2, t2, tauy, by), t2)
plot(y1.real,label="Второй канал")
grid(True)
legend(loc='best')
show()
n = 100001 #порядок фильтра
#ИХ фильтра
h = signal.firwin(n, cutoff = [((f - fco) / (fs * 0.5)), ((f + fco) / (fs *0.5))], pass_zero = False)
title("Сигналы- шум- эффект Доплера после фильтра") 
x2 = filt(x1)
plot(x2.real,label=" Первый канал")
y2 = filt(y1)
plot(y2.real,label="  Второй канал")
grid(True)
legend(loc='best')
show()
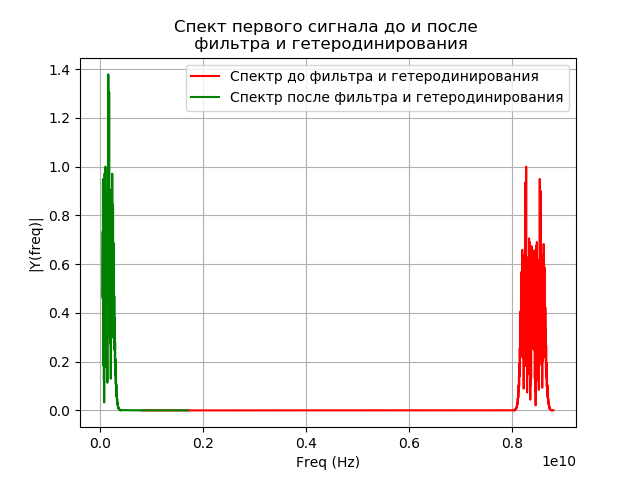
plt.title("Спектр первого сигнала до и после \n фильтра и гетеродинирования") 
a=fs;b=400;c=4400;e='r'
st="Спектр до фильтра и гетеродинирования"
spectrum_wavelet(x,a,b,c,e,st)
a=fs;b=20;c=850;e='g'
st="Спектр после фильтра и гетеродинирования"
spectrum_wavelet(x1,a,b,c,e,st)
show()
X2 = phase_shifter2(x2, t1, tauex, bex)
Y2 = phase_shifter2(y2, t2, tauey, bey)
Corr = corr(X2, Y2)
graf(Corr, t1)


Получим:





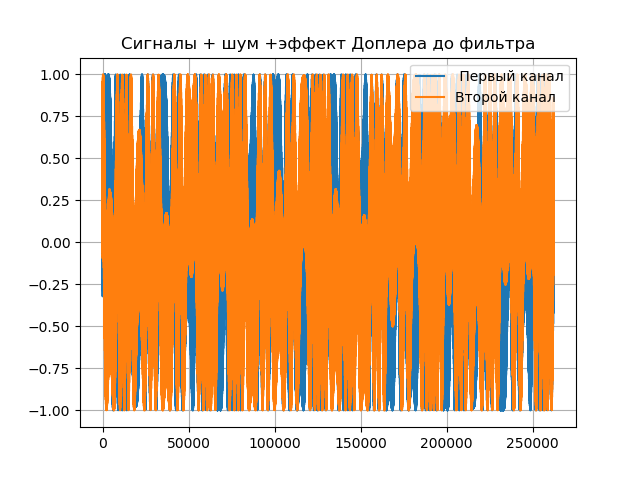
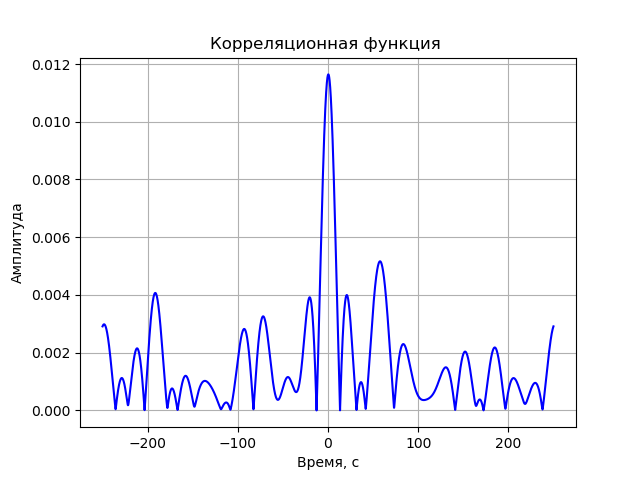
Выводы


  1. Приведена краткая история развития радиоастрономии.
  2. Проанализировано современное состояние РСДБ – сетей.
  3. Рассмотрены задачи, решаемые средствами РСДБ– сетей.
  4. Средствами Python построена модель навигационных сигналов с бинарной (двухпозиционной) фазовой модуляцией – BPSK (binary phase shift key). В модели использован вейвлет анализ фазовой модуляции.
  5. Получена модель источников сигналов, позволяющая определить параметры модуляции, обеспечивающие оптимальную корреляционную функцию по критерию подавления боковых лепестков и максимальной амплитуды центрального лепестка.
  6. Получена модель упрощенной РСДБ – сети, учитывающая шумы и эффект Доплера. Рассмотрены особенности фильтрации с использованием фильтра с конечной импульсной характеристикой.
  7. После краткого изложения теории все модели снабжены демонстрационными программами, позволяющими отслеживать влияние параметров модели.

Комментарии (9)


  1. JC_IIB
    01.07.2019 16:46
    #20345736

    В 1963 был построен уникальный 300-метровый радиотелескоп в Аресибо (Пуэрто-Рико).

    А как же РАТАН-600? Что-то про него в статье вообще ни слова :(


    1. Scorobey Автор
      01.07.2019 16:57
      #20345794
      +1

      Спасибо!.. Цель статьи моделирование радиоинтерферометра со сверхдлинной базой, а не одиночных радиотелескопов.


      1. Javian
        04.07.2019 17:46
        #20357798

        Но упоминается история одиночных радиотелескопов, а не радиоинтерферометров и РДСБ.
        image
        На фото перемещаемый радиоинтерферометр в Owens Valley Radio Observatory в Калифорнии, которым в 1964 году были определены следующие физические характеристики Венеры:

        • температура поверхности планеты T=700 ±50 градусов Кельвина, т.е. выше 400 градусов Цельсия,
        • радиус тела планеты R = 6057 ± 55 км,
        • давление атмосферы у поверхности P 80 ± 50 атм.

        Данные близки к тому, что было обнаружено спускаемыми аппаратами через несколько лет.
        www.prao.ru/History/history_3.html


    1. technarium
      02.07.2019 10:34
      #20347948

      Так и про самый новый и большой китайский 500-метровый с полностью заполненной апертурой — нет. Не о том речь)


  1. vanxant
    01.07.2019 20:56
    #20346624

    Просто замечу, что дифракционный предел lambda / D, точнее даже там еще косинус (проекция D на плоскость фронта волны, картинка есть в статье) — это именно теоретический предел, который еще надо достичь.


  1. Scorobey Автор
    01.07.2019 22:36
    #20346854

    Условие lambda <<D(cos(Teta) близок к 1), очевидно. При большем количестве периодически расположенных антенн ширина главного максимума будет определяться отношением lambda/D а расстояние до боковых максимумов 2*lambda/S, где S расстояние между соседними антеннами. C увеличением количества антенн боковые максимумы будут отдаляться от главного.Как правило, антенны интерферометра делают направленными, понижая уровень боковых лепестков диаграммы направленности интерферометра за счёт ДН отдельных антенн. Потери в высокочастотном кабеле и связанное с ним ослабление сигналов ограничивают базы(расстояние между антеннами, апертура) радиоинтерферометра. Поэтому принятые сигналы сначала усиливаются, преобразовываются в низких частоты и лишь после этого передаются по кабелю. При этом, чтобы не потерять когерентности сигналов и контролировать электрическую длину путей их распространения, передаются вспомогательные сигналы.


  1. ViacheslavMezentsev
    02.07.2019 15:37
    #20349588

    Честно говоря, так и не понял про что это. Реальные сигналы от отдельных телескопов заменены модельными навигационными сигналами со спутников? Где именно происходит мат. обработка? Ведь сигналы от отдельных телескопов значительно удалены. Их оцифровывают перед обработкой? Тогда на каком этапе? Могу предположить, что после гетеродинирования на одну из доступных для дискретизации частот.
    Т.е. должны быть сырые оцифрованные данные, которые поступают в некий центр обработки? Где их уже «коррелируют» с использованием метода БПФ. А для чего нужна корреляционная функция? Чтобы сдвиг по времени между двумя сигналами посчитать? А для чего? Чтобы улучшить отношение сигнал/шум?
    По-моему, в статье не хватает некоторого охвата сверху. Т.е. как именно получаемая «картинка» от телескопа связана с описанным алгоритмом.


    1. Scorobey Автор
      02.07.2019 17:30
      #20350186
      +1

      Радиоинтерферометрия со сверхдлинными базами (РСДБ, англ. Very Long Baseline Interferometry, VLBI) — вид интерферометрии, используемый в радиоастрономии, при котором приёмные элементы интерферометра (телескопы) располагаются не ближе, чем на континентальных расстояниях друг от друга. При этом управление элементами РСДБ интерферометра производится независимо, без непосредственной коммутационной линии связи, в отличие от обычного радиоинтерферометра. Запись данных осуществляется на носители информации с последующей корреляционной обработкой на специализированном вычислительном оборудовании[1] — корреляторе. В статье подробно описана работа FX-коррелятора


      1. ViacheslavMezentsev
        02.07.2019 17:38
        #20350236

        Пришлось диссертацию прочитать, чтобы понять о чём речь: Исследование структуры локальной межзвездной плазмы наземно-космическим интерферометром “РАДИОАСТРОН”