О методах численной оптимизации написано много. Это и понятно, особенно на фоне тех успехов, которые в последнее время демонстрируют глубокие нейронные сети. И очень отрадно, что хотя бы часть энтузиастов интересуется не только тем, как забомбить свою нейросеточку на набравшей в этих ваших интернетах популярность фреймворках, но и тем, как и почему все это вообще работает. Однако мне в последнее время пришлось отметить, что при изложении вопросов, связанных с обучением нейросетей (и не только с обучением, и не только сетей), в том числе на Хабре, все чаще впроброс используется ряд “хорошо известных” утверждений, справедливость которых, мягко говоря, сомнительна. Среди таких сомнительных утверждений:
и т.д. Чем продолжать этот список, лучше перейдем к делу. В этом посте рассмотрим второе утверждение, поскольку его я только на Хабре встречал как минимум дважды. Первый вопрос затрону только в той части, что касается метода Ньютона, поскольку он куда более обширен. Третий и остальные оставим до лучших времен.
Центром нашего внимания будет задача безусловной оптимизации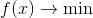 , где
, где 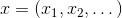 — точка векторного пространства, или просто — вектор. Естественно, что эту задачу решить тем проще, чем больше мы знаем об
— точка векторного пространства, или просто — вектор. Естественно, что эту задачу решить тем проще, чем больше мы знаем об  . Обычно она предполагается дифференцируемой по каждому аргументу
. Обычно она предполагается дифференцируемой по каждому аргументу 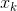 , причем столько раз, сколько требуется для наших грязных дел. Хорошо известно, что необходимым условием того, что в точке
, причем столько раз, сколько требуется для наших грязных дел. Хорошо известно, что необходимым условием того, что в точке 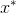 достигается минимум, является равенство градиента функции
достигается минимум, является равенство градиента функции 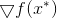 в этой точке нулю. Отсюда моментально получаем следующий метод минимизации:
в этой точке нулю. Отсюда моментально получаем следующий метод минимизации:
Решить уравнение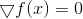 .
.
Задача, мягко говоря, непростая. Точно не проще, чем исходная. Однако на этом моменте сразу можно отметить связь между задачей минимизации и задачей решения системы нелинейных уравнений. Эта связь нам еще аукнется при рассмотрении метода Левенберга-Марквардта (когда до него доберемся). А пока вспомним (или узнаем), что одним из наиболее часто применяемых методов для решения систем нелинейных уравнения является метод Ньютона. Заключается он в том, что для решения уравнения мы, начиная с некоторого начального приближения
мы, начиная с некоторого начального приближения  , строим последовательность
, строим последовательность
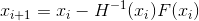 – явный метод Ньютона
– явный метод Ньютона
или
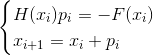 – неявный метод Ньютона
– неявный метод Ньютона
где – матрица, составленная из частных производных функции
– матрица, составленная из частных производных функции  . Естественно, что в общем случае, когда система нелинейных уравнений просто дана нам в ощущениях, требовать что-либо от матрицы
. Естественно, что в общем случае, когда система нелинейных уравнений просто дана нам в ощущениях, требовать что-либо от матрицы  мы не вправе. В случае, когда уравнение представляет собой условие минимума для какой-то функции, то мы можем утверждать, что матрица
мы не вправе. В случае, когда уравнение представляет собой условие минимума для какой-то функции, то мы можем утверждать, что матрица  симметрична. Но не более.
симметрична. Но не более.
Метод Ньютона для решения систем нелинейных уравнений весьма неплохо изучен. И вот ведь штука — для его сходимости не требуется положительная определенность матрицы . Да и не может требоваться — иначе ему была бы грош цена. Вместо этого существуют другие условия, которые обеспечивают локальную сходимость данного метода и которые мы здесь рассматривать не будем, отправляя заинтересованных к специализированной литературе (или в комментарии). Получаем, что утверждение 2 неверно.
. Да и не может требоваться — иначе ему была бы грош цена. Вместо этого существуют другие условия, которые обеспечивают локальную сходимость данного метода и которые мы здесь рассматривать не будем, отправляя заинтересованных к специализированной литературе (или в комментарии). Получаем, что утверждение 2 неверно.
Так?
И да, и нет. Засада здесь в слове локальная перед словом сходимость. Оно означает, что начальное приближение должно быть “достаточно близким” к решению, в противном случае на каждом шаге мы будем все дальше и дальше удаляться от оного. Что же делать? Я не буду вдаваться в детали того, как эту проблему решают для систем нелинейных уравнений общего вида. Вместо этого вернемся к нашей задаче оптимизации. Первая ошибка утверждения 2 на самом деле в том, что обычно говоря о методе Ньютона в задачах оптимизации имеют ввиду его модификацию — демпфированный метод Ньютона, в котором последовательность приближений строится по правилу
должно быть “достаточно близким” к решению, в противном случае на каждом шаге мы будем все дальше и дальше удаляться от оного. Что же делать? Я не буду вдаваться в детали того, как эту проблему решают для систем нелинейных уравнений общего вида. Вместо этого вернемся к нашей задаче оптимизации. Первая ошибка утверждения 2 на самом деле в том, что обычно говоря о методе Ньютона в задачах оптимизации имеют ввиду его модификацию — демпфированный метод Ньютона, в котором последовательность приближений строится по правилу
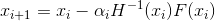 – явный демпфированный метод Ньютона
– явный демпфированный метод Ньютона
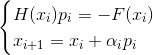 – неявный демпфированный метод Ньютона
– неявный демпфированный метод Ньютона
Здесь последовательность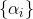 является параметром метода и ее построение представляет собой отдельную задачу. В задачах минимизации естественным при выборе
является параметром метода и ее построение представляет собой отдельную задачу. В задачах минимизации естественным при выборе 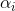 будет требование, чтобы на каждой итерации значение функции f уменьшалось, т.е.
будет требование, чтобы на каждой итерации значение функции f уменьшалось, т.е. 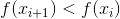 . Возникает закономерный вопрос: а существует ли вообще такое (положительное)
. Возникает закономерный вопрос: а существует ли вообще такое (положительное) 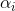 ? И если ответ на этот вопрос положителен, то
? И если ответ на этот вопрос положителен, то  называют направлением спуска. Тогда вопрос можно поставить таким образом:
называют направлением спуска. Тогда вопрос можно поставить таким образом:
когда направление, генерируемое методом Ньютона, является направлением спуска?
И для ответа на него придется посмотреть на задачу минимизации с другого бока.
Для задачи минимизации вполне естественным кажется такой подход: начиная с некоторой произвольной точки, выберем некоторым образом направление p и сделаем в этом направлении шаг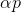 . Если
. Если 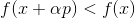 , то возьмем
, то возьмем 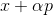 в качестве новой начальной точки и повторим процедуру. Если направление выбирается произвольно, то такой метод иногда называют методом случайного блуждания. Можно в качестве направления брать вектора единичного базиса — то есть делать шаг только по одной координате, такой метод называют методом покоординатного спуска. Стоит ли говорить, что они неэффективны? Для того, чтобы такой подход хорошо работал, нам нужны некоторые дополнительные гарантии. Для этого введем вспомогательную функцию
в качестве новой начальной точки и повторим процедуру. Если направление выбирается произвольно, то такой метод иногда называют методом случайного блуждания. Можно в качестве направления брать вектора единичного базиса — то есть делать шаг только по одной координате, такой метод называют методом покоординатного спуска. Стоит ли говорить, что они неэффективны? Для того, чтобы такой подход хорошо работал, нам нужны некоторые дополнительные гарантии. Для этого введем вспомогательную функцию 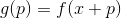 . Думаю, вполне очевидно, что минимизация
. Думаю, вполне очевидно, что минимизация  полностью эквивалентна минимизации
полностью эквивалентна минимизации  . Если
. Если  дифференцируема, то
дифференцируема, то  представима в виде
представима в виде
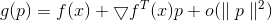
и если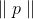 достаточно мало, то
достаточно мало, то 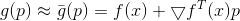 . Можем теперь попробовать подменить задачу минимизации
. Можем теперь попробовать подменить задачу минимизации 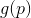 задачей минимизации ее приближения (или модели)
задачей минимизации ее приближения (или модели) 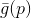 . Кстати, все методы, основанные на использовании модели
. Кстати, все методы, основанные на использовании модели 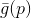 называются градиентными. Но вот ведь беда,
называются градиентными. Но вот ведь беда, 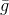 – линейная функция и, следовательно, минимума у нее нет. Для разрешения этой проблемы добавим ограничение на длину шага, который мы хотим сделать. В данном случае это вполне естественное требование — ведь наша модель более-менее корректно описывает целевую функцию только в достаточно малой окрестности. В результате получаем дополнительную задачу условной оптимизации:
– линейная функция и, следовательно, минимума у нее нет. Для разрешения этой проблемы добавим ограничение на длину шага, который мы хотим сделать. В данном случае это вполне естественное требование — ведь наша модель более-менее корректно описывает целевую функцию только в достаточно малой окрестности. В результате получаем дополнительную задачу условной оптимизации:
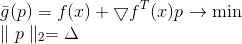
У этой задачи есть очевидное решение: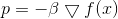 , где
, где  – множитель, гарантирующий выполнение ограничения. Тогда итерации метода спуска примут вид
– множитель, гарантирующий выполнение ограничения. Тогда итерации метода спуска примут вид
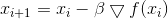 ,
,
в котором мы узнаем широко известный метод градиентного спуска. Параметр , который обычно называют скоростью спуска, теперь приобрел вполне понятный смысл, а его значение определяется из условия, чтобы новая точка лежала на сфере заданного радиуса, очерченной вокруг старой точки.
, который обычно называют скоростью спуска, теперь приобрел вполне понятный смысл, а его значение определяется из условия, чтобы новая точка лежала на сфере заданного радиуса, очерченной вокруг старой точки.
Исходя из свойств построенной модели целевой функции мы можем утверждать, что найдется такое , пусть даже очень маленькое, что если
, пусть даже очень маленькое, что если 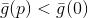 , то
, то  . Примечательно, что в данном случае направление, в котором мы будем двигаться, никак не зависит от величины радиуса этой сферы. Тогда мы можем избрать один из следующих путей:
. Примечательно, что в данном случае направление, в котором мы будем двигаться, никак не зависит от величины радиуса этой сферы. Тогда мы можем избрать один из следующих путей:
Первый подход характерен для методов доверительного региона, второй приводит к постановке вспомогательной задачи т.н. линейного поиска (LineSearch). В данном конкретном случае различия между этими подходами невелики и рассматривать их мы не будем. Вместо этого обратим внимание на следующее:
а почему, собственно, мы ищем смещение , лежащее именно на сфере?
, лежащее именно на сфере?
В самом деле, мы вполне могли бы заменить это ограничение требованием, например, чтобы p принадлежало поверхности куба, то есть выполнялось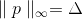 (в данном случае это не слишком разумно, но почему бы и нет), или некоторой эллиптической поверхности? Это уже кажется вполне логичным, если вспомнить про проблемы, возникающие при минимизации овражных функций. Суть проблемы в том, что вдоль одних координатных линий функция изменяется существенно быстрее, чем вдоль других. Из-за этого мы получаем, что если приращение должно принадлежать сфере, то величина
(в данном случае это не слишком разумно, но почему бы и нет), или некоторой эллиптической поверхности? Это уже кажется вполне логичным, если вспомнить про проблемы, возникающие при минимизации овражных функций. Суть проблемы в том, что вдоль одних координатных линий функция изменяется существенно быстрее, чем вдоль других. Из-за этого мы получаем, что если приращение должно принадлежать сфере, то величина  , при которой обеспечивается “спуск”, должна быть очень маленькой. А это ведет к тому, что достижение минимума потребует очень большого количества шагов. Но если вместо этого взять в качестве окрестности подходящий эллипс, то эта проблема как по волшебству сойдет на нет.
, при которой обеспечивается “спуск”, должна быть очень маленькой. А это ведет к тому, что достижение минимума потребует очень большого количества шагов. Но если вместо этого взять в качестве окрестности подходящий эллипс, то эта проблема как по волшебству сойдет на нет.
Условием принадлежности точки эллиптической поверхности может быть записано в виде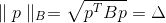 , где
, где  – некоторая положительно определенная матрица, также называемая метрикой. Норму
– некоторая положительно определенная матрица, также называемая метрикой. Норму 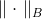 называют эллиптической нормой, индуцированной матрицей
называют эллиптической нормой, индуцированной матрицей  . Что это за матрица и откуда ее взять — рассмотрим позднее, а сейчас приходим к новой задаче.
. Что это за матрица и откуда ее взять — рассмотрим позднее, а сейчас приходим к новой задаче.
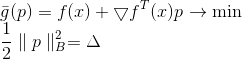
Квадрат нормы и множитель 1/2 здесь исключительно для удобства, чтобы не возиться с корнями. Применив метод множителей Лагранжа, получим связанную задачу безусловной оптимизации
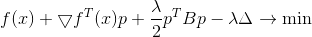
Необходимым условием минимума для нее является
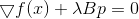 , или
, или 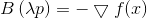 , откуда
, откуда
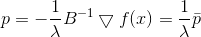
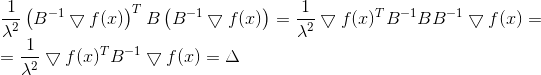
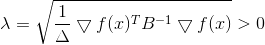
Опять видим, что направление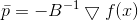 , в котором мы будем двигаться, не зависит от значения
, в котором мы будем двигаться, не зависит от значения  – только от матрицы
– только от матрицы  . И снова, мы можем либо подбирать
. И снова, мы можем либо подбирать  , что чревато необходимостью вычисления
, что чревато необходимостью вычисления  и явного обращения матрицы
и явного обращения матрицы  , либо решать вспомогательную задачу по поиску подходящего смещения
, либо решать вспомогательную задачу по поиску подходящего смещения 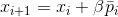 . Поскольку
. Поскольку 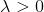 , решение у этой вспомогательной задачи гарантированно существует.
, решение у этой вспомогательной задачи гарантированно существует.
Так что же это должна быть за матрица B? Мы ограничимся умозрительными представлениями. Если целевая функция – квадратичная, то есть имеет вид
– квадратичная, то есть имеет вид 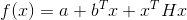 , где
, где  положительно определена, то вполне очевидно, что наилучшим кандидатом на роль матрицы
положительно определена, то вполне очевидно, что наилучшим кандидатом на роль матрицы  является гессиан
является гессиан  , поскольку в этом случае потребуется одна итерация построенного нами метода спуска. Если же H не является положительно определенной, то она не может являться метрикой, и построенные с ней итерации являются итерациями демпфированного метода Ньютона, но не являются итерациями метода спуска. Наконец мы можем дать строгий ответ на
, поскольку в этом случае потребуется одна итерация построенного нами метода спуска. Если же H не является положительно определенной, то она не может являться метрикой, и построенные с ней итерации являются итерациями демпфированного метода Ньютона, но не являются итерациями метода спуска. Наконец мы можем дать строгий ответ на
Вопрос: обязана ли матрица Гессе в методе Ньютона быть положительно определенной?
Ответ: нет, не обязана ни в стандартном, ни в демпфированном методе Ньютона. Но если это условие выполнено, то демпфированный метод Ньютона является методом спуска и обладает свойством глобальной, а не только локальной сходимости.
В качестве иллюстрации посмотрим, как выглядят доверительные регионы в случае минимизации всем известной функции Розенброка методами градиентного спуска и методом Ньютона, и как форма регионов влияет на сходимость процесса.
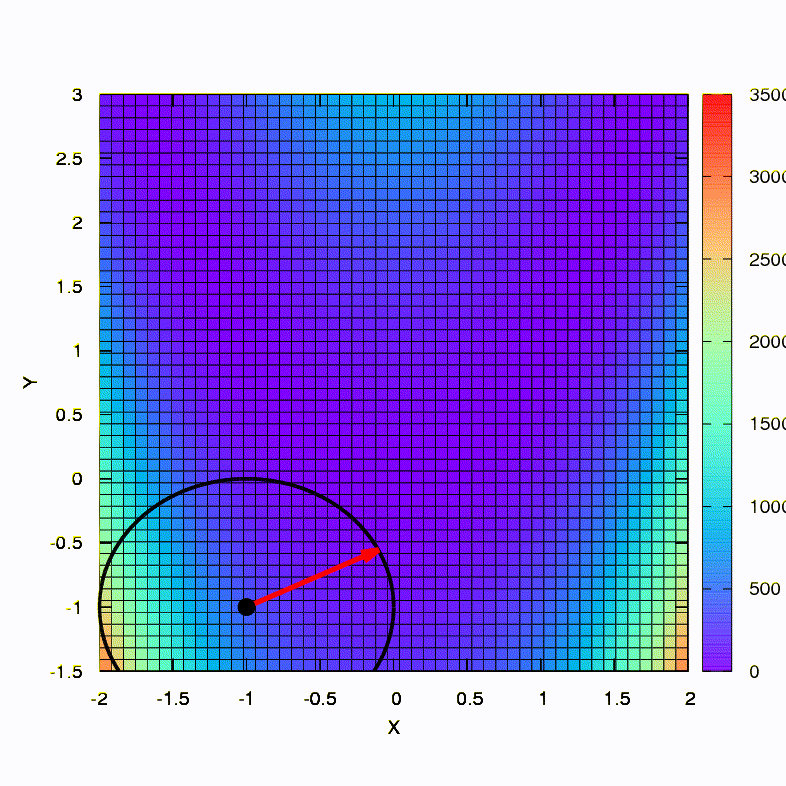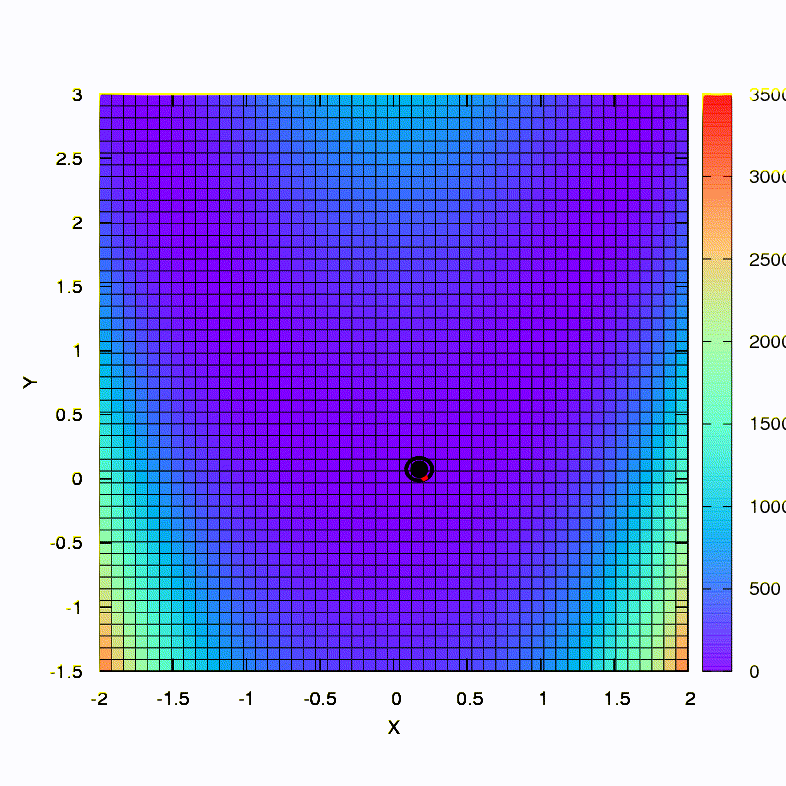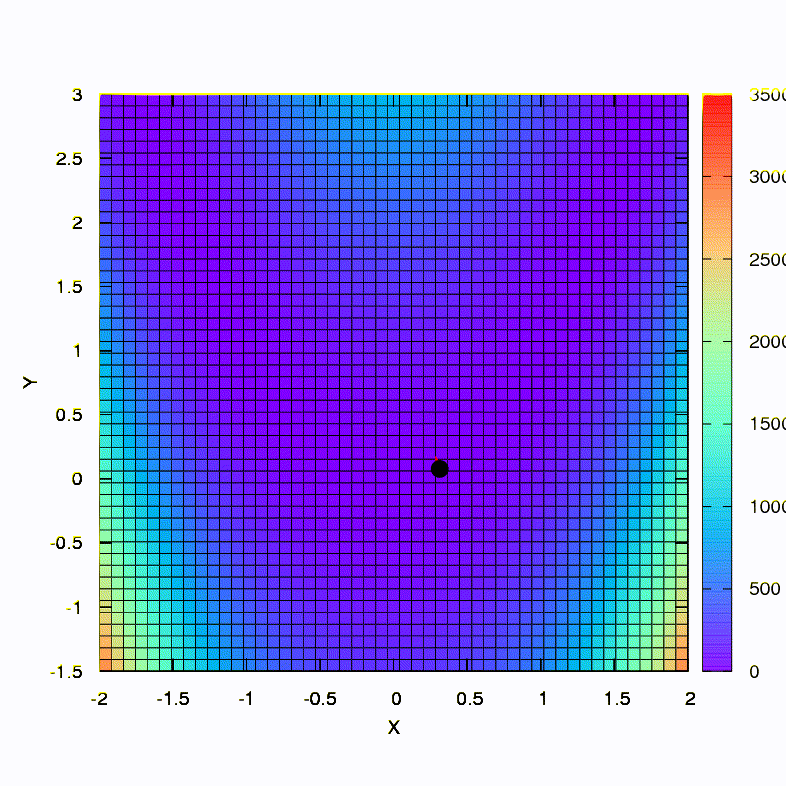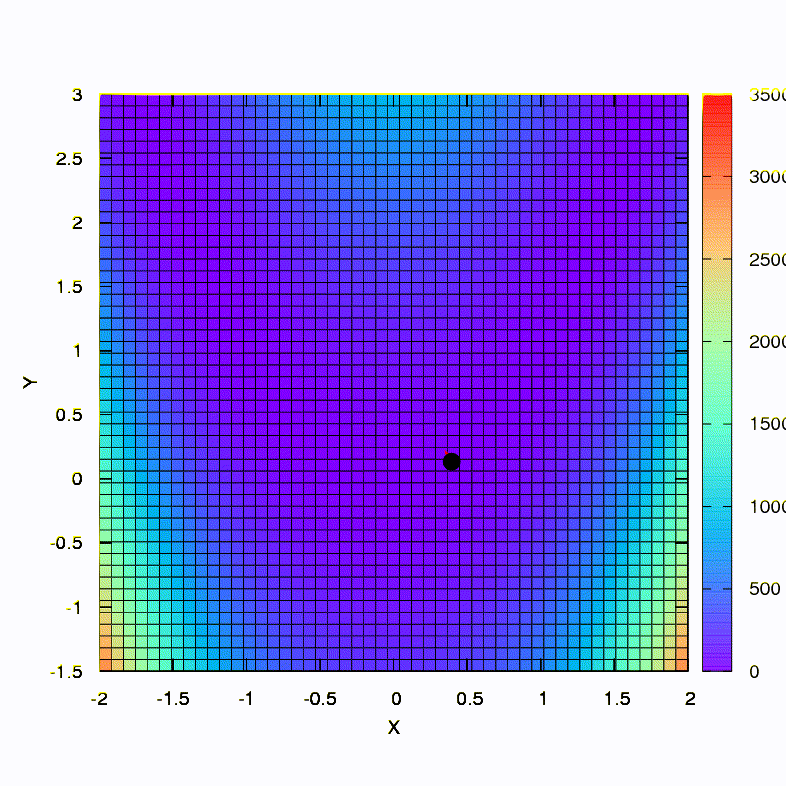
Вот так ведет себя метод спуска со сферическим доверительным регионом, он же — градиентный спуск. Все как по учебнику — мы застряли в каньоне.
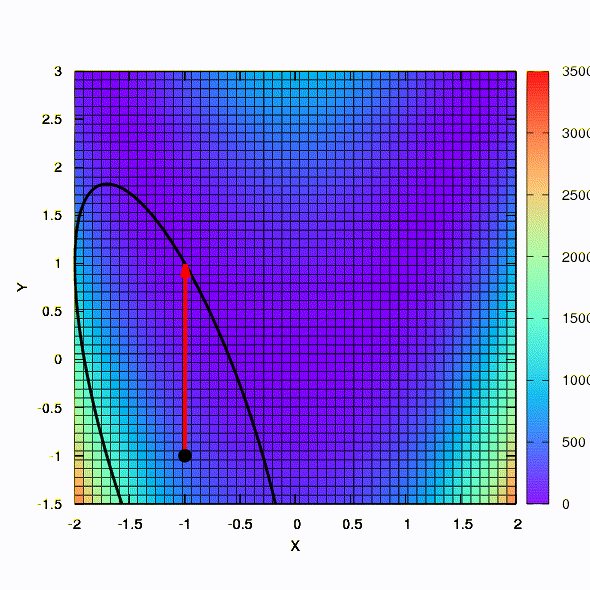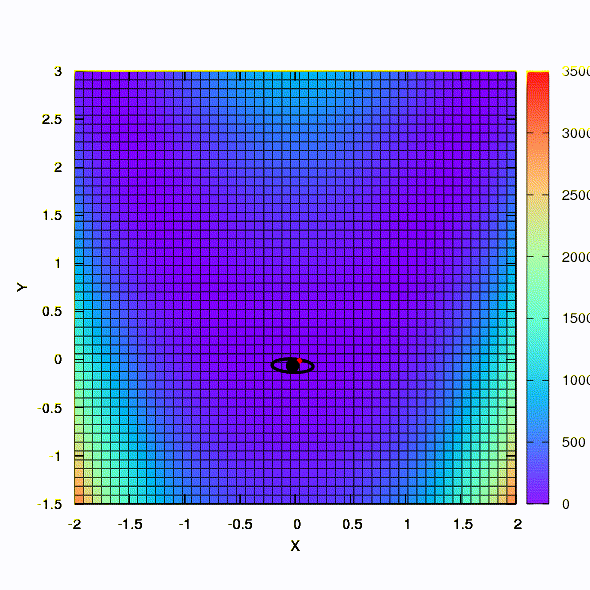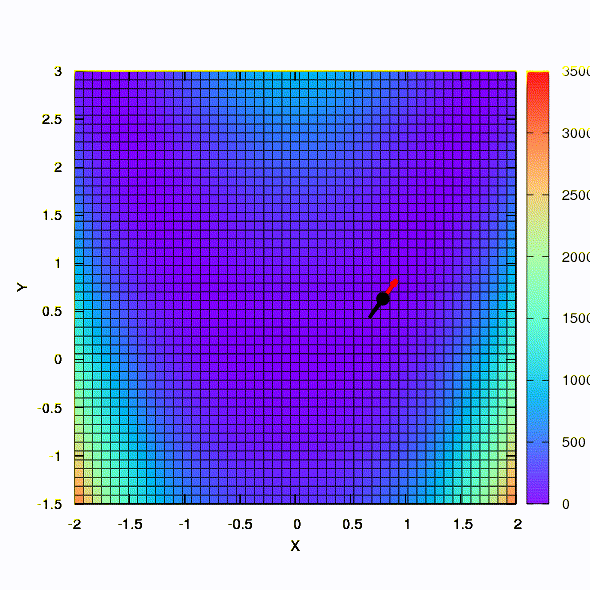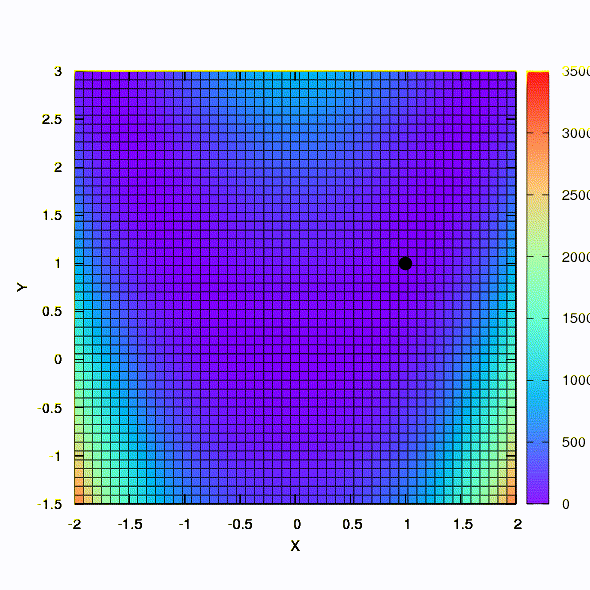
А это мы получаем, если доверительный регион имеет форму эллипса, определяемого матрицей Гессе. Это не что иное, как итерации демпфированного метода Ньютона.
Остался нераскрытым только вопрос о том, что делать, если матрица Гессе не является положительно определенной. Вариантов много. Первый — забить. Может, вам повезет и итерации Ньютона сойдутся и без этого свойства. Такое вполне реально, особенно на финальных этапах процесса минимизации, когда вы уже достаточно близки к решению. В таком случае можно использовать итерации стандартного метода Ньютона, не утруждая себя поисками допустимой для спуска окрестности. Либо использовать итерации демпфированного метода Ньютона и в случае , то есть в случае, когда полученное направление не является направлением спуска, поменять его, скажем, на антиградиент. Только не надо явным образом проверять, является ли гессиан положительно определенным по критерию Сильвестра, как это делалось здесь!!!. Это расточительно и бессмысленно.
, то есть в случае, когда полученное направление не является направлением спуска, поменять его, скажем, на антиградиент. Только не надо явным образом проверять, является ли гессиан положительно определенным по критерию Сильвестра, как это делалось здесь!!!. Это расточительно и бессмысленно.
Более тонкие методы предполагают построение матрицы, в некотором смысле близкую к матрице Гессе, но обладающую свойством положительной определенности, в частности, путем коррекции собственных значений. Отдельную тему составляют квазиньютоновские методы, или методы переменной метрики, которые гарантируют положительную определенность матрицы B и не требуют вычисления вторых производных. В общем, подробное обсуждение этих вопросов сильно выходит за рамки данной статьи.
Да, и кстати, из сказанного следует, что демпфированный метод Ньютона при положительной определенности гессиана — градиентный метод. Как и квазиньютоновские методы. И многие другие, основанные на раздельном выборе направления и величины шага. Так что противопоставлять метод Ньютона градиентным терминологически неверно.
Метод Ньютона, о котором часто вспоминают при обсуждении методов минимизации — это как правило вовсе не метод Ньютона в его классическом понимании, а метод спуска с метрикой, задаваемой гессианом целевой функции. И да, он сходится глобально в случае, если гессиан всюду положительно определен. Это возможно только для выпуклых функций, которые в практике встречаются гораздо реже, чем хотелось бы, так что в общем случае без соответствующих модификаций применение метода Ньютона (все же не будем отрываться от коллектива и продолжим называть его так) не гарантирует правильного результата. Обучение нейросетей, даже неглубоких, обычно приводит к невыпуклым задачам оптимизации с множеством локальных минимумов. И здесь новая засада. Метод Ньютона обычно сходится (если сходится) быстро. В смысле очень быстро. И это, как ни странно, плохо, поскольку мы за несколько итераций приходим к локальному минимуму. А он для функций со сложным рельефом может быть намного хуже глобального. Градиентный спуск с линейным поиском сходится гораздо медленнее, но с большей вероятностью “перескакивает” хребты целевой функции, что очень важно на ранних этапах минимизации. Если вы уже неплохо уменьшили величину целевой функции, а сходимость градиентного спуска существенно замедлилась, то здесь изменение метрики вполне может ускорить процесс, но это — для конечных стадий.
Разумеется, данный аргумент не универсален, не бесспорен и в ряде случаев даже неверен. Как и само утверждение о том, что градиентные методы лучше всех работают в задачах обучения.
- Методы второго и более порядков плохо работают в задачах обучения нейросетей. Потомучто.
- Метод Ньютона требует положительной определенности матрицы Гессе (вторых производных) и поэтому плохо работает.
- Метод Левенберга-Марквардта — компромисс между градиентным спуском и методом Ньютона и вообще эвристичекий.
и т.д. Чем продолжать этот список, лучше перейдем к делу. В этом посте рассмотрим второе утверждение, поскольку его я только на Хабре встречал как минимум дважды. Первый вопрос затрону только в той части, что касается метода Ньютона, поскольку он куда более обширен. Третий и остальные оставим до лучших времен.
Центром нашего внимания будет задача безусловной оптимизации
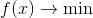 , где
, где 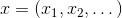 — точка векторного пространства, или просто — вектор. Естественно, что эту задачу решить тем проще, чем больше мы знаем об
— точка векторного пространства, или просто — вектор. Естественно, что эту задачу решить тем проще, чем больше мы знаем об  . Обычно она предполагается дифференцируемой по каждому аргументу
. Обычно она предполагается дифференцируемой по каждому аргументу 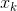 , причем столько раз, сколько требуется для наших грязных дел. Хорошо известно, что необходимым условием того, что в точке
, причем столько раз, сколько требуется для наших грязных дел. Хорошо известно, что необходимым условием того, что в точке 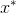 достигается минимум, является равенство градиента функции
достигается минимум, является равенство градиента функции 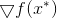 в этой точке нулю. Отсюда моментально получаем следующий метод минимизации:
в этой точке нулю. Отсюда моментально получаем следующий метод минимизации:Решить уравнение
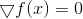 .
.Задача, мягко говоря, непростая. Точно не проще, чем исходная. Однако на этом моменте сразу можно отметить связь между задачей минимизации и задачей решения системы нелинейных уравнений. Эта связь нам еще аукнется при рассмотрении метода Левенберга-Марквардта (когда до него доберемся). А пока вспомним (или узнаем), что одним из наиболее часто применяемых методов для решения систем нелинейных уравнения является метод Ньютона. Заключается он в том, что для решения уравнения
 мы, начиная с некоторого начального приближения
мы, начиная с некоторого начального приближения  , строим последовательность
, строим последовательность 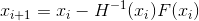 – явный метод Ньютона
– явный метод Ньютонаили
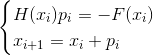 – неявный метод Ньютона
– неявный метод Ньютонагде
 – матрица, составленная из частных производных функции
– матрица, составленная из частных производных функции  . Естественно, что в общем случае, когда система нелинейных уравнений просто дана нам в ощущениях, требовать что-либо от матрицы
. Естественно, что в общем случае, когда система нелинейных уравнений просто дана нам в ощущениях, требовать что-либо от матрицы  мы не вправе. В случае, когда уравнение представляет собой условие минимума для какой-то функции, то мы можем утверждать, что матрица
мы не вправе. В случае, когда уравнение представляет собой условие минимума для какой-то функции, то мы можем утверждать, что матрица  симметрична. Но не более.
симметрична. Но не более.Метод Ньютона для решения систем нелинейных уравнений весьма неплохо изучен. И вот ведь штука — для его сходимости не требуется положительная определенность матрицы
 . Да и не может требоваться — иначе ему была бы грош цена. Вместо этого существуют другие условия, которые обеспечивают локальную сходимость данного метода и которые мы здесь рассматривать не будем, отправляя заинтересованных к специализированной литературе (или в комментарии). Получаем, что утверждение 2 неверно.
. Да и не может требоваться — иначе ему была бы грош цена. Вместо этого существуют другие условия, которые обеспечивают локальную сходимость данного метода и которые мы здесь рассматривать не будем, отправляя заинтересованных к специализированной литературе (или в комментарии). Получаем, что утверждение 2 неверно.Так?
И да, и нет. Засада здесь в слове локальная перед словом сходимость. Оно означает, что начальное приближение
 должно быть “достаточно близким” к решению, в противном случае на каждом шаге мы будем все дальше и дальше удаляться от оного. Что же делать? Я не буду вдаваться в детали того, как эту проблему решают для систем нелинейных уравнений общего вида. Вместо этого вернемся к нашей задаче оптимизации. Первая ошибка утверждения 2 на самом деле в том, что обычно говоря о методе Ньютона в задачах оптимизации имеют ввиду его модификацию — демпфированный метод Ньютона, в котором последовательность приближений строится по правилу
должно быть “достаточно близким” к решению, в противном случае на каждом шаге мы будем все дальше и дальше удаляться от оного. Что же делать? Я не буду вдаваться в детали того, как эту проблему решают для систем нелинейных уравнений общего вида. Вместо этого вернемся к нашей задаче оптимизации. Первая ошибка утверждения 2 на самом деле в том, что обычно говоря о методе Ньютона в задачах оптимизации имеют ввиду его модификацию — демпфированный метод Ньютона, в котором последовательность приближений строится по правилу 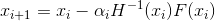 – явный демпфированный метод Ньютона
– явный демпфированный метод Ньютона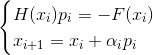 – неявный демпфированный метод Ньютона
– неявный демпфированный метод НьютонаЗдесь последовательность
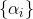 является параметром метода и ее построение представляет собой отдельную задачу. В задачах минимизации естественным при выборе
является параметром метода и ее построение представляет собой отдельную задачу. В задачах минимизации естественным при выборе 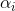 будет требование, чтобы на каждой итерации значение функции f уменьшалось, т.е.
будет требование, чтобы на каждой итерации значение функции f уменьшалось, т.е. 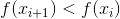 . Возникает закономерный вопрос: а существует ли вообще такое (положительное)
. Возникает закономерный вопрос: а существует ли вообще такое (положительное) 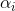 ? И если ответ на этот вопрос положителен, то
? И если ответ на этот вопрос положителен, то  называют направлением спуска. Тогда вопрос можно поставить таким образом:
называют направлением спуска. Тогда вопрос можно поставить таким образом: когда направление, генерируемое методом Ньютона, является направлением спуска?
И для ответа на него придется посмотреть на задачу минимизации с другого бока.
Методы спуска
Для задачи минимизации вполне естественным кажется такой подход: начиная с некоторой произвольной точки, выберем некоторым образом направление p и сделаем в этом направлении шаг
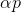 . Если
. Если 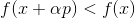 , то возьмем
, то возьмем 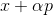 в качестве новой начальной точки и повторим процедуру. Если направление выбирается произвольно, то такой метод иногда называют методом случайного блуждания. Можно в качестве направления брать вектора единичного базиса — то есть делать шаг только по одной координате, такой метод называют методом покоординатного спуска. Стоит ли говорить, что они неэффективны? Для того, чтобы такой подход хорошо работал, нам нужны некоторые дополнительные гарантии. Для этого введем вспомогательную функцию
в качестве новой начальной точки и повторим процедуру. Если направление выбирается произвольно, то такой метод иногда называют методом случайного блуждания. Можно в качестве направления брать вектора единичного базиса — то есть делать шаг только по одной координате, такой метод называют методом покоординатного спуска. Стоит ли говорить, что они неэффективны? Для того, чтобы такой подход хорошо работал, нам нужны некоторые дополнительные гарантии. Для этого введем вспомогательную функцию 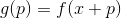 . Думаю, вполне очевидно, что минимизация
. Думаю, вполне очевидно, что минимизация  полностью эквивалентна минимизации
полностью эквивалентна минимизации  . Если
. Если  дифференцируема, то
дифференцируема, то  представима в виде
представима в виде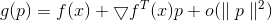
и если
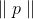 достаточно мало, то
достаточно мало, то 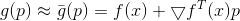 . Можем теперь попробовать подменить задачу минимизации
. Можем теперь попробовать подменить задачу минимизации 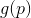 задачей минимизации ее приближения (или модели)
задачей минимизации ее приближения (или модели) 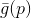 . Кстати, все методы, основанные на использовании модели
. Кстати, все методы, основанные на использовании модели 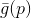 называются градиентными. Но вот ведь беда,
называются градиентными. Но вот ведь беда, 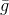 – линейная функция и, следовательно, минимума у нее нет. Для разрешения этой проблемы добавим ограничение на длину шага, который мы хотим сделать. В данном случае это вполне естественное требование — ведь наша модель более-менее корректно описывает целевую функцию только в достаточно малой окрестности. В результате получаем дополнительную задачу условной оптимизации:
– линейная функция и, следовательно, минимума у нее нет. Для разрешения этой проблемы добавим ограничение на длину шага, который мы хотим сделать. В данном случае это вполне естественное требование — ведь наша модель более-менее корректно описывает целевую функцию только в достаточно малой окрестности. В результате получаем дополнительную задачу условной оптимизации: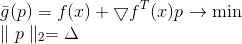
У этой задачи есть очевидное решение:
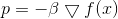 , где
, где  – множитель, гарантирующий выполнение ограничения. Тогда итерации метода спуска примут вид
– множитель, гарантирующий выполнение ограничения. Тогда итерации метода спуска примут вид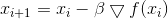 ,
,в котором мы узнаем широко известный метод градиентного спуска. Параметр
 , который обычно называют скоростью спуска, теперь приобрел вполне понятный смысл, а его значение определяется из условия, чтобы новая точка лежала на сфере заданного радиуса, очерченной вокруг старой точки.
, который обычно называют скоростью спуска, теперь приобрел вполне понятный смысл, а его значение определяется из условия, чтобы новая точка лежала на сфере заданного радиуса, очерченной вокруг старой точки.Исходя из свойств построенной модели целевой функции мы можем утверждать, что найдется такое
 , пусть даже очень маленькое, что если
, пусть даже очень маленькое, что если 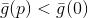 , то
, то  . Примечательно, что в данном случае направление, в котором мы будем двигаться, никак не зависит от величины радиуса этой сферы. Тогда мы можем избрать один из следующих путей:
. Примечательно, что в данном случае направление, в котором мы будем двигаться, никак не зависит от величины радиуса этой сферы. Тогда мы можем избрать один из следующих путей:- Подбирать по некоторой методике величину
 .
. - Поставить задачу выбора соответствующего значения
 , обеспечивающее уменьшение значения целевой функции.
, обеспечивающее уменьшение значения целевой функции.
Первый подход характерен для методов доверительного региона, второй приводит к постановке вспомогательной задачи т.н. линейного поиска (LineSearch). В данном конкретном случае различия между этими подходами невелики и рассматривать их мы не будем. Вместо этого обратим внимание на следующее:
а почему, собственно, мы ищем смещение
 , лежащее именно на сфере?
, лежащее именно на сфере?В самом деле, мы вполне могли бы заменить это ограничение требованием, например, чтобы p принадлежало поверхности куба, то есть выполнялось
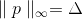 (в данном случае это не слишком разумно, но почему бы и нет), или некоторой эллиптической поверхности? Это уже кажется вполне логичным, если вспомнить про проблемы, возникающие при минимизации овражных функций. Суть проблемы в том, что вдоль одних координатных линий функция изменяется существенно быстрее, чем вдоль других. Из-за этого мы получаем, что если приращение должно принадлежать сфере, то величина
(в данном случае это не слишком разумно, но почему бы и нет), или некоторой эллиптической поверхности? Это уже кажется вполне логичным, если вспомнить про проблемы, возникающие при минимизации овражных функций. Суть проблемы в том, что вдоль одних координатных линий функция изменяется существенно быстрее, чем вдоль других. Из-за этого мы получаем, что если приращение должно принадлежать сфере, то величина  , при которой обеспечивается “спуск”, должна быть очень маленькой. А это ведет к тому, что достижение минимума потребует очень большого количества шагов. Но если вместо этого взять в качестве окрестности подходящий эллипс, то эта проблема как по волшебству сойдет на нет.
, при которой обеспечивается “спуск”, должна быть очень маленькой. А это ведет к тому, что достижение минимума потребует очень большого количества шагов. Но если вместо этого взять в качестве окрестности подходящий эллипс, то эта проблема как по волшебству сойдет на нет.Условием принадлежности точки эллиптической поверхности может быть записано в виде
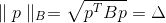 , где
, где  – некоторая положительно определенная матрица, также называемая метрикой. Норму
– некоторая положительно определенная матрица, также называемая метрикой. Норму 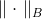 называют эллиптической нормой, индуцированной матрицей
называют эллиптической нормой, индуцированной матрицей  . Что это за матрица и откуда ее взять — рассмотрим позднее, а сейчас приходим к новой задаче.
. Что это за матрица и откуда ее взять — рассмотрим позднее, а сейчас приходим к новой задаче.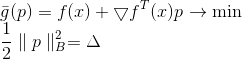
Квадрат нормы и множитель 1/2 здесь исключительно для удобства, чтобы не возиться с корнями. Применив метод множителей Лагранжа, получим связанную задачу безусловной оптимизации
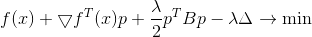
Необходимым условием минимума для нее является
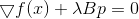 , или
, или 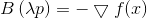 , откуда
, откуда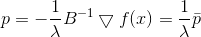
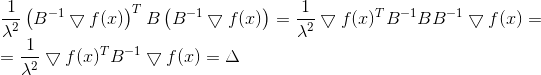
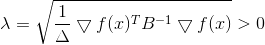
Опять видим, что направление
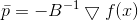 , в котором мы будем двигаться, не зависит от значения
, в котором мы будем двигаться, не зависит от значения  – только от матрицы
– только от матрицы  . И снова, мы можем либо подбирать
. И снова, мы можем либо подбирать  , что чревато необходимостью вычисления
, что чревато необходимостью вычисления  и явного обращения матрицы
и явного обращения матрицы  , либо решать вспомогательную задачу по поиску подходящего смещения
, либо решать вспомогательную задачу по поиску подходящего смещения 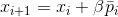 . Поскольку
. Поскольку 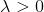 , решение у этой вспомогательной задачи гарантированно существует.
, решение у этой вспомогательной задачи гарантированно существует.Так что же это должна быть за матрица B? Мы ограничимся умозрительными представлениями. Если целевая функция
 – квадратичная, то есть имеет вид
– квадратичная, то есть имеет вид 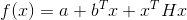 , где
, где  положительно определена, то вполне очевидно, что наилучшим кандидатом на роль матрицы
положительно определена, то вполне очевидно, что наилучшим кандидатом на роль матрицы  является гессиан
является гессиан  , поскольку в этом случае потребуется одна итерация построенного нами метода спуска. Если же H не является положительно определенной, то она не может являться метрикой, и построенные с ней итерации являются итерациями демпфированного метода Ньютона, но не являются итерациями метода спуска. Наконец мы можем дать строгий ответ на
, поскольку в этом случае потребуется одна итерация построенного нами метода спуска. Если же H не является положительно определенной, то она не может являться метрикой, и построенные с ней итерации являются итерациями демпфированного метода Ньютона, но не являются итерациями метода спуска. Наконец мы можем дать строгий ответ на Вопрос: обязана ли матрица Гессе в методе Ньютона быть положительно определенной?
Ответ: нет, не обязана ни в стандартном, ни в демпфированном методе Ньютона. Но если это условие выполнено, то демпфированный метод Ньютона является методом спуска и обладает свойством глобальной, а не только локальной сходимости.
В качестве иллюстрации посмотрим, как выглядят доверительные регионы в случае минимизации всем известной функции Розенброка методами градиентного спуска и методом Ньютона, и как форма регионов влияет на сходимость процесса.

Вот так ведет себя метод спуска со сферическим доверительным регионом, он же — градиентный спуск. Все как по учебнику — мы застряли в каньоне.

А это мы получаем, если доверительный регион имеет форму эллипса, определяемого матрицей Гессе. Это не что иное, как итерации демпфированного метода Ньютона.
Остался нераскрытым только вопрос о том, что делать, если матрица Гессе не является положительно определенной. Вариантов много. Первый — забить. Может, вам повезет и итерации Ньютона сойдутся и без этого свойства. Такое вполне реально, особенно на финальных этапах процесса минимизации, когда вы уже достаточно близки к решению. В таком случае можно использовать итерации стандартного метода Ньютона, не утруждая себя поисками допустимой для спуска окрестности. Либо использовать итерации демпфированного метода Ньютона и в случае
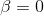 , то есть в случае, когда полученное направление не является направлением спуска, поменять его, скажем, на антиградиент. Только не надо явным образом проверять, является ли гессиан положительно определенным по критерию Сильвестра, как это делалось здесь!!!. Это расточительно и бессмысленно.
, то есть в случае, когда полученное направление не является направлением спуска, поменять его, скажем, на антиградиент. Только не надо явным образом проверять, является ли гессиан положительно определенным по критерию Сильвестра, как это делалось здесь!!!. Это расточительно и бессмысленно. Более тонкие методы предполагают построение матрицы, в некотором смысле близкую к матрице Гессе, но обладающую свойством положительной определенности, в частности, путем коррекции собственных значений. Отдельную тему составляют квазиньютоновские методы, или методы переменной метрики, которые гарантируют положительную определенность матрицы B и не требуют вычисления вторых производных. В общем, подробное обсуждение этих вопросов сильно выходит за рамки данной статьи.
Да, и кстати, из сказанного следует, что демпфированный метод Ньютона при положительной определенности гессиана — градиентный метод. Как и квазиньютоновские методы. И многие другие, основанные на раздельном выборе направления и величины шага. Так что противопоставлять метод Ньютона градиентным терминологически неверно.
Подытожим
Метод Ньютона, о котором часто вспоминают при обсуждении методов минимизации — это как правило вовсе не метод Ньютона в его классическом понимании, а метод спуска с метрикой, задаваемой гессианом целевой функции. И да, он сходится глобально в случае, если гессиан всюду положительно определен. Это возможно только для выпуклых функций, которые в практике встречаются гораздо реже, чем хотелось бы, так что в общем случае без соответствующих модификаций применение метода Ньютона (все же не будем отрываться от коллектива и продолжим называть его так) не гарантирует правильного результата. Обучение нейросетей, даже неглубоких, обычно приводит к невыпуклым задачам оптимизации с множеством локальных минимумов. И здесь новая засада. Метод Ньютона обычно сходится (если сходится) быстро. В смысле очень быстро. И это, как ни странно, плохо, поскольку мы за несколько итераций приходим к локальному минимуму. А он для функций со сложным рельефом может быть намного хуже глобального. Градиентный спуск с линейным поиском сходится гораздо медленнее, но с большей вероятностью “перескакивает” хребты целевой функции, что очень важно на ранних этапах минимизации. Если вы уже неплохо уменьшили величину целевой функции, а сходимость градиентного спуска существенно замедлилась, то здесь изменение метрики вполне может ускорить процесс, но это — для конечных стадий.
Разумеется, данный аргумент не универсален, не бесспорен и в ряде случаев даже неверен. Как и само утверждение о том, что градиентные методы лучше всех работают в задачах обучения.
Комментарии (12)

keine-lust
03.10.2019 22:34Что-то похожее рассказывал Peter Richtarik 27.09.19 в МФТИ mipt.ru/events/fpmi_provodit_na_fiztekhe_vorkshop_po_optimizatsii_i_prilozheniyam, прочитал — улыбнуло)

AC130
Тащемта методы работают плохо потому что в нейросетях, как правило, очень много весов и гессиан тупо не лезет в память, не говоря уже о том чтобы его обращать. Люди трахаются с градиентным спуском (обычным и случайным) не от того, что им нравится усложнять себе жизнь и они любят мазохизм, а от того, что другие методы железо не тянет.
alexkolzov Автор
Это, конечно, совершенно неожиданный и новый для меня аргумент. Можно ещё до кучи добавить, что гессиан долго вычислять. Это безусловно справедливо, если конечно не утруждать себя рассмотрением конкретных деталей в конкретных случаях: не учитывать определяемую архитектурой разреженность матриц, особенностей методов решения линейных систем, где возможно оперировать частями матрицы и т.д. и т.п. Нехватка памяти тоже вопрос ныне решаемый, если затраты окупаются качественным улучшением результата.
И под «плохо работают» я имел ввиду не технические проблемы, а сетования на качество результата работы этих методов.
AC130
Вот конкретный случай: VGG-19. 1, 2. Прошу, можете рассмотреть детали.
alexkolzov Автор
Деталей реализации метода применительно к архитектуре, а не самой архитектуры. На всякий случай напоминаю, что в статье обсуждаются методы оптимизации. Если уж ссылаетесь на публикации, то они должны быть посвящены анализу продуктивности методов обучения, пусть даже применительно к конкретной архитектуре, а не описанию архитектуры и результатов ее тестирования. Если хотели напугать меня количеством свободных параметров — не трудитесь
AC130
Да, конечно, прошу вас, рассмотрите детали реализации метода на примере предложенной НС.
alexkolzov Автор
Вы, конечно, понимаете, что это материал для серьезной научной работы. Но я постараюсь учесть Ваше пожелание.
Pand5461
Я свечку не держал, конечно, но с таким количеством параметров на картинку 224?224 зачем нужна нейросеть? Это уже можно огрубить цвета до 12 бит и протабулировать выходные значения.
Pand5461
Ой, что-то туплю. 224?224 в степень идёт же.
AC130
Можете — если задачу получается решить. Детектор Виолы-Джонса нейросетью не является, тем не менее он вполне работает даже на картинках побольше.
roryorangepants
Надеюсь, это сарказм, потому что скорость и память — это как раз самые первые аргументы против методов оптимизации высших порядков.
Не очень люблю апеллировать к этому, но в данном случае всё же скажу: не думаете же вы, что никто этого не пробовал?
Например, вот статья с ревью этого вопроса. Какие выводы делают авторы статьи?
1. Да, методы второго порядка показывают классные результаты по сравнению с SGD без моментума. К этому выводу у меня две претензии: во-первых, кто ж сейчас учит без моментума? Во-вторых, авторы статьи заменяют ReLU на tanh, потому что с ReLU методы оптимизации второго порядка не дружат.
2. Со скоростью всё очень плохо. На одном и том же железе в альтернативных экспериментах авторы получают такой результат:
При такой разнице по времени тренировка тяжелой сетки на ImageNet, которая сейчас на хорошем сервере занимает пару дней, с методами второго порядка дойдет до аналогичной точности за месяц. В этом просто нет смысла — с SGD за это время инженер может провести не один эксперимент, а, скажем, пять, потюнив гиперпараметры и архитектуру, а потом вывести модель в продакшен и успеть начать следующую задачу.
alexkolzov Автор
Разумеется это сарказм. Еще раз, я не оспариваю повышенные требования к памяти и ресурсам при использовании методов высших порядков, это было бы глупо. Другой вопрос, что идиотизм применять эти методы для систем такого размера простой реализацией ее базовой формулы.
Да ничего, вполне уместное замечание. Нет, я так не думаю. Я думаю, что есть разница между тем, что кто-то как-то пробовал и у него не получилось и утверждением, что что-то невозможно (нецелесообразно, неразумно) в принципе.
За статью большое спасибо, с ней знаком не был. Вывод авторов коротко можно сформулировать так: если методы второго порядка применимы, то они показывают существенно лучшие результаты в плане уменьшения функции за итерацию, но цена итерации оказывается слишком большой.
Первое замечание о методологии. Авторы применяют либо градиентный спуск, либо методы более высокого порядка на протяжении всего процесса обучения. В посте я уже упоминал, что, вообще говоря, на начальном этапе минимизации функций большого количества переменных применение методов высоких порядков обычно нецелесообразно, их лучше применять на завершающих этапах, либо при обнаружении застревания градиентных методов, вероятность которого никакой релаксацией исключено быть не может.
Второе. Авторы применяют методы оптимизации из коробки, не пытаясь учесть особенности архитектуры. Естественно, я не могу сказать сходу, есть ли для конкретной сети какие-то свойства, которые облегчат применение для нее указанных методов. Но делать общие выводы, опуская этот момент, на мой взгляд попросту некорректно. Нейросети — отнюдь не единственная в природе вещь, приводящая к задачам гигантской размерности, но почему-то в других подобных областях считают за правило приспосабливать численный метод к решаемой проблеме, а тут этим обычно не утруждаются.
Третье. Думал, стоит ли касаться этого в статье. Не коснулся. Видимо, зря. Один из используемых при сравнении метод — так называемый Hessian-free, который последнее время стали часто упоминать в публикациях по нейросетям, про него даже на Хабре писали. То есть, во-первых, уважаемые авторы не используют методы второго порядка в сравнении, поскольку этот метод есть просто применение метода сопряженных градиентов к решению определяющей направление линейной системы с аппроксимацией матрицы Гессе конечными разностями первого порядка. То есть это не что иное, как реализация (а вовсе никакой не новый неизученный метод) дискретного демпфированного метода Ньютона (или неточного метода Ньютона). Если ненароком вспомнить теорию, то выяснится, что дискретный метод Ньютона имеет без ограничения на величину приращения только линейный порядок сходимости, то есть сходится сильно хуже всамделешного метода Ньютона. А еще можно вспомнить, что положительная определенность матрицы, которая (см. пост) не гарантирована, является условием устойчивости метода сопряженных градиентов. То есть мало того, что есть вопросы к самому методу, так еще и «second-order methods» в названии, судя по всему, не вполне соответствует действительности. Это не криминал, поскольку в самом деле считать и хранить полную матрицу Гессе при таких размерностях выглядит малоперспективным. Но достаточно показательно.
Аргумент с памятью и вычислительными мощностями совершенно понятен, но на мой взгляд является слабым и выражает всего-навсего желание не вдаваться в детали, а взять готовое решение из коробки. Поэтому я его даже не оспариваю, нет такой задачи. Но делать на основании этого аргумента общие выводы о чем-либо не слишком умно. Конечно, на мой сугубо субъективный взгляд.