
No-communication theorem утверждает, что квантовое запутывание не может использоваться для передачи какой-либо информации. Теорема предполагает, что Боб никак не может отличить начальное состояние ? от состояния P(?) после измерения Алисой. Это доказывается математически, путем сравнения паттерна ? и паттерна P(?). Тот факт, что паттерн никогда не меняется, независимо от действий Алисы, является выводом теоремы об отсутствии связи.
Далее мы увидим, что расчеты no-communication theorem полностью согласуются с экспериментами. Словно квантовый мир использует надежную защиту, чтобы оставить в тайне свои секреты. Но, как мы знаем, любая защита — это лишь генератор ошибок перед правильным кодом. В действительности, мы увидим, что выводы no-communication theorem имеют небольшой изъян, при использование которого возникает возможность передачи информации с использованием квантово-запутанных частиц. Постараемся разобраться с алгоритмами квантового мира и подобрать правильные ключи к тайнам этого удивительного мира.
Данный пост является существенно доработанной и дополненной версией предыдущего поста, содержит подробные математические расчеты и более расширенный материал. Написание данного материала заняло несколько лет упорного труда, результатом которого является данная мегастатья.
Анализ no-communication theorem
Проведем краткий анализ реального эксперимента. Луч лазера попадает на нелинейно-оптическое устройство: кристалл бета-бората бария (BBO), благодаря которому один фотон преобразуется в два запутанных фотона более низкой частоты. Процесс известен как спонтанное параметрическое рассеяние. Полученная пара фотонов следует разными путями, один из которых поступает непосредственно на детектор 1, а второй проходит через двойную щель и попадает на детектор 2 (на каждой из щелей установлены круговые поляризаторы, имеющие противоположные направления круговой поляризации). Оба детектора подключены к схеме совпадений, гарантируя, что будут учитываться только запутанные пары фотонов. Шаговый двигатель перемещает второй детектор и сканирует целевую область, создавая карту интенсивности, которая формирует знакомую картину интерференции.
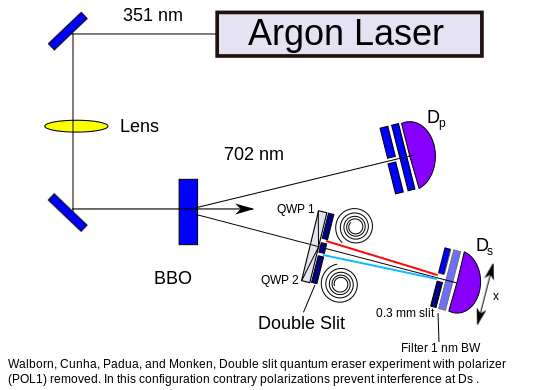
Допустим, что кристалл BBO производит следующее состояние:

Если Алиса помещает круговой поляризатор перед детектором 1, который отфильтровывает фотоны с поляризацией по или против часовой стрелке, то фотоны Боба на детекторе 2 будут описываться в соответствии с волновой функцией:

и

Поскольку Боб не знает, какую поляризацию применила Алиса, то видит на своем экране сумму двух интенсивностей:

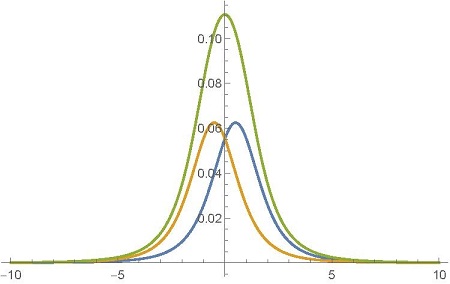
так как они оба производятся в равных количествах кристаллом. Боб может наблюдать только сумму из двух пиков. И только после получения результатов измерения Алисы он сможет увидеть, что для набора фотонов, где Алиса измерила поляризацию по часовой стрелке, подмножество фотонов Боба распределилось согласно
 , а для набора фотонов, где Алиса измерила поляризацию против часовой стрелки, подмножество фотонов Боба распределилось согласно
, а для набора фотонов, где Алиса измерила поляризацию против часовой стрелки, подмножество фотонов Боба распределилось согласно  .
.
Но если Алиса будет использовать линейный поляризатор вместо кругового, то волновая функция системы описывается в терминах состояний линейной поляризации:


Соответственно, Боб видит на своем экране сумму из двух интенсивностей:

и

Имеющих амплитуду волны:


На экране действительно возникает интерференционная картина. Но, поскольку Бобу не сообщили, какая поляризация была использована Алисой (горизонтальная или вертикальная), все, что он видит, является суммой двух интерференций имеющих разность фаз на cos
 . Следовательно, результат,
. Следовательно, результат,
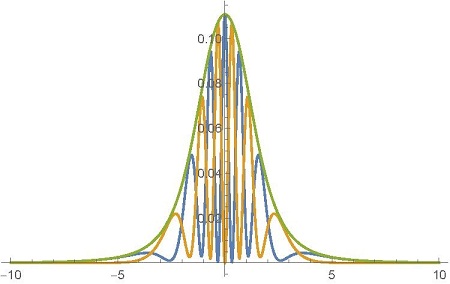
Как видим, расчеты no-communication theorem полностью согласуются с экспериментом. Ключевым моментом является то, что сумма двух интерференций, имеющих разность фаз, взаимно перекрывают друг друга. В результате интерференционная картина на экране не наблюдается.
Полученные результаты коррелируют с измерениями Алисы, поскольку фотоны с горизонтальной поляризацией и вертикальной поляризацией дают два шаблона интерференции, обладающих фазовым сдвигом на половину периода волны. Можно убедиться во взаимосвязанности поляризации и фазы проводя несложный эксперимент.
Экспериментальный анализ
Возьмем кусочек фольги и линейный поляризатор из экрана ЖК-монитора. На фольге аккуратно вырежем две щели расположив их как можно ближе. Щели прикроем двумя кусочками линейного поляризатора, расположив их так, чтобы они имели перпендикулярную поляризацию. Затем, с помощью скотча аккуратно заклеим их по краям.


Теперь мы имеем непрозрачную ширму с двумя щелями с перпендикулярной поляризацией. Установим ее на неподвижную подставку.


На расстояние 3-х метров расположим лист бумаги в качестве экрана и пропустим через щели когерентный луч лазера. Через щели могут пройти фотоны поляризованные либо горизонтально либо вертикально, но ни один фотон не сможет пройти через обе щели одновременно. Соответственно, на экране мы не наблюдаем интерференцию.

Но если перед экраном расположить линейный поляризатор под углом 45°, то происходит квантовое стирание их первоначальной поляризации, и на экране возникает интерференция (эксперимент квантовый ластик). Отметим карандашом интерференционные полосы и повернем линейный поляризатор еще на 90°. В этом случае мы снова увидим интерференцию, но уже из перпендикулярно поляризованных фотонов. Как видно из эксперимента, две картины интерференции из перпендикулярно поляризованных фотонов действительно имеют фазовый сдвиг на половину периода волны.


(получить хорошие фотографии достаточно трудно, но при желании каждый желающий может повторить данный эксперимент)
Волновую функцию мы разберем чуть ниже, но в данном случае она будет аналогична «no-communication theorem»
 для одной интерференции и
для одной интерференции и  для второй. Можно наблюдать каждую интерференцию по отдельности поворачивая линейный поляризатор на 90°. Но сможет ли Боб воспользоваться этой идеей, чтобы рассматривать интерференцию на экране, когда Алиса использует линейный поляризатор? К сожалению, Боб будет наблюдать интерференцию всегда, даже когда Алиса будет использовать круговой поляризатор, так как линейная поляризация на стороне Боба обеспечит дополнительную линейную поляризацию их запутанных пар на стороне Алисы.
для второй. Можно наблюдать каждую интерференцию по отдельности поворачивая линейный поляризатор на 90°. Но сможет ли Боб воспользоваться этой идеей, чтобы рассматривать интерференцию на экране, когда Алиса использует линейный поляризатор? К сожалению, Боб будет наблюдать интерференцию всегда, даже когда Алиса будет использовать круговой поляризатор, так как линейная поляризация на стороне Боба обеспечит дополнительную линейную поляризацию их запутанных пар на стороне Алисы.Краткий анализ квантовых состояний
Рассмотрим для начала обычный двухщелевой эксперимент. Благодаря тому, что фотоны обладают одинаковой вероятностью пройти через первую или вторую щель возникает квантовая суперпозиция, описываемая волновой функцией

Следует учесть, что лазерное излучение изначально являются когерентным, то есть фотоны обладают одинаковой поляризацией и фазой. Предположим, что фотоны на выходе из лазера обладают линейной поляризацией относительно некоторой оси:

Прохождение фотонов через кристалл BBO меняет распределение вероятностей, поскольку кристалл BBO в равных количествах производит фотоны имеющие ортогональные направления поляризации. Соответственно, на выходе кристалла можно получить 50% фотонов с поляризацией в одном направлении, и 50% с поляризацией в ортогональном направлении относительно любой оси измерения. Волновая функция на выходе кристалла BBO имеет вид




 и
и  уже не играют никакой роли, что свидетельствует об отсутствии каких либо скрытых параметров. Наличие во второй части формулы комплексного числа i говорит о том, что квадрат абсолютного значения дает противоположное (инвертированное) значение амплитуды вероятности. Это означает, что во второй части формулы интерференционные максимумы и минимумы поменяются местами. Поэтому, если на выходе кристалла BBO разместить две щели, то интерференционные полосы на экране уже не возникнут, поскольку результат будет аналогичен эксперименту no-communication theorem — сумма из двух интерференций из горизонтально и вертикально поляризованных фотонов будут взаимно перекрывать друг друга благодаря разности фаз. Думаю, теперь мы имеем более полное понимание того, почему Боб никогда не сможет увидеть интерференционные полосы на своем экране.
уже не играют никакой роли, что свидетельствует об отсутствии каких либо скрытых параметров. Наличие во второй части формулы комплексного числа i говорит о том, что квадрат абсолютного значения дает противоположное (инвертированное) значение амплитуды вероятности. Это означает, что во второй части формулы интерференционные максимумы и минимумы поменяются местами. Поэтому, если на выходе кристалла BBO разместить две щели, то интерференционные полосы на экране уже не возникнут, поскольку результат будет аналогичен эксперименту no-communication theorem — сумма из двух интерференций из горизонтально и вертикально поляризованных фотонов будут взаимно перекрывать друг друга благодаря разности фаз. Думаю, теперь мы имеем более полное понимание того, почему Боб никогда не сможет увидеть интерференционные полосы на своем экране. Для более дотошных читателей предлагаю подробные теоретические расчеты в конце статьи (Приложение №1), где Вы сможете узнать каким образом получены формулы волновой функции.
После измерения запутанных пар, Алиса сможет подсказать Бобу какие фотоны обладали горизонтальной поляризацией, а какие вертикальной. Только в этом случае Боб сможет обнаружить наличие интерференционных полос, если подсчитает распределение фотонов для горизонтальной поляризации, и для вертикальной поляризации. Даже если Алиса будет использовать круговые поляризаторы, результат будет аналогичным — Боб сможет подсчитать распределение фотонов для каждого типа круговой поляризации, и обнаружить интерференцию.
Исходя из анализа квантовых состояний можно установить, что используя две щели на выходе кристалла BBO можно получить лишь сумму из двух интерференций, взаимно перекрывающих друг друга из-за фазового сдвига. Мы также узнали, что фотоны участвующие в каждом из двух интерференций всегда имеют взаимно ортогональную поляризацию, и коррелируют с измерениями Алисы. Эти знания помогут нам в дальнейшем найти решение поставленной задачи. Но для этого потребуется в первую очередь разделить сумму из двух интерференций на составляющие. В этом нам поможет устройство, которое называется интерферометр Маха — Цендера.
Интерферометр Маха — Цендера
Рассмотрим подробнее принцип работы данного интерферометра.
На входе интерферометра находится полупрозрачное зеркало, расщепляющее световой поток на два луча. Отражаясь от двух непрозрачных зеркал они сводятся вместе во втором полупрозрачном зеркале. Будь фотон классической частицей то с вероятностью 50% мог бы пройти через первое полупрозрачное зеркало, и с вероятностью 50% отразится от него. Тоже самое произошло бы на втором полупрозрачном зеркале. В результате на выходе интерферометра мы бы наблюдали 50% фотонов направленных вверх, и 50% фотонов направленных вниз.
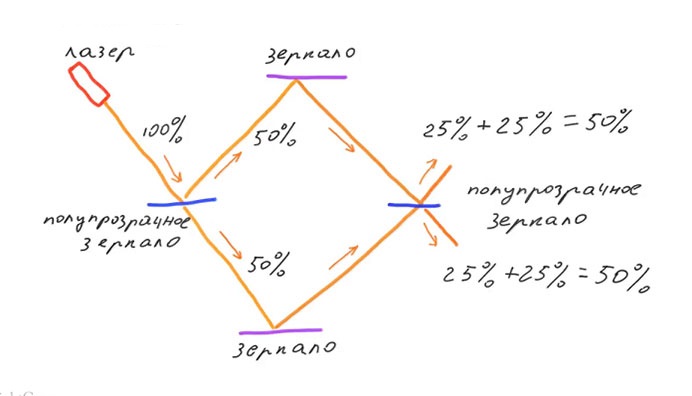
Обозначим базисными кет-векторами со стрелочками два возможных направления движения фотона: вверх и вниз. Тогда изначально фотон будет описываться вектором состояния «вниз». После прохождения первого полупрозрачного зеркала фотон будет в суперпозиции базисных векторов «вверх» и «вниз». Эта суперпозиция является еще одной физической реализацией кубита, наравне со спином электрона и поляризацией фотона.
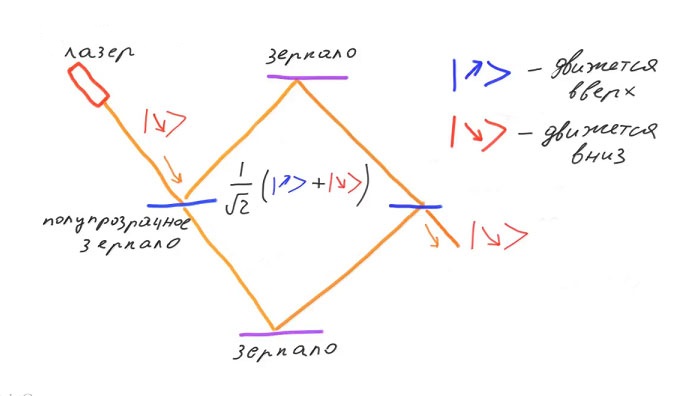
На выходе второго полупрозрачного зеркала наблюдается ни что иное как интерференция фотона с самим собой. При этом интерференционные максимумы направлены вниз, а интерференционные минимумы направлены вверх. Но если мы попытаемся узнать по какому из плечей интерферометра действительно прошел фотон, то интерференция пропадает.
Прохождения квантово-запутанных частиц через интерферометр Маха ? Цендера
Суперпозиция базисных векторов на плечах интерферометра принципиально ничем не отличается от суперпозиции в двухщелевом эксперименте. Соответственно, формулы волновой функции, которые мы приводили для двухщелевого эксперимента, могут быть без изменений применены также для интерферометра Маха ? Цендера. Произведем расчеты с использованием соответствующих квантовых вентилей.
Прохождению первого и второго полупрозрачного зеркала соответствует матрица
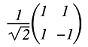
Прохождению зеркала соответствует матрица
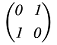
Фазовому сдвигу соответствует эрмитово сопряженная матрица Джонса
для полуволновой пластины

При этом каждый переход описывается оператором эволюции.
Зададим матричный вид вектора состояний
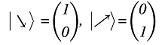
и рассмотрим эволюцию во времени.
Прохождение первого полупрозрачного зеркала (гейт Адамара):
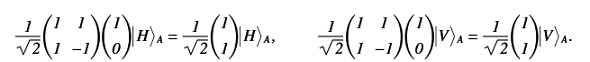
Прохождение зеркала (гейт Паули X):
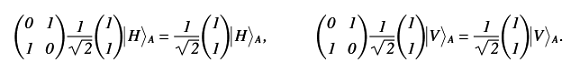
Фазовый сдвиг (матрица Джонса для полуволновой пластины):

Расчеты показывают, что суперпозиция базисных векторов описываются состояниями
 которые в сумме дают формулу волновой функции не нарушающий нормировку и полностью соответствующий волновой функции no-communication theorem:
которые в сумме дают формулу волновой функции не нарушающий нормировку и полностью соответствующий волновой функции no-communication theorem: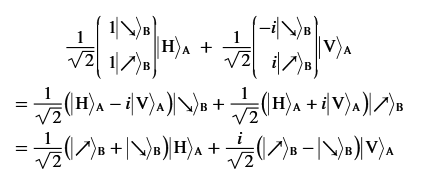
Эрмитово сопряжение матрицы Джонса позволяет рассчитать влияние фазового сдвига на суперпозицию базисных векторов:

Прохождение второго полупрозрачного зеркала (гейт Адамара):
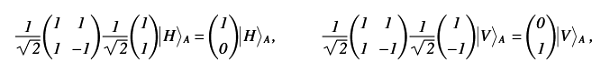
Не трудно заметить, что в зависимости от фазы волны, интерференционные максимумы на выходе интерферометра будут направлены в разные стороны. Следовательно, на выходе интерферометра 50% фотонов будут направлены вверх и 50% фотонов направленны вниз. Причем результаты коррелируют с измерениями Алисы, поскольку фотоны с горизонтальной и вертикальной поляризацией обладают фазовым сдвигом и на выходе направлены в разные стороны.
Амплитуда волны:
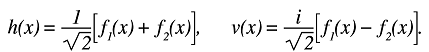
Как правило, поляризация или фаза на входе интерферометра никак не влияет на распределение интерференционных максимумов, поэтому на выходе фотоны всегда направлены в одну сторону. Но при использование квантовой запутанности результат получается совершенно иным. Запутанные пары изначально не имеют определенную поляризацию и фазу. Наличие начальной поляризации или фазы приводит к наличию скрытого параметра, что противоречит экспериментальным данным по проверке неравенства Белла. Это очень важный момент, поскольку само название квантовой нелокальности говорит о том, что локальных объяснений для квантовых корреляций не существует, а все попытки локальных объяснений противоречат экспериментальным данным. Состояние фотона определяется лишь в процессе измерения, и оно всегда случайно. Но в запутанных парах эти случайности всегда коррелируют. По этой причине, фазовый сдвиг возникает случайным образом в процессе декогеренции, при котором происходит также корреляция запутанных пар.
В данном случае, на входе интерферометра фотон обладает фазовой неопределенностью. При прохождении первого полупрозрачного зеркала неопределенность сохраняется, так же как при отражении от зеркал. Но при прохождении второго полупрозрачного зеркала фотон имеет 100% вероятность находиться только в одном из двух состояний, поскольку на втором полупрозрачном зеркале возникает интерференция. Если на выходе интерферометра фотон будет направлен либо вверх либо вниз — это будет означать, что интерференционные максимумы имели соответствующую фазу на втором полупрозрачном зеркале. Соответственно, фазовый сдвиг учитывается при прохождении фотона через второе полупрозрачное зеркало.
Изъян no-communication theorem
Как мы видим, использование интерферометра Маха — Цендера дает не сумму двух интенсивностей как в первоначальном эксперименте, а разности двух интенсивностей. При этом учитывается только фаза волны, что, в свою очередь, не приводит к проблемам, как в случае использования поляризатора. Это является ключом для решения поставленной задачи.
Несмотря на то, что расчеты no-communication theorem абсолютно верны, выводы данной теоремы имеют серьезный изъян. Тот факт, что Боб никогда не сможет увидеть интерференционные полосы на своем экране не является доказательством того, что не существует способов передачи информации с использованием квантово-запутанных частиц. На самом деле существует как минимум два способа для решения этой задачи. Рассмотрим подробнее каждый из них.
Передача информации при помощи квантовой запутанности. Способ №1
Если Алиса будет использовать круговой поляризатор вместо линейного, то фазовый сдвиг возникнет между противоположными направлениями циркулярной поляризации. Волновая функция системы при этом описывается в терминах состояний круговой поляризации

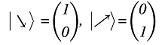 и рассчитаем прохождение квантово-запутанных частиц через интерферометр Маха-Цендера.
и рассчитаем прохождение квантово-запутанных частиц через интерферометр Маха-Цендера.Прохождение первого полупрозрачного зеркала (гейт Адамара):

Прохождение зеркала (гейт Паули X):

Фазовый сдвиг:

Прохождение второго полупрозрачного зеркала (гейт Адамара):

Интерференционные максимумы на выходе интерферометра будут также направлены в разные стороны. Причем фотоны, которые имеют круговую поляризацию по часовой стрелке будут направлены вверх, а фотоны, которые имеют круговую поляризацию против часовой стрелки будут направлены вниз. Это результат квантовых корреляций, возникающих в следствие синглетного состояния фотонов. Поскольку фотоны являются запутанными, они более не являются независимыми. Соответственно, фотоны не могут иметь произвольное направление круговой поляризации на выходе интерферометра.
Эксперимент №1
Если Боб расположит на выходе интерферометра противоположно направленные круговые поляризаторы, то благодаря квантовым корреляциям ни один фотон не попадет на детекторы.

Но если Алиса поменяет круговой поляризатор на линейный, то 25% запутанных частиц попадут на верхний и 25% на нижний детектор, поскольку фотоны с линейной поляризацией имеют равную вероятность круговой поляризации по часовой и против часовой стрелки.

В отличии от эксперимента с двумя щелями, интерференция на выходе интерферометра будет возникать при использование как линейного так и кругового поляризатора. Но в случае использования Алисой кругового поляризатора, запутанные пары на каждом выходе интерферометра будут иметь строго определенное направление круговой поляризации.
Благодаря этому, Боб всегда может узнать какую поляризацию использует Алиса без какой-либо дополнительной информации. Соответственно, данный способ позволяет осуществить передачу информации с использованием квантовой запутанности.
При этом нижнюю ветку на выходе интерферометра использовать не удастся, поскольку на нижний детектор будут направлены не только квантово-запутанные частицы, но и весь шум. На верхней ветке, напротив, окажутся только квантово запутанные частицы. Соответственно, данный способ позволяет использовать до 25% квантово-запутанных частиц для передачи информации без использования детектора совпадений.
Преимуществом данного способа является простота конструкции. Передачу информации можно осуществлять по прямой видимости независимо от углового вращения между приемо-передатчиком. Недостатком данного способа является низкий КПД (не более 25% квантово-запутанных частиц) и непригодность для передачи данных через оптоволоконные каналы. Так как внутреннее отражение оптоволоконного канала приводит к инвертированию направления круговой поляризации, даже небольших внешних колебаний оптоволокна будет достаточно, чтобы серьезно исказить передаваемые данные.
Следующий способ лишен указанных недостатков. Обладает высоким КПД и позволяет осуществить передачу информации по оптоволоконным каналам. Но при этом имеет более сложную конструкцию.
Передача информации при помощи квантовой запутанности. Способ №2
Второй способ подразумевает установку еще одного интерферометра на выходе первого и использование закона Брюстера. Передача информации будет осуществляться зависимости от наличия или отсутствия интерференции в интерферометрах. В этом случае, мы имеем два интерферометра Маха — Цендера расположенных каскадно, и 3 детектора расположенные на их выходе:

При наличии интерференции:
- 50% фотонов попадут в интерферометр №2. При этом, на входе второго интерферометра они имеют базисный вектор направленный вверх, соответственно, на выходе они также будут иметь базисный вектор направленный вверх и попадут на детектор А;
- оставшиеся 50% фотонов попадут на детектор С.
- ни один фотон не попадет на детектор B
При отсутствии интерференции, как мы дальше увидим, почти все фотоны должны будут попасть на детектор B. Но каким образом Алиса сможет разрушить интерференцию на стороне Боба?
Чтобы не сталкиваться с проблемой дополнительного фазового сдвига, необходимо отказаться от использования поляризаторов и найти такое решение, которое позволит определить по какому плечу проходил каждый фотон. И такое решение существует.
Закон Брюстера
Как известно, зако?н Брю?стера — это закон оптики, выражающий связь показателей преломления двух диэлектриков с таким углом падения света, при котором свет, отражённый от границы раздела диэлектриков, будет полностью поляризованным в плоскости, перпендикулярной плоскости падения. При этом преломлённый луч частично поляризуется в плоскости падения, и его поляризация достигает максимального значения (но не 100 %).
Для расчета амплитуд отраженных и преломленных волн пользуются формулами Френеля
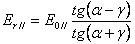 ,
, 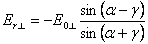 . Угол падения, при котором отражённый луч полностью поляризован, называется углом Брюстера. Оно реализуется только тогда, когда угол между отраженной и преломленной волнами равен
. Угол падения, при котором отражённый луч полностью поляризован, называется углом Брюстера. Оно реализуется только тогда, когда угол между отраженной и преломленной волнами равен 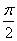 . В этом случае
. В этом случае 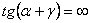 и
и 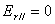 . Но так как
. Но так как 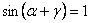 и
и 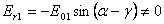 в отраженном свете присутствуют колебания только вектора
в отраженном свете присутствуют колебания только вектора 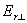 а это означает, что отраженный свет линейно поляризован.
а это означает, что отраженный свет линейно поляризован.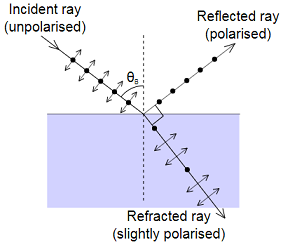
Рассмотрим падение поляризованного луча света на границу раздела двух диэлектриков. Если падающий свет поляризован строго определенным образом, а именно, вектор напряженности электрического поля лежит в плоскости падения, и при этом угол падения расположен под углом Брюстера, то отраженной волны не будет (
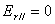 ,
, 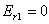 ). Это значит, что луч света, прошедший через линейный поляризатор не отражается от диэлектрической поверхности, если его поляризация находится в плоскости падения, а луч света падает под углом Брюстера. Наглядную демонстрацию данного явления можно увидеть в эксперименте доцента кафедры общей физики МИФИ Гервидса Валериана Ивановича, кандидата физико-математических наук.
). Это значит, что луч света, прошедший через линейный поляризатор не отражается от диэлектрической поверхности, если его поляризация находится в плоскости падения, а луч света падает под углом Брюстера. Наглядную демонстрацию данного явления можно увидеть в эксперименте доцента кафедры общей физики МИФИ Гервидса Валериана Ивановича, кандидата физико-математических наук.Эксперимент №2
Следует заметить, что в интерферометре Маха — Цендера используются именно диэлектрические полупрозрачные зеркала. Разделение луча на отраженные и переломленные составляющие происходит благодаря использованию двойного слоя диэлектрика, из которого состоит полупрозрачное зеркало. Поэтому, если направить на интерферометр луч лазера, поляризованный в плоскости падения и расположенный под углом Брюстера, то на полупрозрачном зеркале отраженной волны не будет. Это значит, что вероятность возникновения суперпозиции окажется минимальной и на выходе не будет интерференции.
Самое интересное заключается в том, что линейный поляризатор может быть расположен на пути запутанных пар (на стороне Алисы). Поскольку квантовая запутанность обеспечивает корреляцию запутанных пар, то это позволит узнать через какое плечо интерферометра прошли фотоны (на стороне Боба). Соответственно, вероятность возникновения суперпозиции в интерферометре будет минимальна.
Как это работает? Допустим, что Алиса будет вращать линейный поляризатор, а Боб расположит интерферометр под углом Брюстера.

(расположение под углом Брюстера слегка меняет геометрическое расположение зеркал)
В определенные моменты вращения плоскость поляризации будет совпадать с плоскостью падения. В эти моменты суперпозиция окажется минимальной, так как станет известно через какое плечо интерферометра прошли фотоны. А поскольку 50% фотонов будут поляризованы в плоскости падения к полупрозрачному зеркалу, а 50% будут ортогональны к ней, то
- все фотоны, поляризованные в плоскости падения к полупрозрачному зеркалу не будут иметь отраженной волны. Соответственно, они не будут отражаться ни на одном полупрозрачном зеркале и попадут на детектор B (на рисунке указаны синими стрелочками);
- все фотоны поляризованные ортогонально к плоскости падения будут иметь минимальный коэффициент преломления. Соответственно, они всегда будут отражаться при прохождении полупрозрачных зеркал и попадут на детектор B (на рисунке указаны красными стрелочками).

С учетом небольшого коэффициента преломления, на выходе первого и второго интерферометров:
• минимальное количество запутанных фотонов попадут на детекторы А и С
• почти все запутанные фотоны попадут на детектор B
При последующем вращении, когда плоскость поляризации уже не будет совпадать с плоскостью падения, на выходе интерферометров возникнет интерференция, соответственно, уже ни один фотон не попадет на детектор B.
На детекторе B будет наблюдаться пульсирующий луч света, причем периодичность пульсации на стороне Боба составит 2N, где N равна одному обороту линейного поляризатора на стороне Алисы — это уже передача информации с использованием квантово-запутанных частиц, так как меняя скорость вращения поляризатора можно передавать разную информацию!
Данный способ передачи информации с использованием квантово-запутанных частиц имеет как свои достоинства, так и недостатки. К достоинствам можно отнести весьма высокий уровень КПД, возможность передачи через оптоволоконные кабели и отсутствие необходимости в детекторе совпадений. К недостаткам можно отнести сложность прецизионной настройки интерферометров. Могут быть использованы более эффективные способы кодирования информации вместо вращения, но в этом случае возникает зависимость от углового вращения между приемником и передатчиком.
Сопутствующие проблемы
Применение таких схем позволит достичь минимальной задержки при передаче информации на большие расстояния. Скорость передачи информации может существенно превосходить скорость света в вакууме. Некоторые утверждают, что СТО/ОТО запрещает передачу информации со скоростью выше скорости света. Идея конечности скорости света была предложена Пуанкаре и получена из формул Максвелла. При этом изначально речь шла об электромагнитном поле, а затем с лёгкой руки Альберта Германовича была распространена на все массивные и безмассовые материальные объекты. Важно подчеркнуть, что об информации речи не было, если открыть любую книжку по СТО/ОТО, информация не присутствует в математическом формализме. Поэтому когда утверждают о том, что СТО/ОТО запрещает передачу информации выше скорости света, делается неявное предположение, что иного способа, кроме как «посадить информацию» на пучок фотонов/электронов и т.д. не существует.
Принцип причинности
Одним из основных проблем мгновенной передачи информации является нарушение принципа причинности. Хотя стоит заметить, что современная физика нигде не требует соблюдения причинности на квантовом уровне, поэтому её среди постулатов физики нет. Однако, от соблюдения причинности человек пока отказаться не может, т. к. это противоречит нашей логике.
Согласно теории относительности Эйнштейна мгновенная передача информации позволяет получить информацию прежде, чем она будет отправлена. Например, если решим отправить информацию самому себе, то можем провести эксперимент таким образом, чтобы получить информацию до того, как мы его отправим. Это может привести к «парадоксу убитого дедушки», когда мы получили одно значение, а решили отправить противоположное.
С точки зрения копенгагенской интерпретации, запутанные пары всегда должны коррелировать, независимо от наших намерений, иначе нарушается закон сохранения импульса. В результате получаем полностью предопределенное будущее, в котором мы ничего не сможем изменить, соответственно, никаким образом не сможем создать «парадокс убитого дедушки».
С точки зрения многомировой интерпретации, каждая запутанная пара должна коррелировать с одним из множества миров. Соответственно, решение отправить противоположное значение вместо увиденного не приведет ни к каким парадоксам. Возможно, с помощью данного эксперимента можно будет подтвердить или опровергнуть одну из двух теорий.
Я же считаю, что полученную информацию из будущего следует рассматривать как статистическую вероятность. Также как нарушение неравенства Белла следует понимать не как строгое доказательство, а как достаточно убедительную статистику, позволяющую считать это утверждение верным. И если решим отправить противоположное значение вместо увиденного, то на выходе интерферометра мы должны получить среднее значение из двух возможных вероятностей, по которому уже не сможем определить какую информацию мы решим отправить себе в будущем. Мы можем отправить любой вариант и это не приведет ни к каким проблемам.
Но это не означает, что нет никакой возможности получить достоверную информацию из будущего. Анализ будущего в детерминированных системах позволит получить достоверный прогноз с высокой степенью вероятности. Например, если мы решим узнать «исчезнет ли завтра Луна», то такая вероятность будет минимальна. Соответственно, результаты эксперимента будут указывать преимущественно на один вариант ответа. Возможности применения в области прогнозирования весьма велики. Попробуем рассмотреть решение данной задачи более подробно.
Квантовые корреляции в пространстве и времени
Для того, чтобы нарушить принцип причинности и заглянуть в будущее, потребуется существенно замедлить скорость света, либо существенно увеличить расстояние между кристаллом BBO и поляризатором на стороне Алисы. Это необходимо для того, чтобы квантово-запутанные частицы сначала прошли через интерферометр Маха-Цендера, а затем через поляризатор на стороне Алисы. В этом случае, информация о состоянии поляризации будет получена прежде, чем запутанные пары смогут пройти поляризатор. Такое возможно благодаря тому, что на квантовом уровне временной порядок не играет никакой роли. Как я уже писал, нарушение причинности противоречит нашей логике, но это не противоречит законам физики.
Согласно специальной теории относительности Эйнштейна по мере увеличения скорости происходит замедление времени. Чем больше скорость движения, тем медленнее течет время. При этом, скорость света является предельной величиной, поэтому для самих частиц света (фотонов) время замедляется до нуля. Правильнее сказать для фотонов не существует времени, для них существует только текущий момент, в котором они пребывают в любой точке своей траектории. Данное явление рассматривается как световой конус в четырёхмерной модели теории относительности Германа Минковского.
Возникает вопрос, каким образом фотон может одновременно находится во всех точках своей траектории? Как известно, по мере увеличения скорости наблюдается эффект релятивистского сокращения длины, согласно формуле:
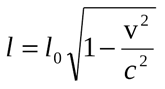
Не трудно заметить, что на скорости света любая длина в пространстве будет сжата до нулевого размера. Это значит, что на скорости света пространство сжимается до планковских размеров, при котором исчезает само понятие о пространстве-времени. В результате фотон может «одновременно» находится во всех точках своей траектории, не зависимо от того, сколько времени прошло относительно наблюдателя.
Временной порядок событий всегда является относительным. То что для наблюдателя кажется прошлым или будущем для фотонов является одновременным. Поэтому, независимо от пройденного расстояния и прошедшего времени относительно наблюдателя, запутанные пары «одновременно» проходят через поляризатор и достигают детектора на выходе интерферометра. Соответственно, квантовые корреляции между прошлым и будущим всегда сохраняются, даже если с ИСО наблюдателя кажется, что следствие опережает причину.
Следует заметить, что немногие физики готовы признать такую теорию. По их мнению, подобное объяснение нелокальных корреляций указывает на то, что фотоны распространяются не в нашем пространстве, а следуют по какому-то «черному ходу» нулевой длины вне его. Единственное, что смогли придумать физики, – это какое-то скрытое воздействие, которое распространяется от Алисы до Боба со скоростью выше световой. Именно так учебники по нерелятивистской физике объясняют эксперименты Белла: утверждается, что измерение, сделанное Алисой, должно повлечь нелокальный коллапс волновой функции на стороне Боба. Хотя такое объяснение противоречит теории относительности, но именно так учат современных студентов.
Такого же мнения придерживались Антуан Суарес и Валерио Скарин, когда выдвинули в 1997 году идею о том, что когда прибор Алисы выдает результат, он дает информацию об этом всей Вселенной, и в частности прибору Боба, на сверхсветовой скорости. И наоборот. То есть первый из них, который выдал результат, информирует второго. Они предложили проверить эту идею экспериментально, воссоздав ситуацию, при котором Алиса и Боб со своими приборами удаляются друг от друга в разные стороны на очень высокой скорости, и поэтому система отсчета, в которой покоится прибор Алисы, отличается от системы, в которой неподвижен прибор Боба. Согласно теории относительности Эйнштейна, хронология, или порядок следования двух событий, наблюдаемых из движущихся относительно друг друга систем отсчета, может быть разной. То есть можно построить эксперимент таким образом, что Алиса в своей системе отсчета делает выбор и фиксирует результат до Боба, и в том же самом эксперименте Боб в своей системе отсчета делает выбор и фиксирует результат до Алисы. Физики описывают этот эксперимент словами «до – до», так как каждый из двух игроков действует раньше другого. По мнению Суареса и Скарани такой эксперимент должен был исключить нарушение неравенства Белла.
В экспериментах, проведенных в Женеве в конце 2000-х в начале 2001 годов Николя Жизэн и Гуго Збинден установили детектор на диске, который вращался со скоростью 10000 оборотов в минуту, что соответствовало линейной скорости на краю диска в 380 км/ч. Такая скорость не выглядит большой, однако, разделение запутанных пар расстоянием свыше 10 км, при хорошей синхронизации позволило добиться релятивистского эффекта «до – до». Антуан Суарес, который внимательно следил за экспериментом, заметил, что в движении должен быть не детектор, а последний светоделитель интерферометра. По мнению Суареса, именно это зеркало было тем местом, где делался окончательный выбор (также, как в наших экспериментах). Но даже после того, как исправили все недостатки эксперимент опроверг гипотезу Суареса и Скарани.
Результаты экспериментов с движущимися измерительными устройствами исключили возможность описания квантовых корреляций с помощью реальных часов, в терминах «раньше» и «позже». Оказалось, что феномен квантовой нелокальности не может быть описан в терминах пространства и времени. Это означало, что для нелокальных корреляций отсутствует упорядочение во времени, так что причинный порядок не может быть сведен к упорядочению во времени. Квантовые корреляции каким-то образом выявляют зависимость между событиями. Эксперимент показывает, что эта зависимость лежит за пределами упорядочения во времени. В реальном проявлении феномен квантовой нелокальности имеет место, но время здесь, как оказалось, не играет роли.
Замедление скорости света
Существенное увеличение расстояния между кристаллом BBO и поляризатором на стороне Алисы представляет большую трудность, поскольку придется иметь дело с расстояниями межпланетных масштабов. Поэтому, наиболее эффективным решением является замедление скорости света.
В любой прозрачной среде свет распространяется медленнее, так как его скорость зависит от показателя преломления среды. Но для существенного замедления скорости света вплоть до полной его остановки, требуется применение более экзотического состояния материи, называемый конденсатом Бозе — Эйнштейна.
Несколько лет назад исследователям из университета Дармштадта (Германия) удалось остановить поток света на одну минуту. Для остановки света, ученые воспользовались так называемой техникой электромагнитно индуцированной прозрачности (EIT). Они использовали непрозрачный кристалл сплава силиката иттрия и празеодима охлажденный до состояния конденсата Бозе — Эйнштейна. Охладив кристалл до сверхнизкой температуры, ученые перевели все атомы вещества в состояние квантовой суперпозиции, в состояние, когда атомы вещества находятся в квантовой неопределенности.
Вначале управляемый луч лазера с определенной длиной волны направляется на кристалл, делая кристалл полностью прозрачным. Затем второй источник света (источник данных) направляется на полностью прозрачный кристалл. После этого управляемый лазер выключается, возвращая кристаллу состояние полной непрозрачности. Это действие позволяет заключить свет, переносящий данные в ловушку кристалла, устраняя его преломление и отражение за счет непрозрачности.
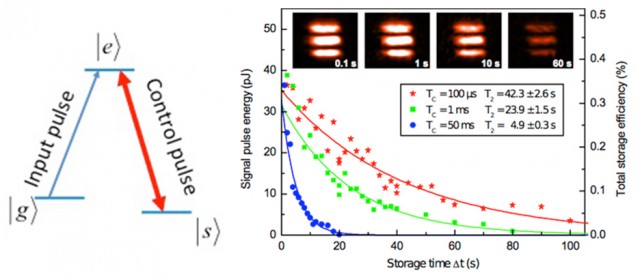
Из-за отсутствия свободы передвижения, энергия фотонов собирается атомами кристалла, а данные, переносимые светом, преобразуются в атомные спины. Чтобы освободить свет из кристалла, производят повторное включение управляемого лазера, делающего кристалл вновь прозрачным, и информация заключенная в атомных спинах выпускаются в виде фотонов.
Фотоны, находившиеся внутри кристалла, сохраняются внутри него в течение 60 секунд
не теряя квантового состояния. Максимальная длительность времени, на которую можно останавливать свет, определяется свойствами кристалла и может быть существенно увеличена. На данный момент ученые ведут поиски более эффективных материалов для решения этой задачи. Предполагается, что использование графена в структуре кристалла может существенно увеличить длительность удержания фотонов. Успехи в данной области помогут создать квантовые ячейки памяти, которые в будущем предполагается применять в квантовых компьютерах.
Эксперимент №3
Рассмотрим схему эксперимента с замедлением скорости света до полной его остановки:

В зависимости от того, какой поляризатор будет использован на выходе криогенно охлажденного кристалла, результаты на выходе интерферометра будут соответственно коррелировать.

Благодаря тому, что непрозрачный кристалл способен удерживать фотоны в «ловушке», полученные данные на выходе интерферометра будут заранее указывать на вероятность того, какая информация будет отправлена в будущем. Если вероятности равны, то на выходе интерферометра 12,5% запутанных фотонов попадут на верхний детектор.
Анализ состояний
Полагаю, не все читатели согласятся с такими выводами, поскольку некоторые убеждены в том, что если запутанная частица сначала проходит через интерферометр и попадает на детектор, это приводит к декогеренции волновой функции, а значит дальнейшие манипуляции Алисы не могут повлиять на наблюдения Боба. Хотя мы уже рассматривали эксперимент «До-До» опровергающий эти выводы, давайте также рассмотрим математические расчеты, чтобы убедится в ошибочности такого мнения.
Допустим, на верхнем выходе интерферометра из 50% запутанных частиц 25% прошли через круговой поляризатор и попали на верхний детектор. В этом случае мы должны полагать, что Алиса будет использовать линейный поляризатор в соответствии с волновой функцией

Но мы убеждены, что дальнейшие манипуляции Алисы не могут повлиять на наблюдения Боба, а значит Алиса может использовать любой поляризатор. Пусть Алиса выбрала круговой поляризатор. В этом случае суперпозиция на плечах интерферометра должна была иметь следующую волновую функцию



Видно, что на каждом выходе интерферометра запутанные фотоны имеют круговую поляризацию только в одном направлении. Соответственно, при использовании Алисой кругового поляризатора на верхний детектор Боба ни один фотон не попадет. Расчеты показывают, что других исходов быть не может, а иначе нарушается закон сохранения импульса. По этой причине, копенгагенская интерпретация предположительно ведет к полной предопределенности будущего. А согласно многомировой интерпретации, на верхний детектор способно попасть от 0 до 25% фотонов в зависимости от распределения вероятности (где 0% — означает, что Алиса будет использовать круговой поляризатор, а 25% означает, что Алиса будет использовать линейный поляризатор).
Перспективы практического применения и последствия
Сложно переоценить важность коммуникаций со сверхсветовой скоростью. Это откроет новые горизонты для технических решений способных привести к революции в области коммуникаций, интернета и телевидения. Позволит существенно сократить задержку сигнала между спутниками и Землей, а также откроет возможность для создания глобальных компьютерных сетей в межпланетных масштабах. Управлять марсоходами можно будет в режиме реального времени, также как управлять спутниками на границах солнечной системы. Не малую важность может иметь также применение в оборонной промышленности.
Анализ будущего с помощью квантовой запутанности позволит определить вероятность того, что произойдет в будущем. Данная вероятность окажется на порядок точнее любых прогнозов на основе логического анализа и классических расчетов. В детерминированных системах это позволит существенно сократить количественные расчеты и сразу же получить готовый результат, например при расчете прогноза погоды. Однако, это может иметь далеко идущие последствия, поскольку знание будущего способно разрушить фондовую биржу, Уолл-стрит, курсы валют и курсы барреля нефти, а значит кардинально изменить всю мировую экономику в целом.
Нельзя отрицать, что данная технология может быть применена как во благо, так и во вред. В недобрых руках данная технология может оказаться страшным оружием. Ведь тот, кто знает будущее будет непобедим. Хочется верить, что люди смогут найти правильное применение, позволяющее предотвратить последствия многих катастроф, природных катаклизмов, мировых конфликтов и войн до того, как они возникнут. В конечном счете, это позволит уберечь человечество от роковых ошибок и обеспечит безопасность нашей планеты в будущем.
<<<<<<<<<<<<<<<>>>>>>>>>>>>>>>
Приложение №1. Теоретические расчеты
Квантовая механика построена на определенных принципах, в которых используются понятия наблюдаемых величин, и предполагается существование лежащего в их основе комплексного векторного пространства, векторы которого представляют состояния системы. Наблюдаемые можно также называть измеряемыми. Это вещи, которые допускают измерение с помощью подходящего прибора. Допустим, что прибор A будет осуществлять измерение системы.
Результат измерений обычно статистически неоднозначен. Однако для любого конкретного измерения есть определенные состояния, результаты которых совершенно однозначны.
Значение каждого принципа
Если прибор A, измеряющий состояние системы, ориентирован вдоль оси Z, то состояние всегда будет приводить к значению
всегда будет приводить к значению  = +1. Аналогично состояние
= +1. Аналогично состояние  всегда будет иметь значение
всегда будет иметь значение  = –1. Из принципа 1 вытекает, что каждая наблюдаемая (
= –1. Из принципа 1 вытекает, что каждая наблюдаемая ( ,
,  и
и  ) отождествляется с определенным линейным оператором в двумерном пространстве состояний. Результат измерения всегда является вещественным числом из множества возможных результатов. Возможные значения для любых компонент ±1.
) отождествляется с определенным линейным оператором в двумерном пространстве состояний. Результат измерения всегда является вещественным числом из множества возможных результатов. Возможные значения для любых компонент ±1.
Принцип 2 определяет связь между оператором, представляющим наблюдаемую, и возможными числовыми результатами измерения. А именно — результат измерения всегда является одним из собственных значений соответствующего оператора.
Принцип 3 наиболее интересен. В нем говорится, что два состояния физически различны, если есть измерение, которое может различить их без какой-либо неоднозначности. Например, и
и  можно различить, измеряя
можно различить, измеряя  . То же самое верно для
. То же самое верно для  и
и  . Различить их можно, измеряя
. Различить их можно, измеряя  . Но если нам сообщили, что состояние системы находится в одном из двух состояний —
. Но если нам сообщили, что состояние системы находится в одном из двух состояний —  или
или  , невозможно провести измерение, чтобы однозначно сказать, каково истинное состояние системы. Измерение
, невозможно провести измерение, чтобы однозначно сказать, каково истинное состояние системы. Измерение  это не обеспечит. Если получилось
это не обеспечит. Если получилось  = +1, то, возможно, исходное состояние было
= +1, то, возможно, исходное состояние было  , поскольку существует 50-процентная вероятность получения такого результата в состоянии
, поскольку существует 50-процентная вероятность получения такого результата в состоянии  . По этой причине говорят, что
. По этой причине говорят, что  и
и  являются физически различимыми, а
являются физически различимыми, а  и
и  — нет. Можно сказать, что внутреннее произведение двух состояний служит мерой невозможности уверенно их различить. Иногда это внутреннее произведение называют перекрытием. Принцип 3 требует, чтобы физически различные состояния представлялись ортогональными векторами состояний, то есть чтобы эти векторы не перекрывались. Так, для состояний
— нет. Можно сказать, что внутреннее произведение двух состояний служит мерой невозможности уверенно их различить. Иногда это внутреннее произведение называют перекрытием. Принцип 3 требует, чтобы физически различные состояния представлялись ортогональными векторами состояний, то есть чтобы эти векторы не перекрывались. Так, для состояний 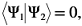 но
но  .
.
Наконец, принцип 4 дает количественное выражение этой идее, формируя правило для вероятности различных исходов эксперимента. Если предположить, что система приготовлена в состоянии и затем измеряется наблюдаемая L, то результатом будет одно из собственных значений
и затем измеряется наблюдаемая L, то результатом будет одно из собственных значений  оператора L. Но в общем случае невозможно сказать, какое из этих значений будет обнаружено. Есть лишь вероятность — назовем ее P(
оператора L. Но в общем случае невозможно сказать, какое из этих значений будет обнаружено. Есть лишь вероятность — назовем ее P( ) — того, что исход будет
) — того, что исход будет  . Принцип 4 говорит, как вычислить эту вероятность, и она выражается через перекрытие
. Принцип 4 говорит, как вычислить эту вероятность, и она выражается через перекрытие  и |
и | >. Более строго, вероятность равна квадрату абсолютной величины этого перекрытия:
>. Более строго, вероятность равна квадрату абсолютной величины этого перекрытия:  или, что эквивалентно,
или, что эквивалентно, 
Важное следствие этого принципа: операторы, представляющие наблюдаемые, — эрмитовы.
Наблюдаемые по оси Z
Рассмотрим , которая имеет фиксированную однозначную величину для состояний
, которая имеет фиксированную однозначную величину для состояний  и
и  , и соответствующие измеренные значения
, и соответствующие измеренные значения  = +1 и
= +1 и  = –1.
= –1.
Наблюдаемые по оси Z соответствуют начальному состоянию параметрически рассеянного луча на выходе кристалла BBO, поскольку кристалл в равных количествах производит фотоны, имеющие ортогональные направления поляризации.
Наблюдаемые по оси X
Попробуем сделать то же самое и для компонента .
.
Собственные векторы — это
— это  и
и  с собственными значениями +1 и ?1 соответственно. Уравнение будет иметь следующий вид:
с собственными значениями +1 и ?1 соответственно. Уравнение будет иметь следующий вид:

При этом и
и  взаимно ортогональны. Другими словами,
взаимно ортогональны. Другими словами,

Если прибор A имеет наблюдаемые или
или  , то по оси
, то по оси  будут равные вероятности обнаружить состояния
будут равные вероятности обнаружить состояния  и
и  . Таким образом, каждое из значений
. Таким образом, каждое из значений  должно быть равно 1/2 — это линейные суперпозиции
должно быть равно 1/2 — это линейные суперпозиции  и
и  , которые соответствуют прохождению фотонов через двухщелевой эксперимент или через интерферометр Маха — Цендера:
, которые соответствуют прохождению фотонов через двухщелевой эксперимент или через интерферометр Маха — Цендера:

Наблюдаемые по оси Y
Наконец, можно проделать то же самое для , которому соответствуют измерения Алисы. Собственные векторы
, которому соответствуют измерения Алисы. Собственные векторы  — это состояния
— это состояния  и
и  с собственными значениями +1 и ?1 соответственно. Уравнение будет иметь следующий вид:
с собственными значениями +1 и ?1 соответственно. Уравнение будет иметь следующий вид:

Состояния и
и  ортогональны друг другу. Другими словами,
ортогональны друг другу. Другими словами,

При этом существуют дополнительные ограничения на векторы и
и  :
:

В первых двух уравнениях играет роль
играет роль  . В двух других уравнениях эту роль играет
. В двух других уравнениях эту роль играет  . Данные условия утверждают, что если фотон ориентирован вдоль оси
. Данные условия утверждают, что если фотон ориентирован вдоль оси  , а затем измерен вдоль
, а затем измерен вдоль  , то он с равной вероятностью будет в состоянии
, то он с равной вероятностью будет в состоянии  или
или  . Следует также ожидать, что если фотон ориентирован вдоль оси
. Следует также ожидать, что если фотон ориентирован вдоль оси  , он также с равной вероятностью будет в состоянии
, он также с равной вероятностью будет в состоянии  или
или  . Это приводит к дополнительным условиям:
. Это приводит к дополнительным условиям:

Данные условия достаточны для определения формы векторов и
и  , за исключением неопределенности фазы. Представим данные в матричном виде и рассчитаем:
, за исключением неопределенности фазы. Представим данные в матричном виде и рассчитаем:

В результате получается:

которая в сумме дает формулу волновой функции по оси Y:

Наличие наблюдаемых значений по оси Y (измерения Алисы) неизбежно вносят свой вклад в волновую функцию по оси X (наблюдаемые Боба). Представим данные в матричном виде и рассчитаем векторы по оси X:

В результате мы получаем волновую функцию «No-communication theorem»:

Наличие во второй части комплексного числа i говорит о том, что квадрат абсолютного значения дает инверсию амплитуды вероятности. Из этого следует, что при наблюдении Бобом интерференции по оси X, интерференционные максимумы первой части волновой функции совпадут с интерференционными минимумами второго, а интерференционные максимумы второго с минимумами первого. Возникнет наложение интерференционных максимумов и взаимное перекрытие двух интерференций, что подтверждается на практике с помощью детектора совпадений:
совпадут с интерференционными минимумами второго, а интерференционные максимумы второго с минимумами первого. Возникнет наложение интерференционных максимумов и взаимное перекрытие двух интерференций, что подтверждается на практике с помощью детектора совпадений:

Благодаря этому, интерференционные максимумы и
и  на выходе интерферометра Маха-Цендера будут направлены в разные стороны, а квантовая запутанность обеспечит соответствующие корреляции между наблюдениями Алисы и Боба.
на выходе интерферометра Маха-Цендера будут направлены в разные стороны, а квантовая запутанность обеспечит соответствующие корреляции между наблюдениями Алисы и Боба.
Приложение №1. Теоретические расчеты
Квантовая механика построена на определенных принципах, в которых используются понятия наблюдаемых величин, и предполагается существование лежащего в их основе комплексного векторного пространства, векторы которого представляют состояния системы. Наблюдаемые можно также называть измеряемыми. Это вещи, которые допускают измерение с помощью подходящего прибора. Допустим, что прибор A будет осуществлять измерение системы.
- Принцип 1. Наблюдаемые или измеряемые величины в квантовой механике представляются линейными операторами L.
- Принцип 2. Возможные результаты измерений являются собственными значениями оператора, который представляет наблюдаемую.
- Принцип 3. Однозначно различимые состояния представляются ортогональными векторами.
- Принцип 4. Если
 — вектор состояния системы, и измеряется наблюдаемая L, то вероятность пронаблюдать значение
— вектор состояния системы, и измеряется наблюдаемая L, то вероятность пронаблюдать значение  равна P(
равна P( ) = <A|
) = <A| ><
>< |A>
|A>
Результат измерений обычно статистически неоднозначен. Однако для любого конкретного измерения есть определенные состояния, результаты которых совершенно однозначны.
Значение каждого принципа
Если прибор A, измеряющий состояние системы, ориентирован вдоль оси Z, то состояние
 всегда будет приводить к значению
всегда будет приводить к значению  = +1. Аналогично состояние
= +1. Аналогично состояние  всегда будет иметь значение
всегда будет иметь значение  = –1. Из принципа 1 вытекает, что каждая наблюдаемая (
= –1. Из принципа 1 вытекает, что каждая наблюдаемая ( ,
,  и
и  ) отождествляется с определенным линейным оператором в двумерном пространстве состояний. Результат измерения всегда является вещественным числом из множества возможных результатов. Возможные значения для любых компонент ±1.
) отождествляется с определенным линейным оператором в двумерном пространстве состояний. Результат измерения всегда является вещественным числом из множества возможных результатов. Возможные значения для любых компонент ±1. Принцип 2 определяет связь между оператором, представляющим наблюдаемую, и возможными числовыми результатами измерения. А именно — результат измерения всегда является одним из собственных значений соответствующего оператора.
Принцип 3 наиболее интересен. В нем говорится, что два состояния физически различны, если есть измерение, которое может различить их без какой-либо неоднозначности. Например,
 и
и  можно различить, измеряя
можно различить, измеряя  . То же самое верно для
. То же самое верно для  и
и  . Различить их можно, измеряя
. Различить их можно, измеряя  . Но если нам сообщили, что состояние системы находится в одном из двух состояний —
. Но если нам сообщили, что состояние системы находится в одном из двух состояний —  или
или  , невозможно провести измерение, чтобы однозначно сказать, каково истинное состояние системы. Измерение
, невозможно провести измерение, чтобы однозначно сказать, каково истинное состояние системы. Измерение  это не обеспечит. Если получилось
это не обеспечит. Если получилось  = +1, то, возможно, исходное состояние было
= +1, то, возможно, исходное состояние было  , поскольку существует 50-процентная вероятность получения такого результата в состоянии
, поскольку существует 50-процентная вероятность получения такого результата в состоянии  . По этой причине говорят, что
. По этой причине говорят, что  и
и  являются физически различимыми, а
являются физически различимыми, а  и
и  — нет. Можно сказать, что внутреннее произведение двух состояний служит мерой невозможности уверенно их различить. Иногда это внутреннее произведение называют перекрытием. Принцип 3 требует, чтобы физически различные состояния представлялись ортогональными векторами состояний, то есть чтобы эти векторы не перекрывались. Так, для состояний
— нет. Можно сказать, что внутреннее произведение двух состояний служит мерой невозможности уверенно их различить. Иногда это внутреннее произведение называют перекрытием. Принцип 3 требует, чтобы физически различные состояния представлялись ортогональными векторами состояний, то есть чтобы эти векторы не перекрывались. Так, для состояний 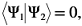 но
но  .
.Наконец, принцип 4 дает количественное выражение этой идее, формируя правило для вероятности различных исходов эксперимента. Если предположить, что система приготовлена в состоянии
 и затем измеряется наблюдаемая L, то результатом будет одно из собственных значений
и затем измеряется наблюдаемая L, то результатом будет одно из собственных значений  оператора L. Но в общем случае невозможно сказать, какое из этих значений будет обнаружено. Есть лишь вероятность — назовем ее P(
оператора L. Но в общем случае невозможно сказать, какое из этих значений будет обнаружено. Есть лишь вероятность — назовем ее P( ) — того, что исход будет
) — того, что исход будет  . Принцип 4 говорит, как вычислить эту вероятность, и она выражается через перекрытие
. Принцип 4 говорит, как вычислить эту вероятность, и она выражается через перекрытие  и |
и | >. Более строго, вероятность равна квадрату абсолютной величины этого перекрытия:
>. Более строго, вероятность равна квадрату абсолютной величины этого перекрытия:  или, что эквивалентно,
или, что эквивалентно, 
Важное следствие этого принципа: операторы, представляющие наблюдаемые, — эрмитовы.
Наблюдаемые по оси Z
Рассмотрим
 , которая имеет фиксированную однозначную величину для состояний
, которая имеет фиксированную однозначную величину для состояний  и
и  , и соответствующие измеренные значения
, и соответствующие измеренные значения  = +1 и
= +1 и  = –1.
= –1. - Принцип 1. Каждая компонента ? представляется линейным оператором.
- Принцип 2. Собственные векторы
 — это
— это  и
и  . Соответствующие собственные
. Соответствующие собственные
значения +1 и –1. Это можно выразить абстрактными уравнениями:

- Принцип 3. Состояния
 и
и  ортогональны друг другу. Это можно выразить в виде
ортогональны друг другу. Это можно выразить в виде

- Принцип 4. Вероятности получения при измерении результатов можно выразить в виде

Наблюдаемые по оси Z соответствуют начальному состоянию параметрически рассеянного луча на выходе кристалла BBO, поскольку кристалл в равных количествах производит фотоны, имеющие ортогональные направления поляризации.
Наблюдаемые по оси X
Попробуем сделать то же самое и для компонента
 .
. Собственные векторы
 — это
— это  и
и  с собственными значениями +1 и ?1 соответственно. Уравнение будет иметь следующий вид:
с собственными значениями +1 и ?1 соответственно. Уравнение будет иметь следующий вид:
При этом
 и
и  взаимно ортогональны. Другими словами,
взаимно ортогональны. Другими словами,
Если прибор A имеет наблюдаемые
 или
или  , то по оси
, то по оси  будут равные вероятности обнаружить состояния
будут равные вероятности обнаружить состояния  и
и  . Таким образом, каждое из значений
. Таким образом, каждое из значений  должно быть равно 1/2 — это линейные суперпозиции
должно быть равно 1/2 — это линейные суперпозиции  и
и  , которые соответствуют прохождению фотонов через двухщелевой эксперимент или через интерферометр Маха — Цендера:
, которые соответствуют прохождению фотонов через двухщелевой эксперимент или через интерферометр Маха — Цендера:
Наблюдаемые по оси Y
Наконец, можно проделать то же самое для
 , которому соответствуют измерения Алисы. Собственные векторы
, которому соответствуют измерения Алисы. Собственные векторы  — это состояния
— это состояния  и
и  с собственными значениями +1 и ?1 соответственно. Уравнение будет иметь следующий вид:
с собственными значениями +1 и ?1 соответственно. Уравнение будет иметь следующий вид:
Состояния
 и
и  ортогональны друг другу. Другими словами,
ортогональны друг другу. Другими словами,
При этом существуют дополнительные ограничения на векторы
 и
и  :
:
В первых двух уравнениях
 играет роль
играет роль  . В двух других уравнениях эту роль играет
. В двух других уравнениях эту роль играет  . Данные условия утверждают, что если фотон ориентирован вдоль оси
. Данные условия утверждают, что если фотон ориентирован вдоль оси  , а затем измерен вдоль
, а затем измерен вдоль  , то он с равной вероятностью будет в состоянии
, то он с равной вероятностью будет в состоянии  или
или  . Следует также ожидать, что если фотон ориентирован вдоль оси
. Следует также ожидать, что если фотон ориентирован вдоль оси  , он также с равной вероятностью будет в состоянии
, он также с равной вероятностью будет в состоянии  или
или  . Это приводит к дополнительным условиям:
. Это приводит к дополнительным условиям:
Данные условия достаточны для определения формы векторов
 и
и  , за исключением неопределенности фазы. Представим данные в матричном виде и рассчитаем:
, за исключением неопределенности фазы. Представим данные в матричном виде и рассчитаем:
В результате получается:

которая в сумме дает формулу волновой функции по оси Y:

Наличие наблюдаемых значений по оси Y (измерения Алисы) неизбежно вносят свой вклад в волновую функцию по оси X (наблюдаемые Боба). Представим данные в матричном виде и рассчитаем векторы по оси X:

В результате мы получаем волновую функцию «No-communication theorem»:

Наличие во второй части комплексного числа i говорит о том, что квадрат абсолютного значения дает инверсию амплитуды вероятности. Из этого следует, что при наблюдении Бобом интерференции по оси X, интерференционные максимумы первой части волновой функции
 совпадут с интерференционными минимумами второго, а интерференционные максимумы второго с минимумами первого. Возникнет наложение интерференционных максимумов и взаимное перекрытие двух интерференций, что подтверждается на практике с помощью детектора совпадений:
совпадут с интерференционными минимумами второго, а интерференционные максимумы второго с минимумами первого. Возникнет наложение интерференционных максимумов и взаимное перекрытие двух интерференций, что подтверждается на практике с помощью детектора совпадений:
Благодаря этому, интерференционные максимумы
 и
и  на выходе интерферометра Маха-Цендера будут направлены в разные стороны, а квантовая запутанность обеспечит соответствующие корреляции между наблюдениями Алисы и Боба.
на выходе интерферометра Маха-Цендера будут направлены в разные стороны, а квантовая запутанность обеспечит соответствующие корреляции между наблюдениями Алисы и Боба.<<<<<<<<<<<<<<<>>>>>>>>>>>>>>>

Shkaff
Мы с bull1251 обсуждали текст до публикации, и на мой взгляд, там есть несколько ошибок, но автор придерживается другого мнения.
Собственно, обойти no-communication нельзя, так как она заложена в самой математике квантовой теории. Поэтому если в расчетах у автора получается, что она обходится, и он при этом пользуется стандартной теорией, значит у автора ошибка (или сама теория содержит противоречия).
Самая главная ошибка в том, что предполагается, что фаза в интерферометре зависит от поляризации входящего света (например, запутанные состояния на входе получают разную фазу внутри состояния). Это математически и физически некорректно. Интерферометр состоит из зеркал, и в нем нет элемента, который менял бы фазу по-разному в зависимости от поляризации света.
Вообще, для любого состояния на входе в интерферометр, выход будет зависеть только от фазы внутри интерферометра, но не от самого состояния на входе.
bull1251 Автор
Shkaff
у меня эти состояния определены не так, как у вас (посмотрите картинку). просто буквы те же.
Это просто частный случай фазы ei? в моих расчетах. Только у вас она появляется почему-то внутри состояния. Вы ошибочно задаете фазовый сдвиг внутри интерферометра как:На самом деле он одинаковый для |H> и |V>, и в общем случае может быть любым значением ?.
bull1251 Автор
Волновая функция в двухщелевом эксперименте ничем не отличается от волновой функции в интерферометре Маха -Цендера. Так как мы рассматриваем волновую функцию «No-communication theorem»:

то никакой ошибки нет. Если бы фазовый сдвиг был одинаковый, то можно было бы не учитывать фазу. В этом случае наличие комплексного числа i в волновой функции не играло бы никакой роли.
Shkaff
Вы не ссылайтесь на другие эксперименты (там тоже есть, что обсудить), а расскажите, какой физический процесс отвечает за приобретение разной фазы для разных поляризаций?
Нет, нельзя — в моих вычислениях это наглядно показано. В зависимости от сдвига у вас будет разная интерференция на выходе. Но сдвиг не зависит от входящего состояния.bull1251 Автор
Сдвиг фазы действительно не зависит от входящего состояния, поскольку зависит от фазы запутанной пары на стороне Алисы.
Shkaff
Такого быть не может. Вы пишете, что преобразование в интерферометре описывается такими матрицами:

Каков физический процесс, обеспечивающий разницу между матрицами для двух поляризаций?
bull1251 Автор
Наличие дополнительной оси измерения запутанной пары на стороне Алисы, позволяющие определить ортогональные вектора состояний в пространстве состояний (наличие дополнительного степени свободы в тензорном произведение векторов).
Shkaff
Нет, Алиса не может влиять на поведение интерферометра. Результаты измерений Алисы и Боба будут коррелированы, но это не будет влиять на распространение волновой функции в интерферометре.
Вы предлагаете какой-то механизм, в котором интерферометр ведет себя по-разному, в зависимости от результата измерения у Алисы. Но такого быть просто не может (разве что они используют обратную связь для управления интерферометром, но тогда какая тут сверхсветовая передача). А представьте, что Алиса еще не измерила свою часть?
bull1251 Автор
Эксперименты по проверке неравенства Белла утверждают обратное. Само название квантовой нелокальности говорит о том, что локальных объяснений для квантовых корреляций не существует, а все попытки локальных объяснений приводят к наличию скрытого параметра и противоречат экспериментальным данным.
Временной порядок не играет никакой роли. Об этом упоминается в статье. А также приводиться описание прекрасного релятивистского эксперемента «До-До» проведенного в Женеве в конце 2000-х в начале 2001 годов.Shkaff
При чем тут нелокальность волновой функции? Вы утверждаете, что Алиса воздействует на интерферометр как-то так, что он на разные состояния действует по-разному. Такого не бывает.
bull1251 Автор
Бывает. Поскольку мы рассматриваем нелокальные состояния, то не возможно разделить квантовое состояние запутанных пар на стороне Алисы и на стороне Боба. Любые воздействия со стороны Алисы будут влиять запутанной паре на стороне Боба. А любые воздействия со стороны Боба будут влиять запутанной паре на стороне Алисы. А любые другие попытки интерпретации приводят к наличию скрытого параметра (наличию перчаток Эйнштейна) которая успешно опровергается при экспериментальной проверке неравенства Белла.
Shkaff
Это не имеет значения. Интерферометр не может влиять по-разному на разные поляризации, будь они в запутанности или нет. Запутанность она между волновыми функциями, а фаза вносится операторами эволюции. Одно на другое никак не влияет.
А если думаете иначе — напишите полную эволюцию волновой функции включая Алису в каждый момент времени, и покажите, как у вас так получается, что для разных поляризаций разная фаза.
Потому что пока у вас только общие высокие слова про «нелокальность» и «неравенства Белла».
mihaild
Насколько я понял, главный момент — магический неунитарный «поляризатор», который из |x>\otimes |b> + |y>\otimes |d> (в каком-то там базисе) делает (с точностью до нормировки) |z> \otimes |d>. Такая штука и правда позволила бы передавать информацию.
Shkaff
Я, признаться, так далеко не зашел в попытках понять, где ошибка. Я увидел, что в матетматике проблема уже на этапе простого интерферометра, где выход зависит от поляризации входа (и от фазы на входе) и остановился на этом.
А где это в тексте?
mihaild
Я как раз не перепроверял перемножение матриц (ну там какие-то числа, наверное перемножено правильно; в конце концов, тут неважно, интерферометр у нас или что, можно считать, что любые унитарные преобразования нам доступны).
 , которая из пары (частица у Боба, частица у Алисы) делает две частицы у Боба… bull1251, что это вообще означает?
, которая из пары (частица у Боба, частица у Алисы) делает две частицы у Боба… bull1251, что это вообще означает?
В явном виде это действительно не написано, но кажется, что сформулированные словами выводы («Если Боб расположит на выходе интерферометра противоположно направленные круговые поляризаторы, то благодаря квантовым корреляциям ни один фотон не попадет на детекторы. Но если Алиса поменяет круговой поляризатор на линейный, то 25% запутанных частиц попадут на верхний и 25% на нижний детектор») соответствуют отбрасыванию в состоянии слагаемых, соответствующих поляризации, которую отфильтровывает поляризатор у Алисы.
Еще присмотревших можно увидеть совсем уж магическую \Rightarrow
Shkaff
Ну да, там магия и раньше (то, на чем я остановился), когда одно и то же преобразование (фазовый сдвиг) описывается двумя разными матрицами в зависимости от поляризации:

Это как раз у него и получается потому, что в зависимости от поляризации на входе меняется распределение вероятностей на выходе. Если бы такое работало, то, конечно, смена поляризации Алисой влияло бы на результаты измерений Бобом.mihaild
Да, правда. Этот момент я пропустил, а откуда взялись две разные матрицы — непонятно.
bull1251 Автор
Две разные матрицы возникают из волновой функции «no-communication theorem», поскольку это матричное представление волновой функции:

mihaild
Так что это за две матрицы? Это явно какие-то преобразования состояния — к какому подпространству они применяются? Почему их две?
(я про матрицы фазового сдвига, а не координатную запись волновой функции)
bull1251 Автор
Если рассматривать данные уравнения

В первом случае применена единичная матрица для фотонов, запутанные пары которых имеют горизонтальную поляризацию на стороне Алисы. Во втором случае применена матрица Джонса для полуволновой пластины для фотонов, запутанные пары которых имеют горизонтальную поляризацию на стороне Алисы.
Преобразования с помощью этих матриц позволяют получить волновую функцию «no-communication theorem» на плечах интерферометра.
mihaild
Это просто вычисления (а давайте применим матрицу к состоянию и посмотрим на результат), или утверждается, что где-то есть физическое устройство, совершающее это преобразование?
bull1251 Автор
Волновая функция «no-communication theorem» описывает не только работу интерферометра на стороне Боба, но также неразрывно связана с измерениями Алисы. В данном случае, измерения Алисы приводят к подобному преобразованию волновой функции на стороне Боба. При этом, не столь важно с помощью чего производиться измерение на стороне Боба — с помощью интерферометра или двух щелей. В обоих случаях возникают два шаблона интерференции обладающих разностью фаз.
mihaild
>В данном случае, измерения Алисы приводят к подобному преобразованию волновой функции на стороне Боба
Что это значит, и где это написано? Никакой «волновой функции на стороне Боба» нет, там максимум матрица плотности, т.к. его частица спутана с внешним миром. И естественно никакого влияния на матрицу плотности у Боба измерения Алисы не оказывают (это примерно одна из формулировок no communication theorem).
В любом случае, вопрос не про теорему, а про предлагаемую вами схему.
bull1251 Автор
В данном случае я хотел показать, что на выходе интерферометра фотоны из первого уравнения будут направлены вниз
mihaild
Нужно уточнять. Если преобразования унитарны, то так происходит. Но тогда поляризатор не может просто вычеркивать слагаемые из волновой функции.
Пусть у нас было состояние 1/\sqrt{2} (|H>\otimes |V> + |V>\otimes |H>). На пути первого фотона мы поставили горизонтальный поляризатор, на пути второго — вертикальный. Что, по-вашему, мы будем наблюдать на детекторах? Изменится ли что-то, если на пути первого фотона поставить диагональный поляризатор?
Можете переписать эти формулы, явно указав, какая компонента относится к Алисе, а какая — к Бобу?
bull1251 Автор
Я не совсем понял описание Вашего вопроса.
Да, я тоже считаю, что это необходимо сделать во избежание путаницы.mihaild
Я не очень понял, что вы не поняли. Какое первое предложение вам непонятно в следующем списке:
Ну сделать это можете только вы, потому что я не понимаю, какая у вас там компонента где.1. Начальное состояние: пара запутанных фотонов, один у Алисы, другой у Боба, в состоянии
2. Боб ставит у себя горизонтальный поляризатор и детектор.
3. Алиса ставит у себя детектор, а перед ним
3а) горизонтальный поляризатор
3б) вертикальный поляризатор
3в) диагональный поляризатор
Очевидно, что есть 4 варианта результатов — сработал ли детектор у Алисы или нет, и сработал ли детектор у Боба или нет. С какой частотой они будут происходить в каждом из пунктов? В частности, будет ли у Боба во всех трех вариантов (а, б, в) одинаковое число срабатываний, или нет?
bull1251 Автор
Shkaff
Ну просто:
У вас не может быть суммы интенсивности и косинуса — чисто из соображения размерности.
bull1251 Автор
Почему вы решили, что это уравнение неправильное? Лично я не вижу никакой ошибки.
Более того, данное уравнение было представлено физиками, которые создали «no-communication theorem» — en.wikipedia.org/wiki/Quantum_eraser_experiment.
Shkaff
Если I1,2имеет размерность интенсивности, вы не можете его прибавить к косинусу, который безразмерный. На вики тоже ошибка. Правильной была бы формула, где у косинуса еще можитель v(I1I2)
bull1251 Автор
Первая половина уравнения описывает квадрат абсолютного значения по модулю, поэтому там не может быть квадратного корня. А вторая половина описывает Эрмитово сопряжение, кстати, интересный вопрос, почему там нет квадратного корня… Но подождите, мы же не ищем амплитуду вероятности, почему вы решили, что там должен быть квадратный корень?
Shkaff
Потому что I1,2 = |f1,2|2, тогда |f1f*2| = v(I1I2)
mihaild
А почему у вас преобразования \Phi_1 \to \Phi_3 и \Phi_2 \to \Phi_4 разные?
>выход будет зависеть только от фазы внутри интерферометра, но не от самого состояния на входе
Это если мы сразу на выходе ставим детекторы. Так-то все преобразования унитарны, и фаза на выходе линейна по фазе на входе.
Shkaff
Я имел в виду «изменение состояния будет зависеть только от фазы внутри». Глобальная фаза, разумеется, сохраняется, но она ни на что и не влияет.
UncleAndy
Очень интересно. Спасибо за статью!
Num
Как обойти No-communication theorem? — Да очень просто, придумать новую физику, в которой такая теорема не выполняется. Делает ли это автор? — Нет.
bull1251 Автор
Опишите пожалуйста ваше предложение на математическом языке, чтобы я мог понять смысл ваших слов.
Num
С удовольствием, изучайте.
появляется чуть ли не после трети всей статьи.Мне нравится как вы структурно оформили статью — сразу в бой и с формулами. В то время как самый существенный абзац:
Вы ставите себе исследовательскую задачу — обойти no-communication theorem и передать информацию быстрее скорости света. Более того, вы признаете, что математический вывод данной теоремы корректен, однако не понимаете либо отказываетесь принимать физический смысл теоремы.
Вы говорите про «изъян» и приводите собственную неверную интерпретацию.
Но даже на этом моменте не всё потеряно: имея одно неверное предположение, корректно оперируя формулами внутри заданного фрэймворка вы бы неизбежно пришли к противоречию. Однако вы не, что означает ошибочность либо вычислений, либо предположений, и мне даже не нужно указывать место, где именно находится ошибка, поскольку вы пытаетесь вывести утверждение, которое в рамках выбранной математической и физической модели принципиально невозможно.
Чтобы
вечный двигательсверхсветовая передача была возможна, вам нужно придумать такую математическую и физическую модель, в которой no-communication theorem не выполняется. И уже после этого проводить вычисления и придумывать эксперимент.Моя рекомендация: начните с азов. Без понимания базовых вещей невозможно вести корректный синтез.
TionRus
Наивно думать, что бит информации может быть передан в прошлое. Потому как, полученный бит можно инвертировать и отправить. Получится что отправленный бит не равен полученному, а значит устройство и собственно теория не сработала.
bull1251 Автор
Почему вы думаете, что законы физики позволят Вам отправить инвертированный бить информации? Судя по копенгагенской интерпретации квантовой механики вы не можете этого сделать не при каком случае, поскольку это противоречит закону сохранения импульса. Согласно многомировой интерпретации это можно сделать, но распределение вероятностей изначально будет совершенно иным (поскольку вы решили отправить инвертированный бит, то изначально Вы получите информацию состоящее на 50% из одного значения и на 50% из другого значения).
Не следует думать, что это является продуктом моей фантазии, это является лишь следствием математических расчетов, которые представлены выше в самом посте.
TionRus
Какие законы физики запрещают инвертировать биты и скармливать их устройству?
Да и если мы говорим что no-communication это теорема, доказанная, то нужно не обходить ее, а искать ошибки в доказательстве либо доказывать, что исходные предпосылки, использованные для ее доказательства не верны.
kauri_39
Вы не задумывались о другом способе реализации сверхсветовой связи? Все мы, и запутанные фотоны тоже, находимся в энергетически плотной среде, а продольные волны её плотности распространяются наверняка быстрее, например, поперечных гравитационных волн. Что если они служат носителем информации для постоянной нелокальной корреляции спинов запутанных фотонов, которая обнаруживается при их измерении?
Я не знаю, какие волны получилось генерировать в начале 80-х в ОИЯИ, но там для их генерации использовали квантовые процессы — накачку молекулярного водорода в одном цилиндре лазерным когерентным излучением. Она должна была порождать в физическом вакууме волну снижения плотности его энергии. И прохождение этой волны через второй цилиндр с ранее возбуждёнными молекулами водорода вызовет у них сброс фотонов, которые регистрируются. С одновременным излучением волны повышенной плотности энергии.
Результаты этих опытов мне не известны, может, кто-то знает. Я уверен в существовании сверхсветовой связи, которой пользуются взрослые цивилизации Вселенной.
math_coder
Главная ошибка здесь не в вычислениях и не в рассуждениях, а в другом — в месте и форме публикации. Такие вещи принято публиковать в научных журналах. Когда вместо этого автор пытается "обаять" широкую публику (вроде публики Хабра), это называется лженаука.
bull1251 Автор
Я не уверен, что такую работу можно опубликовать в научных журналах. Мне кажется, что за такую работу скорее «на костре сожгут» нежели опубликуют.
mihaild
Да не сожгут. Ответят что-то вроде «советуем уточнить формулировки и доказательства» или «первая ошибка в строке такой-то».
Но да, обращение к широкой аудитории вместо специалистов под предлогом «ученые скрывают» — один из стандартных маркеров именно лженауки.
Shkaff
Думаю, даже до рецензии не дойдет. Обойти no-communication в рамках стандартной квантовой теории математически невозможно, как заметил Num выше. Тратить время рецензентов на это ни один редактор журнала не станет.
mihaild
Вроде бы на всё присылаемое дают хоть какой-то ответ. Подробного разбора, естественно, не будет, будет отписка «что-то невнятное», но вежливо сформулированная.
Shkaff
Да, конечно, ответят, только редактор журнала, а не научный рецензент. Напишут что-нибудь красивое, типа «спасибо за проявленный интерес, но сейчас так много статей, что при всем желанию вашу никак не можем рассмотреть к публикации, попробуйте в другой журнал». Плавали, знаем:)
mihaild
Это вроде бы шаблон для случая «ну вроде что-то написано, может быть даже что-то осмысленное, но непонятно, а разбираться смысла не видно».
Shkaff
Наверное, вы правы:) Никогда не пробовал опровержения квантовой теории печатать.
bull1251 Автор
Но тем не менее, некоторые теории опровергались (или дополнялись). По большей части экспериментально. Но, увы, у меня нет возможности провести подобный эксперимент.
Shkaff
Прежде чем делать эксперимент, вам нужно объяснить, почему это должно работать. Пока я вижу странную математику и не очень ясные рассуждения вокруг.
Мы делали подобный эксперимент (только вместо интерферометра был резонатор), и естественно, никаких отклонений от стандартной теории не наблюдали.
Сделать эксперимент как вы описываете тоже не сложно, но это время, которое можно потратить на что-то, что работает хотя бы в теории.
mihaild
А зачем тут эксперименты? Вы же пытаетесь рассуждать в имеющемся формализме. За обнаружение противоречий в математическом аппарате квантмеха (тем более на совсем базовом уровне) дадут нобелевку ничего не спрашивая об экспериментах.
В конце 19 — начале 20 века в физике как раз массово лезли именно математические противоречия. Навскидку могу вспомнить противоречие между механикой Ньютона и уравнениями Максвелла (в механике Ньютона выполнен принцип относительности Галилея, в электродинамике нет) или ультрафиолетовую катастрофу. И вы тут тоже претендуете на в том числе чисто математический результат.