В этой статье я (опять) хочу рассмотреть алгоритм поиска решения задачи полного покрытия, теперь уже с нормальной реализацией через структуру "танцующих ссылок". Заодно на этом примере хочу показать, где и зачем указание типов в Julia критично для производительности, а где оно не обязательно.
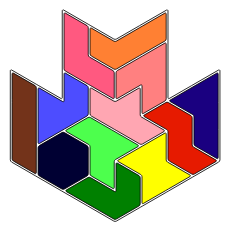
Задача точного покрытия множества некоторым набором его подмножеств состоит в выборе попарно непересекающихся подмножеств , в сумме составляющих . Например, если множество — это геометрическая фигура, а — это кусочки "паркета", то задача точного покрытия спрашивает, можно ли замостить фигуру таким паркетом.
Как пример можно рассмотреть складывание геометрических фигур из фигурок пентамино
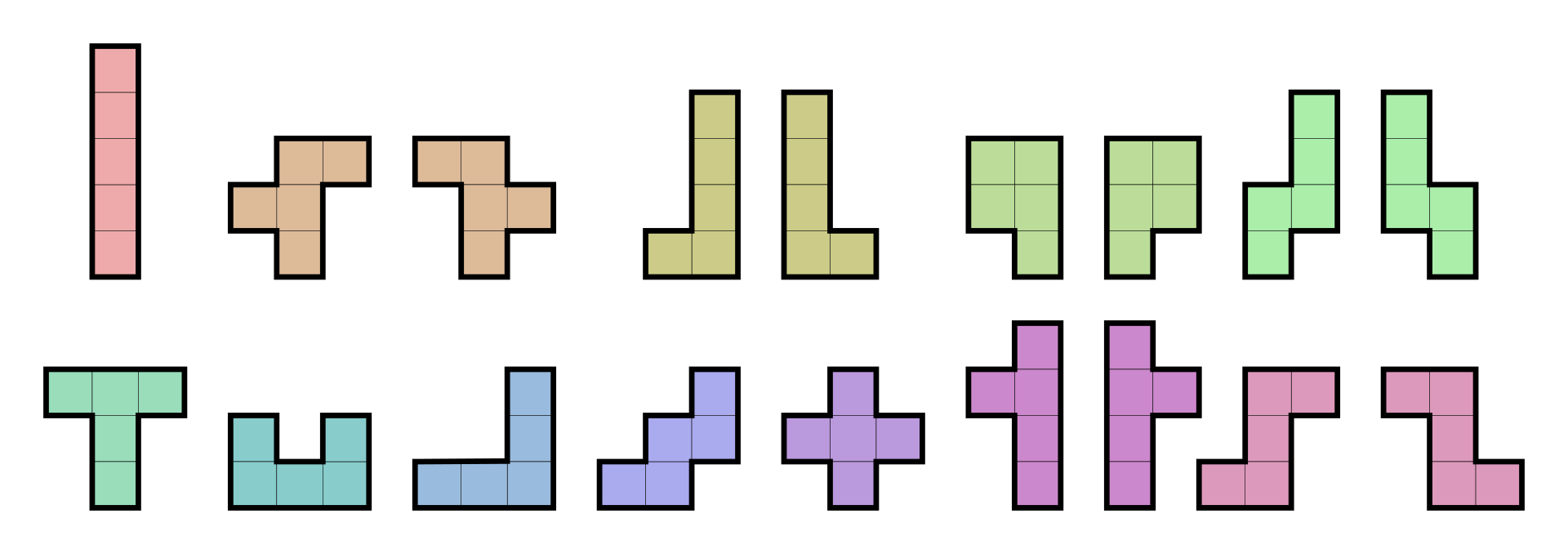
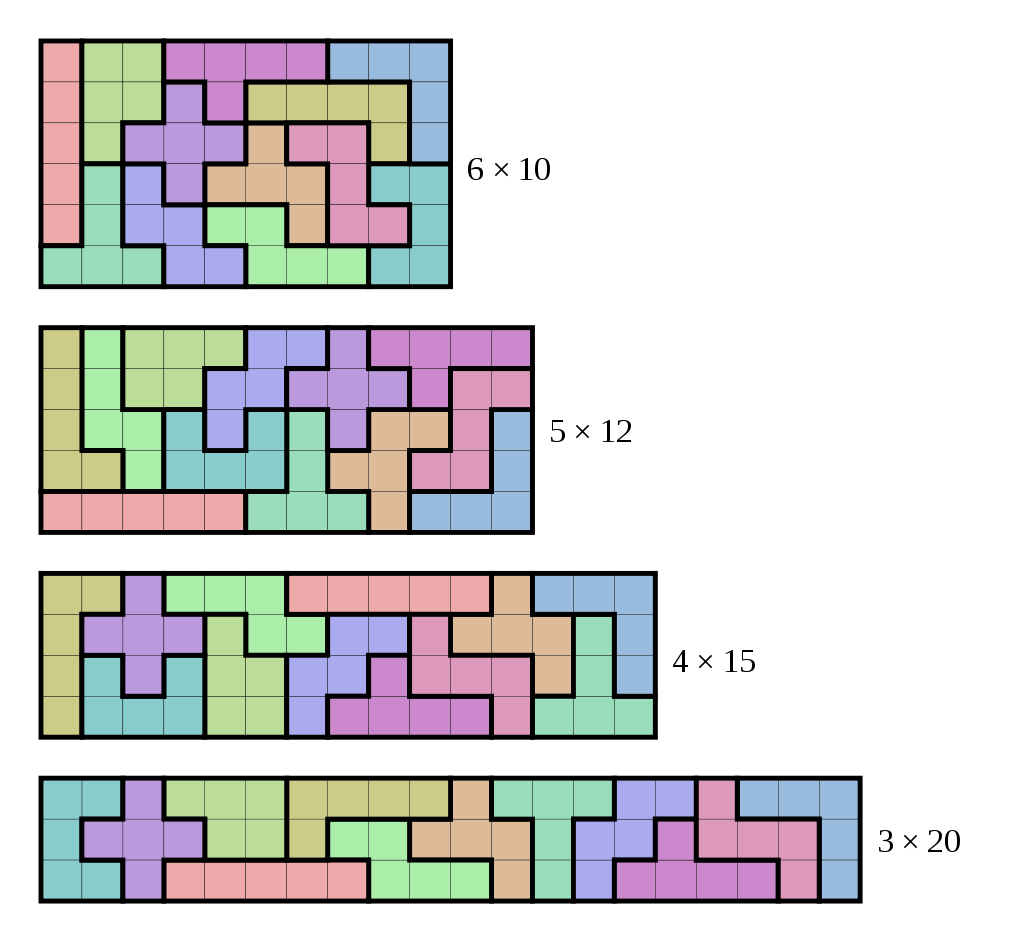
Некоторые решения для прямоугольников (из Википедии):
Для конечного множества и конечного числа подмножеств задача может быть представлена как матрица логических значений (0/1), где в -й строке единицы соответствуют элементам множества , содержащимся в . Задача тогда состоит в выборе таких строк, чтобы в получившейся матрице в каждом столбце была ровно одна единица.
Пример матрицы:
| № строки | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| 2 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 3 | 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| 4 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 5 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 6 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
Строки 1, 4 и 5 составляют точное покрытие.
Задача является NP-полной, поэтому единственным гарантированным способом решения является поиск с возвратом. Особенности задачи позволяют построить специальную структуру данных для такого поиска, популяризованную Дональдом Кнутом, — систему "танцующих ссылок".
"Алгоритм X"
Алгоритм поиска точного покрытия, описанный Кнутом в работе "Танцующие ссылки", представляет собой простой поиск с возвратом. Псевдокод этой процедуры выглядит следующим образом:
Вход:
`matr` - матрица из непокрытых столбцов
`solution` - массив, содержащий строки решения
`k` - указатель на текущий индекс массива
Процедура `Algorithm_x`
Если `matr` не содержит непокрытых столбцов:
Вернуть (или вывести) `solution`.
Иначе выбрать столбец `c`.
Покрыть столбец `c`.
Для всех строк `r`, пересекающихся со стобцом `c`:
Записать `solution[k] = r`.
Для всех столбцов `j`, пересекающихся с `r`:
Покрыть столбец `j`.
Вызвать `Algorithm_x(matr, solution, k+1)`.
Если алгоритм нашёл решение, вернуть его.
(бэктрекинг)
Для всех столбцов `j`, пересекающихся с `r`:
Восстановить столбец `j`.
Восстановить столбец `c`.
Возврат из процедуры."Покрытие" столбца c означает вычёркивание из матрицы его и всех строк, с которыми он пересекается (поскольку если столбец покрыт какой-либо строкой r, то другими строками его покрыть уже нельзя). Восстановление означает вставку удалённого столбца и строк обратно.
Танцующие ссылки
Поскольку алгоритм поиска с возвратом требует удаления некоторых ветвей решения и возвращения их на место, неплохо бы использовать структуру данных, с которой это можно сделать быстро. Кнут в качестве такой структуры данных предлагает "танцующие ссылки", основанные на представлении матрицы в виде тороидально связанного списка.
Идея танцующих ссылок основана на том, что удаление узла node из двусвязного списка делается очень просто: если элемент имеет ссылку prev на предыдущий и next на следующий элемент, то удаление — это
node.next.prev = node.prev
node.prev.next = node.nextПри этом сам узел списка сохраняет информацию о том, какие узлы были его соседями. Благодаря этой информации узел можно восстановить:
node.next.prev = node
node.prev.next = nodeЕсли из списка удалено несколько элементов, то вставка их в порядке, обратном порядку удаления, восстанавливает исходное состояние списка.
Для булевой матрицы можно представлять единичные элементы узлами списка, связанного по двум направлениям. Для приведённой выше матрицы список будет выглядеть так (из статьи Кнута):

h — входной узел для структуры, в узлах A — G хранятся ссылки на соседей и число строк, пересекающих столбец, в остальных узлах хранятся только ссылки на ненулевые элементы в той же строке и в том же столбце. Также внутренние узлы хранят ссылки на заголовки столбцов, на рисунке не показанные.
Процедура покрытия столбца в этой структуре требует следующих действий:
- Отцепить заголовок столбца от правого и левого соседей.
- Проходя по ссылкам вниз, для каждой пересекаемой строки $r$ отцепить от соседей сверху и снизу все ссылки в той же строке, кроме собственно $r$.
Восстановление выполняется в обратном порядке — сначала восстановить для каждой строки (проходя вверх по ссылкам от заголовка столбца) соседей по вертикали, затем восстановить заголовок столбца в ряду. Чтобы структура корректно восстанавливалась, покрытие и восстановление столбцов должны вызываться в строго обратном порядке.
Рассмотрим реализацию этой структуры и алгоритма поиска точного покрытия на языке Julia.
Узел списка содержит ссылки на узлы слева, справа, сверху и снизу и на головной узел столбца, к которому он относится:
mutable struct LinkNode
left
right
above
below
col
# конструктор с привязкой к столбцу
function LinkNode(col)
self = new()
self.above = self.below = self.right = self.left = self
self.col = col
return self
end
# конструктор с пустым столбцом (для входного узла)
function LinkNode()
self = new()
self.above = self.below = self.right = self.left = self
return self
end
endГоловной узел столбца содержит ссылки на соседние элементы, размер и идентификатор.
mutable struct LinkColumn
links
size
id
function LinkColumn(id)
self = new()
links = LinkNode(self)
self.links = links
self.size = 0
self.id = id
return self
end
endСама матрица представляется входным узлом, от которого можно перейти к списку матриц.
struct LinkMatrix
root_node
#=
конструктор создает список столбцов из итерируемого объекта,
содержащего идентификаторы столбцов
=#
function LinkMatrix(ids)
root = LinkNode()
self = new(root)
prev = root
for id in ids
col = LinkColumn(id)
collinks = col.links
collinks.left = prev
collinks.right = root
prev.right = collinks
root.left = collinks
prev = collinks
end
return self
end
endАлгоритм поиска точного покрытия записывается в соответствии с псевдокодом:
function algorithm_x!(matr, solution=FullRow[])
if iscovered(matr)
return solution
end
col = choose_col(matr)
cover!(col)
for node in col
push!(solution, FullRow(node))
for j in RestRow(node)
cover!(j.col)
end
if !isnothing(algorithm_x!(matr, solution))
return solution
end
node = pop!(solution).node
# важен порядок восстановления
for j in Iterators.reverse(RestRow(node))
uncover!(j.col)
end
end
uncover!(col)
return
endВспомогательные структуры данных и процедуры:
# проверка, покрыта ли матрица полностью
iscovered(matr) = matr.root === matr.root.right
# итератор по столбцам матрицы
function Base.iterate(matr::LinkMatrix, next = matr.root.right)
next === matr.root && return
return (next.col, next.right)
end
#=
структура данных, представляющая все узлы в строке,
кроме заданного
=#
struct RestRow
node
end
# итерация по всем узлам в строке, кроме заданного
function Base.iterate(row::RestRow, next = row.node.right)
next === row.node && return
return (next, next.right)
end
# итерация справа налево
function Base.iterate(row::Iterators.Reverse{<:RestRow}, next = row.itr.node.left)
next === row.itr.node && return
return (next, next.left)
end
# строка, содержащая заданный узел
struct FullRow
node
end
# итерация по строке, начиная с заданного узла
function Base.iterate(row::FullRow)
node = row.node
return (node, node.right)
end
function Base.iterate(row::FullRow, next)
next === row.node && return
return (next, next.right)
endВыбор столбца, который пытаемся накрыть следующим, делается на основе "S-эвристики" — выбирается столбец, для которого меньше всего возможных накрывающих его строк:
function choose_col(matr)
bestcol = matr.root.right.col
s = bestcol.size
for col in matr
l = col.size
l < 2 && return col # если возможен только 1 вариант или ни одного, выбираем сразу
if l < s
s, bestcol = l, col
end
end
return bestcol
endПроцедура cover!(col) "отцепляет" столбец от правого и левого соседей (что важно — оставляя связи по вертикали без изменений, чтобы можно было потом восстановить), затем проходится по каждой строке и отцепляет узлы от соседей сверху и снизу (кроме тех ссылок, которые по цепочке ведут к столбцу col). Когда узел отцепляется от соседей по вертикали, размер столбца, где он находился, уменьшаем на единицу.
function cover!(col)
detach_rl!(col.links)
for node in col
for elt in RestRow(node)
detach_ab!(elt)
end
end
end
# отсоединяет от соседей слева и справа
function detach_rl!(node)
node.right.left = node.left
node.left.right = node.right
return node
end
# отсоединяет от соседей сверху и снизу
function detach_ab!(node)
node.above.below = node.below
node.below.above = node.above
node.col.size -= 1
return node
endПроцедура восстановления, uncover!(col) возвращает всё назад:
function uncover!(col)
# важен порядок прохода по столбцу
for node in Iterators.reverse(col)
# порядок прохода по строке не важен
for elt in RestRow(node)
restore_ab!(elt)
end
end
restore_rl!(col.links)
end
function restore_rl!(node)
node.right.left = node
node.left.right = node
return node
end
function restore_ab!(node)
node.above.below = node
node.below.above = node
node.col.size += 1
return node
endВсё, что осталось для удобной жизни — это добавить процедуру добавления строки, которая накрывает столбцы с заданными идентификаторами:
#=
matr - матрица, куда вставляется строка
col_ids - коллекция с идентификаторами
=#
function insert_row!(matr, col_ids)
isempty(col_ids) && return
num_inserted = 0
first_in_row = nothing
prevnode = nothing
# идём по столбцам, если id подходит - создаём новый узел, прицепляем к строке
for col in matr
if col.id in col_ids
newnode = LinkNode(col)
if isnothing(first_in_row)
first_in_row = newnode
end
first_in_row.left = newnode
newnode.right = first_in_row
if !isnothing(prevnode)
prevnode.right = newnode
newnode.left = prevnode
end
prevnode = newnode
num_inserted += 1
# если все идентификаторы найдены - подцепляем строку к матрице
if num_inserted == length(col_ids)
for node in FullRow(first_in_row)
col = node.col
collinks = col.links
lastnode = collinks.above
col.size += 1
node.above = lastnode
node.below = collinks
lastnode.below = node
collinks.above = node
end
return first_in_row
end
end
end
#=
сюда попадаем, если не нашли все идентификаторы
в этом случае строка содержит идентификатор, которого нет в столбцах
игнорируем эту строку и выходим
=#
return
endСкорость работы
Проверим алгоритм на решении судоку и замерим скорость.
Судоку преобразуется в следующую задачу полного покрытия:
(:row, row, num)— в строкеrowесть числоnum(:col, col, num)— в столбцеcolесть числоnum(:block, col, num)— в столбцеblockесть числоnum- (самое хитрое условие)
(:fill, row, col)— на пересечении столбцаcolи строкиrowесть число
Наличие уже заполненных клеток приводит к тому, что часть столбцов уже "накрыта", и их в матрицу задачи вносить не нужно (или можно внести и сразу же "закрыть").
function sudoku2xcover(fill)
ncells = size(fill)
side = ncells[1]
side == ncells[2] || throw(ArgumentError("Invalid matrix size $ncells"))
blockside = isqrt(side)
blockside^2 == side || throw(ArgumentError("Side $side is not a full square"))
row_constr = trues(ncells)
col_constr = trues(ncells)
blk_constr = trues(ncells)
for col in 1:side, row in 1:side
num = fill[row,col]
if num in 1:side
block = col - (col - 1) % blockside + (row - 1) ? blockside
row_constr[row, num] = false
col_constr[col, num] = false
blk_constr[block, num] = false
end
end
constr = collect((:row, row, num) for row in 1:side, num in 1:side if row_constr[row,num])
append!(constr, (:col, col, num) for col in 1:side, num in 1:side if col_constr[col,num])
append!(constr, (:block, block, num) for block in 1:side, num in 1:side if blk_constr[block,num])
append!(constr, (:fill, row, col) for row in 1:side, col in 1:side if !(fill[row,col] in 1:side))
matr = LinkMatrix(constr)
for row in 1:side, col in 1:side, num in 1:side
block = col - (col - 1) % blockside + (row - 1) ? blockside
if row_constr[row,num] && col_constr[col,num] && blk_constr[block,num] && !(fill[row,col] in 1:side)
col_ids = (:row, row, num), (:col, col, num), (:block, block, num), (:fill, row, col)
insert_row!(matr, col_ids)
end
end
return matr
end
function sol2matr(soln, fieldsize)
ans = zeros(Int, fieldsize)
for node in soln
indval = row2indval(node)
ans[indval.ind] = indval.val
end
return ans
end
function row2indval(dlrow)
row, col, n = 0,0,0
for j in dlrow
constr = j.col.id
if constr[1] === :fill
_, row, col = constr
else
_, _, n = constr
end
all(>(0), (row, col, n)) && break
end
return (ind = CartesianIndex(row, col), val = n)
end
function sudoku(fill)
cover = sudoku2xcover(fill)
soln = sol2matr(algorithm_x!(cover), size(fill))
soln .+= fill
return soln
endПосмотрим на время решения "самого сложного судоку" под названием "Золотой самородок"
const testpuzzle = [
0 0 0 0 0 0 0 3 9;
0 0 0 0 1 0 0 0 5;
0 0 3 0 0 5 8 0 0;
0 0 8 0 0 9 0 0 6;
0 7 0 0 2 0 0 0 0;
1 0 0 4 0 0 0 0 0;
0 0 9 0 0 8 0 5 0;
0 2 0 0 0 0 6 0 0;
4 0 0 7 0 0 0 0 0
]
julia> using BenchmarkTools
julia> @btime sudoku(testpuzzle);
33.012 ms (115869 allocations: 3.40 MiB)(ответ не показан, чтобы не спойлить)
Решение требует порядка 0.1 секунды. Быстрее, чем вручную, но как-то не впечатляет. Попробуем "переписать всё в сишном стиле", чтобы ублажить компилятор и ускорить выполнение.
Ускоряем работу, проставив типы
Главная проблема описанной реализации с точки зрения производительности — структуры данных имеют поля с абстрактным типом (когда тип данных поля не указан, он ставится как Any). Поэтому при обращении к полям постоянно требуется боксинг и анбоксинг данных.
Конкретизируем типы полей данных, по возможности. И сразу сталкиваемся с весёлой проблемой. Определение
# так не выйдет
mutable struct LinkNode
left::LinkNode
right::LinkNode
above::LinkNode
below::LinkNode
col::LinkColumn
end
mutable struct LinkColumn
links::LinkNode
size::Int
id::Any
endне проходит, поскольку LinkColumn — неизвестный тип на этапе определения типа LinkNode. По той же самой причине не проходит определение сперва LinkColumn, а потом LinkNode.
Решением в данном случае будут параметрические типы. Поставим тип поля col в структуре LinkNode как параметр, а поле links в LinkColumn будет иметь тип LinkNode{LinkColumn}. Чтобы избавиться от абстрактного типа для id, параметризуем и LinkColumn типом этого поля.
mutable struct LinkNode{C}
left::LinkNode{C}
right::LinkNode{C}
above::LinkNode{C}
below::LinkNode{C}
col::C
function LinkNode(col::C) where {C}
self = new{C}()
self.above = self.below = self.right = self.left = self
self.col = col
return self
end
function LinkNode{C}() where {C}
self = new{C}()
self.above = self.below = self.right = self.left = self
return self
end
end
mutable struct LinkColumn{T}
links::LinkNode{LinkColumn{T}}
size::Int
id::T
function LinkColumn{T}(id) where {T}
self = new{T}()
links = LinkNode(self)
self.links = links
self.size = 0
self.id = id
return self
end
end
LinkColumn(id::T) where {T} = LinkColumn{T}(id)С LinkMatrix проделываем ту же процедуру.
struct LinkMatrix{T}
root::LinkNode{LinkColumn{T}}
function LinkMatrix{T}(ids) where {T}
root = LinkNode{LinkColumn{T}}()
self = new{T}(root)
prev = root
for id in ids
col = LinkColumn{T}(id)
collinks = col.links
collinks.left = prev
collinks.right = root
prev.right = collinks
root.left = collinks
prev = collinks
end
return self
end
end
LinkMatrix(ids) = LinkMatrix{eltype(ids)}(ids)Нужно не забыть указать типы полей во вспомогательных структурах:
struct RestRow{L<:LinkNode}
node::L
end
struct FullRow{L<:LinkNode}
node::L
endПроверяем:
julia> @btime sudoku(testpuzzle);
777.426 ?s (6803 allocations: 209.91 KiB)Время выполнения улучшилось с 33 мс до 0.8 мс при том, что типы переменных не указаны нигде, кроме полей структур, конструкторов и перегруженных методов для iterate, где аннотации типов необходимы для правильной диспетчеризации.
Однако стоит дописать аннотацию типа ещё в одном месте — для аргументов процедуры algorithm_x!, где в качестве аргумента по умолчанию указан контейнер с абстрактным типом элементов. Благодаря множественной диспетчеризации можно напрямую перегрузить метод, вызываемый с одним аргументом.
function algorithm_x!(matr::LinkMatrix{T}) where {T}
RowType = FullRow{LinkNode{LinkColumn{T}}}
solution=RowType[]
return algorithm_x!(matr, solution)
endПроверяем:
julia> @btime sudoku(testpuzzle);
547.812 ?s (3603 allocations: 129.16 KiB)Итого получили ускорение больше чем в полсотни раз. При этом каких-то нечеловеческих усилий для расстановки типов прилагать вовсе не приходится, достаточно это сделать только в ключевых местах, в первую очередь — в полях структур (где, в большинстве случаев, о предполагаемых типах полей так и так нужно задумываться). Сильно в этом помогают параметрические типы — если заранее неизвестно, какого типа может быть поле структуры, чаще всего его стоит не оставлять без типа (т.е. с типом Any), а делать его тип параметром:
struct SomeStruct{T}
data::T
endТак поле data может быть чем угодно, но не придётся жертвовать скоростью выполнения.
Заключение
Дизайн языка Julia позволяет использовать его не только как "язык для математиков". Разумная система типов и активное использование аннотаций типов при JIT компиляции позволяют эффективно реализовывать любые классические Computer Science алгоритмы. Особо заморачиваться с типизацией для получения быстрого кода при этом не нужно, что показано примером реализации алгоритма DLX Кнута. Но выставление аннотаций типов в стратегически выверенных точках вполне может дать прирост скорости на 1-2 порядка, поэтому тем, кто начинает программировать на Julia (и тем, кто пробует язык после других языков с динамической типизацией), стоит потратить некоторое время на понимание концепций абстрактных и конкретных типов, параметрических типов, боксинга и устойчивости типов.
