Введение
В былые времена я увлекался компьютерной графикой, как 2х так и 3х мерной, в том числе математическими визуализациями. Что называется just for fun, будучи студентом, написал программу визуализирующую N-мерные фигуры, вращающиеся в любых измерениях, хотя практически меня хватило только на определение точек для 4-D гиперкуба. Но это только присказка. Любовь к геометрии осталась у меня с тех пор и по сей день, и я до сих пор люблю решать интересные задачи интересными способами.
Одна из таких задач попалась мне в 2010 году. Сама задача достаточно тривиальна: необходимо найти, пересекаются ли два 2-D отрезка, и если пересекаются — найти точку их пересечения. Более интересно решение, которое, я считаю, получилось достаточно элегантным, и которое я хочу предложить на суд читателя. На оригинальность алгоритма не претендую (хотя и хотелось бы), но в сети подобных решений я найти не смог.
Задача
Даны два отрезка, каждый из которых задан двумя точками: (v11, v12), (v21, v22). Необходимо определить, пересекаются ли они, и если пересекаются, найти точку их пересечения.
Решение
Для начала необходимо определить, пересекаются ли отрезки. Необходимое и достаточное условие пересечения, которое должно быть соблюдено для обоих отрезков следующее: конечные точки одного из отрезков должны лежать в разных полуплоскостях, если разделить плоскость линией, на которой лежит второй из отрезков. Продемонстрируем это рисунком.
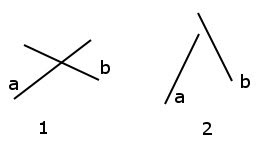
На левом рисунке (1) показаны два отрезка, для обоих из которых условие соблюдено, и отрезки пересекаются. На правом (2) рисунке условие соблюдено для отрезка b, но для отрезка a оно не соблюдается, соответственно отрезки не пересекаются.
Может показаться, что определить, с какой стороны от линии лежит точка — нетривиальная задача, но у страха глаза велики, и всё не так сложно. Мы знаем, что векторное умножение двух векторов даёт нам третий вектор, направление которого зависит от того, положительный или отрицательный угол между первым и вторым вектором, соответственно такая операция антикоммутативна. А так как все вектора лежат на плоскости X-Y, то их векторное произведение (которое обязано быть перпендикулярным перемножаемым векторам) будет иметь ненулевой только компоненту Z, соответственно и отличие произведений векторов будет только в этой компоненте. Причем при изменении порядка перемножения векторов (читай: угла между перемножаемыми векторами) состоять оно будет исключительно в изменении знака этой компоненты.
Поэтому мы можем умножить попарно-векторно вектор разделяющего отрезка на векторы направленные от начала разделяющего отрезка к обеим точкам проверяемого отрезка.
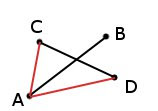
Если компоненты Z обоих произведений будет иметь различный знак, значит один из углов меньше 0 но больше -180, а второй больше 0 и меньше 180, соответственно точки лежат по разные стороны от прямой. Если компоненты Z обоих произведений имеют одинаковый знак, следовательно и лежат они по одну сторону от прямой.
Если один из компонент Z является нулём, значит мы имеем пограничный случай, когда точка лежит аккурат на проверяемой прямой. Оставим пользователю определять, хочет ли он считать это пересечением.
Затем нам необходимо повторить операцию для другого отрезка и прямой, и убедиться в том, что расположение его конечных точек также удовлетворяет условию.
Итак, если всё хорошо и оба отрезка удовлетворяют условию, значит пересечение существует. Давайте найдём его, и в этом нам также поможет векторное произведение.
Так как в векторном произведении мы имеем ненулевой лишь компоненту Z, то его модуль (длина вектора) будет численно равен именно этой компоненте. Давайте посмотрим, как найти точку пересечения.
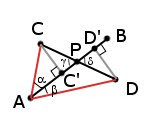
Длина векторного произведения векторов a и b (как мы выяснили, численно равная его компоненте Z) равна произведению модулей этих векторов на синус угла между ними (|a| |b| sin(ab)). Соответственно, для конфигурации на рисунке мы имеем следующее: |AB x AC| = |AB||AC|sin(?), и |AB x AD| = |AB||AD| sin(?). |AC|sin(?) является перпендикуляром, опущенным из точки C на отрезок AB, а |AD|sin(?) является перпендикуляром, опущенным из точки D на отрезок AB (катетом ADD'). Так как углы ? и ? — вертикальные углы, то они равны, а значит треугольники PCC' и PDD' подобны, а соответственно и длины всех их сторон пропорциональны в равном отношении.
Имея Z1 (AB x AC, а значит |AB||AC|sin(?) ) и Z2 (AB x AD, а значит |AB||AD|sin(?) ), мы можем рассчитать CC'/DD' (которая будет равна Z1/Z2), а также зная что CC'/DD' = CP/DP легко можно высчитать местоположение точки P. Лично я делаю это следующим образом:
Px = Cx + (Dx-Cx)*|Z1|/|Z2-Z1|;
Py = Cy + (Dy-Cy)*|Z1|/|Z2-Z1|;
Вот и все. Мне кажется что это действительно очень просто, и элегантно. В заключение хочу привести код функции, реализующий данный алгоритм. В функции использован самодельный шаблон vector<typename, int>, который является шаблоном вектора размерностью int с компонентами типа typename. Желающие легко могут подогнать функцию к своим типам векторов.
1 template<typename T>
2 bool are_crossing(vector<T, 2> const &v11, vector<T, 2> const &v12, vector<T, 2> const &v21, vector<T, 2> const &v22, vector<T, 2> *crossing)
3 {
4 vector<T, 3> cut1(v12-v11), cut2(v22-v21);
5 vector<T, 3> prod1, prod2;
6
7 prod1 = cross(cut1 * (v21-v11));
8 prod2 = cross(cut1 * (v22-v11));
9
10 if(sign(prod1[Z]) == sign(prod2[Z]) || (prod1[Z] == 0) || (prod2[Z] == 0)) // Отсекаем также и пограничные случаи
11 return false;
12
13 prod1 = cross(cut2 * (v11-v21));
14 prod2 = cross(cut2 * (v12-v21));
15
16 if(sign(prod1[Z]) == sign(prod2[Z]) || (prod1[Z] == 0) || (prod2[Z] == 0)) // Отсекаем также и пограничные случаи
17 return false;
18
19 if(crossing) { // Проверяем, надо ли определять место пересечения
20 (*crossing)[X] = v11[X] + cut1[X]*fabs(prod1[Z])/fabs(prod2[Z]-prod1[Z]);
21 (*crossing)[Y] = v11[Y] + cut1[Y]*fabs(prod1[Z])/fabs(prod2[Z]-prod1[Z]);
22 }
23
24 return true;
25 }
Комментарии (33)

Yuuri
17.09.2015 15:28В функции использован самодельный шаблон vector<typename, int>, который является шаблоном вектора размерностью int с компонентами типа typename.
Да это ж std::array!
Скажите, а вы всегда плавучку сравниваете при помощи ==?
vladvic
17.09.2015 15:41Скажите, а вы всегда плавучку сравниваете при помощи ==?
Я понимаю о чём вы, но в данном случае учет погрешности смысла не имеет — если Z даже незначительно больше или меньше нуля, он учтется в ветке, где сравниваются знаки.
MaximNecromant
17.09.2015 18:42Как бы вам это сказать… то что числа с плавающей запятой нельзя сравнивать через == учат на первом семестре любого нормального вуза на соответствующем направлении.

vladvic
18.09.2015 07:16Видите ли, иногда то, чему учат в ВУЗах необходимо переосмысливать. Если вы понимаете, зачем существует это правило, значит вы поймёте, почему в данном случае им можно пренебречь.

MaximNecromant
18.09.2015 12:54+1То что вы проверяете знак не является оправданием. Потому что проверка знака это сравнение с нулем. А сравнение с нулем на вещественных числах тоже делается через введенную точность вычислений. Вы не можете «строго» сравнить с нулем ваше число, т.к. не можете быть уверены что при точности вычислений e, если ваше число меньше e но больше 0, оно точно будет больше 0. Очень странно, что вы не понимаете прописных истин. Нет, конечно если вы берете только «хорошие» случаи, где углы между векторами выражаются в кол-ве градусов больше 1, то на это можно не обращать внимание, но тогда и статью надо было назвать «мое решение задачи с очень ограниченным и практически идеальным набором вариантов». Выше уже писали сколь много случаев вы просто теряете или пренебрегаете ими. Ну вот вам еще один.

vladvic
17.09.2015 15:58Это не совсем std::array, там есть перегруженные операторы и дополнительные функции для работы с векторами.

FransuaMaryDelone
17.09.2015 18:21Попробуйте векторное произведение приладить например к вопросу о пересечении отрезка с треугольником в 3Д. Тоже можно чудно провести время (ну и тут позащищать своё детище).

Aingis
18.09.2015 17:07> Может показаться, что определить, с какой стороны от линии лежит точка — нетривиальная задача, но у страха глаза велики, и всё не так сложно.
Действительно, определить с какой стороны прямой лежит точка — задача тривиальней некуда, и подумать обратное можно только со страху и непривычки.
Достаточно подставить координаты проверяемой точки в уравнение прямой и получившийся знак будет говорить о том, какой полуплоскости принадлежит эта точка. Соответственно, достаточно проверить, что знаки для пары точек каждого отрезка отличаются относительно прямой, которой принадлежит другой отрезок.
Уравнение прямой по двум точкам составляется элементарно: для точек (x1, y1) и (x2, y2) уравнение выглядит как:
(y1 ? y2)·x ? (x1 ? x2)·y + x1·y2 ? x2·y1 = 0
(Равенство нулю, как вы помните, говорит о принадлежности точки прямой.)
Переписываем для точек отрезков (v11, v12) и (v21, v22) и получаем искомое условие:
((v11y ? v12y)·v21x ? (v11x ? v12x)·v21y + v11x·v12y ? v12x·v11y > 0 !=
(v11y ? v12y)·v22x ? (v11x ? v12x)·v22y + v11x·v12y ? v12x·v11y > 0)) &&
((v21y ? v22y)·v11x ? (v21x ? v22x)·v11y + v21x·v22y ? v22x·v21y > 0 !=
(v21y ? v22y)·v12x ? (v21x ? v22x)·v22y + v21x·v22y ? v22x·v21y > 0))
А если использовать функцию определения точки пересечения прямых (которая получается через решение системы уравнений тех же прямых), то достаточно проверить попадания этой точки в отрезки.
Для совсем уж красоты хорошо бы проверять случаи примерного равенства нулю, вычисления чисел с плавающей запятой имеют свойство давать погрешность, но не понимаю чем это сложнее приведённого здесь алгоритма. Это азы аналитической геометрии, которые сложно не знать, имея понятие о векторном произведении.
MaximNecromant
18.09.2015 20:39Не работает в случае нулевого вектора. Вы не сможете проверить на принадлежность полуплоскости, т.к. вы не сможете написать уравнение прямой (иными словами подойдет любое уравнение и что бы вы не подставили всегда будет тождество 0==0). Это действительно нетривиальная задача если рассматривать все а не только очевидные случаи, да еще и с поправкой на формат чисел. Если добавить, что координаты целочисленные, то тогда можно к слову иметь возможность строго говорить о пересечении, совпадении и т.п., т.к. без операций деления мы не выйдем за множество целых чисел (а делить нам нигде не придется, все что при проверках на первый взгляд нужно делить можно преобразовать в операции только умножения).

starosta6123
19.09.2015 11:58Все мы что-то изучаем со временем и переоткрываем, не подозревая, что все уже открыто до нас.
Про себя скажу, что для меня это лучший путь решить задачу и понять логику открытия, чем просто подсмотреть в уже готовое решение.
Ощущения не такие!
Еще в университете «изобрел» один простой способ шифрования данных, но только недавно оказалось, что у него уже есть изобретатель и открыт в 70-х годах. Нужно учитывать, что в то время у меня не было интернета под рукой, чтобы за пять минут найти решение стоящей задачи.
Да, классику нужно знать.

MrShoor
01.10.2015 06:22+1Вот кстати из разряда «То, о чем никогда не задумываешься»:
1. Уравнение прямой в общем виде (ax + by + c = 0) можно записать как вектор (a, b, c)
Тогда чтобы найти точку пересечения двух таких прямых — достаточно взять векторное произведение: Cross( (a1, b1, c1), (a2, b2, c2) ). Мы получим однородные координат в которых лежит наша точка пересечения.
2. У нас есть две точки: (x1, y1) и (x2, y2). Чтобы найти общее уравнение прямой, проходящей через эти точки достаточно взять векторное произведение наших точек в однородных координатах: Cross( (x1, y1, 1), (x2, y2, 1) )
Вот такая красивая симметрия в двух измерениях…

freopen
Каждый начинающий олимпиадник в какой-то момент считает, что пересекать отрезки просто. В вашем случае, например, проблема в том, что один из концов отрезка может лежать на другом отрезке, тогда векторные произведения будут нулевые, однако отрезки будут пересекаться. Попробуйте исправить ваш код так, чтобы он проходил все тесты тут: http://informatics.mccme.ru/mod/statements/view3.php?id=1156&chapterid=280#1.
pehat
Похоже, мы имеем дело с выпускником вуза, который не слышал про книжку Кормена.
vladvic
Про упомянутого Вами автора, каюсь, не слышал.
Ну и выпускник я лет уж как 10.
pehat
Очень популярная книга в узких кругах алгоритмистов и олимпиадных программистов. Один из классических учебников по алгоритмам и структурам данных. Описанный Вами алгоритм можно найти в главе 33. Советую почитать про пирамидальную сортировку, красно-черные деревья, хеш-таблицы, префиксные деревья, систему непересекающихся множеств – очень увлекательные и не менее элегантные штуки, помогающие решать задачи быстро и в относительно небольшом объеме памяти. www.ozon.ru/context/detail/id/22421471
Если захочется попрактиковаться в написании таких алгоритмов – добро пожаловать на codeforces.com, например.
vladvic
Спасибо за наводку. Вот, нашёл в формате djvu www.proklondike.com/var/file/kormen_leiser_algorith.zip
Нашёл указанный Вами алгоритм в главе 35.
Однако в алгоритме у Кормена никак не находится точка пересечения прямых.
vladvic
Спасибо огромное за ценные указания =)
Но видимо, простите, чукча не читатель, чукча писатель? =)
У меня отдельно разобран случай где векторные произведения нулевые, и указано, что считать это пересечением или нет — дело каждого. В моей конкретной реализации этот пограничный случай пересечением не считается.
freopen
Понятно, простота вашего алгоритма заключается в упрощении задачи. Никогда бы не подумал, что бывают люди, считающие совпадающие отрезки непересекающимися…
Уж простите, что не читал, я увидел вот это:
и совсем забил на чтение статьи сосредоточившись на коде.
vladvic
Ну как раз в коде это и учитывается как случай отсутствия пересечения.
А что в этом такого? А еще бывает такое что конечная точка отрезка вообще в отрезок не входит, смотря какой отрезок. Если Вы математику помните, то обозначения вроде (a, b), [a, b], и их комбинации Вам что-то об этом должны напомнить.
freopen
Ни разу не слышал, как (a, b) называют отрезком. Википедия относит к отрезку только [a, b], а (a, b) википедия называет промежутком. Я слышал, как (a, b) называют интервалом, а [a, b) и (a, b] — полуинтервалами, но никогда — отрезками. Но указание вашего учебника математики, в котором это называют отрезками, меня вполне убедит.
Если что, совпадающие отрезки имеют точки пересечения не только в конечных точках, так что очень бы хотелось услышать сколько-нибудь формальное определение пересечения отрезков в котором совпадающие отрезки не пересекаются. Будет совсем здорово, если в этом определении несовпадающие отрезки, которые имеют больше одной общей точки, также не пересекаются.
vladvic
В плане совпадающих отрезков я Вас услышал. Действительно, я лично не уверен, как их классифицировать. В моём случае стояла задача о пересечении отрезков двух различных прямых, но в общем случае Вы правы.
freopen
Соответственно, правильным заголовком будет: «Простой алгоритм пересечения двух интервалов, лежащих на различных прямых». И эта задача решается куда проще.
Первую прямую мы зададим, как A + (B — A) * x, где x — действительное число. Вторую соответственно C + (D — C) * y. Теперь найдем такие x и y, чтобы A + (B — A) * x = C + (D — C) * y. Это и будет точка пересечения, а для проверки принадлежности отрезку (интервалу) надо лишь проверить, принадлежат ли x и y отрезку (интервалу) от нуля до единицы. Доказательство тривиально.
vladvic
Ну во-первых то что вы описали не является алгоритмом. А «найдём такие x и y» подразумевает под собой решение системы двух линейных уравнений.
И, вот, вопрос к вам возник. Является ли пересечением отрезок нулевой длины лежащий на другом отрезке?
freopen
Является в предположении, что мой собеседник знает, как решается система из двух линейных уравнений с двумя неизвестными с предельно щедрой добавкой о ненулевом детерминанте системы. Лично я это проходил в седьмом классе примерно. Поэтому я предположил, что вам будет неинтересно читать о том, как это делается. Но если интересно, скажите, я объясню, там все довольно тривиально.
Является, если принимать во внимание википедийное определение отрезка. Правда он внезапно целиком лежит на прямой другого отрезка, а значит не очень подходит под условие задачи.
vladvic
Ну строго говоря он внезапно лежит на любой прямой проходящей через конечные(ную) точки(ку) нулевого отрезка. Поэтому такая конфигурация подходит под условие и той задачи которая ставилась мне.
Ну и я не вижу, чем решение системы уравнений проще двух векторных произведений.
freopen
Когда я говорил «Лежащих на различных прямых» я имел в виду «Не лежащих на одной прямой», а вовсе не «Существуют две различные прямые такие, что на них можно уложить по отрезку».
Если вы внимательно посмотрите на свой алгоритм, вы поймете, что он не отличает точку лежащую на отрезке и точку, лежащую на прямой, но не на отрезке. Эту разницу просто нельзя вычислить векторными произведениями, которые всегда нулевые, если все лежит на одной прямой.
Строго говоря вычисления более менее одни и те же. Решение системы лучше более простым доказательством и четким пониманием, где оно работает, а где — нет (то, чего так не хватает вашей статье). Ну и бонусом оно нормально работает с отрезками и с многомерными случаями.
vladvic
Ну собственно поэтому я Вам и ответил, что я не учитывал случай отрезков лежащих на одной прямой. Во всех остальных случаях данный алгоритм работать будет.
freopen
На этом я, пожалуй, покину это обсуждение.
vladvic
Вообще говоря, Вы в принципе говорите вещи-то дельные, но Ваш изначально едкий тон совершенно не настраивает на конструктивный разговор.
freopen
Попробуйте в следующий раз прочитать собственную статью перед тем, как упрекать других в том, что они ее не читали.
vladvic
Попробуйте в следующий раз вместо «каждый начинающий олимпиадник» подобрать какое-нибудь более нейтральное обращение, и Вы удивитесь, насколько больше стали прислушиваться к вашим словам.
freopen
Если вы видите предложение, в котором обозначена некоторая группа людей, это не значит, что это обращение. Строго говоря, нет никакой четкой зависимости между этим предложением и этим постом: вы нигде не утверждали, что вы олимпиадник и что вы считаете задачу простой (да, там есть утверждение о тривиальности, но я считал, что это относится к формулировке). Причина существования этого предложения в том, что задача про пересечение отрезков имеет огромное количество простых и неправильных решений, а придумать правильное решение без разбора кучи случаев не очень тривиально, поэтому начинающие олимпиадники пишут первый вариант решения за 10 минут и только через 4 часа двадцать пятый вариант оказывается верным во всех случаях. Я видел столько подобных случаев, что очередное частное решение в виде статьи на хабре не может не вызывать у меня улыбку. Очень жаль, что такое невинное предложение вас обидело, я этого сделать не пытался.
FransuaMaryDelone
Безье бы упомянуть тут.