Почему инициализировать веса нейронной сети одинаковыми значениями (например, нулями)

Главная
Почему инициализировать веса нейронной сети одинаковыми значениями (например, нулями) – это плохая идея

Почему инициализировать веса нейронной сети одинаковыми значениями (например, нулями) – это плохая идея +10

01.12.2021 10:50

ivankrylatskoe 6 3900 Источник

В популярных фреймворках машинного обучения TensorFlow и PyTorch при инициализации весов нейросети используются случайные числа. В этой статье мы попытаемся разобраться, почему для этих целей не используют ноль или какую-нибудь константу.

Кто хочет быстрый и короткий ответ на этот вопрос, вот он: если инициализировать веса нулями, то нейросеть может не обучаться совсем или обучаться плохо.

Кто хочет более развёрнуто узнать, что значит «плохо», может просто перемотать к заключению в конце статьи.

А тем, кто хочет в деталях разобраться с основами обучения нейронных сетей, добро пожаловать в мир математических формул. Мы детально разберём, из-за чего в механизме обучения может произойти «сбой».

Начнём с теории

Рассмотрим однослойный перцептрон с одним выходом и активационной функцией $\DeclareMathOperator{\f}{f}\f$ .

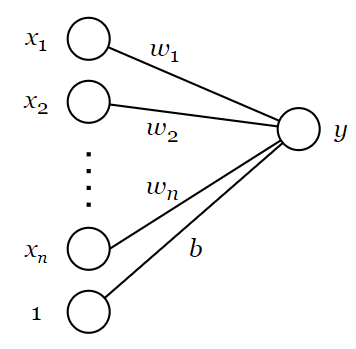
Здесь x_i – -й вход, – количество входов, $\omega_i$ – -й вес, – смещение, – выход. Значение выхода равно $\DeclareMathOperator{\f}{f}\f(z)$ , где $z=\textstyle\sum_{i=1}^nx_iw_i+b$ . В целях упрощения будем считать, что смещение реализуется как ( n+1 )-й вход со значением входа $x_{n+1}=1$ и весом $w_ {n+1}=b$ . Тогда $z=\textstyle\sum_{i=1}^{n+1}x_iw_i$ .

Посмотрим, как будет работать обучение при помощи метода градиентного спуска. Пусть $y^{*}$ – правильное значение выхода для некоторого входа $\overline{x}^*=(x_1^*,x_2^*, \ldots ,x_n^*)$ . В качестве функции ошибки будем использовать среднеквадратичную ошибку (MSE): $L=\textstyle\sum_{j=1}^N(y-y_j^*)^2/N$ , где – число элементов в обучающем наборе данных. Для простоты рассмотрим случай с одним элементом в обучающей выборке, т. е. N=1 , L=(y-y^*)^2 .

В соответствии с методом градиентного спуска, на каждой итерации вектор весов $\overline{w}=(w_1,w_2,...,w_n,w_{n+1})$ обновляется следующим образом: $\overline{w}^{(k+1)}=\overline{w}^{(k)}-\alpha\cdot\nabla L(\overline{w}^{(k)})$ . Здесь $\overline{w}^{(k)}$ – вектор весов на -м шаге обучения, $\alpha$ – коэффициент скорости обучения (learning rate), $\nabla L (\overline{w})$ – градиент функции ошибки, рассчитываемый по формуле:

$\nabla L\left(\vec{w}\right)=\left[\begin{matrix}\frac{\partial L}{\partial w_1}\\\vdots\\\frac{\partial L}{\partial w_{n+1}}\\\end{matrix}\right]\;\;\;\;\;(1)$

Здесь $\frac{\partial L}{\partial w_i}$ – частная производная по w_i . Рассчитаем её значение:

$\frac{\partial L}{\partial w_i}=\frac{\partial (y-y^*)^2}{\partial w_i}=2(y-y^*)\frac{\partial (y-y^*)}{\partial w_i}=2(y-y^*)\frac{\partial y}{\partial w_i}\;\;\;\;\;(2)$

Поскольку

$\DeclareMathOperator{\f}{f} \frac{\partial y}{\partial w_i}=\frac{\partial \f(z)}{\partial w_i}=\frac{\partial \f(z)}{\partial z}\cdot\frac{\partial z}{\partial w_i}=\f'(z)\cdot\frac{\partial\sum_{k=1}^{n+1}x_kw_k}{\partial w_i}=$ $\DeclareMathOperator{\f}{f} =\f'(z)\cdot\frac{\partial x_iw_i}{\partial w_i}=\f'(z)\cdot x_i\;\;\;\;\;\;\;\;\;(3)$

то $\DeclareMathOperator{\f}{f} \frac{\partial L}{\partial w_i}=2\cdot\Delta y\cdot \f'(z)\cdot x_i$ , где $\Delta y=y-y^*$ – величина ошибки предсказания.

Обучение перцептрона осуществляется на значениях из обучающей выборки (в нашем случае на единственном значении вектора $\overline{x}^*$ ), поэтому значение производной ${\partial L}/{\partial w_i}$ необходимо брать в точке $\overline{x}=\overline{x}^*$ .

Таким образом, на каждом шаге обучения каждый вес w_i увеличивается на величину

$\DeclareMathOperator{\f}{f} \Delta w_i=\text{-}2\cdot\alpha\cdot\Delta y\cdot \f'(z)\cdot x_i^*\;\;\;\;\;\;\;\;(4)$

Посмотрим внимательно, какие величины входят в качестве множителей при расчёте величины $\Delta w_i$ :

$\alpha$ – коэффициент скорости обучения,
$\Delta y$ – ошибка предсказания,
$\DeclareMathOperator{\f}{f} \f'(z)$ – значение производной активационной функции $\DeclareMathOperator{\f}{f} \f$ в точке $z=\textstyle\sum_{i=1}^{n{\small+}1}x_i^*w_i$ ,
– значение соответствующего входа на векторе из обучающей выборки.

Заметим, что в общем случае сам вес w_i не входит в эту формулу в качестве множителя в явном виде.

Вывод. Если на некотором шаге обучения вес w_i равен , то это не значит, что на следующем шаге данный вес обязательно останется равным . Он может как увеличиться, так и уменьшиться.

Теперь посмотрим, как это работает на практике

Пусть у нас имеется однослойный перцептрон с одним выходом и линейной активационной функцией $\DeclareMathOperator{\f}{f} \f(z) =z$ . Её производная $\DeclareMathOperator{\f}{f} \f'(z)$ равна 1 для всех . Пусть количество входов n=2 , веса инициализированы нулями и есть обучающая выборка из одного элемента: $\overline{x}^*=(0{,}5;2),$ y^*=42 .

Промоделируем, как будет осуществляться обучение с коэффициентом скорости обучения $\alpha=0{,}1$ .

Вспомним формулы

$\DeclareMathOperator{\f}{f} y=\textstyle\sum_{i=1}^{n+1}x_i^*w_i$

$\Delta y=y-y^*$

$\Delta w_i=\text{-}2\cdot\alpha\cdot\Delta y\cdot x_i^*$

$\overline{w}^{(k+1)}=\overline{w}^{(k)}+\Delta\overline w^{(k)}$

Шаг	Начальное значение $\overline{w}$		$\Delta y$	$\Delta \overline w$
1	(0; 0; 0)	0	-42	(4,2; 16,8; 8,4)
2	(4,2; 16,8; 8,4)	44,1	2,1	(-0,21; -0,84; -0,42)
3	(3,99; 15,96; 7,98)	41,895	-0,105	(0,0105; 0,042; 0,021)
4	(4,005; 16,002; 8,001)	42,00525	0,00525	(-0,00053; -0,0021; -0,00105)
5	(3,99998; 15,9999; 7,99995)	41,99974	-0,00026	(0,00003; 0,00010; 0,00005)
6	(4,00000; 16,00001; 8,00000)	42,00001	0,00001

Здесь все числа приведены с точностью до 5 знаков после запятой.

Как видно, перцептрон довольно быстро пришёл к значениям весов, близких к $\overline w_{sol}=$ (4;16;8) . При $\overline w=\overline w_{sol}$ значение выхода равно $4\cdot0{,}5+16\cdot2+8\cdot1=42$ , а величина ошибки $\Delta y$ равна нулю.

То есть перцептрон вполне успешно обучился, стартуя с весов, инициализированных нулями. Причём, что важно, все веса получились различными.

Более сложные варианты

Рассмотрим перцептрон с несколькими выходами. В этом случае получается та же ситуация — перцептрон успешно обучается и в этом случае. Это следует из того, что перцептрон с выходами можно рассматривать как независимых перцептронов с одним выходом. А перцептроны с одним выходом, как мы выяснили, умеют обучаться при инициализации весов нулевыми значениями.

Это справедливо как для линейной, так и для нелинейных активационных функций с ненулевыми значениями производных ( $\DeclareMathOperator{\sigmoid}{sigmoid} \sigmoid$ , $\tanh$ , $\DeclareMathOperator{\elu}{elu}\elu$ , $\DeclareMathOperator{\leakyRelu}{leakyRelu}\leakyRelu$ и др.). С этими активационными функциями перцептрон успешно обучается, стартуя с нулевых весов.

Однако проблема всё-же возникает при использовании в качестве активационной функции $\DeclareMathOperator{\relu}{relu}\relu$ или $\DeclareMathOperator{\leakyRelu}{leakyRelu}\leakyRelu$ с нулевым коэффициентом наклона для отрицательных чисел (negative slope). В этом случае левая производная в нуле равна нулю, а правая – не равна нулю, поэтому производная математически не определена. Однако для метода градиентного спуска некоторое значение производной активационной функции $\DeclareMathOperator{\f}{f}\f'(z)$ всё же должно быть определено. И в реализациях TensorFlow и PyTorch производная $\DeclareMathOperator{\relu}{relu}\relu$ в нуле считается равной нулю. Из-за этого при инициализации весов нулями величина $\Delta w_i$ для каждого веса равна нулю. Поэтому веса не изменяются, и обучения не происходит.

Но описанная выше проблема с активационной функцией $\DeclareMathOperator{\relu}{relu}\relu$ может проявляться и при весах, инициализированных случайным образом, причём даже с разными знаками. Например, если веса были инициализированы как $\overline w=(0{,}6;\text{-}0{,}3;0{,}2)$ , то на описанном выше обучающем датасете из одного элемента обучение не произойдёт, поскольку значение отрицательно: $z=0{,}6\cdot0{,}5+(\text{-}0{,}3)\cdot2+0{,}2\cdot1=\text{-}0{,}1$ , производная активационной функции $\DeclareMathOperator{\relu}{relu}\relu$ при отрицательных значениях аргумента равна нулю, а нулевое значение производной активационной функции приводит к обнулению изменений весов $\Delta w_i$ .

То есть при использовании $\DeclareMathOperator{\relu}{relu}\relu$ обучение может не происходить как при инициализации весов нулями, так и при инициализации их случайными значениями. Следовательно, описанный выше кейс с $\DeclareMathOperator{\relu}{relu}\relu$ нельзя считать веским аргументом против инициализации весов нулями и константами. Скорее, это довод против использования $\DeclareMathOperator{\relu}{relu}\relu$ .

Так почему бы не инициализировать веса нулями, если это не мешает обучению (если не применять relu)?

Для этого рассмотрим более сложную нейронную сеть

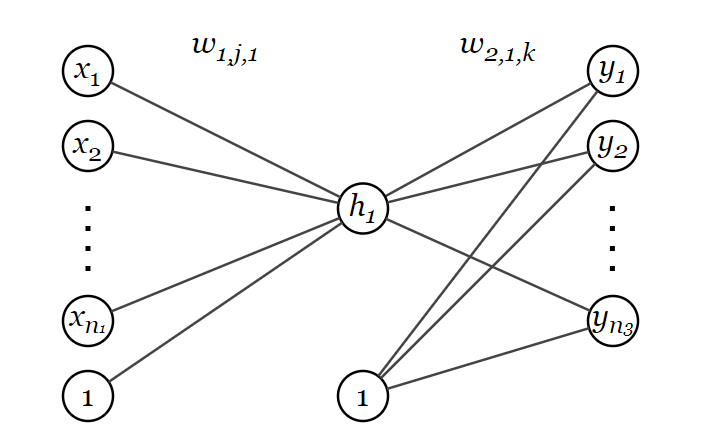
Пусть имеется нейронная сеть состоящая из входного слоя с n_1 элементами, одного скрытого слоя с n_2 элементами и выходного слоя с n_3 элементами.

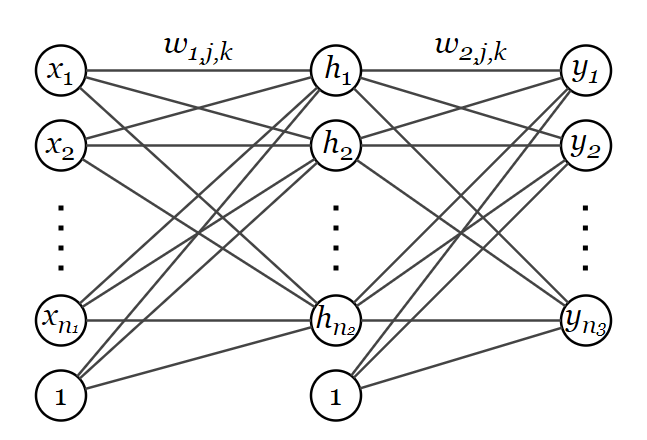
Введём обозначения: x_i – -й вход, h_j – -й элемент скрытого слоя, y_k – -й выход, $\DeclareMathOperator{\f}{f}\f_h(z)$ – активационная функция скрытого слоя, $\DeclareMathOperator{\f}{f}\f_y(z)$ – активационная функция выходного слоя, $w_{1,j,k}$ – вес между -м входом и -м элементом скрытого слоя, $w_{2,j,k}$ – вес между -м элементом скрытого слоя и -м выходом. Как и ранее, считаем, что смещения реализуются через дополнительные элементы: $x_{n_1+1}=1$ , $h_{n_2+1}=1$ .

Обозначим $z_{2,k}=\textstyle\sum_{i=1}^{n_1\small{+}1}x_i w_{1,i,k}$ – значение -го нейрона скрытого слоя до применения активационной функции, тогда $\DeclareMathOperator{\f}{f} h_k=\f_h(z_{2,k})$ – значение -го нейрона скрытого слоя после применения активационной функции. Обозначим $z_{3,k}=\textstyle\sum_{i=1}^{n_2\small{+}1}h_i w_{2,i,k}$ – значение -го нейрона выходного слоя до применения активационной функции, тогда $\DeclareMathOperator{\f}{f} y_k=\f_y(z_{3,k})$ – значение -го нейрона выходного слоя после применения активационной функции.

Пусть у нас имеется обучающая выборка из одной пары векторов $(\overline x^*,\overline y^*)$ . В качестве функции ошибки по-прежнему будем рассматривать среднеквадратичную ошибку (MSE). Тогда $L=\textstyle\sum _{i=1}^{n_3}(y_i-y_i^*)^2$ .

Как происходит обучение многослойной нейронной сети

Для обучения нейронной сети, как и раньше, будем применять формулу $\overline{w}^{(k+1)}=\overline{w}^{(k)}-\alpha\cdot\nabla L(\overline{w}^{(k)})$ , где $\overline w^{(k)}$ – вектор весов на -м шаге обучения, $\alpha$ – коэффициент скорости обучения (learning rate), $\nabla L(\overline w)$ – градиент функции ошибки. Отличие от однослойного перцептрона заключается в том, что частные производные $\partial L/\partial w_i$ считаются по-разному для разных слоёв.

Сначала рассмотрим веса $w_{2,j,k}$ , соединяющие скрытый слой и выходной слой. Вычислим следующую вспомогательную частную производную:

$\DeclareMathOperator{\f}{f} \frac{\partial y_i}{\partial w_{2,j,k}}=\frac{\partial \f_y(z_{3,i})}{\partial w_{2,j,k}}=\frac{\partial \f_y(z_{3,i})}{\partial z_{3,i}}\cdot\frac{\partial z_{3,i}}{\partial w_{2,j,k}}=\f'_y(z_{3,i})\cdot\frac{\sum_{m=1}^{n_2+1}h_m\partial w_{2,m,i}}{\partial w_{2,j,k}}=$ $=\begin{cases}\f'_y(z_{3,i})\cdot h_j&\text{ if }\; i=k\\0&\text{otherwise}\end{cases} \;\;\;\;\;\;\;\;(5)$

Смысл этого равенства следующий. Вес $w_{2,j,k}$ , связывающий -й элемент скрытого слоя и -й выход, влияет только на -й выход нейросети. На остальные выходы он не влияет. Этот факт достаточно очевиден и без применения формул.

Теперь мы можем рассчитать частную производную $\partial L / \partial w_{2,j,k}$ :

$\frac{\partial L}{\partial w_{2,j,k}}=\sum_{i=1}^{n_3}\frac{\partial (y_i-y_i^*)^2}{\partial w_{2,j,k}}=\sum_{i=1}^{n_3}\frac{2\cdot(y_i-y_i^*)\cdot\partial y_i}{\partial w_{2,j,k}}=2\cdot \f_y'(z_{3,k})\cdot h_j\cdot \Delta y_k\;\;\;(6)$

Здесь $\Delta y_k=y_k-y_k^*$ .

Таким образом, мы получили формулу, аналогичную формуле для однослойного перцептрона с одним выходом. Отличие лишь в том, что в данном случае рассматриваются сразу несколько выходов.

Следовательно, обучение весов на последнем слое многослойного перцептрона происходит по тем же правилам, как в однослойном перцептроне. Только в этом случае в качестве входного слоя для весов $w_{2,j,k}$ выступает скрытый слой нейронной сети.

Однако, несмотря на одинаковые правила, обучение нейронной сети со скрытым слоем всё же кардинально отличается от обучения однослойного перцептрона. Чтобы понять причины этого, сначала разберёмся, как рассчитываются частные производные функции ошибки по весам $w_{1,j,k}$ соединяющим входной и скрытый слой.

Для начала вычислим вспомогательные величины:

$\DeclareMathOperator{\f}{f} \frac{\partial h_i}{\partial w_{1,j,k}}=\frac{\partial \f_h(z_{2,i})}{\partial w_{1,j,k}}=\frac{\partial \f_h(z_{2,i})}{\partial z_{2,i}}\cdot\frac{\partial z_{2,i}}{\partial w_{1,j,k}}=\f'_h(z_{2,i})\cdot\frac{\sum_{m=1}^{n_1+1}x_m\partial w_{1,m,i}}{\partial w_{1,j,k}}=$ $=\begin{cases}\f'_h(z_{2,i})\cdot x_j&\text{ if }\; i=k\\0&\text{otherwise}\end{cases}\;\;\;\;\;\;\;(7)$ $\DeclareMathOperator{\f}{f} \frac{\partial y_i}{\partial w_{1,j,k}}=\frac{\partial \f_y(z_{3,i})}{\partial w_{1,j,k}}=\frac{\partial \f_y(z_{3,i})}{\partial z_{3,i}}\cdot\frac{\partial z_{3,i}}{\partial w_{1,j,k}}=\f'_y(z_{3,i})\cdot\frac{\sum_{m=1}^{n_2+1}w_{2,m,i}\partial h_m}{\partial w_{1,j,k}}=$ $=\f'_y(z_{3,i})\cdot w_{2,k,i}\cdot\f_h'(z_{2,k})\cdot x_j\;\;\;\;\;\;\;\;(8)$

Теперь найдём искомую производную:

$\frac{\partial L}{\partial w_{1,j,k}}=\sum_{i=1}^{n_3}\frac{\partial (y_i-y_i^*)^2}{\partial w_{1,j,k}}=\sum_{i=1}^{n_3}\frac{2\cdot(y_i-y_i^*)\cdot\partial y_i}{\partial w_{1,j,k}}=$ $=2\cdot\f_h'(z_{2,k})\cdot x_j\cdot\sum_{i=1}^{n_3}\Delta y_i\cdot\f'_y(z_{3,i})\cdot w_{2,k,i}\;\;\;\;\;\;\;\;(9)$

Заметим, то данная формула очень похожа на формулудля величины $\partial L / \partial w_{2,j,k}$ с той лишь разницей, что вместо производной активационной функции $\f_y'(z_{3,k})$ выходного слоя используется производная активационной функции $\f_h'(z_{2,k})$ скрытого слоя. Вместо значения h_j (значение -го элемента скрытого слоя) используется x_j (значение -го элемента входного слоя). Вместо ошибки $\Delta y_k$ на -м выходе используется следующая величина, которую можно рассматривать как сумму «обратно распространённых» ошибок:

$\Delta h_k=\sum_{i=1}^{n_3}\Delta y_i\cdot\f'_y(z_{3,i})\cdot w_{2,k,i}\;\;\;\;\;\;(10)$

В этом и заключается алгоритм обратного распространения ошибки. Расчёт осуществляется по слоям от выходного слоя к входному. Для каждого нейрона текущего слоя рассчитывается «ошибка». Для выходного слоя ошибка равна разности предсказанного значения и правильного значения из обучающей выборки. Для скрытых слоёв ошибка рассчитывается как взвешенная сумма ошибок на нейронах более поздних слоёв, умноженных на значения производных активационных функций и значения соответствующих весов (см. формулу (10) ).

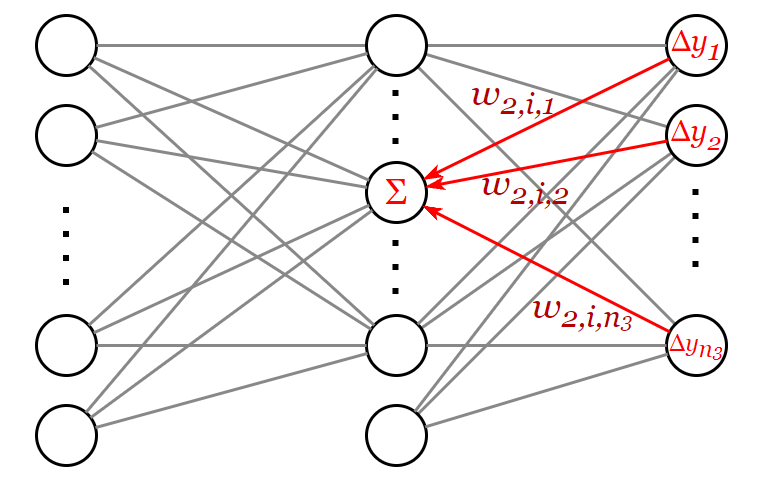
Теперь давайте ещё раз выпишем ключевые формулы для вычисления изменения весов при помощи алгоритма обратного распространения ошибки.

$\Delta h_k=\sum_{i=1}^{n_3}\Delta y_i\cdot\f'_y(z_{3,i})\cdot w_{2,k,i}\;\;\;\;(11)$ $\frac{\partial L}{\partial w_{2,j,k}}=2\cdot \f_y'(z_{3,k})\cdot h_j\cdot \Delta y_k\;\;\;(12)$ $\frac{\partial L}{\partial w_{1,j,k}}=2\cdot\f_h'(z_{2,k})\cdot x_j\cdot\Delta h_k\;\;\;\;\;(13)$ $w_i^{(k+1)}=w_i^{(k)}-\alpha\cdot\frac{\partial L}{\partial w_i}\;\;\;\;\;\;\;(14)$

Выводы по формулам

В этом разделе формулы приведены между любыми двумя соседними слоями. Далее используются обозначения – номер нейрона на текущем слое, – номер нейрона (на следующем слое.

При расчёте ошибки $\Delta h_i$ каждое слагаемое пропорционально:

$\Delta y_j$ – ошибке на следующем слое,
$\DeclareMathOperator{\f}{f} \f'(z_j)$ – значению производной активационной функции на следующем слое,
$w_{i,j}$ – весу соответствующей связи.

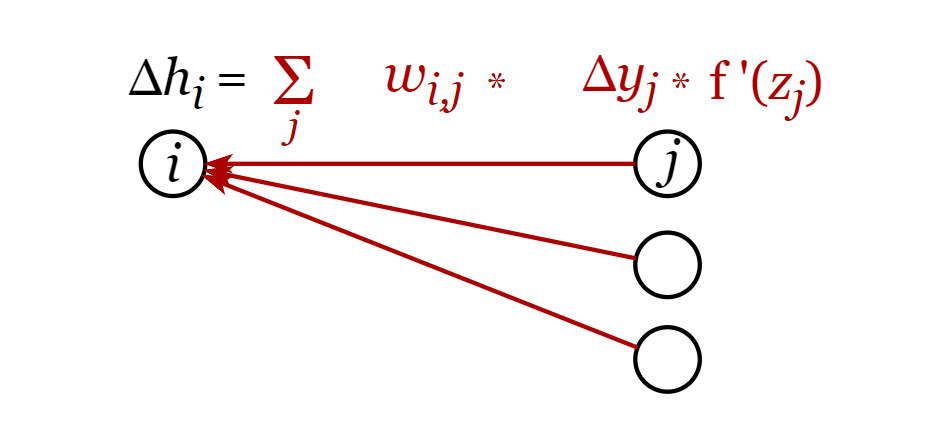
Расчёт ошибки для i-го элемента

Изменение веса $\Delta w_{ij}$ пропорционально:

$\Delta y_j$ – ошибке на следующем слое.
$\f_y'(z_j)$ – значению производной активационной функции на следующем слое,
$\alpha$ – коэффициенту скорости обучения,
– значению -го элемента текущего слоя.

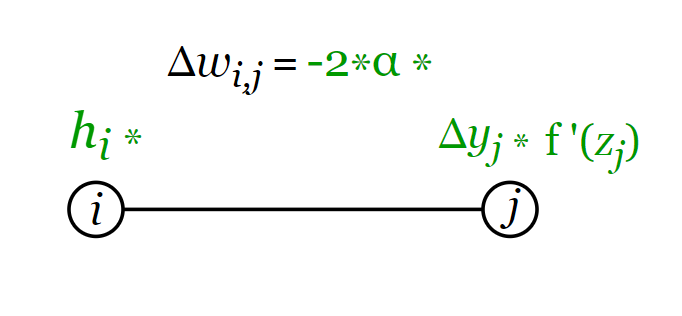
Теперь мы приходим к ответу

Все веса инициализированы нулями

Допустим в начальный момент времени все веса нейронной сети инициализированы нулями. Воспользуемся формулами из предыдущего раздела. Получаем, что все значения h_i на скрытом слое в начальный момент времени нулевые, и все выходы w_i нулевые, а также изменения весов $w_{2,j,k}$ между скрытым и выходным слоем нулевые. При этом ошибка на выходе $\Delta y$ может быть не нулевой. Но из-за того, что веса $w_{2,j,k}$ нулевые, то ошибка $\Delta h$ на скрытом слое по всем элементам равна нулю. Следовательно, изменения весов $\Delta w_{1,j,k}$ равны нулю. Следовательно, никакие веса не изменяются, и обучения не происходит.

Теперь рассмотрим более общий случай

Рассмотрим ситуацию, когда веса $w_{1,j,k}$ инициализированы константой $\const_1$ , а веса $w_{2,j,k}$ инициализированы константой $\const_2$ (возможно, совпадающей с $\const_1$ ).

Первая итерация алгоритма:

$w_{1,j,k}=\const_1$ , по условию кейса
$w_{2,j,k}=\const_2$ , по условию кейса
– все значения на скрытом слое одинаковы (кроме нейрона смещения $h_{n_2+1}=1$ ). Это следует из п. 1.
– все выходы одинаковы (следует из пунктов 2 и 3)
$\Delta y_i$ – ошибки на выходном слое могут быть различными (из-за разных значений в обучающем наборе)
$\Delta h_i$ – ошибки на скрытом слое одинаковы (в т. ч. и для нейрона смещения $\Delta h_{n_2+1}$ ). Это следует из пунктов 2 и 5. В формуле для расчёта величины $\Delta h_i$ суммируются вообще говоря разные слагаемые. Но их сумма одинакова по всем элементам скрытого слоя.
$\Delta w_{2,j,k}$ – все изменения весов, ведущих к одному выходу, одинаковы, т. е. $\Delta w_{2,j_1,k}=\Delta w_{2,j_2,k}$ (кроме весов, исходящих из нейрона смещения). Изменение веса $\Delta w_{2,n_2+1,k}$ , исходящего из нейрона смещения, может отличаться от изменений остальных весов $\Delta w_{2,i,k}$ , ведущих к тому же выходу

Изменения весов, исходящих из одного элемента скрытого слоя, могут отличаться, т.е. $\Delta w_{2,j,k_1}$ и $\Delta w_{2,j,k_2}$ могут отличаться. Это следует из пунктов 3 и 5.
$\Delta w_{1,j,k}$ – изменения весов, ведущих к одному элементу скрытого слоя, могут отличаться, т. е. $\Delta w_{1,j_1,k}$ и $\Delta w_{1,j_2,k}$ могут отличаться. Но изменения весов, исходящих из одного входа, одинаковы, т.е. $\Delta w_{1,j,k_1}=\Delta w_{1,j,k_2}$ . Последнее равенство справедливо также и для входа $x_{n_1+1}=1$ , использующегося для смещения. Это следует из пунктов 1 и 6.

На картинке выше одним и тем же цветом выделены одинаковые веса. Зелёным выделены веса $w_{1,2,k}$ , исходящие из входа x_2 . Все такие веса одинаковы. Красным выделены веса $w_{2,j,2}$ , ведущие к выходу y_2 (за исключением веса $w_{2,n_2+1,2}$ , исходящего из нейрона смещения $h_{n_2+1}$ ). Все такие веса одинаковы. Вес $w_{2,n_2+1,2}$ может отличаться от остальных весов $w_{2,j,2}$ .

Таким образом, исходное условие $w_{1,j,k}=\const_1$ , $w_{2,j,k}=\const_2$ перестаёт соблюдаться. Поэтому рассмотрим вторую итерацию алгоритма.

Вторая итерация алгоритма

$w_{1,j,k_1}=w_{1,j,k_2}$ – веса, исходящие из одного входа, одинаковы (в т. ч для входа смещения $x_{n_1+1}=1$ ) . Это результат первой итерации алгоритма.
$w_{2,j_1,k}=w_{2,j_2,k}$ – веса, ведущие к одному выходу (за исключением весов, исходящих из нейрона смещения $w_{2,n_2\small+1,k}$ ) одинаковы. Это результат первой итерации алгоритма.
– все значения на скрытом слое одинаковы (кроме нейрона смещения $h_{n_2+1}=1$ ). Это следует из того, что $z_{2,i_1}=\textstyle\sum_{j=1}^{n_1+1}x_jw_{1,j,i_1}=\sum_{j=1}^{n_1+1}x_jw_{1,j,i_2}=z_{2,i_2}$ .
– выходы могут быть различны. Это следует из того, что веса, ведущие к разным выходам, могут быть различны.
$\Delta y_i$ – ошибки на выходном слое могут быть различны (из-за различных значений на выходном слое).
$\Delta h_i$ – ошибки на скрытом слое одинаковы (за исключением ошибки на нейроне смещения $\Delta h_{n_2+1}$ ). Это следует из равенства:

$\Delta h_{i_1}=\sum_{j=1}^{n_3}\Delta y_j\cdot\f'_y(z_{3,j})\cdot w_{2,i_1,j}=\sum_{j=1}^{n_3}\Delta y_j\cdot\f'_y(z_{3,j})\cdot w_{2,i_2,j}=\Delta h_{i_2}$ .
$\Delta w_{2,j,k}$ – идентично первой итерации алгоритма.
$\Delta w_{1,j,k}$ – идентично первой итерации алгоритма.

Таким образом, условие, указанное в пунктах 1 и 2, продолжает соблюдаться. И далее процесс обучения повторяется по сценарию второй итерации алгоритма.

Почему это плохо

На каждом шаге алгоритма обучения все значения нейронов скрытого слоя h_i одинаковы (кроме нейрона смещения). Для фиксированного выхода y_k все веса $w_{2,i,k}$ (кроме веса, исходящего из нейрона смещения) одинаковы.

Поэтому данная нейронная сеть будет функционировать и обучаться так же, как некоторая вырожденная нейронная сеть, в которой на скрытом слое всего один нейрон (не считая нейрона смещения). При этом веса $w_{1,j,1}$ вырожденной нейронной сети равны весам $w_{1,j,1}$ исходной нейронной сети (включая нейрон смещения). Веса $w_{2,1,k}$ вырожденной нейронной сети равны значениям $(n_2\cdot w_{2,1,k})$ исходной нейронной сети (за исключением весов нейрона смещения). Веса $w_{2,2,k}$ нейрона смещения вырожденной нейронной сети равны значениям $w_{2,n_2\small+1,k}$ нейрона смещения исходной нейронной сети.

Нейронная сеть с одним элементом на скрытом слое (не считая нейрона смещения)

Интуитивно понятно, что такая вырожденная нейронная сеть обладает более узким пространством ответов, чем нейронная сеть с бóльшим числом нейронов на скрытом слое. То есть она может выдавать меньше различных комбинаций значений выходов. Это следует из того, что вектор выходных значений $\overline y$ начинает зависеть не от n_1 входов, а лишь от одного значения h_1 (вектор выходных значений зависит от весов в обоих случаях, поэтому с этой точки зрения ситуации одинаковы).

Формально это можно доказать на примере задачи XOR.

Суть задачи XOR и доказательство утверждения

Необходимо с помощью нейронной сети реализовать выход функции XOR. То есть:

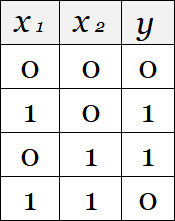
Соответственно, в данной задаче количество выходов n_3 равно 1.

Допустим также, что активационные функции должны быть неубывающими.

Если у нас нет ограничений на количество нейронов на скрытом слое, то для решения задачи XOR достаточно взять нейронную сеть, изображённую на рисунке, с n_2=2 нейронами на скрытом слое и с активационной функцией $\relu$ на скрытом и выходном слоях. Такая нейронная сеть выдаёт на выход значения, равные значениям из описанной выше таблицы для функции XOR.

Решение задачи XOR с активационной функцией relu

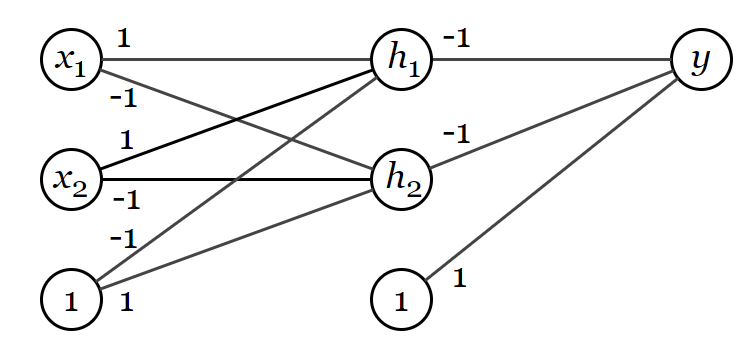
Если же количество нейронов на скрытом слое равно единице, то мы получим следующую схему:

Архитектура нейронной сети для решения задачи XOR с одним нейроном на скрытом слое

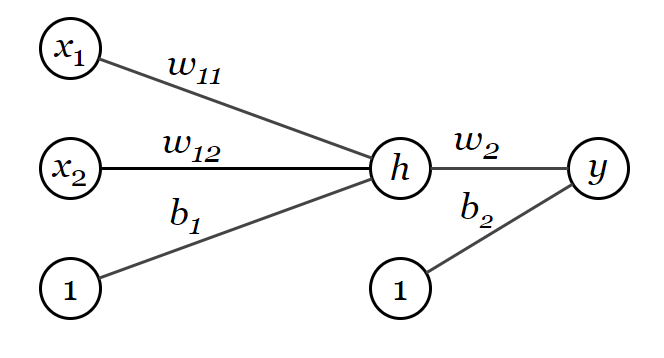
В этом случае $h=\f_h(w_{11}x_1+w_{12}x_2+b_1)$ , $y=\f_y(w_2h+b_2)$ .

Далее докажем, что такая архитектура нейронной сети не может воспроизводить значения из таблицы для функции XOR.

Предположим, что решение задачи найдено. То есть найдены веса, при которых значения выхода зависят от входов x_1 и x_2 , как указано в таблице.

Это означает, что при одних значениях входа значение выхода y=0 , а при других значения выхода значение выхода y=1 . Поскольку мы предположили, что решение задачи уже найдено, т. е. веса найдены и зафиксированы, то значение выхода зависит только от .

Обозначим как H_0 множество значений , при которых $\f_y(w_2h+b_2)=0$ . И обозначим как H_1 множество значений , при которых $\f_y(w_2h+b_2)=1$ . Отметим, что множества H_0 и H_1 не пересекаются, поскольку для $h\in (H_0 \cup H_1)$ значение $\f_y(w_2h+b_2)$ должно было бы одновременно равняться нулю и единице.

Также отметим, что существует число h_d , для которого:

$\forall h_0\in H_0,\forall h_1 \in H_1 \Rightarrow \left[ \begin{array}{l} h_0 \leq h_d \leq h_1 \\ h_1 \leq h_d \leq h_0 \end{array} \right. \;\;\;\;\;\;\;\;(15)$

Это следует из того, что активационная функция $\f_y$ не убывает.

Поскольку $h=\f_h(z)$ , то обозначим как Z_0 множество значений , при которых $\f_h(z) \in H_0$ . Обозначим как Z_1 множество значений , при которых $\f_h(z) \in H_1$ . Отметим, что множества Z_0 и Z_1 не пересекаются, поскольку для $z\in(Z_0 \cup Z_1)$ значение $\f_h(z)$ должно одновременно принадлежать H_0 и H_1 , что невозможно, поскольку множества H_0 и H_1 не пересекаются.

Из условий задачи и свойств множеств Z_0 и Z_1 получаем следующую систему:

$\begin{cases}(w_{11}\cdot 0+w_{12}\cdot0+b_1) \in Z_0\\(w_{11}\cdot 1+w_{12}\cdot0+b_1) \in Z_1\\(w_{11}\cdot 0+w_{12}\cdot1+b_1 )\in Z_1\\(w_{11}\cdot 1+w_{12}\cdot1+b_1 ) \in Z_0 \end{cases}\;\;\;\;\;(16)$

Также отметим, что существует число z_d , для которого:

$\forall z_0\in Z_0,\forall z_1 \in Z_1 \Rightarrow \left[ \begin{array}{l} z_0 \leq z_d \leq z_1 \\ z_1 \leq z_d \leq z_0 \end{array} \right.\;\;\;\;\;(17)$

Это следует из неравенств (15) и того, что активационная функция $\f_h$ не убывает.

Рассмотрим первый случай: $z_0 \leq z_d \leq z_1$ . Второй случай: $z_1 \leq z_d \leq z_0$ рассматривается аналогично.

Составим систему неравенств:

$\begin{cases}w_{11}\cdot 0+w_{12}\cdot0+b_1 \leq z_d\\w_{11}\cdot 1+w_{12}\cdot0+b_1 \geq z_d\\w_{11}\cdot 0+w_{12}\cdot1+b_1 \geq z_d\\w_{11}\cdot 1+w_{12}\cdot1+b_1 \leq z_d \end{cases}\;\;\;\;\;(18)$

Решаем:

$\Rightarrow\begin{cases}b_1 \leq z_d\\w_{11}+b_1 \geq z_d\\w_{12}+b_1\geq z_d\\w_{11}+w_{12}+b_1 \leq z_d \end{cases}\;\;\;\;\;(19)$

Сложим (1) и (4) строчки и (2) и (3). Получаем:

$2\cdot z_d \leq w_{11}+w_{12}+2\cdot b_1 \leq 2\cdot z_d\;\;\;\;\;(20)$ $\Rightarrow z_d = 0{,}5\cdot w_{11}+0{,}5\cdot w_{12}+ b_1\;\;\;\;\;(21)$ $\Rightarrow\begin{cases} w_{11}+b_1 \geq 0{,}5\cdot w_{11}+0{,}5\cdot w_{12}+ b_1\\w_{12}+b_1\geq 0{,}5\cdot w_{11}+0{,}5\cdot w_{12}+ b_1 \end{cases}\;\;\;\;\;(22)$ $\Rightarrow\begin{cases} w_{11} \geq 0{,}5\cdot w_{11}+0{,}5\cdot w_{12}\\w_{12}\geq 0{,}5\cdot w_{11}+0{,}5\cdot w_{12} \end{cases}\;\;\;\;\;(23)$ $\Rightarrow\begin{cases} w_{11} \geq w_{12}\\ w_{12}\geq w_{11}\end{cases} \Rightarrow w_{11}=w_{12}\;\;\;\;\;(24)$ $\Rightarrow z_d=w_{11}+b_1=w_{12}+b_1\;\;\;\;(25)$ $(19), (25) \Rightarrow \begin{cases} b_1 \leq w_{11}+b_1\\ 2\cdot w_{11}+b_1\leq w_{11}+b_1\end{cases}\;\;\;\;\;(26)$ $\Rightarrow \begin{cases} 0 \leq w_{11}\\ w_{11}\leq 0\end{cases} \Rightarrow w_{11}=0\Rightarrow w_{12}=0\;\;\;\;\;(26)$

Однако в этом случае выход нейронной сети всегда равен одному и тому же числу $\f_y(w_2\cdot\f_h(b_1)+b_2)$ , что противоречит условиям задачи.

Таким образом, мы предположили, что нейросеть с одним нейроном на скрытом слое и неубывающими активационными функциями на скрытом и выходном слоях может воспроизвести выходные значения в соответствии с таблицей значений функции XOR. Однако мы пришли к противоречию. Следовательно, нейросеть с такой архитектурой не может моделировать значения функции XOR.

Вывод

Если веса связей между каждыми двумя последовательными слоями инициализированы некоторой константой (вообще говоря, различной для каждой пары последовательных слоёв), то пространство возможных выходных значений нейронной сети сужается по сравнению со случаем, когда все веса инициализированы различными случайными значениями.

Иными словами, нейронная сеть не сможет предсказывать то, что она могла бы предсказать при инициализации весов различными случайными значениями.

Заключение

В этой статье мы разобрали, как обучается однослойный перцептрон и нейронная сеть, состоящая из двух полносвязных слоёв (скрытого и выходного). Основной акцент был сделан на то, как влияют промежуточные значения на значения функции ошибки и в конечном итоге на изменения весов.

Мы убедились на примере, что инициализация весов нулями не мешает однослойному перцептрону обучаться. Также мы выяснили, что при инициализации весов нулями нейронная сеть со скрытым слоем теряет часть пространства возможных выходных значений, поскольку становится эквивалентна нейросети с одним нейроном на скрытом слое.

Комментарии (6)

phenik
02.12.2021 07:45
#23775933
В популярных фреймворках машинного обучения TensorFlow и PyTorch при инициализации весов нейросети используются случайные числа. В этой статье мы попытаемся разобраться, почему для этих целей не используют ноль или какую-нибудь константу.
Интересно, можно инициализировать не случайными числами, а оптимальным набором, кот. сократит время обучения? Очевидно, если сеть с исходными случайными весами обучить распознаванию одного изображения, а затем полученные веса присвоить другой такой же сетке, и обучить ее тому же изображение, то обучение должно завершить намного быстрее, чем в первом случае. В более общей постановке, какую процедуру обработки над обучающей выборкой нужно произвести, чтобы получить из нее оценки оптимального набора весов, присвоить их, и тем самым сократить время обучения на ней? Скорее всего такие процедуры оптимизации исходных весов существуют, постановка вопроса достаточно очевидная.

Подобная оптимизация весов синапсов происходит в биологических сетях развивающего мозга плода и в постнатальный период. Это позволяет произвести предварительную настройку важного с точки зрения выживания функционала, использовать его сразу после рождения, и более эффективно производить дальнейшее обучение в младенчестве, включая по малому числу примеров. Своеобразный период предобучения, настройки ожиданий. Его механизмы, включая генетические, исследуются см. этот комент со ссылками на некоторые источники.
1. AnonimYYYs
  02.12.2021 19:39
  #23778643
  +1
  Обучить нейронку со случайными весами а потом передать эти веса во вторую такую же нейронку и обучить вторую.
  
  Не совсем понимаю, чем это отличается от банально двух эпох обучения одной нейронки на одной картинке?
1. rPman
  02.12.2021 20:07
  #23778709
  +1
  первые слои можно инициализировать весами, скопировав их из нейронной-сети классификатор (она по уму может быть заметно меньше целевой) на основе данных входного вектора.
1. Fell-x27
  02.12.2021 22:39
  #23779151
  Можно подобрать сид рандома, при котором сходимость лучше, если вы об этом. Веса не обязаны быть каждый раз новыми при каждом прогоне - тогда потеряется контроль над ситуацией. Но можно инициализировать одним и тем же случайным набором из раза в раз во время настройки.
1. demidovd98
  03.12.2021 19:16
  #23782453
  Если я правильно понял вашу идею, то Вы только что изобрели fine-tuning :)
1. phenik
  05.12.2021 08:33
  #23787037
  Благодарю за ответы. Идея комента состояла несколько в другом, она во втором абзаце, но чтобы понять о чем речь нужно посмотреть источники по ссылке. Эволюция решала подобную задачу для несравненно более сложного случая, чем сейчас решают специалисты по глубокому обучению для ИНС. Искала способ своеобразного «предобучения» функционала нейронных сетей растущего мозга плода, полезного, с точки зрения выживания, сразу после рождения. Например, распознавание лиц или дискриминация численности объектов, хотя бы приближенная. Однако нет возможности в геноме задать значения весов всех синапсов, как из-за их количества, так неопределенности их локализации в развивающихся сетях мозга. Эволюционное решение состояло в генерации определенной спонтанной активности направленной от формирующихся органов чувств, например, нейронов сетчатки глаз, по восходящим путям мозга к корковым отделам. Своеобразный встроенный «эмулятор реальности» в растущем мозге) Схематически это выглядит так:
  Заголовок спойлера
  
  Источник.
  
  При этом происходит дополнительная эпигенитическая подстройка под текущее состояние среды в которой мать вынашивает ребенка (структуре питания, условиям проживания — температурным, уровню освещенности, и тп).
  
  Как реализовать аналог такой схемы для предобучения ИНС, например, классификатора изображений? Действительно разными методами повторного обучения, как и предлагается в ответах. Но как проделать это без повторного обучения? Эволюция выработала схему генерации оптимальной активности самими структурами мозга, а не повторяет всю эволюционной историю для каждого нового плода. Это равносильно некоторой процедуре обработки обучающей выборки, на выходе кот. получаются оценки весов ИНС. Они присваиваются сетке, и тогда ее обучение может производиться только на подмножестве обучающей выборке. При этом результат обучения должен быть не хуже, чем для обучения на всей выборке. Но время обучения должно уменьшается. Вопрос в затратах на такую процедуру, если он невелики, то должен быть выигрыш в весьма затратных процессах обучения ИНС. Простоя идея такой процедуры состоит в сложение всех изображений из обучающей выборки и усреднения цветов пикселей, или использования другой подходящей статистики. Получившимся результирующим изображением (аналогом спонтанной активности в мозге плода) обучаем сеть, и тем самым присваиваем ей оптимальные начальные значения весов определяемые обучающей выборкой, а не случайными. Затем как обычно производится обучение на обучающей выборке меньшей по числу, чем исходной, использованной в процедуре оценки.
  
  emidovd98
  Если я правильно понял вашу идею, то Вы только что изобрели fine-tuning :)
  Не… передрали у природы) впрочем, как и сама идея ИНС была передрана.