Код, графики, попытка анализа — все под катом.
Решето Эратосфена на новый лад
Нам нужно вычеркнуть из натурального ряда поочередно все числа, кратные 2-м, 3-м, 5-и и так далее? Нет ничего проще! Пустим вдоль оси x функцию «синус» с соответственно подправленным периодом, а сами синусы перемножим:

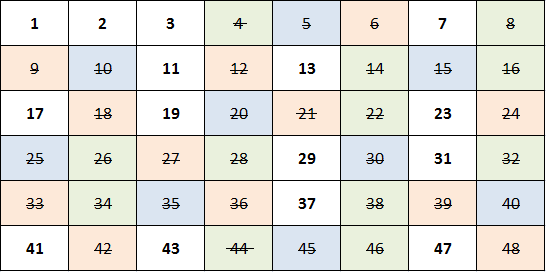
Функция совершенно естественным образом занулится на всех составных числах и обойдет простые. Для 3-х сомножителей таким образом мы найдем все простые вплоть до 47, а дальше останется только домножать на синус со следующим простым числом в аргументе

Тут, признаться, нас ждут проблемы. Хорошо анализировать функцию, когда она определена аналитически сразу на всей числовой оси. А не рекурсивно, как в нашем случае. Более того, даже попытка «сшить» ее в той точке x, где добавляется очередной сомножитель, приводит лишь к непрерывности функции в этой точке, но не гладкости. Похоже, так себе идея.
Что делает человек с университетским образованием, когда видит произведение синусов?

И тут нас ждет некий сюрприз
Пара первых произведений (мы опустили множитель ½ в степени n.)

Вы заметили, да? Числители все сплошь простые числа! Вот почему, как говорят аналитики, так полезно смотреть на данные «глазками». Если копать дальше, то уже на следующем этапе среди числителей начнут попадаться и составные, но, так или иначе, процент простых будет очень велик.
Чтобы исследовать тему дальше, написал простую программу на C#
В первом варианте (тут не показан) я перемножал подряд синусы со всеми натуральными числами подряд – в конце концов, лишний ноль в произведении не помеха, как говорится). Это привело к интересному эффекту – в окончательной сумме синусов, когда мы уже избавились от всех произведений, появлялись подобные слагаемые, некоторые из которых при приведении уничтожали друг друга. Это сразу приводило к многообразию дальнейших вариантов – что делать с теми из них, которые взаимно сокращались, их числители тоже часто были простыми? Однако оказалось, что если брать в качестве новых множителей только простые числа, этот эффект уходит и подобных слагаемых не возникает (это эмпирический факт, без доказательства).
Интересно, что получаемые в этой итерационной последовательности числа (множители в числителе тригонометрических функций) растут с сумасшедшей скоростью. Уже для 15-й итерации (когда мы дошли всего лишь до простого числа 47 как множителя под синусом, на выходе – 16 384 слагаемых) максимальное число превысило 1 квинтиллион (название этой величины — единицы с 18-ю нулями — мне пришлось смотреть в Википедии), а максимальное простое приблизилось к нему. Это уже близко к пределу 64-битной величины long в C#, но причина остановки на 15 итерациях даже не в этом – проверка на простоту начинает занимать непотребно долгое время для следующего шага, во всяком случае, тем тупым лобовым способом, которым я это запрограммировал. Результат:

Интересный вопрос – можно ли каким-то образом избавиться от составных чисел, прореживая результат очередной итерации? Я не нашел никакой закономерности, у полученных составных числителей вполне могут быть простые «потомки» и наоборот, так что этот вопрос остался открытым. Первые 4 поколения выглядят вот так (составные – желтые):

Если взять потомков 3-й итерации, среди которых — 6 простых и 2 составных, то порожденные ими ветки до 15-го поколения включительно дают вот такие количества простых:

Никакой системы не прослеживается.
Ну и еще один подсчет. Известна формула для оценки количества простых чисел, попадающих в некий интервал натуральных. Предположим, что мы берем произвольную выборку чисел из интервала между MIN и MAX в каждой итерации, и сравним теоретическое количество простых с полученным нами:

Предсказание получено по известной формуле MAX/LN(MAX) – MIN/LN(MIN). Как видим, в нашем процессе процент простых чисел заметно выше, хоть и падает.
Если вам не хватило всяких нумерологических загадок в этой статье, то вот еще одна. Сумма модулей числителей в ПРАВОЙ ЧАСТИ таблицы, то есть потомков второго слагаемого в разложении sin πx/2*sin πx/3, а именно cos 5πx/6, выглядит так:

В левой части таблицы все суммы совершенно не круглые
Комментарии (12)

lea
04.02.2022 23:08+4По идее, можно при помощи китайской теоремы об остатках быстро (?) искать простые числа.
Первое простое число - 2. Очевидно, все остальные простые числа сравнимы с единицей по модулю двух.
Второе простое число - 3. Все остальные простые числа по модулю 3 могут быть сравнимы лишь с 1 или с 2.
Система { x mod 2 = 1; x mod 3 = 1 } имеет решение x mod 6 = 1. Не подходит.
Система { x mod 2 = 1; x mod 3 = 2 } имеет решение x mod 6 = 5. То, что нужно. Добавляем x mod 5 = ... в систему уравнений.
С тремя уравнениями находим:
{ x mod 2 = 1; x mod 3 = 1; x mod 5 = 1 } --> x mod 30 = 1 (отбрасываем)
{ x mod 2 = 1; x mod 3 = 1; x mod 5 = 2 } --> x mod 30 = 7 (простое)
{ x mod 2 = 1; x mod 3 = 1; x mod 5 = 3 } --> x mod 30 = 13 (простое)
{ x mod 2 = 1; x mod 3 = 1; x mod 5 = 4 } --> x mod 30 = 19 (простое){ x mod 2 = 1; x mod 3 = 2; x mod 5 = 1 } --> x mod 30 = 11 (простое)
{ x mod 2 = 1; x mod 3 = 2; x mod 5 = 2 } --> x mod 30 = 17 (простое)
{ x mod 2 = 1; x mod 3 = 2; x mod 5 = 3 } --> x mod 30 = 23 (простое)
{ x mod 2 = 1; x mod 3 = 2; x mod 5 = 4 } --> x mod 30 = 29 (простое)Т.е. множество известных простых чисел у нас разрастается очень быстро.
{ 2 },
{ 2, 3 },
{ 2, 3, 5 },
{ 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 }На следующей итерации мы найдём все простые числа, не превышающие 6469693230.
Ещё бы как-то соптимизировать перебор остатков, с которыми требуется решать систему... Хотя даже без оптимизаций он хорошо распараллеливается.

lea
05.02.2022 03:36+1Что-то в этом роде:
import math import operator import itertools def chrem_precalc(a): M = math.prod(a) def gen_factor(a_i): M_i = M // a_i M_i_inv = pow(M_i, -1, a_i) return M_i * M_i_inv return ([gen_factor(a_i) for a_i in a], M) def chrem_solve(r, pre): (f, M) = pre return sum(map(operator.mul, r, f)) % M def gen_all_r(a): r_ranges = [range(1, a_i) for a_i in a] return itertools.product(*r_ranges) def moar_primes(known_primes): pre = chrem_precalc(known_primes) candidates = [chrem_solve(r, pre) for r in gen_all_r(known_primes)] m = max(known_primes) M = pre[1] return known_primes + sorted(list(set([(x + M, x)[x > m] for x in candidates]))) moar_primes([2]) moar_primes([2, 3]) moar_primes([2, 3, 5]) moar_primes([2, 3, 5, 7])
Результат работы для первых простых чисел 
Входные числа / их произведение / к-во простых не превышающих произведение / длина результата. Но всё же результаты надо дополнительно просеивать, т.к. длина результата при последовательном применении функции растет быстрее, чем квадратично.

raamid
04.02.2022 23:35+1Как известно, синус вычисляется через полиномиальный ряд. А что если взять ряд сумм синусов и каждый синус развернуть в полиномиальный ряд. Получится новый ряд, в котором возможно, получится сделать упрощения, а значит сэкономить на вычислениях.

VPryadchenko
05.02.2022 09:10+3Позвольте поинтересоваться, а какова постановка задачи и какой вывод? Какие преимущества у вашего подхода и с чем его вообще корректно сравнивать?

vkomen Автор
05.02.2022 09:25+4Это просто наблюдение. Непонятно, почему плодятся простые, непонятно, почему между ними проскакивают составные)

AxelLx
05.02.2022 12:03+9Да, простые числа — это просто.
Ваши дроби получаются из суммы обратных первым n простым числам.
В числителе все слагаемые кроме одного делятся на p_1, все, кроме одного делятся на p_2 и т.д… Следовательно, числитель не делится на первые n простых.
Получилось обычное решето Эратосфена.

wataru
05.02.2022 12:09+9Вы открыли замечательный факт, что GCD(abс, x) = 1 для чисел, не делящехся на a, b, c.
При раскрытии через сумму вы получаете, что знаменатель — произведение всех ваших простых чисел, а в числителе отсаются взаимно простые.
Далее, с учетом, что любое составное число имеет делитель не превосходящий его корень, вы можете таким методом "найти" все простые до sqrt(abc). Так что, если в вашей таблице возьмете корнень из "максимальное", то у вас останутся только простые числа в этом интервале. А выше этого предела — уж как повезет. Там могут выпасть и простые числа, но в основном будут составные.
Ваш метод есть обобщение эвристики — перебирать в решете только нечетные числа. Или только числа вида 6k+1 и 6k+5.
И главное, этот ваш метод будет на порядки медленнее любого решета. Конечно, красиво, что есть уравнение для простых чисел. Но символьные вычисления над этой конструкцией уж очень неэффективны.

MrAlone
05.02.2022 18:59+4Извините, но судя по КДПВ, 5 не является простым числом. Мы что-то не знаем?

Grigorenkovic
06.02.2022 16:14Когда-то очень интересовался этой задачей и разгадкой. Дошел до того, что попробовал установить последовательность непростых чисел, тех которые имеют одинаковую структуру с простыми (6х+-1). Она, получается, есть, но одной формулой никак не выводилась, потому что непонятно на каждом отрезке, какое количество будет 5 и 7 (5х+7у)




Manrus
Очень сумбурно написано, побольше бы объяснений. А так читать интересно, спасибо