15.03.2022 12:51
AndreyKotlov 1 1600 Источник
Для авиаотрасли 2020 год стал худшим за всю историю ее существования. Из-за COVID-19 более чем на половину сократилось воздушное сообщение, количество маршрутов и общая выручка. Черный лебедь в белой маске, так называют этот кризис. В очередной раз мир «вдруг» снова напомнил всем нам о своей сложности и непредсказуемости. Пожалуй, единственное, чем этот кризис отличается от всех предыдущих, так это растущей убежденностью в том, что мы больше не можем всецело полагаться на простые детерминированные модели. Безусловно, очень трудно учитывать случайность и неопределенность в своих планах и решениях, но только сумасшедший захочет еще раз проверить, во сколько нам обойдется очередное «Авось!»



Для нас логистика это не просто транспорт или доставка, это, прежде всего, рациональное управление ресурсами. В предыдущей статье мы создали довольно простую модель динамического ценообразования, способную подстраиваться под случайные изменения спроса. В этой статье мы попробуем заставить подстраиваться под случайные изменения спроса не только стоимость билетов, но и весь воздушный флот авиакомпании вместе с расписанием его полетов, так же проверим, как получившаяся модель будет вести себя в кризисных ситуациях.

Простейшая модель назначения флота на основе спроса


В математическом моделировании важно сохранять баланс между чрезмерным упрощением и усложнением. Чтобы почувствовать этот баланс, давайте начнем с простейшей задачи распределения самолетов по маршрутам на основе спроса.
Предположим, что в распоряжении авиакомпании находится некоторое множество $F$ различных типов самолетов, обозначаемых индексом $f$. Количество самолетов каждого типа ограничено и равно $N_{f}$. Так же имеется множество маршрутов $I$ c индексом $i$. Авиакомпании необходимо распределить самолеты по маршрутам на некоторый период времени. Если самолет типа $f$ работает на $i$-м маршруте, то он может перевезти $d_{fi}$ пассажиров за некоторый промежуток времени (предполагается, что сюда включены путешествия в оба конца). При этом стоимость эксплуатации самолета равна $c_{fi}$. Допустим, что спрос на билеты одинаков на любом направлении, и если пассажир выходит в промежуточном пункте, то кто-то сразу же занимает его место. Однако, спрос $v_{i}$ на $i$-м маршруте точно предсказать нельзя, поэтому его следует рассматривать как случайную величину, непрерывно распределенную с плотностью вероятности $\varphi_{i}(v_{i})$.
Обозначим через $x_{fi}$ количество самолетов типа $f$$(f \in F)$, обслуживающих $i$-й маршрут $(i \in I)$. Тогда, количество $y_{i}$ пассажиров, которое можно перевезти на всех $x_{fi}$ самолетах $i$-го маршрута, выразится суммой

$\begin{equation*} y_{i} = \sum_{f \in F} d_{fi}x_{fi} \;\;\;\; (i \in I). \tag{1} \end{equation*}$

Если $y_{i} < v_{i}$, т.е. спрос превышает возможности, то авиакомпания не получит той выручки, которую могла бы получить при наличии достаточного количества мест в самолетах $i$-го маршрута. В этом случае из-за недостатка мест не будет перевезено $v_{i} - y_{i}$ пассажиров и недополученная прибыль будет пропорциональна неудовлетворенному спросу $v_{i} - y_{i}$ и выражена как $\pi_{i}(v_{i} - y_{i})$, где $\pi_{i}$ — потенциальная прибыль с одного места, в простейшем случае равная стоимости билета.
Средняя ожидаемая недополученная прибыль от неудовлетворенного спроса на $i$-м маршруте определяется математическим ожиданием $\mathbb {E}_{i}^{'}$ случайной величины $\pi_{i}(v_{i} - y_{i})$.
Математическое ожидание $\mathbb {E}(X)$ непрерывной случайной величины $X$, распределенной с плотностью вероятности $\varphi(x)$, вычисляется по формуле

$\mathbb {E}(X) = \int_{-\infty}^{\infty} x \varphi(x) dx.$

Если $y = f(X)$ — функция от случайной величины $X$, то ее математическое ожидание $\mathbb {E}(f(X))$ выражается формулой

$\mathbb {E}(f(X)) = \int_{-\infty}^{\infty} f(x) \varphi(x) dx.$

Тогда, в нашем случае, математическое ожидание убытков от неудовлетворенного спроса можно определить следующим образом

$\begin{equation*} \mathbb {E}_{i}^{'} = \int_{y_{i}}^{\infty} \pi_{i}(v_{i} - y_{i}) \varphi(v_{i}) dv_{i} \;\;\;\;\; (y_{i} < v_{i} < \infty).\tag{2} \end{equation*}$

Если же $y_{i} > v_{i}$, т.е. количество мест на $i$-м маршруте превышает спрос, то компания так же несет убытки, выражающиеся величиной, пропорциональной количеству мест, оставшихся свободными, т.е. $k_{i}(y_{i} - v_{i})$, где $k_{i}$ — это убыток от каждого незанятого места.
Средние ожидаемые убытки от всех $y_{i} - v_{i}$ свободных мест определяются математическим ожиданием $\mathbb {E}_{i}^{''}$ случайной величины $k_{i}(y_{i} - v_{i})$:

$\begin{equation*} \mathbb {E}_{i}^{''} = \int_{0}^{y_{i}} k_{i}(y_{i} - v_{i}) \varphi(v_{i}) dv_{i} \;\;\;\;\; (0 < v_{i} < y_{i}). \tag{3} \end{equation*}$

Смысл выражений (2) и (3) легко продемонстрировать следующей анимацией
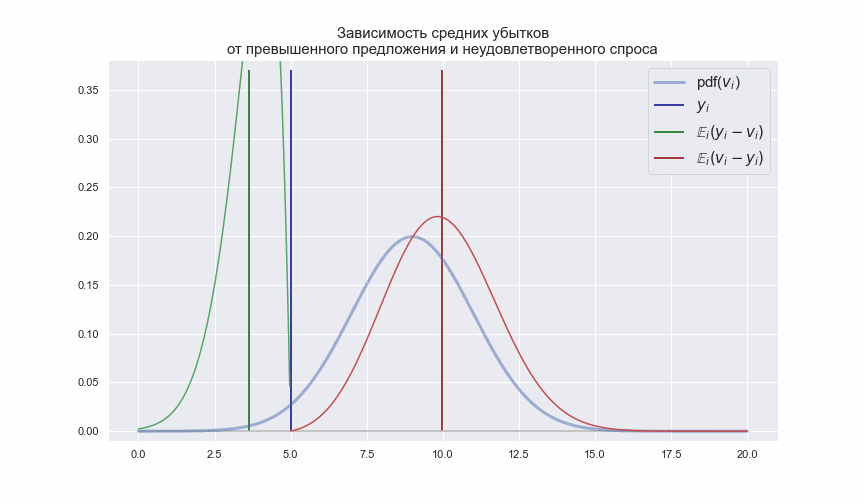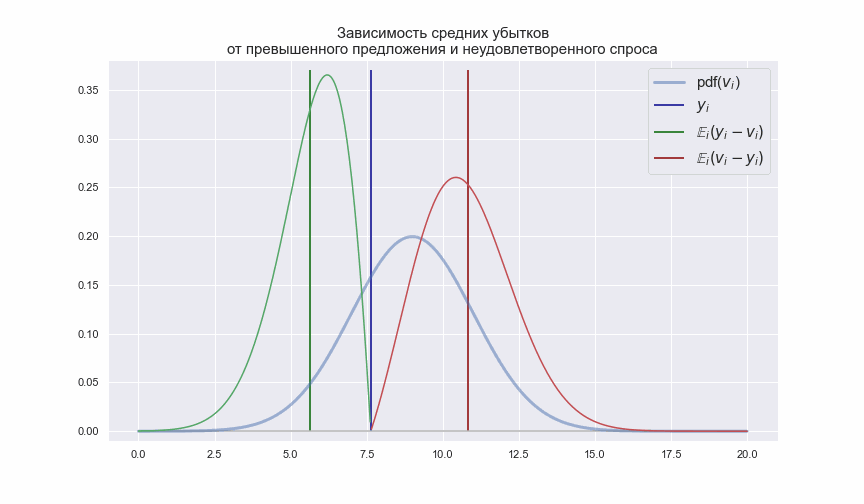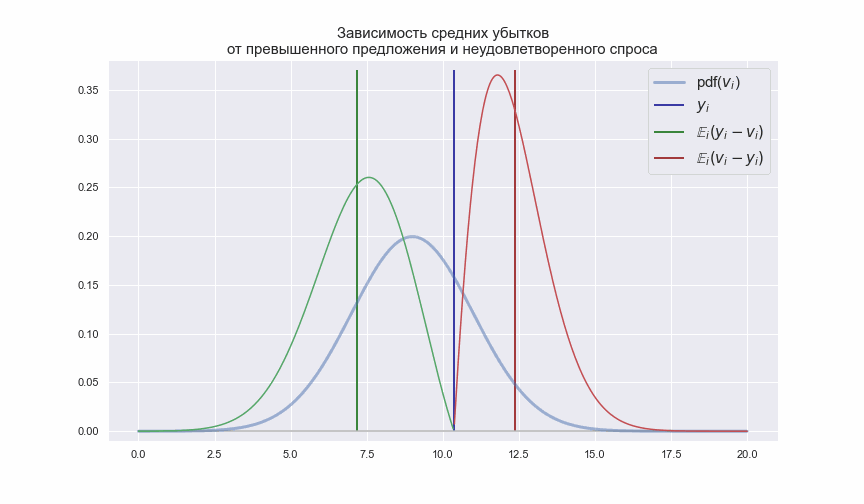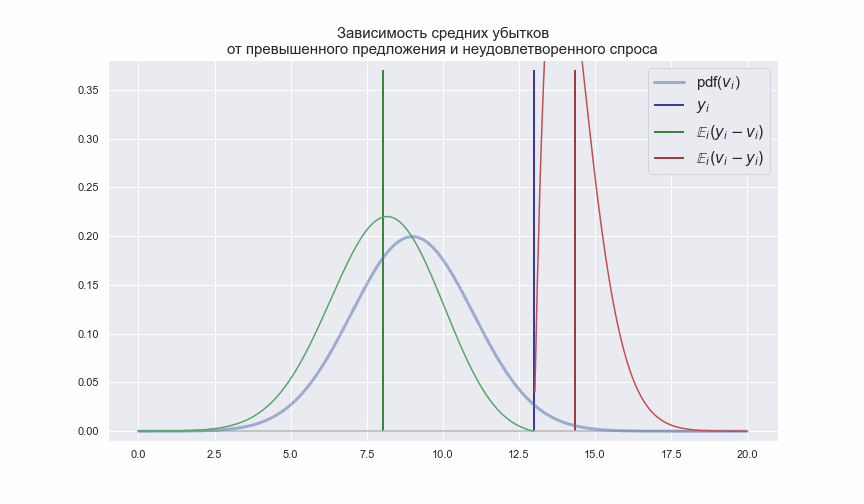
image
Синяя вертикальная линия показывает количество перевозимых пассажиров $y_{i}$ по $i$-му маршруту, а зеленая и красная линии показывают средние значения с которыми случайный спрос $v_{i}$ может быть ниже или выше $y_{i}$. Учитывая, что $\pi_{i} \neq k_{i}$, т.е. убытки от каждого не предоставленного или не занятого кресла отличны друг от друга, значение $y_{i}$ нужно выбирать таким, чтобы выражения (2) и (3) принимали минимальные значения.
Далее необходимо учесть общие эксплуатационные расходы, связанные с работой $x_{fi}$ самолетов на $i$-м маршруте

$\begin{equation*} \sum_{f \in F} c_{fi}x_{fi} \;\;\;\; (i \in I). \tag{4} \end{equation*}$

Средние ожидаемые суммарные потери от эксплуатации самолетов на всех маршрутах из-за неудовлетворенного спроса и избыточного предложения выразятся суммой по всем маршрутам из множества $I$, определяемым выражениями (2)-(4):

$\begin{equation*} z = \sum_{i \in I} \left ( \sum_{f \in F} c_{fi}x_{fi} + \int_{y_{i}}^{\infty} \pi_{i}(v_{i} - y_{i}) \varphi(v_{i}) dv_{i} + \int_{0}^{y_{i}} k_{i}(y_{i} - v_{i}) \varphi(v_{i}) dv_{i} \right ). \tag{5} \end{equation*}$

Необходимо найти такие $x_{fi}$, которые минимизируют функцию (5), при этом можно учесть, что $y_{i}$ могут быть выражены через $x_{fi}$ с помощью равенства (1).
Значения $x_{fi}$ должны удовлетворять следующим условиям: количество самолетов типа $f$, используемых на всех $n$ маршрутах не должно превышать общего количества $N_{f}$ самолетов, находящихся в распоряжении авиакомпании, т.е.

$\begin{equation*} \sum_{i \in I} x_{fi} \leqslant N_{f} \;\;\;\; (f \in F). \tag{6} \end{equation*}$

Еще одно ограничение вытекает из равенства (1)

$ \begin{equation*} \sum_{f \in F} d_{fi}x_{fi} - y_{i} = 0 \;\;\;\; (i \in I). \tag{7} \end{equation*}$

По смыслу задачи

$ \begin{equation*} x_{fi} \geqslant 0 \;\;\;\; (f \in F ; i \in I). \tag{8} \end{equation*}$

$ \begin{equation*} y_{i} \geqslant 0 \;\;\;\; (i \in I). \tag{9} \end{equation*}$

Традиционно, задача расстановки авиапарка решается в линейной и детерминированной форме с заданным значением спроса по каждому маршруту. Сначала может показаться, что если принять во внимание случайность спроса, т.е. стохастическую постановку задачи, то она станет просто не решаемой, к тому же, из-за введения в целевую функцию интегралов (2) и (3) она перестает быть линейной. Но на самом деле функция (5) может быть решена методом линейной аппроксимации, поскольку является выпуклой и сепарабельной, а использование линейной детерминированной формы во многом связано с проблемами прогнозирования величины спроса.

Проблема заключается в том, что из-за ценовой дифференциации спрос классифицируется на уровне тарифов, что в общем-то неудивительно, так как пассажирский пул не является однородным: кто-то предпочитает платить больше за дополнительный комфорт, другие ценят возможность сэкономить. В идеале, модель назначения флота должна учитывать эту неоднородность, что, в принципе, не представляет никаких трудностей. Если ввести множество тарифов $\textrm{Class}$, каждый из которых будет обозначаться индексом $l$, то выражения (2) и (3) просто преобразуются в суммы интегралов где каждое слагаемое соответствует определенному тарифу:

$\begin{equation*} \mathbb {E}_{i}^{'} = \sum_{l \in \textrm{Class}} \int_{y_{il}}^{\infty} \pi_{il}(v_{il} - y_{il}) \varphi(v_{il}) dv_{il} \;\;\;\;\; (y_{i} < v_{i} < \infty),\tag{2'} \end{equation*}$

$\begin{equation*} \mathbb {E}_{i}^{''} = \sum_{l \in \textrm{Class}} \int_{0}^{y_{il}} k_{il}(y_{il} - v_{il}) \varphi(v_{il}) dv_{i} \;\;\;\;\; (0 < v_{i} < y_{i}). \tag{3'} \end{equation*}$

Казалось бы, что абсолютно ничто не мешает создавать прогнозы величины спроса на каждый из тарифов, но парадокс заключается в том, что вместо этого используется так называемая вертикальная и горизонтальная агрегация спроса. В вертикальной агрегации все тарифы объединяются в некий средний тариф, а в горизонтальной величина спроса на этот средний тариф из разных дней недели объединяются в «репрезентативную» дневную величину. В результате такого агрегирования на выходе прогноза получается единственное значение среднего спроса на средний тариф. С фреквентистской точки зрения в таком подходе к прогнозированию все очень разумно, поскольку, как случайная величина, спрос конечно будет испытывать некоторые колебания, но все колебания будут происходить вокруг этого усредненного значения. Раз все кажется более чем приемлемым и абсолютно логичным, то использование стохастических моделей кажется абсолютно бессмысленным.

С Байесовской точки зрения все выглядит несколько иначе. Например, очевидно, что если мы увеличим стоимость билетов, то это приведет к снижению продаж и наоборот, если снизим их стоимость, то будем продавать больше. Однако, так же очевидно, что эти действия влияют на выражения (2') и (3'). Получается, что модель ценообразования и модель управления флотом сильно связаны друг с другом. В линейной и детерминированной модели эта связь не то что бы не очевидна, ее просто не существует, из-за чего задачи ценообразования и расстановки авиапарка воспринимаются как две отдельные задачи. Принцип «разделяй и влавствуй» в этом случае не работает, потому что решение этих задач по отдельности может приводить к противоречивым результатам. Например, идеальное решение задачи ценообразования может привести к тому, что выражения (2') и (3') при большинстве комбинаций самолетов будут иметь очень высокие значения, следовательно, выиграв на продаже билетов, мы проиграем на перевозке.

В предыдущей статье мы подчеркивали, что задача ценообразования во многом зависит от тех целевых показателей, которых мы хотим добиться, но из всего вышесказанного следует, что какими бы ни были наши цели, они должны достигаться с учетом минимизации выражений (2') и (3'). В этом месте снова может показаться, что совместное решение задач ценообразования и расстановки авиапарка не является возможным. Дело в том, что задача (5) относится к классу одноэтапных. Одноэтапная задача может возникнуть перед нами, например, если мы захотим выйти на новый рынок или его сегмент. Сначала придется собрать некоторую аналитику о внутреннем спросе, естественно воспринимая его как набор случайных величин, а потом, с помощью задачи (5), можно спланировать расстановку имеющегося авиапарка или даже его необходимый состав. Такие задачи решаются единожды, а в случае гражданских авиаперевозок, после их решения все движется по старым рельсам. Совместное решение задач ценообразования и расстановки авиапарка в масштабе отдельных рейсов и маршрутов возможно только в многоэтапной форме, так как задача ценообразования имеет протяженность во времени.
Давайте взглянем на то, как выглядит задача ценообразования для максимизации выручки:

$\begin{equation*} \textrm{price}_{fik}^{*} = \underset{\textrm{price}_{fijk}}{\textrm{argmax}} \;\; \left ( \textrm{price}_{fijk} \int_{0}^{\infty} v_{ik} \varphi_{ijk} (v_{ik}) d v_{ik} \right ). \tag{10} \end{equation*}$

Для $i$-го маршрута и самолета типа $f$ оптимальная стоимость билета в $k$-й промежуток времени находится из условия максимизации произведения стоимости билета $\textrm{price}_{fij}$ и мат. ожидания количества билетов, которое можно продать по $j$-й цене. Разумеется оптимальная стоимость билетов зависит от маршрута, но она так же зависит и от типа самолета. Что бы внести ясность в то как мат. ожидание количества проданных билетов меняется от одного промежутка времени к другому, нужно сделать несколько уточнений, а именно разобраться от чего оно зависит. В простейшем случае количество проданных билетов в некоторый промежуток времени зависит от:
  • случайной величины спроса $\rho_{ik}$ с распределением $\varphi (\rho_{ik} , t)$ — количества всех потенциальных покупателей в $k$-й промежуток времени;
  • распределения количества денег у покупателей $\psi (p_{fik}, t)$, которое они готовы отдать за билет в $k$-м промежутке времени.

Действительно, все потенциальные покупатели случайным образом отличаются друг от друга количеством денег, которое они готовы отдать за билет, а значит, тоже как-то распределены. Наличие переменной $t$ в функции $\psi (p_{fik}, t)$ указывает на то что спрос, а точне количество проданных билетов зависит не только от их стоимости, но и от времени, прошедшего с момента начала продаж. Если, для более краткой записи, обозначить стоимость $\textrm{price}$ символом $p$, а время начала $k$-го промежутка времени обозначить как $t_{k}$, то количество проданных билетов по цене $p_{fijk}$ в $k$-м промежутке времени запишется как:

$\begin{equation*} v_{ijk} = \rho_{ik} \cdot \int_{p_{fijk}}^{\infty } \int_{t_{k}}^{t_{k+1}} \psi_{ik} (p_{fik}, t) \, dt \, dp_{fik}. \tag{11} \end{equation*}$

Двойной интеграл в данном выражении просто показывает, какая доля от случайного количества потенциальных покупателей сможет приобрести билет по установленной цене $p_{fijk}$. Математическое ожидание $v_{ijk}$ может быть записано следующим образом:

$\begin{equation*} \mathbb {E}(v_{ijk}) = \int_{0}^{\infty} \int_{p_{fijk}}^{\infty } \int_{t_{k}}^{t_{k+1}} \rho_{ik} \, \varphi_{ik} (\rho_{ik} , t) \, \psi_{ik} (p_{fi}, t) \, dt \, dp_{fi} \, d\rho_{ik}, \tag{12} \end{equation*}$

следовательно, выражение (10) может быть переписано как

$\begin{equation*} p_{fik}^{*} = \underset{p_{fijk}}{\textrm{argmax}} \;\; \left ( p_{fijk} \int_{0}^{\infty} \int_{p_{fijk}}^{\infty } \int_{t_{k}}^{t_{k+1}} \rho_{ik} \, \varphi_{ik} (\rho_{ik} , t) \, \psi_{ik} (p_{fi}, t) \, dt \, dp_{fi} \, d\rho_{ik} \right ). \tag{10'} \end{equation*}$

Прибыль, полученная в $k$-й промежуток времени является случайной величиной

$\begin{equation*} r_{fijk} = p_{fijk} \cdot v_{ijk}, \tag{13} \end{equation*}$,

а общая прибыль будет являться суммой $r_{fijk}$ за все периоды времени $k$

$\begin{equation*} R_{fi} = \sum_{k} r_{fijk} = \sum_{k} p_{fijk} \cdot v_{ijk}. \tag{14} \end{equation*}$

Функция (5) в задаче расстановки флота необходима для минимизации убытков и предполагает, что можно явным образом определить убытки от неудовлетворения спроса и избыточного предложения на каждом маршруте в зависимости от того или иного типа самолета. В то же самое время функция (15) никаких явных возможностей в определении убытков не предполагает и необходима только для максимизации прибыли от продажи билетов на каждый рейс. Получается, что для объединения двух задач необходимо определиться с тем, что мы будем оптимизировать: суммарные убытки или суммарную прибыль. Очевидно, что лучше оставить какие бы то ни было попытки адаптировать мат.ожидания убытков в функции (5) к не стационарному спросу, и просто заменить их на уже адаптированное к такому спросу мат. ожидание прибыли. В результате такой замены и простых преобразований получим окончательное объединение двух задач

$\begin{equation*} z = \sum_{i \in I} \left (\int_{0}^{\infty} \!\! ... \int_{0}^{\infty} \left ( \left ( \sum_{k} p_{fijk} \cdot\rho_{ik} \int_{p_{fijk}}^{\infty } \int_{t_{k}}^{t_{k+1}} \, \psi_{ik} (p_{fi}, t) \right ) \prod_{k} \int_{t_{k}}^{t_{k+1}} \! \varphi_{ik} (\rho_{ik} , t) \right )\, d\rho_{i0}\, d\rho_{i1}\, ... d\rho_{ik} - \sum_{f \in F} c_{fi}x_{fi} \right ). \tag{18} \end{equation*}$

Разумеется, в зависимости от типа самолета функция (15) будет приводить к разным значениям прибыли, так как тип самолета явно учитывается в целевых показателях процесса ценообразования (10') и (16). Следовательно, функция (18) так же будет приводить к разным результатам в зависимости от расстановки всего флота. Смысл оптимизации заключается в максимизации этих результатов, т.е. максимизации суммарной выручки.

Следует сразу отметить, что функция (15) может быть разбита на тарифы в рамках одного рейса, подобно тому как это сделано в выражениях (2') и (3'), но это увеличит и без того громоздкий вид функции (18). Так же индексация временных интервалов в функции (18) сама нуждается в дополнительной индексации, так как одного индекса $k$ не достаточно для того, чтобы отразить тот факт, что временные интервалы, на самом деле, не являются едиными для каждого рейса. Далее будем полагать, что количество временных интервалов и значения их границ для каждого рейса являются уникальными, несмотря на отсутствие дополнительной индексации.

Стоимость применения найденного решения


Для дальнейшего развития задачи назначения флота необходимо учесть тот факт, что самолеты все-таки летают по определенным правилам, а не телепортируются сразу после получения решения. Что бы прояснить смысл данного ограничения давайте взглянем на следующую иллюстрацию расписания для 4-х аэропортов и 20 рейсов между ними.
image
Данный график представляет собой время-расширенную модель расписания, в которой вершинами обозначены события вылета или прилета, а дугами — время между этими событиями. Так же на графе указан конкретный самолет типа $f$ с номером $m$. Глядя на эту модель, можно заметить, что любая реализация текущего решения — это физическая перестройка расстановки флота с одного множества маршрутов на другое, т.е. такая перестройка должна обладать как протяженностью во времени, так и стоимостью, потому что это тоже некоторое множество маршрутов, которое должно быть выполнено из предыдущего состояния для того, чтобы реализовать полученное решение.
Время перестройки важно для процесса ценообразования. Забегая вперед, надо сказать, что, несмотря на динамический характер выражения (15), решение всей задачи основано на его приблизительных оценках, которые в свою очередь основаны на оценках параметров распределения величины спроса, а так же, его внутреннего денежного распределения. Для оценки значения (15) нужно знать: сколько времени осталось до окончания продаж, сколько билетов уже куплено и какой тип у нового самолета. Разумно предположить, что выполнение перестройки для каждого отдельного самолета может обернуться как прибылью, так и убытками. Например, может получиться так, что полученное решение будет требовать незамедлительного назначения некоторого самолета на новый маршрут, в результате чего самолет может отправиться к этому маршруту пустым. Если полученное решение опирается на прогнозируемые параметры спроса, то в этом случае может появиться некоторый запас времени для выполнения перестройки, а значит в ходе ее выполнения можно успеть продать какое-то количество билетов, следовательно, извлечь некоторую прибыль в ходе выполнения такой перестройки.
Стоимость всех перестроек для каждого отдельного самолета должна вычисляться заранее и присутствовать в функции (18). Если обозначить эту стоимость как $C_{ifm}$, то функция (18) примет следующий вид

$\begin{equation*} z = \sum_{i \in I} \left (\int_{0}^{\infty} \!\! ... \int_{0}^{\infty} \left ( \left ( \sum_{k} p_{ifmjk} \rho_{ik} \int_{p_{ifmjk}}^{\infty } \int_{t_{k}}^{t_{k+1}} \, \psi_{ik} (p_{fi}, t) \right ) \prod_{k} \int_{t_{k}}^{t_{k+1}} \! \varphi_{ik} (\rho_{ik} , t) \right )\, d\rho_{i0}\, d\rho_{i1}\, ... d\rho_{ik} - \sum_{f \in F} \sum_{m \in N_{f}}(c_{ifm} + C_{ifm}) x_{ifm} \right ). \tag{19} \end{equation*}$

В конечном счете получается, что каждый этап задачи управления флотом, сам по себе представляет отдельную задачу о назначениях, для решения которой необходимо найти такое отображения множества самолетов на множество маршрутов, при котором функция (19) примет максимальное значение. Переменные $x_{ifm}$ могут принимать всего два значения: 0, если самолет типа $f$ и номером $m$ не назначен на маршрут $i$ и 1, если назначен.

Генерирование множества маршрутов из множества рейсов может выполняться путем поиска в глубину, но таким образом что бы количество переменных сводилось к минимуму. Во многом количество маршрутов снижается, из-за огромного количества естественных ограничений. Например, зачастую выдвигаются требования к цикличности маршрутов. Другие факторы, такие как ограниченная пропускная способность аэропортов или недопустимость чрезмерной сверхурочной работы экипажей, так же являются дополнительными ограничениями для генерируемых маршрутов. Таким образом, комбинаторный взрыв в результате такого генерирования не является существенной проблемой. С другой стороны, от этой проблемы нельзя избавиться окончательно, так как для повышения эффективности решения может потребоваться оптимизация расписания, а это требует введения в модель фиктивных рейсов. Если некоторое решение с использованием фиктивных рейсов является более оптимальным, чем без них, то эти рейсы вносятся в расписание.
Последним недостатком функции (19) является то, что в ней не учитывается наличие отдельных рейсов, из которых, собственно, и состоят маршруты. Пусть $S_{i}$ это множество всех рейсов $s$, из которых состоит $i$-й маршрут, тогда окончательно функцию (19) можно представить следующим образом:

$\begin{equation*} z = \sum_{i \in I} \left (\sum_{s \in S_{i}} \mathbb {E} R_{sfm} - \sum_{f \in F} \sum_{m \in N_{f}}(c_{ifm} + C_{ifm}) x_{ifm} \right ). \tag{20} \end{equation*}$

Как решить задачу?


Генерация множества допустимых маршрутов (расписаний), а так же, расчет стоимости перестановки флота для их реализации, является самой простой частью задачи. Гораздо больше интересных деталей возникает при непосредственной оптимизации функции (20), ведь процесс ценообразования придает задаче динамический (многоэтапный) характер. В общем смысле, данная задача не является задачей, которую можно как-то решить, поскольку на самом деле мы имеем дело с процессом, который состоит из цепочки «Реализация случайных переменных» -> «Решение» -> «Реализация случайных переменных» ->… ->«Решение». Данный процесс можно считать какой-то обозримой задачей если мы говорим о некотором горизонте планирования, например, периоде от начала продаж билетов на некоторый рейс, до вылета самолета по данному рейсу. Нужно сразу отметить, что многоэтапные задачи бывают априорными и апостериорными, т.е. порой очень важно с чего начинается цепочка: с «Решения» или с «Реализации случайных величин». Мы будем предполагать, что у нас всегда есть некоторая аналитика, поэтому любая цепочка всегда будет начинаться с «Реализации случайных величин». Проблема «холодного старта» безусловно существенна, но просто полное отсутствие аналитики очень трудно представить в наше время.

Чтобы решить задачу, надо сначала понять, как вообще возникают многоэтапные задачи. Предположим, что мы занимаемся производством, складированием и продажей некоторого продукта. Благодаря штатному аналитику мы знаем, что спрос $X$ на будущей неделе хоть и будет случайным, но будет иметь гамма-распределение, т.е. $X\thicksim \Gamma (k,\theta )$. Поскольку использование непрерывных случайных величин весьма затруднительно, мы вынуждены аппроксимировать его более простым дискретным распределением. Допустим мы аппроксимировали это распределение пятью значениями $x_{n}$ и их соответствующими вероятностями $p_{n}$, $n \in [1; 5]$, что можно изобразить очень простой схемой:

Изначально может показаться, что нужно ориентироваться либо на самый вероятный исход, либо на мат. ожидание спроса $\mathbb {E}(X)$. Однако, оптимизируемая функция прибыли, хоть и зависит от спроса, но не напрямую. Например, при разных, но довольно близких значениях спроса она может иметь одинаковое значение или наоборот, испытывать очень сильное, скачкообразное изменение. Поэтому, единственное правильное решение — это ориентироваться на мат. ожидание прибыли, которое и должно быть максимальным. Но что если аналитик утверждает, что через следующую неделю спрос будет чуть выше? Очевидно что в этом случае у нас появится 25 сценариев развития событий:

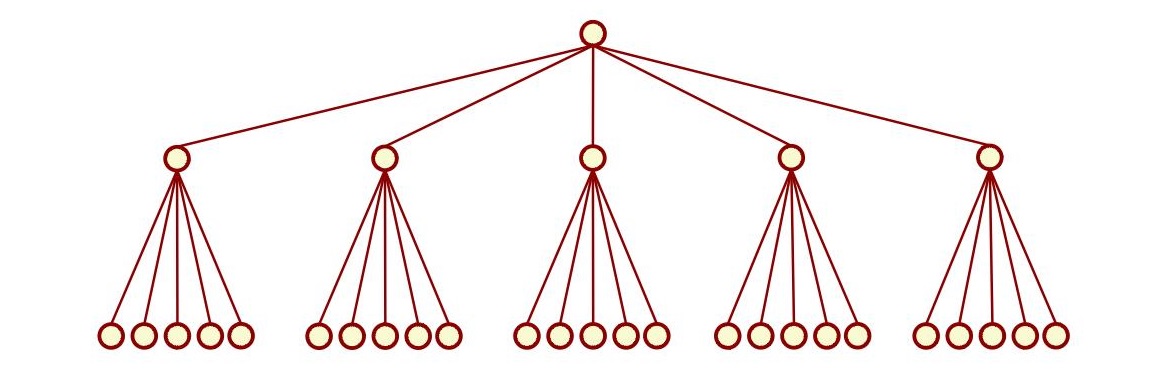
Наш аналитик может пойти еще дальше и сказать, что на третей неделе, вероятнее всего, спрос не изменится, но есть значительная вероятность того, что он вырастет и небольшая вероятность того, что он сильно упадет. В итоге получим 375 сценариев развития событий. Казалось бы, что мы опять должны руководствоваться общим мат. ожиданием прибыли, но так как задача разбита на этапы (недели), то придется учитывать мат. ожидание на каждом из них. Например, если функция прибыли имеет вид $f(X, V)$, где $X$ — это случайная величина спроса, а $V$ — это вектор переменных, то целевая функция примет следующий вид:

$\begin{equation*} z = \mathbb {E} \left [\, \textrm{Max}_{V_{1}} \;\; f(X_{1}, V_{1}) + \mathbb {E} \left [\, \textrm{Max}_{V_{2}} \;\; f(X_{2}, V_{2}) + \mathbb {E} \left [\, \textrm{Max}_{V_{3}} \;\; f(X_{3}, V_{3})\, \right ]\, \right ]\, \right ]. \tag{21} \end{equation*}$

Здесь возникает еще один не совсем очевидный нюанс — неоптимальное решение на текущем этапе может привести к самым оптимальным последствиям на следующем этапе. Например, мы можем две недели подряд при небольшом спросе производить очень много продукции, но если на третьей неделе спрос сильно увеличится, то у нас получится полностью удовлетворить его. Функция (21) требует от нас оптимального решения как для текущего этапа, так и для всего горизонта планирования, т.е. выполнение перепроизводства тоже должно быть оптимальным. Конечно, вероятность разных стечений обстоятельств может оказаться очень маленькой, но как раз для оценки вероятностей таких стечений нам и нужен аналитик.

Многоэтапные задачи больше всего подходят для оптимизации в реальном мире, но как мы уже заметили, для их решения нам нужно уметь две вещи:
  • анализировать имеющиеся данные, чтобы оценивать текущую ситуацию и делать прогнозы;
  • прорабатывать огромное количество сценариев.

Хотелось бы думать, что для первого пункта достаточно обыденных статистических методов. А для второго пункта — параллельных вычислений. Но на качество решения эти пункты влияют не по отдельности, а совместно. Например, мы можем аппроксимировать непрерывные распределения очень большим количеством точек, тогда даже для небольшого горизонта планирования мы получим бесчисленное количество сценариев. Если же мы уменьшим количество аппроксимирующих точек, то сможем очень сильно увеличить горизонт планирования, но решение будет очень грубым и далеко не оптимальным. Необходимо сразу принять во внимание, что для качества решения всегда есть некоторый барьер, определяемый как вычислительными ресурсами, так и применяемыми методами анализа данных. А если вспомнить, что мы решаем данную задачу для всех возможных комбинаций маршрутов, то в чрезвычайной близости и высоте этого барьера можно не сомневаться.

Тем не менее, выход из данной ситуации все-таки имеется. Есть несколько довольно старых статей, в которых доказывается одна простая истина — информация очень важна для многоэтапного стохастического программирования. Абсолютно не важно, каким образом эта информация извлечена из данных, главное, чтобы она имелась в необходимом количестве. А это значит, что мы можем попытаться несколько упростить процесс оптимизации.

В предыдущей статье мы рассматривали спрос как очень простую модель, в которой просто учитывалось, сколько человек в некотором периоде времени обращались к системе за билетом и сколько совершили его покупку. Но на самом деле мы можем учитывать гораздо больше параметров, например:
  • общее число посещений сайта человеком;
  • общее количество покупок совершенных посетителем;
  • время посещения;
  • устройство, с которого посетитель зашел на сайт;
  • сколько страниц с описанием маршрутов просмотрел посетитель;
  • количество билетов, выставленных к продаже на данный момент;
  • периоды времени, на который посетитель искал билеты.

Это лишь малая часть тех параметров, которые могут быть собраны на самом деле. Очевидно, что чем больше данных мы собираем о посетителях, тем больше информации о спросе мы можем извлечь. Но точно так же очевидно, что обычными статистическими методами эту информацию извлечь не получится, поскольку у нас нет самых главных данных о том, сколько денег посетитель был готов отдать за билет в действительности. Давайте еще раз вспомним, что нам необходимо знать для решения задачи ценообразования:
  • $\varphi (\rho_{ik} , t)$ — распределение количества всех потенциальных покупателей билетов на рейс $i$ в $k$-й промежуток времени;
  • $\psi (p_{fik}, t)$ — распределение количества денег которое каждый из посетителей готов отдать за билет в $k$-м промежутке времени на $i$-й рейс, выполняемый самолетом типа $f$.

Для величины спроса $\rho_{ik}$ никаких проблем с данными нет и мы можем чуть ли не в автоматическом режиме выбирать самые подходящие алгоритмы для анализа и прогноза. Для финансового распределения $\psi (p_{fik}, t)$ есть только скрытые данные, все что можно увидеть из этих данных это то, что посетитель:

был готов отдать за билет либо больше, либо столько же денег, сколько указано в его цене, если он его купил;
рассчитывал приобрести билет за меньшую цену, если он его не купил.

Фактически перед нами встает задача из области машинного обучения — построение двух моделей данных, перая модель для величины спроса, вторая для его внутреннего финансового распределения. Подобрать самую оптимальную модель для прогнозирования величины спроса довольно легко, так как мы имеем дело с обычным временным рядом. А вот для прогнозирования финансового распределения подобрать модель уже несколько сложнее. Самое простое, что можно придумать — использовать в качестве основы нормальное распределение, параметры которого зависят от времени, например, линейно:

$\begin{equation*} N(\varepsilon_{1}t + \mu_{0}, (\varepsilon_{2}t + \sigma_{0})^{2}). \tag{22} \end{equation*}$

Такая модель, даже несмотря на свою простоту, может очень хорошо отражать то, как меняется распределение $p_{fit}$ с течением времени в $k$-м периоде, а следовательно, и вероятность продажи одного билета по заданной цене в этом периоде. Например, если распределение плотности вероятности $p_{fik}$ задано как $N(0.5t + 9, (0.3t + 1)^{2})$, то можно проследить как будет меняться вероятность продажи одного билета на протяжении двух дней:

Тогда распределение $\psi (p_{fik}, t)$ можно представить, как смесь из таких распределений, т.е.

$\begin{equation*} \psi (p_{fik}, t_{k}, t_{k+1}) = \frac{\int_{t_{k}}^{t_{k+1}}f(p, t)dt}{\int_{-\infty}^{\infty}\int_{t_{k}}^{t_{k+1}}f(p, t)dtdp}, \tag{23} \end{equation*}$

где

$\begin{equation*} f(p, t) = \frac{1}{\sqrt{2\pi}(\varepsilon_{2}t + \sigma_{0})}e^{-\frac{(p - (\varepsilon_{1}t + \mu_{0}))^{2}}{2(\varepsilon_{2}t + \sigma_{0})^{2}}}. \tag{24} \end{equation*}$

При очень быстром или небольшом, но продолжительном изменении параметров, смеси могут принимать самые разные формы:

Как оказалось, учет формы таких распределений при анализе параметров $\psi (p_{fik}, t)$ требует очень много данных и вычислительных ресурсов, при этом итоговые оценки все равно получаются очень грубыми. На практике выяснилось, что параметры действительно могут меняться очень быстро, но так как время удержания цены является непродолжительным, то результирующие смеси практически не отличаются от нормального распределения, разве что имеют незначительную асимметрию:

На графике видно, что результирующая смесь распределений $N(0.5t + 9, (0.3t + 1)^{2})$ для $t \in [2, 4]$ практически полностью совпадает с плотностью распределения $N(10.5,1.9^{2})$, а результирующая вероятность продажи одного билета по 13.5 тыс. рублей составляет около 0.062, что для смеси, что для $N(10.5,1.9^{2})$.
Такое простое упрощение позволяет очень сильно сократить объем необходимых данных о недавних продажах и позволяет довольно легко оценивать параметры распределения спроса. Например, данных о продаже билетов по последним двум ценам $\textrm{price}_{k}$ и $\textrm{price}_{k+1}$, достаточно для того, чтобы довольно точно оценить $\mu_{k}$. Предположим, что $\mu_{k+1} = \varepsilon_{1}\mu_{k}$, а $\sigma_{k+1} = \varepsilon_{2}\sigma_{k}$, где $\varepsilon_{1}$ и $\varepsilon_{2}$ небольшие коэффициенты, тогда вероятности исходов двух продаж могут быть оценены как:

$\begin{equation*} \widehat{p}_{k} = C_{u + z}^{u}\left ( 1 - \frac{1}{\sigma_{k, i_{2}} \sqrt{2 \pi}}\int_{-\infty }^{\textrm{price}_{k}} e ^{-\frac{(x-\mu_{k, i_{1}})^2}{2\sigma_{k, i_{2}}^{2}}}d x \right )^{u}\left (\frac{1}{\sigma_{k, i_{2}} \sqrt{2 \pi}}\int_{-\infty }^{\textrm{price}_{k}} e ^{-\frac{(x-\mu_{k, i_{1}})^2}{2\sigma_{k, i_{2}}^{2}}}d x \right )^{z} \\ \widehat{p}_{k+1} = C_{u + z}^{u}\left ( 1 - \frac{1}{\varepsilon_{2, i_{4}}\sigma_{k, i_{2}} \sqrt{2 \pi}}\int_{-\infty }^{\textrm{price}_{k+1}} e ^{-\frac{(x-\varepsilon_{1, i_{3}}\mu_{k, i_{1}})^2}{2\varepsilon_{2, i_{4}}\sigma_{k, i_{2}}^{2}}}d x \right )^{u}\left (\frac{1}{\varepsilon_{2, i_{4}}\sigma_{k, i_{2}} \sqrt{2 \pi}}\int_{-\infty }^{\textrm{price}_{k+1}} e ^{-\frac{(x-\varepsilon_{1, i_{3}}\mu_{k, i_{1}})^2}{2\varepsilon_{2, i_{4}}\sigma_{k, i_{2}}^{2}}}d x \right )^{z} , \tag{25} \end{equation*}$

где $u$ — это количество посетителей, которые купили билет, а $z$ — количество посетителей, которые его не купили. Тогда, решая следующее уравнение

$\begin{equation*} (\mu_{k, i_{1}}^{*}, \sigma_{k, i_{2}}^{*}, \varepsilon_{1}^{*}, \varepsilon_{2}^{*} ) = \underset{(\widehat{\mu}, \widehat{\sigma}, \widehat{\varepsilon}_{1}, \widehat{\varepsilon}_{2})}{\textrm{argmax}}\;\;(\widehat{p}_{k, i_{1},i_{2},i_{3},i_{4}} \cdot \widehat{p}_{k+1, i_{1},i_{2},i_{3},i_{4}}), \tag{26} \end{equation*}$

можно найти наилучшую оценку $\mu_{k, i_{1}}^{*}$. Сразу возникает вопрос: почему не $\mu_{k, i_{1}}^{*}$ и $\sigma_{k, i_{2}}^{*}$ одновременно? Дело в том, что даже очень большие приращения дисперсии и коэффициента $\varepsilon_{2}$ приводят к небольшим изменениям общего произведения, поэтому значения $\sigma_{k, i_{2}}^{*}$ являются практически случайными. На нижеследующем графике показано, как выглядят оценки параметров модели спроса, которые со временем увеличиваются линейно:

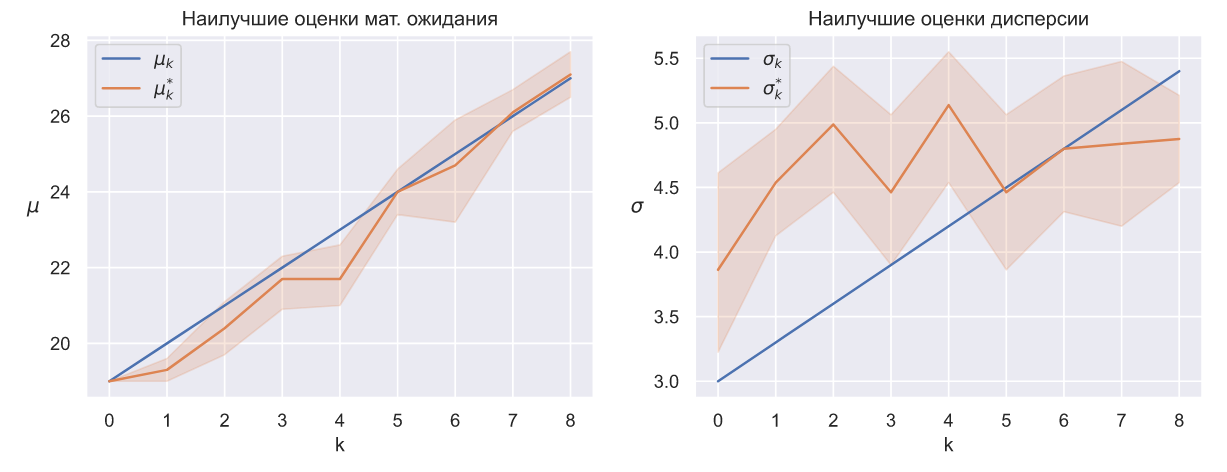
А на этом графике параметры сначала линейно увеличиваются, а затем так же линейно уменьшаются:

С другой стороны, если есть оценки мат. ожидания, то можно попробовать применить метод максимального правдоподобия. Для примера, предположим, что распределение $\psi (p_{fik}, t)$ задано как $N(0.3t + 950, (0.2t + 150)^{2})$, тогда процесс продажи билетов на протяжении 20 дней может выглядеть так:

Синими точками отмечены те посетители, которые приобрели билет, т.е. были готовы отдать за билет столько, сколько указано в его стоимости или больше. Зелеными точками отмечены посетители, которые рассчитывали приобрести билет по меньшей стоимости. Благодаря вышеописанному методу мы можем довольно точно установить, что $\mu_{t} = 0.28t + 930$, а значит параметры $\varepsilon_{1}$ и $\mu_{0}$ в выражении (23) имеют довольно хорошие оценки. Тогда мы можем оценить вероятность того, что посетитель не купит билет как

$\begin{equation*} P_{i, 0}(p_{fik} < \textrm{price}_{i}) = \int_{-\infty }^{\textrm{price}_{i}}f(p, t_{i})d p, \tag{27} \end{equation*}$

а вероятность того, что он его приобретет как

$\begin{equation*} P_{i, 1}(p_{fik} \geqslant \textrm{price}_{i}) = 1 - \int_{-\infty }^{\textrm{price}_{i}}f(p, t_{i})d p, \tag{28} \end{equation*}$

Благодаря формулам (27) и (28) мы можем оценить вероятность приобретения или не приобретения посетителем одного билета при различных значениях параметров $\varepsilon_{2}, \sigma_{0}$. Если в некоторый период времени $T$ к системе обратилось $n$ посетителей, а факт приобретения или неприобретения билета каждым из них записан как массив $U = [u_{0}, u_{1},..,u_{i}]$, то оценить подходящие параметры $\varepsilon_{2}, \sigma_{0}$ можно исходя из принципа максимального правдоподобия:

$\begin{equation*} P_{n, T}=\sum_{i=0}^{n} \ln (P_{i, u_{i}}), \tag{29} \end{equation*}$

Причем, параметры $\varepsilon_{2}, \sigma_{0}$ из формулы (23) подбираются так, чтобы значение $P_{n, T}$ было максимальным.

Если сделать последовательные срезы по 200 посетителей и применить данный метод к каждому из срезов, то увидим следующую картину:

Даже несмотря на то, что средние значения оценок довольно близки к истинным значениям, такой результат не вызывает абсолютного доверия, особенно это касается оценок $\sigma_{0}$, которые явно ограничены искусственно. Дело в том, что ограничение действительно имеется и является частью настроек процесса оптимизации. Если не вводить ограничения, то $\sigma_{0}$ может очень сильно отклоняться и в то же самое время ограничения нужны хотя бы потому что у $\sigma_{0}$ должны быть какие-то разумные пределы. В конечном счете, если применить бутстреп метод к такому срезу (или любому другому), то картина будет следующей:

На этом графике видно, что значения, близкие к ограничениям, могут быть отброшены и это никак не повлияет на точность оценок. Хотя, надо сразу отметить, что иногда оценки могут быть очень грубыми и от этого никуда не деться, поэтому ограничений требуют не только оцениваемые параметры, но и максимально возможные изменения цен, на которые они влияют. В принципе, можно целиком и полностью положиться на последовательный анализ Вальда, который очень быстро реагирует на изменение вероятности продажи одного билета, но даже несколько билетов, проданных по крайне низким ценам, означают потерю прибыли, так что лучше всегда использовать разумные ограничения везде, где есть риски.

S-кривая и реальное изменение спроса


Описание динамики спроса линейными функциями очень хорошо подходит для стационарных приращений, но в действительности такое описание зачастую непригодно. Рост (или падение) спроса на некоторые товары, как правило, характеризуется тремя фазами:
  1. подготовка
  2. рост (или падение)
  3. стагнация

Чтобы понять суть этих фаз, достаточно вспомнить, как меняется спрос на шампанское. Например, вы вряд ли увидите, как кто-то покупает шампанское к Новому году в начале ноября. Да, кто-то покупает этот напиток, но вплоть до 20-х чисел ноября в этих продажах практически нет никакой динамики. С 20-х чисел спрос на шампанское начинает расти. Далее, за несколько дней до Нового года спрос приобретает максимальное значение и на какое-то время останавливается. В предельном случае, когда есть бесконечное количество потребителей и бутылок шампанского, спрос на него должен экспоненциально стремиться к бесконечности. Но, поскольку любой ресурс ограничен, то вместо бесконечного роста мы всегда наблюдаем эффект насыщения.

Все это справедливо и для авиабилетов. Если взять усредненные данные по продажам на некоторый рейс, то картина будет примерно следующей:

Безусловно, на форму кривой, описывающей динамику ежедневных объемов продаж, будет влиять процесс изменения цены, но, в любом случае, необходимо учитывать её S-образную форму. Очевидно, что такая форма так же относится и к внутреннему финансовому распределению спроса, т.е. мат. ожидание и дисперсия распределения количества денег $p_{fi}$, которое посетители готовы заплатить за билет, не могут расти бесконечно и так же должны испытывать эффект насыщения. Если принять, что в «нормальной» модели

$\begin{equation*} \psi (p_{fi}, t) = N(\mu (t), (\sigma (t))^{2}) \tag{30} \end{equation*}$

математическое ожидание и отклонения заданы как

$\begin{equation*} \mu(t) = \frac{\varepsilon_{1}}{1 + e^{\varepsilon_{2}(t + \varepsilon_{3})}} + \varepsilon_{4}, \tag{31} \end{equation*}$

$\begin{equation*} \sigma(t) = \frac{\varepsilon_{5}}{1 + e^{\varepsilon_{6}(t + \varepsilon_{7})}} + \varepsilon_{8}, \tag{32} \end{equation*}$

то мы получим модель, которая гораздо больше соответствует действительности. Однако, в этой модели целых 8 параметров, оперативная оценка которых по небольшому набору данных о продаже билетов по разным ценам просто невозможна. В самом деле, если мы смоделируем процесс продажи билетов для этой модели в раках одного рейса, то картина будет следующей:

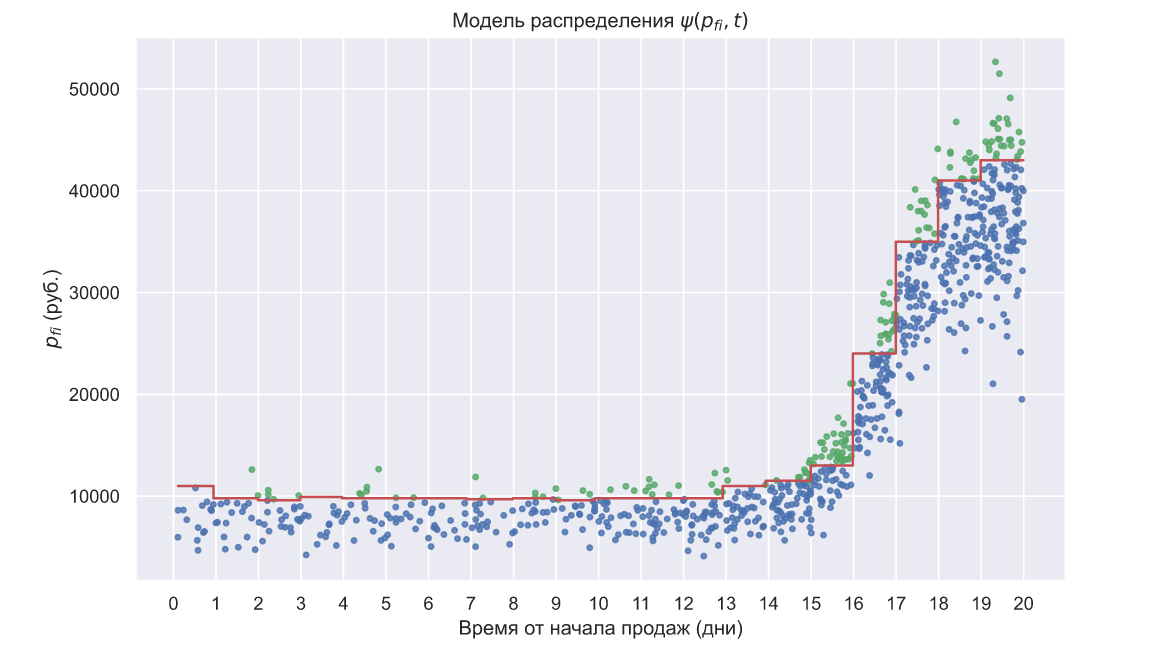
Но если у нас имеются данные по значительному количеству рейсов, то мы можем без особого труда довольно точно оценить все параметры $\mu(t)$ и $\sigma(t)$. На первый взгляд кажется, что для оперативного оценивания параметров это не приносит никакой пользы, но выше мы уже видели, что нормальные смеси для небольших интервалов времени практически ничем не отличаются от нормального распределения. Анализируя данные по продажам на некоторое количество состоявшихся рейсов, можно установить разумные границы для $\mu_{k}$ и $\sigma_{k}$ для любого $k$-го интервала. С учетом того, что изменение цены в $k$-м интервале времени происходит только тогда, когда вероятность продажи одного билета в последовательном анализе покидает область безразличия, мы можем оценивать отклонения $\mu_{k}$ и $\sigma_{k}$ опираясь на распределение количества посетителей, которое необходимо для того, чтобы покинуть эту область. Если количество посетителей, после которого была покинута область безразличия, слишком сильно отклоняется от среднего значения, то это становится сигналом того, что $\mu_{k}$ и $\sigma_{k}$ действительно отклонились от значений, рассчитанных по историческим данным.

Важную роль в оперативной оценке $\mu_{k}$ и $\sigma_{k}$, а также параметров $\mu(t)$ и $\sigma(t)$ играет анализ самих посетителей. Если задуматься о том, что может повлиять на изменение $\mu_{k}$ и $\sigma_{k}$ в некотором периоде времени, то окажется, что причин не так уж и много. Например, в некотором городе может быть запланирована масштабная IT-конференция на определенную дату. Тогда на рейсы, близкие к этой дате, увеличится не только спрос, но и готовность отдать за билет больше денег. Что в этом случае могло увеличиться: мат. ожидание или отклонение? Очевидно, что и то и другое. В принципе, можно представить довольно много разных ситуаций, но ни в одной из них мы не увидим разнонаправленного изменения $\mu_{k}$ и $\sigma_{k}$, а это тоже, несколько облегчает их текущую оценку. Точно так же очевидно, что для изменения параметров $\mu(t)$ и $\sigma(t)$ должны происходить какие-то массовые явления, влияющие на большинство или всех потенциальных покупателей, например, приближение сезона отпусков или закрытие воздушных границ над некоторыми странами.

Оценка текущих $\mu_{k}$ и $\sigma_{k}$, а также краткосрочное прогнозирование их значений для $k+1, k+2, ...$ периодов продаж на конкретный рейс по некоторому направлению очень важно для того, чтобы понимать, как должна меняться цена. Но если анализируя $\mu_{k}$ и $\sigma_{k}$ мы вдруг понимаем, что их отклонение не является краткосрочным и вызвано изменением параметров $\mu(t)$ и $\sigma(t)$, то в этом случае стоит действительно задуматься о необходимости перестановки самолетов. Значительное изменение параметров — это и есть один из критериев, который определяет момент, в который возникает необходимость решения общей задачи назначения флота. Фактически, мы решаем общую задачу о назначении, только если какие-то ее параметры начали или будут сильно меняться, а не для каждого периода времени, что позволяет значительно снизить требования к вычислительным ресурсам.

Кажется, что решение задачи уже близко, но давайте еще раз взглянем на выражение (19)

$\begin{equation*} z = \sum_{i \in I} \left (\int_{0}^{\infty} \!\! ... \int_{0}^{\infty} \left ( \left ( \sum_{k} p_{ifmjk} \rho_{ik} \int_{p_{ifmjk}}^{\infty } \int_{t_{k}}^{t_{k+1}} \, \psi_{ik} (p_{fi}, t) \right ) \prod_{k} \int_{t_{k}}^{t_{k+1}} \! \varphi_{ik} (\rho_{ik} , t) \right )\, d\rho_{i0}\, d\rho_{i1}\, ... d\rho_{ik} - \sum_{f \in F} \sum_{m \in N_{f}}(c_{ifm} + C_{ifm}) x_{ifm} \right ). \tag{19} \end{equation*}$

Оно содержит два распределения, а это значит, что даже для небольших периодов продаж мы получим огромное количество сценариев. То есть для окончательного решения, вместо всего этого множества интегралов, мы должны получить единственную числовую оценку мат. ожидания прибыли для каждого конкретного самолета. Если использовать распределения в исходном виде, то для получения этих оценок не хватит никаких вычислительных ресурсов. С другой стороны, мы можем очень сильно упростить задачу, если разобьем исходные распределения на участки, которые хорошо аппроксимируются линейными функциями. Любопытно, но такое преобразование не приводит к сколь бы то ни было значительным ошибкам. В задаче ценообразования такое преобразование действительно может снизить объем выручки, но для быстрой оценки общей прибыли, такое приближение более чем пригодно.

В определенном смысле, перед нами все та же задача назначения флота, но только нам удалось привязать ее к данным о продажах. В обычном режиме мы решаем задачу ценообразования для каждого отдельного рейса, в ходе решения этой задачи у нас неизбежно накапливаются данные, которые пригодны для создания моделей спроса на каждый из таких рейсов и если параметры этих моделей сильно изменились или мы уверены в том, что они будут меняться, то мы используем эти модели для того, чтобы оценить мат. ожидание прибыли для каждого самолета на каждом рейсе. Полученные значения прибыли можно подставить в функцию (20) и решать ее как типичную задачу о назначениях. После перестановки мы снова решаем только задачи ценообразования до тех пор, пока какие-то параметры опять не изменятся слишком сильно. Можно сказать, что в этой задаче мы просто учитываем процесс ценообразования для каждого самолета, который мог бы выполняться на произвольно выбранном рейсе.

Моделирование


Для моделирования процесса управления флотом была создана следующая сеть аэропортов

Данная сеть обладает кластерной структурой, причем спрос в разных кластерах меняется со временем по-разному. Чем темнее дуга, тем больше спрос между аэропортами, которые она соединяет. Конечно, можно было обойтись и более простыми сетями, но мы хотели смоделировать нечто вроде кризисной ситуации, когда спрос падает в большей части сети. На данной сети было смоделировано два процесса управления флотом. Первый алгоритм, который мы назвали GenFAM, во многом основан на вышеизложенных идеях. Второй алгоритм, названный нами OldFAM, создан сугубо для сравнения и отражает текущее положение дел.

В общей сложности, между всеми аэропортами выполняется 64 рейса, но для GenFAM введено еще 32 фиктивных рейса.

Если для OldFAM расписание является довольно жестким, так как 32 рейса являются обязательными (обозначены красным цветом), а остальные могут быть отменены (обозначены черным цветом), то для GenFAM расписание является более гибким, поскольку к необязательным рейсам добавляются еще и фиктивные. Так же в OldFAM не учитывается стоимость перестановок, что приводит к весьма эффективным решениям, но дорогостоящей реализации этих решений. В GenFAM эффективность решений рассматривается как с точки зрения удовлетворения спроса, так и с точки зрения стоимости перестановок, которая может быть снижена за счет использования фиктивных рейсов. В обеих моделях учитывалась выплата компенсаций за отмену рейсов, размер которых был тем больше, чем ближе к вылету происходила его отмена.

Обе модели использовали один и тот же флот, состоящий из 38 самолетов 4-х типов. Продажи билетов для любых рейсов начинались не менее, чем за 5 дней до вылета. В OldFAM билеты продавлись только исходя из прогнозов на один день вперед, в то время как в GenFAM использовалось стохастическое программирование и довольно грубое прогнозирование на всю глубину продаж. В условиях резкого роста или падения спроса даже такие прогнозы довольно часто побуждали модель к заблаговременным оптимальным перестановкам, которые зачастую были гораздо менее убыточными чем в OldFAM. Количество отмененных рейсов в обеих моделях было практически одинаковым, но в GenFAM выплаты компенсаций покрывались гораздо меньшими последующими убытками. Для каждого предстоящего рейса в GenFAM, даже при аппроксимации спроса тремя прямыми линиями, выходило около 760 тысяч сценариев. Чтобы получить решения для ценообразовании и оценки средней выручки с рейса, пришлось использовать только 500 случайных сценариев, однако, даже такого количества хватило, чтобы получить вполне приемлемые результаты.

На вышеприведенном графике GenFAM демонстрирует поведение, которое учитывает множество сценариев. Это приводит к тому, что рост и падение выручки не испытывает значительного ускорения даже в кризисных ситуациях. Например, когда спрос снизился одновременно сразу в двух больших кластерах, объем выручки в GenFAM упал на 35%, когда в OldFAM он упал на 75%.

Чтобы оценить влияние только стохастического программирования, были созданы еще три модификации алгоритма OldFAM, результаты которых представлены на нижеследующем графике:

Данные модификации позволяют оценить эффект от расширенения простой модели. OldFAM1 учитывает стоимость перестановок, но это не принесло ощутимого результата. Если к стоимости перестановок добавить возможность использовать фиктивные рейсы, как в OldFAM2, то это уже приносит заметный эффект. В OldFAM3 были добавлены прогнозы на всю глубину продаж, но эти прогнозы использовали только один самый вероятный сценарий, который не уточнялся по мере поступления данных о продажах. Хоть это и принесло самый значимый результат в сравнении с двумя предыдущими моделями, тем не менее значительная часть прогнозов сбывалась далеко не точно, из-за чего для значительной части самолетов принимались не самые оптимальные решения. Причем у таких ошибок всегда проявлялся накопительный эффект, приводящий к неизбежному резкому падению выручки.

Если сравнить среднюю выручку всех моделей, то результаты окажутся следующими:
  • OldFAM — 4.303 млн. рублей;
  • OldFAM1 — 4.571 млн. рублей (+6.23% к результатам OldFAM);
  • OldFAM2 — 5.143 млн. рублей (+12.53% к результатам OldFAM1);
  • OldFAM3 — 6.090 млн. рублей (+18.40% к результатам OldFAM2);
  • GenFAM — 6.893 млн. рублей (+13.18% к результатам OldFAM3 или +60.2% к OldFAM).

Мы получаем фантастический прирост, но на самом деле в нем нет ничего необычного. При отсутствии колебаний спроса стохастическое программирование ничем не отличается от обычного детерминированного, но если колебания происходят часто и с большой амплитудой, то разница становится ощутимой. Например, OldFAM2 является полностью детерминированной, но если при оптимизации учитывать случайные факторы и неопределенность, как в GenFAM, то мы получаем 34% прироста к средней выручке.

В заключение


Детерминированные модели долгое время служили верой и правдой, но совокупные ошибки, которые неизбежно возникают и накапливаются при их использовании в случайном мире, порой приводят к катастрофическим последствиям. Стохастическое программирование наоборот, помогает учесть множество сценариев и помогает добиться устойчивого равновесия. В этом равновесии нет таких понятий как «повезло» или «не повезло», нет феерических или панических настроений от сказочных прибылей или кризисов, только «ровное» развитие всех процессов и систем.

В данной статье, для упрощения демонстрации, мы использовали крайне упрощенный вариант GenFAM. Тем не менее, эта модель, состоящая из большого числа упрощений и ограничений, демонстрирует очень важный принцип — рассмотрение даже небольшого количества вариантов развития событий позволяет избежать очень плохих последствий. В общем случае, при более масштабном моделировании, алгоритм позволяет увеличить прибыль в среднем на 30%.

Стохастическое программирование не является каким-то волшебным способом увеличения прибыли, даже наоборот, оно заставляет нас направлять часть собственных доходов и ресурсов на преодоление неблагоприятных событий, которые, по воле случая, могут произойти или не произойти. Это разумно и рационально. Но если правила таковы, что основным способом победить в конкурентной борьбе является риск, то предусмотрительность становится слабостью, гарантирующей отставание и поражение. Следовательно, преодоление кризисных ситуаций одними методами стохастического программирования невозможно. В следующей статье, мы расширим модель до нескольких авиакомпаний (игроков) и попробуем выяснить, каких результатов позволят добиться их согласованные действия.

Комментарии (1)


  1. XaBoK
    15.03.2022 17:54
    #24168539

    Было интересно, на за один раз не осилил. Не то, что можно быстро пролистать под чашку кофе. Математика не сложная и формула строиться по ходу статьи, но продолжать читать приходиться опять с начала...