У каждого человека есть набор возможных действий в различных ситуациях, которые можно разделить по степени предпочтительности. Очевидно, что мы всегда будем стараться к чувству защищенности и удовлетворения, то есть когда наши действия приводят к предполагаемому результату и оборачиваются пользой. Мы интуитивно придерживаемся границ зоны комфорта, внутри которой нет места сложным альтернативам. Однако, вопреки нашим стремлениям к комфорту, мир так или иначе вынуждает нас сталкиваться с необходимостью совершать сложный выбор, причем чаще всего это становится неотъемлемой частью профессиональной деятельности. Остро ощущается такая проблема в сферах, где еще не сформировался развитый вспомогательный инструментарий, облегчающий поиск наилучших решений, например, в арбитраже криптовалют. В этой статье рассмотрим, как проблема выбора может быть формализована и решена, а также оценим прибыльность от использования такого решения.

Введение
В арбитраже источником прибыли являются так называемые связки, которые чаще всего являются цепочками обменов типа (покупка некоторого количества криптовалюты за меньшее количество той же самой криптовалюты). Проблема выбора заключается в том, что связок может быть очень много и они могут отличаться друг от друга доходностью, длиной и временем жизни. Успех во многом определяется умением ранжировать данные связки по этим параметрам и реализовывать только лучшие из них. Самым очевидным решением такой проблемы является введение функции полезности. В предыдущей статье мы установили, что она имеет следующий вид:
Функция легко интерпретируется и позволяет четко определять критерии предпочтительности одних связок другим. Например, аргумент - это доходность. Чем доходность у связки больше, тем лучше, но, если длина связки
является слишком большой, то мы отдадим предпочтение другой, более короткой связке, пусть и с несколько меньшей доходностью. Такое предпочтение объясняется тем, что реализация связок требует временных затрат, вследствие чего величина получаемой прибыли сильнее зависит от количества реализуемых связок, а не доходности каждой из них. Аргумент
определяет вероятность разрыва цепочки обменов за время, необходимое для ее реализации: чем меньшее данное значение у связки, тем большее предпочтение мы готовы ей отдать.
Числовые значения функции не имеют никакого особого смыслового значения - в данном случае важно только то, что эти значения позволяют упорядочить все имеющиеся связки по степени привлекательности. Все было бы хорошо, если бы не одна проблема на пути к ее непосредственному использованию: аргументы
и
являются простыми характеристиками самой связки, в то время как аргумент
требует определенной, далеко не тривиальной работы по вычислению его значения.
Чтобы разобраться в чем именно кроется проблема, начнем с простого примера. Предположим, что у нас имеется простая короткая связка:
Разумеется, для выполнения обменов требуется некоторое время. Пусть для обмена это время оценивается как
, а для обмена
как
, тогда существует некоторая вероятность того, что цепочка обменов разорвется раньше, чем она будет реализована. Запишется эта вероятность следующим образом:
где - это время жизни ордера. Формула для вычисления
будет выглядеть так:
Если обмены могут выполняться параллельно, то если нет, то
. Идея параллельного выполнения цепочек может натолкнуть на мысль, что функция полезности в этом случае обязана претерпеть некоторые изменения, но на самом деле нет. Если рассматривать некий офис, в котором люди могут распределять обмены звеньев цепочек между собой, то для них предпочтения будут формироваться точно на таких же принципах, как и для отдельно взятого арбитражера.
Вычисление значения аргумента требует предварительного вычисления вероятностей
. Если учесть, что делать это нужно для сотен валютных пар, то сам метод вычисления должен быть неким компромиссом между точностью и вычислительной сложностью. На первый взгляд, в этом нет серьезной сложности, ведь очевидное решение лежит на поверхности - непараметрическая статистика, то есть определение
должно основываться на минимуме гипотез о параметрах функции плотности (PDF).
Самая простая оценка вероятностного распределения - это гистограмма, а конкретно для нашей задачи лучше всего воспользоваться эмпирической функцией распределения плотности вероятности (EPDF). Нас интересует распределение времени жизни ордеров, появляющихся на некоторой глубине (расстоянии от цен bid и ask в книге ордеров). Для нашего простого примера процесс определения
может быть выполнен следующим образом:
Производим некоторое количество наблюдений за временем жизни ордеров, которые появились на тех же глубинах, что и ордеры
и
, используемые в связке (допустим, 100-300 наблюдений);
Выполняем построение EPDF;
Вычисляем интегралы под полученными кривыми от 0 до
и
, по которым можно вычислить значения
и
соответственно;
Вычисляем произведение
и
и вычитаем его из единицы - это и есть значение аргумента
в функции полезности.
Визуально определение и
на основе данных выглядит так:
Python
# Делаем необходимые импорты
import pandas as pd
import numpy as np
from scipy.stats import uniform, norm, expon, levy_stable, invgamma, invgauss, gamma, binom, gaussian_kde
from scipy.optimize import curve_fit, minimize
import matplotlib.pyplot as plt
%matplotlib inline
%config InlineBackend.figure_format = 'png'
plt.rcParams["figure.figsize"] = (10 ,5.5)
import seaborn as sns
sns.set()
np.random.seed(42)
# Моделируем данные:
data_1 = expon.rvs(scale=1.5, size=100)
data_2 = expon.rvs(scale=2.5, size=100)
x_1 = np.linspace(0, 5, 11)
x_2 = np.linspace(0, 10, 11)
# Вычисляем гистограмму, по значениям которой будет
# строиться полигон:
f_1 = np.histogram(data_1, bins=x_1, density=True)[0]
f_2 = np.histogram(data_2, bins=x_2, density=True)[0]
# Нормируем площадь под кривой до 1:
f_1 = f_1 / np.trapz(f_1, x_1[:-1])
f_2 = f_2 / np.trapz(f_2, x_2[:-1])
f, ax = plt.subplots(1, 2, figsize=(10, 4))
ax[0].plot(x_1[:-1], f_1)
ax[1].plot(x_2[:-1], f_2)
ax[0].fill_between([0. , 0.5, 1. ], f_1[:3], alpha=0.5, color='g')
ax[0].axvline(1, color='r', label=r'$\tau_{1}$')
ax[0].axvline(0, color='0.3', lw=1)
ax[0].axhline(0, color='0.3', lw=1)
ax[1].fill_between([0., 1., 2.], f_2[:3], alpha=0.5, color='g')
ax[1].axvline(2, color='r', label=r'$\tau_{2}$')
ax[1].axvline(0, color='0.3', lw=1)
ax[1].axhline(0, color='0.3', lw=1)
# Определяем необходимые вероятности:
p_1, p_2 = np.trapz(f_1[:3], x_1[:3]), np.trapz(f_2[:3], x_2[:3])
ax[0].text(1.5, .35, r'$P_{1}(t<\tau_{1})=$' + str(round(p_1, 3)))
ax[1].text(3, .15, r'$P_{2}(t<\tau_{2})=$' + str(round(p_2, 3)))
ax[0].legend()
ax[1].legend()
ax[0].set_title(r'EPDF(t) ордеров $X \to Y$')
ax[1].set_title(r'EPDF(t) ордеров $Y \to X$')
ax[0].set_xlabel('t (min)')
ax[0].set_ylabel('Density')
ax[1].set_xlabel('t (min)')
ax[1].set_ylabel('Density');
Таким образом, для смоделированных данных по связке аргумент
будет равен:
Вероятность разрыва данной связки за время, необходимое для ее реализации, составляет 0.798.
Много это или мало? И как вообще интерпретировать получаемые таким образом вероятности? Определенно, чем меньше , тем лучше. Стоит также учитывать, что это все-таки вероятность, а не гарантия или прогноз. Поскольку значение
определяется эмпирически, то
следует воспринимать как оценку вероятности, а не ее истинное значение. Фактически, это означает, что мы оперируем некоторой величиной, которая всегда немного отклоняется от своего истинного значения, причем мы не можем сформировать какие-то границы неопределенности (доверительные интервалы), так как имеем дело с динамическим процессом, параметры которого всегда меняются. Имея значение
, мы можем только сказать, что исходя из последней истории наблюдений за временем жизни ордеров их вероятностное распределение не должно меняться кардинальным образом в ближайшем будущем. Это значит, что оценка
может быть использована при формировании предпочтений.
Нетрудно догадаться: мы можем уменьшать значение , например, выполняя обмены параллельно или сокращая время, затрачиваемое на обмены. В общем случае стоит учитывать, что изначально оценка
должна определяться индивидуально под каждого отдельного арбитражера, а именно учитывать параметры скорости его действий. Пока мы используем аргумент
в роли обобщенного показателя, высчитываемого для некоторого усредненного арбитражера, который тратит на один обмен от 45 до 120 секунд (в зависимости от биржи). Такой подход позволяет снизить к минимуму количество предоставляемых короткоживущих связок.
Даже в краткосрочной перспективе точная оценка параметра крайне полезна: если не использовать данный параметр вовсе, то доля разрывов может составлять 15-25%. Все это приводит к потере времени и, соответственно, снижению прибыли. Также важно учесть конкуренцию, ведь арбитражер, способный оценивать вероятность разрыва цепочек, будет использовать наименее рискованные связки, увеличивая долю рискованных среди оставшихся для остальных арбитражеров.
Почему именно полигон из значений? Почему бы не воспользоваться более точными тестами для оценки параметров распределения? Чтобы более или менее разобраться с практической стороной вопроса, нам нужен вводный материал. Возьмем посекундные снимки книги ордеров пары BTC/USDT биржи Binance. Всего в нашем распоряжении 2760 снимков (46 минут), и каждый из них содержит по 1000 ордеров со стороны спроса и предложения. Хочется надеяться, что данные будут качественными, но даже в финансовой сфере это случается довольно редко: в нашем случае время между снимками практически никогда не равно точно 1 секунде, а также время создания последующего снимка может оказаться меньше времени создания предыдущего снимка. Предположим, что снимки действительно создаются последовательно, а время между ними равно в точности одной секунде. Для усреднения времени между снимками до одной секунды можно использовать следующую гистограмму временных дельт:

Допущение значения в строго 1 секунду для временных дельт является очень грубым, однако наша оценка должна работать даже при таких условиях. У ордеров нет уникальных идентификаторов, которые позволяли бы отслеживать их наиболее точным образом, что представляется дополнительной трудностью. Предположим (снова), что каждый ордер может быть отслежен по указанной в нем цене. Время жизни ордеров (со стороны спроса) мы посчитали заранее и собрали в отдельный файл:
Python
data = pd.read_csv('btc_usdt_binance_1s_buy.csv', index_col=0)
print(data.head(2))Результат
t depth
0 1.0 0.0
1 1.0 0.0Данные показывают, сколько времени прожил ордер (столбец t) и на какой глубине он появился (depth). Распределение количества ордеров по глубине выглядит следующим образом:
Python
def depth_count(data):
tmp_data = data.depth
return [len(tmp_data[tmp_data == i]) for i in np.r_[:1000]]
plt.plot(depth_count(data))
plt.title('Распределение количества ордеров по глубине')
plt.xlabel('depth')
plt.ylabel('count');
Данный график имеет несколько примечательных особенностей: во-первых, в "горячей" зоне, близкой к цене bid, где ожидаемо идет наиболее активная торговля, количество ордеров с увеличением глубины не убывает монотонно, а образует два четких пика в районе depth, равного 25 и 100. Появление таких пиков связано с тем, что некоторая часть игроков со стороны спроса делала ставку на некоторый рост предложения. Во-вторых, пик в районе наибольшей глубины снимков объясняется тем, что используемой глубины не хватает для вмещения всех ордеров спроса. Это значит, что какие-то из них могут появляться на более глубоких позициях, смещаться из этих позиций в снимок, находиться в нем какое-то время, а затем снова уходить на большую глубину. Такое предположение является верным ввиду того, что ордеры на позициях глубже 200 живут очень долго.
Рассмотрим конкретный ордер, скажем, на 400-й позиции с ценой, равной 12273.43 USDT:

Выходит, что примерно с 200-й позиции все ордеры со стороны спроса являются "долгожителями" и определить время их жизни на основе имеющихся данных невозможно.
Рассмотрим распределение времени жизни ордеров в конкретной позиции, например, в 10-й:
Python
tmp_data = data[data.depth == 10].t
sns.histplot(tmp_data[tmp_data < 15]-0.5, bins=np.arange(0, 14))
plt.xlabel('t (s)')
plt.title('Распределение времени жизни ордеров на depth = 10');
Гистограмма показывает, что продолжительность жизни ордеров укладывается в одинаковые промежутки времени длиной в 1 секунду. Любая гистограмма является лишь некоторым приближением к реальному распределению, но в нашем случае это приближение очень грубое. Связано это с тем, что точное время жизни ордеров неизвестно, а с учетом того, что исполнение ордеров происходит автоматически, то следует иметь ввиду, что некоторая часть ордеров может жить меньше 1 секунды и не попасть в первый столбец. Мы можем относительно доверять только тем данным, в которые попадают ордеры с временем жизни больше 1 секунды.
В таком случае мы имеем дело с цензурированной и ограниченной выборкой. Если на основе такой выборки приближать распределение плотности вероятности полигоном, как мы это делали выше, то оценки аргумента наверняка будут получаться крайне грубыми. В реальности снимки совершаются не каждую секунду, а раз в несколько минут, поэтому следует ожидать, что совершаемые оценки
будут скорее неверными, чем грубыми.
Другой особенностью распределения времени жизни ордеров является наличие очень длинного и легкого хвоста. Например, приведенное выше распределение мы ограничили 15 секундами, хотя максимальное время жизни ордера составляет 1264 секунды. Если прибегнуть к логарифмированию времени, то то мы все равно увидим длинный легкий хвост:
Python
bins = np.hstack(([0], np.log(np.unique(tmp_data+1)))) + 0.001
sns.histplot(np.log(tmp_data+1), stat='density', bins=bins)
plt.xlabel(r'$\ln(t+1)$');
Время жизни ордеров, появляющихся на небольшой глубине, может принимать очень большие значения, что будет вполне естественным и распространенным явлением. Такие значения нельзя отбрасывать, а само наличие длинных хвостов является обыденным явлением в биржевой торговле. Таким образом мы приходим к простому выводу - непараметрическая статистика нам ничем не поможет. Единственный способ оценивать аргумент - это попытаться подобрать подходящий закон распределения и каким-то образом оценить его параметры по той части выборки, которой можно больше всего доверять.
Устойчивое распределение Леви
Чтобы делать оценки, мы должны быть уверены в том, что распределение времени жизни ордеров имеет какое-то конкретное распределение. Первое, что сильно бросается в глаза - количество ордеров в зависимости от логарифма времени их жизни убывает очень быстро:
Python
bins = np.hstack(([0], np.log(np.unique(tmp_data+1)))) + 0.001
x_data = [np.mean(bins[i:i+2]) for i in range(len(bins)-1)]
y_data = np.histogram(np.log(tmp_data+1), bins=bins, density=True)[0]
plt.scatter(x_data, y_data, marker = 'x', c='k', zorder=100)
sns.histplot(np.log(tmp_data+1), bins=bins, edgecolor = 'k',
lw=1, stat='density', alpha=0.2)
def func1(x, a, b, c):
return a / (b + x) + c
def func2(x, l):
return l*np.exp(-l*x)
popt1, pcov = curve_fit(func1, x_data, y_data)
popt2, pcov = curve_fit(func2, x_data, y_data)
xf = np.linspace(0.25, 7, 300)
plt.plot(xf, func1(xf, *popt1), color='red', lw=2,
label=r'$\frac{0.26}{x-0.11}-0.06$', zorder=101)
plt.plot(xf, func2(xf, *popt2), color='blue', lw=2,
label=r'$1.9e^{-1.9x}$', zorder=102)
plt.title('Распределение количества ордеров по логарифму времени их жизни',
fontsize=18)
plt.xlabel('ln(t+1)')
plt.legend(fontsize=18)
plt.ylim(-0.1, 1.25);
Распределение на графике носит скорее гиперболический, а не экспоненциальный характер. Учитывая, что в первый интервал попадает лишь часть ордеров, это различие только усиливается. К тому же, незнание точного количества ордеров в первом временном интервале заставляет нас трепетнее относиться к хвостовой части распределения. Гиперболическое распределение в этой части убывает так же медленно, как и высоты столбцов.
Анализ данных по разным криптовалютам и разным биржам показывает, что распределения в целом очень схожи. Например, так выглядят распределения количества ордеров на покупку/продажу пары BTC/USDT в зависимости от глубины в книге ордеров:

Гистограммы распределения количества ордеров в зависимости от времени жизни и глубины также очень похожи:


Конечно, принадлежность выборок одному и тому же распределению - это всего лишь гипотеза. Если установить тип распределения по имеющимся высокочастотным данным, и принять, что оно является общим, станет возможным искать параметры этого распределения для других данных. Необходимо только выяснить, что это за распределение.
Что нам известно абсолютно точно из того, что не видно на гистограмме? Значение PDF в точке должно быть равно 0 - это следует из того факта, что ордеры не могут жить 0 секунд. Поскольку исполнение ордеров выполняется автоматически, то вполне возможно, что некоторые из них могут находиться в книге мили-, микро- или даже наносекунды. Ордеры могут жить очень недолго, но эта величина должна иметь какое-то минимальное значение, после которого идет быстрый рост, а затем более медленный спад. Таким образом, распределение, во-первых, должно быть одновершинным с очень большими коэффициентами асимметрии и эксцесса; во-вторых, должно иметь длинный и тонкий хвост.
Наилучшими кандидатами на роль таких распределений являются обратное Гауссово и гамма распределения, а также устойчивое распределение Леви:
Python
f, ax = plt.subplots(1, 3, figsize=(12, 4))
x = np.linspace(0, 3, 300)
y_levy = levy_stable.pdf(x, alpha=0.4, beta=1, loc=0, scale=1)
y_igamma = invgamma.pdf(x, a=1.2, loc=0, scale=0.3)
y_gamma = gamma.pdf(x, a=5, loc=0, scale=0.05)
y_invgauss = invgauss.pdf(x, mu=0.8, loc=0, scale=0.8)
ax[0].axvline(0, color='0.3', lw=1)
ax[0].axhline(0, color='0.3', lw=1)
ax[0].plot(x, y_levy, color='blue', label = 'levy', lw=1)
ax[0].plot(x, y_igamma, color='orange', label='invgamma', lw=1)
ax[0].plot(x, y_gamma, color='green', label='gamma', lw=1)
ax[0].plot(x, y_invgauss, color='red', label='invgauss', lw=1)
ax[0].legend()
ax[0].set_title('Общий вид')
x = np.linspace(0, .2, 300)
y_levy = levy_stable.pdf(x, alpha=0.4, beta=1, loc=0, scale=1)
y_igamma = invgamma.pdf(x, a=1.2, loc=0, scale=0.3)
y_gamma = gamma.pdf(x, a=5, loc=0, scale=0.05)
y_invgauss = invgauss.pdf(x, mu=0.8, loc=0, scale=0.8)
ax[1].axvline(0, color='0.3', lw=1,)
ax[1].axhline(0, color='0.3', lw=1)
ax[1].plot(x, y_levy, color='blue', label = 'levy')
ax[1].plot(x, y_igamma, color='orange', label='invgamma')
ax[1].plot(x, y_gamma, color='green', label='gamma')
ax[1].plot(x, y_invgauss, color='red', label='invgauss')
ax[1].legend()
ax[1].set_title('Характер роста')
x = np.linspace(2, 11, 300)
y_levy = levy_stable.pdf(x, alpha=0.4, beta=1, loc=0, scale=1)
y_igamma = invgamma.pdf(x, a=1.2, loc=0, scale=0.3)
y_gamma = gamma.pdf(x, a=5, loc=0, scale=0.05)
y_invgauss = invgauss.pdf(x, mu=0.8, loc=0, scale=0.8)
ax[2].axvline(0, color='0.3', lw=1)
ax[2].axhline(0, color='0.3', lw=1)
ax[2].plot(x, y_levy, color='blue', label = 'levy', lw=2)
ax[2].plot(x, y_igamma, color='orange', label='invgamma', lw=2)
ax[2].plot(x, y_gamma, color='green', label='gamma', lw=2)
ax[2].plot(x, y_invgauss, color='red', label='invgauss', lw=2)
ax[2].legend()
ax[2].set_title('"Хвосты"');
На первом графике изображены: простое гамма, обратное гамма и Гауссово распределения, а также устойчивое распределение Леви. На среднем графике виден характер роста распределений: у подходящего кандидата он должен быть как можно круче. Данные распределения, за исключением устойчивого Леви распределения, могут быть параметризованны так, чтобы неплохо описывать лишь часть данных из выборки с небольшим временем жизни. Однако такая параметризация приводит к исчезновению хвостов, что хорошо видно на третьем графике. Устойчивое распределение Леви действительно является наилучшим кандидатом на роль общего распределения времени жизни ордеров:
Python
f, ax = plt.subplots(1, 2, figsize=(12, 6))
sns.histplot(np.log(tmp_data+1), bins=bins, edgecolor = 'k',
lw=1, stat='density', alpha=0.3, ax=ax[0])
sns.histplot(np.log(tmp_data+1), bins=bins, edgecolor = 'k',
lw=1, stat='density', alpha=0.3, ax=ax[1])
x = np.linspace(0, 6, 300)
y_levy = levy_stable.pdf(x, alpha=0.75, beta=1., loc=0., scale=0.15)
y_igamma = invgamma.pdf(x, a=1.5, loc=0, scale=0.4)
ax[0].axvline(0, color='0.3', lw=1,)
ax[0].axhline(0, color='0.3', lw=1)
ax[1].axvline(0, color='0.3', lw=1,)
ax[1].axhline(0, color='0.3', lw=1)
ax[0].plot(x, y_levy, label = 'stable_levy', lw=1, color='red')
ax[1].plot(x, y_igamma, label='invgamma', lw=1, color='red')
ax[0].set_xlabel('log(t)')
ax[1].set_xlabel('log(t)')
ax[0].legend()
ax[1].legend()
ax[0].set_ylim(-0.1, 2.5)
ax[1].set_ylim(-0.1, 2.5)
ax[0].set_xlim(0, 6)
ax[1].set_xlim(0, 6);
Визуально распределения похожи по форме, но из-за различий в характере убывания площадь под кривой изменяется по-разному. Например, в интервале от 0 до 1 получим следующее:
Python
p_ls = levy_stable.cdf(1, alpha=0.75, beta=1., loc=0., scale=0.15)
p_ig = invgamma.cdf(1, a=1.5, loc=0, scale=0.4)
print(f'Устойчивое Леви: P(0 < t < 1) = {p_ls:.3f}')
print(f'Обратное гамма: P(0 < t < 1) = {p_ig:.3f}')Результат
Устойчивое Леви: P(0 < t < 1) = 0.761
Обратное гамма: P(0 < t < 1) = 0.849Устойчивое распределение Леви имеет следующую характеристическую функцию:
где - это функция, возвращающая 1 или -1, в зависимости от знака
, а
задает параметризацию распределения:
Характеристическая функция не является комплексной в привычном понимании этого слова, так как переменная является вещественной, но возвращаемые значения принадлежат множеству комплексных чисел. Чтобы получить функцию плотности распределения, необходимо выполнить обратное преобразование Фурье:
До преобразования подынтегральная функция может принимать весьма необычные для обыденной статистики формы. Например, для значения и разных значениях параметров
и
получатся следующие графики:

После преобразования по множеству значений мы получаем привычные PDF:

Семейство устойчивых распределений задают 4 параметра: - параметр устойчивости;
- параметр асимметрии,
и
- параметры сдвига и масштаба соответственно.
Функция плотности лишь в редких случаях может быть задана аналитически, в остальных случаях ее построение выполняется на основе приближенных вычислений. Переход от характеристической функции к функции плотности выполняется с помощью преобразования Фурье:
где ,
. Функцию
под знаком суммы удобнее представить в виде
, которые определяются следующим образом:
После некоторых простых преобразований получаем следующую формулу для вычисления значений функции плотности в некоторой точке :
Если , а
, то область определения функции плотности будет находиться в
. Учитывая, что
, то для
это будет как раз тем, что нам необходимо. Взглянем еще раз на аппроксимацию времени жизни ордеров на глубине, равной 10:
Python
sns.histplot(np.log(tmp_data+1), bins=bins, edgecolor = 'k',
lw=1, stat='density', alpha=0.3)
x = np.linspace(0, 4, 300)
y_levy = levy_stable.pdf(x, alpha=0.78, beta=1., loc=0., scale=0.13)
plt.plot(x, y_levy, label = 'stable_levy', lw=2, color='red')
plt.ylim(-0.1, 2.5)
plt.xlim(0, 4);
Исходя из формы распределения следует, что ордеров с временем жизни меньше 0.15 секунды не существует, а наиболее вероятное время жизни ордеров приблизительно равно 0.32 секунды и далее оно увеличивается вплоть до нескольких минут.
На первый взгляд кажется, что распределение плотности задано с параметром сдвига, значение которого больше 0. Однако в данном распределении плотности , а сдвиг обеспечен только значением параметра
. Технически это даже нельзя считать сдвигом графика в прямом смысле этого слова. Если мы взглянем на распределение плотности около нуля, то увидим, что при приближении к 0 функция не принимает нулевых значений:
Python
f, ax = plt.subplots(1, 3, figsize=(12, 4))
x = np.linspace(0, 0.15, 300)
y_levy = levy_stable.pdf(x, alpha=0.78, beta=1., loc=0., scale=0.13)
ax[0].plot(x, y_levy, label = 'stable_levy', lw=2, color='red')
x = np.linspace(0, 0.12, 300)
y_levy = levy_stable.pdf(x, alpha=0.78, beta=1., loc=0., scale=0.13)
ax[1].plot(x, y_levy, label = 'stable_levy', lw=2, color='red')
x = np.linspace(0.01, 0.07, 300)
y_levy = levy_stable.pdf(x, alpha=0.78, beta=1., loc=0., scale=0.13)
ax[2].plot(x, y_levy, label = 'stable_levy', lw=2, color='red');
Такое поведение устойчивого распределения точно соответствует положению вещей: например, параметр сдвига не может быть отличен от 0, так как это значило бы, что вероятности встретить ордеры с временем жизни меньше некоторого значения равны 0. Что касается параметра
, то, помимо смещения, он также приводит к "вытягиванию" самого распределения:
Python
plt.figure(figsize=(12, 6))
x = np.linspace(0, 12, 200)
for alpha in [0.4, 0.6, 0.8, 0.9]:
y_levy = levy_stable.pdf(x, alpha=alpha, beta=1)
plt.plot(x, y_levy, label=r'$\alpha$ = ' + str(alpha))
plt.legend();
Такое поведение хорошо соответствует действительности, так как гистограммы распределения времени жизни при увеличении глубины тоже смещаются и вытягиваются.
Стоит также отметить, что параметр не может быть больше 1, а параметр
должен быть строго равен 1, чтобы распределение находилось строго в положительной области значений. В данном случае математическое ожидание не определено, а дисперсия равна бесконечности, что также согласуется с наблюдаемыми данными о времени жизни ордеров.
Пожалуй, самая главная трудность применения устойчивых распределений на практике - это большая вычислительная сложность. Однако в нашем случае есть возможность значительно ускорить процесс вычислений.
При , а
устойчивые распределения выделяются в отдельное семейство односторонних устойчивых распределений с распределением плотности, задаваемым следующим образом:
где ,
. В таком виде все равно приходится вычислять интеграл для каждой точки распределения, но при этом можно снизить точность вычислений самих интегралов:
Python
def one_sided(x, a, c):
q = np.exp(-1j*a*np.pi/2)
re_q = np.real(q)
im_q = np.imag(q)
t = np.linspace(0, 300, 1000)
k = np.cos(a*np.pi*0.5)**(1/a)
func = np.exp(-re_q*t**a)*np.sin(t*np.c_[x]*k/c)*np.sin(-im_q*t**a)
f_x = 2*k*np.trapz(func, t)/(np.pi*c)
return f_x
x = np.linspace(0, 5, 200)
y = one_sided(x, 0.6, 1.2)
y_levy = levy_stable.pdf(x, alpha=0.6, beta=1, loc=0, scale=1.2)
plt.plot(x, y, lw=6, c='r', alpha=0.7, label='integral')
plt.plot(x, y_levy, c='k', label='fft')
plt.legend(fontsize=16);
Между построенной и теоретической функциями нет никаких отличий, зато появился значительный прирост в скорости вычислений:
Python
%%time
s = one_sided(x, 0.6, 1.2)Результат
Wall time: 15 msPython
%%time
s = levy_stable.pdf(x, alpha=0.6, beta=1, loc=0, scale=1.2)Результат
Wall time: 1.24 sТочность вычислений быстрого преобразования Фурье также может быть снижена, но это приведет к гораздо большим отклонениям от теоретической функции.
Устойчивое распределение очень схоже с гиперболическим: при больших значениях аргумента они убывают практически в точности, как гиперболы. Это очень хорошо аппроксимирует поведение хвостов распределений количества ордеров по времени жизни. В то же время наблюдаемые распределения чаще всего лишь похожи на гиперболы, из-за чего правильнее называть их квази-гиперболическими. Наблюдение квази-гиперболы является поводом для поиска некоторой системной случайности, но вовсе не гарантирует ее наличия. В наиболее общем смысле квази-гиперболичность проявляется в любых системах, где элементы и процессы могут иерархически зависеть от нескольких других элементов и процессов.
Устойчивое распределение хорошо подходит для объяснения процессов в биржевой торговле. Объясняется это тем, что поведение игроков определяется результатом влияния огромного объема информации, а благодаря памяти происходит ее накопление. Согласно центральной предельной теореме, если сумма большого числа независимых одинаково распределенных случайных величин имеет предельное распределение, то предельное распределение должно принадлежать к устойчивому классу. Именно поэтому предположение, что процессы в биржевой торговле хотя бы приблизительно определяются устойчивыми распределениями, является более чем логичным.
Если биржевые процессы действительно определяются устойчивым распределением с бесконечной дисперсией, то сама деятельность игроков оказывается более рискованной, чем в чисто Гауссовском мире. В нем нормальное распределение является наиболее известным и легко вычисляемым устойчивым распределением, поэтому предполагается, что либо оно, либо логнормальное распределение объясняет наблюдаемые распределения. Судя по всему, это не так, а значит внезапные и резкие движения цен превращаются в более чем возможные события. Все это подвергает сомнению такие аспекты биржевой деятельности, как защита от рисков или применение моделей ценообразования.
Восстановление распределения по ограниченной и цензурированной выборке
Данные по динамике книги ордеров являются цензурированными, так как мы не знаем точного времени появления ордеров. Сбор данных выполняется через приблизительно равные промежутки времени (в нашем случае 2 минуты), поэтому реальное время жизни ордеров всегда округляется (цензурируется) до значений, кратных этим минимальным интервалам времени. Данные уже являются готовой гистограммой, в которой просто отражается количество ордеров из разных временных интервалов продолжительности жизни. Помимо этого есть проблема некоторого ограничения: часть ордеров существует намного меньше интервалов времени, через которые выполняется обход бирж. Такие ордеры могут попадать в выборку, но какая-то часть ордеров в ней никогда не окажется. Это значит, что ограничения накладываются лишь на первый столбец, но в случае устойчивых распределений с большой асимметрией оставшаяся часть данных, которой можно доверять, является ни чем иным как хвостовой частью.
Попытаемся разобраться с тем, какие идеи для восстановления распределения необходимо использовать. Сгенерируем данные из простого распределения, с которым будет не так сложно работать - пусть это будет банальное :
Python
data = norm.rvs(size=50000)
sns.histplot(data);
Теперь представим, что у нас есть данные только из "хвостовой" части. Пусть выборка ограничивается значением 1.5, значит в выборку попадут все элементы, значения которых больше 1.5:
Python
tail = data[data > 1.5]
sns.histplot(tail);
Теперь у нас есть ограниченная выборка, которую осталось цензурировать. Для этого разобьем интервал значений на равные промежутки и будем просто подсчитывать количество их попаданий в соответствующие промежутки:
Python
bins = np.r_[1.5 : 3.75 : 0.25]
hist = np.histogram(tail, bins=bins, density=True)[0]
hist, bins
sns.histplot(tail, bins=bins);
Полученная гистограмма хорошо моделирует реальные данные. Теперь нужно понять, как по этим модельным данным восстановить исходное нормальное распределение с математическим ожиданием, равным 0, и отклонением, равным 1.
Первое, что приходит на ум - аппроксимация распределения по гистограмме. Вполне распространенный метод, но в нашем случае он возможен только в том случае, если мы знаем, из какого именно закона распределения взялись данные. Создавая метод, мы аппроксимируем модельные данные известной функцией:
Данная функция отличается от реальной только одним коэффициентом . Его введение необходимо, так как мы не знаем объема всей выборки, а, значит, не можем выполнить нормализацию. Важно учитывать, что каждый столбец диаграммы отличается от нормализованного пропорционально какому-то коэффициенту.
Осталось решить несложную оптимизационную задачу по аппроксимации:
Python
np.random.seed(42)
# Задаем функцию:
def func(x, k, mu, sigma):
return 1/(sigma*k*(2*np.pi)**0.5)*np.exp(-0.5*((x - mu)/sigma)**2)
x = bins[:-1] + np.diff(bins[:2])/2
y = hist.copy()
# Находим подходящие коэффициенты:
popt, pcov = curve_fit(func, x, y)
print(f'μ = {popt[1]:.3f}')
print(f'σ = {popt[2]:.3f}')Результат
μ = 0.106
σ = 0.963Данные значения далеки от реальных, но, если провести множество экспериментов, то получим следующую картину:
Python
np.random.seed(42)
M, S = [], []
for i in range(100):
data = norm.rvs(size=50000)
tail = data[data > 1.5]
bins = np.r_[1.5 : 3.75 : 0.25]
hist = np.histogram(tail, bins=bins, density=True)[0]
x = bins[:-1] + np.diff(bins[:2])/2
y = hist.copy()
popt, pcov = curve_fit(func, x, y)
M.append(popt[1])
S.append(popt[2])
f, ax = plt.subplots(1, 3, figsize=(12, 3))
ax[0].plot(M)
ax[1].plot(S)
ax[0].set_title('Мат. ожидание')
ax[1].set_title('Отклонение')
ax[2].set_title('P(x < 0.5)')
mu_rm = [np.mean(M[i:i+10]) for i in np.r_[0:90]]
sigma_rm = [np.mean(S[i:i+10]) for i in np.r_[0:90]]
ax[0].plot(np.r_[10:100], mu_rm, color='r')
ax[0].axhline(np.mean(M), c='k', label=r'$\mathbb{E}(\mu)$ = ' + f'{np.mean(M):.2f}')
ax[1].plot(np.r_[10:100], sigma_rm, color='r')
ax[1].axhline(np.mean(S), c='k', label=r'$\mathbb{E}(\sigma)$ = ' + f'{np.mean(S):.2f}')
C = norm.cdf(0, M, S)
c_rm = [np.mean(C[i:i+10]) for i in np.r_[0:90]]
ax[2].plot(C)
ax[2].plot(np.r_[10:100], c_rm, color='r')
ax[2].axhline(np.mean(C), c='k', label=r'$\mathbb{E}(p)$ = ' + f'{np.mean(C):.2f}')
ax[0].legend()
ax[1].legend()
ax[2].legend();
На графике виден большой разброс и тенденция к смещению оценок. Даже если пользоваться усредненными значениями, скажем, по последним 10-ти оценкам (красная линия), то отклонения все равно получаются очень большими, особенно математические ожидания. Если построить графики распределения плотности для каждой пары оцененных параметров, то мы увидим вполне ожидаемое смещение влево:
Python
x = np.linspace(-10, 10, 300)
y = norm.pdf(x, loc=np.c_[M], scale=np.c_[S]).T
plt.plot(x, y, c='b', alpha=0.2)
y = np.sum(y, axis=1)
y = y / np.trapz(y, x)
plt.plot(x, norm.pdf(x, 0, 1), lw=4, c='red', alpha=0.7,
label='N(0, 1)')
plt.plot(x, y, c='k')
plt.legend();
На графике изображена PDF стандартного нормального распределения, а также нормированная сумма PDF для каждой пары оцененных параметров - различие не так велико, как ожидалось изначально. Мы взяли хвост от нормального распределения, а у устойчивого распределения Леви хвост гораздо длиннее и тоньше.
Можно предположить, что из-за шумов: с такими данными будет работать намного сложнее, поэтому нужно придумать какие-то способы улучшения метода. Самое простое - это использование принципов бутстрэп: можем многократно моделировать распределение данных внутри интервалов, например, с помощью равномерного распределения, а далее специальным образом менять их ширину.
Python
np.random.seed(42)
data = norm.rvs(size=50000)
start_tail = 1.5
tail = data[data > start_tail]
fig, ax = plt.subplots(1, 2, figsize=(10, 4))
bins = np.r_[1.5 : 3.75 : 0.25]
hist = np.histogram(tail, bins=bins, density=True)[0]
hist, bins
sns.histplot(tail, bins=bins, stat='density', ax=ax[0]);
ax[0].vlines(np.r_[1.5 : 3.75 : 0.25], 0, 0.2, color='r')
ax[0].vlines(np.r_[1.5 + 0.25/4 : 3.75 : 0.25/2], 0, 0.3, color='k')
BINS = np.r_[start_tail : 3.75 : 0.25]
HIST = np.histogram(tail, bins=BINS)[0]
sample = np.hstack([uniform.rvs(loc=BINS[j], scale=0.25, size=HIST[j]) for j in np.r_[:len(HIST)]])
bins = np.r_[start_tail + 0.25/4 : 3.75 : 0.25/2]
hist = np.histogram(sample, bins=bins, density=True)[0]
sns.histplot(tail, bins=bins, stat='density', ax=ax[1]);
На графике выше видно, что это приводит к увеличению количества интервалов, а из-за многократного моделирования высота столбцов в этих интервалах будет случайным образом слегка отклоняться. Это позволит получать не точечные значения оценок, а их распределения.
Попробуем взглянуть, как будет выглядеть оценка параметров не для разных выборок, а для одной:
Python
np.random.seed(42)
data = norm.rvs(size=50000)
start_tail = 1.5
tail = data[data > start_tail]
L = len(tail)
k, M, S = [], [], []
BINS = np.r_[start_tail : 3.75 : 0.25]
HIST = np.histogram(tail, bins=BINS)[0]
for i in range(1000):
sample = np.hstack([uniform.rvs(loc=BINS[j], scale=0.25, size=HIST[j]) for j in np.r_[:len(HIST)]])
bins = np.r_[start_tail + 0.25/4 : 3.75 : 0.25/2]
hist = np.histogram(sample, bins=bins, density=True)[0]
x = bins[:-1] + np.diff(bins[:2])/2
y = hist.copy()
try:
popt, pcov = curve_fit(func, x, y)
except:
pass
k.append(popt[0])
M.append(popt[1])
S.append(popt[2])
fig, ax = plt.subplots(1, 3, figsize=(12, 3))
sns.kdeplot(k, ax=ax[0], alpha=0.5)
sns.kdeplot(M, ax=ax[1])
sns.kdeplot(S, ax=ax[2])
kde1 = gaussian_kde(M)
x = np.linspace(min(M), max(M), 300)
y = kde1(x)
mo_M = x[np.argmax(y)]
ax[1].axvline(mo_M, c='k', label = r'$\mathbb {Mo}(\mu)$ = ' + f'{mo_M:.2f}')
ax[1].legend()
kde1 = gaussian_kde(k)
x = np.linspace(min(k), max(k), 300)
y = kde1(x)
mo_k = x[np.argmax(y)]
ax[0].axvline(mo_k, c='k', label = r'$\mathbb {Mo}(k)$ = ' + f'{mo_k:.2f}')
ax[0].legend()
kde1 = gaussian_kde(S)
x = np.linspace(min(S), max(S), 300)
y = kde1(x)
mo_S = x[np.argmax(y)]
ax[2].axvline(mo_S, c='k', label = r'$\mathbb {Mo}(\sigma)$ = ' + f'{mo_S:.2f}')
ax[2].legend()
ax[0].set_title('k')
ax[1].set_title('Мат. ожидание')
ax[2].set_title('Отклонение');
Моделирование значений внутри интервалов и уменьшение длины самих интервалов позволяет увидеть, каким на самом деле может быть разброс значений оцениваемых параметров. Черными вертикальными линиями обозначены моды распределений. Вполне логично предположить, что, если в качестве оценок использовать именно моды, то мы увидим гораздо меньший разброс оценок. Проведем 100 испытаний для разных выборок и взглянем на результат:
Python
np.random.seed(42)
m_res, s_res = [], []
for n_i in range(100):
print(n_i, end='\r')
data = norm.rvs(size=50000)
start_tail = 1.5
tail = data[data > start_tail]
L = len(tail)
k, M, S = [], [], []
BINS = np.r_[start_tail : 3.75 : 0.25]
HIST = np.histogram(tail, bins=BINS)[0]
for i in range(500):
sample = np.hstack([uniform.rvs(loc=BINS[j], scale=0.25, size=HIST[j]) for j in np.r_[:len(HIST)]])
bins = np.r_[start_tail + 0.25/4 : 3.75 : 0.25/2]
hist = np.histogram(sample, bins=bins, density=True)[0]
x = bins[:-1] + np.diff(bins[:2])/2
y = hist.copy()
try:
popt, pcov = curve_fit(func, x, y)
except:
pass
k.append(popt[0])
M.append(popt[1])
S.append(popt[2])
kde1 = gaussian_kde(M)
x = np.linspace(min(M), max(M), 300)
y = kde1(x)
m_res.append(x[np.argmax(y)])
kde1 = gaussian_kde(S)
x = np.linspace(min(S), max(S), 300)
y = kde1(x)
s_res.append(x[np.argmax(y)])
f, ax = plt.subplots(1, 3, figsize=(12, 3))
ax[0].plot(m_res)
ax[1].plot(s_res)
ax[0].set_title('Мат. ожидание')
ax[1].set_title('Отклонение')
ax[2].set_title('P(x < 0.5)')
mu_rm = [np.mean(m_res[i:i+10]) for i in np.r_[0:90]]
sigma_rm = [np.mean(s_res[i:i+10]) for i in np.r_[0:90]]
ax[0].plot(np.r_[10:100], mu_rm, color='r')
ax[0].axhline(np.mean(m_res), c='k', label=r'$\mathbb{E}(\mu)$ = ' + f'{np.mean(m_res):.2f}')
ax[1].plot(np.r_[10:100], sigma_rm, color='r')
ax[1].axhline(np.mean(s_res), c='k', label=r'$\mathbb{E}(\sigma)$ = ' + f'{np.mean(s_res):.2f}')
C = norm.cdf(0, m_res, s_res)
c_rm = [np.mean(C[i:i+10]) for i in np.r_[0:90]]
ax[2].plot(C)
ax[2].plot(np.r_[10:100], c_rm, color='r')
ax[2].axhline(np.mean(C), c='k', label=r'$\mathbb{E}(p)$ = ' + f'{np.mean(C):.2f}')
ax[0].legend()
ax[1].legend()
ax[2].legend();
Мы не только избавились от больших выбросов, но также значительно снизили разброс самих значений. А сглаженные по последним 10-ти наблюдениям оценки испытывают гораздо меньшие отклонения.
Можно ли каким-то образом еще сильнее уменьшить разброс оценок? При моделировании данных внутри интервалов мы использовали равномерное распределение, хотя интуитивно понятно, что даже внутри интервалов они должны сохранять свою настоящую форму. Шаг в сторону увеличения точности заключается в том, чтобы использовать не равномерное а какое-то линейно-скошенное распределение. Такого распределения нет в стандартной библиотеке, поэтому придется создать его самостоятельно.
Функция плотности:
Python
def uniskew_pdf(x, loc=0, scale=1, k=0):
b = 2/((k + 1)*scale)
y = np.zeros_like(x)
idx = (loc <= x) & (x < loc + scale)
y[idx] = b*(((x[idx] - loc)*(k - 1))/scale + 1)
return yФункция распределения:
Python
def y(x, loc=0, scale=1, k=0):
b = 2/((k + 1)*scale)
return b*(((k-1)*(loc-x)**2)/(2*scale)-loc+x)Для генерации случайных значений нужна обратная функция, но, так как интегрирование получается очень сложным, то воспользуемся результатами символьных вычислений. Конечный вид обратной функции распределения будет следующим:
Python
def Y(x, loc=0, scale=1, k=0):
b = 2/((k + 1)*scale)
B = b*(k-1)*loc/scale
A = ((b*(k-1)*loc**2)/(2*scale)-b*loc-x)
return scale*((B - b)+((b - B)**2 - (2*b*(k-1)*A)/scale)**0.5)/(b*(k-1))Имея обратную функцию распределения, можем создать генератор случайных значений с необходимыми параметрами скошенности, смещения и масштаба:
Python
def uniskew_rvs(loc=0, scale=1, size=1, K=0):
X = uniform.rvs(size=size, loc=0, scale=1)
return Y(X, loc, scale, k=K)
sns.histplot(uniskew_rvs(loc=1, scale=0.5, size=10000, K=0.2),
stat='density')
x = np.linspace(0.9, 1.6, 1000)
plt.plot(x, uniskew_pdf(x, loc=1, scale=0.5, k=0.2), c='k')
plt.title('Функция плотности линейно-скошенного распределения',
fontsize=14);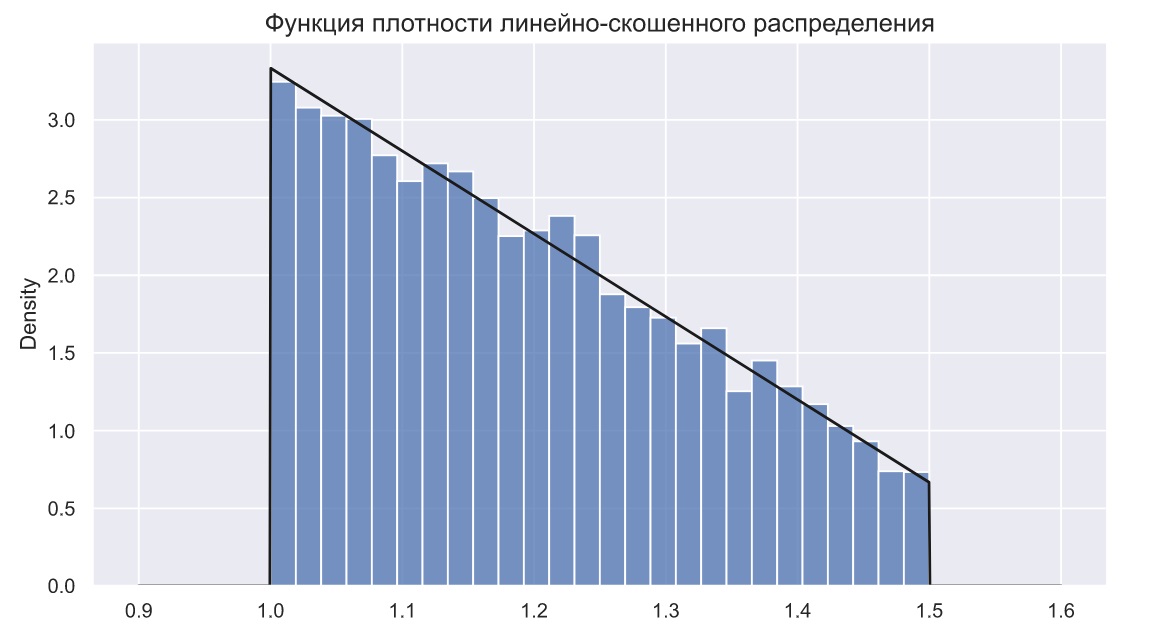
Теоретически применение такого распределения для моделирования данных внутри интервалов должно увеличить точность оценок значений параметров. Однако является ли аппроксимация единственным способ решения данной задачи? Смоделируем нашу выборку несколько сотен раз и взглянем на распределение высот столбцов гистограммы:
Python
for i in range(100):
data = norm.rvs(size=50000)
tail = data[data > start_tail]
bins = np.r_[1.5 : 3.75 : 0.25]
hist = np.histogram(tail, bins=bins, density=True)[0]
plt.plot(bins[:-1], hist, drawstyle='steps-post', c='b', alpha=0.1, lw=0.5)
plt.plot(bins[:-1], hist, drawstyle='steps-post', c='red', lw=1);
Синие линии свидетельствуют о том, что высоты столбцов имеют какое-то собственное распределение. Красная линия показывает одну из возможных гистограмм, факт наблюдения которой имеет свою вероятность, причем эта вероятность будет максимальна при интересующих нас значениях параметров.
Вероятность попадания случайной величины в некоторый интервал равна:
где - это функция плотности вероятности. Поскольку сейчас мы рассматриваем хвост нормального распределения, то данная вероятность запишется так:
Мы не знаем точного количества элементов в выборке, однако, если обозначить это количество буквой , то мы можем оценить вероятность наблюдения
попаданий случайной величины в заданный интервал с помощью формулы биномиального распределения:
Плотность вероятности, что гистограмма из столбцов примет определенный вид с высотами, заданными некоторым случайным вектором
, примет следующий вид:
Необходимо найти такие значения ,
и
, при которых
. Большие значения
, которые могут быть порядка тысяч и десятков тысяч элементов в силу центральной предельной теоремы, приводят к тому, что биномиальное распределение
асимптотически приближается к нормальному
. Вероятности попадания в интервалы могут быть очень малы, а значит для того, чтобы
, значение
должно быть колоссальным. Обычные методы оптимизации для данной функции непригодны, но, чтобы взглянуть на результаты, можно воспользоваться обычным брутфорсом:
Python
np.random.seed(42)
n_res, m_res, s_res = [], [], []
for i in range(100):
data = norm.rvs(size=50000)
tail = data[data > start_tail]
bins = np.r_[1.5 : 3.75 : 0.25]
hist = np.histogram(tail, bins=bins)[0]
M = np.linspace(-2, 2, 25)
S = np.linspace(0.5, 2, 25)
N = np.linspace(30000, 70000, 25)
res = None
P = np.inf
for m in M:
for s in S:
for n in N:
p = np.diff(norm.cdf(bins, loc=m, scale=s))
P_tmp = -np.sum(np.log(binom.pmf(k=hist, n=int(n), p=p)))
if P > P_tmp:
res = (n, m, s)
P = P_tmp
n_res.append(res[0])
m_res.append(res[1])
s_res.append(res[2])
f, ax = plt.subplots(1, 3, figsize=(12, 3))
ax[0].plot(n_res)
ax[1].plot(m_res)
ax[2].plot(s_res)
n_rm = [np.mean(n_res[i:i+10]) for i in np.r_[0:90]]
mu_rm = [np.mean(m_res[i:i+10]) for i in np.r_[0:90]]
sigma_rm = [np.mean(s_res[i:i+10]) for i in np.r_[0:90]]
ax[0].plot(np.r_[10:100], n_rm, color='r')
ax[1].plot(np.r_[10:100], mu_rm, color='r')
ax[2].plot(np.r_[10:100], sigma_rm, color='r')
ax[0].set_title('N')
ax[1].set_title('Мат. ожидание')
ax[2].set_title('Отклонение')
ax[0].axhline(np.mean(n_res), c='k', ls=':',
label=r'$\mathbb{E}(N)$ = ' + f'{np.mean(n_res):.2f}')
ax[1].axhline(np.mean(m_res), c='k', ls=':',
label=r'$\mathbb{E}(\mu)$ = ' + f'{np.mean(m_res):.2f}')
ax[2].axhline(np.mean(s_res), c='k', ls=':',
label=r'$\mathbb{E}(\mu)$ = ' + f'{np.mean(s_res):.2f}')
ax[0].legend()
ax[1].legend()
ax[2].legend();

Кажется невероятным, но разброс значений уменьшился еще сильнее, что также верно для значений оценки .
Python
C = norm.cdf(0, m_res, s_res)
c_rm = [np.mean(C[i:i+10]) for i in np.r_[0:90]]
plt.plot(C)
plt.plot(np.r_[10:100], c_rm, color='r')
plt.axhline(np.mean(C), c='k', label=r'$\mathbb{E}(p)$ = ' + f'{np.mean(C):.2f}')
plt.legend()
plt.title('P(x < 0)', fontsize=16);
Однако такую оптимизацию нельзя считать глобальной: метод имитации отжига показывает, что глобальный максимум может располагаться далеко от реальных значений параметров. Уменьшить разброс можно было бы с помощью моделирования, точно так же, как это делалось выше. Проблема в этом случае заключается в том, что простые реализации алгоритма имитации отжига не всегда добираются до глобального максимума, а иногда и вовсе не находят решений. Более сложные реализации получаются очень затратны в вычислительном плане. Также не стоит забывать, что функция правдоподобия требует вычисления вероятностей попадания значений в заданный интервал то есть интегрирования по PDF устойчивого распределения, а это еще сильнее увеличивает время вычислений.
Поскольку метод максимального правдоподобия оказался очень медленным, да и не таким уж правдоподобным, как хотелось бы, то остается только аппроксимация. Посмотрим, как она работает на реальных данных:
Python
data = pd.read_csv('btc_usdt_binance_1s_buy.csv', index_col=0)
tmp_data = data[data.depth == 10].t
bins = np.hstack(([0], np.log(np.unique(tmp_data+1)))) + 0.001
x_data = [np.mean(bins[i:i+2]) for i in range(len(bins)-1)]
y_data = np.histogram(np.log(tmp_data+1), bins=bins, density=True)[0]
Y = y_data[1:]
X = bins[1:]
X = X[:-1] + np.diff(X)/2
def least_sqr(x):
return np.sum((Y - one_sided(X, a=x[0], c=x[1])/x[2])**2)
x0 = np.array([0.5, 0.15, 0.96])
bounds = [(0, 1), (0, 0.5), (0.8, 1)]
res = minimize(least_sqr, x0, method='Powell', bounds=bounds)
res['x']
print(f"alpha = {res['x'][0]:.3f}")
print(f"scale = {res['x'][1]:.3f}")
print(f"k = {res['x'][2]:.3f}")
sns.histplot(np.log(tmp_data+1), bins=bins, edgecolor = 'k', lw=1, stat='density')
x_res = np.linspace(0, 6, 500)
y_res = levy_stable.pdf(x_res, alpha=res['x'][0], beta=1., loc=0., scale=res['x'][1])/res['x'][2]
plt.plot(x_res, y_res, color='r', zorder=101)
plt.scatter(X, Y, marker = 'x', c='k', zorder=100)
plt.title('Bybit, BTC/USDT, depth=10');Результат
alpha = 0.773
scale = 0.150
k = 0.963
Полученная PDF хорошо аппроксимирует эмпирические значения. Зачем же тогда были нужны все эти танцы с бубном, проделанные выше? Все дело в том, что первый столбец содержит значительную часть выборки: точное количество элементов в выборке нам неизвестно, а значит необходимо стремиться к наименьшему разбросу оценок. Небольшое отклонение от истинных значений параметров приводит к довольно сильному отклонению получаемых оценок.
Можно взглянуть на то, как меняется функция плотности в зависимости от глубины:

С ростом глубины вершина распределения смещается вправо. Происходит это вследствие того, что с ростом глубины минимальное время жизни ордеров увеличивается. Некоторый игрок может посчитать, что через определенное время актуальная цена изменится, и выставляет ордер с ценой, сильно отличающейся от цен bid или ask. Такие ордеры могут появляться на большой глубине, а значит и существовать они могут гораздо дольше, как минимум до тех пор, пока рыночная цена не приблизится к цене, заявленной в ордере. Если рыночная цена начинает двигаться в противоположном направлении, то ордер может существовать еще дольше, ведь в этом случае игрок может сам отозвать свой ордер или терпеливо ждать и надеяться, что рано или поздно рынок начнет двигаться в необходимую ему сторону.
Несомненно, совокупное поведение игроков является очень сложным и определяется многими факторами. Это делает еще более интересным тот факт, что подстройка распределения плотности во многом определяется именно параметром устойчивости, а не смещения. А также напоминает нам о том, что устойчивое распределение хорошо подходит для описания процессов в таких сложных системах.
Время ликвидности ордеров
У каждого ордера есть объем (простое произведение объявленной в ордере цены актива на количество продаваемого или покупаемого актива). Вполне естественна ситуация, когда ордер в цепочке не исчезает раньше времени ее реализации, а уменьшается в объеме. В таком случае функция полезности будет выглядеть так:
где - это вероятность того, что объем ордера уменьшится раньше, чем цепочка будет реализована. Чем меньше
, тем лучше.
Чтобы понять, как определять , рассмотрим данные об изменении объема ордеров в паре MANA/ETH на бирже Binance:
Python
data = pd.read_csv('volume_mana_eth_binance_buy.csv', index_col=0)
print(data.head())Результат
t depth v_dead v_appear price
0 2.0 0.0 0.629426 0.613372 0.000303
1 2.0 0.0 0.077112 0.336269 0.000302
2 2.0 0.0 0.336269 0.077112 0.000302
3 2.0 0.0 0.207446 0.336269 0.000302
4 2.0 0.0 0.642329 0.933224 0.000303В биржевых книгах ордеры с одинаковой ценой объединяются. Для оценки времени жизни ордера это неважно, но для оценки времени ликвидности это имеет ключевое значение. В первом случае объединенные ордеры можно воспринимать как единственный, который либо существует в книге, либо нет. Во втором случае объем может как уменьшаться, так и увеличиваться, причем такие изменения происходят между моментами снимков книги, и их нельзя отследить.
Посмотрим, у скольких ордеров и в какую сторону менялся объем:
Python
data['v_delta'] = data.v_appear - data.v_dead
print(data.head())Результат
t depth v_dead v_appear price v_delta
0 2.0 0.0 0.629426 0.613372 0.000303 -0.016054
1 2.0 0.0 0.077112 0.336269 0.000302 0.259157
2 2.0 0.0 0.336269 0.077112 0.000302 -0.259157
3 2.0 0.0 0.207446 0.336269 0.000302 0.128822
4 2.0 0.0 0.642329 0.933224 0.000303 0.290895Python
count_all = [len(data[data.depth == i]) for i in np.r_[0:100]]
count_increase = [len(data[(data.depth == i) & (data.v_delta < 0)]) for i in np.r_[0:100]]
count_decrease = [len(data[(data.depth == i) & (data.v_delta > 0)]) for i in np.r_[0:100]]
plt.plot(count_all, label='all count')
plt.plot(count_increase, label=r'$\Delta V^{+}$ count')
plt.plot(count_decrease, label=r'$\Delta V^{-}$ count')
plt.legend()
plt.title('Распределение количества ордеров с измененным \
объемом по глубине\n(' + str(sum(count_all))+' ордер из 5011)')
plt.xlabel('depth')
plt.ylabel('count');
Изменение объема наблюдается примерно у половины всех ордеров, а это чрезвычайно значительная часть. Если вспомнить, что ордер - это своего рода ставка на определенное поведение рынка, то неудивительно, что несколько игроков могут сделать ставку на одну и ту же цену (увеличение ордера). Несколько игроков могут наоборот отозвать свои ставки на некоторую цену (уменьшение ордера). Такое поведение также объясняет то, что с увеличением глубины количество изменений объема ордеров постепенно уменьшается. Количества ордеров, объем которых уменьшался и увеличивался, примерно равны, что свидетельствует об отсутствии выраженных и долгосрочных бычьего или медвежьего трендов.
Если взглянуть, как на некоторой глубине величина изменения объема зависит от изначального объема ордера, то можно увидеть, что ордеры с изначально низким объемом увеличиваются в объеме, и, наоборот, ордеры с изначально большим объемом уменьшаются:
Python
sns.histplot(x = data[data.depth == 10].v_appear,
y = data[data.depth == 10].v_delta)
plt.xlabel('Начальный объем ордера (ETH)')
plt.ylabel('Дельта объема (ETH)')
plt.title('Изменение объема ордеров в зависимости\nот их начального объема (MANA/ETH Binance)');
Мы можем оценивать вероятность как уменьшения объема ордера, так и увеличения: обозначим эти оценки как и
соответственно. Польза от оценки вероятности уменьшения объема очевидна. Польза от оценки вероятности увеличения объема заключается в том, что в ситуации, когда некий ордер в цепочке имеет недостаточный объем, то мы могли бы все равно начать ее реализацию, если бы вероятность увеличения объема такого ордера была достаточно велика. При этом мы должны учитывать возможный дисбаланс в поведении спроса и предложения, а значит обе оценки должны присутствовать в функции полезности, вследствие чего она примет следующий вид:
Данные об изменении объема являются крайне неполными, то есть в выборку попадают далеко не все ордера, объем которых изменялся в промежутках между снимками. Даже имеющихся данных по каждой позиции глубины крайне мало для аппроксимации гистограмм. Если учесть, что небольшие изменения объема, скажем, меньшие чем 0.1 ETH, не оказывают никакого ощутимого влияния на работу арбитражеров, то после удаления ордеров с такими изменениями выборка уменьшится еще сильнее. Распределение изменений объема выглядит следующим образом:
Python
sns.histplot(data.v_delta[(data.v_delta > -4) & (data.v_delta < 4)])
plt.xticks(np.r_[-4:4.1:0.5])
plt.xlabel(r'$\Delta V$ (ETH)')
plt.title('Распределение изменений объема ордеров');
Если удалить данные по небольшим изменениям, то объем всей выборки сократится чуть более чем в 3 раза - что очень много. Легко представить, насколько после этого станут неинформативными гистограммы по отдельным значениям глубины.
Взглянем, как будет выглядеть итоговое распределение ордеров с десятой позиции глубины, чей объем уменьшился более чем на 0.1 ETH:
Python
bins = np.hstack(([0], np.log(np.unique(data[data.depth==10].t)))) + 0.001
sns.histplot(np.log(data[(data.v_delta > 0.1) & (data.depth == 10)].t),
bins=bins)
plt.xlabel(r'$\ln (t)$')
plt.title(r'Распределение ордеров с $\Delta V^{-}>0.1$ ETH и depth=10');
Есть все предпосылки к тому, чтобы объяснить эту гистограмму односторонним устойчивым распределением, но, если в оценке времени жизни выборка была ограничена лишь в первом столбце, то в данном случае мы имеем ограничение количества элементов более чем по одному столбцу. Тем не менее, мы можем все равно выводить оценки для и
, интерпретируя их отношение как показатель дисбаланса. В то же время это является не лучшей идеей, так как увеличение или уменьшения объема ордера зависит от его изначального объема (с учетом небольшого объема выборки учесть эту особенность при оценке не получится). Наверняка, можно сказать только одно: пока лучше обойтись без оценки
, а ограничиться только
.
Оценить можно с помощью простого вычисления отношения количества интересующих нас случаев уменьшения объема ордеров в некотором столбце (или столбцах) к общему количеству ордеров в данном столбце. Например, вероятность, что объем некоторого ордера уменьшится более чем на 0.1 ETH менее чем через 2 минуты в зависимости от глубины, будет выглядеть следующим образом:
Python
all_data = pd.read_csv('datasets/cc3_mana_eth_binance_buy.csv')
liq_buy_data = data[(abs(data.v_delta) > 0.1) & (data.v_delta > 0)]
Q_m = [sum(liq_buy_data.depth==i) / sum(all_data.depth==i) if sum(all_data.depth==i) !=0 else 0 for i in np.r_[0:100]]
plt.plot(Q_m, 'bo', ms=4, ls='-');
В конечном счете функция полезности должна выглядеть следующим образом:
И снова можно заметить странное противоречие - выходит, что в знаменателе "смешиваются" две оценки: - крайне грубая и
- для повышения точности и уменьшения разброса которой было приложено так много усилий. В конце концов, если задуматься, то исчезновение ордера - это уменьшение его ликвидности ровно на 100%. Может действительно стоит прогнозировать только изменение ликвидности? Дело в том, что изначально достигнутое уменьшение количества разрывов на 15-25% как раз и было достигнуто с помощью банального частотного подхода и следующей функции полезности:
Допустим, нам интересны вероятности определенных изменений ликвидности некоторого ордера спустя две минуты после его попадания в снимок. Все, что нам нужно это посчитать частоты определенных изменений за некоторый период времени:
Python
bid_data = pd.read_csv('vec_feature_mana_eth_binance.csv')
sns.histplot(bid_data[bid_data.depth == 10].delta_q,
stat='probability')
N = len(bid_data[bid_data.depth == 10])
p_dq_plus = len(bid_data[(bid_data.depth == 10) & (bid_data.delta_q >= 0)]) / N
p_dq_minus = len(bid_data[(bid_data.depth == 10) & (bid_data.delta_q <= -0.25)]) / N
plt.text(0.5, 0.4, r'$P(\Delta Q \geqslant 0)$ = ' + f'{p_dq_plus:.3f}' + '\n' + \
r'$P(\Delta Q \leqslant -0.25)$ = ' + f'{p_dq_minus:.3f}',
fontsize = 13)
plt.title('Вероятности изменений ликвидности ордера\n( MANA/ETH Binance, depth=10)')
plt.xlabel(r'$\Delta Q$ (%)');
Логично предположить, что улучшение метода получения оценок должно уменьшить количество разрывов цепочек еще сильнее. Однако после улучшения количество разрывов снизилось всего на 0.5-1.5%. Представленный метод также потребовал еще целого ряда доработок, прежде чем был использован на практике. Распределение является асимметричным, что потребовало ввода дополнительных ограничений на целевую функцию. Вычисление функции плотности при некоторых значениях параметров устойчивости и масштаба все-таки потребовало значительного увеличения точности. Также оказалось, что некоторые валютные пары сильно выбиваются из общей картины.
Можно ли было взять и перепрыгнуть с тривиальных методов сразу на методы машинного обучения? Да, мы можем конструировать целое множество самых разных признаков ордеров, например:
Python
print(bid_data.head(2))Результат
offer_time quantity price trade_type depth delta_q mp_0 \
0 10 6.977281 0.000302 buy 0 -1.000000 0.000303
1 10 7.853993 0.000302 buy 1 -0.965839 0.000303
mp_m1 mp_m2 mp_m3 mp_m4 i_buy trend
0 0.000304 0.000303 0.000302 0.000301 -0.000107 -4.107
1 0.000304 0.000303 0.000302 0.000301 -0.000107 -4.107 К имеющемуся набору данных добавлена целевая переменная delta_q - значение изменения количества объема ордера, наблюдаемое через 2 минуты. Переменные - это текущее и предыдущие значения mid-price. Переменная trend показывает силу тренда, а переменная i_buy совокупное движение спроса.
Можем снизить размерность данного набора до трех компонентов и взглянуть на результат:
Python
bid_data = pd.read_csv('vec_feature_mana_eth_binance.csv', index_col=0)
bid_data = bid_data[bid_data.depth <= 20]
bid_data.index =np.arange(len(bid_data))
bid_data['quantity'] = np.log(bid_data['quantity'])
X = bid_data[['quantity', 'depth', 'mp_0', 'mp_m1', 'mp_m2', 'mp_m3', 'mp_m4', 'i_buy', 'trend']]
y = np.where(bid_data.delta_q < -0.25, 0, 1)
idx = X.depth == 10
X_d10 = X[idx]
y_d10 = y[idx]
from sklearn.decomposition import PCA
pca = PCA(n_components=3)
data_projected = pca.fit_transform(X_d10)
q_plus = data_projected[y_d10 == 1]
q_minus = data_projected[y_d10 == 0]
fig, ax = plt.subplots(1, 3, figsize=(12, 3.7))
ax[0].scatter(q_plus[:, 0], q_plus[:, 1], c='g', marker='x', s=10, alpha=0.5)
ax[0].scatter(q_minus[:, 0], q_minus[:, 1], c='r', marker='o', s=10, alpha=0.5)
ax[0].set_xlabel('x')
ax[0].set_ylabel('y', rotation=0)
ax[1].scatter(q_plus[:, 0], q_plus[:, 2], c='g', marker='x', s=10, alpha=0.5)
ax[1].scatter(q_minus[:, 0], q_minus[:, 2], c='r', marker='o', s=10, alpha=0.5)
ax[1].set_xlabel('x')
ax[1].set_ylabel('z', rotation=0)
ax[2].scatter(q_plus[:, 1], q_plus[:, 2], c='g', marker='x', s=10, alpha=0.5)
ax[2].scatter(q_minus[:, 1], q_minus[:, 2], c='r', marker='o', s=10, alpha=0.5)
ax[2].set_xlabel('y')
ax[2].set_ylabel('z', rotation=0)
fig.suptitle('Применение метода PCA к данным об изменении\n\
ликвидности ордеров (MANA/ETH Binance, depth=10)', y=1.05);
Между признаками, очевидно, есть какая-то зависимость. Применим случайный лес для классификации изменений ликвидности ордеров:
Python
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn import metrics
Xtrain, Xtest, ytrain, ytest = train_test_split(X, y, random_state=42)
model = RandomForestClassifier(n_estimators=100)
model.fit(Xtrain, ytrain)
ypred = model.predict(Xtest)
print(metrics.classification_report(ypred, ytest))Результат
precision recall f1-score support
0 0.79 0.75 0.77 1112
1 0.80 0.83 0.82 1340
accuracy 0.79 2452
macro avg 0.79 0.79 0.79 2452
weighted avg 0.79 0.79 0.79 2452Удивительно, но простой случайный лес без каких-либо специальных настроек способен обеспечить довольно точную классификацию изменений ликвидности.
Стоило ли тратить так много усилий на разработку метода аппроксимирования гистограмм устойчивым распределением ради 0.5-1.5% улучшения? Здесь вопрос не в количестве, а в качестве. Задачи прогнозирования времени ликвидности ордеров и прогнозирования изменения цены (mid-price) очень сильно связаны между собой, а это значит, что умение прогнозировать время ликвидности ордеров позволяет заниматься не только арбитражем, но и алготрейдингом.
Никто не гарантировал, что классические методы финансовой математики и математической статистики будет легко применять на практике, но без них невозможно понять истинную суть наблюдаемых явлений. Преимущество рынка криптовалют заключается в его волатильности: большая волатильность позволяет извлекать большую доходность, но и риски в этом случае также сильно возрастают. Устойчивое распределение свидетельствует о том, что на самом деле эти риски намного значительнее, чем может показаться. Использовать устойчивое распределение для прогнозирования крайне трудно и бессмысленно. Однако его применение для моделирования, управления портфелем и рисками более чем обоснованно и не так дорого в вычислительном плане.
Опыт работы с книгами ордеров заставляет еще сильнее сомневаться в эффективности рынка криптовалют. В целом, на небольших промежутках времени изменение цены актива практически всегда выглядит, как случайное блуждание, но этого нельзя сказать о динамике книги ордеров. Доказать это крайне непросто, но то, что изменение ликвидности ордеров поддается классификации, косвенно подтверждает данную гипотезу о неэффективности рынка. Следовательно, торговые стратегии должны учитывать как динамику, так и состояние книг ордеров.
Заключение
Актуальной задачей для нас по-прежнему остается построение непрерывных распределений изменений ликвидности. Для арбитража, выполняемого в ручном режиме, это не дало практически никакого преимущества, но с приходом средств автоматизации наличие распределений может стать решающим фактором. Разумеется, над проблемой увеличения частоты снимков книг ордеров мы тоже постоянно работаем, так как сейчас это самый простой способ повышения точности используемых оценок.
В данной статье мы продемонстрировали, как фундаментальные и прикладные, казалось бы, бессмысленные исследования могут открыть новые перспективы. Иногда очень трудно обосновать необходимость выхода из зоны комфорта, в нашем случае освоения новой сферы деятельности, но именно так мы решили заняться еще и алготрейдингом.
Комментарии (7)

cliver
07.09.2023 04:29+2Устойчивое распределение очень схоже с гиперболическим: при больших значениях аргумента они убывают практически в точности, как гиперболы.
Кстати вы не пробовали сделать такую не совсем стандартную вещь как начертить гистограмму в двойных логарифмических координатах (возможно даже точками а не барами)? Так как вы рассматриваете устойчивые распределения с
и
, то есть те которые определены на положительной полуоси, если модельное распределение согласуется с эмпирическим, то вы увидите асимптотическое приближение точек к некоторой прямой хвоста на таком графике (эта прямая хвоста в таких координатах и есть гипербола). Вообще гиперболический хвост у L-устойчивого распределения должен убывать как
(A - некоторая константа). Если мы считаем модель верной, то по углу наклона этой прямой можно также определять параметр
.
То, что устойчивые распределения вылезают в данных изменениях цен и биржевых котировок (причем там альфа как правило больше 1) - это в принципе известно (хотя не так широко как хотелось бы), а вот что так распределено время жизни ордеров в стакане - немного подозрительно звучит. Я бы все же присмотрелся к хвосту. Как я указал выше, если такая модель верна, то он не может убывать быстрее чем
, а если брать максимальную альфу в модели, то не может убывать быстрее чем
. То есть, если хвост по эмпирическим данным убывает быстрее чем
, я бы не стал рассматривать такое распределение в качестве модельного для данного случая.

AndreyKotlov Автор
07.09.2023 04:29Благодарю за столь детальный комментарий с подробным разъяснением. Результаты вышли следующими, это однозначно стоило рассмотреть:

Действительно, для основательной проверки того, что время жизни ордеров лучше всего описывается односторонним устойчивым распределением, нужны данные лучшего качества. Из-за ограничений API данные были еще хуже, ввиду чего параметры любого подходящего закона можно подкручивать к данным практически идеально, поэтому от данной идеи пришлось полностью отказаться.
В целом, все обусловлено принципами работы с большими данными и операциями над ними, поэтому решили пробовать извлекать полезную информацию из книг методами ML.

cliver
07.09.2023 04:29То, что так теоретическая PDF против гиперболы выглядит это ожидаемо. Интересно все таки попробовать точки нанести эмпирических данных на такой log-log график (каждая точка = (<cредняя точка интервала бара гистограммы>, <относительная частота бара гистограммы>)). Неужели там очень сильный разброс получается?
Фактически на этом графике, что у вас в статье по оси частот log шкалу сделать, бары убрать, точки оставить
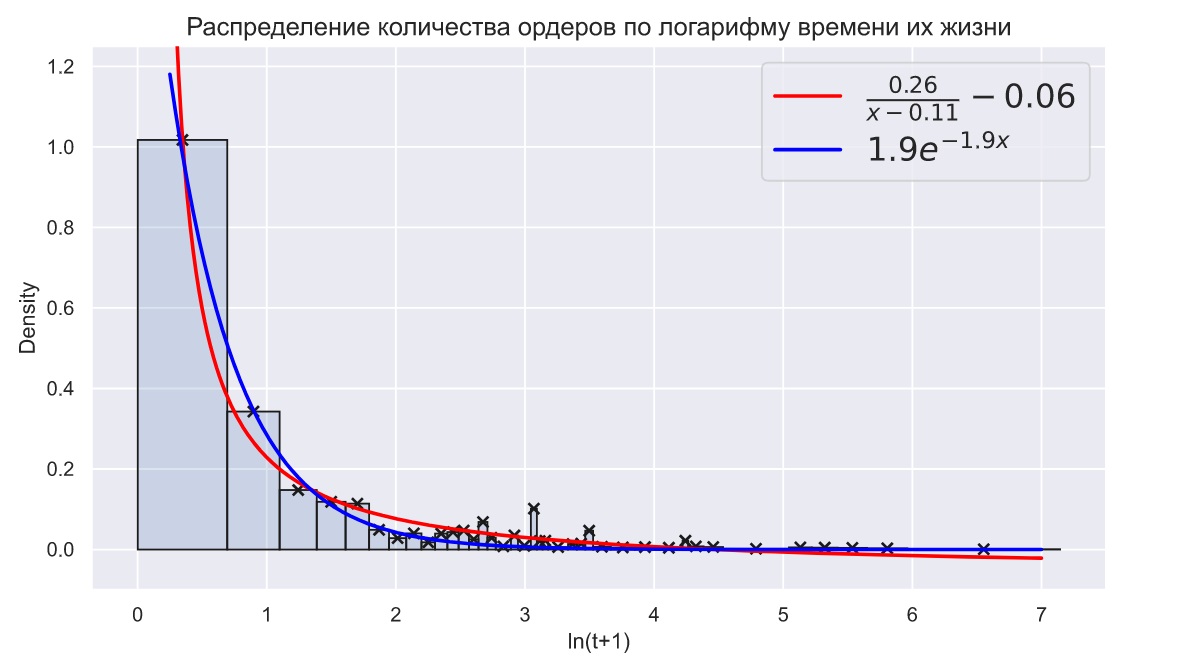
гистограмма 
cliver
07.09.2023 04:29Хотя судя по этому графику может оказаться, что там бары в хвосте с нулевыми значениями есть - то есть придется перестраивать с другими интервалами, чтобы что-то вменяемое получить.

AndreyKotlov Автор
07.09.2023 04:29+1Метод максимального правдоподобия тут неуместен, просто потому что сама выборка является ограниченной и цензурированной. Получить что-то вменяемое действительно есть как цель, но это не должно быть достигнуто путем "подкручивания". Устойчивое одностороннее распределение - это именно гипотеза.
Взгляните еще раз на гифку в статье - это самый идеальный "подгон", и проблема как раз именно в этом. Книга ордеров - это место, в котором статистические методы как минимум перестают быть надежными. В этом случае уже ML выходит на передний план.


paluke
Все это исследование времени жизни заявок для арбитража никакого значения не имеет. При возникновении возможности арбитража заявки выкупаются за миллисекунды hft-роботами.
AndreyKotlov Автор
Во-первых, цепочек обменов может быть очень много. В этом случае поиск выигрышной стратегии, допустим, для двух арбитражеров с абсолютно одинаковыми техническими возможностями становится нетривиальной задачей. В предыдущей статье я как раз рассматривал пример, где наглядно показывается, что скорость вовсе не является гарантией успеха.
Во-вторых, на некоторых рынках, например, на p2p-платформах возможности для арбитража могут существовать неделями, но нет возможности для их автоматизации. В качестве примера также можно привести «синтетические» офферы: когда ставку делает сам арбитражер, создавая «звено» цепочки, вследствие чего модель становится вероятностной.