24.02.2023 01:07
samsergey 57 10000 Источник

Продолжаю знакомить вас с наработками к занятиям математического кружка. В этой статье собраны два сюжета, связанные друг с другом одной темой: математика углов и тригонометрия. Каким образом обосновываются угловые меры? Какие из них для чего более пригодны? Почему значения тригонометрических функций от рациональных долей окружности почти все иррациональны и, наоборот, почему в рациональной тригонометрии только восемь рациональных углов и те, по большей части тривиальны? Материал рассчитан на школьников, но он приоткрывает двери в большую математику, поэтому здесь появятся элементы теории чисел, теории алгебраических полей и полиномы Чебышёва.

В чём лучше измерять углы?

— А вам зачем? Определить направление в море, или, может быть, узнать уклон дороги? Хотите найти расстояние на сфере, либо угловое расстояние между звёздами? Или вам для геометрических нужд, треугольничек построить или звезду пятиконечную? Может, вас тригонометрия интересует, синус вычислить, координату какую отыскать, или фигуру Лиссажу нарисовать даме к 8 марта? Или вы больше по физике: вращения, колебания, гармонические функции, спектры, дифференциальные уравнения. А топологию окружности или группу поворотов изучить не желаете?

Для разных задач годятся разные меры, и какую попало выбирать не стоит. Во-первых, надо, что бы углы выражались числами (желательно, удобными — целыми или рациональными) и были пригодны для бытового использования. Во-вторых, они должны быть удобны для геометрических построений, имели внятные значения для часто встречающихся геометрических фигур. И, в-третьих, помогали нам дружить с тригонометрией и алгеброй — не одними же только циркулем и линейкой вычислять!

Обороты

Для длины абсолютной единицы не существует, выбирай, хоть аршин, хоть астрономическую единицу, хоть планковскую. А вот с оборотами не так. Полный оборот — сам себе единица. Вещь в себе, так сказать. Раз такое дело, самым естественным решением будет измерять углы оборотами и его долями. Нормальный способ, именно его мы используем для измерения частоты вращения, когда пишем об/минуту или когда просим кого нибудь повернуться на четверть-оборота для фотографии.

Типичный тахометр измеряющий обороты
Типичный тахометр измеряющий обороты

Однако, для геометрических нужд имеет смысл оборот представить, не как единицу, а как двойку, точнее, как два развернутых угла. Преимущества этого способа могут быть заметны при измерении углов правильных многоугольников, все они будут выражаться понятными говорящими дробями. Сумма углов в треугольнике тогда будет равна 1, в правильном многоугольнике с n вершинами — n - 2Углы в квадрате: 1/4, в равностороннем треугольнике — 1/3, в пятиугольной звезде — 1/10, в пятиугольнике — 3/5. Удобно.

Грады и градусы

Но правильные дроби нравятся не всем. Так вышло, что законодателями мод в измерении углов были моряки и астрономы, и именно им принадлежат основные практичные угловые меры.

Мореходы и землемеры, в своё время, решили, что разделить угол между Севером и Востоком на 100 частей будет в самый раз! Так получились грады. Прямой угол — 100 град, развёрнутый — 200 град, полный оборот — 400. Кстати, при таком способе 1 град это 1% от прямого угла, можно было бы записывать углы в процентах.

Компас с делениями в градах
Компас с делениями в градах

Есть у град один конструктивный недостаток: у числа 400 сравнительно немного делителей: 2, 4, 5, 8, 10, 16, 20, 25, 40, 50, 80, 100, 200 и среди них нет чисел, кратных трём. Так что у равностороннего треугольника получится угол в 133⅓ града, которые в десятичной дроби представляются лишь периодичной дробью. Давайте поищем что-нибудь получше. Взглянем на то, как растёт количество делителей у чисел в первой тысяче:

Для детализации небольших значений горизонтальная шкала логарифмическая.
Для детализации небольших значений горизонтальная шкала логарифмическая.

Как видите, есть такие числа, которые имеют наибольшее число делителей, среди всех предыдущих. Среди них значится знакомое число 360. Так что, если вам хочется рисовать правильные многоугольники, у которых 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 24, 30, 36, 40, 45, 60, 72, 90, 120 и 180 вершин, имеющие целые значения углов, или заниматься астрономией, в которой угловые размеры Солнца и Луны составляют половину деления, то 360° — ваш выбор!

Ну, а если вам до зарезу нужны семиугольники, то вместо 360 делений выбирайте, например, 420. Делителей у этого числа столько же, что и у трёхсот шестидесяти, но среди них есть кратные 7. Если полный оборот принять за 420 единиц, то прямой угол будет равен 105, углы в правильном треугольнике — 70, в пятиугольнике — 127, в шестиугольнике — 140, семиугольнике — 150. Красота!

Часы

А ещё мне по душе штурманский способ измерять угол в часах и минутах. Разделив оборот на 24 часа, а час — на 60 минут, мы получим привычное бытовое деление суточного периода. К тому же, число 24 относится к числам с наибольшим числом делителей в своей весовой категории. Более того, 24×60 = 1440 имеет целых 34 делителя!

Так что углы во всех привычных правильных многоугольниках будут иметь вполне аккуратное выражение: треугольник — 4ʰ, квадрат — 6ʰ, пятиугольная звезда — 2ʰ24ᵐ, а пятиугольник — 7ʰ12ᵐ. Это менее привычно, чем десятичная запись, но легко ложится на визуальный образ циферблата. Вместо 24 делений можно использовать и 12 часов, но тогда половина прямого угла будет выражаться как 1ʰ 30ᵐ. Зато транспортир превратится в хорошо знакомый и привычный для нас часовой циферблат.

Но особенно мне нравится, как выглядит таблица тригонометрических функций, в которой аргумент выражен в часах:

\begin{array}{c|ccccccc} x & 0^h & 1^h & 2^h & 3^h & 4^h & 5^h & 6^h \\\hline \sin(x) & 0 & \frac{\sqrt{3}-1}{2\sqrt{2}} & \frac{1}{2} & \frac{\sqrt{2}}{2} & \frac{\sqrt{3}}{2} & \frac{\sqrt{3}+1}{2\sqrt{2}} & 1 \\ \cos(x) & 1 & \frac{\sqrt{3}+1}{2\sqrt{2}} & \frac{\sqrt{3}}{2} & \frac{\sqrt{2}}{2} & \frac{1}{2} & \frac{\sqrt{3}-1}{2\sqrt{2}} & 0 \\ \mathrm{tg}(x) & 0 & 2-\sqrt{3} & \frac{\sqrt{3}}{3} & 1 & \sqrt{3} & \sqrt{3}-2 & \infty \end{array}

Кроме привычных значений, в этой таблице можно разместить две дополнительные величины в 1 час и в 5 часов, соответствующие 15° и 75°. Значения синусов и косинусов для них громоздковаты, конечно, но во второй части статьи мы с вами убедимся в том, что это хорошие величины: они имеют алгебраическую степень равную четырём, но при этом выражаются в виде внятного сочетания корней. Таким образом, все целые часы имеют относительно неплохие значения тригонометрических функций.

Румбы

Углы это не только части оборота, это ещё и способ обозначать направления. В отличие от оборотов, направления образуют модулярную арифметику, то есть, не бывает направления соответствующего 25 часам. Так что 25ʰ = 1ʰ и 20ʰ + 6ʰ = 2ʰ. Ещё более явно эту особенность алгебры направлений демонстрируют румбы и азимуты.

К любому углу можно подобраться с помощью дихотомии или методом деления пополам. Сначала выясняем в какой полуплоскости лежит нужное нам направление, потом — в какой четверти, потом — в какой из половинок четвертей и так далее. Так с незапамятных времён делили горизонт моряки, измеряя углы в румбах, разделив окружность на 2⁵ = 32 части, и дав им звучные имена, типа вест-зюйд-вест, норд-ост-тень-ост или даже стрик встока к обеднику, которые очень прикольно выкрикивать хриплым голосом, стоя на мостике.

Наконец, углы можно измерять даже в пальцах, как это делают бывалые морские и речные волки, идя "на два пальца левее Алголя".

Изображения с сайта: http://shturman-tof.ru/Bibl/Bibl_1/Bibl_1_43vremy.html
Изображения с сайта: http://shturman-tof.ru/Bibl/Bibl_1/Bibl_1_43vremy.html

Однако, степени двойки, не могут похвастаться большим числом делителей, у числа 32 их всего 5 и все... степени двойки. Так что, поскольку 1/6 выражается только в виде бесконечной двоичной дроби:

\frac16 = 0.0(01)_2 = \frac18 + \frac1{32} + \frac1{128} + \frac1{512}+...

используя номенклатуру румбов, угол в равностороннем треугольнике придётся выражать бесконечным символом. И о тригонометрии на языке румбов говорить будет нелегко, поскольку косинусы углов, являющихся степенями двойки, кроме четверти и восьмой части оборота, вычисляются не особо изящно:

\cos(NbE) = \frac12\sqrt{2+\sqrt{2+\sqrt{2}}}

Ну, а для других румбов тригонометрические дела обстоят и того хуже!

Радианы

Все описанные выше способы деления окружности, более или менее, подходят для базовой тригонометрии и бытового использования. Но если вы решите вычислить производную от какого-нибудь синуса, то она не будет равна косинусу, покуда аргумент будет измеряться в оборотах, градах, часах или румбах. Однако, при равномерном вращении, скорости изменения прямоугольных координат точки выражаются именно так: \dot{y} = x, \dot{x}= -y

Если в качестве угловой меры взять расстояние, на которое прокатится колесо единичного радиуса, при известном повороте, то угол поворота будет измеряться в радианах, то есть, в отношениях длины дуги, стягиваемой углом, к её радиусу. При этом появится иррациональное число π, но этот значок не хуже значка ° или, например, ₽. Если вместо "пи" произносить "развёрнутый угол", то смысл угла, выраженного в радианах станет яснее. Например, угол в правильном треугольнике равен π/3, то есть трети развёрнутого угла, а у квадрата — π/2, сиречь половина развёрнутого угла. А формула Эйлера e^{i\pi} =-1гласит, что число −1, если рассматривать его, как комплексное -1+0i, имеет аргумент, равный развёрнутому углу.

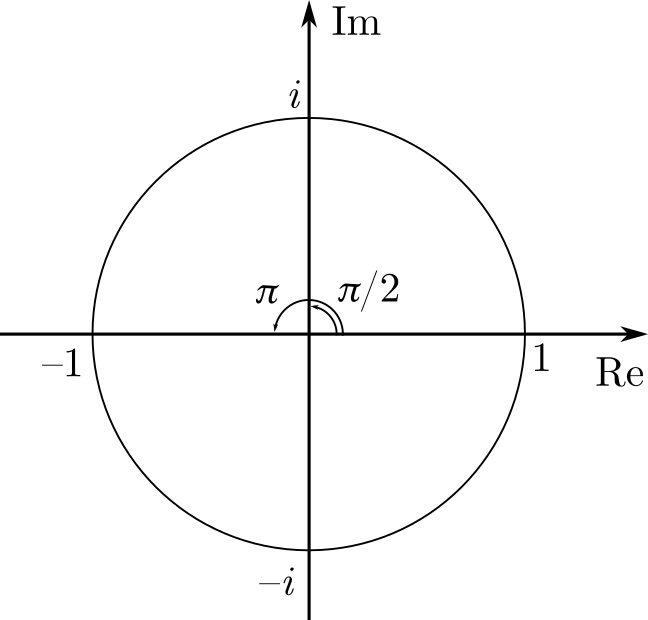
Иллюстрация к формуле Эйлера
Иллюстрация к формуле Эйлера

Несомненные выгоды от использования радиан начинаются при занятиях серьёзной тригонометрией и матанализом. В радианах синусы и косинусы решают дифференциальное уравнение: f''(x)=-f(x),их можно раскладывать в ряды, и использовать методы приближённых вычислений, типа \sin(x) \approx xдля малых углов. С аргументом, выраженным в радианах, тригонометрия позволяет решать задачи на движение, строить теорию функций комплексного переменного и методы разложения в ряды Фурье для решения задач матфизики. Начиная с первого курса физфака или мехмата, про градусы можно забыть.

Уклоны

Наконец, можно отказаться от равномерных делений и сразу измерять углы в тангенсах. Именно этот способ используется на дорожных знаках, где уклон дороги, то есть тангенс угла, образуемого дорогой к горизонту, выражен в процентах. Этот подход полезен в геодезии и в дорожном строительстве. И даже позволяет кое-где упростить тригонометрию.

Например, если величина угла выражается через его тангенс рациональной дробью, то нетрудно точно посчитать его синус и косинус, не используя калькулятор:

\mathrm{tg}(x)=\frac{p}{q},\quad\sin(x)=\frac{p}{\sqrt{p^2+q^2}},\quad\cos(x)=\frac{q}{\sqrt{p^2+q^2}}.

Но есть и существенные проблемы. Уклон в равностороннем треугольнике будет равен 1/√3 ≈57.73%, а вот угол квадрата, простите, будет неопределён, ибо тангенс для прямого угла терпит разрыв. Но самое главное: углы, измеряемые таким образом, перестают быть аддитивными. Это значит, что сумма двух уклонов или, скажем, удвоение уклона будут вычисляться весьма нетривиально, особенно, с учётом разрывов.

От геометрии к алгебре

Эти ограничения можно обойти, если использовать не дробь для выражения тангенса, а пару чисел: (числитель, знаменатель). Тогда прямой угол примет безопасное "значение" (1,0), а его половина может быть выражена, как (1,1) или (√2,√2) — это одно и тоже. Последовательно развивая такое представление, можно прийти к теоретикогрупповому представлению об угле, как о повороте, то есть, действии на множестве точек пространства или элементов поля.

Решение нехитрой задачки на определение угла между заданными отрезками.
Решение нехитрой задачки на определение угла между заданными отрезками.

Если разглядеть в упомянутых выше парах чисел комплексные числа, то алгебру углов можно определить, как мультипликативную группу комплексных чисел, факторизованную по норме (модулю). Тогда аддитивная абелева группа поворотов становится изоморфна мультипликативной группе комплексных чисел. Сложению углов (композиции поворотов) соответствует умножение соответствующих комплексных чисел, а вычитанию — умножение на сопряжённое число.

Ограничившись только такими парами чисел (a,b), что a^2 + b^2 = 1, получим полноценную алгебру, в которой повороты можно складывать таким образом: (a,b) + (c,d) = (ac - bd, ad + bc). Если все числа в парах будут рациональными, то результаты тоже окажутся парами рациональных чисел. Так можно построить группу рациональных точек окружности и рациональную тригонометрию, в которой нет корней, зато полно дробей с пугающими числами.

Наконец, окончательно абстрагировавшись от угловых мер, градусов, румбов и даже радиан, можно рассматривать углы, как топологическое пространство \mathrm{S}^1и унитарную группу первого порядка U(1)изоморфную группе вращений двумерного вещественного пространства SO(2). Впрочем, этот подход, необходимый для определения базовых понятий в геометрии, для решения прикладных геометрических и инженерных задач, всё-таки, не очень удобен. Даже тот фундаментальный для евклидовой геометрии факт, что сумма углов в треугольнике равна развёрнутому углу, будет непросто выразить и доказать, оперируя комплексными числами или рациональными точками на окружности. Но в следующей части статьи именно такой взгляд на углы станет нашим основным инструментом.

Эй, тригонометрия, ты почему такая иррациональная?!

Вернёмся к таблице тригонометрических функций, заучиваемой в школе. Почему в школьной таблице синусов и косинусов так мало чисел, которые легко запомнить? Почему тангенсы, синусы и косинусы от "хороших" углов имеют "нехорошие" значения?

Взгляните ещё раз на привычную таблицу тригонометрических функций:

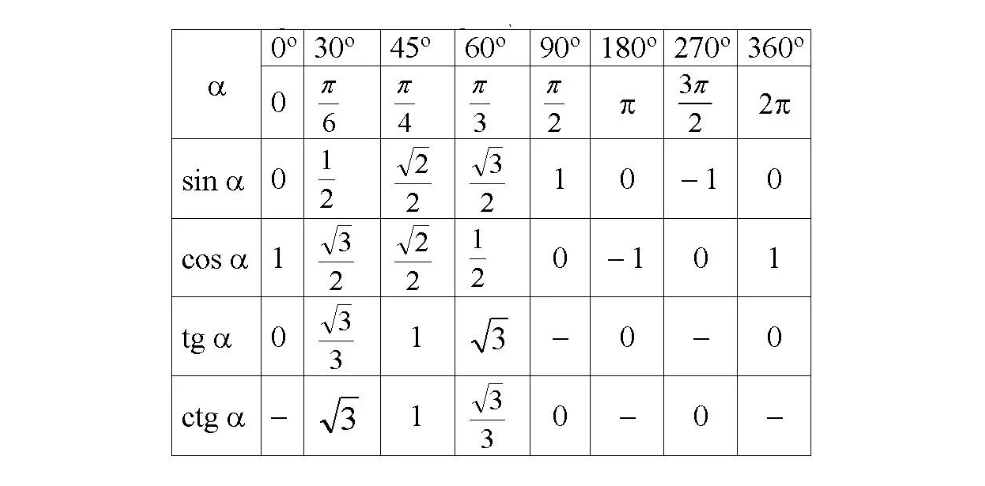
Вся эта красота врывается в жизнь восьмиклассника и способна здорово отравить её неинтуитивными иррациональными значениями, содержащими корни не то из 2 не то из 3, которые как-то надо запоминать. Рациональные значения представлены в этой таблице только четырьмя числами: 0,1/2 и ±1, все же остальные содержат квадратные корни. Наконец, в таблице кроме нулевого и прямого, нет таких углов, для которых все тригонометрические функции принимали бы рациональные значения одновременно.

Из-за этой сплошной иррациональности полностью решить прямоугольный треугольник, то есть узнать все точные значения углов, сторон и их отношений, возможно лишь в двух особых случаях: в треугольнике с углами (45°, 45°, 90°) и с углами (30°, 60°, 90°). Этим треугольникам в школьной программе можно смело ставить памятник!

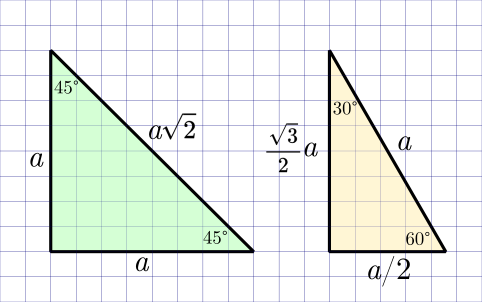
Вот они, два классических школьных треугольника, под которые даже выпускаются специальные линейки.
Вот они, два классических школьных треугольника, под которые даже выпускаются специальные линейки.

Что же делает перечисленные углы "хорошими", и почему именно их мы заучиваем в школе? Они выражаются целыми числами в угловой мере, то есть, являются делителями 360°, или полного оборота. Может быть, мы не те углы выбрали для таблицы? Давайте взглянем на некоторые другие рациональные доли полного оборота:

Жуть! Ещё хуже стало. Получается, что в школьную таблицу попали те углы, для которых тригонометрия ещё терпимо иррациональна. У других шансов получить звание "хороших" очень невелики.

В то же самое время, все тригонометрические функции, это ведь просто отношения длин сторон в прямоугольном треугольнике. В обыкновенной тетрадке в клеточку мы можем нарисовать сколько угодно прямоугольных треугольников с целочисленными сторонами, для которых все тригонометрические функции будут принимать внятные рациональные значения:

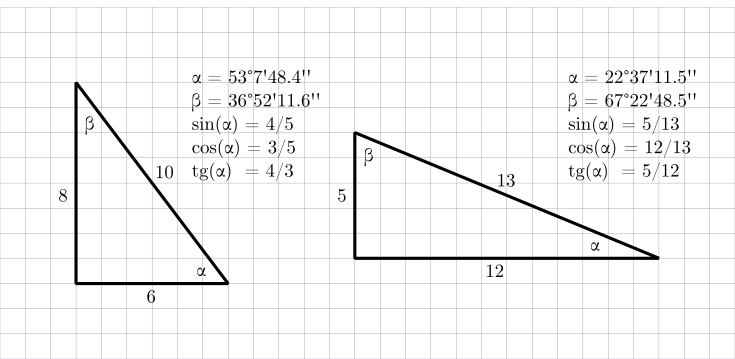
Пара целочисленных треугольников с рациональной тригонометрией из огромного их множества.
Пара целочисленных треугольников с рациональной тригонометрией из огромного их множества.

Почему же эти значения не оказываются в таблицах тригонометрических функций? Дело в том, что для этих чудесных треугольников невозможно точно вычислить углы: они не будут рациональными долями 360° или полного оборота.

Получается, что либо углы рациональны, но тогда тригонометрия превращается в нагромождение корней, либо тригонометрия рациональна, а углы — нет. Одновременно всё становится рациональным только в самых примитивных случаях для 0°, 90°, 180° и 270°. Это значит, что углы и тригонометрические функции почти всегда несоизмеримы друг с другом. И дело тут не в выборе конкретной угловой меры, а в более фундаментальном свойстве евклидова пространства, в котором мы работаем.

А почему не вместе?

Все прямоугольные треугольники с рациональной тригонометрией имеют стороны, образующие, так называемые, пифагоровы тройки: целые числа a,b и c, такие что a^2+b^2=c^2. И все они могут быть построены на регулярной прямоугольной решётке. Но увы, кажется, на этой же решётке невозможно построить никакой угол, выражающийся через рациональную долю полного оборота, кроме тех, что кратны 45°.

Для того, чтобы убедиться в этом, нужно представить точки на регулярной квадратной решётке, как комплексные числа с целыми вещественной и мнимой частями. Они называются гауссовыми числами. Они образуют алгебраическое кольцо и для этих чисел действует основная теорема арифметики и любое гауссово число раскладывается на простые множители не единственным, но вполне определённым способом. Эти разложения имеют некоторые особенности, существенно отличающие их от разложения вещественных целых чисел и из этих особенностей можно вывести следующее утверждение:

Если гауссово число a+bi при возведении в степень n становится вещественным, то либо a=0, либо b=0, либо a=\pm b.

Схема доказательства

Пусть a+ib = z, \gcd(a,b)=1и z^n=m\in \mathbb{Z}. Обозначим как w один из простых делителей z, тогда и сопряжённое ему число \bar{w}, должно быть делителем числа m, поскольку m, по нашему предположению, вещественное. Отсюда следует, что \bar{w} делит z^n, а значит, и z. Таким образом, мы можем заключить, что если w это простой делитель гауссова числа z, то вещественное целое w\bar{w} тоже является делителем z.

Поскольку \gcd(a, b) = 1число z раскладывается на простые множители, каждый из которых должен быть ассоциирован со своим сопряжённым. Для числа c+di ассоциированными являются три числа:-d+ci,\ -d-di,\ d-ci. Сопряжённое число может быть ассоциированным только если c = 0, или d = 0, или c = \pm d. Первые два случая соответствуют вещественным множителям. Из третьего случая следует, что c=\pm 1 для любого простого делителя z, а это значит, что z должно быть ассоциированным числу M(1+i) для какого-то целого числа M.

Из этого свойства вытекает следующее:

Углы, которые опираются на узлы регулярной квадратной решётки либо кратны 45°, либо несоизмеримы с 360°.

Доказательство

Доказать это утверждение можно, если вспомнить, что любое комплексное число a+bi можно представить в форме r\exp(\theta i). В такой форме удобно перемножать комплексные числа и возводить в степень. Так, в частности, (a+bi)^n = r^n\exp(n\theta i).

Рассмотрим гауссово число a+bi, образующее с горизонталью (вещественной осью) угол \theta =k\pi/n, где n — натуральное число, а k— целое. Тогда число (a+bi)^n = r^n\exp(k\pi i) =-r^n  будет вещественным. Это для гауссовых чисел означает, что либо a = 0 и \theta = k\pi/2, либо b = 0 и \theta = 0, либо a=\pm b и \theta = k\pi/4. Во всех же остальных случаях многократное умножение на a+bi, эквивалентное повороту вектора(a,b) на угол \theta и одновременному увеличению его длины в rраз, никогда не приведёт к вещественному значению, а значит, этот угол несоизмерим с 360°.

Осталось показать, что это свойство относится не только к углам, отсчитываемым от горизонтальной оси, но справедливо для любого угла, опирающегося на узлы решётки. Это легко продемонстрировать на рисунке, который показывает, что переходя к регулярным подрешёткам, легко можно свести любой угол к доказанному случаю.

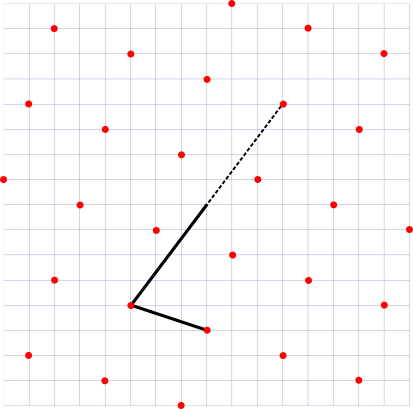
Угол между векторами (3, −1) и (3, 4) при переходе на подрешётку, генерируемую первым вектором, является углом между вектором (1, 3) и горизонтальной осью на этой подрешётке
Угол между векторами (3, −1) и (3, 4) при переходе на подрешётку, генерируемую первым вектором, является углом между вектором (1, 3) и горизонтальной осью на этой подрешётке

Таким образом, школьные задачи, подразумевающие внятный ответ, в которых нужно найти углы, опирающиеся на узлы квадратной сетки, скорее всего, имеют решение 45°, 90° или 135°. Либо задача формулируется на поиск тангенса угла.

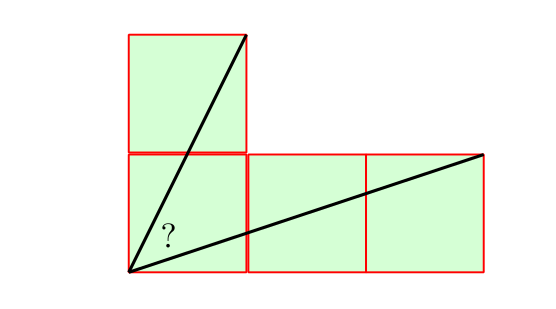
В этой популярной задаче нужно найти точное значение угла, а значит, это может быть только 45°. Её можно решить разными способами, с привлечением геометрии, векторов, вычисляя арктангенсы, но если вас спрашивают про угол, то единственный возможный точный ответ, в принципе, вы уже знаете.

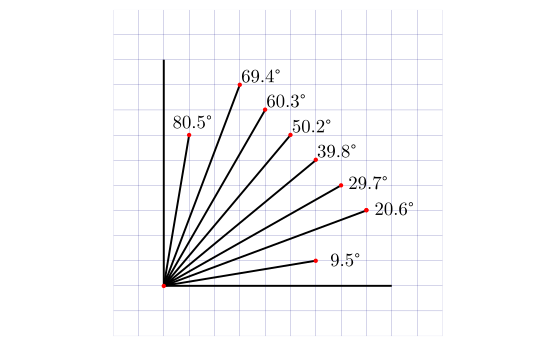
В сети легко найти множество рекомендаций по построению приближений к углам, кратным 10° или даже 5°. Однако, очень мало где говорится, то это только приближения, причём, удобно работающие только для построения углов, отсчитываемых от горизонтали. Впрочем, для быстрых построений они, действительно, могут быть полезны.

Копаемся в тригонометрическом лайфхаке

На многих ресурсах, созданных для облегчения жизни школьникам, то и дело появляются разнообразные лайфхаки: приёмы, существенно облегчающие запоминание чего-либо или упрощающие вычисления. Отношение у педагогов к таким приёмам неоднозначное. Одни с удовольствием их пропагандируют, продвигая мысль, что "Математика — это просто!". Другие возражают: "Ученик — не попка, заученное, но не понятое бесполезно", и считают лайфхаки, шпаргалки и линейки с формулами вредными.

Мне не нравится считать математику простой. Она сложна, но невероятно интересна, а главное, она познаваема! Это же относится и к жизни. Не уверен, что хочу прожить "простую" жизнь, в которой "всё понятно", потому что есть "правильные ответы", найденные кем-то для меня и выученные мною до автоматизмов. Это не вопрос "свободы выбора" или "права на самовыражение". Это про удовольствие, про красоту, про интерес, про мастерство, как в математике, так и в жизни. Так что, мне кажется очень полезным и интересным рассмотреть ответы, найденные другими, и самостоятельно постараться понять, что они означают и откуда взялись.

Выходит, я отношусь тем, кто любит лайфхаки, и с удовольствием о них рассказывает, но использует их, как повод заглянуть "под капот", и разобраться с тем почему, как и при каких условиях они работают. Многие "простые приёмы" имеют под собой интереснейшие и глубокие основания, открывающие двери в разделы серьёзной математики.

Уверен, многие из вас встречали этот симпатичный способ запомнить табличные значения тригометрических функций, синуса и косинуса, в первой четверти, который столь же часто рекомендуют, сколько поругивают:

\begin{array}{c|ccccc} \alpha & 0 & \pi/6 & \pi/4 & \pi/3 & \pi/2\\\hline \sin(\alpha) & \sqrt{\frac{0}{4}} & \sqrt{\frac{1}{4}} & \sqrt{\frac{2}{4}} & \sqrt{\frac{3}{4}} & \sqrt{\frac{4}{4}}\\ \cos(\alpha) & \sqrt{\frac{4}{4}} & \sqrt{\frac{3}{4}} & \sqrt{\frac{2}{4}} & \sqrt{\frac{1}{4}} & \sqrt{\frac{0}{4}}\\ \end{array}
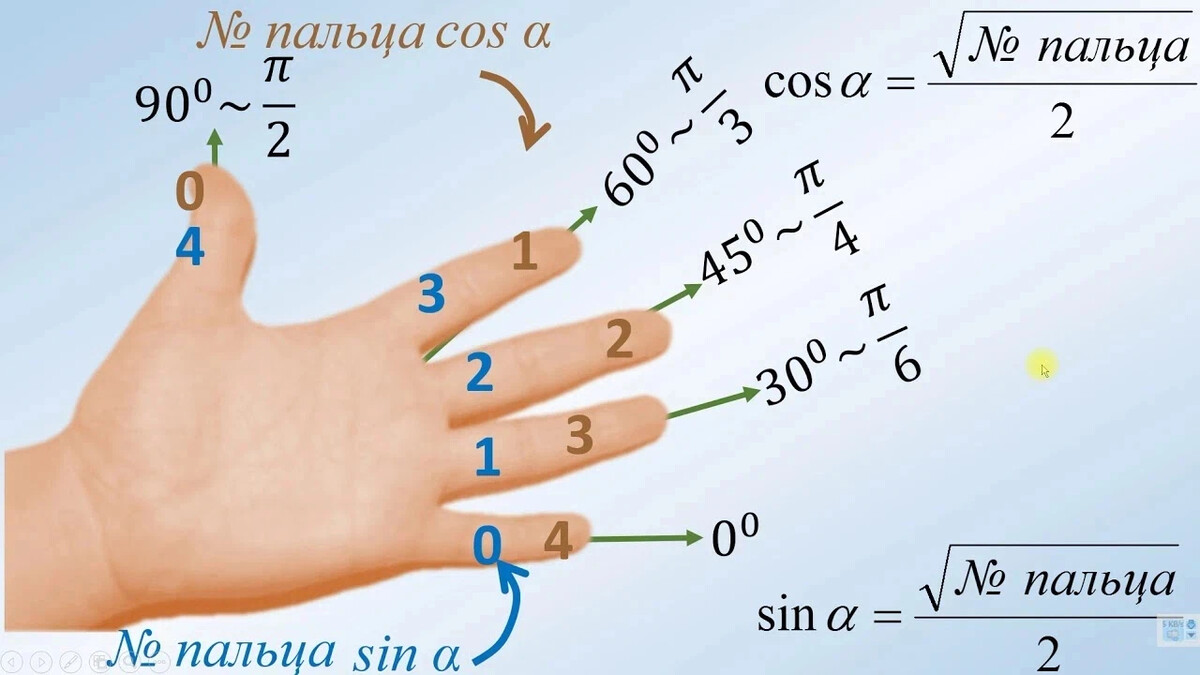
К нему даже приспособили растопыренные пальцы для пущей понятности.
К нему даже приспособили растопыренные пальцы для пущей понятности.

Польза от этого способа есть, он позволяет не только запомнить значения синуса и косинуса, но и усвоить кто из них растёт, а кто убывает в первой четверти. Но есть в нём кое-что любопытное. Аргумент \alpha меняется неравномерно, а под корнями при этом наблюдаются линейные зависимости. Но мы же прекрасно понимаем, что тригонометрия не ограничивается квадратными корнями. О чём говорит нам эта линейная зависимость? Почему значений именно пять, а не больше? И почему под корнями равномерно перебираются четверти?

Откуда взялась линейность

Давайте сначала посмотрим на то, как этот способ выглядит графически. Нанесём значения синуса и косинуса из таблицы, как точки на координатной плоскости.

Ожидаемо получим пять точек, лежащих на окружности с единичным радиусом. Точки, соответствующие подкоренным выражениям (зелёные), при этом выстраиваются в аккуратную линию. В этом тоже нет ничего неожиданного, если вспомнить, что \sin^2(x) + \cos^2(x) = 1, а значит, квадраты синуса и косинуса, действительно, связаны линейным соотношением.

Почему значений только пять?

В теории полей, есть такой термин степень алгебраического числа. Им обозначается минимальная степень многочлена, корнем которого может быть число.

Например, целые и рациональные числа имеют алгебраическую степень, равную единице, потому что они могут быть решением уравнения ax+b=0 для целых коэффициентов a и b. Числа \sqrt2, i или золотое сечение имеют степень равную двум, потому что являются корнями квадратных уравнений, так же как и гауссовы числа, не являющиеся вещественными. А вот кубический корень, решая квадратное уравнение с рациональными коэффициентами получить не выйдет, тут требуется уравнение третьей степени. Так что \sqrt[3]2 имеет алгебраическую степень, равную трём.

Методами теории полей можно показать, что алгебраическая степень значений тригонометрических функций от угла вида 2k\pi/n зависит от числа n:

\begin{eqnarray*} D\left(\cos\left(\frac{2k\pi}{n}\right)\right) &=& \frac{\varphi(n)}{2},\\ D\left(\sin\left(\frac{2k\pi}{n}\right)\right) &=& \left\{ \begin{array}{ll} \varphi(n), &\mathrm{if}\ n \ne 0 \mod 4,\\ \varphi(n)/2, &\mathrm{if}\ n = 0 \mod 8,\\ \varphi(n)/4, &\mathrm{if}\ n = 4 \mod 8. \end{array} \right.\\ D\left(\mathrm{tg}\left(\frac{2k\pi}{n}\right)\right) &=& \left\{ \begin{array}{ll} \varphi(n), &\mathrm{if}\ n \ne 0 \mod 4,\\ \varphi(n)/4, &\mathrm{if}\ n = 0 \mod 8,\\ \varphi(n)/2, &\mathrm{if}\ n = 4 \mod 8. \end{array} \right. \end{eqnarray*}

В приведённой выше формуле используется функция Эйлера \varphi(n), которая играет очень важную роль в теории чисел. Она определена на множестве натуральных чисел и равна количеству чисел, не превышающих n и взаимно с ним простых.

Взгляните на первые двенадцать значений функции Эйлера, а также на соответствующие доли круга и алгебраические степени косинуса и синуса для этих долей:

Эту таблицу можно продолжить и дальше, но чем больше оказывается число n, тем больше можно отыскать чисел с ним взаимно простых. Вот как растёт функция Эйлера:

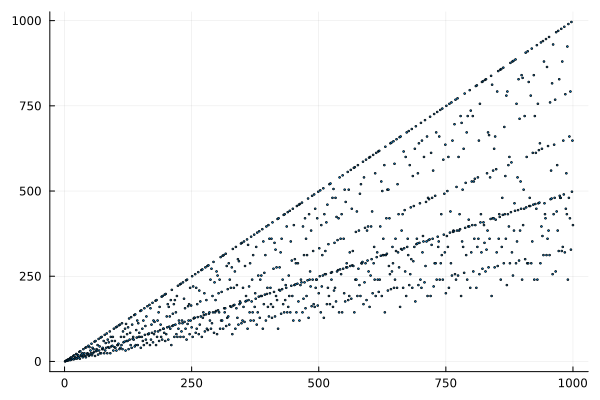
Более или менее удобоваримыми можно считать числа с алгебраической степенью 1 и 2. Но \varphi(n) становится больше 2, для всех n>6 , а если n>12, то \varphi(n) уже не опустится ниже четырёх. Это значит, что в табличке мы перечислили все возможные рациональные доли окружности, в которых косинус и синус имеют шанс попасть на страницы школьного учебника. Таких углов в первой четверти оказывается всего пять, и это ровно те углы, что оказались в таблице, с которой начался наш разговор.

Вот как выглядит распределение по углам максимального значения алгебраических степеней для тригонометрических функций.

Здесь каждый чёрный кружок показывает угол и максимальную алгебраическую степень тригонометрических функций для него, как расстояние от центра координат (логарифмированное для наглядности). Зелёный, розовый и голубой круги в середине ограничивают величины с алгебраической степенью 1, 2 и 3.
Здесь каждый чёрный кружок показывает угол и максимальную алгебраическую степень тригонометрических функций для него, как расстояние от центра координат (логарифмированное для наглядности). Зелёный, розовый и голубой круги в середине ограничивают величины с алгебраической степенью 1, 2 и 3.

Табличные значения углов попадают внутрь радиуса, ограничивающего алгебраические степени меньше 3.

А причём тут четвёрки?

Итак, почему чисел в таблице всего пять, мы разобрались. Понятно также почему они образуют линейную зависимость под корнем. Но каким образом они оказались расположены на одинаковом расстоянии друг от друга, и отчего во всех подкоренных выражениях в знаменателях четвёрки?

Пора нам взглянуть на те самые алгебраические уравнения, о решениях которых мы говорили, когда рассуждали об алгебраических степенях.

В школьном курсе значения тригонометрических функций от примечательных углов выводятся геометрически. Однако эти вычисления можно свести к решению чисто алгебраических задач.

Из формул косинуса суммы несложно получить полезное соотношение:

\cos(n\alpha) = 2\cos[(n-1)\alpha]\cos(\alpha) - \cos[(n-2)\alpha].

Подставляя натуральные числа n, можно вывести следующие равенства:

\begin{array}{cll} \cos(0\alpha) &&= 1\\ \cos(1\alpha) &&= \cos(\alpha)\\ \cos(2\alpha) &= 2\cos(1\alpha)\cos(\alpha)-1 &= 2\cos(\alpha)^2-1\\ \cos(3\alpha) &= 2\cos(2\alpha)\cos(\alpha)-\cos(1\alpha) &= 4\cos(\alpha)^3 - 3\cos(\alpha)\\ \cos(4\alpha) &= 2\cos(3\alpha)\cos(\alpha)-\cos(2\alpha) &= 8\cos(\alpha)^4 - 8\cos(\alpha)^2 - 1\\ \cos(5\alpha) &= 2\cos(4\alpha)\cos(\alpha)-\cos(3\alpha) &= 16\cos(\alpha)^5 - 20\cos(\alpha)^3 + 5\cos(\alpha)\\ \vdots&& \end{array}

Если теперь заменить \cos(α)на формальную переменную x и ввести обозначение \cos(nα) = T_n(x)то мы получим последовательность многочленов:

\begin{array}{l} T_0(x) = 1\\ T_1(x) = x\\ T_2(x) = 2x^2 - 1\\ T_3(x) = 4x^3 - 3x\\ T_4(x) = 8x^4 - 8x + 1\\ T_5(x) = 16x^5 - 20x^3 + 5x\\ \vdots \end{array}

для которых выполняется общее правило:

T_n(x) = 2xT_{n-1}(x) - T_{n-2}(x).

Мы получили семейство многочленов Чебышёва (первого рода), которые используются в широком ряде задач от приближённых вычислений и численного интегрирования, до теории сигналов и радиосвязи.

Приравнивая многочлен T_n(x) к значениям косинуса какого-нибудь угла, можно вычислить косинус от n-ной доли этого угла. Например, решив уравнение T_3(x) = \cos(\alpha) = 4x^3 − 3x, мы найдём a=\cos(\alpha/3).

Так можно найти все значения из обсуждаемой нами волшебной таблицы. Например, для x = \cos(π/6) = \cos((π/2)/3)мы получаем:

T_3(x) = \cos(\pi/2)\quad \Rightarrow\quad 4x^3-3x = 0\quad \Rightarrow\quad x^2 = 3/4

вы можете найти сами алгебраические значения \cos(π/4) и \cos(π/3), и чтобы почувствовать себя крутым математиком, косинусы румбов NNE и NbE.

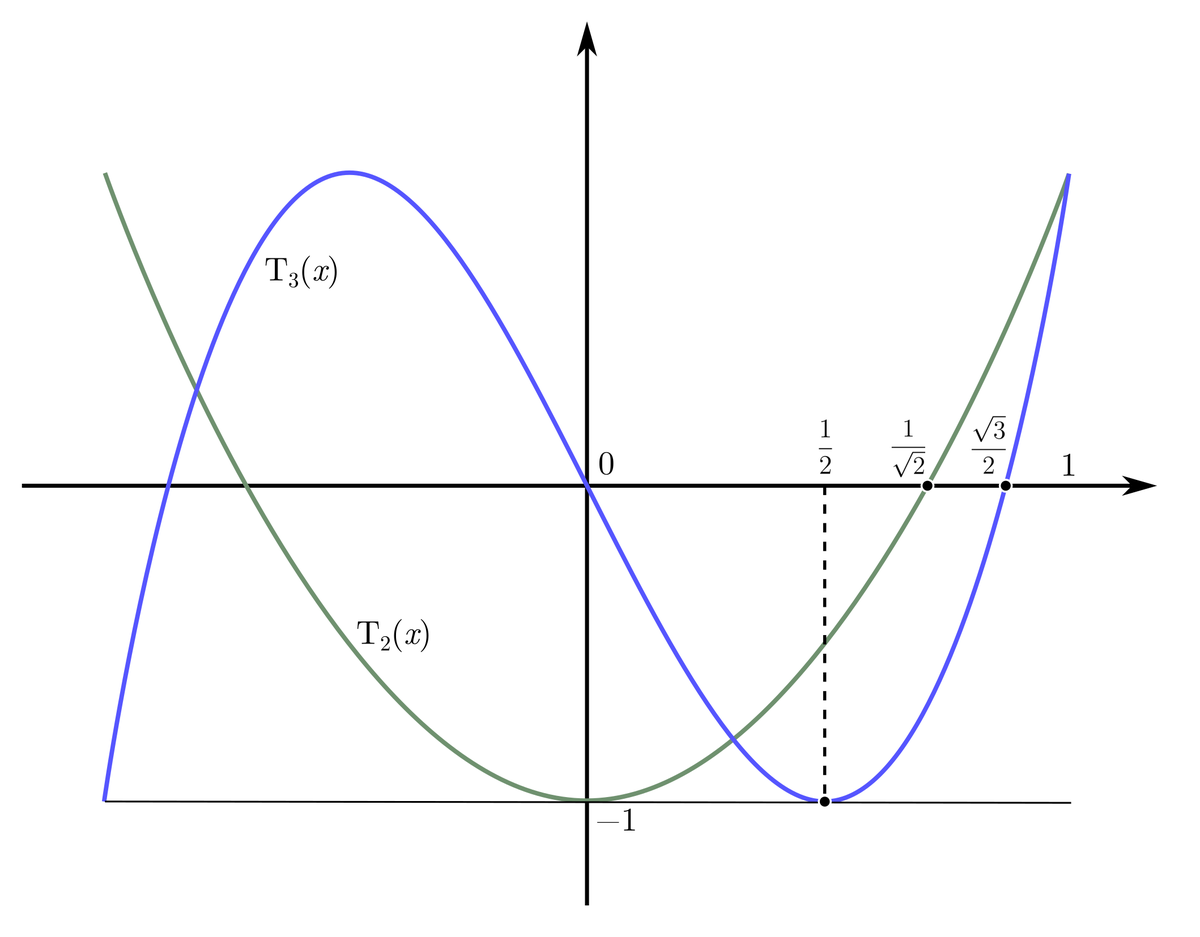
Графики двух многочленов Чебышёва и связь их корней с табличными значениями тригонометрических функций.
Графики двух многочленов Чебышёва и связь их корней с табличными значениями тригонометрических функций.

Имея общий вид для многочленов Чебышёва, можно увидеть откуда берутся четвёрки в таблице-лайфхаке. Обратите внимание на то, что все многочлены T_n(x) имеют коэффициент при старшей степени вида 2^n, который появляется из-за двойки в рекуррентном определении многочленов. В то же время, все пять значений из мнемонической таблицы получаются из уравнений, вытекающих из T_2(x)и T_3(x). А в них старшие коэффициенты равны 2 или 4. В результате, все квадраты значений с алгебраической степенью не превышающей 2, можно записать так, чтобы старший коэффициент был равен 4. Для других долей окружности порядки уравнений становятся выше, и либо их решения будут выражаться через нагромождение корней и дробей, либо не решаются в конечной форме вовсе.

Подведём итог нашей вылазки. Мы выяснили, что среди углов, являющихся рациональной долей полного круга, есть только пять, для которых значения синуса и косинуса имеют алгебраическую степень 1 или 2. Для всех этих углов уравнения, выводимые из многочленов Чебышёва имеют старший коэффициент 2 или 4, таким образом, все эти значения будут квадратными корнями из рациональных чисел со знаменателем 4. Так как все они должны оказаться в интервале [0, 1], то в нашем распоряжении оказывается ровно пять таких рациональных чисел: 0/4, 1/4, 2/4, 3/4 и 4/4. Иные значения возможны, но будут иметь более сложную структуру и более высокую алгебраическую степень.

Используя теорию чисел, можно составить исчерпывающий список значений уклонов, имеющих алгебраическую степень 2, соответствующих углам, соизмеримым с 2π. И убедиться в том, что все они выражаются целыми значениями, если измерять углы в часах.

\begin{array}{ll} \mathrm{tg}(\pi/3) = \sqrt{3} & \mathrm{tg}(2\pi/3) = -\sqrt{3}\\\rule{0pt}{4ex} \mathrm{tg}(\pi/6) = \sqrt{3}/3 & \mathrm{tg}(5\pi/6) = -\sqrt{3}/3 \\\rule{0pt}{4ex} \mathrm{tg}(\pi/8) = \sqrt{2}-1 & \mathrm{tg}(3\pi/8) = \sqrt{2}+1 \\ \mathrm{tg}(5\pi/8) = -\sqrt{2}-1 & \mathrm{tg}(7\pi/8) = 1-\sqrt{2} \\\rule{0pt}{4ex} \mathrm{tg}(\pi/12) = 2-\sqrt{3} & \mathrm{tg}(5\pi/12) = \sqrt{3}+2 \\ \mathrm{tg}(7\pi/12) = -\sqrt{3}-2 & \mathrm{tg}(11\pi/12) = \sqrt{3}-2 \end{array}

По-моему, теория чисел и теория полей — это круто! Здорово иметь возможность не просто вычислять какие-то значения, а ещё до начала вычислений знать, в какой мере эти значения вычислимы. Именно благодаря таким рассуждениям удалось дать исчерпывающий ответ на давний вопрос: какие задачи можно решить с помощью циркуля и линейки, а какие нельзя.

Благодарю за храбрость тех, кто пробрался вместе со мной сквозь дебри теории! Вместе не так страшно. А тех, кому интересно, приглашаю на Дзен-канал Онлайн-кружок математики, в котором занимательно-математические статьи появляются в облегчённом варианте.

Предыдущие статьи в серии Математическая продлëнка:

Квадратные уравнения во всей красе

Теория чисел на пальцах

Комментарии (57)


  1. Tyusha
    00.00.0000 00:00
    #25263708
    +2

    Спасибо, очень интересно.


  1. wataru
    00.00.0000 00:00
    #25264404

    Именно этот способ используется на дорожных знаках, где уклон дороги, то есть тангенс угла,

    А точно тангенс, а не синус? Я всегда интересовался, а вот как эти проценты меряются — от длины дорожного полотна (тогда это синус) или от смещения по горизонтали (тогда это тангенс). С практической точки зрения первое мерять проще. Есть какой-нибудь источник?


    1. iShrimp
      00.00.0000 00:00
      #25264928
      +1

      В геодезии расстояния и площади измеряются в горизонтальной проекции (сайт не АИ, но общее представление получить можно)


  1. Andy_U
    00.00.0000 00:00
    #25264464
    +5

    Автор еще про "военный" метод не упомянул: " противник на 2 часа!". Тут обычный 12-часовой цифрблат подразумевается.


    1. vivlav
      00.00.0000 00:00
      #25280246
      +1

      У военных есть тысячные (в нато схожие милы). И там по угловым размерам объектов (их можно в биноклях, прицелах смотреть как насечки) и их реальным размерам можно высчитывать расстояния.


    1. Crocodilus
      00.00.0000 00:00
      #25304756
      +2

      Есть ещё классические "полшестого".


  1. thevlad
    00.00.0000 00:00
    #25264582
    +3

    Для меня до сих пор загадка. Почему школьную тригонометрию дают исключительно, как кучку не очевидных формул для преобразования одного в другое. А ни через комплексные числа.


    1. mianoki
      00.00.0000 00:00
      #25264690
      +3

      Потому что тригонометрия - это греки палкой на песке чертили.
      А комплексные числа - ультра-костыль современной математики. Вот и ответ.


      1. thevlad
        00.00.0000 00:00
        #25264718
        +3

        Прям уж и костыль. Их вообще можно вводить на пальцах, как двухмерные вектора и довольно очевидные операции над ними. А дальше показывать выполнимость над ними аксиом поля и сказать, что алгебра над ними "точно такая же" как и над "обычными числами".

        Да и комплексные числа хотя бы имеют пользу во многих реальных применениях инженерии и науки. А единственное приложение формул из школьной тригонометрии это заваливание школьников на ЕГЭ.


        1. Andy_U
          00.00.0000 00:00
          #25265424
          -2

          Да и комплексные числа хотя бы имеют пользу во многих реальных применениях инженерии и науки

          Ага, пользу приносят, но вот только в физической реальности не наблюдаются/не существуют.


          1. thevlad
            00.00.0000 00:00
            #25265444
            +1

            Так в физической реальности и других чисел, кроме натуральных, которыми можно овец считать, вроде как и не существует. Где вы отрицательное количество овец видели? А число Пи к примеру в реальности существует, или где-то полностью записано? )


            1. Andy_U
              00.00.0000 00:00
              #25265450

              Число pi существует? Итого уже не только натуральные. Отрицательные - векторные скорости, ускорения, да и сами кооординаты. Целые отрицательные - деньги - долги.


              1. thevlad
                00.00.0000 00:00
                #25265456
                +3

                Так вот я и спрашиваю, с чего вы взяли что число пи существует в реальности, где его можно потрогать, или увидеть полную запись? А где можно потрогать или увидеть отрицательно количество денег или овец? А волновая функция у элементарной частицы действительно существует? Или весь этот ваш квантмех бесовщина и живем мы на плоской земле?


                1. Andy_U
                  00.00.0000 00:00
                  #25265528

                  Число Pi - это отношение длины окружности к диаметру. И так далее. А с использованием комплексных чисел в той же (линейной) электротехнике немножко другая история, начинающаяся с утверждения, "пусть у нас входное напряжение - комплесное число виде U*exp(-i*omega*t)", чего в природе не встречается. Потом, а конце, мы мнимую компоненту убъем. Т.е. чисто математический трюк, убиваемый любым диодом. И еще, как перешли в 3D, так и нет комплексных чисел. И


                  1. thevlad
                    00.00.0000 00:00
                    #25265538

                    Число Pi - это отношение длины окружности к диаметру.

                    А комплексные числа это просто двухмерные вектора с заданными свойствами, при помощи которых можно сокращать вычисления с тригонометрическими функциями. Ровно так же как и отрицательное значение являясь долгом, упрощают вычисления с деньгами . Но если вас даже примеры с отрицательными овцами, не наводят на размышления. То я спрошу еще раз существует ли в реальности волновая функция?


                    1. Andy_U
                      00.00.0000 00:00
                      #25265650

                      То я спрошу еще раз существует ли в реальности волновая функция?

                      А та же фигня, что с эфиром в 19 веке. Был реальностью, но сплыл.


                      1. thevlad
                        00.00.0000 00:00
                        #25265814

                        То есть ученые всех нас обманывают? А как быть со всякими квантмеханическими моделями, где эти бесовские комплексные числа повсюду, и о боже - получаются плотности вероятности(их то уж точно в реальности не существует)?


                      1. Andy_U
                        00.00.0000 00:00
                        #25266402

                        Что, плотность вероятности в реальности? В реальности событие или случается, или нет. А плотность - это модель для предсказания. Она не в реальности, а в мозгах.


                      1. thevlad
                        00.00.0000 00:00
                        #25266420
                        +1

                        Так эти вероятности считаются на богомерзких комплексных числах которых не существует. А по поводу, что плотность вероятности в мозгах, это верно, перенесите этот подход и на комплексные числа.


                      1. Andy_U
                        00.00.0000 00:00
                        #25266422

                        Так я все время об этом и говорю?


                      1. thevlad
                        00.00.0000 00:00
                        #25266434

                        Отлично, теперь осталось понять где пролегает эта граница между математикой которая в мозгах и которая в физической реальности. По большому счету, где-то на уровне подсчета овец.


                      1. Andy_U
                        00.00.0000 00:00
                        #25266460

                        Я там ниже, надеюсь, ответил.


                      1. Tyusha
                        00.00.0000 00:00
                        #25266218
                        +1

                        У математики в отличие от других наук отсутствует предметная область. Поэтому не надо требовать приложения математических конструкций к реальности.


                      1. energo_2000
                        00.00.0000 00:00
                        #25291210

                        Не сплыл.

                        Это будущее, и все новые разработки будут воплощением теории эфира.

                        Нынешняя теория упёрлась в свой тупик.


                      1. Andy_U
                        00.00.0000 00:00
                        #25291838

                        Тупик, не тупик, но СТО "эфир" убила. Что-нибудь новенькое наверняка появится, будет интересно, наука ведь не религия.


                  1. wataru
                    00.00.0000 00:00
                    #25265540
                    +1

                    А в реальном мире вообще есть эти окружности-то?


                    1. Andy_U
                      00.00.0000 00:00
                      #25265654

                      2 колышка, веревка и ровный участок, вот и окружность.


                      1. wataru
                        00.00.0000 00:00
                        #25266342
                        +1

                        Нет. Это лишь приближение к математическому объекту "окружность" будет. Знаете этот популярный факт, что всего 40 знаков после запятой хватит, чтобы вычислить длину окружности всей наблюдаемой вселенной с точностью до планковской длины? А вот колышками у вас там будут: дрожание руки, неровность "ровного участка", разное растяжение веревки (доли процента, но оно есть), отклонения колышка от вертикальной оси… Так что окружность вы так точно не получите. И даже циркулем на бумаге тоже, хоть там и поточнее будет.


                      1. Andy_U
                        00.00.0000 00:00
                        #25266408

                        Согласен, а теперь придумайте физический экперимент, приводящий доказательству, что i^2==-1.


                      1. thevlad
                        00.00.0000 00:00
                        #25266430
                        +1

                        Алё, математика она не про физическую реальность, это наука которая создает абстракции и ими оперирует. По большому счёту это просто игра в абстракции(или головоломки) основанная на мат. логики. По счастливой случайности(на самом деле нет), некоторые из этих абстракций имеют приложения в других науках. А отождествление математики с физической реальностью, заканчивается где-то на уровне натуральных чисел и подсчёта овец. Хотя даже с овцами не уверен, что вы когда ни буть сможете увидеть счетную бесконечность.


                      1. Andy_U
                        00.00.0000 00:00
                        #25266456
                        +1

                        Я вынужден признать, что с математической точки зрения ваша точка зрения более последовательна.

                        Только я - физик. И у меня все волосы дыбом встают, когда из применимости комплексных чисел в электротехнике, используя рассуждения типа "давайте предположим, что переменный ток, это лишь вещественная часть комплексного тока/напряжения, посчитаем, что будет на выходе, проигнорируем мнимую часть, убедимся в эксперименте, что предсказали правильно", делают утверждения о реальности комплексных чисел.

                        Про обычные числа вы правы, тоже мат.модель реальности. Не могу сформулировать, но что-ли более прямая и непосредственная. и проверяемая без мозговывертов и альтернативных вариантов. Без комлексных чисел в электротехнике можно обойтись. В физике хуже. Сталкивался с вариантами, когда интеграл аналитически без вылезания в комплексную плоскость не посчитать.


                      1. lgorSL
                        00.00.0000 00:00
                        #25270866

                        Если взять вместо электротехники оптику и эксперимент с фотоном и двумя щелями, то окажется, что складываются именно те самые комплексные волны, а не вероятности пролететь через одну или другую щель.


                      1. samsergey Автор
                        00.00.0000 00:00
                        #25266448
                        +1

                        Поверните что-нибудь два раза на 90°, вот и эксперимент ????


                      1. Andy_U
                        00.00.0000 00:00
                        #25266470

                        В 3D?


                      1. samsergey Автор
                        00.00.0000 00:00
                        #25266484

                        Если в 3D, то ещё более абстрактные кватернионы могут пригодиться.

                        Я к тому, что "умножить на i" ничуть не хуже "повернуть на 90°" Тоже абстракция.


                      1. Andy_U
                        00.00.0000 00:00
                        #25266502

                        Именно, что совсем другая абстракция. Но реальность то у нас одна?


                      1. samsergey Автор
                        00.00.0000 00:00
                        #25266516

                        И как абстрактность абстракций делает вас слабее при работе с реальностью? Используете их с умом, знаете пределы применимости, как грамотный физик и всë в порядке.


                      1. Andy_U
                        00.00.0000 00:00
                        #25266536
                        +1

                        Да, но разговор то начался с предложения использовать комплексные числа в школе для облегчения понимания тригонометрии. Да даже не в школе. Что-то я не вижу в самолетах индикаторов пространственного положения, где бы на экран выводились параметры квартернионов. На том же авиафоруме срач на тему сравнения прямой и обратной индикации не затихает много лет. Какие кватернионы?


                      1. Radisto
                        00.00.0000 00:00
                        #25266796
                        +1

                        Реальность вам недоступна. У вас есть только модель реальности (и не самая лучшая), которую строит вам ваш неокортекс. И если вы знакомы с нейрологией, то наверное знаете, что эта модель сильно неполна. Вы не видите (буквально не видите) некоторые вещи, которые есть и наоборот, видите некоторые вещи, которых нет. Что для вас реальность?


                      1. Andy_U
                        00.00.0000 00:00
                        #25266960

                        Так, сначала не меня напали математики, теперь еще и специалисты по нейрологии :) Кто еще? :)

                        А по сути, Доступна, недоступна, частично, напрочь, не важно. Но таки одна единственная. И не в каменном веке живем? Использовать приборы никто не мешает. Т.е. чем дальше, тем модель точнее. И, возвращаясь к нашим баранам, не видно ничего такого, чтобы для измерения этого нам потребовались бы комплексные числа.

                        P.S. А нейрология, это что за наука? Код специальности в ВАК есть? Или хотя бы институтская специальность?


                      1. wataru
                        00.00.0000 00:00
                        #25266708

                        Вот ни числа пи, ни мнимых чисел, ни дробей в физическом мире не существует. С некоторой натяжкой — есть только натуральные числа. Это все математические абстракции. Которые удобно ложатся на многие модели, которыми мы описываем физический мир.


                      1. vasyakolobok77
                        00.00.0000 00:00
                        #25266344

                        Окружность – это чисто идеальная модель. В реальной жизни у нас появляется гранулярность пространство. Начиная от песчинок на земле, заканчивая "атомами" и планковскими длинами.


        1. Trabant_Vishnya
          00.00.0000 00:00
          #25265482
          +2

          Подумал хорошенько - из вышмата лично мне пригодились системы уравнений и производные первого порядка.

          Другое дело, что за счет натренированности чтение НОРМАЛЬНОГО учебника по матанализу или геометрии (в моем школьном детстве образца середины 00-х это Виленкин и Атанасян) не вызывает сложности, как и воспроизводство упоминаемых там выражений в дальнейшем.

          Так что в конечном итоге это не столько заваливание, сколько тренировка умения читать FUCKING MANUALS правильно.


      1. amberovsky
        00.00.0000 00:00
        #25268958

        Вся математика - это костыль. Изучение целых / вещественных чисел начинается с ввода аксиоматики. Потому что не можем доказать.

        А уж если у нас целые числа строятся на наборе правил, в которые мы просто верим , что уж говорить про всё остальное.


        1. samsergey Автор
          00.00.0000 00:00
          #25269036
          +1

          Как-то вы неуважительно: "костыль". И далеко мы без этого костыля ушкандыбаем? А что не костыль? Опыт? Без анализа, обобщения и абстракции помрëт с экспериментатором. Интуиция? Так себе основание для научного метода.

          И про веру вы как-то непонятно сказали. Аксиомы Пеано требуют веры? Аксиомы Гильберта и определения топологии тоже? Лямбда-исчисление, может быть, на вере основано. Так вы проверьте их опытом. И, говоря про "остальное", это вы что имели в виду? Индукцию, абстракцию, логический метод, что с ними не так?


          1. charypopper
            00.00.0000 00:00
            #25269108
            +1

            конечно требуют, ведь доказательства нет, мы не понимаем и не чувствуем базы, можем жить жизнь, но не понять ее основы. Когда выдумали аксиомы, из них удобно складываются доказательства, это позволяет много инструментов сделать и жить легче\дольше, это замечательно, но это не делает их истинными или ложными. Те проблемы которые есть в математики которые Гёдель открыл - это показывают. Возможно все не так, но из-за ограниченности человек может только этим оперировать и не понимать что происходит на самом деле. Вот пример - модель геоцентрическая, в ней были сложные формулы для описания движения небесных тел, и они достоверные, потому что математики могли это описать, абстракции работают, движение становится предсказуемым, и хотя модель неверна, она давала верные результаты. Потом переделали в гелиоцентричную, и стало проще считать. Нет никакой гарантии, что завтра вместо базовых абстракций и аксиом к которым все привыкли, не будут открыты новые, которые опишут наблюдаемую жизнь проще и возможно даже достоверно


            1. samsergey Автор
              00.00.0000 00:00
              #25269198

              Ура, Гëдель в ход пошëл! Который, правда, не про всю математику неполноту доказал, а про формальные системы, содержащие в себе индуктивные построения, изоморфные арифметике Пеано. Но всë, после Гëделя мы к математике относимся только скептически и с подозрением! Не наука она, а лишь формальная стстема. То ли дело, реальность.

              Правда, во время и после Гëделя были Феликс Кляйн, Анри Пуанкаре, Давид Гильберт, Бертран Рассел, Алонзо Чëрч, Алан Тьюринг, Александр Гротендик, Герман Вейль, Андрей Колмогоров, Джон Конвей... и им неполнота по Гëделю не мешала работать и дарить нам обалденные инструменты для работы с реальностью при помощи скромных наших мозгов.


              1. ksbes
                00.00.0000 00:00
                #25280428
                +1

                Ну это потому что математека — весьма практичная наука. Правда даже многие профессиональные математики, с которыми я общался, не понимали её предмет. И в этом есть некоторая проблема.

                А предмет довольно прост — проведение и интерпритация измерений в частности (и последовательностей действий вообще). Т.е. любое число, хоть натуральное, хоть гиперкомплексное — это набор алгоритмов из множества наборов алгоритмов определённым образом связанных.
                Т.е. «7» — это и подсчёт (не результат, а сам подсчёт!) камешков поочерёдным выниманием из мешка, и овец с загибанием пальцев, и много других подобных алгоритмов у которых есть определённые свойства (в основном связанные с алгоритмом «6»), которые позволят абстрагироваться от конкретного подсчёта и обобщить. Так же как физики абстрагируются и обобщают свойства конкретного газа в конкретном объёме.

                Так что в таком рассмотрении не удивительна ни не полнота математики, ни её дальнейшее развитее. Я бы даже сказал — сложно найти более практичную вещь чем математика! Необразованный крестьянин без знаний даже правила рычага проживёт, а без умения считать запасы и площади посевов — нет.


              1. charypopper
                00.00.0000 00:00
                #25291432

                Как и любой иснтурмент математика нуждается в адекватности и скепсису. Подозрение - уместно, а серебренных пуль - нет


  1. Surrogate
    00.00.0000 00:00
    #25264632
    +3

    Жаль, что 30 лет назад в школе никто мне так наглядно и популярно не объяснял!


  1. kylikovskix
    00.00.0000 00:00
    #25265898
    -1

    Зачем "городить огород", если sin(x) = p и cos(x) = q ?


    1. SomeAnonimCoder
      00.00.0000 00:00
      #25265980
      +5

      А если tg x = 1023/1024?


      1. kylikovskix
        00.00.0000 00:00
        #25330140

        согласен )). извиняюсь за необоснованную критику.


  1. VladimirLadynev
    00.00.0000 00:00
    #25275648

    Эти ограничения можно обойти, если использовать не дробь для выражения тангенса, а пару чисел: (числитель, знаменатель). Тогда прямой угол примет безопасное "значение" (0, 1)

    Если (числитель, знаменатель), то значение прямого угла (1,0). Так?


    1. samsergey Автор
      00.00.0000 00:00
      #25275654

      У тангенса числитель -- это синус, который в обычной координатной системе задает ординату точки. То есть, точке с координатами (x, y) соответствует угол arctg(y/x).


      1. VladimirLadynev
        00.00.0000 00:00
        #25277156
        +1

        (чис, знам) = (sin(\theta), cos(\theta)) = (sin(\pi/2), cos(\pi/2) = (1, 0)

        Ведь так?


        1. samsergey Автор
          00.00.0000 00:00
          #25277262
          +1

          А ведь вы правы, неоднозначная у меня вышла фраза. Спасибо, за замечание!