W-функция Ламберта, ее приближения, и как она помогает строить доверительные интервалы / forpes.ru

Главная
W-функция Ламберта, ее приближения, и как она помогает строить доверительные интервалы

W-функция Ламберта, ее приближения, и как она помогает строить доверительные интервалы +11

07.07.2023 07:02

e1vanov 4 1600 Источник

Читателям, которые не знают, что такое W-функция Ламберта, какие у нее есть ветви и как с ее помощью можно решать различные полиномиально-экспоненциальные уравнения, предлагаю ознакомиться с первой статьей.

В этой же статье мы сначала поговорим о том, как можно приближать значения различных ветвей W-функции Ламберта, а после применим полученные результаты для решения задачи поиска кратчайших доверительных интервалов. Немного о пороге входа: читателю понадобятся базовые знания в теории вероятностей, математической статистике и, что менее банально, комплексном анализе (хотя в более-менее серьезном виде он понадобится для получения только одного выражения, которое можно принять на веру).

О приближениях W-функции Ламберта

Начнем с первого, что приходит на ум, когда говорят о приближениях - рядах Тейлора. Изучим вопрос того, как хорошо или плохо раскладывается W-функция в степенной ряд в окрестности нуля. Для этого сразу предлагается сбежать в комплексный анализ и ввести следующую функцию:

Теперь воспользуемся теоремой Лагранжа об обращении рядов. Приведем ее формулировку. Здесь не стоит пугаться того, что она дана в терминах ТФКП, просто с обращением функций и разложением их в ряд в этой науке проще, чем в действительном братце.

Теорема (Лагранжа, об обращении рядов). Пусть функция голоморфна в точке , причем $f'(z_0) \ne 0$ , тогда в некоторой окрестности точки функция, обратная к может быть представлена в виде следующего ряда:

$f^{-1}(w) = z_0+\sum_{n=1}^\infty\frac{1}{n!}\cdot\frac{d^{n-1}}{dz^{n-1}}\left(\frac{z-z_0}{f(z)-f(z_0)}\right)^n\bigg|_{z=z_0}\cdot(w-f(z_0))^n$

Посмотрим на то, как перепишется утверждение данной теоремы применительно к W-функции Ламберта:

$W_0(w) = \sum_{n=1}^\infty \frac{1}{n!}\cdot \frac{d^{n-1}}{dz^{n-1}}\left(\frac{z}{ze^{z}}\right)^n\bigg|_{z=0}\cdot w^n$

Осталось найти соответствующие коэффициенты:

$\frac{d^{n-1}}{dz^{n-1}}\left(\frac{z}{ze^{z}}\right)^n\bigg|_{z_0}=\frac{d^{n-1}}{dz^{n-1}}e^{-nz}\bigg|_{z=0}=(-n)^{n-1}$

Как итог, получаем следующую симпатичную формулу, правда, с пока неизвестной областью применимости:

$W_0(z) = \sum_{n=1}^\infty\frac{(-n)^{n-1}}{n!}z^n$

Найдем радиус сходимости этого степенного ряда с помощью теоремы Коши-Адамара и формулы Стирлинга:

$R^{-1}=\lim_{n\to\infty}\sqrt[n]{\left|\frac{(-n)^{n-1}}{n!}\right|}=\lim_{n\to\infty}\sqrt[n]{\frac{n^n}{n!}}=\exp\left\{\lim_{n\to\infty}\frac{n\ln n - \ln n!}{n}\right\}=\\ =\exp\left\{\lim_{n\to\infty}\frac{n\ln n - \ln[\sqrt{2\pi n}\cdot n^n \cdot e^{-n}\cdot (1+o(1))]}{n}\right\}=\\=\exp\left\{\lim_{n\to\infty}\frac{n\ln n - \frac{1}{2}\ln(2\pi n) - n\ln n+n+\ln(1+o(1))}{n}\right\}=e$

Итак, полученный степенной ряд сходится в открытом круге $\{|z| < e^{-1}\}$ .

О приближении степенным рядом. На графике - сумма первых 7 членов

Далее обсудим то, как можно использовать схожесть графика функции в окрестности точки с параболой. Для этого воспользуемся теоремой Тейлора с остаточным членом в форме Пеано с центром в точке -1:

$xe^x = xe^x\bigg|_{x=-1}+\frac{d}{dx}(xe^x)\bigg|_{x=-1} (x+1) + \frac{d^2}{dx^2}(xe^x)\bigg|_{x=-1}\frac{(x+1)^2}{2}+o((x+1)^2)$ $xe^x = -\frac{1}{e}+\frac{(x+1)^2}{2e}+o((x+1)^2)$

Теперь так как нас интересуют обратные функции отражаем картинку относительно и получаем следующие предельные равенства:

$\lim_{x\to -e^{-1}}\left[W_0(x)-\left(\sqrt{2(ex+1)}-1\right)\right]=0\\ \lim_{x\to -e^{-1}}\left[W_{-1}(x)-\left(-\sqrt{2(ex+1)}-1\right)\right]=0$

Полученные приближения хороши при "не сильно больших" $e^{-1}$ . Казалось бы, зачем они нам при наличии сходящегося ряда, однако ближе к граничным точкам интервала $|x|<e^{-1}$ этот ряд сходится медленно и даже если взять 10 первых слагаемых, то около $-e^{-1}$ приближение будет хуже, чем при описанном выше методе, который к тому же оказывается полезным при оценке значений "минус первой" ветви.

Замечание. Можно раскладывать в Тейлора до члена третьей степени и дальше решать кубическое уравнение и получать лучшую аппроксимацию, но мы не будем этого делать, чтобы не устраивать радикальное безумие имени Кардано.

Теперь же мы приступаем к самой интересной с математической точки зрения части статьи. Если Вам не интересен комплексный анализ или не хочется вникать в математические выкладки (хотя дальше таковых будет не очень много), то сразу переходите на абзац с полученным результатом.

Итак, введем следующую функцию: $f(z)=e^{-z}-1-\sigma z+\tau$ . Она целая (то есть голоморфна во всей комплексной плоскости) и зависит от двух комплексных параметров $\sigma$ и $\tau$ .

Утверждение 1. Существует такое число , что при $|\sigma| < a, \: |\tau| < a$ функция имеет в точности один нуль внутри открытого круга $\{|z| < \pi\}$ .

Доказательство. Пусть $\delta := \min|e^{-z}-1|$ на окружности $|z|=\pi$ . Заметим, что $\delta>0$ в силу того, что $|e^{-z}-1|$ - это строго положительная непрерывная на компакте $\{|z|=\pi\}$ функция. Внутри этого круга ее единственный ноль -. Теперь явно укажем значение и покажем, что оно действительно подходит:

$a=\frac{\delta}{2(\pi+1)}$

Далее нам понадобится теорема Руше, сформулируем ее.

Теорема (Руше). Пусть $D\subset\mathbb C$ - ограниченная область с кусочно-гладкой границей $\partial D$ , функции голоморфны в области , компактно содержащей и всюду на $\partial D$ верно, что , тогда в области количество нулей с учетом кратности функции совпадает с количеством нулей с учетом кратности функции .

Звучит страшновато, но смысл простой: если на границе области одна из функций по модулю строго меньше другой, то и внутри области ее прибавление не оказывает достаточного влияния на другую функцию в смысле изменения количества нулей.

Вернемся к доказательству, которое по указанной выше теореме завершается следующей цепочкой неравенств:

$|-\sigma z+\tau|\le|\sigma||z| + |\tau|<\frac{\delta}{2}<|e^{-z}-1|$

Утверждение 2. Пусть - единственный корень в круге $\{|z|<\pi\}$ . Тогда верно следующее равенство:

$u = \frac{1}{2\pi i}\int_{|z|=\pi}\frac{-e^{-\xi}-\sigma}{e^{-\xi}-1-\sigma\xi+\tau}\xi d\xi$

Доказательство. Учитывая единственность особенности подыинтегральной функции, по теореме Коши о вычетах достаточно показать, что

$\mathop{\mathrm{res}}_{u}\frac{zf'(z)}{f(z)}=u$

Для этого рассмотрим предел, который равен "минус первому" члену в ряде Лорана. Преобразуем его, используя, что .

$\lim_{z\to u}\frac{zf'(z)}{f(z)}\cdot(z-u)=\lim_{z\to u}\frac{zf'(z)}{\frac{f(z) - f(u)}{z-u}}=u$

На этом доказательство утверждения завершено.

Сделаем следующий шаг: разложим знаменатель в ряд Тейлора, который в силу утверждения 1 будет абсолютно сходящимся (это позволяет не просто утверждать, что такое представление справедливо, но еще и менять порядок суммирования).

$\frac{1}{e^{-\xi}-1-\sigma\xi+\tau} = \frac{1}{e^{-\xi}-1}\cdot\frac{1}{1 - \left(\frac{\sigma\xi}{e^{-\xi}-1}-\frac{\tau}{e^{-\xi}-1}\right)}=\\=\frac{1}{e^{-\xi}-1}\sum_{n=0}^\infty \left(\frac{\sigma\xi-\tau}{e^{-\xi}-1}\right)^n=\sum_{n=0}^\infty(e^{-\xi}-1)^{-n-1}\sum_{k=0}^nC_n^k\sigma^k\xi^k(-\tau)^{n-k}$

Меняем порядок суммирования с "зеленых" направлений на "синие" (см. рисунок)

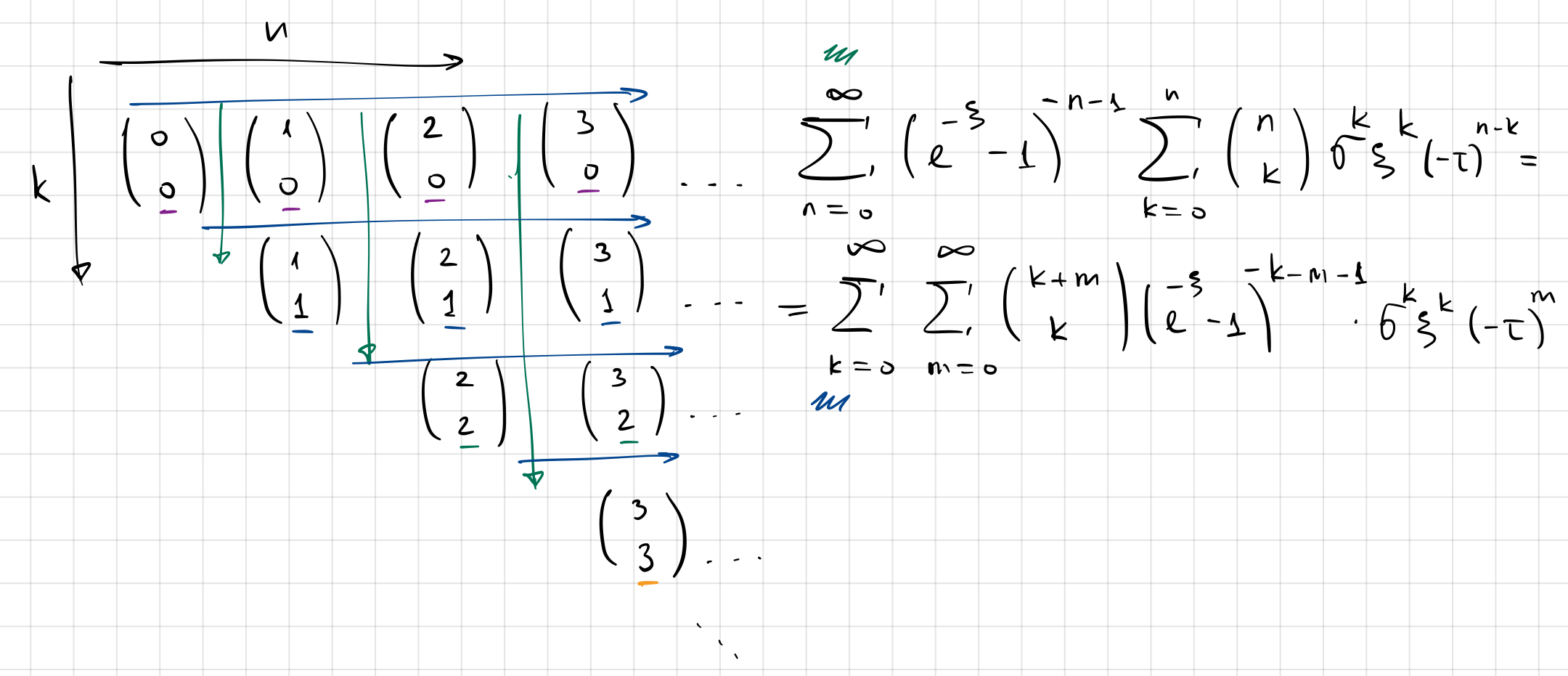
Полученное в виде двойного ряда представление подставляем в изначальное интегральное равенство из утверждения 2 и меняем порядок операций.

$u=\sum_{k=0}^\infty\sum_{m=0}^\infty C_{k+m}^k\sigma^k(-\tau)^m\frac{1}{2\pi i}\int_{|z|=\pi}(e^{-\xi}-1)^{-k-m-1}(-e^{-\xi}-\sigma)\xi^{k+1} d\xi$

Заметим, что если (иными словами, соответствующий моном не содержит $\tau$ ), то подыинтегральная функция не имеет особенностей: порядок нуля знаменателя и порядок нуля числителя совпадают и равны , а значит по интегральной теореме Коши соответствующий коэффициент равен 0. Как итог имеем следующее равенство, в котором $c_{km}$ - не зависящие от $\sigma$ и $\tau$ коэффициенты.

$u=\sum_{k=0}^\infty\sum_{m=1}^\infty c_{km} \sigma^k\tau^m$

Можно найти явный вид этих коэффициентов, они выражаются через числа Стирлинга первого рода, однако доказательство этого факта проводить не будем.

Пока что это были отвлеченные от W-функции Ламберта рассуждения, но зато теперь мы готовы их с ней связать. Сделаем в основном Ламбертовом тождестве замену (берем основную ветвь комплексного логарифма): $W(z) = \ln z-\ln\ln z + u(z)$ . Наводящие на именно такое преобразование соображения приведены в [1] вместе с англоязычным доказательством.

$W(z)e^{W(z)}=z\\ \frac{(\ln z-\ln\ln z + u) ze^u}{\ln z} =z$

Сокращаем на и приходим к следующему равенству:

$1-\frac{\ln\ln z}{\ln z}+\frac{u}{\ln z}=e^{-u}$

Очень похоже на ту функцию, с которой мы начали разложение, правда? Если теперь сделать замену, то мы получим ее в явном виде:

$\sigma = \frac{1}{\ln z}, \: \tau=\frac{\ln\ln z}{\ln z}$

Для доказательства прекрасной формулы осталось заметить, что при достаточно больших и, наоборот, достаточно малых по модулю соответствующие значения $\sigma$ и $\tau$ "зайдут" в границы, описанные в утверждении 1, а значит будет справедливо представление в виде двойного ряда, которое в терминах W-функции Ламберта перепишется следующим образом:

$W_0(z) = \ln z - \ln\ln z + \sum_{k=0}^\infty\sum_{m=1}^\infty c_{km}\frac{(\ln\ln z)^m}{(\ln z)^{k+m}}$

Кроме того, аналогичное представление верно и для "минус первой" ветви, только взять нужно $\ln(-z)$ и $\ln(-\ln(-z))$ соответственно.

Замечание. На самом деле таким методом можно получить представление для любой ветви W-функции Ламберта (просто нас интересуют только "нулевая" и "минус первая"), нужно лишь брать другую ветвь внутреннего логарифма.

Снова вернемся в действительный мир и распишем несколько первых членов (в смысле степени знаменателя) ряда:

$W_{-1}(x)=\ln(-x)-\ln(-\ln(-x))+\frac{\ln(-\ln(-x))}{\ln(-x)} +\\+ \frac{\ln(-\ln(-x))(-2+\ln(-\ln(-x)))}{2\ln^2(-x)}+O\left(\frac{\ln(-\ln(-x))}{\ln(-x)}\right)^3$

О приближении двойным рядом и логарифмов

Подведем промежуточные итоги. Что мы умеем?

приближать "нулевую" ветвь около 0
приближать "нулевую" и "минус первую" ветвь около $-e^{-1}$
приближать "минус первую" ветвь всюду

Теперь перейдем к применению полученных результатов.

Немного сведений из теории вероятностей

Раз мы заглянули в комплексный анализ, то нечего нам уже останавливаться и будем пользоваться удобным аппаратом характеристических функций.

Определение. Характеристической функцией случайной величины $\xi$ называется функция $\varphi_\xi:\mathbb R\to\mathbb C$ , определяемая следующий выражением:

$\varphi_\xi(t)=\mathsf E\left[\exp\{it\xi\}\right]=\int_{\mathbb \Omega} \exp\{it\omega\}\mathsf P(d\omega)$

Основная прелесть характеристических функций заключается в следующей теореме:

Теорема (Леви, о непрерывности). Пусть $\{\xi_n\}_{n=1}^\infty$ - последовательность случайных величин, тогда:

если $\xi_n\to \xi$ по распределению при $n\to\infty$ , то поточечно $\varphi_{\xi_n}\to\varphi_{\xi}$
если $\varphi_{\xi_n}\to\varphi$ поточечно, причем $\varphi$ непрерывна в нуле, то существует случайная величина $\xi$ такая, что $\varphi_\xi\equiv \varphi$ и $\xi_n\to \xi$ по распределению при $n\to\infty$

С помощью этого прекрасного результата можно доказать, например, закон больших чисел в форме Хинчина или центральную предельную теорему, нам же он понадобится для определения вида распределения функций от случайных величин, имеющих гамма-распределение.

Определение. Говорят, что случайная величина $\xi$ имеет гамма-распределение с параметром масштаба $\theta > 0$ и параметром формы , если ее плотность вероятности имеет следующий вид:

$p_{\xi}(x) = \mathbb I\{x>0\}\frac{\theta^{k}}{\Gamma(k)}x^{k-1}e^{-\theta x}$

Обозначение: $\xi\sim\Gamma(\theta, k)$

Замечание. Как в википедии, так и в нескольких математических пакетах используется определение, получающееся из приведенного выше заменой $\theta\mapsto\theta^{-1}$ , однако автор считает идейно правильным умножать на параметр масштаба, а не делить, хотя это вопроса вкуса и простоты выкладок в конкретной задаче.

Гамма-распределение прекрасно тем, что многие другие распределения являются его частными случаями, например, экспоненциальное распределение с параметром $\lambda$ это $\Gamma(\lambda, 1)$ .

Характеристическая функция случайной величины $\xi\sim\Gamma(\theta, k)$ имеет вид:

$\varphi_{\xi}(t)=\left(1-\frac{it}{\theta}\right)^{-k}$

Вывод этого факта оставляем читателю в качестве упражнения. Теперь мы можем сказать, например, как распределена случайная величина $\eta:=\theta\xi$ :

$\varphi_\eta(t)=\mathsf E[\exp\{it\eta\}]=\mathsf E[\exp\{it\theta\xi\}]=\varphi_{\xi}(\theta t) = (1-it)^{-k}\Rightarrow \eta\sim\Gamma(1,k)$

Утверждение 3. Пусть $\xi_1,\dots\xi_n$ - независимые одинаково распределенные случайные величины, причем $\xi_i\sim\Gamma(\theta,k)$ , тогда случайная величина $\theta\sum\xi_i\sim \Gamma(1, nk)$ .

Доказательство. Воспользуемся одним из свойств характеристических функций. Оно звучит так: характеристическая функция суммы независимых случайных величин равна произведению их характеристических функций. Это почти очевидное следствие свойств математических ожиданий и показательной функции.

$\varphi_{\xi_1+\dots+\xi_n}(t) = \prod_{i=1}^n\varphi_{\xi_i}(t)=\varphi_{\xi_1}^n(t) = \left(1-\frac{it}{\theta}\right)^{-nk}\Rightarrow\sum_{i=1}^n\xi_i\sim\Gamma(\theta, nk)$

Осталось заметить, что о распределении умноженной на число случайной величины мы уже говорили.

О построении кратчайших доверительных интервалов

Для начала освежим в памяти понятие доверительного интервала. Пусть выборка $\mathbb X=(X_1,\dots,X_n)$ состоит из независимых одинаково распределенных случайных величин , а множество распределений $\{\mathsf P_\theta\}$ параметризовано с помощью $\Theta\subset\mathbb R$ .

Определение. Интервал $[L(\mathbb X), R(\mathbb X)]$ называется доверительным интервалом с уровнем доверия $\gamma$ , если для любого $\theta\in\Theta$ вероятность того, что он накроет неизвестный параметр, равна $\gamma$ :

$\mathsf P_\theta\{L(\mathbb X)\le\theta\le R(\mathbb X)\} = \gamma$

Постановка задачи. Пусть $X_1,\dots,X_n\sim \Gamma(\theta, k)$ и дополнительно . Нужно построить кратчайший доверительный интервал для параметра $\theta$ .

Решение. Сначала разберемся с тем, что доверительный интервал должен быть кратчайшим, то есть нужно решить следующую оптимизационную задачу (здесь - плотность распределения случайной величины, как-то слепленной из выборки, пока это не важно, нужно уточнить другой момент):

$\int_{l}^rp(x)dx = \gamma, \: r -l \to \min$

Будем решать ее методом множителей Лагранжа, составим функционал и будем его безусловно минимизировать:

$\mathcal L(r, l, \lambda) = r-l-\lambda\left[\int_{l}^rp(x)dx-\gamma\right]$

Необходимое условие экстремума запишется следующим образом:

$\frac{\partial \mathcal L}{\partial r} = 1 - \lambda \cdot p(r)=0, \frac{\partial\mathcal L}{\partial l} = -1 + \lambda \cdot p(l)=0\Rightarrow p(r)=p(l)$

То есть если минимум достигается, то значения плотности в концах доверительного интервала должны быть равны. Запомним это.

Решать поставленную задачу будем с помощью метода центральной случайной величины: для этого нужно найти такую случайную величину $G(\mathbb X, \theta)$ , распределение которой не зависит от параметра $\theta$ , тогда можно, используя, например, квантили этого распределения и монотонную зависимость от параметра, перейти от интервала для центральной случайной величины к интервалу для параметра. В нашей задаче в качестве центральной случайной величины будем использовать (вид распределения следует из утверждения 3):

$G(\mathbb X, \theta) = \theta\sum_{i=1}^nX_i\sim\Gamma(1, nk)\Rightarrow p_G(x) = \frac{x^{m-1}e^{-x}}{\Gamma(m)}$

Тогда верны следующие равенства:

$\mathsf P_\theta\{l\le G\le r\}= \mathsf P_\theta\{l\le \theta\sum X_i\le r\} = \mathsf P_\theta\{\frac{l}{\sum X_i}\le \theta\le \frac{r}{\sum X_i}\}$

Вспоминаем рассуждения в задаче минимизации и получаем переформулированную постановку: нужно найти такой уровень , что если - упорядоченные решения уравнения , то

$\int_{l}^rp_G(x)dx = \gamma$

Делать это можно, например, с помощью бинарного поиска с заданной точностью, начиная из и .

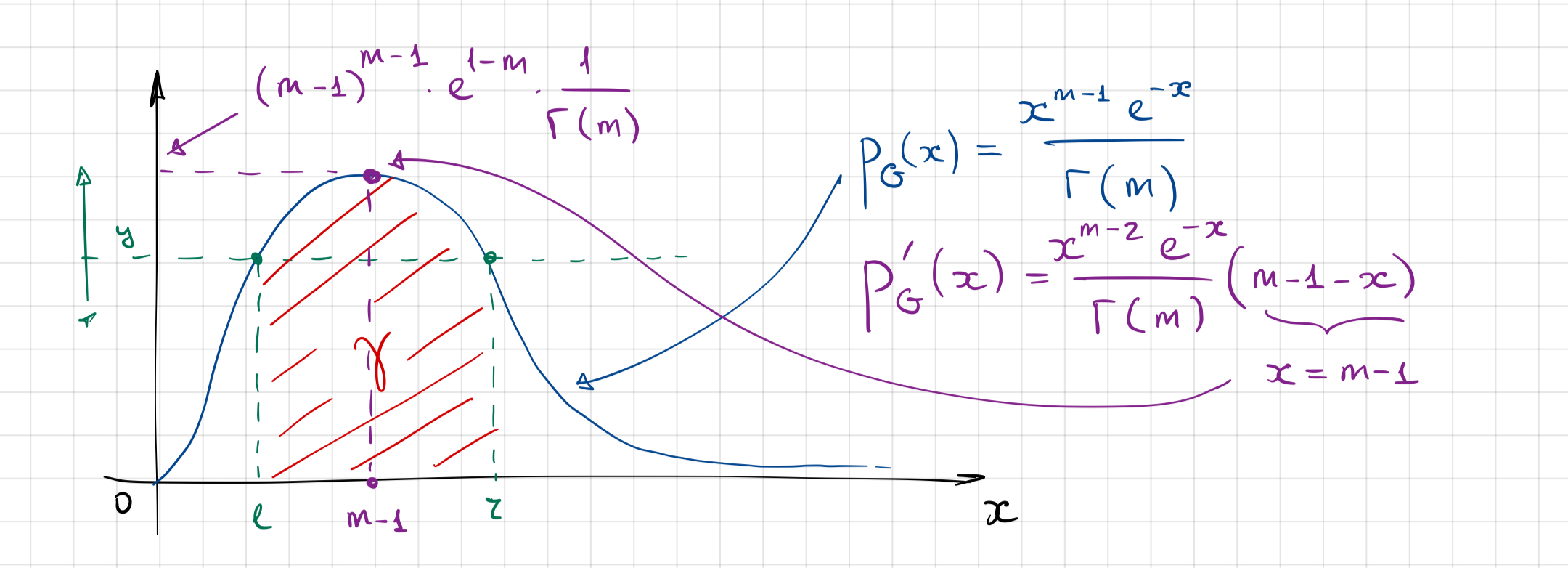
Замечание. Дополнительное условие на величину было поставлено, чтобы плотность имела именно такой вид, как на рисунке, или, строго говоря, не имела особенностей в нуле.

Для начала научимся по заданному уровню определять значения точек и . Грубо говоря, о решении подобных уравнений и была первая статья, поэтому сейчас без пояснений и лишних выкладок сразу выписываем решение:

$l,r=(1-m)\cdot W_{0,-1}\underbrace{\left(\frac{\sqrt[m-1]{y\cdot\Gamma(m)}}{1-m}\right)}_{\alpha}$

Обратим внимание на то, что $-e^{-1}<\alpha<0$ , поэтому при реализации алгоритма мы можем пользоваться приближениями, полученными в первой части статьи.

Теперь у нас есть два варианта, как считать определенный интеграл:

Пользоваться численными методами (прямоугольников, трапеций, парабол) и получать погрешность, во-первых, из-за границ интегрирования, во-вторых, из-за самих численных методов.
Предположить, что $nk\in\mathbb N$ , явно выписать первообразную и вычислить нужную величину по формуле Ньютона-Лейбница. Тогда погрешность будет накапливаться из-за возведения значений границ интегрирования в степени.

С первым методом все понятно, рассмотрим подробнее второй.

Утверждение 4. $\int\frac{ x^{m}e^{-x}}{m!}dx=- e^{-x}\sum_{j=0}^m\frac{x^j}{j!} + C$

Доказательство. Оставляем читателю в качестве упражнения по методу математической индукции и интегрированию по частям.

Вычисляем определенный интеграл:

$\frac{1}{\Gamma(m)}\int_{l}^rx^{m-1}e^{-x}dx=\frac{1}{\Gamma(m)}\sum_{j=0}^{m-1}\frac{(m-1)!}{j!}x^j e^{-x}\bigg|_{r}^l=\\=e^{(m-1)W_0(\alpha)}\sum_{j=0}^{m-1}\frac{(1-m)^jW_0^j(\alpha)}{j!}-e^{(m-1)W_{-1}(\alpha)}\sum_{j=0}^{m-1}\frac{(1-m)^jW_{-1}^j(\alpha)}{j!}$

Далее пользуемся основным Ламбертовым тождеством:

$W(z)e^{W(z)} = z\Rightarrow e^{W(z)}=\frac{z}{W(z)}$ $\frac{1}{\Gamma(m)}\int_{l}^rx^{m-1}e^{-x}dx = \alpha^{m-1}\sum_{j=0}^{m-1}\frac{(-1)^j(m-1)^j[W_0^{j-m+1}(\alpha)-W_{-1}^{j-m+1}(\alpha)]}{j!}$

Делая замену , получаем чуть более простой вид:

$\frac{1}{\Gamma(s+1)}\int_{l}^rx^{s}e^{-x}dx = \alpha^s\sum_{j=0}^s\frac{(-s)^j[W_0^{j-s}(\alpha) - W_{-1}^{j-s}(\alpha)]}{j!}$

Заметим, что множитель перед суммой симпатично выглядит, если раскрыть его по определению:

$\alpha^s=\left[\frac{\sqrt[s]{y\cdot\Gamma(s+1)}}{-s}\right]^s=\frac{y\cdot\Gamma(s+1)}{(-s)^s}$

Подставляем и делаем замену индекса суммирования:

$\frac{1}{\Gamma(s+1)}\int_{l}^rx^{s}e^{-x}dx =y\cdot\Gamma(s+1)\sum_{k=0}^s\frac{(-s)^{-j}[W_0^{-j}(\alpha) - W_{-1}^{-j}(\alpha)]}{(s-j)!}$

Перед изучением результатов тестирования программы на языке Python докажем небольшой результат о состоятельности данного метода. Состоятельность здесь понимается в смысле улучшения качества работы при увеличении размера выборки (для доверительного интервала мерой качества, очевидно, является его длина).

Теорема. Пусть - четное число, - интервал для $\theta\sum X_i$ , найденный описанным выше методом, тогда для любого $\theta>0, \:\varepsilon>0$

$\mathsf P_{\theta}\left\{\frac{r - l}{\sum X_i}\ge \varepsilon\right\}\to 0, \: n\to\infty$

Доказательство. Опишем его идейно, без лишних выкладок. Во-первых, введем случайную величину $Y = \sum X_i\sim\Gamma(\theta, s+1)$ . Во-вторых, вспоминаем, что наш доверительный интервал - кратчайший, а значит, что достаточно доказать утверждение теоремы для любого другого интервала. Мы будем использовать $[z_{\frac{1-\gamma}{2}}(\theta, s), z_{\frac{1+\gamma}{2}}(\theta, s)]$ , где $z_{\dots}(\dots)$ - это квантили $\Gamma(\theta, s+1)$ порядка нижнего индекса. Проводим равносильные преобразования:

$\mathsf P\left\{\varepsilon Y\le z_{\frac{1+\gamma}{2}}-z_{\frac{1-\gamma}{2}}\right\}\to0,\: n\to\infty$

В [2] можно найти асимптотическую формулу для квантилей, которая справедлива в условиях теоремы. Применяем ее и получаем, что разность в правой части неравенства есть $O(\sqrt s)$ , что в свою очередь позволяет расписать эту вероятность по определению и оценить сверху сходящейся к 0 последовательностью.

Итак, перейдем к результатам тестирования. Метод с явным вычислением первообразной хорош в тех случаях, когда - невелико, в противном случае его начинает по понятным причинам штормить вплоть до удивительных явлений в виде вероятности, большей единицы. Далее приводятся результаты экспериментов для метода, в котором при подсчете интеграла использовались численные методы, а именно функция $\texttt{scipy.integrate.quad}$ . Всюду в экспериментах проводилось 2000 запусков, уровень доверия $\gamma=0.95$ .

$\theta$		Раз-р выборки,	Ср. длина инт-ла
0.5	0.1	50	1.03
		100	0.67
		200	0.47
1	0.2	50	1.34
		100	0.92
		200	0.65
2	0.5	50	1.64
		100	1.15
		200	0.8
3	0.75	50	2.0
		100	1.39
		150	1.13
0.25	1	25	0.21
		50	0.14
		100	0.1

Литература

Corless, R.M., Gonnet, G.H., Hare, D.E.G. et al. On the LambertW function. Adv Comput Math 5, 329–359 (1996)
В. И. Пагурова, “О вычислении квантилей Γ-распределения”, Теория вероятн. и ее примен., 10:4 (1965), 746–749; Theory Probab. Appl., 10:4 (1965), 677–680

Комментарии (4)

Tyusha
07.07.2023 08:30
#25726826
+2
Большое спасибо. Понимаю, что Хабр не совсем об этом, но подобные статьи — именно то, что я жду, и всегда радуюсь. Такие материалы расширяют кругозор и дают знания, которые полезны, но по разным причинам до сих пор проходили мимо.

domix32
07.07.2023 08:30
#25727072
Пусть функция голоморфна в точке ,

из вики

Функция является голоморфной в области когда комплексно дифференцируема в каждой точке $z\in A$ .

То есть я правильно понимаю, что мы областью в данном случае выбираем ровно одну точку от которой и генерируем наш ряд?
1. e1vanov Автор
  07.07.2023 08:30
  #25727148
  +2
  Под голоморфностью в точке подразумевается голоморфность в малой окрестности этой точки (возможно, мне стоило это указать). В качестве области взять точку не получится, потому что область по определению должна быть открытым множеством, а множество из одной точки замкнуто.
  1. domix32
    07.07.2023 08:30
    #25727968
    Было бы неплохо. Заодно и в вики поправить, т.к. в теореме Лагранжа там тоже голоморфность в точке указана. Без подходящего бэкраунда не самое очевидное утверждение.