Привет! Меня зовут Глеб Рыжаков, я научный сотрудник Сколтеха. Я занимаюсь математикой, а точнее, линейной алгеброй, и её приложениями к практическим задачам. Сегодня я расскажу вам о нашем исследовании, которое может помочь справиться с проблемой проклятия размерности, которая возникает во множестве статистических задач, включая машинное обучение.

Понятие «проклятие размерности» появилось в середине прошлого века в пионерской работе Ричарда Беллмана, посвященной методам решения сложных задач путём разбиения их на более простые подзадачи. Сегодня оно понимается в более общем смысле, а именно как экспоненциальный — O(n^d) — рост количества необходимых данных и, как следствие, количества памяти, необходимой для их хранения, с ростом размерности пространства d. Когда задачу можно свести к работе с многомерными массивами в общем случае комплексных чисел, удобно говорить о d-мерных тензорах и использовать достижения мультилинейной алгебры. Хорошая новость заключается в том, что там существует такая процедура, как тензорное разложение, которое в ряде случаев может помочь преодолеть проклятие размерности.

Разложение матриц

Прежде, чем говорить о разложении тензоров, взглянем на то, как это делается с матрицами — просто двумерными таблицами. Под разложением матрицы понимается её представление в виде произведения других матриц, обладающих более простыми или симметричными свойствами. Такую задачу, например, непрерывно решают процессоры в наших мобильных телефонах.

Среди прочего важно уметь производить ранговую факторизацию матриц. Представьте, что у вас есть матрица m×n ранга r (назовем ее A). Тогда ранговой факторизацией будет называться нахождение матриц U и V размерами m×r и r×n, произведение которых даст A. В реальности ранги матриц r могут не обязательно быть малыми. В этом случае может помочь малоранговая аппроксимация, которая заключается в ранговой факторизации в некотором приближении. С такой задачей лучше всего справляется сингулярное разложение, для которого есть множество эффективных численных реализаций. В индексном виде его результат можно записать как

где матрица Σ является диагональной, т.е. вне основной диагонали у неё находятся нули. Объединяя матрицу Σ с одной из матриц U или V, получаем малоранговое разложение. В идеальном случае ранг r много меньше, чем m и n.

Но что будет, если вместо A_i,j мы будем иметь дело с A_i,j,k или большим числом индексов, словом, с тензорами? Здесь уже требуются методы тензорного разложения, которые исследованы не так хорошо, как в случае матриц.

Методы тензорного разложения

Одним из самых первых способов делать это стало каноническое разложение. Оно появилось как обобщение ранговой факторизации для матриц, где количество матриц в произведении равно числу размерности тензора:

Несмотря на свою распространённость в том или ином виде, каноническое разложение сталкивается с трудностями при больших рангах. Задача сама по себе NP-сложная, и для неё нет быстрых и универсальных алгоритмов.

Этих проблем нет в разложении Таккера. В нём у матриц индексы суммирования не общие, а связанные некоторым склеивающим множителем. Разложение Таккера всегда устойчиво, но для его исполнения требуется много места для многомерного множителя, что делает обход проклятия размерности с его помощью практически бесполезным. Вот так оно выглядит:

Еще один способ — лепить большие двумерные матрицы из наших тензоров. Для этого одну часть индексов объявляем строчными, а другу — столбцовыми индексами нашей мегаматрицы. В результате сингулярное разложение обеспечивает нас меньшими матрицами, приобретающими дополнительный индекс, к которым можно снова применить эту процедуру:

где

Этот рекурсивный подход давал некоторое преимущество в скорости, но его довольно сложно программировать и он требователен к вычислительным ресурсам.

Тензорный поезд

Вместо этого Иван Оселедец, работающий ныне в Сколтехе и AIRI, более десяти лет назад предложил самый простой вид этой структуры, который получил название тензорного поезда (tensor train, TT). В этом разложении суммирование ведется по попарно общим индексам соседних трехмерных тензоров, стоящих в произведении (TT-ядер). Лучше слов эту идею проиллюстрирует формула для некоторого тензора K

Оказалось, что такой подход позволяет добиться O(ndr²), где r — это средний ранг ядер, что для целого ряда задач позволяет преодолеть проклятие размерности. Потом, как это часто бывает, выяснилось, что он не первый, кто придумал подобное. В квантовой физике подобные конструкции носят название состояния матричного произведения (matrix product states) и используются для описания квантовых тензорных сетей. Но хорошую вещь надо открыть как минимум дважды — иначе не очень понятно, хорошая ли она.

TT-разложение оказалось очень плодотворной идеей, особенно в машинном обучении. Например, вот в этой работе тензорные поезда используются для решения многомерных параболических уравнений в частных производных с d порядка сотни. Это побудило нас и наших коллег искать оптимальные способы вычисления ядер. Было сделано несколько таких попыток, среди которых крестовая TT-аппроксимация, чередующийся метод наименьших квадратов или чередующиеся линейные схемы. Все эти подходы объединяет одна деталь: они игнорируют возможную аналитическую связь между компонентами тензора и их индексами. Из-за этого существующие методы имеют большое время работы и плохую сходимость, даже если точное решение известно.

Учёт аналитических зависимостей

Чтобы задействовать этот ресурс мы с Иваном Оселедцем в своей недавней статье предложили новый метод построения ядер ТТ-разложения, который учитывает аналитическую зависимость компонент тензора от индексов (под аналитической зависимостью мы понимаем известную символьную формулу значения тензора, а не определение термина в рамках комплексного анализа). Технически это реализовано через цепочку функций, которые получили название производящих. Каждая из них зависит от индекса тензора, а также от результата применения другой функции на предыдущем шаге.

В общем случае процесс построения ТТ-разложения можно представить как последовательное преобразование (линейное) вектора в каждом «вагоне», начиная с конца поезда. Функции же могут не обязательно быть линейными. Решение этой проблемы оказалось довольно простым: мы присваиваем каждому возможному входному и выходному значению производящей функции различные базисные векторы, благодаря чему нужное нам преобразование может быть представлено как умножение матрицы на вектор.

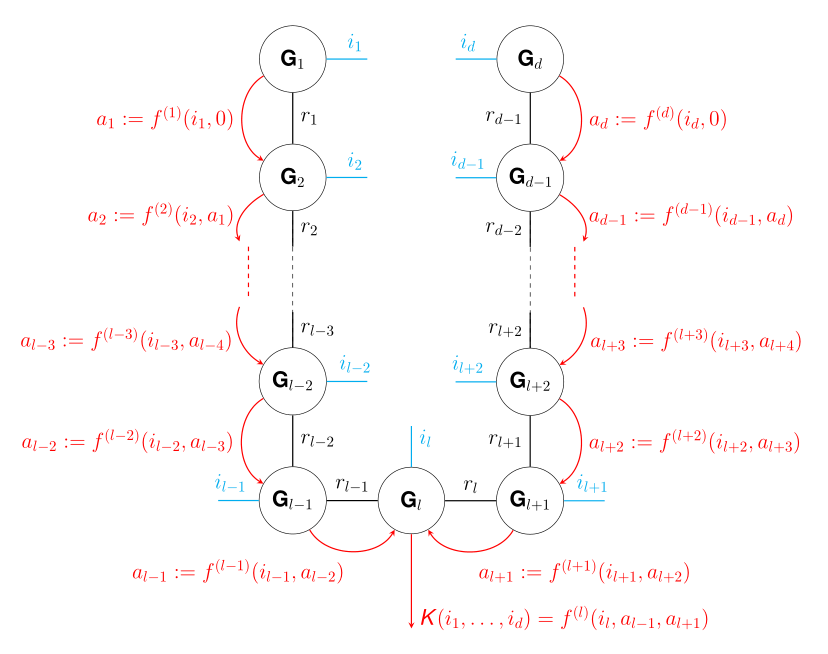
На рисунке выше схематически изображен процесс ТТ-разложения некоторого тензора K, каждый элемент которого вычисляется с помощью движения по поезду с двух сторон: слева и справа. Ядра разложения обозначаются чёрными кружочками, входные индексы тензоров — синими линиями. Чёрные линии, соединяющие ядра, снабжены числом, равным размерности суммирования. Наконец, красными стрелками показано соответствие между выходным вектором, полученным последовательным перемножением ядер (слева и справа) и значениями производящих функций.

К сожалению, не существует единого алгоритмического подхода для построения последовательности производящих функций по заданной аналитической зависимости значения тензора от его индексов. Более того, такое представление не единственно, и разные представления могут привести к разным рангам результирующего тензора. Однако оказывается, что существуют достаточно общие закономерности для производящих функций, и мы надеемся, что на основе приводимых нами примеров будет несложно строить нужные последовательности по аналогии.

Проверка на практике

Предложенный нами подход работает лучше всего в тех случаях, когда производящие функции вместе с самим тензором имеют небольшое количество возможных значений. При этом ТТ-ядра, полученные новым методом, сильно разрежены, т.е. в них много нулевых элементов, что дает дополнительный выигрыш в производительности.

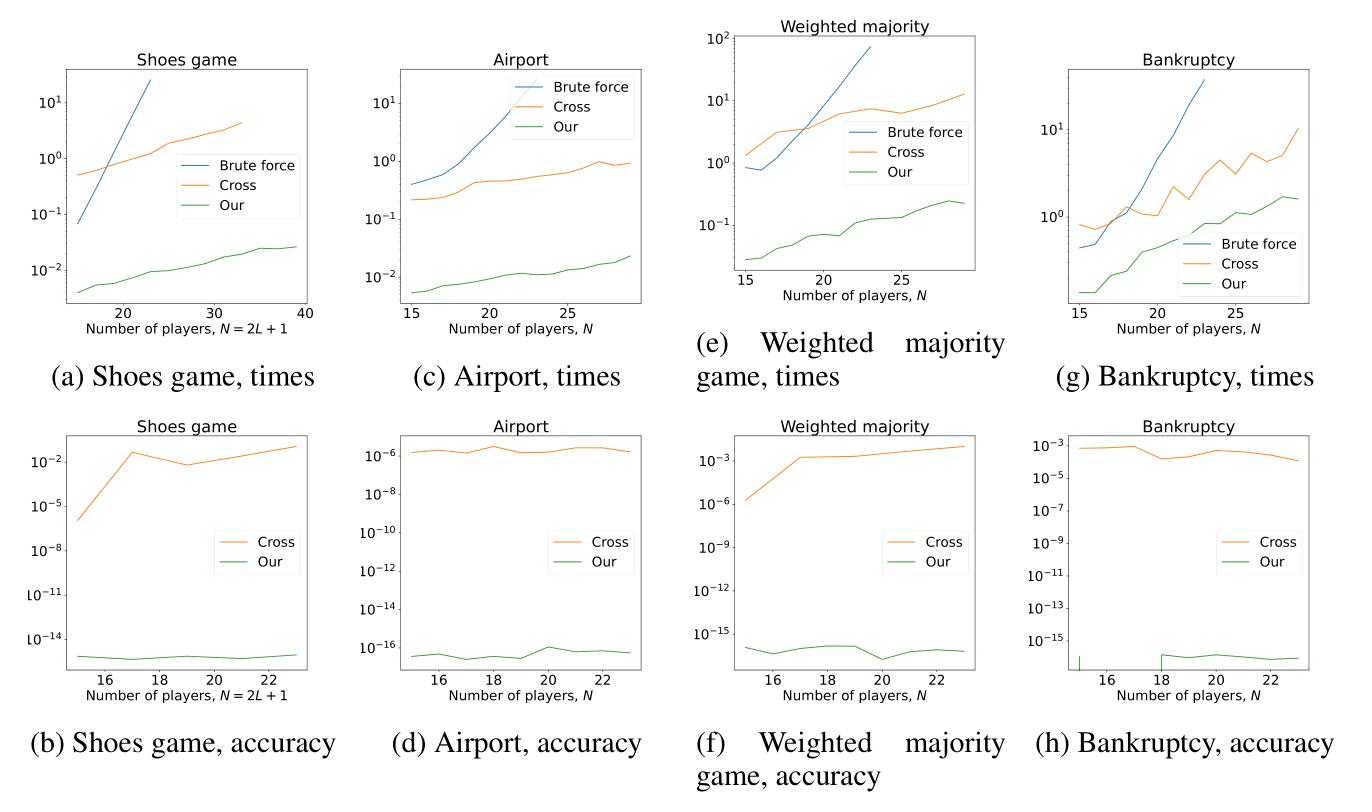
Мы убедились в этом, применив алгоритм к ряду задач, включающему в себя кооперативные игры, задачу о рюкзаке, задачу о расстановке n ферзей, вычисления перманента матрицы и многое другое. Так, в кооперативных играх новый подход показал превосходство, как по времени выполнения, так и по точности по сравнению с существующими методами. В случае же с вычислением перманента оценочное число операций оказалось всего в два раза больше, чем в оптимизированном ad hoc методе на основе гамильтоновых блужданий. Важно, что предложенный подход не только решает проблему проклятия размерности, но и реализует алгебру для TT-тензоров.

Конечно, метод не лишен недостатков: если размер множества образов, которым обладают производящие функции, слишком велик, ранг ядер растёт довольно быстро. Вообще-то, эту проблему можно решить с помощью специальной процедуры ограничения рангов, и мы планируем расширить свой алгоритм и на такой случай.