Георг Кантор родился в Санкт-Петербурге в 1845 году, но с 11 лет жил в Германии. Там он начал заниматься математикой и сделал свои первые открытия. Несмотря на то, что научное сообщество отказывалось принимать доказательства его концепций, сейчас он известен как создатель теории множеств и отец современной математики. Мы подготовили материал про труды Кантора на основе статьи, опубликованной в интернет-журнале Medium.

Концепция бесконечности Кантора

Кантор всю жизнь увлекался математикой и делал открытия. Однажды коллега ученого Эдуард Гейне задал Кантору вопрос, который полностью изменил известные основы математики. Он заключался в следующем: если задано множество E из [0, 2π], то означает ли сходимость тригонометрического ряда из E, что все коэффициенты равны 0?

Кантор задумался над вопросом и пришел к невероятному открытию. Рациональные числа не могут быть сопоставлены с иррациональными. Совпадение двух бесконечных множеств должно означать, что величины их бесконечностей различны. Кантор обнаружил, что то, что люди на протяжении тысячелетий считали одной бесконечностью, на самом деле больше, чем одна.

В 1884 году Кантор представил идею бесконечности на основе счетности. Принято считать, что N = {0, 1, 2, 3, ...} представляет собой множество натуральных чисел. Кантор впервые добавил «бесконечное число» в конец 0, 1, 2, 3, ... и обозначил его ω (омега):

0, 1, 2, 3, …, ω.

Однако Кантор на этом не остановился и продолжил добавлять числа:

1, 2, 3, ..., ω, ω +1, ω +2, ω +3, …

Он продолжал складывать числа до 2ω:

1, 2, 3, ..., ω, ..., 2ω.

Кантор понял, что можно продолжать складывать числа:

1 , 2 , 3 , … , ω, …, 2ω, …, 2ω+1 , 2ω+2 , 2ω+3 , …

1 , 2 , 3 , … , ω, …, 2ω, …, 3ω, …, 4ω, …, 5ω, …

1 , 2 , 3 , … , ω, …, 2ω, …, ω², …, ω³, …, ω⁴, …, ω⁵, …

1 , 2 , 3 , … , ω, …, 2ω, …, ω², …, ω³, …, …, ω^ω

1 , 2 , 3 , … , ω, …, 2ω, …, ω², …, ω³, …, ω^ω, …, ω^ωω, …,

1 , 2 , 3 , … , ω, …, 2ω, …, ω², …, ω^ω, …, (ω^ω)^(ω)^(ω), …

Однако через некоторое время Кантор подумал, что понятие бесконечности само по себе ничего не значит. Ведь бесконечность — это лишь противоположность конечного. Поэтому Кантор определил понятие «бесконечность» и соотнес его с понятием «множества». До этого множества были конечными вещами, которые состояли из объектов, но Кантор решил объективировать бесконечность с помощью множеств.

Георгу впервые пришлось дать определение понятию множества. Он подошел к решению этой задачи с математической серьезностью. В статье, опубликованной в 1874 году, он описал множества так: Множество — это любая совокупность определенных и отдельных объектов нашей интуиции или мышления.

Например:

{x: x - нечетное положительное целое число}

{x: x - простое число, меньшее 9 999}.

Проще говоря, множество — это совокупность объектов. Если в математике, говоря «объекты», имеются в виду числа или множества, то, согласно Кантору, для того чтобы объект можно было определить как множество, он не должен отвечать определенным требованиям, и любой объект мог составить множество.

После того, как ученый определил понятие «множество», Кантор стал размышлять, что значит два одинаковых по размеру «множества». Тогда он открыл одну из своих фундаментальных идей — идею соответствия один-к-одному. Используя этот метод, Кантор доказывал, есть ли в двух множествах одинаковое количество объектов.

Логика Кантора была простой. Два человека чертили на стене линию для каждого животного, на которое они охотились. Кантор использовал и сопоставлял понятие бесконечности, например, вещественных чисел, с другими бесконечными множествами.

Согласно Кантору, если можно сопоставить все объекты множества А со всеми объектами множества B, и при этом в обоих множествах нет ни одного несопоставимого объекта, то они равны по размеру. Простым примером может служить сопоставление пальцев на левой руке с пальцами на правой руке.

Соответствие один-к-одному сильно отличается от счета. Когда речь идет об объектах в каждом из множеств, то их не считают по одному, а устанавливают соответствие. Вместо того чтобы сказать, что в этих двух наборах столько-то объектов, говорят, что в них одинаковое количество объектов.

Однако самая блестящая идея Кантора заключалась в том, чтобы использовать метод соответствия один-к-одному не только для конечных, но и для бесконечных множеств. После введения этого метода множества стали делиться на конечные и бесконечные, а бесконечные еще и по величине.

Кантор показал бы, что бесконечность натуральных чисел (N) равна бесконечности рациональных чисел (Q) и что бесконечность действительных чисел (R) больше бесконечности натуральных чисел (N). В конце концов, Кантор доказал, что бесконечность не единственна.

Математическое установление соответствий

Следует начать с множества натуральных чисел, которые имеют вид 1, 2, 3, 4, 5, 6, ... и  предполагается, что продолжаются до бесконечности. Согласно Кантору, множество натуральных чисел является счетным. Поэтому, если можно сопоставить ему другое множество, то это множество тоже будет счетное.

Попробуем сопоставить набор натуральных чисел с двойным набором натуральных чисел. Пусть N представляет собой множество натуральных чисел: N= {1, 2, 3, 4, 5, 6, 7, ...}. А E представляет собой двойное множество натуральных чисел: E= {2, 4, 6, 8, ...}.

Как видно из приведенной выше таблицы, все элементы N и E могут быть сопоставлены друг другу по правилу: n → 2n. Таким образом, в этих двух множествах одинаковое количество объектов.

Используя тот же метод, можно сопоставить всем натуральным числам целые числа. На этот раз Z будет представлять целые числа:

Z = {… -3, -2, -1, 0, 1, 2, 3, …}.

Если сопоставить 1 с 0, то увидим, что всем последующим числам можно поставить в соответствие сначала положительное, а затем отрицательное число. Таким образом,  два множества имеют соответствие один к одному.

До сих пор объединялись в пары только два множества, между которыми нет пробелов. Это означает, что между двумя последовательными числами в множестве натуральных и целых чисел нет пробелов. Например, между 1 и 2 нет натуральных чисел.

Будет ли этот метод работать в рациональных и иррациональных множествах, в которых между числами есть бесконечные элементы? Этот вопрос интригует, потому что рациональные числа интересны. Например, можно поместить любое количество объектов (чисел) между 1 и 2. Но самый простой метод заключается в том, что среднее из двух чисел будет находиться где-то посередине между ними:

• между 1 и 2 находится ровно 3/2;

• между 1 и 3/2 находится ровно 5/4;

• между 1 и 5/4 находится ровно 9/8;

• между 1 и 9/8 находится ровно 17/16;

• и так далее, потому что выполнять эту операцию можно бесконечно долго.

Вероятностный подход к математической философии

Соответствие один-к-одному можно использовать во всех положительных рациональных числах. На изображении ниже в первой строке и столбце записаны натуральные числа до бесконечности. Затем, следуя определенной схеме, записаны все рациональные числа. Например, сначала записали все числители как единицу и сделали так, чтобы знаменатели становились больше.

В следующем ряду повторяется тот же процесс, только в качестве числителя написано два. Далее продолжаются эти действия до бесконечности. Если следовать этому методу установления соответствия, то можно заметить, что в действительности возможно соответствие один к одному — 1 к 2, 2 к ½, ½ к ⅓, ⅓ к 3 и т.д.

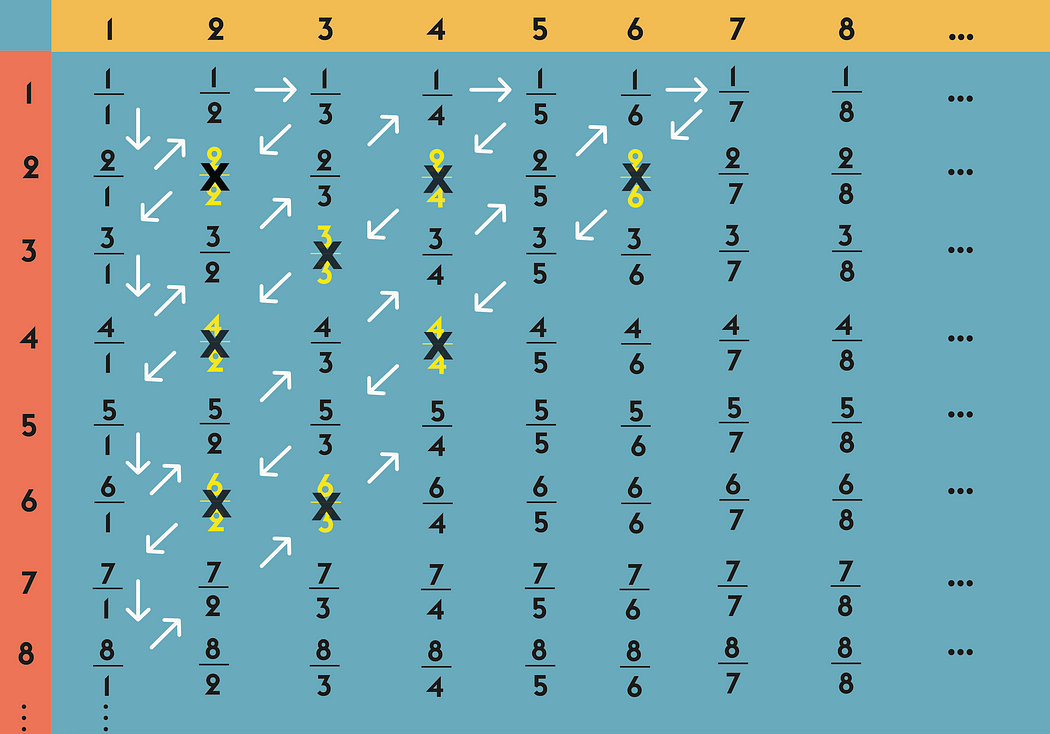
Получается, что можно сопоставить всем натуральным числам положительные рациональные числа. При желании по этой же логике можно сопоставить всем рациональным числам целые числа. Таким образом, можно предположить, что рациональные числа являются счетными.

Вещественные числа не поддаются счету. Доказывая это, Кантор использовал метод противоречия, чтобы показать, что интервал между (0-1) несчетно велик. Сначала он предполагает, что интервал между (0-1) счетен, а когда доказывает, что это не так, то получается противоречие.

Сначала Кантор пишет все натуральные числа от 1 до n, начиная с левого верхнего края пустого листа бумаги. Затем он предполагает, что пишет все числа между (0-1) справа от них, называя их x₁, x₂, x₃ и так далее:

1 → x₁ = 0.256173…

2 → x₂ = 0.654321…

3 → x₃ = 0.876241…

4 → x₄ = 0.60000…

5 → x₅ = 0.67678…

6 → x₆ = 0.38751…

. . . .

n → xₙ = 0.a₁a₂a₃a₄…aₙ…

Согласно первому предположению, Кантор считает, что он не должен найти никакого другого числа между (0-1). Однако он также знает, что должен доказать это математически. Поэтому он начинает искать число, которое, по его мнению, не находится между (0-1), - b.

Используя прямой подход, Кантор находит число b. Прежде всего, он берет первое число, которое он написал x₁, увеличивает его первый десятичный разряд на единицу и пишет b в первом десятичном разряде. Таким образом, он превращает два в три и пишет b = 0,3... Затем он говорит, что b отличается от x₁.

Затем он делает второй десятичный знак x₂ на единицу больше и пишет b во втором десятичном знаке. Таким образом, он превращает 5 в 6 и говорит, что b = 0,36... Затем он говорит, что b отличается от x₂.

После этого он увеличивает третий знак после запятой у x₃ на единицу и ставит b на место третьего знака после запятой. Таким образом, 6 превращается в 7, и он пишет, что b = 0,367... Затем он говорит, что число b отличается от x₃.

Кантор продолжает эту схему и находит число в интервале (0-1), отличное от всех чисел, которые он записал ранее. Тогда он признает, что его предположение ложно. Используя метод противоречия, он приходит к выводу, что вещественные числа несчетны, поскольку при соответствии один к одному многие числа остаются несопоставленными.

Реальные числа не поддаются подсчету

Кантор опубликовал революционное доказательство того, что реальные числа не поддаются подсчету, в статье под названием Über eine elementere Frage der Mannigfaltigkeitslehre.

В своей работе он рассказал, что обнаружил существование бесконечных множеств с разным числом элементов. Проще говоря, он сказал, что «хотя и натуральные, и вещественные множества имеют бесконечное число объектов, множество вещественных чисел имеет больше объектов».

Находка Кантора вызвала споры в мире глубокой философии. Например, Тобиас Данциг в своей книге «Число, язык науки» написал, что доказательство Кантором этой теоремы — триумф человеческой изобретательности.

Во времена Георга Кантора многие ведущие математики не понимали его. Зато гений того времени Гильберт оказался в числе тех, кто понял ученого. В 1900 году на конференции в Париже Гильберт задал 23 вопроса и первым выбрал вопрос о гипотезе непрерывности Кантора. Напоследок Гильберт сказал: «Из рая, созданного для нас Кантором, нас никто не выгонит».

«Теория типов» Бертрана Рассела

Согласно канторовскому определению множества, к объекту не предъявлялось никаких требований, чтобы он был множеством. Любой объект мог считаться множеством. Кантор не знал, что, когда он изложит свою теорию множеств, это вызовет разногласия в мире математики. Некоторое время математики считали все объекты множествами. Так было до тех пор, пока Бертран Рассел не задал неизбежный вопрос: является ли множество всех множеств множеством?

Бертран Рассел нашел способ решить поставленный им парадокс. В 1908 году Рассел выдвинул «теорию типов», которая ранжирует все множества. Например, чтобы определить множество третьего уровня, необходимо использовать множества первых двух уровней. При таком правиле Рассела множество всех множеств не будет считаться множеством. Однако эта теория оказалась сложной для математиков, поэтому впоследствии они заменили ее на более простую.

Парадокс Гильберта о гранд-отеле

В 1924 году, уже после смерти Кантора, Давид Гильберт в своей лекции Über das Unendliche задал свой знаменитый вопрос об отеле: в гостинице есть счетное число бесконечных номеров, и каждый из них занят. Однажды вечером, когда в номер заходит новый клиент, менеджеру гостиницы необходимо найти способ не потерять его. Но как?

В литературе вопрос получил название «Парадокс бесконечного отеля» или «Гранд-отель Гильберта». Проблема Гильберта была популяризирована Джорджем Гамоу в его книге «Раз два три... Бесконечность».

Парадокс бесконечного отеля, который большинство людей с трудом понимают, можно объяснить с помощью упомянутой выше трансфинитной теории Кантора.

Предположим, что управляющий гостиницы — это Георг Кантор. Кантор нашел бы номер для клиента простым методом и попросил бы всех клиентов переместиться в следующий номер. Это означает, что клиент из номера 1 перейдет в номер 2, 2 - в номер 3, а клиент из номера n - в номер n + 1. Из этого можно сделать вывод, что если к счетному множеству добавить какой-либо объект, то это множество все равно будет счетным.

На следующую ночь, когда все номера уже заполнены, подъезжает автобус со 100 людьми. Кантор быстро просит всех своих клиентов пересесть на 100 номеров. Это означает, что человек из номера 1 переезжает в номер 101, человек из номера 2 — в номер 102, человек из номера 102 — в номер 202 и так далее. Таким образом, первые 100 номеров были освобождены. Это означает, что если Кантор получит счетное число клиентов, то он сможет найти решение задачи.

Однако на следующий вечер происходит нечто интересное. Подъезжает автобус с бесконечным количеством людей.

Тогда Кантор подбирает бесконечное число клиентов, как и ранее, то есть просит всех своих клиентов переехать в удвоенный номер комнаты. Таким образом, все нечетные номера освобождаются, и он может принять еще бесконечное число новых клиентов.

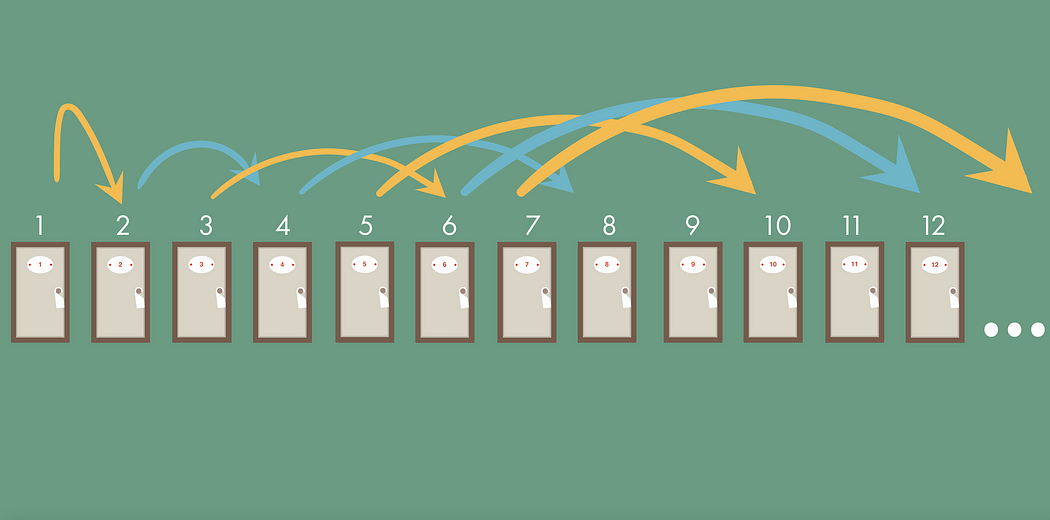
Однако позже к гостинице подъезжает бесконечное число автобусов с бесконечным числом людей. После некоторого размышления Кантор представляет отель в виде пирамиды.

В первом ряду есть только 1. Во втором ряду есть 2 и 3. В третьем ряду — 4, 5 и 6. И так продолжается до бесконечности. Кантор начинает раскрашивать двери комнат в соответствии со своим рисунком.

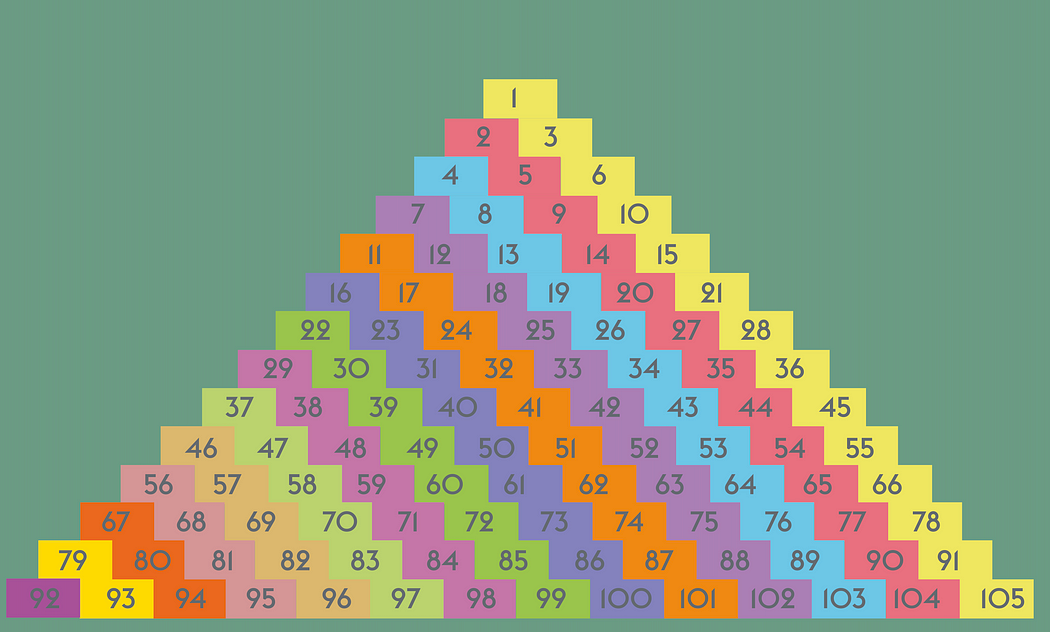
Затем Кантор перемещает всех клиентов, которые находятся в гостинице, в номера с желтыми дверями. После этого он помещает клиентов первого бесконечного автобуса в номера с красной дверью, а второй из бесконечных автобусов клиентов отправляется в теперь уже опустевшие номера с синей дверью.

Таким образом, если у Кантора есть счетное бесконечное число клиентов, то он может разместить в номерах еще одно счетное бесконечное число новых клиентов.

Неприятие идей Кантора и «кризис оснований математики»

Открытия Кантора представляли собой совершенно новый подход к математике, и хотя они были подкреплены доказательствами, многие математики, такие как Леопольд Кронекер и Анри Пуанкаре, считали их опасными. Если бы слова Кантора были верны, то всю математику пришлось бы переосмыслить.

Ученые яростно выступали против идей Кантора и отстаивали концепцию бесконечности Аристотеля. Через некоторое время Пуанкаре и его близкие друзья стали оскорблять Кантора. Из-за этого математик, чье психологическое здоровье и без того было плохим, регулярно попадал в больницу и приостанавливал свою работу. 

Еще одной причиной массового неприятия Кантора стало то, что церковь отвергла его и объявила вне закона. Хотя большую часть своей жизни ученый писал о сходстве между математической и божественной бесконечностью, идеи Кантора доставляли неудобство церкви. Когда Георг выдвинул идею о том, что «бесконечности также бесконечны», христианские богословы посчитали, что это прямо противоречит убеждению, что «единственное бесконечное — это Бог». Они утверждали, что идеи Кантора о бесконечности связаны с пантеизмом.

Вопросы и сомнения относительно логических оснований, на которых была построена математика, привела к глубокому кризису науки. Спустя годы период конца XIX-начала XX века назовут «Кризисом оснований математики». Единственным выходом из него был отказ от классических методов математики. Именно так и произошло. Математики решили, что «теория множеств» аксиоматична, стали строить математику на ее основе и сразу после этого математизировали определение бесконечности.