Привет, дорогие читатели Хабра!

С радостью хочу поделиться с вами своей статьей о параметризованных кривых, написанная простыми словами. Математика вдохновляет своей красотой и применимостью, и параметризованные кривые – это увлекательная область, которая заслуживает внимания.

В этой статье мы рассмотрим:

1. Параметризованные кривые: В тексте рассматривается понятие параметризованных кривых как векторных функций, которые позволяют описывать движение и форму объектов в пространстве. Они играют важную роль в математике, физике и других науках.

2. Параметризация и её применение: Рассматривается метод параметризации для представления кривых в пространстве с помощью переменных. Этот подход полезен для описания движения объектов и анализа их формы.

3. Свойства параметризованных кривых: Говорится о гладкости и регулярности параметризованных кривых, а также о классах гладкости, которые определяют степень дифференцируемости кривой.

4. Диффеоморфизмы и вычисление длины дуги: Вводится понятие диффеоморфизмов как гладких отображений между многообразиями, а также рассматривается вычисление длины дуги параметризованных кривых через интеграл длины дуги.

5. Задание линий в геометрии: Обсуждается понятие линии как геометрического объекта и способы её задания с использованием параметризованных кривых.

6. Заключение

Введение

Параметризованные кривые играют важную роль в математике, физике и других науках, позволяя описывать и изучать движение и форму объектов в пространстве. В этой статье мы рассмотрим понятие параметризованных кривых, их использование, свойства и классы гладкости.

Параметризованные кривые и их свойства

Определение:

Параметризованная кривая – это векторная функция скалярного аргумента, которая принимает скалярное значение в качестве аргумента и возвращает векторное значение. Она задается как , где , и – скалярные функции, определяющие компоненты вектора в зависимости от параметра .

Параметризация и её применение

Параметризация – метод представления кривой, поверхности или объекта в пространстве с помощью одной или нескольких переменных, называемых параметрами. Параметризация позволяет описывать траекторию объекта на кривой или поверхности, изменяя значение параметра. Это гибкий подход для изучения и анализа форм и движений объектов.

Примером использования параметризованных кривых является описание движения объектов в пространстве в зависимости от времени или других переменных. Такие функции также применяются в других научных областях, где векторы зависят от одной переменной.

Носитель параметризованной кривой

Носитель параметризованной кривой – это множество точек в пространстве, которые кривая охватывает в течение своего параметризованного диапазона. Это область, где находятся все точки, соответствующие значениям параметра, используемым для параметризации кривой.

Если у нас есть параметризованная кривая с параметром и координатами , то носителем этой кривой будет множество всех точек, представленных как при изменении параметра в интервале, на котором кривая определена.

Примеры параметризованных кривых:

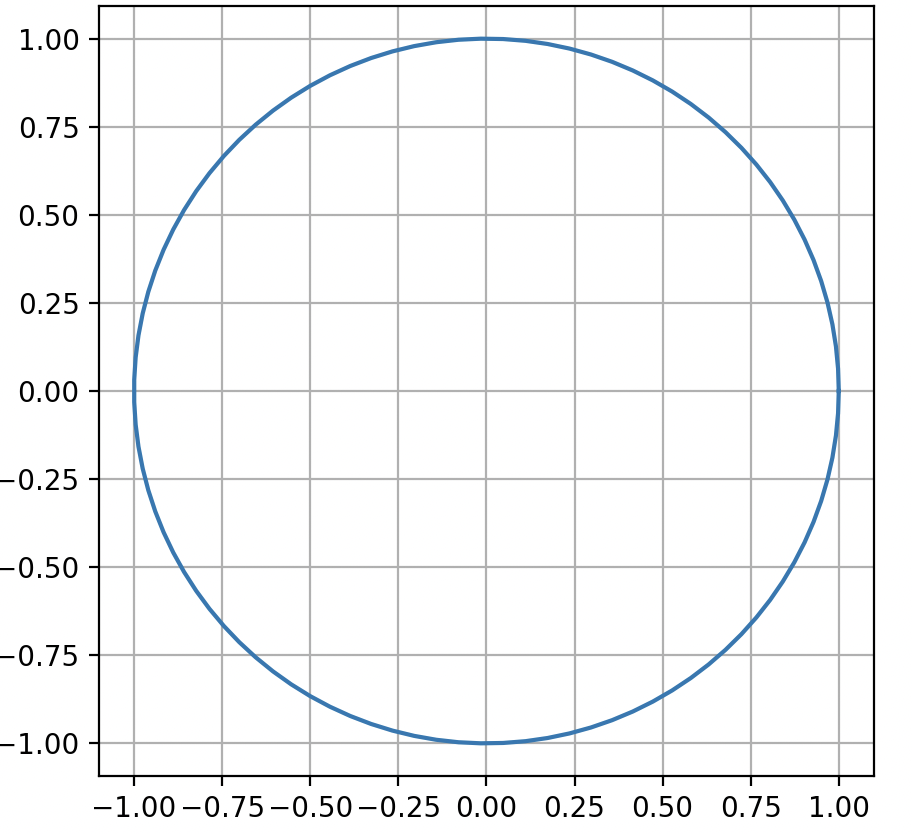
Окружность в двумерном пространстве:

Рассмотрим параметрические уравнения, описывающие движение точки по окружности:

Здесь – радиус окружности, а – параметр времени. Такие уравнения задают векторную функцию скалярного аргумента . При различных значениях параметра , точка будет двигаться по окружности радиуса в двумерном пространстве.

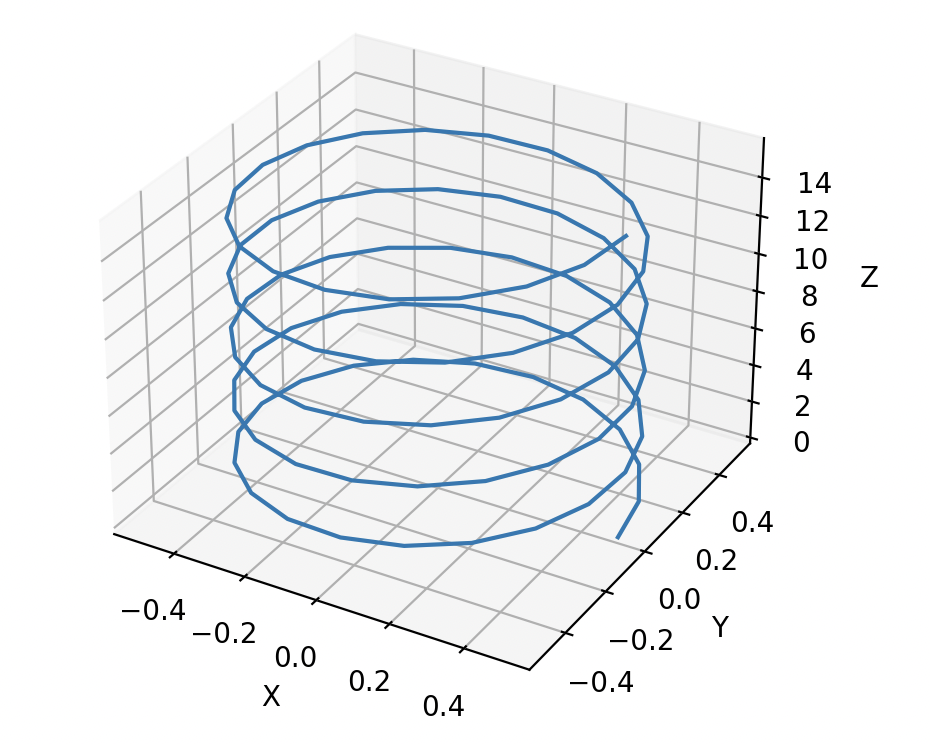
Винтовая линия в трёхмерном пространстве:

Винтовая линия описывает спиральное движение в трёхмерном пространстве. Её параметризация может выглядеть следующим образом:

Здесь – параметр (угол поворота), – радиус спирали, – высота подъема за каждый полный оборот, , , – начальные координаты.

Свойства параметризованных кривых:

(Гладкость и регулярность)

Гладкость кривой означает отсутствие резких углов и изломов. Кривая считается гладкой, если её компоненты имеют непрерывные производные.

Регулярность кривой связана с отсутствием самопересечений и сохранением интринсических характеристик. Регулярные кривые не имеют вырожденных точек и параметризация не теряет информацию о кривой.

Познакомившись с двумя выше определениями, можно рассмотреть Классы Гладкости.

Кривая принадлежит классу , если её компонентные функции также принадлежат этому классу. Классы гладкости определяются степенью непрерывной дифференцируемости кривой.

• : Непрерывная кривая.

• : Кривая с непрерывной первой производной.

• : Кривая с непрерывными первой и второй производными.

• : Кривая с непрерывными производными до -го порядка.

Чем выше класс гладкости, тем плавнее и "естественнее" выглядит кривая.

Диффеоморфизмы, Длина дуги и Задание линий в Геометрии

Диффеоморфизм класса C^k:

Диффеоморфизм класса C^k - это биективное отображение между двумя гладкими многообразиями, которое обладает определенной гладкостью. Формально, диффеоморфизм класса C^k - это гладкое отображение f: M -> N, где M и N - гладкие многообразия класса C^k, удовлетворяющее условиям:

• f является биективным отображением.

• Обратное отображение f^(-1) также принадлежит классу C^k.

Диффеоморфизмы позволяют устанавливать гладкую эквивалентность между различными кривыми или многообразиями. Если две параметризованные кривые связаны диффеоморфизмом, то они считаются диффеоморфно эквивалентными и могут быть рассмотрены как одна и та же кривая с различными параметризациями. Такие диффеоморфные кривые принадлежат одному классу эквивалентности, что позволяет сохранять геометрические свойства при различных параметризациях.

Пример:

Для лучшего понимания, представьте две параметризованные кривые r1(t) и r2(t), между которыми существует диффеоморфизм f, то есть r1(t) = f(r2(t)). В этом случае r1(t) и r2(t) считаются диффеоморфно эквивалентными кривыми. Это означает, что они обладают одинаковой гладкостью и регулярностью в зависимости от параметра t.

Введем первую кривую, которая образуется по параметризации x = cos(t), y = sin(t), а вторая кривая получается из первой кривой путем поворота на угол θ и изменения масштаба в α раз. Обе кривые являются эквивалентными, так как можно сопоставить каждой точке на одной кривой точку на другой кривой без пересечений.

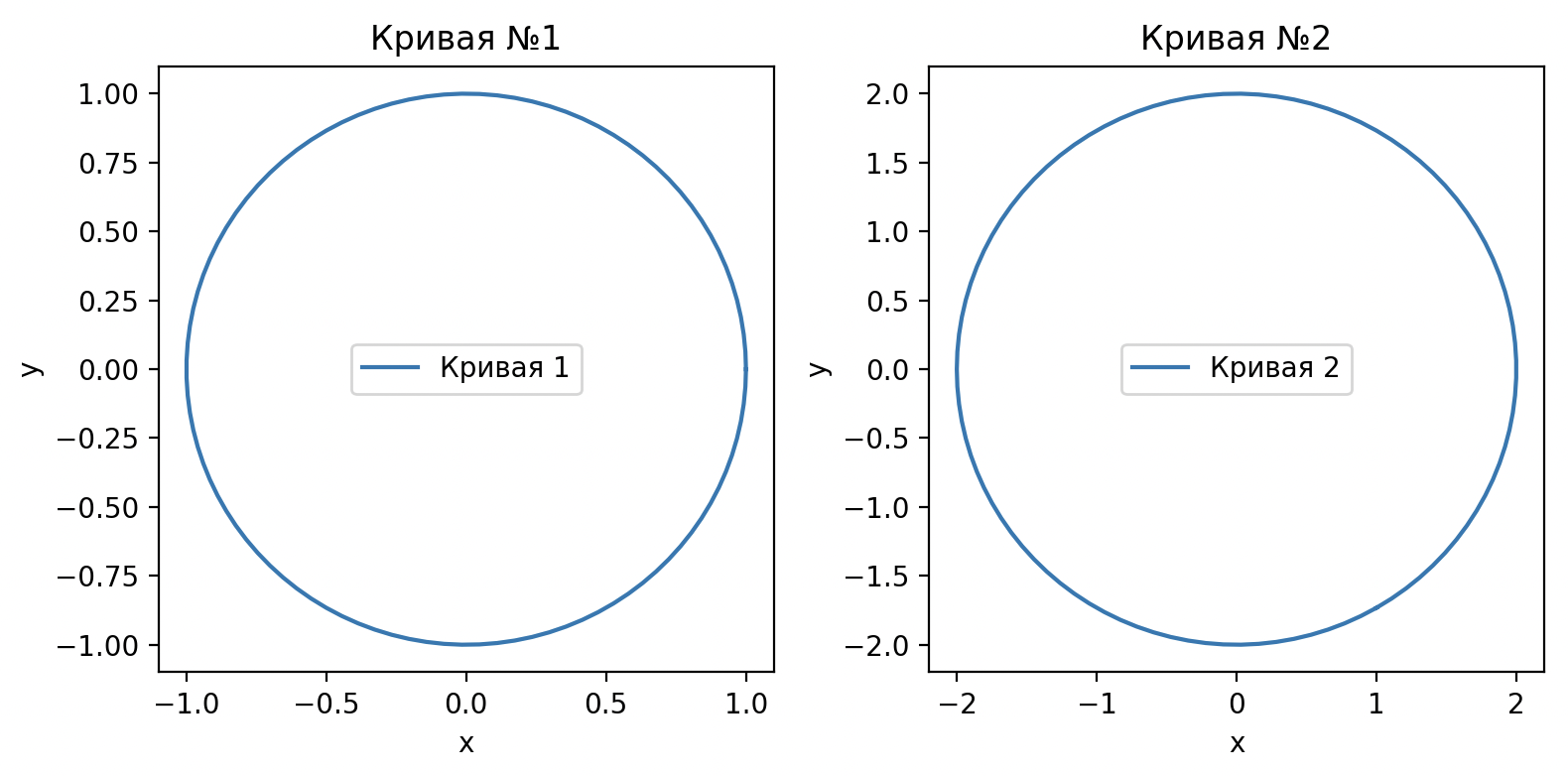
Вычисление длины дуги параметризованных Кривых.

Длина дуги между двумя точками на параметризованной кривой играет важную роль в геометрии. Для её вычисления используется интеграл длины дуги, который зависит от производной параметризации.

Математически, длина дуги вычисляется по формуле:

Здесь r(t) - векторная функция, параметризующая кривую, r'(t) - её производная по параметру t (тангенциальный вектор), |r'(t)| - модуль этого вектора.

Немножко про линии в геометрии

Линия - это геометрический объект, представляющий собой подмножество М трехмерного пространства R^3. В контексте трехмерного пространства, параметризованные кривые часто используются для описания линий.

Линию M пространства R^3 считают линией, если для каждой точки α на ней существует параметризованная кривая (I, r), носитель которой r(I) является окрестностью точки α. Понятие "точка α", "регулярная параметризованная кривая" и "носитель" играют важную роль:

• Точка α: Точка на линии, подлежащая покрытию параметризованной кривой.

• Регулярная параметризованная кривая (I, r): Функция r, отображающая интервал I в пространство R^3.

• Носитель r(I): Множество точек r(t) для t из интервала I, описывающее окрестность точки α.

Таким образом, каждая точка на линии может быть охвачена параметризованной кривой, что позволяет задавать линию с использованием параметризованных кривых.

Если для линии существует параметризация, покрывающая всю линию, она называется простой линией. Глобальная параметризация охватывает всю линию, обеспечивая полное описание каждой точки на ней. Линии в трехмерном пространстве могут иметь различные формы и свойства. Некоторые из них являются прямыми линиями, которые не имеют изгибов или изломов, а другие могут быть закрытыми кривыми, образующими окружности или эллипсы.

Заключение

Параметризация кривых и линий открывает перед нами возможность изучать их свойства и поведение под различными условиями. Регулярность функций позволяет нам определить гладкость кривых и линий, а диффеоморфизмы позволяют нам описать их преобразования, сохраняющие основные геометрические свойства. Эта тема даёт нам глубокий взгляд в мир форм и структур.

Геометрические аспекты параметризации кривых и линий также имеют широкое применение в компьютерной графике, криптографии и других областях.