Квантовые компьютеры. С точки зрения традиционного программиста-математика. Часть 5 / forpes.ru

Главная
Квантовые компьютеры. С точки зрения традиционного программиста-математика. Часть 5

Квантовые компьютеры. С точки зрения традиционного программиста-математика. Часть 5 +10

08.09.2023 10:16

java_prog 2 1500 Источник

Универсальные логические операции на квантовых гейтах

В прошлых частях мы рассмотрели семейство квантовых гейтов: Инвертор, C-NOT, Адамара, инверсия фазы. Но, согласитесь, как-то не похожи они на привычные нам гейты классических компьютеров: AND, OR, XOR, NOT. Ну, ладно, с NOT это я хватил лишку, NOT это вполне тоже самое, что квантовый инвертор, который мы рассмотрели самым первым гейтом в прошлых частях.

А как быть с остальными? Можем ли мы как-то сделать, к примеру, квантовый AND?
И да, и нет. Как вы помните из второй части, квантовая операция обязана обладать двумя важными свойствами:

свойство обратимости, которое мы рассматривали, что если применить операцию к квантовому регистру повторно, то регистр вернется в исходное состояние.
свойство сохранения нормы, которое заключается в том, что сумма вероятностей всех возможных состояний должна быть 1. А значит сумма квадратов всех амплитуд должна быть равна 1.

Как вы, может, помните с первым свойством я в прошлых частях приврал. На самом деле, свойство обратимости заключается в том, что для каждой квантовой операции существует обратная квантовая операция, которую можно вычислить из исходной определенными математическими действиями. Нам просто до сих пор везло, что обратные операции для гейтов Адамара, инвертора, C-NOT и инверсии фазы являлись теми же самыми операциями. Поэтому я и приврал тогда, что обратимость операции, это квантовая цепь, примененная дважды возвращает систему в исходное состояние. Нет, забудьте, это неправда. Теперь обратимость сформулируем следующим образом.

Для любой квантовой операции существует обратная операция $U^\dagger$ , которую можно получить из исходной операции определенными математическими преобразованиями.

Пока опустим, что это за математические преобразования надо совершить. Иногда эта операция равняется исходной операции, $U\equiv U^\dagger$ , как у нас было с теми гейтами, что нам встречались до сих пор. Но, как вы понимаете, такое работает не всегда.

Это очень важное свойство всех квантовых операций. Теперь, когда у нас есть любой квантовый регистр $|x\rangle$ емкостью в несколько кубит, и мы подвергаем этот регистр квантовому преобразованию, какому-нибудь n-кубитному гейту

То теперь мы можем быть уверены, что существует обратная операция $U^\dagger$ , благодаря которой мы можем совершить обратное преобразование. И если мы результат операции $U|x\rangle$ подадим на вход операции $U^\dagger$ , мы снова вернемся к исходному состоянию $|x\rangle$

И что из этого следует? Что мы не сможем так просто сделать операцию AND, XOR, OR квантовыми гейтами, ведь операции AND, XOR, OR не обратимы. Из одного бита результата никак не узнать, каковы были исходные два бита. Но не будем отчаиваться, а посмотрим на пару примеров. Рассмотрим гейт CNOT

Мы помним, что если на управляющем входе гейта CNOT будет $|1\rangle$ , то состояние управляемого входа инвертируется. Получается, по своей сути действия, этот гейт может выполнять операцию xor. При этом на втором выходе гейта у нас сохраняется один из аргументов операции XOR, что позволяет эту операцию обратить.

Вторым примером рассмотрим новый трехкубитный квантовый гейт, который называется CSWAP гейт, иногда его называют вентилем Фредкина. Обозначается он в схемах следующим образом:

Иногда его рисуют вверх-ногами, в зависимости от того, с какой стороны его надо вставить в схему. Вход обозначаемый черной жирной точкой - управляющий. На рисунке выше это вход C.

Аналитически его действие можно описать следующим образом.

Квантовой состояние, подаваемое на вход C проходит гейт на выход без изменений. На то оно и управляющее Как помните, у CNOT тоже есть управляющий вход, который проходит гейт без изменений. Если на вход C подать состояние $|0\rangle$ , то квантовые состояния, поданные на входы A и B, пройдут также без изменений через гейт.

Если на вход C подать $|1\rangle$ , то квантовые состояние A и B поменяются местами. То состояние, что на входе A, выйдет из гейта напротив входа B. И наоборот, то, что подавалось на вход B, выйдет из гейта напротив входа A. На досуге можете попробовать нарисовать матрицу этого преобразования. Это будет матрица $8\times 8$ , но мы уже с этой темой разобрались и заниматься этим не будем.

Очевидно, что это преобразование обратимо, и если применить CSWAP два раза, то мы получим исходное состояние трехкубитного регистра.

А теперь давайте применим этот гейт следующим способом: на вход A мы будем всегда подавать состояние $|0\rangle$ . И будем наблюдать то состояние, что на выходе, что находится напротив входа A. Как тогда будет работать гейт?

1-ый случай. Если на входе C будут подавать состояние $|0\rangle$ , то сигналы поданные на все входы проходят без изменений, и напротив входа A будет $|0\rangle$ , независимо от того, что за состояние подается на вход B.

2-ой случай. Если на управляющем входе C будут подавать состояние $|1\rangle$ , а на входе B подается состояние $|0\rangle$ . В этом случае гейт меняет местами входные сигналы и напротив входа A выйдет тот самый $|0\rangle$ , что мы подавали на вход B.

3-ий случай.Если на управляющем входе C будут подавать состояние $|1\rangle$ , а на входе B подается состояние $|1\rangle$ . В этом случае гейт меняет местами входные сигналы и напротив входа A выйдет тот самый $|1\rangle$ , что мы подавали на вход B.

Итак, подведем предварительный итог. Напротив выхода A будет состояние $|1\rangle$ только если на входе B будет состояние $|1\rangle$ и одновременно на входе C будет состояние $|1\rangle$ . Во всех остальные случаях напротив входа A будет состояние $|0\rangle$ .

Вот мы и повторили AND в квантовом варианте, используя гейт CSWAP. Но, кроме двух кубитов, что являлись аргументами, нам потребовался еще третий входной кубит, который мы закоротили на $|0\rangle$ . А второй нюанс, что кроме выхода с результатом операции AND у нас на выходе еще 2 кубита с "мусором", который нам не нужен.

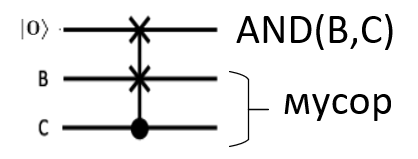
А теперь обобщим ситуацию и ответим на вопрос, поставленный вначале этой части. Да, мы можем повторить элементарные логические функции F(x) классического компьютера, используя квантовые гейты. Но при этом:

нам, вероятно, придется добавить еще один или несколько входов в схему. Чаще всего на все такие входы подают состояние $|0\rangle$ .
На выходе, кроме результата операции нам понадобятся еще аргументы операции, а также образуется "мусор", который нам не нужен, но от которого нам необходимо избавляться. Просто откинуть и забыть этот мусор не получится, ведь кубиты на мусорных выходах спутаны с результатом операции и с аргументом операции.

Задачу утилизации "мусора" программисты квантовых компьютеров решили довольно быстро и изящно. Для этого можно воспользоваться свойством обратимости любой квантовой операции. Посмотрите на вот эту схему:

Какую бы мы не проделали квантовую операцию мы можем быть уверены, что существует обратная операция $U^\dagger$ , благодаря которой мы можем совершить обратное преобразование. А значит на выходе мы получим тоже самое, что на входе. Это будет аргумент функции и состояния $|0\rangle$ , которые мы подавали на добавленные входы. Отлично, можем утилизировать (например измерением), все нулевые кубиты, эти кубиты ни с кем не спутаны. Если конечно мы не подавали на входы уже ранее спутанные кубиты, но это не наш случай.

Отлично, то отлично, но ведь и ответ, результат функции F(x) мы тоже потеряли в процессе обратного преобразования.

А чтобы не потерять ответ, можно использовать наш старый знакомый гейт C-NOT.

И вот, благодаря этому изящному решению, у нас есть и результат операции, и аргумент сохранился, и мусор, который можем легко утилизировать, так как он не спутан с остальными регистрами.

Еще пара замечаний.

Те нулевые кубиты, что входят в U_f они никому не интересны, сколько их вошло, столько их и вышло, они ни с кем не спутались, так что можем их даже не рисовать.

Что касается тех нулевых кубитов, что проходят через CNOT: что если на эти входы подать кубиты ненулевые? Ничего страшного, результат операции является результатом работы несколько CNOT с этим кубитами в качестве управляемых. А мы выше разобрали что по сути действия CNOT это тот же xor. Поэтому в результате операции будет исходные кубиты на которые наложена маска xor с результатом операции. Очевидно, что в частном случае, когда мы подаем нули, xor ничего не изменит, имея нулевую маску, и на выходе мы получим чистый результат операции. Часто это то, что нам и надо.

Но бывает случаи когда программисту надо провести xor результата операции с какой то маской. В этом случае программист может сэкономить и сразу подать вместо нулевых кубит нужную маску.

С учетом этих двух замечаний, перерисуем схему так:

Схема получилась громоздкой, но если мы с ней разобрались, то кратко можем записывать ее в дальнейшем так:

Выводы:

Квантовыми гейтами можно реализовать логические функции классического компьютера. В общем случае на такие схемы подаются аргументы логической функции и несколько дополнительных кубит, количество которых равно разрядности результата операции. На выходе такой реализации мы будем иметь маску XOR([результат функции], [добавленные кубиты]) и аргумент. Чаще всего добавленные кубиты это нули, в этом случае на выходе будет чистый результат операции.
Все такие квантовые реализации классических логических операций обратимы. Действительно, ведь они построены из элементарных обратимых гейтов и чтобы получить обратную квантовую цепь, надо просто повторить эти гейты в обратном порядке. А вернее повторить обратные гейты $U^\dagger$ .

Преобразование Адамара для n-кубитного регистра

Как вы помните, в третьей части мы рассмотрели двухкубитный гейт Адамара и сформулировали самостоятельное задание, рассчитать этот гейт для общего случая, n-кубитный гейт Адамара $H^{(n)}$ Уверен, вы справились самостоятельно, но в любом случае пришла пора нам решить эту задачу.

Как мы помним, по устройству, такой n-кубитный гейт, это просто n однокубитных гейтов Адамара в одной коробке:

А каждый однокубитный гейт Адамара описывается следующим аналитическим способом: Состояние $|0\rangle$ преобразуется гейтом в состояние $\frac{1}{\sqrt 2}(|0\rangle+|1\rangle)$

Состояние $|1\rangle$ преобразуется гейтом в состояние $\frac{1}{\sqrt 2}(|0\rangle-|1\rangle)$

Что будет на выходе?

Преобразуем каждый $|0\rangle$ и $|1\rangle$ по правилам для однокубитного гейта Адамара получим:

$H^{(4)}|0101\rangle=\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)\otimes\frac{1}{\sqrt{2}}(|0\rangle-|1\rangle)\otimes\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)\otimes\frac{1}{\sqrt{2}}(|0\rangle-|1\rangle)$

Перемножим, раскроем скобки и получим:

$H^{(4)}|0101\rangle=\frac{1}{2^\frac{4}{2}}(|0000\rangle-|0001\rangle+|0010\rangle-|0011\rangle-|0100\rangle+|0101\rangle-|0110\rangle+|0111\rangle+$ $+|1000\rangle-|1001\rangle+|1010\rangle-|1011\rangle-|1100\rangle+|1101\rangle-|1110\rangle+|1111\rangle)$

Кстати, а чего это мы мучаемся и пишем в двоичном виде эти громоздкие выражения? Давайте перепишем в привычной десятичной форме то выражение, что только что получили:

$H^{(4)}|5\rangle=\frac{1}{2^\frac{4}{2}}(|0\rangle-|1\rangle+|2\rangle-|3\rangle-|4\rangle+|5\rangle-|6\rangle+|7\rangle+$ $+|8\rangle-|9\rangle+|10\rangle-|11\rangle-|12\rangle+|13\rangle-|14\rangle+|15\rangle)$

Посчитали конкретный случай. Какие выводы мы можем распространить на общий случай? Во-первых, очевидно, что впереди всегда будет стоять множитель $\frac{1}{2^\frac{n}{2}}$ , где n - разрядность гейта Адамара.

Во вторых, очевидно, что в сумме будут присутствовать все возможные состояния для n двоичных разрядов от $|0\rangle$ до $|2^n-1\rangle$

$H^{(n)}|y\rangle=\frac{1}{2^\frac{n}{2}}\sum_{x=0}^{2^n-1}{\pm |x\rangle}$

И вот только со знаками самая неприятная загвоздка. Как понять, где будет плюс, а где будет минус. Не будем мучить, а просто скажу ответ, который доказывается, к примеру матиндукцией: $(-1)^{p(x \land y)}$

Где знак $(\land)$ это побитовое И - логическое AND. А функция - функция четности, считает количество единиц в двоичном представлении числа. Например выше, где мы считали $H^{(4)}|5\rangle$ давайте вычислим, какой знак будет в сумме у состояния $|12\rangle$ , вычислим по предоставленной формуле:

$5\otimes 12=0101_b \land 1100_b=0100_b$

В двоичном представлении числа всего одна единица, поэтому функция четности p(0100_b)=1

Следовательно $(-1)^{p(5 \land 12)}=-1$

И получается, что состояние $|12\rangle$ войдет в сумму всех состояний с отрицательным знаком, и это сходится с ответом выше. Итого перепишем начисто формулу для гейта Адамара разрядности n

$H^{(n)}|y\rangle=\frac{1}{2^\frac{n}{2}}\sum_{x=0}^{2^n-1}{(-1)^{p(x \land y)} |x\rangle}$

Квантовый параллелизм. Задачи с черными ящиками

Гейт Адамара очень важен в задачах решаемых квантовыми алгоритмами тем, что позволяет легко получить такое состояние квантового регистра, где все элементарные состояния равновероятны. Как мы видели в формуле выше, результатом этого преобразования будут все возможные элементарные состояния квантового регистра от $|0\rangle$ до $|2^n-1\rangle$ и все эти элементарные состояния будут с равными вероятностями.

Во многих задачах классического компьютера: задача факторизации и др, наивному алгоритму, зачастую надо перебрать в цикле все значения регистра и проверить, удовлетворяет ли значение поставленным условиям задачи. Каким то алгоритмам требуется на это линейное время, каким то экспоненциальное, в любом случае зависящее от количества проверяемых значений в классическом цикле.

Сила квантовых алгоритмов в том, что гейтом Адамара можно получить состояние, где все значения равновероятны. Далее в квантовой цепи можно построить такую цепочку гейтов, что состояния, которые удовлетворяют условию поставленной задачи отфильтруются, а амплитуды состояний не удовлетворяющих условию задачи занулятся. И все, остается только измерить результат и получить то состояние, которое будет ответом на поставленную задачу. И все это за один проход алгоритма, без всяких циклов. Такой принцип называется квантовым параллелизмом.

Существует целое семейство задач на "черный ящик", как для квантовых алгоритмов, так и для классических алгоритмов. Общая постановка этих задач в том, что черный ящик выполняет какое-то функциональное преобразование. Мы скармливаем черному ящику различные аргументы, и по выходному результату пытаемся установить параметры этого скрытого преобразования. Классический алгоритм требует цикла для перебора этих аргументов. А квантовые алгоритмы проявляют в таких задачах свою силу, благодаря квантовому параллелизму.

Вот и давайте разберем простейшую такую задачу, которая имеет малое практическое применение, но подходит для демонстрации силы квантового параллелизма.

Задача. Черный ящик принимает на вход любое n-разрядное двоичное число от 0 до $2^{n-1}$ . Внутри черный ящик выполняет преобразование результатом которого будет один бит $p(x \land u)\; mod\; 2$ где $(\land)$ это побитовое И - логическое AND. Функция - функция четности, считает количество единиц в двоичном представлении числа. $mod\; 2$ - это остаток от деления на 2, u - это неизвестное n-разрядное двоичное число, которое является постоянным скрытым параметром черного ящика. Задача состоит в том, чтобы установить это u.

Например, имеем 4-х разрядный ящик, с u=0101_b На вход черному ящику подаем число x=1111_b . Черный ящик выполняет преобразования. Вначале он посчитает

$x \land u=1111_b \land 0101_b=0101_b$

Затем функция четности p подсчитывает количество единиц в результате и получает 2. Наконец, вычисляем остаток от деления на 2, $2\; mod\; 2=0$ Значит на выходе черного ящика будет 0.

Как бы мы решали эту задачу на классическом компьютере. Нам нет нужды перебирать все возможные значения. Например, взять двоичное число 000...001_b , тогда

$000...001_b \land u=\; младший(нулевой)\; бит\; u$

Далее берем число 000...010_b , и получим

$000...010_b \land u=\; первый\; бит\; u$

И так далее, нам придется перебрать в цикле n чисел и в итоге мы вычислим все биты числа u. Можно ли сделать алгоритм оптимальнее, с меньшим числом проходов? Нет, каждое обращение к черному ящику дает в результате всего один бит информации и построить ответ на информации меньше, чем n бит никак не получится.

В квантовой постановке данной задачи, мы имеем гейт-черный ящик, который совершает наше преобразование:

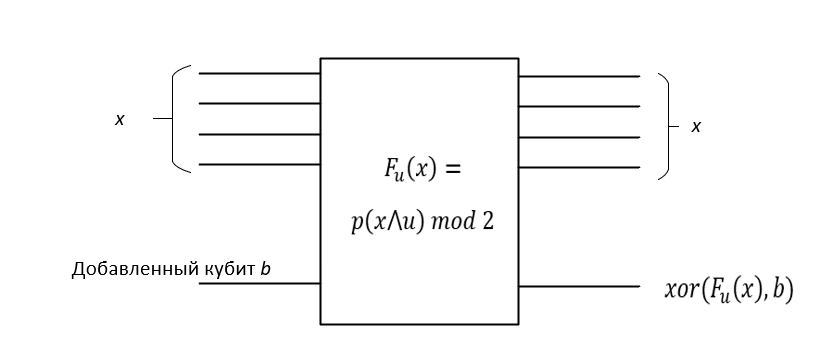
Как мы уже разбирали выше в этой части, нам потребуется подать на вход черного ящика кроме аргумента x, еще и дополнительный кубит b. На выходе будем иметь снова аргумент x и результат операции $p(x \land u)\; mod\; 2$ , в случае если на вход b подавался $|0\rangle$ . Если же мы подавали какое то другое состояние на вход b, то будет применена однобитная маска $xor(p(x \land u)\; mod\; 2,b)$ Как будем решать эту задачу? План предлагается следующий:

Используя черный ящик и другие гейты, получить состояние $\frac{1}{2^\frac{n}{2}}\sum_{x=0}^{2^n-1}{(-1)^{p(x \land u)} |x\rangle}$
Подать это состояние в гейт Адамара и получить u.

Начнем с конца. Почему это состояние, поданное в гейт Адамара даст в результате u?
Допустим, нам было бы известно u и мы подали бы его на вход в гейт Адамара. По общей формуле выше на выходе мы получили бы состояние.

$\frac{1}{2^\frac{n}{2}}\sum_{x=0}^{2^n-1}{(-1)^{p(x \land u)} |x\rangle}$

А далее, помня, что гейт Адамара обратим, мы можем подать это состояние снова в гейт Адамара и получится u. Все просто. Вот только u нам неизвестно, поэтом надо получить это состояние каким то другим способом, используя черный ящик. то есть выполнить пункт 1.
Для этого используем квантовый параллелизм. Возьмем черный ящик и подадим на вход x состояние, которое является равновероятной суперпозицией всех возможных состояний.

$\frac{1}{2^\frac{n}{2}}\sum_{x=0}^{2^n-1}{|x\rangle}$

Черный ящик для каждого элементарного состояния вычислит свое однобитное значение F_u(x) и на выходе мы будем иметь состояние

$\frac{1}{2^\frac{n}{2}}\sum_{x=0}^{2^n-1}{|x\rangle}\otimes F_u(x)=$ $=\frac{1}{2^\frac{n}{2}}\sum_{x=0}^{2^n-1}{|x\rangle}\otimes |p(x \land u)\; mod\; 2\rangle$

Почти то, что нам надо, но немного не то. И тут мы вспоминаем, что на вход b можно подавать не обязательно $|0\rangle$ .

Давайте подадим на этот вход состояние $\frac{1}{\sqrt 2}(|0\rangle-|1\rangle)$ , которое легко можно получить однокубитным гейтом адамара. Тогда на выходе b вместо состояния $|F_u(x)\rangle$ будет состояние

$|xor(b,F_u(x))\rangle=\frac{1}{\sqrt 2}(|xor(0,F_u(x))\rangle-|xor(1,F_u(x))\rangle)=$

Используем тот факт, что для однобитного исключающего или xor(0,x)=x, xor(1,x)=not(x), получаем

$=\frac{1}{\sqrt 2}(|F_u(x)\rangle-|not(F_u(x))\rangle)$

Давайте распишем два случая, когда $F_u(x)=0\; и \; F_u(x)=1$

В первом случае получится состояние

$=\frac{1}{\sqrt 2}(|0\rangle-|1\rangle)$

Во втором случае получится состояние

$=\frac{1}{\sqrt 2}(|1\rangle-|0\rangle)=-\frac{1}{\sqrt 2}(|0\rangle-|1\rangle)$

То есть, мы получаем по сути одно и то же состояние, только меняется знак. В случае если F_u(x)=0 будет знак +, если будет F_u(x)=1 будет знак -.

Давайте этот знак запищем в виде множителя $(-1)^{F_u(x)}$

Тогда в обоих случаях у нас получится один и тот же ответ:

$=(-1)^{F_u(x)}\frac{1}{\sqrt 2}(|0\rangle-|1\rangle)$

Тогда общее состояние на выходе из черного ящика, с учетом x

$=\frac{1}{2^\frac{n}{2}}\sum_{x=0}^{2^n-1}{|x\rangle\otimes (-1)^{F_u(x)}\frac{1}{\sqrt 2}(|0\rangle-|1\rangle)}=$ $=\frac{1}{2^\frac{n+1}{2}}\sum_{x=0}^{2^n-1}{(-1)^{p(x \land u)}|x\rangle\otimes (|0\rangle-|1\rangle)}$

Вот и получилось именно то, что нам нужно. За добавленный справа кубит с состоянием $(|0\rangle-|1\rangle)$ беспокоится не надо, это состояние никак не спутано с нашим состоянием, можем его измерить или пропустить дополнительным разрядом в гейт Адамара, это не важно, данный кубит независим от полученной суперпозиции.

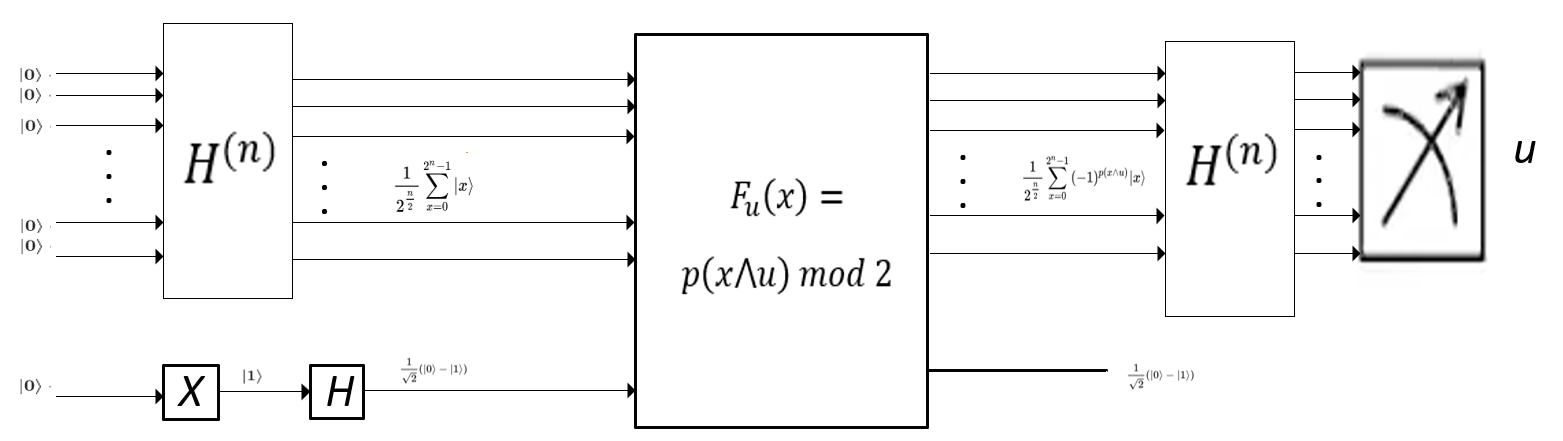
Ну теперь, давайте запишем ответ, квантовая цепь, которая решает исходную задачу, на отдельных этапах цепи подписаны состояние на этих этапах:

Комментарии (2)

green_nebula
11.09.2023 04:44
#25951304
Во многих задачах классического компьютера: задача факторизации и др,
наивному алгоритму, зачастую надо перебрать в цикле все значения
регистра и проверить, удовлетворяет ли значение поставленным условиям
задачи. Каким то алгоритмам требуется на это линейное время, каким то
экспоненциальное,

При переборе всех значений регистра длиной n бит нужно перебрать 2^n значений.
Т. е. задача делает экспоненциальное количество шагов от длины регистра.
Может ли существовать классический алгоритм, который переберет в цикле все эти значения за линейное время?
1. java_prog Автор
  11.09.2023 04:44
  #25951588
  Тут не очень удачно выразился. "требуется на это" имеется в виду не для перебора всех значений, а для решения задачи.
  
  И далее перечисляю, что наивному алгоритму надо перебрать все значения для решения задачи. Другим алгоритмам может потребоваться для решения задачи линейное и т.д.
  
  Если речь о так называемом наивном алгоритме, то да, надо перебрать все значения, чтобы решить задачу. Далее я имел в виду, что многие алгоритмы, не требуют перебора всех значений. Например, в задаче черного ящика в примере из последней части нам было достаточно перебрать только все степени двойки для ее решения, что делает алгоритм линейным

Квантовые компьютеры. С точки зрения традиционного программиста-математика. Часть 5 +10

Универсальные логические операции на квантовых гейтах

Преобразование Адамара для n-кубитного регистра

Квантовый параллелизм. Задачи с черными ящиками

Комментарии (2)

green_nebula

java_prog Автор