Добро пожаловать в новый мир новых технологий вычислений!

В быту, когда мы смотрим на разные предметы, мы пытаемся понять - похожи ли они или нет, и на сколько они похожи.

Так и в математике - когда мы смотрим на последовательностей чисел, мы пытаемся понять - похожи ли они или нет, и насколько они похожи.

Одним из таких критериев "похожести" является совпадение частотных характеристик этих последовательностей.

Рассмотрим вопрос, как реализовать такую проверку с использованием квантовых вычислений и напишем программку-тест на Q-sharp для проверки этих рассуждений.

Для понимания данного туториала вам потребуются базовые знания по

• теории вероятности

• алгебре

• булевым функциям

• свёртке, корреляции, скалярному произведению

• квантовым вычислениям (кубиты и трансформации)

• программированию на Q-sharp

Получение частотных характеристик числовой последовательности

Пусть задана последовательность x(i) целых чисел из 0..m-1, где i=0..l-1

Спросим себя - можно ли для регистра (массива) кубитов получить состояние SUM SQRT(P(v))|v>, где P(v) - частота символа v в последовательности x(i)?

Ответ - а почему бы и нет (но с оговорками)!

Что означает запись x(i), где i=0..l-1 ?

Это фактически означает, что у нас имеется отображение (функция) x: 0..l-1 to 0..m-1

Пусть

kl - количество бит, достаточных для хранения чисел 0..l-1
km - количество бит, достаточных для хранения чисел 0..m-1

Преобразуем отображение x: 0..l-1 to 0..m-1 в трансформацию для квантовых вычислений Ux(i,z)=(i,z xor x(i))
где i - регистр из kl кубитов, а z - регистр из km кубитов

Очевидно, что если выполнить трансформацию Ux(H|0>,|0>), то (поскольку i пробегает значения от 0..2^kl-1) в регистре z сформируется подсчёт статистики появления разных символов в последовательности.

Но есть небольшая проблема - у нас не известны значения функции x на диапазоне аргумента l..2^kl-1.

Есть ли варианты решения? Конечно!

Самый простой вариант - дополнить последовательность на участке l..2^kl-1 случайными равновероятными числами из 0..m-1

И вуаля ...

Имеем x:0..2^kl-1 to 0..m-1 и Ux(i,z)=(i,z xor x(i))

1. Задаём начальное состояние (i,z)=(H|0>,|0>)

2. Выполняем трансформацию Ux

3. И в регистре z содержатся частотные характеристики последовательности (ну немного усреднённые, за счёт сгенерированного хвоста из случайных равновероятных чисел)

Как сделать реализацию трансформации Ux ?

Пусть у нас имеется базовый набор гейтов - X и Controlled X

Пусть x|j:0..2^kl-1 to 0..1 - отображение полученное взятием j-го бита из значения x:0..2^kl-1 to 0..m-1

То есть x = SUM 2^j*x|j

Как и всякая булева функция, x|j может быть представлена в дистрибутивной форме, а значит Ux|j может быть вычислена как Ux|j(i,z|j) = SUM x|j(k)(Controlled X(X(i) xor k), z|j)

NB. Мы не будем сейчас рассматривать вопросы минимизации количества гетов, например, путём вычисления минимальной дистрибутивной формы

Что дальше?

Мы поняли, что имея произвольную последовательность чисел, можно сформировать состояние регистра кубитов, которое будет отражать частотные характеристики этой последовательности

Рассмотрим теперь две последовательности чисел из 0..m-1

• x: 0..lx-1 to 0..m-1

• y: 0..ly-1 to 0..m-1

Можем ли мы, используя квантовые вычисления быстро проверить - совпадают или нет частотные характеристики этих двух последовательностей?

Пусть k - количество бит, достаточных для хранения чисел из диапазона 0..max(lx,ly)-1

Так же, как и ранее доопределим отображения x и y на недостающем диапазоне

• x: 0..lx-1 to 0..m-1 lx..2^k-1 to rand(m)

• y: 0..ly-1 to 0..m-1 ly..2^k-1 to rand(m)

И построим соответствующие трансформации

• Ux(i,z)=(i,z xor x(i))

• Uy(i,z)=(i,z xor y(i))

Вычисление скалярного произведения через инверсию и свёрку

Пусть у нас есть кольцо с операцией op и пара функций a и b, отображающих кольцо в поле, например комплексных чисел.

Операцией свёрки a и b мы будем называть функцию c = a x b, такую что c(i) = SUB a(ix)b(iy)|i=ix op iy

Пусть у нас есть кольцо с операцией op и функция f, отображающих кольцо в поле, например комплексных чисел.

Операцией инверсией аргумента назовём функцию inv f , такую что (inv f)(i) = f( -i ), где i op -i == 0

Скалярным произведением a и b называют (a,b) = SUM a(i)b(i) (=(a,b)(0) где (a,b)(i) = SUM a(ix)b(iy)|i=ix-iy)

Легко убедиться самостоятельно, что (a,b) = a x (inv b)

Пусть для регистров кубитов a и b

• a = SUM A(i)|i>

• b = SUM B(i)|i>

Тогда, если op:

• xor: (a,b)(i) = SUM A(ix)B(iy)|i>|i=ix xor ~iy

• add: (a,b)(i) = SUM A(ix)B(iy)|i>|i=ix + (-iy)

Что даёт нам вычисление функции-скалярного произведения a и b?

Ответ - асли A(i)~=B(i) для всех i и распределения отличны от тривиальных, то значение (a,b)(0) является максимальным (по модулю) среди других значений этой функции
А значит, если мы имеем пару регистров кубитов, содержащих частотные характеристики двух последовательностей, то

1. вычисление свёртки этих двух регистров,

2. проверка, что в результате значение |0> имеет максимальную вероятность,

3. даст нам ответ, что две статистики совпадают.

а если нет - то в качестве бонуса - значение |j>, которое имеет максимальную вероятность, вероятнее всего будет "сдвигом" при генерации второго распределения из первого (например, при шифровании гаммирования повторяющимся ключом, то есть окажется ключом шифра).

Как будет выглядеть вычисление скалярного произведения двух регистров кубитов?

Весьма просто - например, для xor - это будет трансформация scalar(a,b)=(a,a xor X(b)), а для add - scalar(a,b)=(a, a add X(b) add |1>)

Таким образом получилась следующая схема алгоритма

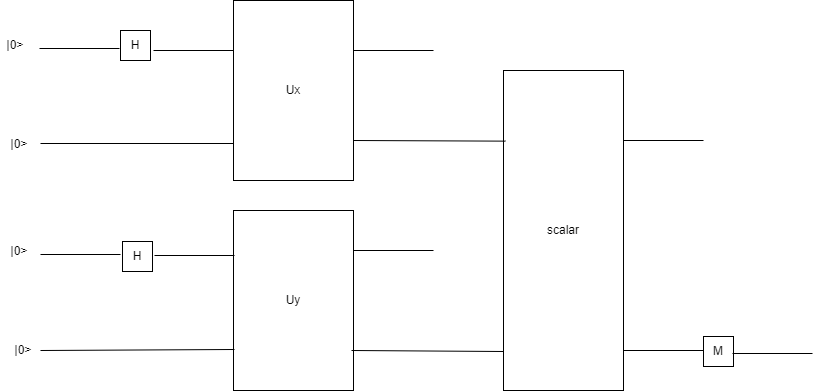
Проверим рассуждения написанием программы на Q-sharp и прогона тестов

1. Нам потребуются арифметические операции

• инкремента регистра (упорядоченного массива) кубитов

• суммирования значений отдельных кубитов в регистр (упорядоченный массив) кубитов

• измерение значения регистра (упорядоченного массива) кубитов в виде целого числа

• изменение значения регистра (упорядоченного массива) кубитов в соответствии с двоичным представлением целого числа (xor)

• копирование регистра кубитов в другой регистр кубитов

    /// # Описание
    /// увеличение на единицу числового значения в массиве кубитов (рассматриваемых как регистр)
    /// то есть трансформация вида |k> -> |k+1>
    operation Inc(target: Qubit[]) : Unit is Ctl {
        let n = Length(target);
        for idx in 1..n {
            Controlled X(target[0..n-idx-1], target[n-idx]);
        } 
    }

    /// # Описание
    /// Реализация операции суммирования, то есть трансформации |abcde...> -> |a+b+c+d+e+...>
    /// Это не самая эффективная реализация, но самая простая для кодирования
    operation Sum(qubits: Qubit[], register: Qubit[]) : Unit {
        for q in qubits {
            Controlled Inc([q], register);
        }
    }
    
    /// # Описание
    /// измерение значений (коллапсирование) кубитов в массиве (который рассматриваем как один регистр)
    /// и возврат числа (равного полученной двоичной последовательности)
    operation Measure(qubits: Qubit[]) : Int {
        let results = ForEach(M, qubits);
        let i = ResultArrayAsInt(results);
        return i;
    }

    /// # Описание
    /// побитовое изменение на указанную величину числового значения в массиве кубитов (рассматриваемых как регистр)
    /// то есть трансформация вида |k> -> |k xor value>
    operation Xor(target: Qubit[], value: Int) : Unit {
        let n = Length(target);
        let bools = IntAsBoolArray(value, n);
        for idx in 0..n-1 {
            if(bools[idx]) {
                X(target[idx]);
            }
        }
    }

    /// # Описание
    /// вспомогательный метод для копирования значений массива кубитов
    operation Copy(source: Qubit[], target: Qubit[]) : Unit {
        let n = Length(source);
        for i in 0..(n-1) {
            Controlled X([source[i]], target[i]);
        }
    }

2. Статистические методы

• получение в регистре кубитов значений с биномиальным распределением

• генерация случайного значения с биномиальным распределениемм (и xor сдвиг на заданные величину)

• генерация случайного значения с равновероятным распределением

    /// # Описание
    /// Реализация операции биноминального распределения, то есть n -> SUM SQRT(C(k,n))|k>
    operation Binom(n: Int, register: Qubit[]) : Unit {
        use qubits = Qubit[n] {
            ApplyToEach(H, qubits);
            Sum(qubits, register);
            ResetAll(qubits);
        }
    }

    /// # Описание
    /// Генерация случайного целого числа из диапазона 0..m-1
    /// Равновероятное распределение
    operation RandomRandom(m: Int) : Int {
        let k = BitSizeI(m-1);
        mutable i = 0;
        repeat {
            use qubits = Qubit[k] {
                ApplyToEach(H, qubits);
                set i = Measure(qubits);
                ResetAll(qubits);
            }
        }
        until (0<=i and i<m);
        return i;
    }

    /// # Описание
    /// Генерация случайного целого числа из диапазона 0..m-1
    /// Биноминальное распределение
    /// Дополнительный параметр a позволяет сместить распределение
    operation RandomBinom(a: Int, m: Int) : Int {
        let k = BitSizeI(m-1);
        use register = Qubit[k] {
            Binom(m-1, register); 
            let i = Measure(register);
            ResetAll(register);
            return Microsoft.Quantum.Bitwise.Xor(i,a)  % m;
        }
    }

3. Методы для реализации описанного алгоритма

• применение трансформации Ux по заданному массиву x

• вычисление скалярного произведения для двух регистров

• нахождение индекса элемента массива с наибольшим значением

• Многократное повторение измерения смещения распределения и возврат наилучшего (наиболее вероятного) значения смещения

    /// # Описание
    /// Выполнение трансформации для получения частотных характеристик последовательности чисел 0..m-1
    operation U(m: Int, l: Int, x: Int[], z: Qubit[]) : Unit {
        let kl = BitSizeI(l-1);
        let km = Length(z);
        let total = 2^kl;

        use (index) = (Qubit[kl]) {
            ApplyToEach(H, index);
            for i in 0..total-1 {
                Xor(index, i);
                mutable value = 0;
                if(i < l) {
                    set value = x[i];
                }
                else {
                    set value = RandomRandom(m);
                }
                let bools = IntAsBoolArray(value, km);
                for j in 0..km-1 {
                    if(bools[j]) {
                        Controlled X(index, z[j]);
                    }
                }
                Xor(index, i);
            }
            ResetAll(index);
        }
    }
    
    /// # Описание
    /// Вычисление скалярного произведения содержимого регистров кубитов
    operation ScalarTransformation(a: Qubit[], b: Qubit[]) : Unit
    {
        let n = Length(a);
        ApplyToEach(X, b);
        for i in 0..n-1 {
            Controlled X([a[i]], b[i]);
        }
    }

    /// # Описание
    /// Нахождение индекса элемента с максимальным значением в массиве чисел
    operation IndexOfMax(arr: Int[]) : Int {
        mutable result = 0;
        let n = Length(arr);
        for i in 1..n-1 {
            if(arr[result]<arr[i]) {
                set result = i;
            }
        }
        return result;
    }


    /// # Описание
    /// Многократное повторение измерения смещения распределения для заданных двух массивов
    /// и возврат лучшего (наиболее верооятного) значения смещения
    operation TestArrays(m: Int, x: Int[], y: Int[], tests: Int): (Int, Int[]) {
        let lx = Length(x);
        let ly = Length(y);
        mutable l = lx;
        if(ly>lx) {
            set l = ly;
        }
        let kl = BitSizeI(l-1);
        let km = BitSizeI(m-1);
        let s = 2^km;

        // Аллокируем массив для подсчёта количества исходов экспериментов
        mutable arr = [0, size = s];
        
        for _ in 1..tests {
            use (a, b) = (Qubit[km], Qubit[km]){
                
                U(m, l, x, a);
                U(m, l, y, b);

                ScalarTransformation(a, b);

                let i = Measure(b);
                
                // Добавим полученное значение в счётчик
                set arr w/= i <- arr[i] + 1;
                
                ResetAll(a);
                ResetAll(b);
            }

        }
        return (IndexOfMax(arr), arr);
    }

    /// # Описание
    /// Многократное повторение измерения смещения распределения для двух массивов
    /// которые создаются с помощью заданных генераторов случайных числел
    /// и возврат лучшего (наиболее верооятного) значения смещения

    operation Test(m: Int, randX: (Int)=>Int, randY: (Int)=>Int, l: Int, tests: Int) : (Int, Int[]) {
        mutable x = [0, size = l];
        mutable y = [0, size = l];

        for i in 0..l-1 {
            set x w/= i <- randX(m);
        }
        for i in 0..l-1 {
            set y w/= i <- randY(m);
        }
        
        Message($"x = {x} / y = {y}");

        return TestArrays(m, x, y, tests);
    }

4. И, собственно, сам тест с параметрами запуска

    @EntryPoint()
    operation Main(n: Int, l: Int, t: Int) : Unit {
        let m=2^n;

        Message("Hello quantum world!");
        Message($"Binom0/Binom0: {Test(m, RandomBinom(0,_), RandomBinom(0,_), l, t)}");
        Message($"Binom0/Binom1: {Test(m, RandomBinom(0,_), RandomBinom(1,_), l, t)}");
        Message($"Binom3/Binom1: {Test(m, RandomBinom(3,_), RandomBinom(1,_), l, t)}");
        Message($"Binom0/Random: {Test(m, RandomBinom(0,_), RandomRandom, l, t)}");
        Message($"Random/Random: {Test(m, RandomRandom, RandomRandom, l, t)}");
        Message($"Random/Binom0: {Test(m, RandomRandom, RandomBinom(0,_), l, t)}");
    }

Полный код программы можете взять здесь https://github.com/dprotopopov/qcompare

Запускаем и получаем результат ...

PS C:\Projects\qcompare> dotnet run -n 3 -l 32 -t 100
Hello quantum world!
x = [7,6,5,4,2,3,3,3,2,4,4,5,6,3,4,4,5,4,4,4,5,4,3,4,5,4,5,4,6,3,2,3] / y = [2,5,1,2,2,3,6,6,3,2,1,5,5,5,3,3,6,5,2,4,4,6,6,2,4,5,5,4,4,4,3,3]
Binom0/Binom0: (7, [15,16,16,6,4,10,15,18])
x = [4,5,6,3,5,3,2,5,7,6,3,4,5,1,2,1,4,2,4,2,1,4,4,2,2,6,2,3,3,5,4,3] / y = [4,5,4,2,3,2,4,5,0,3,1,2,4,2,4,5,3,2,2,5,2,3,5,2,2,2,2,2,5,7,2,3]
Binom0/Binom1: (1, [14,21,9,18,3,6,16,13])
x = [3,5,7,5,6,1,1,7,1,7,6,1,1,7,7,1,1,0,7,0,6,1,1,6,6,4,6,1,0,0,6,7] / y = [2,5,5,2,2,4,0,5,3,2,5,7,4,5,2,0,5,5,5,0,2,5,2,0,2,3,2,4,4,0,5,4]
Binom3/Binom1: (2, [9,6,24,20,18,10,10,3])
x = [6,4,4,2,2,3,3,4,3,4,2,3,3,4,3,4,4,3,4,2,3,5,4,2,5,4,4,3,3,3,5,5] / y = [6,6,0,2,4,1,2,5,3,1,0,2,4,4,3,3,5,0,1,6,3,2,1,3,2,1,0,0,5,7,4,0]
Binom0/Random: (1, [13,16,11,15,7,9,15,14])
x = [4,4,3,4,4,1,3,7,5,6,1,3,1,4,0,1,5,4,0,0,1,2,4,5,5,0,0,4,2,6,7,3] / y = [4,6,7,5,2,4,5,2,6,6,5,7,0,4,3,0,5,3,0,1,7,3,6,7,6,7,0,7,4,1,5,1]
Random/Random: (3, [11,10,11,21,9,10,18,10])
x = [7,2,3,3,5,7,4,4,3,0,2,0,5,3,0,4,7,6,6,7,7,6,2,4,2,6,7,4,0,0,0,4] / y = [5,3,5,5,4,3,3,4,3,3,2,5,3,3,3,2,4,3,5,3,4,6,2,4,4,3,4,3,4,3,3,5]
Random/Binom0: (7, [10,15,10,15,14,7,12,17])

Вроде всё правильно ...

Примечание. То, что Binom0/Binom0 совпало со смещением 7 - то это тоже правильный ответ, поскольку биноминальное распределение симметрично, то есть С(k, 7) = C(k xor 7, 7)

Ссылки

• https://github.com/dprotopopov/qcompare

• https://learn.microsoft.com/ru-ru/azure/quantum/user-guide/host-programs?tabs=tabid-copilot

• https://learn.microsoft.com/ru-ru/training/modules/qsharp-create-first-quantum-development-kit/2-install-quantum-development-kit-code

Ранее

• Изучаем Q#. Алгоритм Гровера. Не будите спящего Цезаря

• Изучаем Q#. Делаем реализацию биноминального распределения

• Первые шаги в Q#. Алгоритм Дойча