Нормальное распределение по-пацански: часть 1 / forpes.ru

Главная
Нормальное распределение по-пацански: часть 1

Нормальное распределение по-пацански: часть 1

18.12.2023 10:34

start_ds 7 1400 Источник

В интернете маловато доступного материала про нормальное распределение на русском. И мы, вдохновившись видео от 3b1b про ЦПТ и статьёй про нормальное распределение от Boris Again, решили написать свою.

Её цель - дать читателю интуитивное понимание нормального распределения: почему его график – колокол, его формула выглядит так страшно, где нормальное распределение встречается в повседневной жизни и как оно связано с Центральной Предельной Теоремой.

Сумма случайных величин

Для начала давайте определим, что такое случайная величина.

Случайной называют величину, которая в результате испытания примет одно и только одно числовое значение, зависящее от случайных факторов и заранее непредсказуемое.

В пример случайной величины обычно приводят бросок монетки, игрального кубика, вытягивание карты из колоды и т. д.
Возьмем монетку. Тогда наша случайная величина будет следующей:

$X = \begin{cases} 1, & p = 0.5 \\ 0 & p = 0.5 \end{cases}$

Давайте подбросим монетку 10 раз и каждый раз будем записывать 0, если выпал орёл, и 1, если выпала решка. Проведем симуляцию этого эксперимента в python

Код

import random
import matplotlib.pyplot as plt

def simulate_coin_toss(num_tosses):
    results = []
    for _ in range(num_tosses):
        # Возможные исходы – решка (1) и орёл (0). Они равновероятны 
        outcome = random.choice([0, 1]) 
        results.append(outcome)
    return results

def plot_coin_toss_results(results):
    heads_count = results.count(1)
    tails_count = results.count(0)
    
    labels = ['Решка', 'Орёл']
    counts = [heads_count, tails_count]
    
    plt.bar(labels, counts, color=['blue', 'green'])
    plt.title(f'Симуляция {len(results)} бросков монеты')
    plt.xlabel('Исход')
    plt.ylabel('Количество')
    plt.show()


num_tosses = 10
toss_results = simulate_coin_toss(num_tosses)
print("Результаты 10 бросков монеты:", toss_results)
plot_coin_toss_results(toss_results)

А теперь давайте возьмем другую случайную величину. Это будет уже не случайная величина, которая принимает равновероятно значения 1 или 0, а случайная величина, обозначающая количество выпавших решек в эксперименте с n бросками монетки.

То есть:

$Y = \sum_{i=1}^{n} X_i$

Проведем симуляцию m экспериментов c n бросками в каждом из них в Python

Код

import random
import matplotlib.pyplot as plt

def simulate_coin_toss(num_tosses):
    results = []
    for _ in range(num_tosses):
        # Возможные исходы – решка (1) и орёл (0). Они равновероятны
        outcome = random.choice([0, 1])
        results.append(outcome)
    return results

def run_experiments(num_experiments, num_tosses_per_experiment):
    experiment_results = [0] * (num_tosses_per_experiment + 1)
    for _ in range(num_experiments):
        toss_results = simulate_coin_toss(num_tosses_per_experiment)
        experiment_results[sum(toss_results)] += 1
    return experiment_results

def plot_experiment_results(ax, experiment_results, experiments_num):
    ax.bar(range(1, len(experiment_results)+1), experiment_results, color='blue')
    ax.set_title(f'{experiments_num} экс, {len(experiment_results)-1} брос')
    ax.set_xlabel('Количество решек')
    ax.set_ylabel('Количество экспериментов')
    left_lim = 0
    right_lim = len(experiment_results) - 1
    while experiment_results[left_lim] == 0:
      left_lim += 1
    while experiment_results[right_lim] == 0:
      right_lim -= 1
    ax.set_xlim(left_lim, right_lim)


num_experiments = 10
num_tosses_per_experiment = 10

all_experiment_results = run_experiments(num_experiments, num_tosses_per_experiment)


fig, axes = plt.subplots(2, 3, figsize=(15, 8))

# Разворачиваем массив подграфиков в одномерный массив
axes = axes.flatten()

for i in range(3):
    toss_results = simulate_coin_toss(num_tosses_per_experiment)

    # Используем текущий подграфик для построения результатов
    plot_experiment_results(axes[i], run_experiments(num_experiments=10**(i+1), num_tosses_per_experiment=10), experiments_num=10**(i+1))
for i in range(3):
    toss_results = simulate_coin_toss(num_tosses_per_experiment)
    plot_experiment_results(axes[i+3], run_experiments(num_experiments=10**(i+3), num_tosses_per_experiment=10**(3)), experiments_num=10**(i+3))
    print('Done')

# Регулировка расположения подграфиков
plt.tight_layout()

# Показываем графики
plt.show()

По картинке можно увидеть, что, при увеличении количества экспериментов и количества бросков в каждом эксперименте, график эмпирической плотности нашей случайной величины Y напоминает знакомый колокол.
Проверим, что будет, если мы изменим случайную величину X. Останется ли график распределения Y такой же?

Пусть теперь X - количество очков, которое выпало на подброшенном кубике.

$X = \begin{cases} 1, & p = \frac{1}{6} \\ 2, & p = \frac{1}{6} \\ 3, & p = \frac{1}{6} \\ 4, & p = \frac{1}{6} \\ 5, & p = \frac{1}{6} \\ 6, & p = \frac{1}{6} \\ \end{cases}$

Случайная величина Y остается прежней

$Y = \sum_{i=1}^{n} X_i$

Снова проведем симуляцию m экспериментов с n бросками в каждом

Код

import random
import matplotlib.pyplot as plt

def simulate_dice_roll(num_rolls):
    results = []
    for _ in range(num_rolls):
        # Теперь возможные исходы - все числа на гранях кубика
        outcome = random.choice([1, 2, 3, 4, 5, 6])
        results.append(outcome)
    return results

def run_experiments(num_experiments, num_rolls_per_experiment):
    experiment_results = [0] * (num_rolls_per_experiment*6 + 1)
    for _ in range(num_experiments):
        rolls_results = simulate_dice_roll(num_rolls_per_experiment)
        experiment_results[sum(rolls_results)] += 1
    return experiment_results

def plot_experiment_results(ax, experiment_results, experiments_num):
    ax.bar(range(1, len(experiment_results)+1), experiment_results, color='green')
    ax.set_title(f'm = {experiments_num} экс, n = {len(experiment_results)-1} брос')
    ax.set_xlabel('Y - Сумма выпавших очков')
    ax.set_ylabel('Количество экспериментов')
    left_lim = 0
    right_lim = len(experiment_results) - 1
    while experiment_results[left_lim] == 0:
      left_lim += 1
    while experiment_results[right_lim] == 0:
      right_lim -= 1
    ax.set_xlim(left_lim, right_lim)


fig, axes = plt.subplots(2, 3, figsize=(15, 8))

# Разворачиваем массив подграфиков в одномерный массив
axes = axes.flatten()

for i in range(3):
    toss_results = simulate_coin_toss(num_tosses_per_experiment)

    # Используем текущий подграфик для построения результатов
    plot_experiment_results(axes[i], run_experiments(num_experiments=10**(i+1), num_rolls_per_experiment=10), experiments_num=10**(i+1))
for i in range(3):
    toss_results = simulate_coin_toss(num_tosses_per_experiment)
    plot_experiment_results(axes[i+3], run_experiments(num_experiments=10**(i+3), num_rolls_per_experiment=10**(3)), experiments_num=10**(i+3))
    print('Done')

# Регулировка расположения подграфиков
plt.tight_layout()

# Показываем графики
plt.show()

Видим, что так же, с увеличением количества бросков в эксперименте и количества экспериментов, график эмпирической плотности распределения становится похож на колокол.

Причем когда мы увеличиваем количество бросков, у нас как бы увеличивается “разрешение” этого колокола, а когда увеличиваем количество экспериментов, колокол становится более явным.

Окей, мы поняли, что сумма случайной величины, вне зависимости от того, сколько значений она принимает, с увеличением количества экспериментов становится похожей на колокол. Но мы рассмотрели случайные величины с равновероятными исходами. Может, если кубик будет со смещенным центром тяжести, для него это не будет работать?

$X = \begin{cases} 1, & p = \frac{1}{10} \\ 2, & p = \frac{1}{10} \\ 3, & p = \frac{1}{10} \\ 4, & p = \frac{1}{10} \\ 5, & p = \frac{3}{10} \\ 6, & p = \frac{3}{10} \\ \end{cases}$

Код

import random
import matplotlib.pyplot as plt

def simulate_dice_roll(num_rolls):
    results = []
    for _ in range(num_rolls):
        # Возможные исходы - все числа на гранях кубика. Но числа 5 и 6 выпадают с большей вероятностью
        outcome = random.choice([1, 2, 3, 4, 5, 5, 5, 6, 6, 6])
        results.append(outcome)
    return results

def run_experiments(num_experiments, num_rolls_per_experiment):
    experiment_results = [0] * (num_rolls_per_experiment*6 + 1)
    for _ in range(num_experiments):
        rolls_results = simulate_dice_roll(num_rolls_per_experiment)
        experiment_results[sum(rolls_results)] += 1
    return experiment_results

def plot_experiment_results(ax, experiment_results, experiments_num):
    ax.bar(range(1, len(experiment_results)+1), experiment_results, color='orange')
    ax.set_title(f'm = {experiments_num} экс, n = {len(experiment_results)-1} брос')
    ax.set_xlabel('Y - Сумма выпавших очков')
    ax.set_ylabel('Количество экспериментов')
    left_lim = 0
    right_lim = len(experiment_results) - 1
    while experiment_results[left_lim] == 0:
      left_lim += 1
    while experiment_results[right_lim] == 0:
      right_lim -= 1
    ax.set_xlim(left_lim, right_lim)


fig, axes = plt.subplots(2, 3, figsize=(15, 8))

# Разворачиваем массив подграфиков в одномерный массив
axes = axes.flatten()

for i in range(3):
    toss_results = simulate_coin_toss(num_tosses_per_experiment)

    # Используем текущий подграфик для построения результатов
    plot_experiment_results(axes[i], run_experiments(num_experiments=10**(i+1), num_rolls_per_experiment=10), experiments_num=10**(i+1))
for i in range(3):
    toss_results = simulate_coin_toss(num_tosses_per_experiment)
    plot_experiment_results(axes[i+3], run_experiments(num_experiments=10**(i+3), num_rolls_per_experiment=10**(3)), experiments_num=10**(i+3))
    print('Done')

# Регулировка расположения подграфиков
plt.tight_layout()

# Показываем графики
plt.show()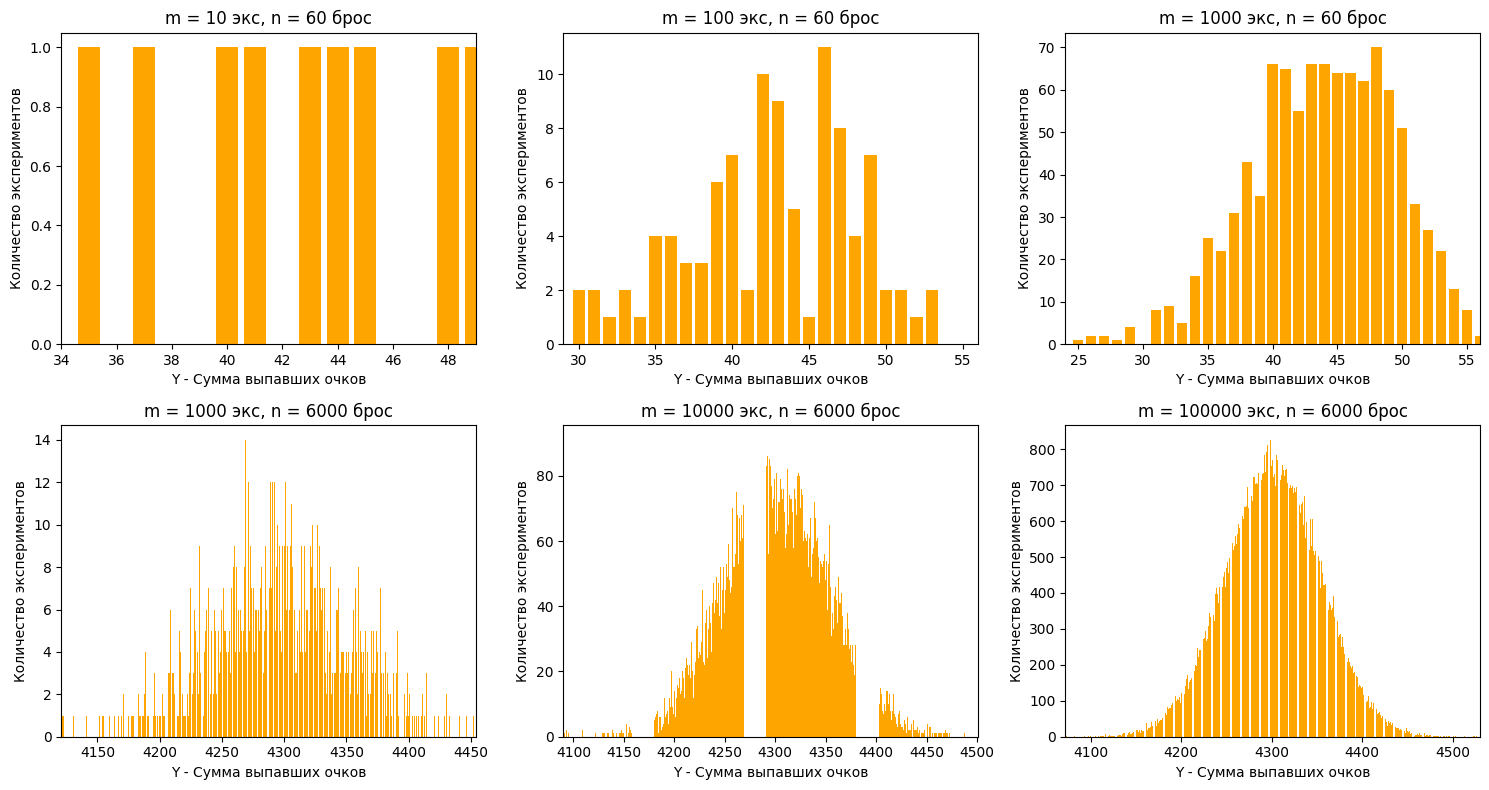

Эмпирическое распределение величин с разновероятными исходами тоже стремится к колоколу

Почему так получается?

Давайте в качестве примера случайной величины X возьмем обычный игральный кубик. Вот наша случайная величина:

$X = \begin{cases} 1, & p = \frac{1}{6} \\ 2, & p = \frac{1}{6} \\ 3, & p = \frac{1}{6} \\ 4, & p = \frac{1}{6} \\ 5, & p = \frac{1}{6} \\ 6, & p = \frac{1}{6} \\ \end{cases}$

Теперь будем бросать кубик два раза. Первый бросок обозначим $X_1$ , второй бросок обозначим $X_2$
Построим распределение случайной величины $X_1 + X_2$. Минимальное значение, которое она принимает - 2. Это может произойти, когда на обоих кубиках выпала единица. То есть $P_{X_1+X_2=2}=P_{X_1=1}\cdot P_{X_2=1} = \frac{1}{6} \cdot \frac{1}{6} = \frac{1}{36}$ .
Обобщить это можно следующей формулой:

$\mathbb{P}(X_1+X_2=k)=\sum_{i=1}^{6}{\mathbb{P}(X_1=i)\cdot \mathbb{P}(X_2=k-i)}$

А вот момент из видео 3b1b, который отлично демонстрирует распределение

Теперь поработаем со смещенным кубиком

$X = \begin{cases} 1, & p = \frac{1}{16} \\ 2, & p = \frac{7}{16} \\ 3, & p = \frac{1}{16} \\ 4, & p = \frac{1}{16} \\ 5, & p = \frac{3}{16} \\ 6, & p = \frac{3}{16} \\ \end{cases}$

Код

import numpy as np
import matplotlib.pyplot as plt

# Задаем значения на игральном кубике
dice_values = np.arange(1, 7)

# Задаем вероятности (смещенный кубик)
probabilities = [1/16, 7/16, 1/16, 1/16, 3/16, 3/16]

# Строим график
plt.bar(dice_values, probabilities, color='blue', alpha=0.7, label='Смещенный кубик')
plt.xlabel('Значение на кубике')
plt.ylabel('Вероятность')
plt.title('Распределение вероятности смещенного игрального кубика')
plt.legend()
plt.show()

Пойдем по такому же алгоритму:

$\mathbb{P}(X_1+X_2=k)=\sum_{i=1}^{6}{\mathbb{P}(X_1=i)\cdot \mathbb{P}(X_2=k-i)}$

Построим распределение суммы случайных величин:

Что-то не похоже на колокол :( . А если мы увеличим количество бросков кубика? В эксперименте прокатило, может и тут получится?

Запишем формулу вероятности суммы $n$ случайных величин в общем виде

$\mathbb{P}(X_1+X_2+...+X_n=k)=\\=\sum_{i_1=1}^{6}\sum_{i_2=1}^{6}...\sum_{i_{n-1}=1}^{6}\mathbb{P}(X_1=i_1)\cdot \mathbb{P}(X_2=i_2)\cdot...\cdot\mathbb{P}(X_n = k -(i_1+...+i_n-1))$

Напишем по этой формуле код, который построит нам графики

Код

from itertools import product
import math
def plot_experiment_results(ax, variables_amount, probabilities):
    sum_probab = np.zeros(variables_amount*6) 
    for prod in product([1, 2, 3, 4, 5, 6], repeat=variables_amount):
        product_probab = math.prod([probabilities[i-1] for i in prod])
        sum_probab[sum(prod)-1] += product_probab
    ax.bar([i for i in range(1, variables_amount*6 + 1)], sum_probab, color='orange')
    ax.set_xlabel('Значение суммы')
    ax.set_ylabel('Вероятность')
    ax.set_title('Распределение суммы {0} величин'.format(variables_amount))
fig, axes = plt.subplots(2, 3, figsize=(15, 8))
# Разворачиваем массив подграфиков в одномерный массив
axes = axes.flatten()
for num, ax in enumerate(axes):
  plot_experiment_results(ax, num+2, probabilities)
# Регулировка расположения подграфиков
plt.tight_layout()

# Показываем графики
plt.show()

Видим, что с увеличением количества бросков кубиков мы опять пришли к колоколу, только на этот раз этот колокол - не эмпирическое, а теоретическое распределение суммы случайных величин

Сравним с эмпирическим распределением при 10 000 экспериментах:

Код

import random
import matplotlib.pyplot as plt
import numpy as np

def simulate_dice_roll(num_rolls):
    results = []
    for _ in range(num_rolls):
        # Возможные исходы - все числа на гранях кубика. Но числа 5 и 6 выпадают с большей вероятностью
        outcome = random.choice([1]+[2]*7+[3]+[4]+[5]*3+[6]*3)
        results.append(outcome)
    return results

def run_experiments(num_experiments, num_rolls_per_experiment):
    experiment_results = [0] * (num_rolls_per_experiment*6 + 1)
    for _ in range(num_experiments):
        rolls_results = simulate_dice_roll(num_rolls_per_experiment)
        experiment_results[sum(rolls_results)] += 1
    experiment_results = np.array(experiment_results)
    return experiment_results / sum(experiment_results)

def plot_experiment_results_1(ax, experiment_results, experiments_num):
    ax.bar(range(1, len(experiment_results)), experiment_results[1:], color='blue', alpha=1, label="Эмпирическое распределение")



fig, axes = plt.subplots(2, 3, figsize=(15, 8))

# Разворачиваем массив подграфиков в одномерный массив
axes = axes.flatten()

for i in range(6):
    # Используем текущий подграфик для построения результатов
    plot_experiment_results_1(axes[i], run_experiments(num_experiments=100000, num_rolls_per_experiment=i+2), experiments_num=100000)

for num, ax in enumerate(axes):
  plot_experiment_results(ax, num+2, probabilities)

# Регулировка расположения подграфиков
plt.tight_layout()

# Показываем графики
plt.show()

Мы подобрались к одному и тому же колоколу с двух сторон - с эмпирической и с теоретической.

Итак, что же самое главное мы выяснили после всех проведенных манипуляций?
График распределения суммы случайных величин при увеличении их количества образует колокол.
Конечно, это правило действует не во всех ситуациях, для него должны быть выполнены определенные условия, о которых мы расскажем в следующих статьях

Надеемся, после прочтения этого текста вам стало понятно, откуда в принципе в теории вероятностей возник колокол. В следующих частях мы попробуем как-то описать этот колокол формулой и разберемся в Центральной Предельной Теореме

Stay tuned!

Комментарии (7)

nikolz
18.12.2023 11:38
#26279010
Вообще-то, Вы просто проверяете программный датчик случайных чисел, у которого какой-то закон распределения значений и о "чудо" у этого датчика похоже на колокол. Так это уже заложено в его алгоритм. Верно?

Может монетку покидаете 10000 раз по 1000 раз?
1. Zenitchik
  18.12.2023 11:38
  #26279132
  А в чём проблема? Алгоритм показывает, как имея генератор случайных чисел с равномерным распределением, построить генератор с колоколообразным распределением.
  1. nikolz
    18.12.2023 11:38
    #26279192
    Т е статья именно о том, как построить генератор с колоколообразным распределением. Верно?
    
    А причем здесь нормальное распределение?
    
    Вот здесь вроде бы написано как сделать датчик нормального закона распределения.
    
    https://habr.com/ru/articles/331560/
    
    Zenitchik
    18.12.2023 11:38
    #26279236
    Нет, я бы не сказал, что это инструкция по построению такого генератора - показан дюже неоптимальный алгоритм для практического применения.
    
    Скорее, это статья о том, что сумма равномерно распределённых случайных чисел, распределена колоколообразно. А в пределе на бесконечности - нормально.
    
    nikolz
    18.12.2023 11:38
    #26279246
    "А в пределе на бесконечности - нормально." В статье про это ничего нет. Приведите доказательство, так как программный датчик периодический. Бесконечностью не пахнет.
    
    Zenitchik
    18.12.2023 11:38
    #26279382
    Логично.

Jury_78
18.12.2023 11:38
#26279152
В интернете маловато доступного материала про нормальное распределение на русском.

Неожиданно... По мне так этого добра более чем, но пусть будет еще... :)