Многорукие бандиты в задаче ритейла / forpes.ru

Главная
Многорукие бандиты в задаче ритейла

Многорукие бандиты в задаче ритейла

28.12.2023 10:31

muxeu 2 1300 Источник

Введение

В настоящее время набирают популярность модели Reinforcement Learning для решения прикладных задач бизнеса. В этой статье мы рассмотрим подмножество этих моделей, а именно многоруких бандитов (multi-armed bandits). Также мы:

обсудим, какие задачи теоретически могут быть решены с помощью этих моделей;
рассмотрим некоторые популярные реализации моделей многоруких бандитов;
опишем симулятор ценообразования, применим эти алгоритмы в нём и сравним их эффективность.

Многорукие бандиты – практические примеры

Идея методов многоруких бандитов заключается в том, что исследуется множество возможных вариантов (“ручек”) так, чтобы найти ручку с максимальным выигрышем и с минимальными затратами на поиск этой самой ручки. Подход многоруких бандитов может быть полезен в ситуациях, когда у нас есть фиксированный набор действий/вариантов, которые нацелены на увеличение некоторого показателя, но об отклике на это действие заранее мы практически ничего не знаем.

Приведём несколько примеров, где может быть применима такая логика.

Пример из маркетинга
Предположим, что мы начисляем бонусные баллы клиентам с целью решения каких-то маркетинговых задач. Клиенту можно предложить 500, 1000 или 1500 баллов и, очевидно, что эффекты по итоговой выручке/трафику будут разными.
Ещё схожий пример можно взять из ритейла техники: при покупке смартфона можно предложить скидку в зависимости от минимальной цены аксессуара(ов), соответственно, в такой ситуации многорукий бандит будет искать оптимум по условиям скидки, что проиллюстрировано в таблице:

Условие	Минимальная стоимость аксессуаров	Скидка	Спрос
№1	1000	500	?
№2	1500	500	?
№3	2000	1000	?

Пример из ценообразования
Довольно часто встречается ситуация, когда история продаж товара содержит только одну цену, например, из-за новизны товара, или из-за специфики модели ценообразования и спроса. В таких случаях, мы ничего не знаем о том, как бы он продавался по другой цене. Потенциально цена может быть неоптимальной с точки зрения выручки или валового дохода, в этом случае для выбора оптимальной цены также могут помочь многорукие бандиты:

цена	80	90	100	110	120
продажи, шт.	?	?	500	?	?
продажи, руб.	?	?	500000	?	?
валовый доход, руб.	?	?	100000	?	?

Поиск кратчайшего пути
Интересный пример применения многоруких бандитов был рассмотрен авторами статьи, в которой ставится задача поиска оптимального пути в графе из одной вершины в другую. Про граф известно только наличие связей, но не стоимость переходов через промежуточные вершины (такая задача может возникнуть, например, в построении оптимальных маршрутов), так как выбор маршрута является дискретным, то здесь может быть применена стратегия многоруких бандитов.

Симулятор задачи ценообразования для сети магазинов

Создадим симулятор, в котором под средой мы будем понимать множество магазинов с известным случайным распределением спроса на товар, а агентом будет какая-то математическая модель, использующая данные среды для расчёта цен. В симуляторе также добавим ограничения офлайн магазина:

Допустимо изменять цену в магазине не чаще одного раза в неделю;
Цена может меняться не более чем на 10%.

Для генерации спроса будем использовать следующую модель спроса (которую мы уже применяли в одной из предыдущих статей):

$\lambda(p) = Q_0 \cdot \exp\bigg(E \cdot \Big(\frac{p}{p_0} - 1\Big)\bigg),$ $Q(p) \sim Poisson(\lambda(p)),$

где
- средний спрос в шт/кг,
- текущая цена,
- искомая цена, которая берется из заданной сетки цен(ручек), $p \in \{P_1, P_2, ..., P_m \}$ ,
- эластичность спроса от цены.

Оборот и прибыль определяются следующими выражениями:

$S = p \cdot Q(p),$ $M = (p - c) \cdot Q(p),$

где - себестоимость товара.

Оптимальное решение по цене для прибыли в предложенной модели можно найти аналитически: $p^* = (c \cdot E - p_0) / E$ .

Ниже приведены графики спроса и прибыли, на которых видно, что оптимум по прибыли в этой модели сильно зависит от значения эластичности:

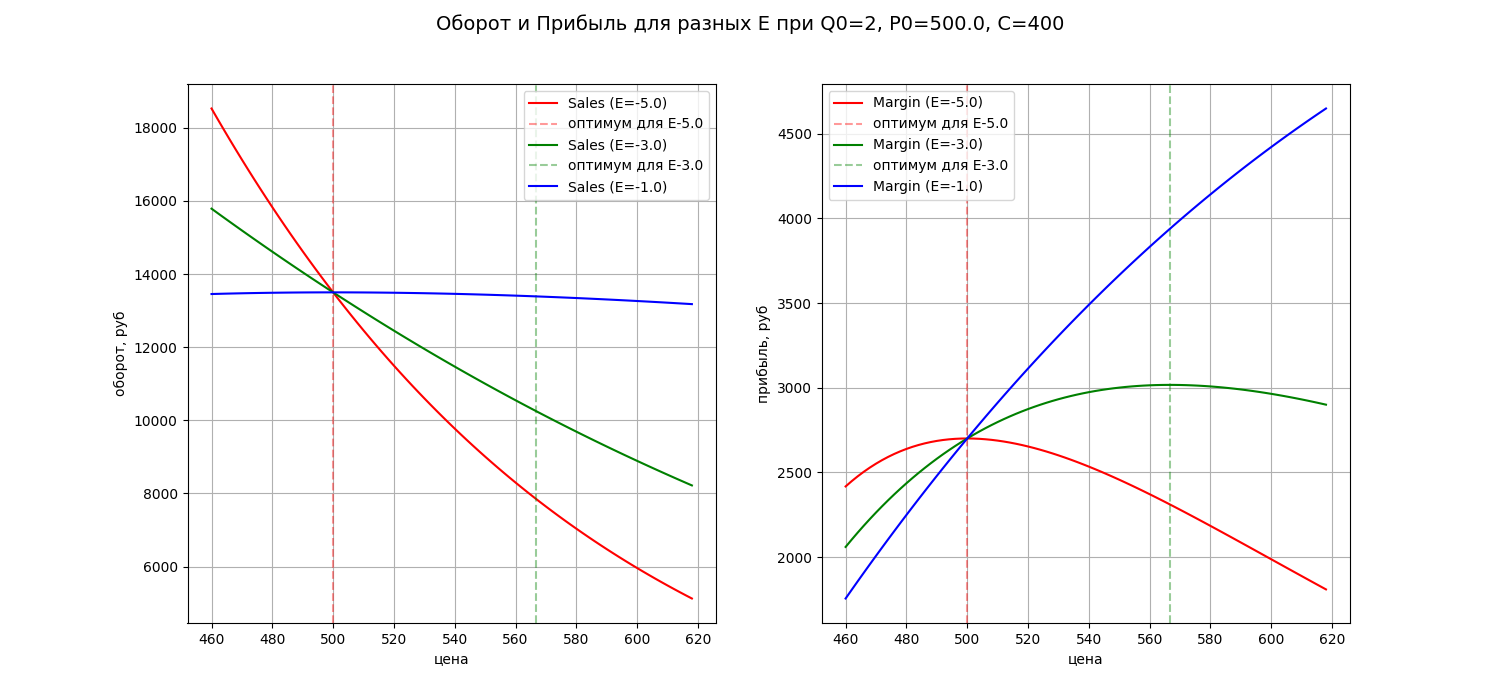
Эластичность
Если есть исторические данные спроса при разных ценах, то можно аппроксимировать зависимость продаж от цены, откуда получить параметр эластичности. Для этого будем использовать линейную пуассоновскую модель следующего вида:

$\lambda(p) = \exp(a \cdot p + b),$

учитывая, что

$\lambda(p) = Q_0 \cdot \exp\bigg(E \cdot \Big(\frac{p}{p_0} - 1\Big)\bigg) = \exp\bigg(\frac{E}{p_0}\cdot p + \ln(Q_0) - E\bigg)$

можно, сопоставляя, формулы выше выразить параметры модельного спроса через параметры аппроксимации следующим образом: $E = a\cdot p_0, Q_0 = \exp(b + a\cdot p_0)$ .
Найденную таким образом зависимость спроса от цены мы можем использовать для поиска лучшего решения на заданной сетке цен, а полученное решение будем далее сравнивать с решениями других моделей.

Стратегии многоруких бандитов

Сделаем краткое описание алгоритмов, которые будем сравнивать в симуляторе ценообразования, в этом контексте некоторые детали будет проще пояснять.
Для задачи ценообразования ручкой является одна из перебираемых цен на товар, наградой или откликом – прибыль, полученная для конкретной цены, сожаление (Regret) – недополученная прибыль. Так как мы знаем точное решение, то Regret можно точно рассчитать как разницу откликов между текущей и оптимальной (если точнее, то ближайшая к оптимуму цена исследуемого множества

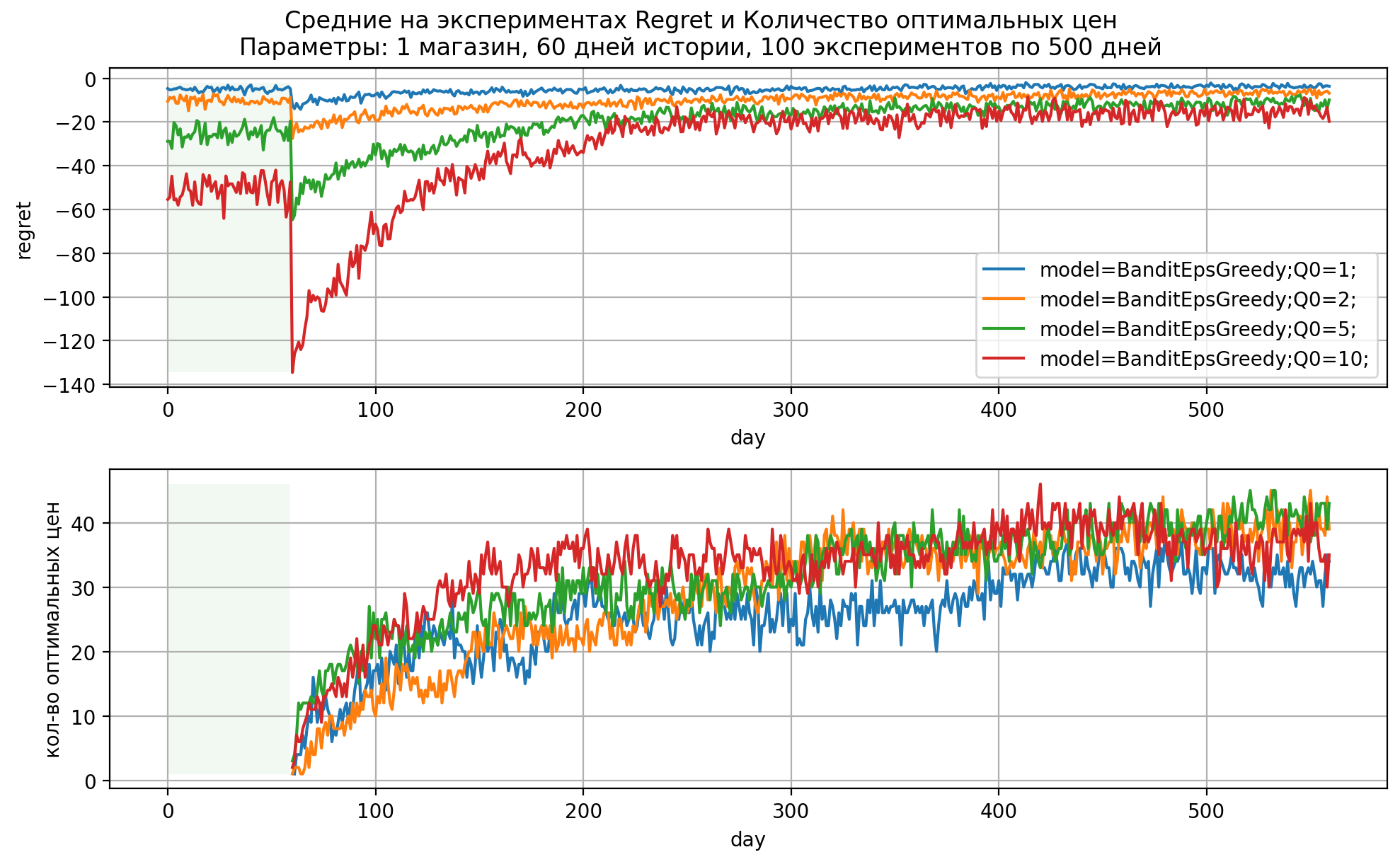
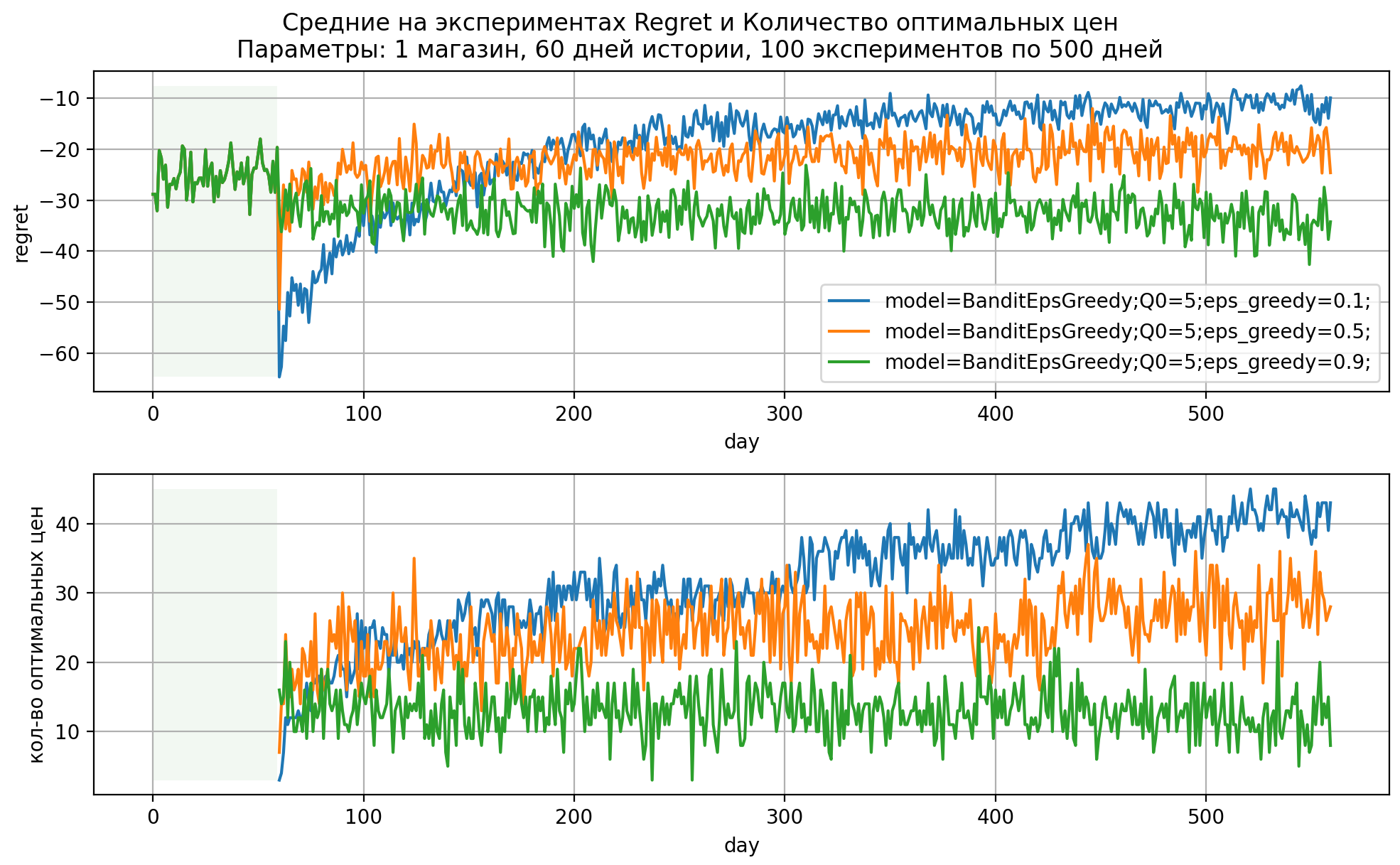
Жадные стратегии greedy/epsilon-greedy/epsilon-decay

Жадная (greedy) стратегия заключается в выборе лучшей ручки по собранному за время экспериментов отклику. Если отклик является не случайным и стационарным, то данная стратегия точно скажет, какая ручка лучшая. В реальности отклик является случайной величиной, поэтому после проведения исследования не гарантируется, что ручка с наибольшим средним будет действительно лучшей.

В каком-то смысле жадная стратегия выступает аналогом АБ-тестирования для рассматриваемых ручек, в начале эксперимента цены случайно в одинаковых количествах отправляются в магазины на всю продолжительность эксперимента, далее выбирается лучшая ручка по среднему отклику.

Эпсилон-жадная (eps-greedy) стратегия является модификацией greedy стратегии.
В ней с вероятностью $1- \epsilon$ мы выбираем лучшую на данный момент эксперимента ручку, а с вероятностью eps – случайную любую другую. Таким образом появляется возможность дополнительно проверять другие ручки, что позволяет повысить шансы на выбор лучшей ручки в ходе итераций.

В eps-greedy стратегии мы асимптотически $100 \cdot \epsilon \ \%$ действий тратим на исследование, что может быть затратно. Стратегия eps-decay снижает $\epsilon$ во времени, например, по правилу $\epsilon_0/(1 + j \cdot d)$ , где – номер итерации, – параметр скорости затухания $\epsilon$ . Если , то стратегия совпадает с eps–greedy при $\epsilon = \epsilon_0$ .

Рис 3. Динамика показателей модели EpsGreedy

Рис 3.1 Динамика показателей модели EpsGreedy при различных Q0

Softmax
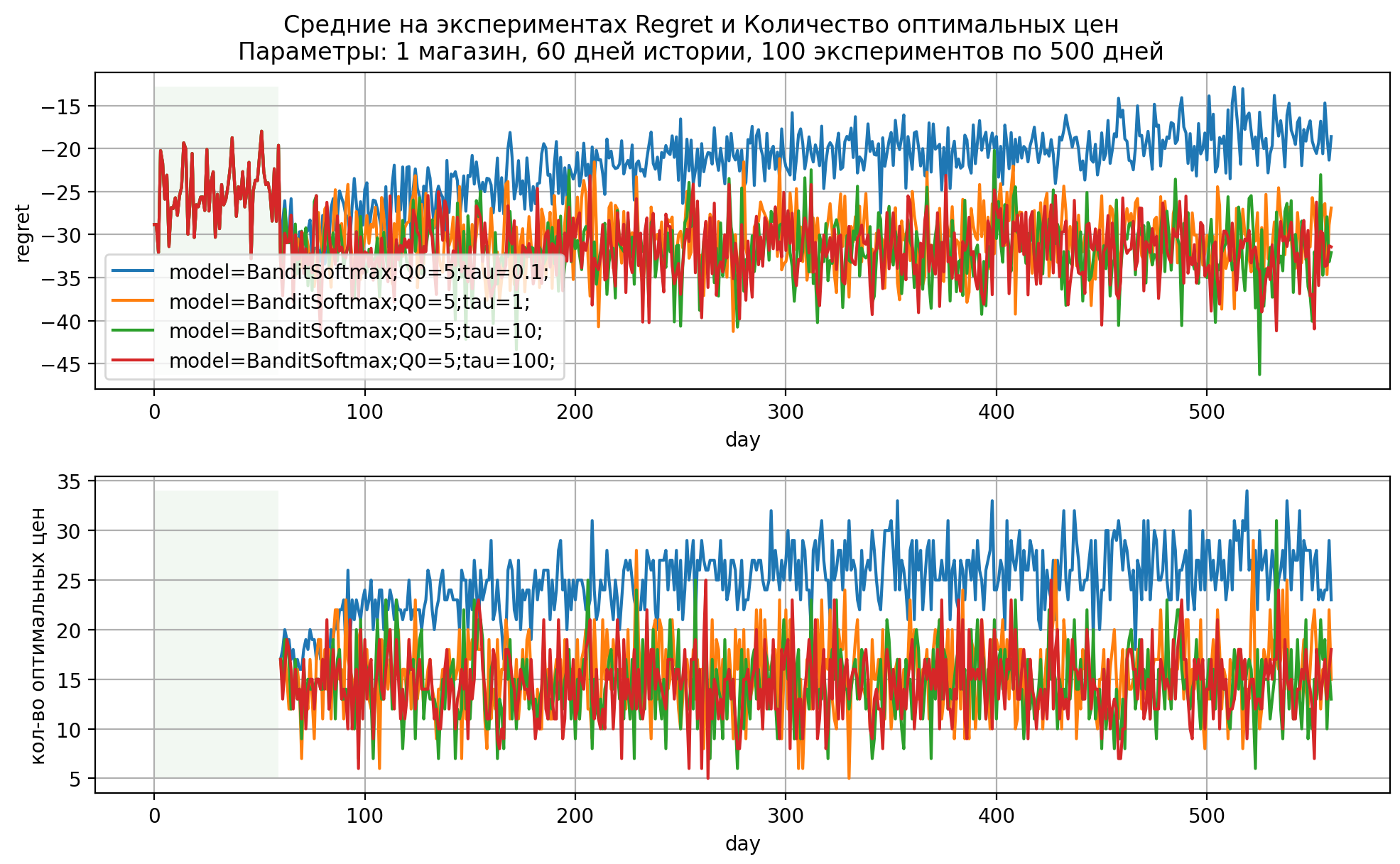
Данная стратегия (её также можно встретить в литературе как Boltzman Exploration) основана на вероятностном выборе ручек согласно значениям вероятностей по формуле:

$P_i = \frac{\exp(Q_i / \tau)}{\sum_{i=1}^{m}\exp(Q_i/\tau)}$ ,

здесь – вероятность выбора ручки , – текущая оценка средней награды ручки , $\tau$ – параметр температуры.
Как видим из формулы, с наибольшей вероятностью стратегия будет выбирать ручку с наибольшим значением текущей оценки среднего вознаграждения, а сама вероятность регулируется параметром температуры . Если $\tau$ стремится к бесконечности, то все ручки становятся равнозначны, то есть бандит производит только исследование всех ручек. В случае если tau стремится к нулю, то вероятность выбора самой лучшей ручки на текущий момент стремится к 1, таким образом бандит производит только использование самой лучшей ручки, по факту превращаясь в жадную стратегию. Данную стратегию можно модифицировать, задавая расписание изменения параметра $\tau$ (как в стратегии $\epsilon$ -decay) – как правило, это охлаждение, то есть постепенное снижение температуры $\tau$ . Здесь мы будем брать $\tau$ равным среднему отклику.

Рис 4. Динамика показателей модели SoftMax при различных параметрах

UCB
Стратегия Upper Confidence Bounds или коротко UCB заключается в следующем – на каждой итерации выбираем ту ручку, которая даёт наибольшее значение величины:

$Q_{i} + c \cdot \sqrt{\frac{\ln{n}}{n_i}},$

где - номер ручки, – среднее значение отклика для ручки, – количество наблюдений (сколько раз была выбрана любая ручка), – количество выбора ручки .

Здесь первое слагаемое отвечает за использование лучшей ручки к текущему шагу, а второй – за исследование ручек. Параметр отвечает за баланс между использованием/исследованием, если – то по факту получаем жадный алгоритм, если $c \to \infty$ , то все ручки будут равноправны – то есть получается случай только исследования. Отметим также, что параметрнеобходимо подбирать так, чтобы достичь лучшей сходимости алгоритма. Как правило, на выбор оказывает влияние дисперсия отклика и разница между минимальным и максимальным значением отклика на всех ручках.

UCB+QBC
Данная стратегия является развитием стратегии UCB, к которой добавляется элемент активного обучения. Здесь, если ручки – это дискретный набор из непрерывной переменной, то можно попробовать аппроксимировать функцию отклика от этой переменной, причём сделать это с помощью разных функций (например, параболой, гауссианой и т.п.) и использовать данные о расхождениях моделей для лучшего уточнения аппроксиматоров – такая концепция называется Query by Committee (или коротко QBC). В таком случае алгоритм выбора следующей ручки заключается в выборе той, которая даёт максимальное значение выражению:

$\hat{F}(p_i) + c \sqrt{\frac{\ln{n}}{n_i}} + d\sqrt{\frac{1}{M}\sum_{j=1}^M\bigg(F_j(p_i) - \hat{F}(p_i)\bigg)^2},$ $\hat{F}(p_i) = \frac{1}{M} \sum_{j=1}^{M}F_j(p_i),$

где – количество моделей-функций, с помощью которых аппроксимируется зависимость отклика; – – ая функция из набора разных функций, с помощью которой производится аппроксимация зависимости отклика от цены.

Здесь первые слагаемые играют ту же роль, что и в обычном UCB, описанном выше, только теперь на первом месте стоит среднее от оценок модели $\hat{F}(p_i)$ , третье слагаемое здесь отвечает за расхождение в комитете моделей для каждой ручки(QBC).

В качестве функций аппроксимации мы выбрали 7 параметрических функций, часть из которых имеют один глобальный максимум. Перечислим их:

Функции для аппроксиматоров

1) Функция, похожая на скошенное нормальное распределение
$\phi(x)$ - нормальное распределение.
Введём $\Phi(x) = 0.5 \cdot(1 + erf(x))$ , где – функция распределения стандартного нормального распределения. Тогда функция вводится как:

$F(x) = c\cdot2\phi\bigg(\frac{x-x_0}{s}\bigg)\Phi\bigg(a\cdot\frac{(x-x_0)}{s}\bigg),$

где – отвечает за “скошенность” колокола, – центр нескошенного колокола, – ширина колокола

2) Квадратичная функция:

$F(x) = a \cdot(x-x_0)^2 + b$

3) Функция, похожая на гамма распределение:

$F(x) = a \cdot x^b \cdot \exp(-c \cdot x)$

4) Линейная функция:

$F = a \cdot x + b$

5) Функция Гаусса:

$F(x) = a \cdot \exp\bigg(-\Big(\frac{x-b}{c}\Big)^2\bigg)$

6) Функция Лоренца:

$F(x) = \frac{a}{1+\big(\frac{x-b}{c}\big)^2}$

7) Случайный лес из библиотеки sklearn с параметрами по умолчанию, кроме max_depth=2.

Иллюстрация аппроксиматоров для модели UCB+QBC

Thompson sampling
В данной стратегии каждой ручке ставится в соответствие некоторое случайное распределение отклика (точнее, распределение его математического ожидания) и на каждом шаге производится сэмплирование случайных чисел из этих распределений, далее выбирается ручка с максимальным значением. После получения фактического отклика производится обновление параметров распределения, как правило, с помощью применения методов байесовского вывода.

В экспериментах для данной статьи продажи по цене моделируются распределением Пуассона, которое описывается одним параметром $\lambda_i$ – математическое ожидание случайной величины . Сопряжённым для распределения Пуассона является гамма распределение $\Gamma(\alpha, \beta)$ , поэтому оно используется для оценки распределения по Байесу, математическое ожидание оценки $\alpha/\beta$ , дисперсия $\alpha/\beta^2$ , обновление параметров гамма распределения после получения одного наблюдения производится по формулам $\alpha \gets \alpha + d$ , $\beta\gets\beta+1$ , где – это результат сэмплирования из пуассоновского распределения. Здесь мы исследуем поиск оптимума валовой маржи, то есть величины $(p_i - c) \cdot Q_i$ , она отличается от исходного пуассоновского распределения фиксированным множителем , и для такой случайной величины, как несложно проверить, гамма распределение будет иметь параметры $\Gamma((p_i-c)\cdot\alpha, \beta)$ , и в таком случае формула для обновления параметров будет иметь такой же вид, только теперь d – это результат сэмплирования валовой маржи.

Итого: для каждой ручки (цены) задаём априорное Гамма распределение параметров: $\rho(\theta) = \Gamma(\alpha_i, \beta_i)$ . В нашем случае это априорное распределение валовой маржи для каждой ручки-цены. Для первого шага случайно выбираем ручки и отправляем в эксперимент. Далее:

Обновляем параметры $\alpha_i \gets\alpha_i + d_i$ значение отклика, $\beta_i \gets \beta_i + n_i$ , которые отвечают за сумму прибыли и количество наблюдений, соответственно, для ручки
Семплируем ручки из обновлённого априора.
Выбираем ту ручку, которая максимизирует целевую функцию и отправляем её в следующий эксперимент.

С более подробным описанием и иллюстрацией работы алгоритма для поиска оптимальной цены можно ознакомиться тут.

Рис 6. Динамика показателей модели Thompson Sampling при различных Q

Разобравшись с описанием сравниваемых алгоритмов, перейдём к описанию параметров экспериментов и результатам моделирования.

Результаты экспериментов

Зафиксируем параметры , , . Количество недель – 6, длина истории – 60 дней, количество ручек – 7, количество магазинов – 100, количество экспериментов – 500.

По результатам экспериментов мы будем считать долю верно угаданных оптимальных цен на последней неделе и средний суммарный на эксперименте Regret, а также среднее суммарное число изменений цен.

Здесь оптимальной ручкой/ручками будем считать те, на которых значение прибыли составляет значение более чем 99% от максимума на рассматриваемой сетке; цены на истории определяются случайно на заданном допустимом интервале цен с шагом в 5 рублей, а цены для поиска – равномерно делят искомый диапазон исследования. Также на первой итерации эксперимента цены не проходят через ограничение на изменение цен, так как было выявлено сильное влияние текущих цен при наличии ограничения на максимальное изменение текущей цены на 10%.

Рис 7 Результаты расчётов при разном количестве цен на истории

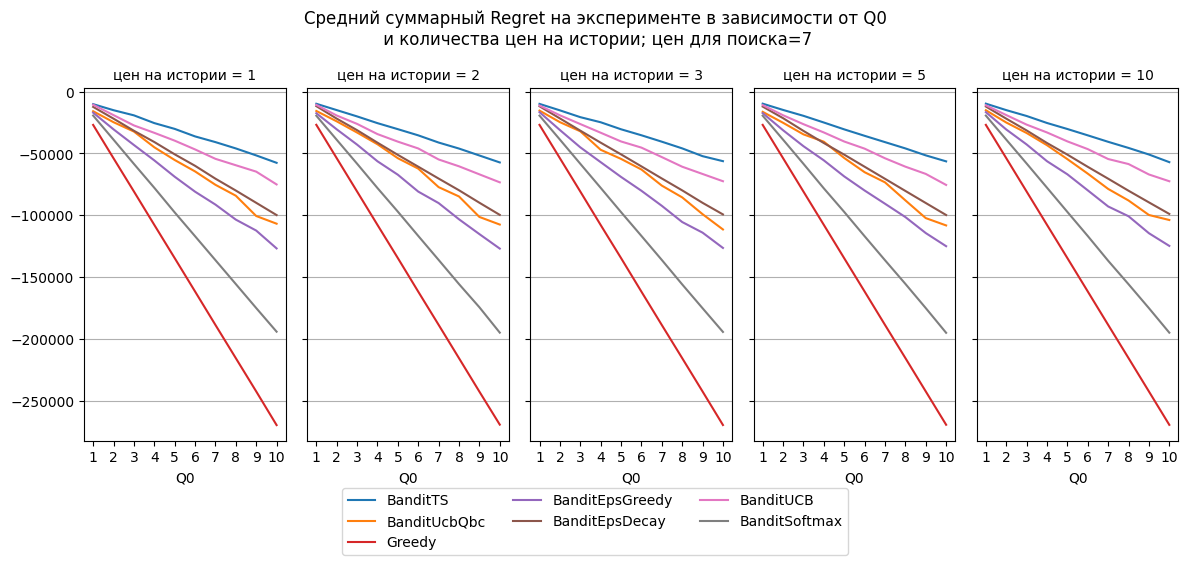
При росте количества цен на истории эластичность аппроксимируется точнее, что ожидаемо, так как мы использовали точную формулу для её аппроксимации. На практике так угадать, скорее всего, не получится, поэтому исключим эту модель из графиков далее.
Лучшей по доле верно найденных ручек оказалась модель TS и Greedy, но по Regret Greedy показывает худший результат, а TS – лучший во всех экспериментах. Худшие результаты получились у EpsGreedy/Decay и SoftMax.

Рис 8. Результаты расчётов при разном количестве ручек (и с двумя на истории)

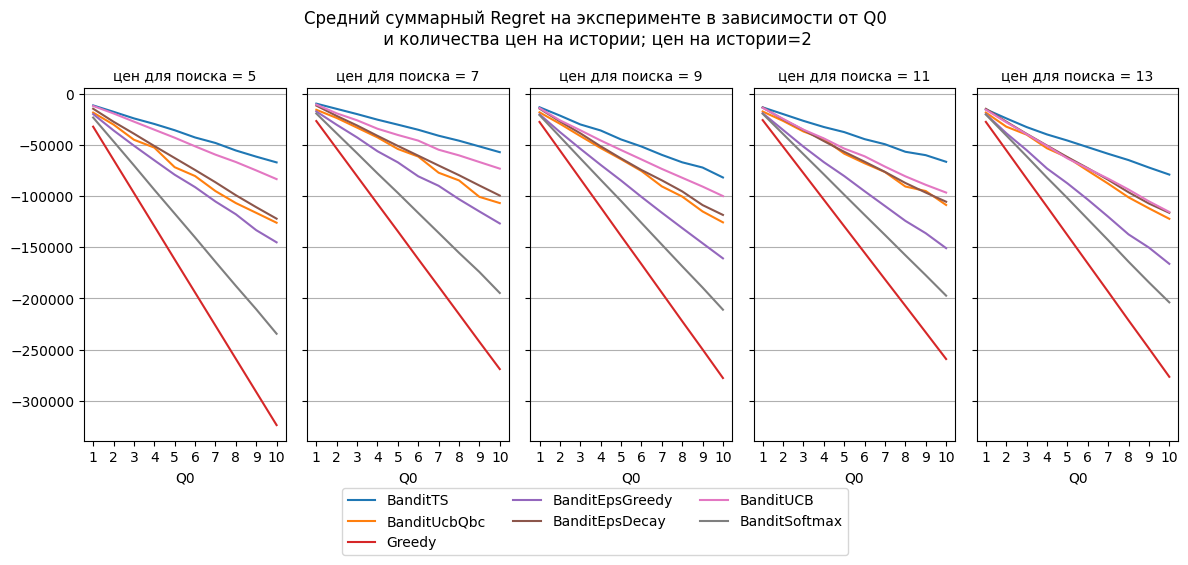
Явного победителя по всем рассмотренным вариантам количества ручек нет. Для 5 и 7 ручек лучшими по доле верно угаданных оказались TS и Greedy, для 11 и 13 ручек – UcbQbc, TS и Greedy. Как и в предыдущих экспериментах Greedy очень дорого обходится по метрике Regret.
Резкое снижение метрик моделей в случае с 9 ручками связано с тем, что в оптимальный набор попадаем только одна цена, а, например, для 7 ручек – две, соответственно, доля попаданий методов в две ручки намного выше, чем в случае с одной.

Оптимизация ценников.
В офлайн ценообразовании смена ценника стоит определённую сумму (труд на переклейку ценника, расходы на печать – это основные составляющие), поэтому целесообразно сократить количество смен ценников, но при этом сохранить ручки при исследовании. В связи с этим в симулятор добавлена логика перераспределение ценников так, чтобы минимизировать “работу” на изменение ценников в магазинах, что является задачей о назначениях и решается пакетом SciPy.

Рис 9. Изменение количества ценников с оптимизацией (с оптимизацией / без оптимизации)

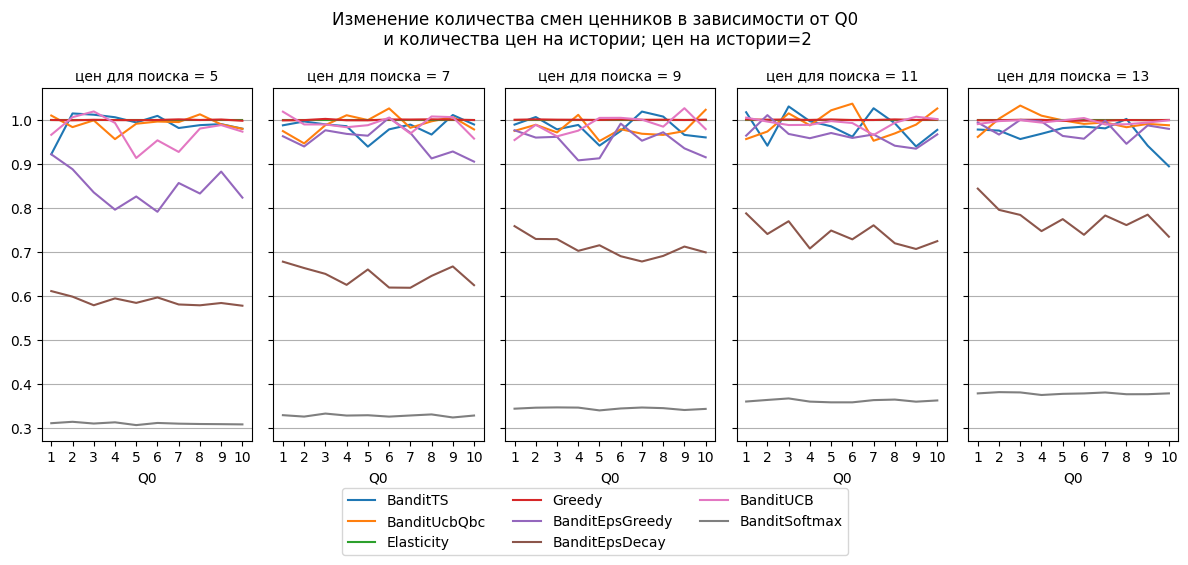
Оптимизация назначений ценников сильно снижает количество изменений ценников для Softmax и EpsDecay. Для остальных методов существенного изменения не происходит.

Заключение

Мы разобрали наиболее популярные на данный момент стратегии многоруких бандитов, сравнили их эффективность на модельной задаче ценообразования. Оценивая результаты расчётов, мы получили вывод, что для рассмотренных экспериментов победителями стали TS, UcbQbc. Greedy по доле верно найденных ручек даёт хороший результат, но сильно уступает по Regret. Надо отметить, что данный вывод может оказаться иным для других моделей спроса, а также при других параметрах моделей и эксперимента.

Над статьёй работали Будылин Михаил и Денисов Антон.

Комментарии (2)

katerina_chernykh
28.12.2023 13:27
#26316732
Спасибо, было интересно

mike_bell
28.12.2023 13:27
#26325500
Привет! Спасибо за статью, очень интересно!

Есть вопрос касательно того, как выбрать варианты цен для ценообразования. На практике чаще всего как происходит: менеджеры составляют какие то ценовые стратегии или ,например, вы используете какое-то ML решение ?