10.01.2024 00:58
anikengur 4 2000 Источник

Мы рассматриваем задачи рекомендаций. Нужно порекомендовать пользователю что-нибудь (айтемы): статьи, фильмы, сериалы, музыку, видео, картинки, товары, и т.п.

Описание пользователя можно представить по-разному:

  1. Как неупорядоченный набор айтемов с которыми пользователь провзаимодействовал (список пролайканых треков)

  2. Как неупорядоченный набор айтемов с оценками (оценка пользователем фильмов, или какой-то другой агрегат, например, сколько раз пользователь прослушал трек)

  3. Как последовательность айтемов с оценками

  4. Как последовательность взаимодействий с учетом контекста

В статье, в основном, будет говориться о первом и втором случае.

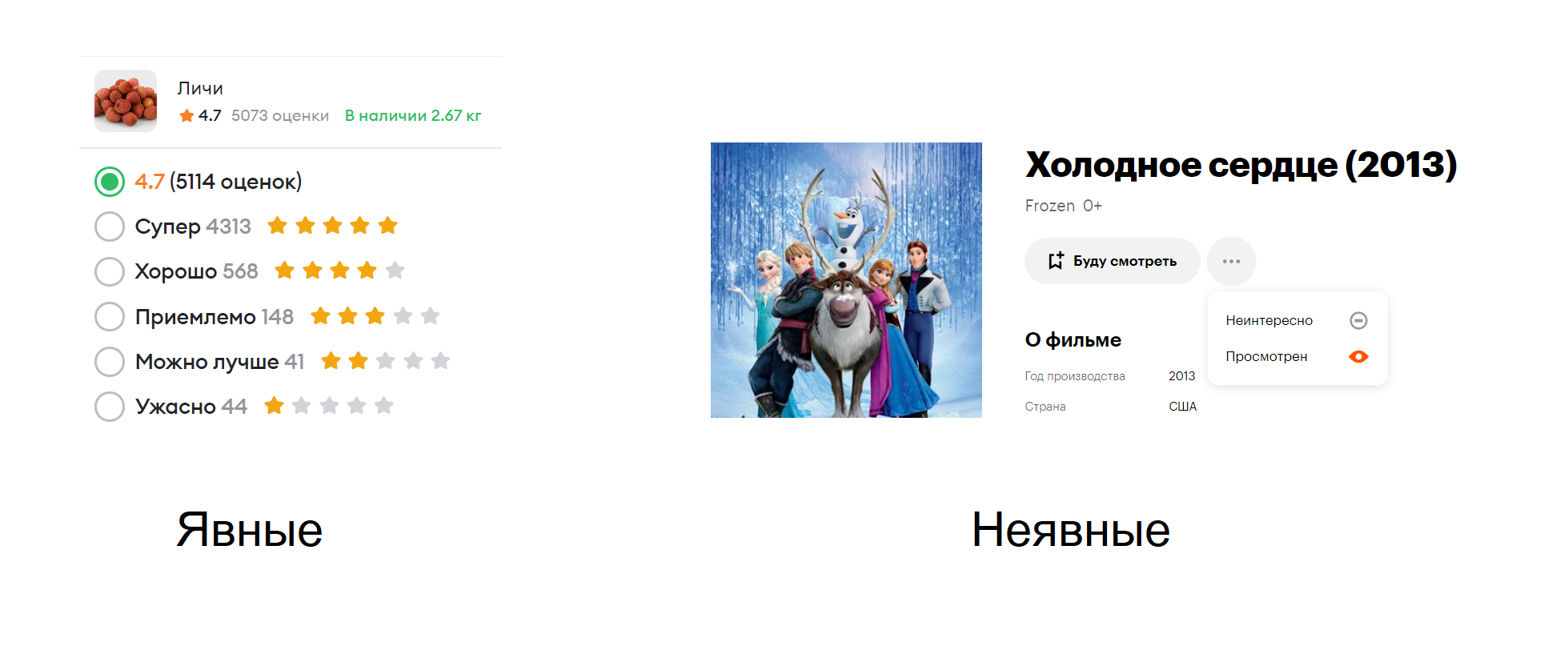
Фитбек пользователя, в свою очередь, бывает явным (оценки, лайки) или неявным (клики, скипы). Причем, у нас нет какого-то строго различия между явным и неявным фитбеком. Позже, при решении задачи рекомендаций, нам понадобится некая уверенность в нашем фитбеке.

Взаимодействия пользователей и айтемов хранятся в матрице оценокR(таблица, в которой каждая строка представляет собой пользователя, каждый столбец - товар). Обратите внимание, что это очень разреженная матрица (содержит много нулей).

Простейшими решениями для задач рекомендаций являются Item- и User-based подходы.

Коллаборативная фильтрация (CF)

  • User2User - ищем похожесть между юзерами (топ ближайших пользователей, усредненные фитбеки разных пользователей)

  • Item2Item - ищем похожести между айтемами (например, средняя оценка по наиболее похожим фильмам)

Ниже будут приведены формулы для Item2Item, но, с точность до замен переменных, они верны для User2User.

Пусть s(i, j) - матрица похожестей (насколько айтемы i и j похожи).

В случае оценок (explicit фитбек) в качестве похожести можно считать корреляцию:

corr(i, j) = \frac{ \sum_u (r_{ui} - \overline r_{i}) (r_{uj} - \overline r_{j})}{ \sqrt{\sum_u (r_{ui} - \overline r_{i})^2 (r_{uj} - \overline r_{j})^2}}

В случае взаимодействий (implicit фитбек) можно посчитать меру Жаккара:

J(A, B) = \frac{|A \cup B|}{|A \cap B|} = \frac{|A \cup B|}{|A| + |B| - |A \cup B|}

Посчитав похожести айтемов (получится матрица Item \times Item) предсказание для пользователя для i-го айтема считается как:

\hat r_{u i} = \frac{\sum_j s(i, j) (r_{uj} - r_{u})}{\sum_j |s(i, j)|} + r_u

Однако, считать в больших задачах корреляцию довольно тяжело. Обычно, в качестве похожести в каждой строчке для Item2Item оставляют ТОП. То есть, у каждого айтема есть какое-то топовое количество айтемов на которые он похож (с весами похожести или без). Тогда текущий айтем будет просто усреднением ТОПа. Что, в каком-то смысле, похоже на KNN.

Выбор между Item2Item и User2User зависит от количества оценок на пользователя и на айтем - чем больше, тем надежнее похожесть. Это же приводит к возможности предрасчета: если оценок много, то добавление пары оценок ничего не изменит. Тогда можно обновляться раз в какое-то время. Сами похожести можно использовать для других задач (кандидат-генерация, контекстные рекомендации).

В продакшене в качестве чистого алгоритма рекомендаций ни Item2Item, ни User2User сегодня не используют. Однако, часто используют как какая-то часть рекомендаций.

Матричные факторизации

Еще один подход основан на методе главных компонент (PCA) и матричном разложении (SVD).

Задача PSA - понизить размерность точек в многомерном пространстве линейным способом. Выбрать линейное подпространство L_k такое, чтобы сумма расстояний до него была минимальной (они наилучшим образом приближались этой линейной плоскостью).

Цель - сопоставить каждой точке проекцию на L_k.

\sum dist(x_i, L_k) \rightarrow min

Какая же связь у PSA с матричным разложением

Наша исходная матрица оценок Rполучила новые координаты в новом пространстве L_k. Пространство L_k имело какие-то базисные вектора (L_k матрица базиса или поворота). Если мы их запишем, они будут в матричке V.

R_{M \times N} \approx U_{M \times k} \times V^T_{k \times N} + B_{1 \times N}

Таким образом, мы пытаемся представить исходную марицу R в виде произведения двух матриц и добавить какое-то смещение:

r_{ij} = \overline u_i^T \overline v_j + b_i

Что же представляет из себя SVD

SVD раскладывает исходную матрицу оценок на произведение трех матриц:

R = U \Sigma V^T\\U U^T = U^T U = I_M\\V V^T = V^T V = I_N

причем, U и V - матрицы поворота.

Если мы будем умножать вектор на SVD-разложение, то сначала мы вектор повернем, потом растянем и еще раз повернем.

При этом, в матрице \Sigma оставляют столько, сколько было не нулевых компонентов (rank(R)).

R = U \Sigma V^T \\l = rank(R) \\U^T U = V^T V = I_l

В результате мы получим усеченные матрицы поворота. А отбросив самые малозначимые сингулярные числа в матрице \Sigma мы получим самое лучшее приближение для исходной матрицы R.

Поставим задачу оптимизации:

R \approx U \Sigma V^T \\ U^T T = V^T V = I_k \\\sum_{\forall i, j} \big( r_{ij} - u_i^T \Sigma v_j \big)^2 \rightarrow \min_{U, V, \Sigma} U \Sigma V^T = X Y^T \\ X^T X \not = I_k, Y^T Y \not = I_k

Эквивалентная задача:

\sum_{\forall i, j} \big( r_{ij} - x_i^T y_j \big)^2 \rightarrow \min_{X, Y} \min_{X, Y} \sum_{\forall i, j} \big( r_{ij} - x_i^T y_j \big)^2 + \lambda \sum_{i} \|x_i\|^2 C_i + \lambda \sum_{j} \|y_j\|^2 C_j

где x_i называем вектором пользователя, а y_j - вектором айтема, C_i - коэффициент взаимодействия.

C_i = \frac{ \big| \{ j|r_{ij} > 0 \} \big| ^{\alpha} \big|\{i\}\big| }{\sum_i \big| \{ j|r_{ij} > 0 \} \big| ^{\alpha}}

Причем, мы не можем просто применить SVD разложение. Поскольку матрица R содержит большое количество нулей, то и решение всегда будет близко к нулю. Идея Funk SVD в том что мы восстанавливаем матрицу R только по заданным элементам. Такая задача оптимизации решается градиентным спуском и довольно хорошо сходится.

Интерпретация SVD

Если вернуться к исходной постановке с SVD и развернуть матрицы X и Y правильно, чтобы они стали ортогональными, а нормы вынести в отдельную матрицу \Sigma между ними, то у этих векторов неожиданно будет появляться какой-то геометрический смысл. Часто можно подобрать какую-то интерпретацию (например, если речь про фильмы, то это могут быть популярность, комедия, ужастик и тд.).

Похожесть между айтемами измеряем как сosine similarity. Но результате, мы выдаем новые айтемы для пользователя, которые дают большое скалярное произведение с вектором пользователя. Чаще всего это будут айтемы с большой нормой. Но, регуляризация, в том числе, борется и с этим.

Алгоритм метода чередующихся наименьших квадратов (Alternating Least-Squares, ALS):

  • Инициализируем X и Y случайными значениями

  • В цикле:

    • Фиксируем матрицу X (пользователей).

    • Находим оптимальную матрицу Y (решаем гребневую регрессию для каждого товара).

    • И наоборот

ALS - шаг по x_i

Задача предствляет собой квадратичный функционал. Положим, если мы знаем вектор айтема, то получим квадратичную задачу по вектору юзера.

Минимизируя вектор айтема по оптимальному пользовательскому вектору, очевидно, что не нужно оптимизировать сумму квадратов айтемных векторов (они уже константно заданы).

\require{cancel} \min_{X, Y} \sum_{\forall i, j} \big( r_{ij} - x_i^T y_j \big)^2 + \lambda \sum_{i} \|x_i\|^2 C_i + \cancel{ \lambda \sum_{j} \|y_j\|^2 C_j }

Раскроем скобки. Уберем сумму квадратов элементов матрицы R, которая ни на что не влияет.

\arg \min_{x_i} \cancel{ \sum r_{ij}^2 } - 2 \sum r_{ij} x_i^T y_j + \sum (x_i^T y_j)^2 + \lambda \langle x_i, x_i \rangle C_i

Еще немного преобразуем (красным выделила места преобразований):

\arg \min_{x_i} -2 \color{red}{ x_i^T }\sum r_{ij} y_j + \sum \color{red}{ x_i^T y_j y_j^T x_i } + \lambda C_i \color{red}{ x_i^T x_i }\arg \min_{x_i} -2 \color{red}{ x_i^T } \big( \sum r_{ij} y_j \big) + \color{red}{ x_i^T } \big( \sum y_j y_j^T + \lambda C_i \big) \color{red}{ x_i }

Нужно получить оптимальное решение для:

\arg \min_{x_i} -2 x_i^T B_i + x_i^T A_i x_i

Матрично продифференцируем и прировняем к нулю:

-2B_i + 2A_ix = 0 \\ x_i = A_i^{-1} B_i

Таким образом оптимальная точка:

\arg \min_{x_i} -2 x_i^T B_i + x_i^T A_i x_i = A_i^{-1} B_i = \big( \sum y_j y_j^T + \lambda C_i \big) ^{-1} \big( \sum r_{ij} y_j \big)

IALS немного изменяет функционал оптимизации, что позволяет учитывать места, которые важно хорошо оптимизировать (было много взаимодействий).

Итоги SVD:

Матричные факторизации (MF) не считывают похожести товаров напрямую (как коллаборативная фильтрация (CF)). Они пытаются описать пользователей и товары маленьким набором характеристик (часто меньше 100), объясняющих оценки. Причем, эти характеристики могут быть неинтерпретируемыми, но, как минимум, векторы айтемов и юзеров будут определены с точностью до поворота.

Комментарии (4)


  1. 19Zb84
    10.01.2024 04:51
    #26359182
    +1

    А есть возможность это же самое рассказать языком, более приближенным к разговорному ?


    1. vova_sam
      10.01.2024 04:51
      #26359850

      Думаю кому то надо список публикаций, а чтобы вы поняли о чем речь :)


  1. Ababaj
    10.01.2024 04:51
    #26360710

    Разговорным языком с искусственным интеллектом сама статья, а на самом деле это линейная алгебра, которую должны знать все технари - о математиках я не говорю!


  1. dmagin
    10.01.2024 04:51
    #26362244

    Какой-то набор слов получился, не? Это ChatGPT нагенерил?

    Ну те, кто уже знает, что такое SVD, наверное, поймут, о чем речь. Остальным и вникать не стоит.