Меня зовут Антон Сорока, я математик и аналитик данных, и это моя первая статья на Хабр.

Я хотел бы рассказать об алгоритме, который выделяет кусочно-линейный тренд из временного ряда и сам определяет точки изменения тренда. Другими словами, это алгоритм для автоматического кусочно-линейного приближения любой функции. Это может понадобиться, если вам важно анализировать линейные тренды ряда, но единственная линия явно недостаточно точно описывает ряд, и самостоятельно искать точки, где тренд менялся, неудобно. Схожую задачу, но немного другим способом, решают и Prophet с их trend changepoints detection. А реализация именно этого алгоритма есть в open-source библиотеке для анализа изменений временных рядов anomeda, написанной на Python.

Зачем нужен такой алгоритм?

Тренд во временном ряде можно наивно понимать как очищенные от сезонных и случайных колебаний значения временного ряда. Тренд должен сохранить “общее направление движения” и “средний уровень” временного ряда, убрав всё остальное. Иногда делать выводы о поведении временного ряда удобнее по его тренду, чем по реальному временному ряду со всеми его выбросами и сезонными колебаниями. Кроме того, выделение тренда упрощает анализ сезонности и поиск аномальных значений.

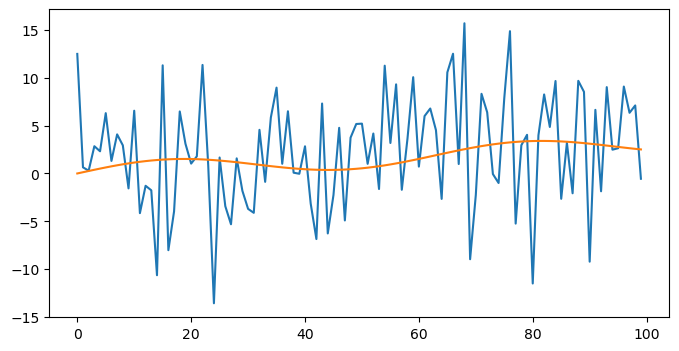
Я бы выделил два подхода для выделения тренда:

1. Moving average приближение и его производные

2. Кусочно-линейное приближение

Первый подход, приближение с помощью moving average, прост в использовании, гибок, подходит для визуального анализа и не накладывает вообще никаких ограничений на то, как ведёт себя временной ряд – метод опишет тренд более-менее адекватно. Желательно только, чтобы в ряде не было больших аномалий, потому что они могут сильно изменить среднее. Впрочем, влияние можно уменьшить увеличением размера окна. В свою очередь, это сделает период, для которого может быть рассчитан тренд, короче.

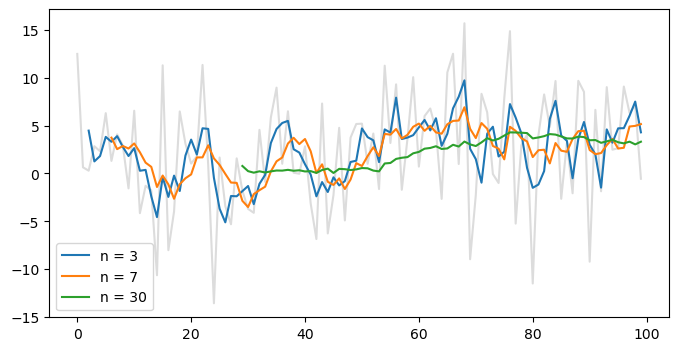
С другой стороны есть кусочно-линейное приближение тренда. На мой взгляд, его главное преимущество заключается в легкости описания полученных трендов. А легкость эта достигается с помощью двух параметров a и b, которыми полностью определяется каждый линейный тренд, представляемый в виде функции:

Эти параметры позволяют делать человекопонятные выводы о том, как ведет себя тренд. А главное, они позволяют понять, как тренд меняется. Например, если раньше мы видели тренд с a = 1.2 и b = 5, и вдруг он стал a = -0.5 и b = 4, это может стать поводом для беспокойства. Как минимум, это повод обратить свое внимание на показатель, который описывается временным рядом.

Вот так мог бы выглядеть кусочно-линейно тренд для примера выше:

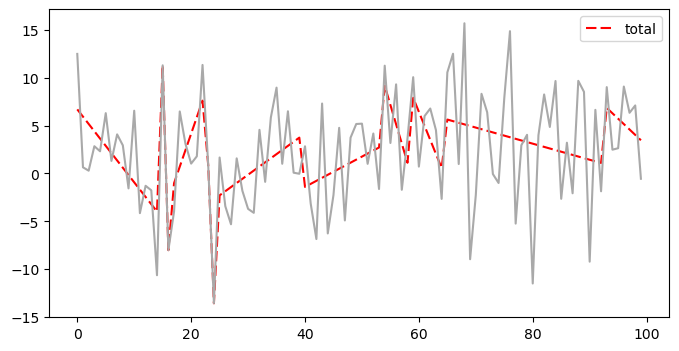
Если ваша задача входит в список тех, которые хорошо решаются с помощью кусочно-линейного приближения временных рядов, то вам не всегда захочется вручную искать точки, где меняется тренд, а затем приближать каждую из частей временного ряда. Это может быть долго, а местоположение такой точки не всегда очевидно.

Попытка приблизить временной ряд кусочно-линейной функцией таким образом, чтобы точки переломов трендов определялись автоматически, привела меня к варианту алгоритма, который эту задачу решает, и впоследствии к написанию этой заметки.

Строим алгоритм

Конечная цель – построить алгоритм, который может приближать временной ряд кусочно-линейной функцией с достаточной для нас степенью точности. При этом заранее мы можем не знать, сколько раз изменяется тренд, и в каких точках это происходит, то есть эти параметры должны определяться самим алгоритмом.

Алгоритм будет работать итерационно, то есть сначала строить приближение временного ряда одной линейной функцией, затем искать лучшую точку, чтобы сделать из одного тренда два, затем лучшую точку, чтобы сделать из двух трендов три, и так далее, до момента выхода из алгоритма.

Приближение ряда одной линейной функцией

Это задача решается просто: подбираются такие параметры a и b для функции f(x) = ax + b, чтобы выбранная нами метрика “расстояния” между линейной функцией f и временным рядом T была минимальна, то есть (a, b) = argminM(f, T).

В качестве метрики расстояния часто используют MSE (Mean Squared Error), поскольку тогда параметры легко подобрать с помощью градиентного спуска, считая градиент для параметров a и b. Однако никто не запрещает использовать другие метрики и другие методы оптимизации.

Примечание. Простой способ приблизить линейную функцию с помощью Python - методы scipy.stats.linregress или scipy.optimize.curve_fit

На этом этапе нам важно зафиксировать разброс реальной, а не абсолютной ошибки полученного приближения. Сделать это можно с помощью расчета дисперсии или стандартного отклонения ошибки. Это понадобится нам в следующих шагах.

Добавляем линейные функции и увеличиваем точность приближения

Приближение временного ряда одной линейной функцией может оказаться недостаточно точным, если в действительности существует больше одного линейного тренда.

Что если один тренд мы постараемся разбить на два? В этом случае нам необходимо понять, в какой точке заканчивается первый тренд и начинается второй. В этом алгоритме мы не будем  пытаться найти точку аналитически (по формуле). Вместо этого мы будем оценивать каждую точку-кандидата с помощью метрики, вычисляющей, насколько хорошо точка “дробит” тренд на два новых.

В виде кандидатов могут выступать как все доступные точки, так и точки, выбранные из какого-либо распределения. А вот основа метрики, которая используется  для описания качества дробления в данном алгоритме:

Метрика усредняет дисперсии абсолютных ошибок приближения “левым” и “правым” трендами с весами, соответствующими объему точек, попавшие в каждую из частей. Дисперсия абсолютной ошибки описывает то, насколько качественно каждый из трендов описывает свою часть.

Подсчитывая эту метрику для каждой точки-кандидата, мы можем выбрать ту точку, у которой значение метрики минимально, затем построить два новых тренда и заменить ими изначальный. Проходя по точкам-кандидатам раз за разом и находя наилучшую, мы можем выделить столько трендов, сколько нам необходимо.

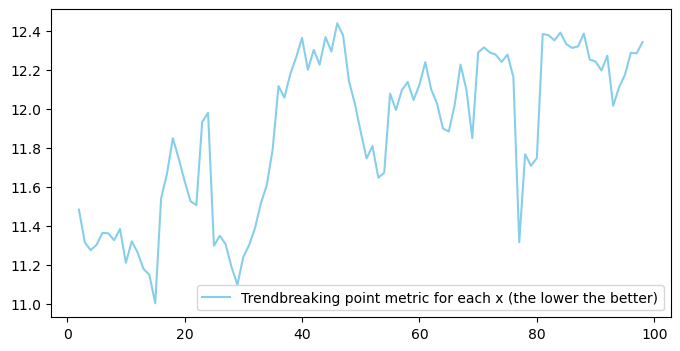
Если перебирать все точки слишком дорого, то как можно определить, какие точки выбирать? Как я упомянул выше, можно выбирать случайные наборы точек, и выбирать только среди них. Выбирать их мы можем как из равномерного распределения (тогда мы допускаем, что точка перелома тренда может находиться где угодно), так и из любых других распределений – так мы будем отдавать предпочтения точкам, которые находятся в определенных промежутках нашей временной шкалы. Частный случай этого – когда мы проверяем только фиксированный набор точек, известных заранее. При этом вероятность выбора точки не из данного набора равна нулю.

Когда остановиться?

Точек выхода у алгоритма может быть несколько:

• Мы выделили достаточное количество трендов;

• Мы приблизили временной ряд достаточно хорошо.

В реализации алгоритма в библиотеке anomeda доступны оба варианта, работающие одновременно.

“Достаточное количество” трендов – это просто число трендов, после которого мы хотим остановиться. Но что есть “достаточно хорошее” приближение? Один из способов понимать это – оценить то, насколько сильно мы снизили разброс ошибки приближения единственным трендом (дисперсию или стандартное отклонение) приближением множеством трендов. В этом случае при приближении одним трендом разброс ошибки будет максимальным, или 100%, а минимальным будет разброс, равный 0. Нулевого разброса можно достичь, если просто провести линию через все известные точки временного ряда. В этом случае разброс будет равен 0, поскольку ошибка в каждой точке приближения будет равна 0. В редких случаях такой разброс будет говорить о том, что приближение оказалось хорошее. Чаще это сигнализирует об overfitting. 

Таким образом, если мы установим порог относительного снижения разброса в 75%, то мы остановимся тогда, когда тренды снизят разброс ошибки на 75% по сравнению с разбросом ошибки от приближения одним трендом. 

Это дает нам два универсальных и довольно интуитивных гиперпараметра, управляющие точностью нужного нам приближения и выходом из алгоритма.

Псевдокод

На вход алгоритм получает значения временного ряда {x, f(x)} и два гиперпараметра: maxTrends и minErrorVarianceReduction.

1. Построить приближение временного ряда одной линейной функцией. Зафиксировать разброс ошибки

2. “Дробить” имеющиеся тренды до выхода из алгоритма

   1. Перебрать точки-кандидаты для перелома имеющихся трендов. Для каждой точки рассчитать метрику, оценивающую качество дробления тренда в этом месте. Выбрать наилучшую точку и соответствующий ей тренд

   2. Заменить тренд, в котором была найдена точка, на два новых тренда, разделенных точкой дробления. Зафиксировать текущий разброс ошибки приближения всеми трендами

   3. Если общее количество трендов равно maxTrends или отношение текущего и изначального разброса ошибки меньше либо равно minErrorVarianceReduction, завершить алгоритм

Поскольку мы всегда можем добиться приближения с нулевым разбросом ошибки, выход из алгоритма гарантирован спустя конечное количество шагов.

Пример работы

Как было сказано в начале статьи, реализация такого алгоритма на Python встроена в библиотеку anomeda, поэтому воспользуемся методами оттуда.

Алгоритм реализован в методе anomeda.fit_trends. Он принимает данные о временном ряде в виде numpy массивов либо встроенного класса anomeda.DataFrame, а также параметр trend_fitting_conf типа dict, содержащий два описанных выше гиперпараметра. Значения по умолчанию {max_trends: ‘auto’, min_var_reduction: 0.75} означают, что нам не важно количество трендов, но мы хотим снизить изначальный разброс ошибки на 75%. 

Для выбора точек-кандидатов метод anomeda.fit_trends использует равномерное распределение. Метод старается перебрать все доступные точки, если их не очень много, а если их число растет, начинает перебирать случайные выборки точек объемом от 75% от всех кандидатов.

Метод также использует нечто вроде регуляризации для метрики при выборе точек близко к краям промежутка, поскольку это может снизить разброс ошибки из-за малого количества примеров на концах промежутка. Функция регуляризации пропорционально увеличивает дисперсию абсолютной ошибки для тренда по доле наблюдений, которые этот тренд охватывает. Если их очень мало или очень много, штраф будет больше. 

В качестве функции для регуляризации используется Beta(0.4, 0.4). Ее можно поменять переопределением метода anomeda.utils.__regularizer. График функции для промежутка (0, 1) выглядит следующим образом.

Метод возвращает список трендов с промежутками, в которые этот тренд наблюдался. Далее тренды можно визуализировать и проанализировать поведение вашего показателя, или даже создать автоматические триггеры по “подсвечиванию” неожиданных изменений тренда в важных для вас метриках.

А вот и полный пример работы алгоритма:

from math import sin

import anomeda
import numpy as np
import matplotlib.pyplot as plt

# Generate data
n_points = 100
x = np.arange(n_points)
noise = np.random.randn(n_points)
y = 1.5 * x / 50 + np.array(list(map(sin, x / 10)))
y_noised = y + 5 * noise

# Fit trends
trends = anomeda.fit_trends((x, y_noised), trend_fitting_conf={'max_trends': 3})

# Plot trends
plt.subplots(figsize=(8, 4))
anomeda.plot_trends(trends, colors={'total': 'red'})
plt.plot(x, y_noised)

Я буду рад, если вы поделитесь своим мнением о реализации и применимости алгоритма в вашей работе. Надеюсь, он сделает вашу жизнь немного лучше.