Свою работу «Комбинаторная теория музыки» инженер-программист и музыкант Эндрю Дункан начинает со слов о том, что нет профессий более далеких, чем музыкант и математик — однако, как это ни парадоксально для самих музыкантов и математиков, музыка и ее создание может служить отличным примером работы ряда математических концепций.

В материалах из этой серии мы вспомним некоторые интересные примеры и явления, связывающие музыку, математику (в данном случае — комбинаторику) и даже историю.

Фотография Pascal / PD

«Волшебное» число 5

На самом деле, «магических» чисел в музыке множество: от знакомых нам с детства «семи нот», то «волшебного числа три» в трезвучии и 12 звуков хроматической гаммы. Однако среди всех чисел, так или иначе связанных с музыкой, одно заслуживает особого внимания — это число 5 и связанная с ним пентатонная гамма.

Интересна эта гамма в первую очередь тем, что отличается от «традиционной» западной (диатонической) семинотной версии (слово «пентатонная» происходит от греческого «пять» — по числу нот в пентатонной гамме), при этом не является усеченной версией обычной интервальной системы (просто пентатонический ряд — в отличие от диатонического — не содержит полутонов). И несмотря на то, что сейчас все привыкли к «диатонической музыке», пентатоническая музыкальная традиция, пусть она и звучит немного непривычно для современного слуха, намного старше.

Говоря «намного», стоит иметь в виду не тысячи, а десятки тысяч лет. Именно на пентатонную гамму были настроены самые старые музыкальные инструменты в мире (обнаруженные на сегодняшний день). В 2008 году археологи проводили раскопки на юге Германии и в одной из пещер нашли флейты из кости стервятника и бивней мамонта, возраст которых составляет примерно 35-40 тысяч лет.

То, что возраст пентатонной гаммы — настолько древний, позволяет делать предположения о том, какую роль такая музыка играла в жизни первобытных людей. Итан Хайн, профессор музыки в Государственном университете города Монтклер, США, вдохновившись фильмом Вернера Херцога Cave of forgotten dreams, в котором демонстрировались эти флейты, делает предположение о том, что пентатонная гамма и «пентатонная музыка» были для древних сакральными — хотя бы потому, что изготовление такой флейты в каменном веке было невероятно сложным и крайне трудозатратным процессом.

Кстати, на флейте, настроенной на пентатонную гамму, можно сыграть и «диатоническую» музыку — что и делает один из палеонтологов, вооружившись современной копией древнего инструмента:

Еще пара слов о числе 5

Еще одно понятие в музыке, тесно связанное с числом 5 — так называемый квинтовый круг. Квинтовый круг — графическая схема, позволяющая музыкантам систематизировать знания о тональностях, «знаках при ключе» и в некоторых случаях облегчающая импровизацию и написание музыки.

Квинтовый круг минорных и мажорных тональностей и их знаки в ключе Wiki / CC

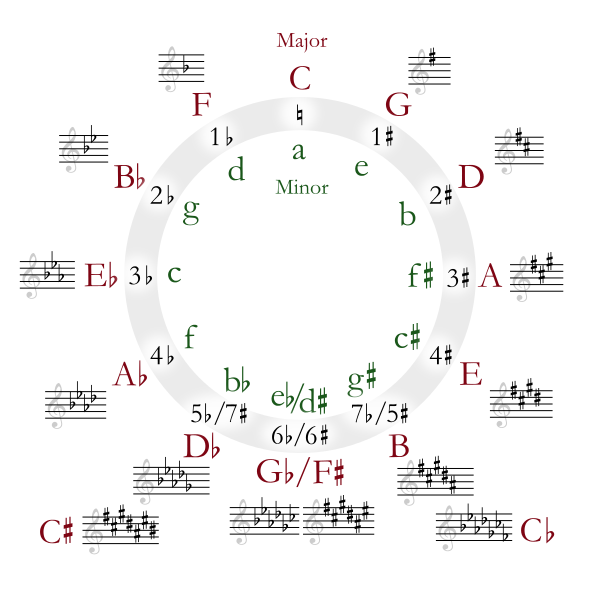
Впервые квинтовый круг был описан в книге «Идея грамматики мусикийской» от 1679 года русско-украинского композитора Николая Дилецкого (хотя, конечно, самая идея такой связи между тональностями существовала и раньше). Подробно о том, как (в том числе с «комбинаторной» точки зрения) строится квинтовый круг, мы уже рассказывали здесь.

Стоит только добавить, что в рамках одной мелодии смена тональности на «соседку» по квинтовому кругу не только логична с позиции математики, но и на слух воспринимается как гармоничный музыкальный переход. При этом, как отмечает все тот же Итан Хайн, смена тональностей в рамках круга обычно зависит и от жанра — в джазе тональности сменяются против часовой стрелки, в роке — по часовой.

Кстати, пентатонная гамма и квинтовый круг связаны — фактически, на квинтовом круге ноты пентатонной гаммы идут подряд (подробнее об этом — а также о том, как древняя пентатонная гамма может звучать в современном джазовом репертуаре — можно почитать в блоге американского саксофониста Антона Шварца).

Как можно визуализировать ноты

Вопрос, который мучает многих музыкантов-новичков — почему музыка записывается именно так? Здесь есть несколько объяснений, кроме того, современные исследователи не оставляют попыток придумать новую систему музыкальной нотации — более удобную для новоиспеченных музыкантов или даже ученых.

Исторический экскурс: читаем по рукам и чертим геометрические фигуры

Гвидонова рука. Миниатюра из мантуанской рукописи конца XV века Wiki / PD

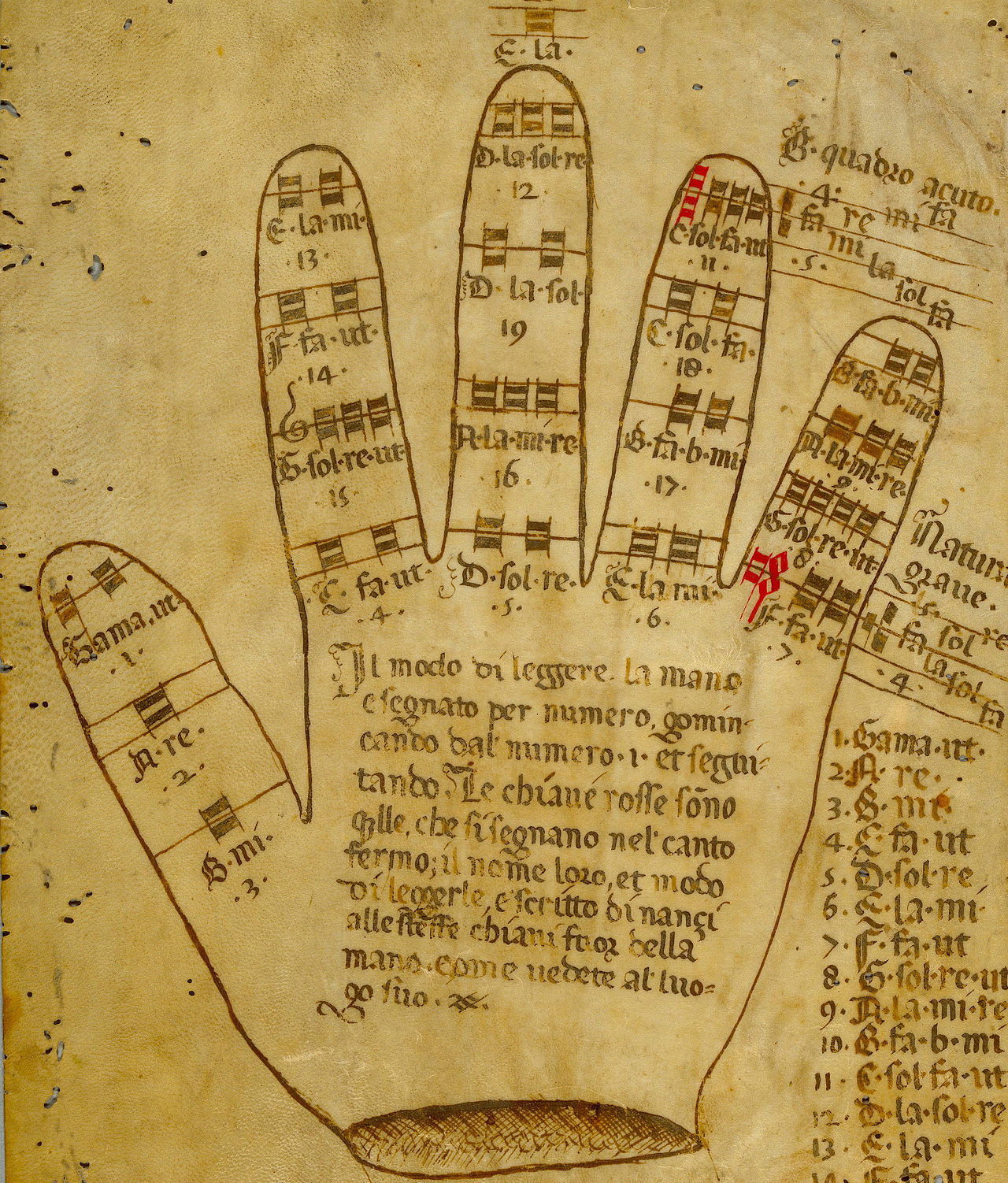
Исторически, одной из ранних версий нотной записи (наряду с буквенными нотациями) была так называемая Гвидонова рука, придуманная монахом бенедиктинского ордена Гвидо д’Ареццо (Guido d'Arezzo) (ок. 991 — 1033). Такая система записи помогала послушникам быстрее заучить мелодии хорала, высчитывать интервалы и определять высоту звуков и являлась основой западной музыкальной теории в течение сотен лет (подробнее о том, как «работает» Гвидонова рука, мы рассказывали здесь).

Строго говоря, это система, позволяющая разобраться во взаимосвязи нот и интервалов в рамках гексахордов и заучить ту или иную мелодическую последовательность, — для записи классической и современной музыки она мало подходит хотя бы потому, что не дает никаких указаний относительно ритма мелодии, длительности звука (и многих других особенностей, которые принято отражать в современных музыкальных произведениях).


Фотография Brandon Giesbrecht / PD

Современная музыкальная нотация (или то, что большинство музыкантов привыкли использовать сейчас) гораздо подробнее и содержит множество уточняющих моментов и нюансов относительно ритма и темпа, особенностей игры, высоты звука, уровня экспрессивности и других деталей исполнения. Стоит отметить, что «современная» музыкальная нотация стала такой не сразу — по мере развития европейской музыкальной традиции она также усложнялась.

Основная проблема современной музыкальной нотации — в ее сложности. Именно поэтому, например, многие исполнители-гитаристы не утруждают себя ее изучением, ограничиваясь табулатурами (кстати, в Европе 16-17 веков были популярны не только гитарные, но и органные и клавесинные табулатуры, и в целом этот вид нотной записи тогда составлял конкуренцию тому, что мы считаем «классическими нотами»).

Кстати, в начале 19 века была предпринята попытка немного упростить классическую систему музыкальной нотации: вместо стандартной записи нот овалами было предложено записывать их различными геометрическими фигурами. Этот способ нотации, правда, не прижился — хотя немногочисленные исследования показывали, что читать с листа такие ноты действительно проще.

Современные варианты: как «видят» музыку юзабилист и программист

Однако наряду с «традиционной» нотацией современные музыканты, композиторы и даже ученые не оставляют попыток вывести новую систему схематической записи нот (и даже делают попытки составить «периодическую музыкальную систему» — по аналогии с таблицей Менделеева — но об этом чуть ниже). Например, UX-специалист и большой любитель музыки Alex Couch предложил современный вариант музыкальной нотации, удобный для новичков.

В своей статье на medium он приводит вариант записи (и несколько музыкальных произведений, записанных таким образом), который подойдет начинающим пианистам и в особенности тем, кто хочет быстро освоить песни современных поп-исполнителей. Такая нотация (как подтверждает сам автор) не дает информации о ритме и скорости игры — для того, чтобы понять, как в действительности нужно играть произведение, автор советует обратиться к оригиналу и послушать трек в записи.

Однако это не единственный современный вариант визуализации музыки. Так, например, уже упомянутый во вступлении к статье Эндрю Дункан задался целью посчитать, сколько существует вариаций 12-тонной хроматической гаммы и как эти вариации, а также аккорды и интервалы связаны между собой.

Для этого он (так же, как и в случае с квинтовым кругом) решил объединить ноты в замкнутый круг из 12 элементов, в котором каждый элемент (или полутон) окрашивается черным (в случае, если он присутствует в выбранной тональности/интервале/аккорде) или белым (в противном случае) [в видео, размещенном ниже, логика окрашивания элементов прямо противоположная — как говорит сам автор, это изменение первоначальной концепции сделано для простоты восприятия].


В итоге, как несложно догадаться, автор получил 2^12=4096 различных вариаций. Интерес здесь представляет то, какое визуальное отображение получила эта гигантская схема: на одном изображении исследователь не просто уместил все полученные варианты тональностей, интервалов и аккордов, но и окрасил их в соответствующие цвета по классам их эквивалентности (в рамках этого исследования эквивалентными считались две и больше комбинаций, строящихся по одним и тем же принципам от разных нот — например, все кварты или все мажорные трезвучия).

По сути, на этой схеме отображена вся теория музыки или, как говорит сам автор, «музыкальная периодическая система» (в статье, посвященной этому исследованию автора, есть еще больше интересных выводов, которые позволяет сделать такая схема визуальной репрезентации).

P.S. В следующих материалах из этой серии мы продолжим рассказывать о теории музыки, развитии музыкальных жанров и о том, как музыка связана с точными науками.

P.P.S. Сегодня мы проводим Аудиопонедельник — большую распродажу, которая продлится только один день (пока товары имеются в наличии).