Коротко о главном
Ключевые слова
Внутренняя сортировка; Равномерное распределение; Средняя временная сложность; Статистический анализ; Статистическая оценка
Сундараджан и Чакраборти [10] представили новую версию быстрой сортировки, удаляющую обмены. Крейзат [1] отметил, что алгоритм хорошо конкурирует с некоторыми другими версиями быстрой сортировки. Однако он использует вспомогательный массив, увеличивая пространственную сложность. Здесь мы предоставляем вторую версию, где мы удалили вспомогательный массив. Эта версия, называемая нами K-sort, упорядочивает элементы быстрее пирамидальной при значительном размера массива (n <= 7 000 000) для входных данных равномерного распределения U[0, 1] (в статистическом смысле — прим. перев).
1. Введение
Существует несколько методов внутренней сортировки (где все элементы могут храниться в основной памяти). Простейшие алгоритмы, такие как пузырьковая сортировка, обычно занимают время O (n2) упорядочивая n объектов и полезны только для малых множеств. Одним из самых популярных алгоритмов больших множеств является Quick sort, занимающий O(n*log2n) в среднем и O (n2) в худшем случае. Подробно об алгоритмах сортировки читайте у Кнута [2].
Сундараджан и Чакраборти [10] представили новую версию быстрой сортировки, удаляющую обмены. Крейзат (Khreisat) [1] обнаружил, что этот алгоритм хорошо конкурирует с некоторыми другими версиями Quick sort, такими как SedgewickFast, Bsort и Singleton sort для n [3000..200 000]. Поскольку в алгоритме сравнения преобладают над обменами, удаление обменов не делает сложность этого алгоритма отличной от сложности классической быстрой сортировки. Другими словами, наш алгоритм имеет среднюю и худшую сложность, сравнимую с Quick sort, то есть O(n*log2n) и O(n2) соответственно, что также подтверждается Крейзатом [1]. Однако он использует вспомогательный массив, тем самым увеличивая пространственную сложность. Здесь мы предлагаем вторую улучшенную версию нашей сортировки, которую мы называем K-sort, где удалён вспомогательный массив. Обнаружено, что сортировка элементов с K-sort выполняется быстрее пирамидальной при значительном размере массива (n <= 7 000 000) равномерно распределённых входных U[0, 1].
1.1 K-sort
Step-1: Initialize the first element of the array as the key element and i as left, j as (right+1), k = p where
p is (left+1).
Step-2: Repeat step-3 till the condition (j-i) >= 2 is satisfied.
Step-3: Compare a[p] and key element. If key <= a[p]
then
Step-3.1: if ( p is not equal to j and j is not equal to (right + 1) )
then set a[j] = a[p]
else if ( j equals (right + 1)) then
set temp = a[p] and flag = 1
decrease j by 1 and assign p = j
else (if the comparison of step-3 is not satisfied i.e. if key > a[p] )
Step-3.2: assign a[i] = a[p] , increase i and k by 1 and set p = k
Step-4: set a[i] = key
if (flag = = 1) then
assign a[i+1] = temp
Step-5: if ( left < i - 1 ) then
Split the array into sub array from start to i-th element and repeat steps 1-4 with the sub array
Step-6: if ( left > i + 1 ) then
Split the array into sub array from i-th element to end element and repeat steps 1-4 with the sub array
Демонстрация
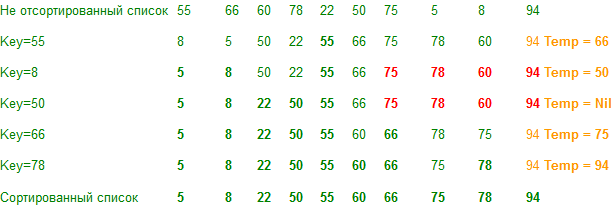
Примечание. Если вспомогательный массив имеет одно значение, его не нужно обрабатывать.
2. Эмпирическая (средняя временная сложность)
Компьютерный эксперимент представляет собой серию прогонов кода для различных входов (см. Сакс [9]). Проводя компьютерные эксперименты на Borland International Turbo 'C ++' 5.02, мы могли бы сравнить среднее время сортировки в секундах (среднее значение приняло более 500 чтений) для разных значений n для K-sort и Heap. Используя симуляцию Монте-Карло (см. Кеннеди и Джентл [7]), массив размером n был заполнен независимыми непрерывными однородными U[0, 1] вариациями, и скопирован в другой массив. Эти массивы сортировались сравниваемыми алгоритмами. Таблица 1 и рис. 1 показывает эмпирические результаты.
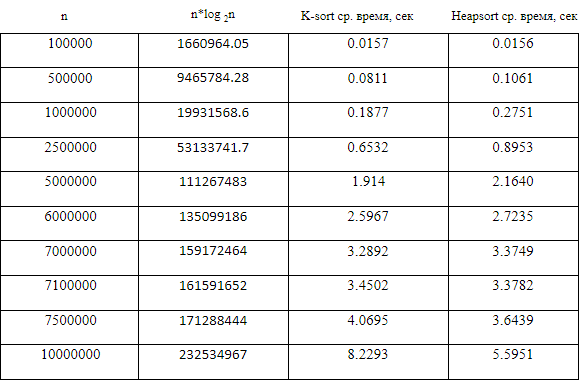

Рис. 1 График сравнения
Наблюдаемые средние значения времени из непрерывного равномерного распределения U(0,1) для рассматриваемый сортировок представлены в таблице 1. Рисунок 1 вместе с таблицей 1 показывают сравнение алгоритмов.
Точки на графике, построенном из таблицы 1, показывают, что среднее время выполнения для K-сортировки меньше, чем у сортировки кучей, когда размер массива меньше или равен 7 000 000 элементов, а выше этого диапазона Heapsort выполняется быстрее.
3. Статистический анализ эмпирических результатов с использованием Minitab версии 15
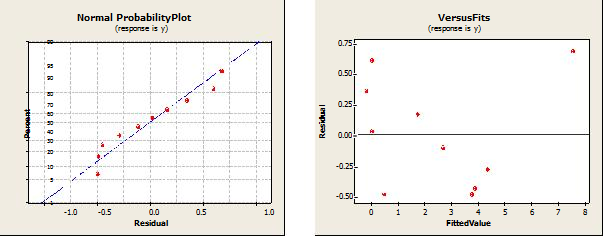
3.1. Анализ для K-sort: регрессирование среднего времени сортировки y(K) по n*log 2 (n) и n
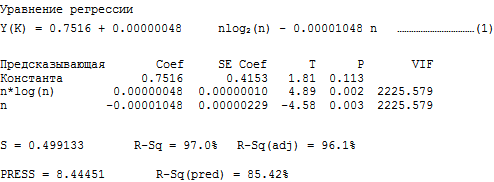

R обозначает наблюдение с большими стандартизованными остатками.
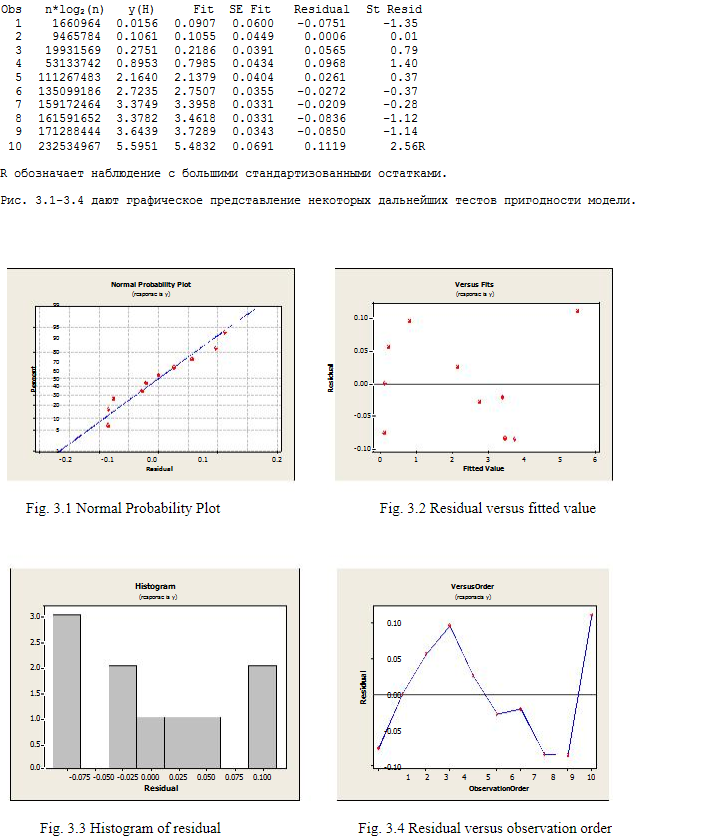
Рис. 2.1-2.4 показывает наглядный итог некоторых дополнительных испытаний модели.

4. Дискуссионная часть
Легко видеть, что сумма квадратов, внесенных n*log(n) в регрессионную модель как в сортировке K-sort, так и в Heap, существенна, по сравнению с суммой, полученной n. Напомним, что оба алгоритма имеют среднюю сложность O(n*log2n). Таким образом, экспериментальные результаты подтверждают теорию. Мы сохранили n-член в модели, потому что взгляд на математический оператор, приводящий к сложности O(nlog2n) в сортировке Quick sort и Heap, предполагает n-член (см. Кнута [2]).
Сравнительное уравнение регрессии для среднего случая получается просто путем вычитания y(H) из y(K).
Имеем, y(K) — y(H) = 0.52586 + 0.00000035 n*log2(n) – 0.00000792 n ……..(3)
Преимущество уравнений (1), (2) и (3) состоит в том, что мы можем прогнозировать среднее время выполнения обоих алгоритмов сортировки, а также их разность даже при огромных значениях n, громоздких для выполнения. Такое «дешевое предсказание» является девизом в компьютерных экспериментах и ??позволяет нам проводить стохастическое моделирование даже для неслучайных данных. Другим преимуществом является то, что достаточно знать только размер ввода, чтобы сделать прогноз. То есть весь вход (для которого ответ фиксирован) не требуется. Таким образом, предсказание через стохастическую модель не только дешево, но и более эффективно (Сакс, [9]).
Важно отметить, что когда мы непосредственно работаем над временем выполнения программы, мы фактически рассчитываем статистическую оценку в конечном диапазоне (компьютерный эксперимент не может быть выполнен для ввода бесконечного размера). Статистическая оценка отличается от математической оценки в том смысле, что в отличие от математической она взвешивает, а не точно рассчитывает вычислительные операции и, как таковая, способна смешивать различные операции в концептуальную оценку, тогда как математическая сложность специфична для операции. Здесь время операции принимается за ее вес. Общее обсуждение статистической оценки, включающей формальное определение и другие свойства, см. Чакраборти и Соубик [5]. Смотрите также Чакраборти, Моди и Паниграхи [4], чтобы понимать, почему статистическая оценка является идеальной границей параллельных вычислений. Предположение о статистической оценке получается путем запуска компьютерных экспериментов, где весам присваиваются численные значения в конечном диапазоне. Это означает, что достоверность связанной оценки зависит от правильной разработки и анализа нашего компьютерного эксперимента. Связанную литературу по компьютерным экспериментам с другими областями применения, такими как проектирование СБИС, сжигание, теплопередача и т. Д., Можно найти в (Фанг, Ли и Суджианто, [3]). Смотрите также обзор (Чакраборти [6]).
5. Заключение и предложения для будущей работы
K-sort, очевидно, быстрее, чем Heap для количества элементов сортировки до 7 000 000, хотя оба алгоритма имеют одинаковый порядок сложности O(n*log2n) в среднем случае. Будущая работа включает исследование параметризованной сложности (Mahmoud, [8]) по этой улучшенной версии. В качестве заключительного комментария мы настоятельно рекомендуем K-sort по крайней мере для n <= 7 000 000.
Тем не менее, мы соглашаемся выбрать Heap-sort в худшем случае из-за того, что он поддерживает сложность O (n*log2n) даже в худшем случае, хотя программировать её сложнее.
N.B. Продолжение работы, 2012
[2] Knuth, D. E., The Art of Computer Programming, Vol. 3: Sorting and Searching, Addison
Wesely (Pearson Education Reprint), 2000
[3] Fang, K. T., Li, R. and Sudjianto, A., Design and Modeling of Computer Experiments
Chapman and Hall, 2006
[4] S. Chakraborty, S., Modi, D. N. and Panigrahi, S., Will the Weight-based Statistical Bounds
Revolutionize the IT?, International Journal of Computational Cognition, Vol. 7(3), 2009, 16-22
[5] Chakraborty, S. and Sourabh, S. K., A Computer Experiment Oriented Approach to
Algorithmic Complexity, Lambert Academic Publishing, 2010
[6] Chakraborty, S. Review of the book Design and Modeling of Computer Experiments authored by K. T. Fang, R. Li and A. Sudjianto, Chapman and Hall, 2006, published in Computing Reviews, Feb 12, 2008,
www.reviews.com/widgets/reviewer.cfm?reviewer_id=123180&count=26
[7] Kennedy, W. and Gentle, J., Statistical Computing, Marcel Dekker Inc., 1980
[8] Mahmoud, H.,Sorting: A Distribution Theory, John Wiley and Sons, 2000
[9] Sacks, J., Weltch, W., Mitchel, T. and Wynn, H., Design and Analysis of Computer Experiments, Statistical Science 4 (4), 1989
[10] Sundararajan, K. K. and Chakraborty, S., A New Sorting Algorithm, Applied Math. and Compu., Vol. 188(1), 2007, p. 1037-1041
Комментарии (18)

daiver19
20.07.2017 06:33+2Код ну совсем тяжко читать: с отступами непонятно что, зато комментарии вроде «затем установите a[j] = a[p]». Псевдокод чисто на английском все бы поняли, я думаю.
А вообще неясно, почему не сравнивали с классической быстрой сортировкой (или она вообще по умолчанию отстой для маленьких н?). Еще неясно, можно ли её рандомизировать для поддержки ожидаемого времен н лог н или вообще обеспечить гарантированный н лог н? Короче, вроде есть какой-то анализ, а по сути нет.
AleksandrK
20.07.2017 18:11+2Действительно, странная логика — быстрая сортировка (quick sort), модификацией которой является представленный алгоритм, имеет временную сложность O(n^2) в худшем случае. Пирамидальная (heap) сортировка в худшем случае O(n*log(n)), да еще и стабильна. Сравнение теплого с мягким.

netch80
21.07.2017 20:02+2> Пирамидальная (heap) сортировка в худшем случае O(n*log(n)), да еще и стабильна.
Если «стабильна» это сохранение порядка равных элементов, то этого свойства как раз у пирамидальной никогда не было.
> быстрая сортировка (quick sort), модификацией которой является представленный алгоритм, имеет временную сложность O(n^2) в худшем случае
Только если её неправильно реализовать. Даже случайный выбор разделяющего элемента асимптотически снижает вероятность такого до нуля. С помощью медианы медиан получается гарантированное O(n log n), причём всё равно дешевле в большинстве окружений, чем пирамидальная.
Если авторы не знают этой возможности гарантировать время для быстрой сортировки, то что они вообще знают, простите?

joossy
21.07.2017 14:55+1И вовсе не отстой она для маленьких N. Qsort легко модифицируется заменой рекурсивных вызов алгоритмом сортировки вставками когда N становится «маленьким».

daiver19
21.07.2017 17:31+1Ну правильно, для маленьких н как раз хип сорт и используют, а для совсем маленьких вставки. Так что сравнивать логичнее сразу с пирамидальной. Другое дело, что 7000000 — это далеко е маленько н, и думаю что тот же std::sort и раньше побьет.

stranger777
21.07.2017 20:08Поправил. Спасибо. С отступами да, непонятно что… потестирую в черновиках, посмотрю, как ведёт себя source (кстати, тега не было, его добавил либо хабр автоматически, либо какие-то неизвестные корректоры статей).
Ваши вопросы спрошу у автора, если ответит — добавлю ответ и отпишу сюда.
valemak
22.07.2017 18:05Пытался реализовать этот псевдокод, сортировка не работает.
Также вообще непонятно, по какому принципу работает алгоритм. Псевдокод представляет собой набор бессмысленных инструкций, в статье о принципах сортировки тоже ничего не сказано (кроме беглого упоминания, что это якобы «разновидность quicksort»). Гугл также по поводу «k-sort source» абсолютно ничем не порадовал (кроме ссылки на эту хабрастатью).
Если всё-таки попробуете связаться с авторами и они даже что-то ответят — поинтересуйтесь, пожалуйста, есть ли у них работающий код этой сортировки на любом языке программирования?
VaalKIA
20.07.2017 07:44+2Эта версия, называемая нами K-sort, упорядочивает элементы быстрее пирамидальной при значительном размера массива (n <= 7 000 000) для входных данных равномерного распределения
Суть статьи: мы быстрее, на заранее подготовленных данных, а теперь и без вспомогательного массива — хвалите нас!

kovserg
20.07.2017 18:11+1Обычно проводят множество экспериментов с разными данными и на разных машинах и потом усредняют и получают данные с доверительными интервалами. У вас на графиках погрешностей что-то не видно.
Современные процессоры не так просты как может показаться: Сache, Branch prediction, AMD SenseMI, ...
Так что в вашем частном случаем может и быстрее. А если еще использовать и возможности современных процессоров то можно сделать еще быстрее. Но на теоретическую асимптотику это не повлияет.
С другой стороны сортировка пирамидой имеет очень простой алгоритм и понятную асимптотику
struct PSort { virtual void swp(int i,int j)=0; virtual void cmp(int i,int j)=0; void psort(int n) { // O(n*ln(n)) int i,r,c; for(i=n/2;i>=0;i--) { pfix(i,n); } for(i=n-1;i>=0;i--) { swp(0,i);pfix(0,i); } } void pfix(int i,int n) { int c,r; for(r=i;r*2<n;r=c) { c=r*2; if (c<n-1 && cmp(c,c+1)<0) c++; if (cmp(r,c)>=0) break; swp(r,c); } } };
stranger777
20.07.2017 19:06+1У вас на графиках погрешностей что-то не видно.
Residual error — остаточная ошибка, она же погрешность.
http://normative_reference_dictionary.academic.ru/98777/50.1.040-2002%3A_Статистические_методы._Планирование_экспериментов._Термины_и_определения. Я не переводил термин, полагая его понятным интуитивно.
https://www.amazon.com/Computer-Experiment-Oriented-Algorithmic-Complexity/dp/3838377435 — книга о компьютерных экспериментах из литературы к статье.
Конечно, на низком уровне из-за оптимизаций в кэше может быть много сюрпризов, но во-первых тут уклон в математику именно, а не в особенности работы памяти. То есть на сферическом языке в вакууме (или на языке, в котором нет этих эвристических трюков с процессорами) по статистическим данным закономерность продолжит работать.
И — в конце концов — это научная статья, а не прикладная. Прикладное исследование — отдельная работа и этим будут заниматься уже не доктора, а скорее заинтересованные лица и энтузиасты.

nickolaym
27.07.2017 13:46Я конечно извиняюсь, но почему переводчик сумел перевести весь текст статьи, но оставил как есть описание алгоритма на лютом псевдо-коболе?
Почему авторы статьи дали описание на лютом псевдо-коболе — это, как раз, понятно. Это чёртов наукообразный стиль, редакторы журналов от него млеют и тают.

stranger777
27.07.2017 17:56Пока комментарий про желательность псевдокода на английском не набрал два плюса, он был на русском. Мнения разделились, как говорится.

nickolaym
27.07.2017 19:09Понятно :(
Всё-таки, читать код на псевдо-коболе — это одинаковая кровь из глаз, что на русском, что на английском.
Во-первых, он наглухо неотформатирован.
Во-вторых, весёлая смесь из "=", "= =" и "equals to", всяких операций "decrease j by 1" и прочего.
Вот буквальный перевод этой литературы на питон:
def ksort(a, left, right) : # Step 1 key = a[left] i = left j = right+1 k = left+1 p = left+1 # Step 2 while j-i < 2 : # Step 3 if key <= a[p] : # Step 3.1 if p != j and j != right+1 : a[j] = a[p] else if j == right+1 : temp = a[p] flag = True j -= 1 p = j else : # Step 3.2 a[i] = a[p] i += 1 k += 1 p = k # Step 4 a[i] = key if flag : a[i+1] = temp # Step 5 if left < i-1 : ksort(a, start, i) # Step 6 if left > i+1 : ksort(a, i, right)
Если кто возьмётся расставить здесь осмысленные названия переменных, прокомментировать происходящее и выловить ошибки, — человечество только выиграет.

nickolaym
27.07.2017 17:31Хипсорт вдвое медленнее квиксорта в среднем — потому что сперва за логлинейное время строит пирамиду, а потом за логлинейное время разбирает её. Зато хипсорт в худшем случае логлинейный (в отличие от квадратного квиксорта).
А что же с К-сортом? В начале статьи упоминаются всякие варианты квиксорта, а потом начинаются сравнения с хипсортом.
Если К-сорт в худшем случае квадратный, то и сравнивать его надо было с квиксортом. Разве нет?
Если он в худшем случае логлинейный, то зачем вводные слова про квиксорт?


Centimo
Почему-то по графику виден перелом (где K-sort расходится с heap; такое ощущение, что после этой точки рост линейный) — в чём причина?
khoramus
Линейный рост для сортировки это очень даже хорошо)