02.10.2017 05:58
A3a 27 12500 Источник


Как бы вы подошли к симуляции дождя, ну или любого другого продолжительного физического процесса?

Симуляцию, будь это дождь, поток воздуха над крылом самолёта или же падающий по ступенькам слинки (помните игрушку-пружинку радугу из детства?), можно представить, если знать следующее:

  1. Состояние всего в момент начала симуляции.
  2. Как это состояние меняется из одного момента времени в другой?

Под «состоянием всего» я подразумеваю любые переменные данные, которые либо определяют как выглядит окружение, либо же изменения, происходящие с течением времени. Как пример состояния можно привести положение капли дождя, направление ветра, либо же скорость каждой части пружинки слинки.

Если положить, что всё наше состояние окружения это один большой вектор $\vec{y}$, то можно сформулировать нужные нам данные, указанные выше, в следующее:

  1. Найти значение $y_0$, удовлетворяющее $y(t_0) = y_0$?
  2. Найти функцию $f$ такую, что $\frac{dy(t)}{dt} = f(t, y(t))$.

Зачем нам надо хранить состояние всего в одном векторе, я объясню чуть позже. Это один из тех случаев, когда кажется что мы перебарщиваем с обобщением задачи, но я обещаю, в таком подходе есть свои интересности.

Теперь взглянем как можно хранить всю информацию об окружении в одном векторе на простом примере. Допустим, у нас есть 2 объекта в 2D симуляции. Каждый объект определяется своим положением $\vec x$ и скоростью $\vec v$.


Таким образом, чтобы получить вектор $\vec y$, нам надо объединить вместе вектора $\vec x_1, \vec v_1, \vec x_2 ~и~ \vec y_2$ в один, состоящий из 8 компонент, вот так:

$\vec y = \begin{bmatrix} \vec x_1 \\ \vec v_1 \\ \vec x_2 \\ \vec v_2 \end{bmatrix} = \begin{bmatrix} x_{1x} \\ x_{1y} \\ v_{1x} \\ v_{1y} \\ x_{2x} \\ x_{2y} \\ v_{2x} \\ v_{2y} \end{bmatrix}$


Если вас смущает, почему мы хотим найти $f(t, y(t))$, а не начальное определение $\frac{dy(t)}{dt}$, то смысл в том, что производная нам нужна как выражение, зависящее только от текущего состояния, $y(t)$, констант и самого времени. Если же это невозможно, то наверняка какая либо информация о состоянии не была учтена.

Начальное состояние


Чтобы определить начальное состояние симуляции, нужно определить вектор $\vec y_0$. Таким образом, если начальное состояние нашего примера с двумя объектами выглядит приблизительно так:


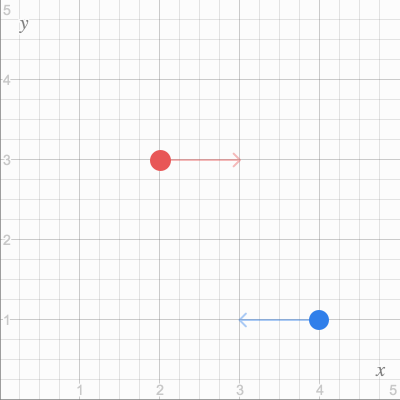
То в векторном виде это можно представить следующим образом:

$\vec x_1(t_0) = \begin{bmatrix} 2 \\ 3 \end{bmatrix}, \vec v_1(t_0) = \begin{bmatrix} 1 \\ 0 \end{bmatrix}, \vec x_2(t_0) = \begin{bmatrix} 4 \\ 1 \end{bmatrix}, \vec v_2(t_0) = \begin{bmatrix} -1 \\ 0 \end{bmatrix}$


Если объединить это всё в один вектор, мы получим нужный нам $\vec y_0$:

$\vec y_0 = \vec y(t_0) = \begin{bmatrix} x_{1x} \\ x_{1y} \\ v_{1x} \\ v_{1y} \\ x_{2x} \\ x_{2y} \\ v_{2x} \\ v_{2y} \end{bmatrix} = \begin{bmatrix} 2 \\ 3 \\ 1 \\ 0 \\ 4 \\ 1 \\ -1 \\ 0 \end{bmatrix}$


Производная функция


$\vec y_0$ определяет начальное состояние и теперь всё что нам нужно это найти способ перехода из начального состояния в состояние происходящее мгновение после него, а с полученного состояния ещё чуть дальше во времени и так далее.

Для этого, решим уравнение $\frac{dy(t)}{dt} = f(t, y(t))$ для $f$. Найдём производную от $y(t)$:

$\frac{dy(t)}{dt} = \frac{d}{dt} \begin{bmatrix} x_{1x} \\ x_{1y} \\ v_{1x} \\ v_{1y} \\ x_{2x} \\ x_{2y} \\ v_{2x} \\ v_{2y} \end{bmatrix} = \begin{bmatrix} \frac{dx_{1x}}{dt} \\ \\ \frac{dx_{1y}}{dt} \\ \\ \frac{dv_{1x}}{dt} \\ \\ \frac{dv_{1y}}{dt} \\ \\ \frac{dx_{2x}}{dt} \\ \\ \frac{dx_{2y}}{dt} \\ \\ \frac{dv_{2x}}{dt} \\ \\ \frac{dv_{2y}}{dt} \end{bmatrix}$


Ого! Высокая получилась формула! Но можно привести её в более читаемый вид, если разобьём наш вектор $\vec y$ обратно на составные части.

$\begin{aligned} \frac{d \vec x_1(t)}{dt} = \begin{bmatrix} \frac{dx_{1x}}{dt} \\ \\ \frac{dx_{1y}}{dt} \end{bmatrix}, \frac{d \vec v_1(t)}{dt} = \begin{bmatrix} \frac{dv_{1x}}{dt} \\ \\ \frac{dv_{1y}}{dt} \end{bmatrix} \\ \\ \frac{d \vec x_2(t)}{dt} = \begin{bmatrix} \frac{dx_{2x}}{dt} \\ \\ \frac{dx_{2y}}{dt} \end{bmatrix}, \frac{d \vec v_2(t)}{dt} = \begin{bmatrix} \frac{dv_{2x}}{dt} \\ \\ \frac{dv_{2y}}{dt} \end{bmatrix} \end{aligned}$


$\vec x_1$ и $\vec x_2$ связаны аналогичными правилами, равно как и $\vec v_1$ с $\vec v_2$, поэтому несмотря на кучу выражений сверху, всё что нам действительно нужно найти, это следующие 2 вещи:

$\frac{d \vec x}{dt}~~\text{и}~\frac{d \vec v}{dt}$


От определения этих двух производных и зависит качество симуляции, именно в них вся сила. И чтобы симуляция не походила на программу где всё случается хаотичным образом, можно обратиться к физике за вдохновением.

Кинематика и динамика


Кинематика и динамика — необходимые ингредиенты для создания интересной симуляции. Начнём с самых основ на нашем примере.

За положение в пространстве отвечает $\vec x$, и первая производная положения точки по времени это его скорость $\vec v$. В свою очередь, производная от скорости по времени это ускорение, $\vec a$.

Может показаться, что мы уже нашли нужную нам функцию $f$, т.к. мы уже знаем следующее:

$\frac{d \vec x}{dt} = \vec v ~~\text{ и } ~\frac{d \vec v}{dt} = \vec a$


И в самом деле мы блестяще справились с $\frac{d \vec x}{dt}$, т.к. $\vec v$ это часть нашего вектора состояния $\vec y(t)$, но нам нужно ещё чуточку разобрать вторую формулу, потому что с $\vec a$ не всё так просто.

Тут нам поможет второй закон Ньютона: $\vec F = m \vec a$. Если предположить что масса наших объектов известна, то переставив переменные в выражении, мы получим:

$\frac{d \vec v}{dt} = \vec a = \frac{\vec F}{m}$


Так, погодите ка, $\vec a$ и $\vec F$ не являются частью $\vec y(t)$, поэтому это сложно назвать продвижением (помните, нам нужна производная функция зависящая только от $\vec y(t)$ и $t$). Но тем не менее мы продвинулись вперёд, потому что мы нашли все полезные формулы которые определяют поведение объектов в нашем физическом мире.

Предположим, что в нашем простом примере, единственной силой, которая воздействует на объекты является гравитационное притяжение. В таком случае, мы можем определить $\vec F$, используя закон всемирного тяготения Ньютона:

$F = G \frac{m_1 m_2}{r^2}$


Где $G$ это гравитационная постоянная $6.67 \times 10^{-11} \frac{Нм^2}{кг^2}$, а $m_1$ и $m_2$ это массы наших объектов (которые, мы предположим, являются константами).

Для создания самой симуляции, также нам понадобится направление и как то указать $r$ через компоненты вектора $\vec y(t)$. Если предположить что $\vec F_1??$ это сила действующая на первый объект, то можно сделать это следующим образом:

$\begin{aligned} \vec F_1 &= G \frac{m_1 m_2}{|\vec x_2 - \vec x_1|^2} \left[ \frac{\vec x_2 - \vec x_1}{|\vec x_2 - \vec x_1|} \right] = G \frac{m_1 m_2(\vec x_2 - \vec x_1)}{|\vec x_2 - \vec x_1|^3} \\ \\ \vec F_2 &= G \frac{m_2 m_1}{|\vec x_1 - \vec x_2|^2} \left[ \frac{\vec x_1 - \vec x_2}{|\vec x_1 - \vec x_2|} \right] = G \frac{m_2 m_1(\vec x_1 - \vec x_2)}{|\vec x_1 - \vec x_2|^3} \end{aligned}$


Подытожим. Изменение состояний в нашей системе из двух объектов полностью выражено через переменные $\vec x_1, \vec v_1, \vec x_2, ~и~ \vec v_2$. И изменения такие:

$\begin{aligned} \frac{d \vec x_1}{dt} &= \vec v_1 \\ \\ \frac{d \vec x_2}{dt} &= \vec v_2 \\ \\ \frac{d \vec v_1}{dt} &= \vec a_1 = \frac{\vec F_1}{m_1} = G \frac{m_2 (\vec x_2 - \vec x_1)}{|\vec x_2 - \vec x_1|^3} \\ \\ \frac{d \vec v_2}{dt} &= \vec a_1 = \frac{\vec F_1}{m_1} = G \frac{m_1 (\vec x_1 - \vec x_2)}{|\vec x_1 - \vec x_2|^3} \end{aligned}$


Теперь у нас есть всё, что отличает нашу симуляцию от всех других симуляций: $\vec y_0$ и $f$.

$\begin{aligned} \vec y_0 &= \vec y(0) &= \begin{bmatrix} \vec x_1(0) \\ \vec v_1(0) \\ \vec x_2(0) \\ \vec v_2(0) \end{bmatrix} &= \begin{bmatrix} (2, 3) \\ (1, 0) \\ (4, 1) \\ (-1, 0) \end{bmatrix} \\ \\ f(t, y(t)) &= \frac{d\vec y}{dt}(t) &= \begin{bmatrix} \frac{d\vec x_1}{dt}(t) \\ \\ \frac{d\vec v_1}{dt}(t) \\ \\ \frac{d\vec x_2}{dt}(t) \\ \\ \frac{d\vec v_2}{dt}(t) \end{bmatrix} &= \begin{bmatrix} \vec v_1(t) \\ \\ G \frac{m_2 \big(\vec x_2(t) - \vec x_1(t)\big)}{|\vec x_2(t) - \vec x_1(t)|^2} \\ \\ \vec v_2(t) \\ \\ G \frac{m_1 \big(\vec x_1(t) - \vec x_2(t)\big)}{|\vec x_1(t) - \vec x_2(t)|^2} \end{bmatrix} \end{aligned}$


Но как, имея строго определённую симуляцию, превратить её в красивую анимацию?

Если у вас был опыт написания симуляции или игры, то возможно вы предложите нечто такое:

x += v * delta_t
v += F/m * delta_t

Но давайте чуть остановимся и разберём почему это сработает.

Дифференциальные уравнения


Прежде чем мы приступим к реализации, нужно определиться, какая информация у нас уже имеется и что нам нужно. У нас есть значение $y_0$, которое удовлетворяет $y(t_0) = y_0$, так же есть $f$, удовлетворяющее $\frac{dy}{dt}(t) = f(t, y(t))$. А нужна нам функция, которая даст нам состояние системы в любой момент времени. Математически, нам нужна функция $y(t)$.

Имея это ввиду и приглядевшись к $\frac{dy}{dt}(t) = f(t, y(t))$, можно заметить, что это уравнение связывает $y$ со её производной $\frac{dy}{dt}$. Это означает что наше уравнение дифференциальное! Обыкновенное дифференциальное уравнение первого порядка, если быть точнее. Если его решить, то мы найдём функцию $y(t)$.

Задача нахождения $y(t)$ по данным $y_0$ и $f$ называется задачей Коши.

Численное интегрирование


Для некоторых примеров задач Коши можно легко найти ответ аналитическим методом, но в сложных симуляциях аналитический подход может оказаться очень сложным. Поэтому попробуем найти способ поиска аппроксимированного решения задачи.

Для примера возьмём простую задачу Коши.
Дано: $y(0) = 1$ и $\frac{dy}{dt}(t) = f(t, y(t)) = y(t)$. Найти аппроксимированное решение для $y(t)$.

Рассмотрим задачу с геометрической точки зрения и посмотрим на значение и касательную в точке $t = 0$. Из того, что нам дано, имеем $y(0) = 1$ и $\frac{dy}{dt}(t) = y(t) = 1$


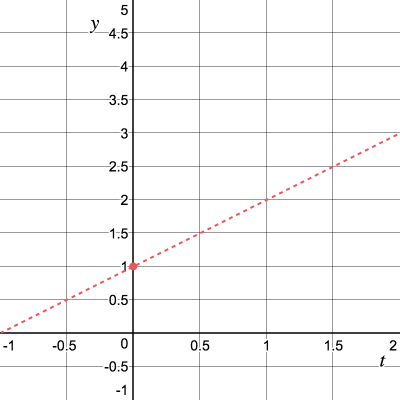
Мы пока не знаем как выглядит $y(t)$, но мы знаем что возле точки $t=0$, значение близко к касательной. Теперь постараемся вычислить $y(0 + h)$ для маленького значения $h$, воспользовавшись касательной. Для начала попробуем $h = 0.5$.


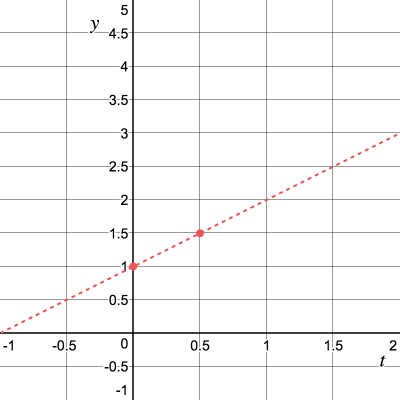
Если расписать, то мы приближаем значение $y(h)$ следующим образом:

$\begin{aligned} y(h) \approx y(0) + h \frac{dy}{dt}(0) &= y(0) + h f(0, y(0)) \\ &= y(0) + h y(0) \\ &= 1 + h \end{aligned}$


Так, для $h = 0.5, y(h) \approx 1.5 $.
??
Теперь мы можем продолжить вычислять для других точек. Хотя, конечно, мы нашли не точное значение $y(h)$, но если наше приближённое значение очень близко к точному, то аппроксимированная касательная тоже будет очень близка к действительной!

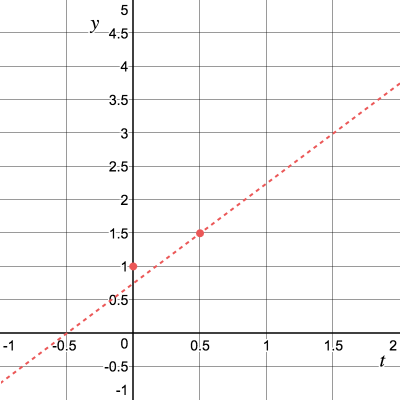
$$display$$\begin{aligned}?f(t,y(t))&?=y(t)\\?f(0.5,1.5)?&=1.5??\end{aligned}$$display$$



Далее, продвинемся ещё на $h$ единиц вправо по касательной.


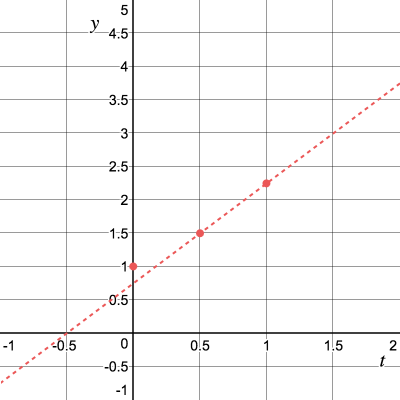
Повторим процесс и получим угловой коэффициент касательной $f(t,y(t))=f(1,2.25)=2.25$:


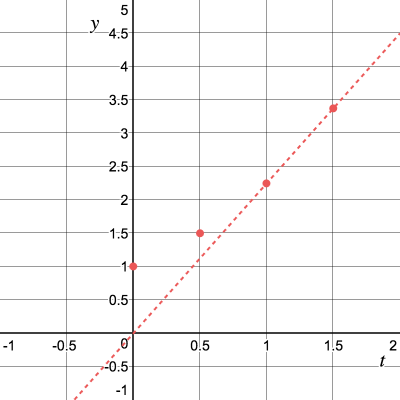
Процедуру можно проводить рекурсивно и для этого выведем формулу:

$\begin{aligned} t_{i+1} &= t_i + h \\ y_{i+1} &= y_i + h f(t_i, y_i) \end{aligned}$


Данный численный метод решения дифференциальных уравнений называется методом Эйлера. Для общего случая шаг x += v * delta_t.

В нашем конкретном случае, пошаговое решение выглядит так:

$\begin{aligned} t_{i+1} &= t_i + h \\ y_{i+1} &= y_i + h y_i \end{aligned}$


Используя данный метод, результаты удобно представлять в виде таблицы:

$\begin{aligned} t_0 &= 0, & y_0 &= 1 & & &\\ t_1 &= 0.5, & y_1 &= y_0 + h y_0 &=& 1 + 0.5 (1) &=& 1.5 \\ t_2 &= 1, & y_2 &= y_1 + h y_1 &=& 1.5 + 0.5 (1.5) &=& 2.25 \\ t_3 &= 1.5, & y_3 &= y_2 + h y_2 &=& 2.25 + 0.5 (2.25) &=& 3.375 \\ \end{aligned}$


Оказывается, у нашей задачи есть красивое аналитическое решение $y(t) = e^{?t} ??$:

График функции y(t) = e^?t

Как вы думаете, что произойдёт, если в методе Эйлера уменьшить шаг?


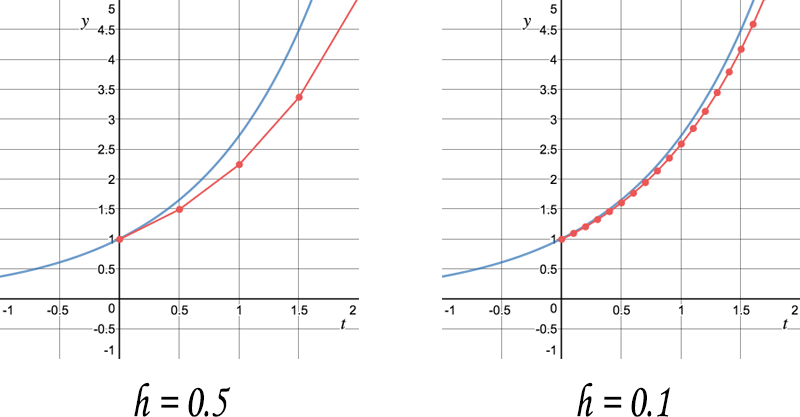
Разница между аппроксимированным и точным решениями уменьшается с уменьшением $h$! К тому же, вдобавок к уменьшению шага, можно использовать и другие методы численного интегрирования, которые могут привести к лучшему результату, такие как метод средних прямоугольников, метод Рунге-Кутты и метода Адамса.

Настало время кодить!


С таким же успехом как мы вывели математическое представление описания симуляции, мы можем написать реализацию симуляции программно.

Т.к. я больше всего знаком с JavaScript, и мне нравится ясность, которую добавляют в код аннотации, все примеры будут написаны на TypeScript.

А начнём мы с версии, в которой подразумевали, что $y$ это одномерный массив чисел, прямо как в нашей математической модели. 

function runSimulation(
    // y(0) = y0
    y0: number[],
    // dy/dt(t) = f(t, y(t))
    f: (t: number, y: number[]) => number[],
    // показывает текущее состояние симуляции
    render: (y: number[]) => void
) {
    // Шаг вперёд на 1/60 секунды за тик
    // Если анимация будет 60fps то это приведёт к симуляции в рельном времени
    const h = 1 / 60.0;

    function simulationStep(ti: number, yi: T) {
        render(yi)
        requestAnimationFrame(function() {
            const fi = f(ti, yi)

            // t_{i+1} = t_i + h
            const tNext = ti + h

            // y_{i+1} = y_i + h f(t_i, y_i)
            const yNext = []
            for (let j = 0; j < y.length; j++) {
                yNext.push(yi[j] + h * fi[j]);
            }

            simulationStep(tNext, yNext)
        }
    }
    simulationStep(0, y0)
}

Оперировать с одномерными массивами не всегда удобно, можно абстрагировать функции сложения и умножения процесса симуляции в интерфейс и получить краткую обобщённую реализацию симуляции используя TypeScript Generics.

interface Numeric<T> {
    plus(other: T): T
    times(scalar: number): T
}

function runSimulation<T extends Numeric<T>>(
  y0: T,
  f: (t: number, y: T) => T,
  render: (y: T) => void
) {
    const h = 1 / 60.0;

    function simulationStep(ti: number, yi: T) {
        render(yi)
        requestAnimationFrame(function() {
            // t_{i+1} = t_i + h
            const tNext = ti + h
            // y_{i+1} = y_i + h f(t_i, y_i)
            const yNext = yi.plus(f(ti, yi).times(h))
            simulationStep(yNext, tNext)
        })
    }
    simulationStep(y0, 0.0)
}

Положительной стороной данного подхода является возможность сконцентрироваться на основе симуляции: что именно эту симуляцию отличает от любой другой. Используем пример симуляции с двумя объектами, упомянутыми выше:

Код симуляция двух объектов
// Состояние симуляции двух объектов в один тик времени
class TwoParticles implements Numeric<TwoParticles> {
    constructor(
        readonly x1: Vec2, readonly v1: Vec2,
        readonly x2: Vec2, readonly v2: Vec2
    ) { }

    plus(other: TwoParticles) {
        return new TwoParticles(
            this.x1.plus(other.x1), this.v1.plus(other.v1),
            this.x2.plus(other.x2), this.v2.plus(other.v2)
        );
    }

    times(scalar: number) {
        return new TwoParticles(
            this.x1.times(scalar), this.v1.times(scalar),
            this.x2.times(scalar), this.v2.times(scalar)
        )
    }
}

// dy/dt (t) = f(t, y(t))
function f(t: number, y: TwoParticles) {
    const { x1, v1, x2, v2 } = y;
    return new TwoParticles(
        // dx1/dt = v1
        v1,
        // dv1/dt = G*m2*(x2-x1)/|x2-x1|^3
        x2.minus(x1).times(G * m2 / Math.pow(x2.minus(x1).length(), 3)),
        // dx2/dt = v2
        v2,
        // dv2/dt = G*m1*(x1-x1)/|x1-x2|^3
        x1.minus(x2).times(G * m1 / Math.pow(x1.minus(x2).length(), 3))
    )
}

// y(0) = y0
const y0 = new TwoParticles(
    /* x1 */ new Vec2(2, 3),
    /* v1 */ new Vec2(1, 0),
    /* x2 */ new Vec2(4, 1),
    /* v2 */ new Vec2(-1, 0)
)

const canvas = document.createElement("canvas")
canvas.width = 400;
canvas.height = 400;
const ctx = canvas.getContext("2d")!;
document.body.appendChild(canvas);

// Текущее состояние симуляции
function render(y: TwoParticles) {
    const { x1, x2 } = y;
    ctx.fillStyle = "white";
    ctx.fillRect(0, 0, 400, 400);

    ctx.fillStyle = "black";
    ctx.beginPath();
    ctx.ellipse(x1.x*50 + 200, x1.y*50 + 200, 15, 15, 0, 0, 2 * Math.PI);
    ctx.fill();

    ctx.fillStyle = "red";
    ctx.beginPath();
    ctx.ellipse(x2.x*50 + 200, x2.y*50 + 200, 30, 30, 0, 0, 2 * Math.PI);
    ctx.fill();
}

// Запускаем!
runSimulation(y0, f, render)


Если подшаманить с числами, то можно получить симуляцию орбиты Луны!

Симуляция орбиты Луны, 1 пикс. = 2500 км. 1 сек. симуляции равна 1 дню на Земле. Пропорция Луны к Земле увеличена в 10 раз

Столкновения и ограничения


Приведённая математическая модель и в самом деле симулирует физический мир, но в некоторых случаях метод численного интегрирования, к сожалению, ломается.

Представьте симуляцию прыгающего на поверхности мячика.

Состояние симуляции можно описать так:

$\vec y = \begin{bmatrix} x \\ v \end{bmatrix}$


Где $x$ это высота мяча над поверхностью, а $v$ его скорость. Если отпустить мяч с высоты 0.8 метра, то получим:

$\vec y_0 = \begin{bmatrix} 0.8 \\ 0 \end{bmatrix}$


Если изобразить график $x(t)$, то получим нечто следующее:


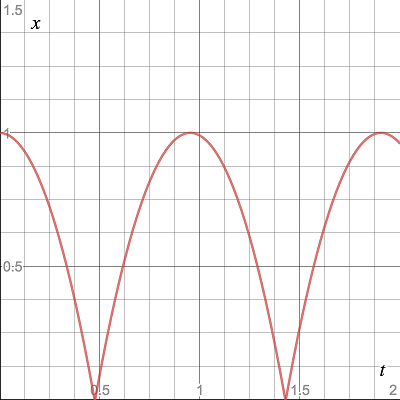
Во время падения мяча производная функции $f$ вычисляется достаточно легко:

$f(t,y(t)) = \frac{dy}{dt}(t) = \begin{bmatrix} \frac{dx}{dt}(t) \\ \\ \frac{dv}{dt}(t) \end{bmatrix} = \begin{bmatrix} v \\ a \end{bmatrix}$


С ускорением свободного падения, $a = -g = -9.8 \frac{m}{s^2}$.

Но что произойдёт, когда мяч коснётся поверхности? То, что мяч достиг поверхности мы можем узнать по $x=0$. Но при численном интегрировании, в один момент времени мяч может находиться над поверхностью, а уже в следующий под ней: $x_i > 0, x_{i+1} < 0$.

Можно было бы решить эту задачу путём определения момента столкновения $t_{?c} ~ (t_i < t_c < t_{i+1})$. Но даже если этот момент найти, как определить ускорение $ \frac{dv}{dt}$ так, чтобы оно менялось в противоположную сторону.

Можно, конечно, определить столкновение в ограниченном промежутке времени и применить другую силу $F$ на этот отрезок времени $\Delta t$, но гораздо легче определить дискретную константу ограничивающую симуляцию.

А чтобы уменьшить величину проницания мячом поверхности, можно за один тик вычислять сразу несколько шагов симуляции. В совокупности с этим, код нашей симуляции изменится так:


function runSimulation<T extends Numeric<T>>(
  y0: T,
  f: (t: number, y: T) => T,
  applyConstraints: (y: T) => T,
  iterationsPerFrame: number,
  render: (y: T) => void
) {
    const frameTime = 1 / 60.0
    const h = frameTime / iterationsPerFrame

    function simulationStep(yi: T, ti: number) {
        render(yi)
        requestAnimationFrame(function () {
            for (let i = 0; i < iterationsPerFrame; i++) {
                yi = yi.plus(f(ti, yi).times(h))
                yi = applyConstraints(yi)
                ti = ti + h
            }
            simulationStep(yi, ti)
        })
    }
    simulationStep(y0, 0.0)
}

И теперь уже можно написать код нашего прыгающего мячика:

Код прыгающего мячика

const g = -9.8; // m / s^2
const r = 0.2; // m

class Ball implements Numeric<Ball> {
    constructor(readonly x: number, readonly v: number) { }
    plus(other: Ball) { return new Ball(this.x + other.x, this.v + other.v) }
    times(scalar: number) { return new Ball(this.x * scalar, this.v * scalar) }
}

function f(t: number, y: Ball) {
    const { x, v } = y
    return new Ball(v, g)
}

function applyConstraints(y: Ball): Ball {
    const { x, v } = y
    if (x <= 0 && v < 0) {
        return new Ball(x, -v)
    }
    return y
}

const y0 = new Ball(
    /* x */ 0.8,
    /* v */ 0
)

function render(y: Ball) {
    ctx.clearRect(0, 0, 400, 400)
    ctx.fillStyle = '#EB5757'
    ctx.beginPath()
    ctx.ellipse(200, 400 - ((y.x + r) * 300), r * 300, r * 300, 0, 0, 2 * Math.PI)
    ctx.fill()
}

runSimulation(y0, f, applyConstraints, 30, render)




Внимание разработчикам!


Хоть у такой модели есть свои плюсы, она не всегда ведёт к производительным симуляциям. По мне, такой фреймворк полезен для представления поведения симуляции, даже если в ней происходит много чего лишнего.

Например, симуляция дождя в начале этой статьи [прим. В оригинальной статье, в начале вставлена красивая интерактивная симуляция дождя, рекомендую посмотреть воочию] не была создана с использованием, описанного в статье, шаблона. Это был эксперимент с использованием Entity–component–system. Исходники симуляции можно найти тут: симуляция дождя на GitHub.

До скорого!


Я нахожу пересечение математики, физики и программирования чем-то действительно впечатляющим. Создание работающей симуляции, её запуск и рендеринг это некий особенный вид чего-то из ничего.

На всё изложенное меня вдохновили материалы лекции SIGGRAPH, точно так же как и в симуляции жидкости. Если хотите найти более исчерпывающую информацию о вышеизложенном, то взгляните на материалы курса SIGGRAPH 2001 «Введение в физическое моделирование». Привожу ссылку на курс 1997 года, т.к. Pixar похоже удалила версию 2001.

Хочу поблагодарить Maggie Cai за чудесную иллюстрацию пары под зонтом и за терпение при кропотливом подборе цветов, в то время как я не могу отличить синее от серого.

А если вас интересует, то иллюстрации были созданы в Figma.

Комментарии (27)


  1. kovserg
    02.10.2017 10:00
    #10447218
    +1

    Лучше переведите Rigid Body Dynamics motion with constraints, там больше интересного. И метод решения уравнений для статического равновесия. Еще есть интересные статьи как эта математика распараллеливается на gpu.


    1. A3a Автор
      02.10.2017 10:41
      #10447292

      По поиску нашёл только мастер тезис Michael Bradley Cline 1999 года на 111 страниц. Вы же не его мне предлагаете переводить, правда? Поиск статьи слово в слово ничего не дал, если не сложно киньте ссылку пожалуйста.


      1. kovserg
        02.10.2017 13:21
        #10447568
        +1

        У вас же есть ссылка на siggraph
        David Baraff
        www.cs.cmu.edu/afs/cs.cmu.edu/user/baraff/www/index.html
        www.cs.cmu.edu/~baraff/pbm/rigid2.pdf — я вот это имел ввиду

        про gpu Erwin Counmans
        www.gdcvault.com/play/1017756/GPU-Rigid-Body
        www.multithreadingandvfx.org/course_notes/GPU_rigidbody_using_OpenCL.pdf
        www.nvidia.com/content/GTC/documents/1077_GTC09.pdf
        www.cs.rpi.edu/~trink/RSS-2011/Presentations/coumans.pdf


        1. A3a Автор
          02.10.2017 13:32
          #10447592

          Спасибо большое за ссылки, я не понял сразу что вы на материалы курса ссылались. Да, курс на первый взгляд очень интересный у них. Надо бы выжимку на досуге сделать.


  1. Idot
    02.10.2017 12:08
    #10447460

    Реально Круто! Всегда мечтал о таком!


    А реализация через OpenCL или CUDA будет?


    1. A3a Автор
      02.10.2017 12:14
      #10447472

      Да тут же простенькие симуляции, и четверти ядра хватит :)


  1. midday
    02.10.2017 13:00
    #10447532
    +3

    У вас луна улетает от земли тихонько.


    1. A3a Автор
      02.10.2017 13:09
      #10447546

      Я думаю это из-за недостатка Солнца


      1. A3a Автор
        02.10.2017 14:17
        #10447682
        +3

        Нет, всё же это из-за погрешности при численном интегрировании.


        1. Itanium_Next
          02.10.2017 22:50
          #10448364
          +4

          Разумеется из-за погрешностей. Метод Эйлера (тем более явный) — решение «в лоб». Для более точного решения стоит использовать хотя бы leap-frog (вычисляем попеременно то координату, то скорость). Будет и энергия сохраняться, и орбита.

          А «большие дяди» используют хотя бы метод Рунге-Кутты 4 порядка. Пишется в 4 строчки, а погрешность — O(h^2).


          1. bfDeveloper
            04.10.2017 13:07
            #10451646

            Вот за этим я всегда прихожу в комменты, за leap-frog первый раз слышу, хотя написал немало методов. Он очевиден и легко «изобретается», но не знал про его свойства.
            Рунге-Кутты 4 порядка всё же имеет 4-й порядок сходимости, соответственно O(h^4). Может вы имели в виду Рунге-Кутты 2-го порядка? Он действительно в 4 строчки.


            1. Itanium_Next
              04.10.2017 13:49
              #10451846

              Да, разумеется, О(h^4). Второпях набирал =)

              Если еще хотите поэкспериментировать с N-body, гуглите в сторону метода потенциалов: вычисляем не силу, действующую на каждое тело, а потенциал (например, гравитационный) в нужной точке. С него потом можно переходить на Practical Mesh и Tree-Code


    1. bfDeveloper
      02.10.2017 14:46
      #10447742

      Тоже хотел про это написать и даже был готов возмущаться, как так можно было написать. А потом подумал, как сделать симуляцию устойчивую к этой проблеме. Не поднять точность, а принципиально избавить метод от подобных ошибок. Конкретно эту задачу решить несложно — задача двух тел решается аналитически. А как быть с тремя телами? Пока могу придумать только количественные решения, например, методы высоких порядков сходимости (Р-К 4).


      1. kovserg
        02.10.2017 19:39
        #10448178
        +1

        Консервативные схемы интегрирования нужны. Короче насильно закон сохранения энергии и импульса поддерживать.


      1. Itanium_Next
        04.10.2017 13:55
        #10451864

        Задача трех тел аналитически не решается (строго говоря, нашелся один финн, который смог ее решить при помощи ну уж ооооочень медленно сходящихся рядов, так что это практического смысла не имеет).

        Чуть выше уже написал, что можно делать в случае, когда тел не меньше трех.


  1. xaoc80
    02.10.2017 14:31
    #10447706

    Касаемо симуляции прыгающего мячика. Когда-то я моделировал движение турбины, которая могла соприкасаться со статором и изучал хаотические колебания ротора. Модель соударения я моделировал в приближении Герца, то есть в момент удара действует упругая сила. В этом случае, если использовать метод Адамса для решение ОДУ, то решение получается довольно гладким. Вообще для таких задач надо тщательно выбирать метод численного решения.


  1. FadeToBlack
    03.10.2017 07:06
    #10448560

    Интересно, а как все сделано в PowderToy?


  1. nsinreal
    03.10.2017 13:22
    #10449072

    Когда писал себе симулятор гравитации обнаружил, что при сближении объектов (столкновение, а не движение по стабильной орбите) все идет в тартары. А именно: объекты после столкновения разлетаются с сильно увеличенной скоростью и нарушением закона сохранения энергии. Ваша реализация точно также ведет себя, если обнулить скорость Луны.
    Есть какие-то способы это обойти?


    1. Idot
      03.10.2017 14:08
      #10449200

      Гравитационный манёвр?


    1. bfDeveloper
      04.10.2017 13:12
      #10451676

      А как столкновение обрабатывали? Если это было именно столкновение, то уже 100 раз написано в множестве физдвижков и куча статей про это.
      Если же вы не обрабатывали это отдельно, а это был пролёт очень близко к центру масс, то всё ещё проще. Скорости около центров огромные, а влияние малейших изменений расстояния очень велико, поэтому любые погрешности (как метода, так и вычислительные) резко усиливаются. Выше писали про leap-frog, он не даст супер точности, но с энергией должно быть хорошо.


      1. nsinreal
        04.10.2017 18:55
        #10453204

        Столкновение никак не обрабатывалось. Строго говоря я не хотел бы вообще их обрабатывать до того момента как пойму, что моя модель корректно работает на гравитации. Про корректность: я ожидал что два идеальных шарика в вакууме (изначально с нулевой скоростью) будут бесконечно мотыляться вдоль одного ограниченного отрезка. За leapfrog посмотрю как оно себя ведет, спасибо.


        1. nsinreal
          04.10.2017 19:00
          #10453224

          Уточнение: под столкновением в оригинальном комментарии я подразумевал такое сближение объектов, что их координаты при максимально точных рассчетах должны были рано или поздно совпасть. Самого столкновения не было


          1. bfDeveloper
            05.10.2017 12:40
            #10455118

            leap-frog поможет на больших расстояниях, Луна перестанет стабильно удаляться. В вашем случае этого может не хватить, потому что рядом с нолём сила уходит в бесконечность и правильно проинтегрировать вряд ли получится. Методы более высоких порядков дадут выше точность, но всё равно ничего не гарантируют. Метод потенциалов, выше, осилит подобное.
            Но скорее всего в вашей задаче не нужна эта безумная точность в окрестности ноля, для небесной механики достаточно ограничить расстояние радиусом планет. При сближении на такое расстояние посчитать соударение шариков (неупругих с потерями на нагрев).


            1. nsinreal
              05.10.2017 15:08
              #10455602

              По глупости изначально решил, что метод потенциалов не поможет, но сейчас понял что был не прав. Спасибо.
              А вот касательно безумной точности вы не совсем правы. Когда клацал по чужим симуляторам (которые «решали» эту проблему через соударение) в некоторых случаях добивался точно такого же нарушения. Либо их писали раки, либо это частичное решение проблемы.
              Но у меня задача была по моделированию разных вариантов гравитации для собственного любопытства. Тут именно максимальная точность нужна.


              1. bfDeveloper
                05.10.2017 15:46
                #10455712

                Либо их писали раки

                Как бы грубо не звучало, но скорее всего так. В физдвиижках давно научились правильно обрабатывать столкновения. Это же два бильярдных шара, там всё банально считается в лоб. Вывести формулы скоростей после соударения, да тут первокурсник справится! Главное правильно отследить момент удара, а не давать погружаться телам друг в друга за один кадр.
                Для любопытства это здорово, но планета — не материальная точка, у неё размер есть. Взаимодействия на сравнимых с размером дистанциях уже интереснее. Материальной точке пофиг, а протяжённые объекты получат приливной градиент. Внутри планеты тоже всё будет не так. Ровно в центре гравитация вообще 0, а не бесконечность как в формуле G*M/R^2.
                Моя мысль в том, что малые расстояния находятся за пределами применимости формул небесной механики, не надо пытаться добиваться точности от них.


    1. KodyWiremane
      04.10.2017 13:21
      #10451732

      Видимо, происходит абсолютно упругое столкновение, т. е. не учитывается переход энергии движения в деформацию / разрушение / нагрев. Надо особо это обрабатывать. Даже мячик в симуляции выше не должен бы прыгать вечно.


      1. nsinreal
        04.10.2017 19:01
        #10453226

        Ответил выше, я некорректно выразился.