19.03.2018 09:42
ffriend 20 9500 Источник

image
(source)


Иногда мне приходится рассказывать другим людям как работает машинное обучение и, в частности, нейронные сети. Обычно я начинаю с градиентного спуска и линейной регрессии, постепенно переходя к многослойным перцептронам, автокодировщикам и свёрточным сетям. Все понимающе кивают головой, но в какой-то момент кто-нибудь прозорливый обязательно спрашивает:


А почему так важно, чтобы переменные в линейной регрессии были независимы?

или


А почему для изображений используются именно свёрточные сети, а не обычные полносвязные?

"О, это просто", — хочу ответить я. — "потому что если бы переменные были зависимыми, то нам пришлось бы моделировать условное распределение вероятностей между ними" или "потому что в небольшой локальной области гораздо проще выучить совместное распределение пикселей". Но вот проблема: мои слушатели ещё ничего не знают про распределения вероятностей и случайные переменные, поэтому приходится выкручиваться другими способами, объясняя сложнее, но с меньшим количеством понятий и терминов. А что делать, если попросят рассказать про батч нормализацию или генеративные модели, так вообще ума не приложу.


Так давайте не будем мучить себя и других и просто вспомним основные понятия теории вероятностей.


Случайные переменные


Представим, что у нас есть анкеты людей, где указаны их возраст, рост, пол и количество детей:


age height gender children
32 175 1 2
28 180 1 1
17 164 0 0
... ... .... ....

Каждая строчка в такой таблице — это объект. Каждая ячейка — значение переменной, характеризующей этот объект. Например, возраст первого человека — 32 года, а рост второго — 180см. А что, если мы хотим описать некоторую переменную сразу для всех наших объектов, т.е. взять целую колонку? В этом случае у нас будет не одно конкретное значение, а сразу несколько, каждое со своей частотой встречаемости. Список возможных значений + соответсвующая вероятность и называется случайной переменной (random variable, r.v.).


Дискретные и непрерывные случайные переменные


Чтобы это отложилось в голове, я повторю ещё раз: случайная переменная полностью задаётся распределением вероятностей своих значений. Есть 2 основных типа случайных переменных: дискретные (discrete) и непрерывные (continuous).


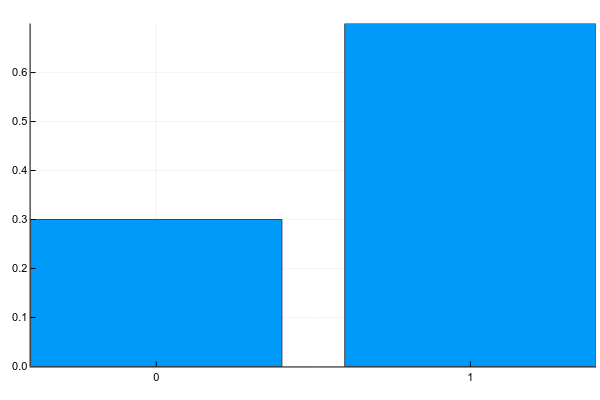
Дискретные переменные могут принимать набор чётко разделимых значений. Обычно я изображаю их как-нибудь так (probability mass function, pmf):



Код на Julia
Pkg.add("Plots")
using Plots
plotly()

plot(["0","1"], [0.3, 0.7], linetype=:bar, legend=false)

А текстом это обычно записывается так (g — gender):


$p(g=0) = 0.3\\ p(g=1) = 0.7$


Т.е. вероятность того, что случайно взятый человек из нашей выборки окажется женщиной ($g=0$) равна 0.3, а мужчиной ($g=1$) — 0.7, что эквивалентно тому, что в выборке было 30% женщин и 70% мужчин.


К дискретным же переменным относятся количество детей у человека, частота встречаемости слов в тексте, количество просмотров фильма и т.д. Результат классификации на конечное число классов, кстати, — это тоже дискретная случайная переменная.


Непрерывные переменные могут принимать любое значение в определённом интервале. Например, даже если мы записываем, что рост человека — 175см, т.е. округляем до 1 сантиметра, на самом деле он может быть 175.8231см. Изображают непрерывные переменные обычно с помощью кривой плотности вероятности (probability density function, pdf):



Код
Pkg.add("Distributions")
using Distributions

xs = 140:0.1:200
ys = [pdf(Normal(172, 10), x) for x in xs]
plot(xs, ys; xlabel="h", ylabel="p(h)", legend=false, show=true)

График плотности вероятности — штука хитрая: в отличие от графика массы вероятности для дискретных переменных, где высота каждой колонки показывает непосредственно вероятность получить такое значение, плотность вероятности показывает относительное количество вероятности вокруг некоторой точки. Саму же вероятность в этом случае можно посчитать только для интервала. Например, в этом примере вероятность, что случайно взятый человек из нашей выборки будет иметь рост от 160 до 170см равна примерно 0.3.


Код
d = Normal(172, 10)
prob = cdf(d, 170) - cdf(d, 160)

Вопрос: может ли плотность вероятности в какой-то точке быть больше единицы? Ответ — да, конечно, главное, чтобы общая площадь под графиком (или, говоря математически, интеграл плотности вероятности) был равен единице.


Ещё одна трудность с непрерывными переменными состоит в том, что их плотность вероятности не всегда возможно красиво описать. Для дискретных переменных у нас просто была таблица значение -> вероятность. Для непрерывных это уже не прокатит, поскольку значений у них, вообще говоря, бесконечное множество. Поэтому обычно стараются аппроксимировать набор данных каким-нибудь хорошо изученным параметрическим распределением. Например, график выше — это пример т.н. нормального распределения. Плотность вероятности для него задаётся формулой:


$p(x) = \frac{1}{\sqrt{2\pi \sigma^2}}e^{-\frac{(x - \mu)^2}{2\sigma^2}}$


где $\mu$ (мат. ожидание, mean) и $\sigma^2$ (дисперсия, variance) — параметры распределения. Т.е. имея всего 2 числа мы можем полностью описать распределение, посчитать его плотность вероятности в любой точке или суммарную веростность между двумя значениями. К сожалению, далеко не для любого набора данных найдётся распределение, которое сможет его красиво описать. Есть много способов бороться с этим (взять хотя бы смесь нормальных распределений), но это уже совсем другая тема.


Другие примеры непрерывного распределения: возраст человека, интенсивность пикселя на изображении, время ответа от сервера и т.д.


Совместное, маргинальное и условное распределения


Обычно мы рассматриваем свойства объекта не по одному, а в комбинации с другими, и здесь появляется понятие совместного распределения (joint probability) нескольких переменных. Для двух дискретных переменных мы можем изобразить его в виде таблицы (g — gender, c — # of children):


c=0 c=1 c=2
g=0 0.1 0.1 0.1
g=1 0.2 0.4 0.1

Согласно этому распределению, вероятность встретить в нашем наборе данных женщину с 2-мя детьми равна $p(g=0, c=2) = 0.1$, а бездетного мужчину — $p(g=1, c=0) = 0.2$.


Для двух непрерывных переменных, например, роста и возраста, нам снова придётся задать аналитическую функцию распределения $p(h, a)$, аппроксимировав его,
например, многомерным нормальным. Таблицей это не запишешь, зато можно нарисовать:



Код
d = MvNormal([172.0, 30.0], [10 0; 0 5])
xs = 160:0.1:180
ys = 22:1:38
zs = [pdf(d, [x, y]) for x in xs, y in ys]
surface(zs)

Имея совместное распределение, мы можем найти распределение каждой переменной по отдельности, просто суммировав (в случае дискретных) или интегрировав (в случае непрерывных) остальные переменные:


$p(g) = \sum_c p(g, c)\\ p(h) = \int p(a, h) da$


Это можно представить в виде суммирования по каждой строке или столбцу таблицы и вынесением результат на поля таблицы:


c=0 c=1 c=2
g=0 0.1 0.1 0.1 0.3
g=1 0.2 0.4 0.1 0.7

Так мы снова получаем $p(g=0) = 0.3$ и $p(g=1) = 0.7$. Процесс вынесения на поля (margin) даёт название и самому получившемуся распределению — маргинальное (marginal probability).


А что, если мы уже знаем значение одной из переменных? Например, мы видим, что перед нами мужчина и хотим получить распределение вероятностей количества его детей? Таблица совместной вероятности и тут нам поможет: поскольку мы уже точно знаем, что перед нами мужчина, т.е. $g=1$, мы можем выбросить из рассмотрения все остальные варианты и рассматривать только одну строчку:


c=0 c=1 c=2
g=1 0.2 0.4 0.1

$\bar{p}(c=0 | g=1) = 0.2\\ \bar{p}(c=1 | g=1) = 0.4\\ \bar{p}(c=2 | g=1) = 0.1$


Поскольку вероятности так или иначе должны суммироваться в единицу, получившиеся значения нужно нормализовать, после чего получится:


$p(c=0 | g=1) = 0.29\\ p(c=1 | g=1) = 0.57\\ p(c=2 | g=1) = 0.14$


Распределение одной переменной при известном значении другой называется условным (conditional probability).


Правило цепи


А соединяются все эти вероятности одной просто формулой, которая называется правилом цепи (chain rule, не путать с правилом цепи в дифференцировании):


$p(x, y) = p(y|x)p(x)$


Формула эта симметричная, поэтому так тоже можно:


$p(x, y) = p(x|y)p(y)$


Интерпретация правила очень простая: если $p(x)$ — вероятность того, что я пойду на красный свет, а $p(y|x)$ — вероятность того, что человек, переходящий на красный свет, будет сбит, то совместная вероятность пойти на красный свет и быть сбитым как раз и равна произведению вероятностей этих двух событий. Но вообще лучше ходите на зелёный.


Зависимые и независимые переменные


Как уже говорилось, если у нас есть таблица совместного распределения, то мы знаем про систему всё: можно вычислить маргинальную веростность любой переменной, можно условное распределение одной переменной при известной другой и т.д. К сожалению, на практике составить такую таблицу (или просчитать параметры непрерывного распределения) в большинстве случаев невозможно. Например, если мы захотим посчитать совместное распределение встречаемости 1000 слов, то нам понадобится таблица из


107150860718626732094842504906000181056140481170553360744375038837035105112493612
249319837881569585812759467291755314682518714528569231404359845775746985748039345
677748242309854210746050623711418779541821530464749835819412673987675591655439460
77062914571196477686542167660429831652624386837205668069376


(чуть больше 1e301) ячеек. Для сравнения, количество атомов в наблюдаемой вселенной равно примерно 1e81. Пожалуй, покупкой дополнительной планки памяти тут не обойдёшься.


Но есть одна приятная деталь: не все переменные зависят друг от друга. Вероятность того, пойдёт ли завтра дождь, вряд ли зависит от того, перехожу ли я дорогу на красный свет. Для независимых переменных условное распределение одной от другой равно просто маргинальному распределению:


$p(y|x) = p(y)$


По-честному, совместная вероятность 1000 слов записывается так:


$p(w_1, w_2, ..., w_{1000}) = p(w_1) \times p(w_2|w_1) \times p(w_3|w_1, w_2) \times ... \times p(w_{1000}|w_1, w_2, ...)$


А вот если мы "наивно" предположим, что слова не зависят друг от друга, то формула превратится в:


$p(w_1, w_2, ..., w_{1000}) = p(w_1) \times p(w_2) \times p(w_3) \times ... \times p(w_{1000})$


А чтобы сохранить вероятности $p(w_i)$ для 1000 слов нужна таблица всего с 1000 ячеек, что вполне приемлемо.


Почему тогда не считать все переменные независимыми? Увы, так мы потеряем массу информации. Представим, что мы хотим посчитать вероятность того, что пациент болен гриппом в зависимости от двух переменных: боли в горле и повышенной температуры. Отдельно боль в горле может говорить как о болезни, так и том, что пациент только что громко пел. Отдельно повышенная температура может говорить как о болезни, так и о том, что человек только что вернулся с пробежки. А вот если мы одновременно наблюдаем и температуру, и боль в горле, то это уже серьёзная причина выписать пациенту больничный.


Логарифм


Очень часто в литературе можно увидеть, что используется не просто вероятность, а её логарифм. Зачем? Всё довольно прозаично:


  1. Логарифм — монотонно возрастающая функция, т.е. для любых $p(x_1)$ и $p(x_2)$ если $p(x_1) > p(x_2)$, то и $\log p(x_1) > \log p(x_2)$.
  2. Логарифм произведения равен сумме логарифмов: $\log (p(x_1) p(x_2)) = \log p(x_1) + \log p(x_2)$.

В примере со словами вероятность встретить любое слово $p(w_i)$, как правило, сильно меньше единицы. Если мы попробуем перемножить много маленьких вероятностей на компьютере с ограниченной точностью вычислений, догадываетесь что будет? Ага, очень быстро наши вероятности округляться к нулю. А вот если мы сложим много отдельных логарифмов, то выйти за пределы точности вычислений будет практически невозможно.


Условная вероятность как функция


Если после всех этих примеров у вас сложилось впечатление, что условная вероятность всегда вычисляется подсчётом количества раз, которое встретилось некоторое значение, то спешу развеять это заблуждение: в общем случае условная вероятность — это некоторая функция одной случайной переменной от другой:


$p(y|x) = f(x) + \epsilon$


где $\epsilon$ — это некоторый шум. Виды шума — это тоже отдельная тема, в которую мы сейчас влезать не будем, а вот на функции $f(x)$ остановимся поподробней. В примерах с дискретными переменными выше в качестве функции мы использовали простой подсчёт встречаемости. Это само по себе хорошо работает во многих случаях, например, в наивном байесовском классификаторе для текста или поведения пользователей. Чуть более сложная модель — линейная регрессия:


$p(y|x) = f(x) + \epsilon = \theta_0 + \sum_i\theta_ix_i + \epsilon$


Здесь тоже делается предположение о том, что переменные $x_i$ независимы друг от друга, но распределение $p(y|\mathbf{x})$ уже моделируется с помощью линейной функции, параметры которой $\mathbf{\theta}$ нужно найти.


Многослойный перцептрон — это тоже функция, но благодаря промежуточным слоям, на которые влияют все входные переменные сразу, MLP позволяет моделировать зависимость выходной переменной от комбинации входных, а не только от каждой из них по отдельности (вспомните пример с болью в горле и температурой).


Свёрточная сеть работает с распределением пикселей в локальной области, покрываемой размером фильтра. Рекуррентные сети моделируют условное распределение следующего состояния от предыдущего и входных данных, а также выходной переменной от текущего состояния. Ну, в общем, вы поняли идею.


Теорема Байеса и умножение непрерывных переменных


Помните правило сети?


$p(x, y) = p(y|x)p(x) = p(x|y)p(y)$


Если убрать левую часть, то получим простое и очевидное равенство:


$p(y|x)p(x) = p(x|y)p(y)$


А если теперь перенесём $p(x)$ направо, то получим знаменитую формулу Байеса:


$p(y|x) = \frac{p(x|y)p(y)}{p(x)}$


Про произношение

Итересный факт: русское произношение "байес" в английском звучит как слово "bias", т.е. "смещение". А вот фамилия учёного "Bayes" читается как "бэйс" или "бэйес" (лучше послушать в Yandex Translate).


Формула настолько избитая, что каждая её часть имеет своё название:


  • $p(y)$ называется априорным распределением (prior). Это то, что мы знаем ещё до того, как увидели конкретный объект, например, общее количество людей, вовремя выплативших кредит.
  • $p(x|y)$ носит название правдоподобия (likelihood). Это вероятность увидеть такой объект (описанный переменной $x$) при таком значении выходной переменной $y$. Например, вероятность того, что у человека, отдавшего кредит, двое детей.
  • $p(x) = \int p(x, y) dy$ — маргинальное правдоподобие, вероятность вообще увидеть такой объект. Оно одинаково для всех $y$, так что его чаще всего не считают, а просто максимизируют числитель формулы Байеса.
  • $p(y|x)$ — апостериорное распределение (posterior). Это распределение вероятностей переменной $y$ после того, как мы увидели объект. Например, вероятность того, что человек с двумя детьми отдаст кредит вовремя.

Байесовская статистика — штука жутко интересная, но влезать в неё сейчас мы не будем. Единственный вопрос, который хотелось бы затронуть, — это перемножение двух распределений непрерывных переменных, которое у нас встречается, например, в числителе формулы Байеса, да и вообще в каждой второй формуле над непрерывными переменными.


Допустим, что у нас есть два распределения $p_1(y)$ и $p_2(y)$:



Код
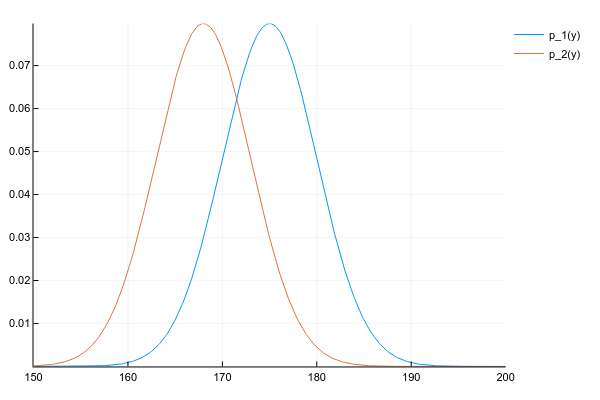
d1 = Normal(175, 5)
d2 = Normal(168, 5)
space = 150:0.1:200
y1 = [pdf(d1, y) for y in space]
y2 = [pdf(d2, y) for y in space]
plot(space, y1, label="p_1(y)")
plot!(space, y2, label="p_2(y)")

И мы хотим получить их произведение:


$p(y) = p_1(y)p_2(y)$


Мы знаем плотность вероятности обоих распределений в каждой точке, поэтому, по-честному и в общем случае, нам нужно перемножить плотности в каждой точке. Но, если мы вели себя хорошо, то $p_1(y)$ и $p_2(y)$ у нас заданы параметрами, например, для нормального распределения 2-мя числами — матожиданием и дисперсией, а для их произведения придётся считать вероятность в каждой точке?


К счастью, произведение многих известных распределений даёт другое известное распределение с легко вычислимыми параметрами. Ключевое слово здесь — conjugate prior.


Как бы мы не вычисляли, произведение двух нормальных распределений даёт ещё одно нормальное распределение (правда, ненормализованное):



Код
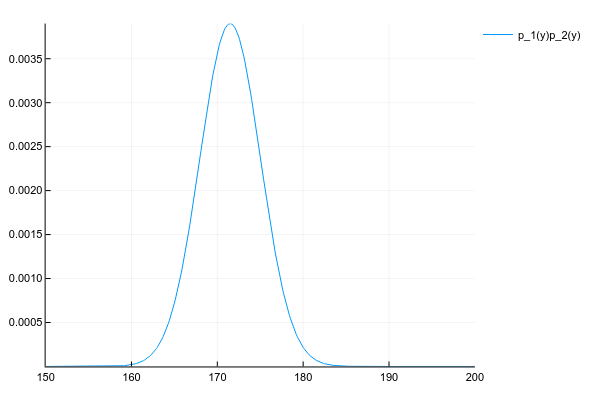
# честно перемножаем плотности вероятности в каждой точке
# неэффективно, но работает для любых распределений
plot(space, y1 .* y2, label="p_1(y)p_2(y)")

Ну и просто для сравнения распределение смеси 3х нормальных распределений:



Код
plot(space, [pdf(Normal(130, 5), x) for x in space] .+ 
                 [pdf(Normal(150, 20), x) for x in space] .+ 
                 [pdf(Normal(190, 3), x) for x in space])

Вопросы


Раз уж это туториал и кто-нибудь наверняка захочет запомнить то, что здесь было написано, вот несколько вопросов для закрепления материала.


Пусть рост человека — нормально распределённая случайная переменная с параметрами $\mu=172$ и $\sigma^2=10$. Какова вероятность встретить человека ростом ровно 178см?

Ответ

Правильными ответами можно считать "0", "бесконечно мала" или "не определена". А всё потому что вероятность непрерывной переменной считается на некотором интервале. Для точки интервал — это её ширина, в зависимости от того, где вы учили математику, длину точки можно считать нулём, бесконечно малой или вообще не определённой.


Пусть $x$ — количество детей у заёмщика кредита (3 возможными значения), $y$ — признак того, отдал ли человек кредит (2 возможных значения). Мы используем формулу Байеса для предсказания, отдаст ли конкретный клиент с 1 ребёнком кредит. Сколько возможных значений может принимать априорное и апостериорное распределения, а также правдоподобие и маргинальное правдоподобие?

Ответ

Таблица совместного распредления двух переменных в данном случае небольшая и имеет вид:


c=0 c=1 c=2
s=0 p(s=0,c=0) p(s=0,c=1) p(s=0,c=2)
s=1 p(s=1,c=0) p(s=1,c=1) p(s=1,c=2)

где $s$ — признак успешно отданного кредита.


Формула Байеса в данном случае имеет вид:


$p(s|c) = \frac{p(c|s)p(s)}{p(c)}$


Если все значения известны, то:


  • $p(c)$ — это маргинальная вероятность увидеть человека с одним ребёнком, считается как сумма по колонке $с=1$ и является просто числом.
  • $p(s)$ — априорная/маргинальная вероятность того, что случайно взятый человек, про которого мы ничего не знаем, отдаст кредит. Может иметь 2 значения, соответствующих сумме по первой и по второй строке таблицы.
  • $p(c|s)$ — правдоподобие, условное распределение количества детей в зависимости от успешности кредита. Может показаться, что раз уж это распределение количества детей, то возможных значений должно быть 3, но это не так: мы уже точно знаем, что к нам пришёл человек с одним ребёнком, поэтому рассматриваем только одну колонку таблицы. А вот успешность кредита пока под вопросом, поэтому возможны 2 варианта — 2 строки таблицы.
  • $p(s|c)$ — апостериорное распределение, где мы знаем $c$, но рассматриваем 2 возможных варианта $s$.

Нейронные сети, оптимизирующие расстояние между двумя расспределениями $q(x)$ и $p(x)$, зачастую используют в качестве оптимизационной цели кросс-энтропию (cross entropy) или расстояние Кульбака-Лейблера (Kullback-Leibler divergence). Последнее определяется как:

$KL(q||p) = \int q(x) \log \frac{q(x)}{p(x)}dx$


$\int q(x) (.) dx$ — это мат. ожидание по $q(x)$, а почему в основной части — $\log \frac{q(x)}{p(x)}$ — используется деление, а не просто разница между плотностями двух функций $q(x) - p(x)$?

Ответ

$\log \frac{q(x)}{p(x)} = \log q(x) - \log p(x)$


Другими словами, это и есть разница между плотностями, но в логарифмическом пространстве, которе является вычислительно более стабильным.

Комментарии (20)


  1. myrslok
    19.03.2018 15:31
    #10715636

    Придирка к задаче про рост: вероятность одноточечного множества может быть и ненулевой, это зависит от распределения. Реально рост распределен более-менее нормально, но в формулировке это не сказано.


    1. ffriend Автор
      19.03.2018 18:17
      #10715928

      А ведь и правда, пропустил эту деталь. Добавил "нормально распределённая случайная переменная".


      Спасибо!


      1. yorgo
        19.03.2018 21:21
        #10716248

        А разве здесь важно конкретное распределение или же значения его параметров? Коль скоро распределение непрерывно, вероятность точечного события равна нулю (что, вообще говоря, не означает невозможности наступления этого события).


        1. ffriend Автор
          19.03.2018 21:25
          #10716258

          Всё верно, задача с небольшим подвохом, чтобы ответ совсем уж очевидным не был.


  1. vsuragin
    19.03.2018 18:21
    #10715936
    +1

    «Дискретные переменные имеют конечное множество чётко разделимых значений»

    Возможно я подзабыл курс универской математики, но разве дискретная переменная обязательно имеет конечное множество значений? Дискретность противопоставляется непрерывности, а не размерности множества.
    Да и само по себе определение дискретности подразумевает в себе 'разделимость' значений, так что звучит для меня как тавтология.


    1. ffriend Автор
      19.03.2018 18:49
      #10715994

      Если быть точным, то значения дискретной переменной могут принадлежать конечному (finite) либо счётному (countable) множеству. Счётное множество — это, например, множество всех возможных строк из символов таблицы ASCII. В теории для них тоже можно построить распределение вероятностей, свойства которого будут чем-то средним между свойствами непрерывного и конечного дискретного распределения. На практике мне ещё не приходилось работать с бесконечным набором признаков объекта, да и окунать читателя в детали теории множеств не особо хотелось. Поэтому, я надеюсь, вы простите мне эту маленьку ложь.


      (В статье, кстати, ещё много примеров маленькой лжи. Самая большая маленькая ложь, пожалуй, это определение вероятности, которую я сначала показываю на примере подсчёта встречаемости, потом обзываю функцией с шумом, а на самом деле это мера, да ещё и с несколькими возможными интерпретациями; а случайная переменная, соответсвенно, — это измеримая функция. Но последний раз, когда я пытался быть математически точным, люди начинали похрапывать минуте на 8й и выходили с полным отсутствием понимания).


      1. Deosis
        20.03.2018 07:44
        #10716530

        Самый простой пример дискретной случайной величины с бесконечным множеством значений:
        Подбрасывать монетку, пока не выпадет орел.
        Результатом измерения случайной величины считать количество подбрасываний.


        1. ffriend Автор
          20.03.2018 15:39
          #10717214

          Хм, согласен. Наверное, распределение Пуассона сюда тоже попадёт, хотя я его плохо знаю. Убрал "конечное", спасибо за пример.


        1. RoykerZen
          20.03.2018 20:31
          #10717770

          А простой натуральный ряд не из той же серии? Элементы — дискретны, количество элементов — бесконечно…


          1. ffriend Автор
            20.03.2018 20:49
            #10717816

            Над самим по себе натуральным рядом не определена вероятность, так что распределением он не является. Хотя он учвствует в определении счётного множества, которое является основой для бесконечных дискретных распределений, это да.


  1. rotor
    19.03.2018 22:10
    #10716288

    Годнота!
    Вот такие статьи по ML хочу видеть на Хабре.


  1. ntkj666
    20.03.2018 04:10
    #10716480

    "кривой плотоности"


  1. ntkj666
    20.03.2018 04:24
    #10716486

    "органиченной точностью"


    1. ffriend Автор
      20.03.2018 15:39
      #10717216

      Поправил, спасибо.


  1. ChePeter
    20.03.2018 09:50
    #10716576
    -1

    Для понимания сути явления вероятности нужны труды Мартина Лёфа.
    Применять алгоритмическую парадигму к полностью неалгоритмической, классической теории вероятностей как то вызывает настороженность и сомнения.


    1. ffriend Автор
      20.03.2018 15:52
      #10717232
      +1

      Это уже зависит от целей. Если цель — построить красивую теоретическую систему, то да, наверное это важно. Если же цель менее благородная, но более практическая, то обычно и наивного представление о вероятности хватает для любого практического применения.


      1. ChePeter
        20.03.2018 15:59
        #10717250

        Правильная теория — половина решения
        Ну и Земля тоже бывает плоской
        ))
        Выше это шутка

        Красивые теоретические системы строят не от любви к системам
        Это серьезно


    1. Kwent
      21.03.2018 22:53
      #10719596

      А какие именно труды, если не секрет?


  1. ChePeter
    22.03.2018 09:04
    #10719780

    The definition of random sequences
    Martin-Lof
    Если строить алгоритмы, то нужно использовать такое определение как начало рассуждений.


  1. KsandrFreeman
    22.03.2018 14:45
    #10720318
    +1

    Коллеги! А подскажите, пожалуйста, толковую литературу/курс по Байесовским нейронным сетям.