25.03.2018 20:17
Rumyantsev 13 3400 Источник

Введение


Ввиду того, что при решении задач оптимизации, дифференциальных игр, и в 2D и 3D расчётах, а вернее при написании софта, который проводит вычисления для их решения одними из наиболее часто выполняемых операций являются векторно-матричные преобразования типа $aX+bY$, где $a,b$ — скалярные значения, $X, Y\in R^n$ — вектора или матрицы размерности $R^{n\times m}$.


Собственно вот такие:


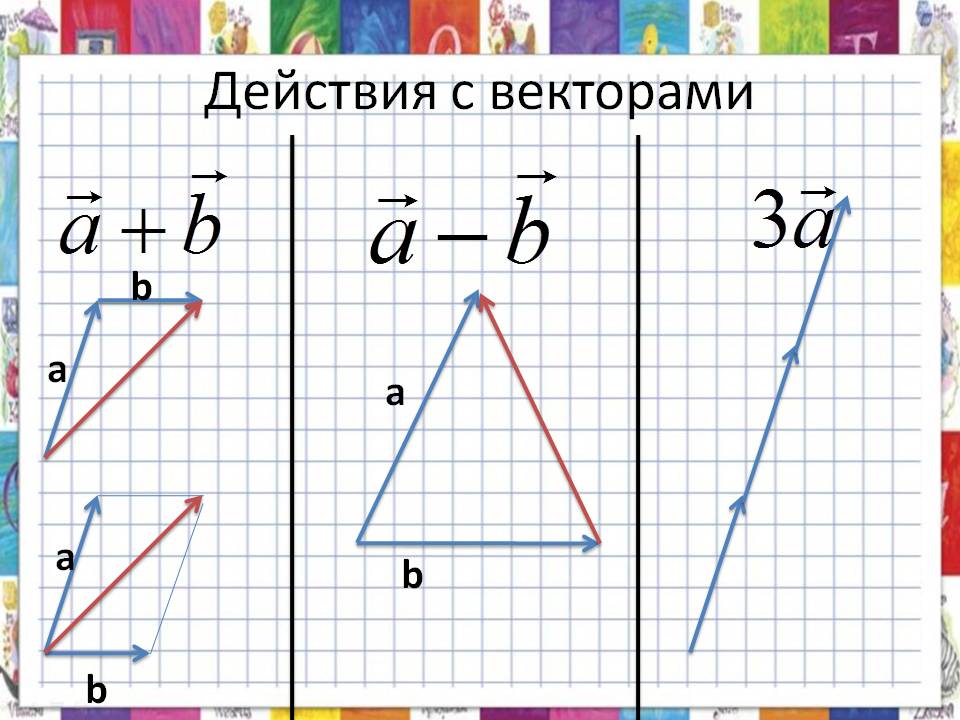
image
(источник).


Так, чтобы не углубляться в теорию оптимизации за примерами достаточно вспомнить формулу численного интегрирования Рунге-Кутты четвёртого порядка:


$Y_{n+1}=Y_n+\frac{h}{6}(k_1 + 2 k_2 + 2 k_3+k_4),$


где $Y_i$ — очередное значение интегрируемой функции $f(t,Y)$ $h$ — шаг метода, а $k_i$, $i=1..4$ — значения интегрируемой функции в некоторых промежуточных точках — в общем случае векторах.


Как можно заметить основную массу математических операций как для векторов, так и для матриц составляют:


  • сложение и вычитание — более быстрые;
  • умножение и деление — более медленные.

О сложности вычислений хорошо написано в соответствующем курсе МФТИ.


Помимо этого, довольно существенные расходы при реализации векторных вычислений приходятся на операции управления памятью — создание и уничтожение массивов представляющих собой матрицы и вектора.


Соответственно есть смысл заняться снижением количества операций привносящих наибольшую сложность — умножения (математика) и операции управления памятью (алгоритмика).


Снижение вычислительной сложности


Произвольный вектор $x\in R^n$ представим в виде $x = aX$, где
$a\in R^1$, $X\in R^n$, обозначим как $[a,X]$. Операцией приведения такого вектора назовем вычисление $[a,X]=x\in R^n$, — обратную операцию, вычислительная сложность которой составляет $n$ операций действительного умножения.


Соответственно под экономией будем понимать экономию операций умножения.


На чём можно сэкономить при операциях с векторами :


  1. Умножение на константу $b[a,X]= [ab,X]$ — экономится $n-1$ операция умножения.
  2. Сложение $k$ сонаправленных векторов $\sum\limits_{i=1}^{k} [a_i,X]= \left[\sum\limits_{i=1}^{k}a_i,X\right]$
    • откладывается вычисление $n$ умножений;
    • экономится $(k-2)n$ умножений.
  3. Сложение не сонаправленных векторов $[a,X]+[b,Y]= [a,X+b/a\ Y]$ — откладывается вычисление $n-1$ операция умножения, при $a \ne 0$.
  4. Умножение матрицы на вектор: $A[a,x]=[a,Ax]$, где $A\in R^{m\times n}$ — что позволяет отложить вычисление $m$ операций умножения.
  5. Скалярное произведение векторов $([a,X],[b,Y])= ab(X,Y)$ — экономится $n-1$ операция действительного умножения.

Аналогично, если представить матрицу в виде $Y = a\bar Y$, где
$a\in R^1$, а $\bar Y, Y\in R^{n\times m}$, обозначим как $[a,\bar Y]$. Соответственно операцией приведения — вычисление $[a,\bar Y]=Y\in R^{n\times m}$, — обратную операцию, вычислительная сложность которой составляет $n\cdot m$ операций действительного умножения.


Аналогичны и возможности экономии (1-4) с той той лишь разницей, что операция скалярного произведения (5) отсутствует, а для остальных операций возможности сэкономить умножения становится больше в $m$ раз, что довольно приятно, особенно при необходимости хранения в матричном представлении массивов векторов для проведения над ними различных массовых операций.


Понятно, что приведенные выше способы экономии не бесплатны в смысле необходимости иметь дополнительную память для хранения коэффициентов, и накладных затрат связанных с контролем состояния вычисляемых объектов.


Помимо чисто математических оптимизаций данный подход вполне применим при вычислениях на сетках т.е., например, если значение сеточной функции, представленной вектором, надо сначала умножить на некоторую константу, а потом найти градиентным методом (не перебирая все значения) её максимум.


Снижение алгоритмической сложности


Как видно из предшествующих рассуждений, — реальная экономия возникает для:


  • умножения вектора/матрицы на число и скалярных произведений векторов;
  • операций над векторами и матрицами, отличающимися только коэффициентами.

Соответственно для того, чтобы обеспечить оптимизацию скалярных вычислений необходимо построить структуру данных следующего вида:


class Vector {
public:
   sVec *v; //массив для данных
   double upd; //коэфф. a
   bool updated; //признак  того, что a==1
//....
};

Возможно не самым очевидное здесь — назначение переменной updated, ввиду того, что если upd = 1, то вроде как дополнительные проверки избыточны. Но если вспомнить, что последовательное деление и умножение следующего вида:


a_ /= b_;
a_ *= b_;

не обязано сохранять значение a_ из-за округлений, то видно, что данная страховка не лишняя.


Далее, если обратить внимание на, то, что если у векторов $[a,X]$ и $[b,X]$ сам $X$ одинаков, то нет смысла хранить его дважды, а достаточно создать единственный объект класса базовый вектор $X$ и ссылаться на него в расчётах, т.е. 


class sVec {
public:
    unsigned long size;
    double *v;//собственно массив данных
    long linkCount;//счётчик ссылок
//..
};

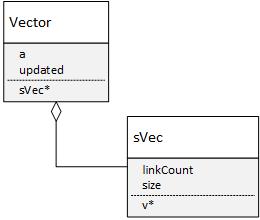
image


Динамический массив здесь необходим для того, чтобы отрабатывать склонность векторов менять размерность при умножении на матрицу, подход связанный с учётом ссылок — для того, чтобы убрать "под капот" логику связанную с созданием и отслеживанием дубликатов объектов, при использовании перегруженных операторов для векторных и матричных операций в С++.


Особенности реализации


Для примера (который можно взять на github) рассмотрим достаточно простые вычисления, связанные с векторно-матричной арифметикой в разрезе экономии операций умножения. Итак: сначала создадим необходимые объекты:


    Vector X(2), Y(2), Z(2); //три вектора из R^2
    double a = 2.0; // коэфф. для проверки умножения на скаляр

и инициализируем их как единичный вектор для X=[1,1] и нулевой для Y=[0,0]


    X.one(); //единичный вектор [1,1]
    Y.zero();// создаём нулевой вектор [0,0]
    cout<<"Вектор X: "<<X<<" Счётчик ссылок X: "<<X.v->linkCount<<" Адрес массива: "<<X.v<<endl;
    cout<<"Вектор Y: "<<Y<<" Счётчик ссылок Y: "<<Y.v->linkCount<<" Адрес массива: "<<Y.v<<endl;

Получаем, что внутренние вектора указывают на разыве массивы и оба счётчика ссылок равны единице.


Вектор X: [1,1]; Счётчик ссылок X: 1 Адрес массива: 448c910
Вектор Y: [0,0]; Счётчик ссылок Y: 1 Адрес массива: 448c940

Далее приравниваем вектора:


    Y=X;// теперь приравниваем X и Y
    cout<<"Вектор X: "<<X<<" Счётчик ссылок X: "<<X.v->linkCount<<" Адрес массива: "<<X.v<<endl;
    cout<<"Вектор Y: "<<Y<<" Счётчик ссылок Y: "<<Y.v->linkCount<<" Адрес массива: "<<Y.v<<endl;

и видим, что теперь оба вектора указывают на один и тот же адрес, а счётчик ссылок увеличился на 1:


Вектор X: [1,1];  Счётчик ссылок X: 2 Адрес массива: 448c910
Вектор Y: [1,1];  Счётчик ссылок Y: 2 Адрес массива: 448c910

После чего домножаем вектор X на 2 


    X*=a;  //домножаем вектор на коэффициент 2.0
    cout<<"Вектор X: "<<X<<" Счётчик ссылок X: "<<X.v->linkCount<<" Адрес массива: "<<X.v<<" Коэфф. a вектора X: "<<X.upd<<endl;
    cout<<"Вектор Y: "<<Y<<" Счётчик ссылок Y: "<<Y.v->linkCount<<" Адрес массива: "<<Y.v<<" Коэфф. a вектора Y: "<<Y.upd<<endl;

и получаем, что несмотря на то, что оба вектора как и раньше указывают на один и тот же адрес, и счётчик ссылок как и прежде 2, у .X сохранённый коэффициент 2, а у Y соответственно равен 1:


Вектор X: [2,2]; Счётчик ссылок X: 2 Адрес массива: 448c910 Коэфф. a вектора X: 2
Вектор Y: [1,1]; Счётчик ссылок Y: 1 Адрес массива: 448c910 Коэфф. a вектора Y: 1

И в конце, сложив X+Y 


    Z= X+Y;
    cout<<"Вектор Z: "<<Z<<" Счётчик ссылок Z: "<<Z.v->linkCount<<" Адрес массива: "<<Z.v<<" Коэфф. a вектора Z: "<<Z.upd<<endl;

получаем Z=[3,3]:


Вектор Z: [3,3]; Счётчик ссылок Z: 1 Адрес массива: 448c988 Коэфф. a вектора Z: 1

Для матриц все вычисления аналогичны:


    Matrix X_(2), Y_(2), Z_(2); //создаём 3 единичных диагональных матрицы 2x2

    cout<<"Матрица X: "<<endl<<X_<<" Счётчик ссылок X: "<<X_.v->linkCount<<" Адрес массива: "<<X_.v<<endl;
    cout<<"Матрица Y: "<<endl<<Y_<<" Счётчик ссылок Y: "<<Y_.v->linkCount<<" Адрес массива: "<<Y_.v<<endl;

    Y_=X_;// теперь приравниваем X_ и Y_
    cout<<"Матрица X: "<<endl<<X_<<" Счётчик ссылок X: "<<X_.v->linkCount<<" Адрес массива: "<<X_.v<<endl;
    cout<<"Матрица Y: "<<endl<<Y_<<" Счётчик ссылок Y: "<<Y_.v->linkCount<<" Адрес массива: "<<Y_.v<<endl;

    X_*=a;  //домножаем матрицу на коэффициент 2.0
    cout<<"Матрица X: "<<endl<<X_<<" Счётчик ссылок X: "<<X_.v->linkCount<<" Адрес массива: "<<X_.v<<" Коэфф. a матрицы X: "<<X_.upd<<endl;

    Z_= X_+Y_;
    cout<<"Матрица Z: "<<endl<<Z_<<" Счётчик ссылок Z: "<<Z_.v->linkCount<<" Адрес массива: "<<Z_.v<<" Коэфф. a матрицы Z: "<<Z_.upd<<endl;

Вывод также аналогичен:


Матрица X:
[1,0]
[0,1];
 Счётчик ссылок X: 1 Адрес массива: 44854a0
Матрица Y:
[1,0]
[0,1];
 Счётчик ссылок Y: 1 Адрес массива: 44854c0
Матрица X:
[1,0]
[0,1];
 Счётчик ссылок X: 2 Адрес массива: 44854a0
Матрица Y:
[1,0]
[0,1];
 Счётчик ссылок Y: 2 Адрес массива: 44854a0
Матрица X:
[2,0]
[0,2];
 Счётчик ссылок X: 2 Адрес массива: 44854a0 Коэфф. a матрицы X: 2
Матрица Z:
[3,0]
[0,3];
 Счётчик ссылок Z: 1 Адрес массива: 4485500 Коэфф. a матрицы Z: 1

Библиотечка доступна на GitHub.


Пользуйтесь, критикуйте.

Комментарии (13)


  1. Antervis
    26.03.2018 06:03
    #10724782

    Лабораторная работа по оптимизации вычислений и даже без реальных замеров производительности.

    Понятно, что приведенные выше способы экономии не бесплатны в смысле необходимости иметь дополнительную память для хранения коэффициентов ...

    обращение к памяти — более дорогая операция, чем умножение.


    1. CrazyFizik
      26.03.2018 14:39
      #10725310
      -1

      А) Операции умножения бывают разными. Какая именно операция умножения?
      Б) Памяти бывают тоже разные. К какой памяти обращение?
      В) Любая операция подразумевает обращение к памяти. Хорошо если данные уже лежат в регистрах процессора, только вот им туда надо сначала попасть.
      Г) Умножение в общем случае всегда дороже. Оно не просто само по себе медленнее сложения, оно принципе отжирает немалую часть кристалла, так что много их в ЦП не будет — места всем не хватит. Например, в Ьульдозере всего одно 256 битное FPU состоящие из 4-х блоков сложения-умножения по 64 бита каждое, в Skylake уже 4 FPU, но 256-и битных FPU максимум 3 (что кагбэ намекает на ч0рную магию) — для векторных вычислений это ниачом, так что любая нормальная видеокарточка (не заглушка, конечно же) сделает любой ЦП (Quadra P5000 vs двухголовый Intel Xeon на 64 ядра, ну примерно ~24:1, мобильная 960 vs Intel i7 ну примерно ~16:1), т.к. там нет недостатка в умножителях… зато там есть есть недостаток быстрой памяти...


      Так что нет. Размен памяти на производительность — нормальная практика, даже не смотря на то что у нас есть бутылочное горлышко межу ЦП и ОЗУ, в разумных пределах конечно же.


      1. Antervis
        26.03.2018 15:05
        #10725352

        А) Операции умножения бывают разными. Какая именно операция умножения?
        Б) Памяти бывают тоже разные. К какой памяти обращение?
        В) Любая операция подразумевает обращение к памяти. Хорошо если данные уже лежат в регистрах процессора, только вот им туда надо сначала попасть.

        Вещественное умножение — 4-6 тактов в зав-ти от архитектуры (вектор/скаляр), комплексное — 10-16 (avx: скалярное и векторное de-interleaved), 13-16 (sse: скалярное и векторное de-interleaved), 11-14 (комплексное avx interleaved). Обращение к кешу L1 ~20 тактов. Т.е. больше любого умножения. В статье рассматривается случай экономии на умножениях за счет использования буфера, так что случай «данные уже в регистрах» не рассматривается.

        так что любая нормальная видеокарточка (не заглушка, конечно же) сделает любой ЦП

        для начала чиселки надо загрузить в память видеокарты, и оттуда же их и достать. Подозреваю, что для сравнительно дешевых операций (дешевле чем load/store), это будет медленнее, чем прогнать на проце.


        1. Rumyantsev Автор
          26.03.2018 16:55
          #10725564

          Ну да, рассчитывал собственно на оптимизацию компилятором.


        1. CrazyFizik
          26.03.2018 17:27
          #10725616

          У вас неверные цифры. Доступ к L1 — 4 такта, L2 — 10 тактов, и только к L3 от 40 тактов начинается. Это вот у всяких Скайлейков.


          Чисто операция сложения — 1 такт, целочисленного умножения — 3 такта, для чисел с плавающей запятой — 4 такта, для деления — 25 тактов, и эти циферки уже с учетом ч0рной магии, т.е. Циферки уже познакомились с Dispatch Unit их построили в рядочек и отправили куда надо, а к нему еще нужно попасть (а откуда они попадают? Явно что не из Нарнии) а число вычислительных блоков не впечатляет: у Бульдозера как я выше написал всего 4 вещественные умножалки с плавающей запятой на 64 бита, а у Скалэйк вероятно 12 штук, так что обращаться к кэшу в любом случае придется часто. А для тех же комплексных чисел потребуется по 3 умножалки и и по 5 сумматоров или 4 умножалки и 2 сумматора, кому-что нравиться — так шо кватернионам например будет уже грустно, а это все операции поворота в 3D.


          Что касается сравнительно дешевых операций на видеокартах, то да, [sarcasm]видеокарты были разработаны именно для того чтобы складывать два целых числа, однозначно, а циферки в регистры CPU падают из Нарнии, бесплатно, инфа 145%[/sarcasm] Если говорить о всяких load/store в любом случае придется протаскивать данные из ОЗУ и обратно, пофиг, CPU это или GPU, ну а внутри процессоров еще предстоят увлекательные путешествия по кэшам разных уровней. Разница только в том, что видеокарта будет потолще по количеству вычислительных боков и реализует MIMD, а не SIMD как обычные процы, и пропускная способность GRAM-GPU, несколько побольше (так что L3 им и не нужен), чем RAM-CPU, так что вектора, матрицы и тензоры, пока видеопамяти хватает, GPU будет переваривать на порядок быстрее, не смотря на то что тактовая частота у видюшек все же ниже, чем у CPU. Есть только один способ обогнать видеокарты в матричных вычислениях с большим числом операций умножения/деления — фигачить вычислительные кластеры из Xeon Phi или делать свой ASIC под конкретные задачи, но это уже решения совершенно другого уровня.


          1. Antervis
            26.03.2018 18:00
            #10725670

            У вас неверные цифры.

            и то верно, спасибо.
            … целочисленного умножения — 3 такта, для чисел с плавающей запятой — 4 такта, для деления — 25 тактов...

            Вы говорите про latency, есть еще throughoutput. Если операция умножения выполняется за 4 такта и попадает в конвейер за такт, то иметь больше 4-х векторных умножителей на ядро процессору в принципе не нужно. В общем-то, правильно переставляя операции (это компилятор умеет) мы получаем умножение за такт
            а циферки в регистры CPU падают из Нарнии, бесплатно, инфа 145%

            Допустим, исходные данные уже в RAM. На проце мы загрузили из RAM, посчитали, сунули в RAM. На видюхе — скопировали RAM -> GPU RAM, посчитали, скопировали GPU RAM -> RAM. Я не утверждаю, что на проце в принципе вычисления быстрее (понимаю, что это не так). Но в частных случаях её использование не оправдано


      1. Rumyantsev Автор
        26.03.2018 16:54
        #10725560

        Спасибо.


        a) Операции действительного умножения
        b) Память из кучи, т.к. при умножении вектора на матрицу и матрицы на матрицу хочется убрать учёт их размерностей "под капот"
        в) Тут надеюсь на оптимизатор компилятора
        г) Как лучше задействовать вычисления через видеокарту, т.к. требуется не только умножения, но и вычисления довольно сложных функций типа sin, cos, abs и т.п.?


        1. CrazyFizik
          26.03.2018 17:46
          #10725648

          B) Вообще размерность результата матричных операций всегда можно предсказать, зная размерность входных массивов. Поэтому лучше использовать сразу заготовленные массивы. А с указателями на память в условиях неопределенности (хз какой участок потребуется) — можно нарваться на кучу неприятных ошибок, а всякие контейнеры с динамически изменяемым размером, тот же vector например — резервируют память всегда с запасом, как только коэффициент заполнения станет большим — он расширит область памяти под свои нужды, опять таки с запасом. Неоптимально.
          В) Вот тут бы я на компилятор не надеялся бы. Компиляторы C/C++ глупее даже чем компиляторы фортрана, тот же алиасинг памяти, например, не обойдет если не прописать квалификатор restrict там где надо. Ну эт так пример, первый какой в голову пришел.
          Тут вот поминали всякие бласы и лппаки, так вот, в том же openBLAS жесткий си-хардкод, в том числе и с заточкой под конкретную архитектуру CPU
          Г) CUDA. На сайте nvidia висит халявный тулкит с примерами. Только надо иметь ввиду, что максимальный перфоманс достигается тогда, когда объем входных данных приближается к 0.4 от размера видеопамяти.
          Что же касается функций всяких, ну abs — дешевая функция. А вот косинусы-синусы — очень дорогие, на синус потребуется тактов в несколько раз больше чем на операцию деления. Так что их надо избегать по максимуму, можно еще лук-ап тейбел использовать (хэш-таблицы значений синусов-косинусов) если не боитесь потерять в точности. Если же синус от малого угла — то он равен собственно аргументу. Ну и т.д.


  1. saluev
    26.03.2018 13:56
    #10725250
    +1

    Сложение несонаправленных векторов начинает требовать n умножений, хотя обычно требует лишь n сложений. Круто сэкономили, да.

    Фактически экономия появляется только при умножении на константу и сложении сонаправленных векторов. Второе почти не встречается, первое в реальных алгоритмах ничего не стоит по сравнению с другими вычислениями (например, умножением матрицы на вектор).

    Автор, возьмите какую-нибудь реальную программу, замените в ней стандартные массивы и вызовы BLAS/LAPACK на свою поделку и сравните скорость. Спойлер: вы проиграете.


    1. Rumyantsev Автор
      26.03.2018 16:48
      #10725546

      Насчёт сложений несонаправленных векторов: смотрите появляется одно доп. деление, за счёт-того, что n- умножений переносятся на более поздний срок, а число сложений как было n — так и остаётся. и если потом так получится, что возникнет операция сложения с сонаправленным вектором, то эффект будет, если нет — заплатили умножением.


      У меня экономии вылезают, скажем, при необходимости поэтапно "раздувая" выпуклую фигуру, проверить поглощение ей какой либо точки или множества. Соотв. на практике домножаю сетку вектора на коэфф. для первого шага, запоминаю вектор, на котором расстояние между искомой точкой и фигурой было наименьшее, повторяю до тех пор пока не будет поглощения. И, если на первом шаге требуется пройти условно "пол-фигуры" градиентным методом и, описанное выше не очень эффективно, то при поледующщих шагах поиск минимума будет не более чем за О(d), где d размерность — и тут это довольно эффективно.


      1. saluev
        26.03.2018 17:00
        #10725572

        Ну это значит, что вы придумали эффективный алгоритм для своей задачи, только и всего. Но никак не глобально «более лучшую» векторную арифметику.


        1. Rumyantsev Автор
          26.03.2018 17:14
          #10725596

          Так и не претендую, на "более лучшую".
          Если есть задачи, требующие массовых операций, например, на сеточных функциях и позволяющие использовать поиски без перебора — эффект есть. Если есть простые задачи — типа просто сложений и умножений, — эффект вполне может оказаться и обратным.


  1. potan
    26.03.2018 15:27
    #10725382

    сложение и вычитание — более быстрые;
    умножение и деление — более медленные.

    На суперскалявных процессорах это не так. Для работы конвеера требуется что бы все конвейризируемые операции выполнялись на одинаковое количество тактов, по этому сложение специально замедляется. В смысле количества тактов от старта команды до фиксации результатов — все равно на каждом такте, в идеале, с одного устройства выходит один результат.