Серия «Белый шум рисует черный квадрат»

История цикла этих публикаций начинается с того, что в книге Г.Секей «Парадоксы в теории вероятностей и математической статистике» (стр.43), было обнаружено следующее утверждение:


Рис. 1.

По анализу комментарий к первым публикациям (часть 1, часть 2) и последующими рассуждениями созрела идея представить эту теорему в более наглядном виде.

Большинству из участников сообщества знаком треугольник Паскаля, как следствие биноминального распределения вероятностей и многие сопутствующие законы. Для понимания механизма образования треугольника Паскаля развернем его детальнее, с развертыванием потоков его образования. В треугольнике Паскаля узлы формируются по соотношению 0 и 1, рисунок ниже.


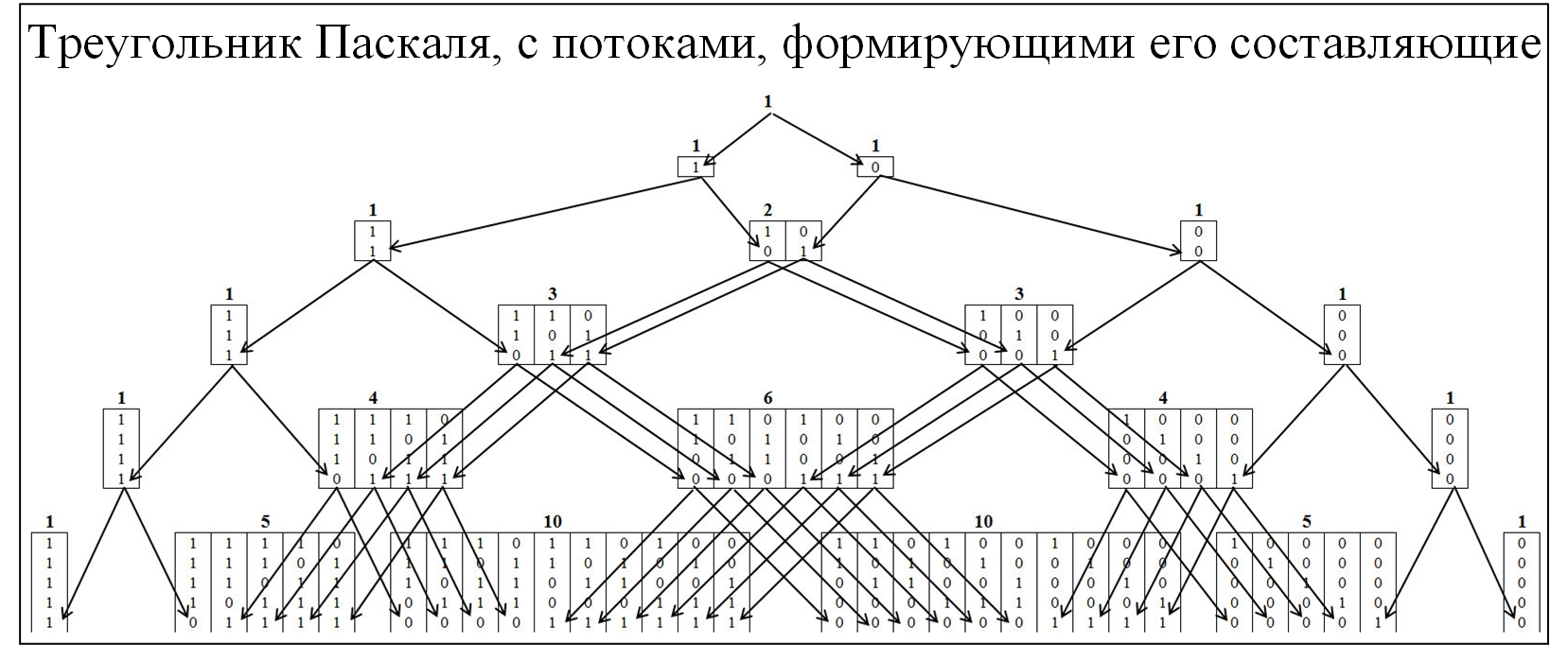
Рис. 2.

Для понимания теоремы Эрдёша-Реньи составим аналогичную модель, но узлы будут формироваться из значений, в которых присутствуют наибольшие цепочки, состоящие последовательно из одинаковых значений. Кластеризации будет проводиться по следующему правилу: цепочки 01/10, к кластеру «1»; цепочки 00/11, к кластеру «2»; цепочки 000/111, к кластеру «3» и т.д. При этом разобьём пирамиду на две симметричные составляющие рисунок 3.


Рис. 3.

Первое что бросается в глаза это то, что все перемещения происходят из более низкого кластера в более высокий и наоборот быть не может. Это естественно, так как если цепочка размера j сложилась, то она уже не может исчезнуть.

Определяя алгоритм концентрации чисел, удалось получить следующую рекуррентную формулу, механизм которой показан на рисунках 4-6.

Обозначим элементы, в которые концентрируются числа J. Где n количество знаков в числе (количество бит), а длину максимальной цепочки — m. И каждый элемент получит индекс n;mJ.
Обозначим что количество перешедших элементов из n;mJ в n+1;m+1J, n;mjn+1;m+1.


Рис. 4.

По рисунку 4 видно, что для первого кластера определить значения каждой строки не составляет трудности. И эта зависимость равна:


Рис. 5.

Определяем для второго кластера, с длиной цепочки m=2, рисунок 6.


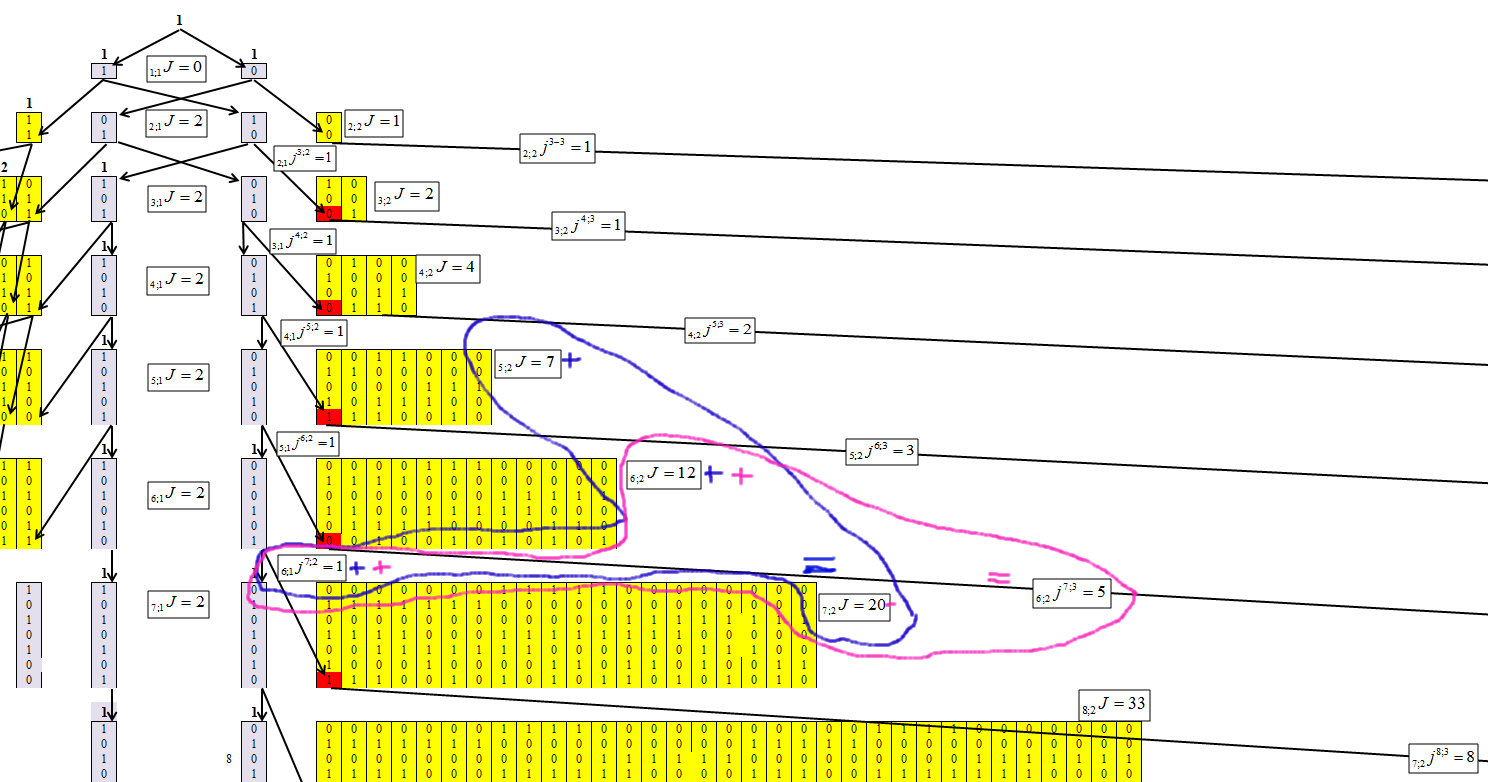
Рис. 6.

По рисунку 6 видно, что для второго кластера зависимость равна:


Рис. 7.

Определяем для третьего кластера, с длиной цепочки m=3, рисунок 8.


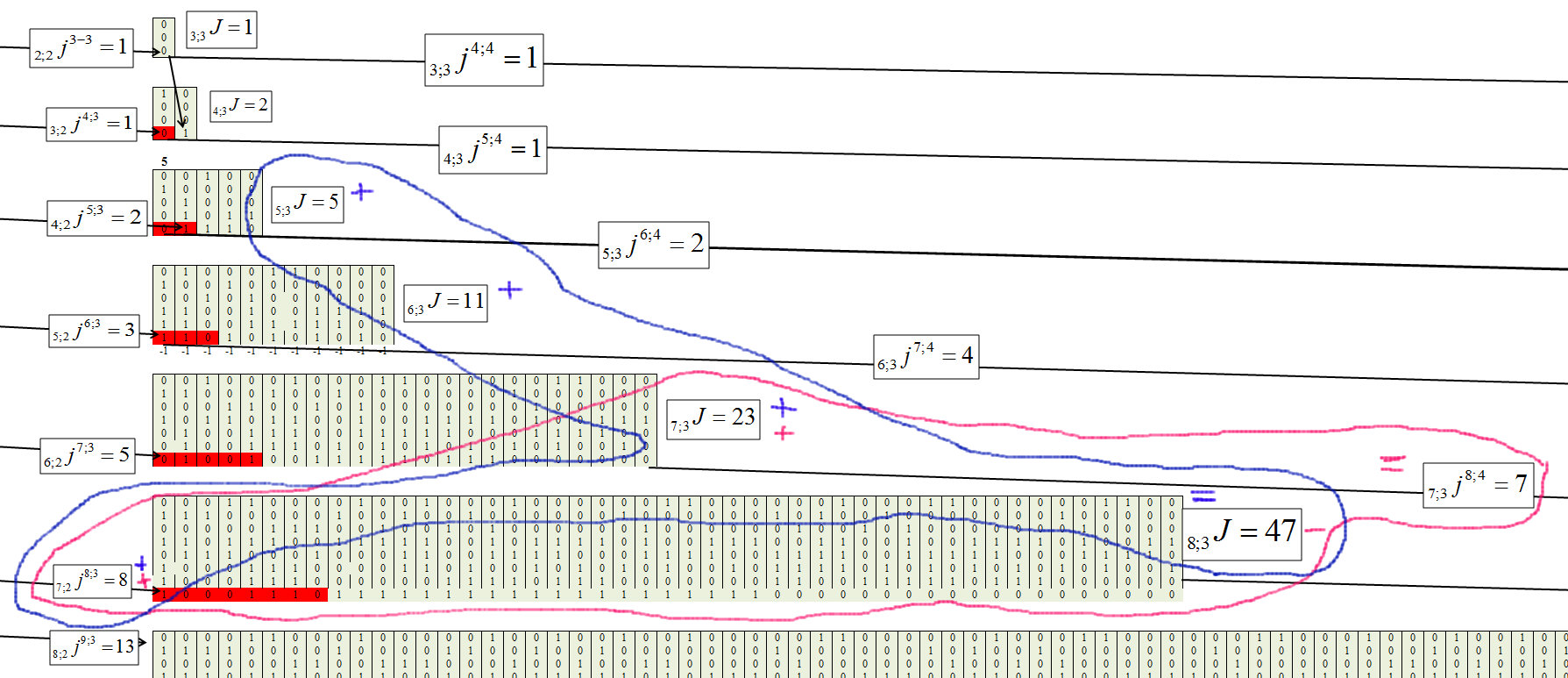
Рис. 8.

Рис. 9.

Общая формула каждого элемента принимает вид:


Рис. 10.


Рис. 11.

Проверка.

Для проверки используем свойство данной последовательности, которое показано на рисунке 12. Оно заключается в том, что последние члены строки с определенного положения принимают единственное значение для всех строк с увеличением длины строки.


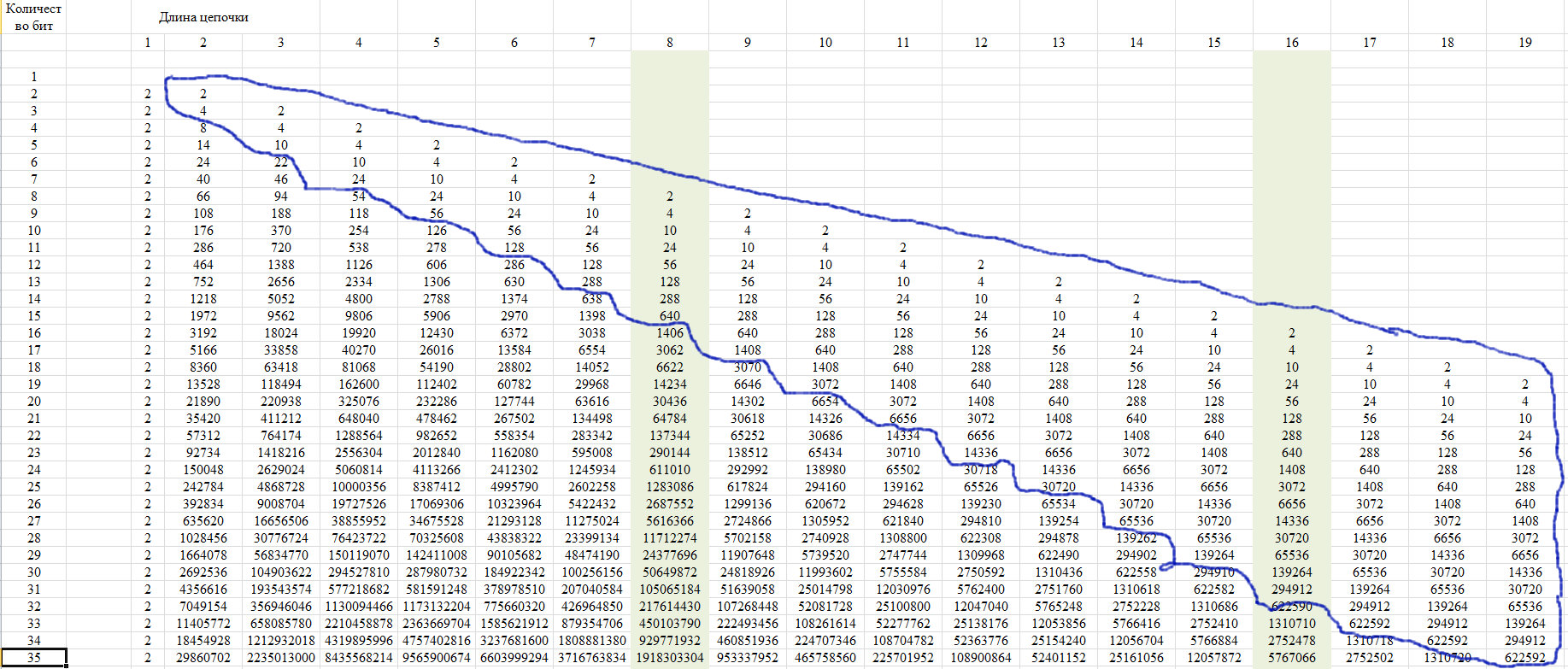
Рис. 12.

Это свойство связано с тем, что при длине цепочки более чем половина всего ряда, то возможна только одна такая цепочка. Покажем это на схеме рисунка 13.


Рис. 13.

Соответственно для значений k < n-2 получаем формулу:


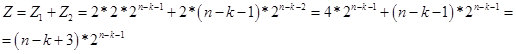
Рис. 14.

По сути, значение Z – это потенциально возможное количество чисел (вариантов в строке из n бит), в которых содержится цепочка из k одинаковых элементов. А по рекуррентной формуле мы определяем количество чисел (вариантов в строке из n бит), в которых, цепочка из k одинаковых элементов, является наибольшей. Пока предполагаю, что величина Z является виртуальной. Поэтому в районе n/2 она переходит в реальное пространство. На рисунке 15, скрин с расчетами.


Рис. 15.

Покажем на примере 256-битного слова, что можно определить по данному алгоритму.


Рис. 16.

Если определяться стандартами 99,9% надежности для ГСПЧ, то 256-битный ключ должен содержать последовательные цепочки одинаковых символов с количеством от 5 до 17. То есть по нормативам для ГСПЧ, чтоб он с 99,9% надежностью удовлетворял требованию подобия случайности он, ГСПЧ, в 2000 испытаниях (выдаче результата в форме 256-битного бинарного числа) должен только один раз выдать результат, в котором максимальная длина серии из одинаковых значений: либо меньше 4, либо больше 17.


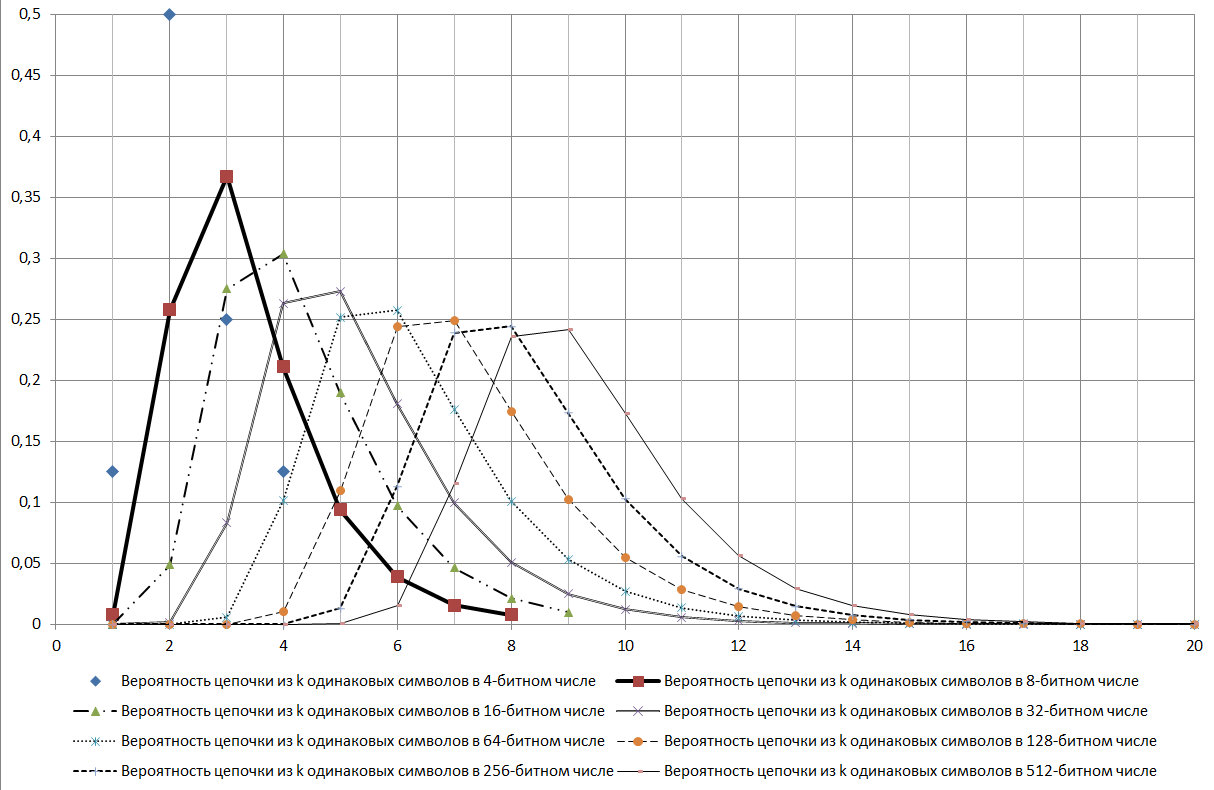
Рис. 17.

Как видно из представленной на рисунке 17 диаграммы цепочка log2N является модой для рассматриваемого распределения.

В процессе исследования было обнаружено много признаков различных свойств данной последовательности. Вот некоторые из них:

• она должна неплохо проверяться по критерию хи-квадрат;
• подает признаки существования фрактальных свойств;
• может быть неплохим критериям выявления различных случайных процессов.

И еще много других связей.

Проверил существует ли такая последовательность и на The On-Line Encyclopedia of Integer Sequences (OEIS) (Онлайн-энциклопедия целочисленных последовательностей) в последовательности под номером A006980, дается ссылка на издание J. L. Yucas, Counting special sets of binary Lyndon words, Ars Combin., 31 (1991), р. 21-29, где на 28 странице приведена последовательность (в таблице). В издании, строки пронумерованы на 1 меньше, но значения те же. В целом издание о словах Линдона, то есть вполне возможно, что исследователь даже не подозревал, что этот ряд имеет отношение к такому аспекту.

Вернемся к теореме Эрдёша-Реньи. По проведенному в данной публикации, можно сказать, что в той формулировке, которая представлена, данная теорема относится к общему случаю, который определяется теоремой Муавра-Лапласа. И указанная теорема, в этой формулировке, не может быть однозначным критерием случайности ряда. Но фрактальность, а для данного случая это выражается что цепочки указанной длины могут находиться с совокупности с цепочками большей длины, не позволяют так однозначно отвергать эту теорему, так как возможна неточность в формулировке. Примером может служить тот факт, что если для 256-битного вероятность числа, где максимальная цепочка длиной 8 бит составляет 0,244235, то в совокупности с остальными, более длинными последовательностями вероятность того, что в числе присутствует цепочка из 8 бит, уже составляет — 0,490234375. То есть пока, однозначной возможности, отвергнуть эту теорему, нет. Но данная теорема достаточно неплохо укладывается в другом аспекте, который будет показан дальше.

Практическое применение

Обратимся к примеру, который представил пользователь VDG: «… Дендритные ветки нейрона можно представить как битовую последовательность. Ветка, а затем и весь нейрон, срабатывает, когда в любом её месте активируется цепочка синапсов. У нейрона есть задача не срабатывать на белый шум, соответственно, минимальная длина цепочки, насколько помню было у Нументы, равна 14 синапсам у пирамидального нейрона с его 10 тысячами синапсов. И по формуле получаем: Log_{2}10000 = 13,287. То есть, цепочки длиной меньше 14 будут возникать из-за естественного шума, но не будут активировать нейрон. Прямо вот идеально легло».

Построим график, но с учетом того, что Excel не считает значения больше чем 2^1024, то ограничимся числом синапсов 1023 и, с учетом этого будем интерполировать результат на коммент, по рисунку 18.


Рис. 18.

Есть биологическая нейронная сеть, которая срабатывает, когда составляется цепочка из m = log2N = 11. Данная цепочка является модальным значением, при этом достигается пороговое значение, вероятности, какого-то изменения ситуации в 0,78. И вероятности ошибки 1- 0,78 = 0,22. Допустим, сработала цепочка из 9 сенсоров, где вероятность определения события 0,37, соответственно вероятность ошибки 1 – 0,37 = 0,63. То есть, чтобы достичь снижения вероятности ошибки с 0,63 до 0,37 необходимо, чтобы сработало 3,33 цепочки по 9 элементов. Разница между 11 и 9 элементами 2 порядка, то есть 2^2 = 4 раза, что если округлить до целых, так как элементы дают целочисленное значение, то 3,33 = 4. Смотрим дальше, чтобы снизить ошибку при обработке сигнала из 8-ми элементов, нам уже потребуется 11 срабатываний цепочек из 8-ми элементов. Предполагаю, что это механизм, который позволяет оценивать ситуацию и принимать решение об изменении поведения биологического объекта. Достаточно разумно и эффективно, на мой взгляд. И с учетом того, что мы знаем о природе то, что она максимально экономно использует ресурсы, допускать гипотезу, что биологическая система использует этот механизм, оправдано. Да и когда мы обучаем нейронную сеть, мы, по сути, снижаем вероятность ошибки, так как для полного исключения ошибки нам необходимо найти аналитическую зависимость.

Обратимся к анализу числовых данных. При анализе числовых данных мы стараемся подобрать аналитическую зависимость в форме y=f(xi). И на первом этапе находим ее. После ее нахождения, имеющийся ряд можно представить в виде бинарного, относительно уравнения регрессии, где положительным значениям присваиваем значения 1, а отрицательным 0. И далее проводим анализ на серии одинаковых элементов. Определяем наибольшую, по длине цепочку, распределение более коротких цепочек.

Далее обращаемся к теореме Эрдёша-Реньи, из нее следует, что при проведении большого количества испытаний случайной величины обязательно должна образоваться цепочка одинаковых элементов во всех регистрах генерируемого числа, то есть m = log2N. Сейчас, когда мы исследуем данные, мы не знаем каков на самом деле объем ряда. Но если посмотреть обратно, то эта максимальная цепочка и дает нам основания предполагать что R это параметр, характеризующий поле случайной величины, рисунок 19.


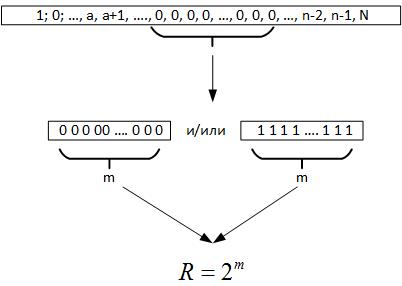
Рис. 19.

То есть сравнивая R и N мы можем сделать несколько выводов:

1. Если R<N, то случайный процесс повторяется несколько раз на исторических данных.
2. Если R>N, то случайный процесс имеет размерность выше, чем имеющиеся данные, либо мы неверно определили уравнение целевой функции.

Тогда для первого случая проектируем нейронную сеть с 2^m сенсорами, предполагаю, что можно добавить по паре сенсоров, чтобы уловить переходы, и проводим обучение этой сети на исторических данных. Если сеть в результате обучения не сможет обучиться и будет выдавать правильный результат с вероятностью 50%, то это означает, что найденная целевая функция оптимальна и улучшить ее невозможно. Если сеть сможет обучиться, то проводим дальнейшее улучшение аналитической зависимости.

В случае если размерность ряда больше размерности случайной величины, то можно использовать свойство фрактальности случайной величины, так как любой ряд размера m содержит в себе все подпространства низших размерностей. Предполагаю, что в этом случае имеет смысл обучение нейронной сети проводить на всех данных, кроме цепочек m.

Другим подходом при проектировании нейронных сетей может быть прогнозный период.

В заключении необходимо сказать, что по дороге к этой публикации было обнаружено множество аспектов, где величина размерности случайной величины и обнаруженные свойства ее, пересекались с другими задачами при анализе данных. Но пока это все в очень сыром виде и оставим для будущих публикаций.

Предыдущие часть: Часть 1, Часть 2