Немного матчасти
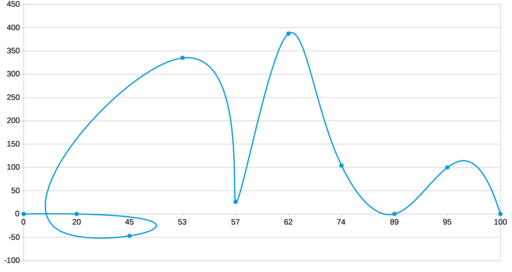
Восстановление промежуточных значений функции, которая в данном случае задана таблично в виде точек P1 ... Pn, называется интерполяцией. Есть множество способов интерполяции, но все они могут быть сведены к тому, что надо найти n – 1 функцию для расчёта промежуточных точек на соответствующих сегментах. При этом заданные точки обязательно должны быть вычислимы через соответствующие функции. На основе этого и может быть построен график:

Функции fi могут быть самыми разными, но чаще всего используют полиномы некоторой степени. В этом случае итоговая интерполирующая функция (кусочно заданная на промежутках, ограниченных точками Pi) называется сплайном.
В разных инструментах для построения графиков — редакторах и библиотеках — задача «красивой интерполяции» решена по-разному. В конце статьи будет небольшой обзор существующих вариантов. Почему в конце? Чтобы после ряда приведённых выкладок и размышлений можно было поугадывать, кто из «серьёзных ребят» какие методы использует.
Ставим опыты
Самый простой пример — линейная интерполяция, в которой используются полиномы первой степени, а в итоге получается ломаная, соединяющая заданные точки.
Давайте добавим немного конкретики. Вот набор точек (взяты почти с потолка):
0 0
20 0
45 -47
53 335
57 26
62 387
74 104
89 0
95 100
100 0
Результат линейной интерполяции этих точек выглядит так:
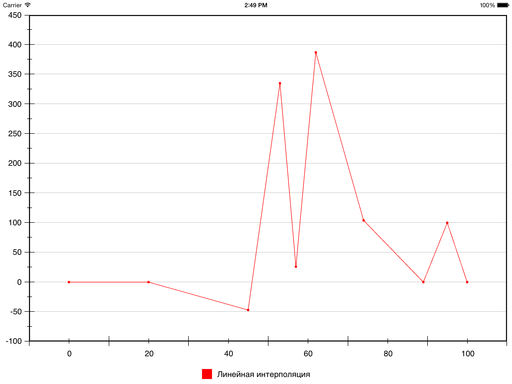
Однако, как отмечалось выше, иногда хочется получить в итоге гладкую кривую.
Что есть гладкость? Бытовой ответ: отсутствие острых углов. Математический: непрерывность производных. При этом в математике гладкость имеет порядок, равный номеру последней непрерывной производной, и область, на которой эта непрерывность сохраняется. То есть, если функция имеет гладкость порядка 1 на отрезке [a; b], это означает, что на [a; b] она имеет непрерывную первую производную, а вот вторая производная уже терпит разрыв в каких-то точках.
У сплайна в контексте гладкости есть понятие дефекта. Дефект сплайна — это разность между его степенью и его гладкостью. Степень сплайна — это максимальная степень использованных в нём полиномов.
Важно отметить, что «опасными» точками у сплайна (в которых может нарушиться гладкость) являются как раз Pi, то есть точки сочленения сегментов, в которых происходит переход от одного полинома к другому. Все остальные точки «безопасны», ведь у полинома на области его определения нет проблем с непрерывностью производных.
Чтобы добиться гладкой интерполяции, нужно повысить степень полиномов и подобрать их коэффициенты так, чтобы в граничных точках сохранялась непрерывность производных.
Традиционно для решения такой задачи используют полиномы третьей степени и добиваются непрерывности первой и второй производной. То, что получается, называют кубическим сплайном дефекта 1. Вот как он выглядит для наших данных:

Кривая, действительно, гладкая. Но если предположить, что это график некоторого процесса или явления, который нужно показать заинтересованному лицу, то такой метод, скорее всего, не подходит. Проблема в ложных экстремумах. Появились они из-за слишком сильного искривления, которое было призвано обеспечить гладкость интерполяционной функции. Но зрителю такое поведение совсем не кстати, ведь он оказывается обманут относительно пиковых значений функции. А ради наглядной визуализации этих значений, собственно, всё и затевалось.
Так что надо искать другие решения.
Другое традиционное решение, кроме кубических сплайнов дефекта 1 — полиномы Лагранжа. Это полиномы степени n – 1, принимающие заданные значения в заданных точках. То есть членения на сегменты здесь не происходит, вся последовательность описывается одним полиномом.
Но вот что получается:
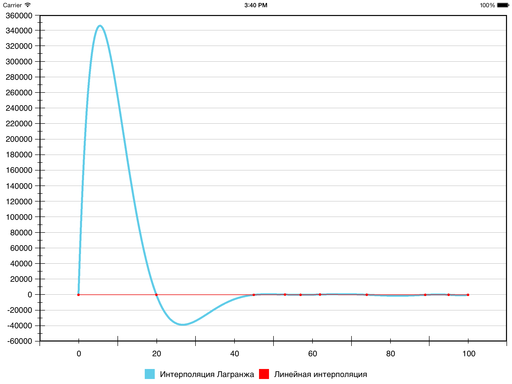
Гладкость, конечно, присутствует, но наглядность пострадала так сильно, что… пожалуй, стоит поискать другие методы. На некоторых наборах данных результат выходит нормальный, но в общем случае ошибка относительно линейной интерполяции (и, соответственно, ложные экстремумы) может получаться слишком большой — из-за того, что тут всего один полином на все сегменты.
В компьютерной графике очень широко применяются кривые Безье, представленные полиномами k-й степени.
Они не являются интерполирующими, так как из k + 1 точек, участвующих в построении, итоговая кривая проходит лишь через первую и последнюю. Остальные k – 1 точек играют роль своего рода «гравитационных центров», притягивающих к себе кривую.
Вот пример кубической кривой Безье:

Как это можно использовать для интерполяции? На основе этих кривых тоже можно построить сплайн. То есть на каждом сегменте сплайна будет своя кривая Безье k-й степени (кстати, k = 1 даёт линейную интерполяцию). И вопрос только в том, какое k взять и как найти k – 1 промежуточную точку.
Здесь бесконечно много вариантов (поскольку k ничем не ограничено), однако мы рассмотрим классический: k = 3.
Чтобы итоговая кривая была гладкой, нужно добиться дефекта 1 для составляемого сплайна, то есть сохранения непрерывности первой и второй производных в точках сочленения сегментов (Pi), как это делается в классическом варианте кубического сплайна.
Решение этой задачи подробно (с исходным кодом) рассмотрено здесь.
Вот что получится на нашем тестовом наборе:

Стало лучше: ложные экстремумы всё ещё есть, но хотя бы не так сильно отличаются от реальных.
Думаем и экспериментируем
Можно попробовать ослабить условие гладкости: потребовать дефект 2, а не 1, то есть сохранить непрерывность одной только первой производной.
Достаточное условие достижения дефекта 2 в том, что промежуточные контрольные точки кубической кривой Безье, смежные с заданной точкой интерполируемой последовательности, лежат с этой точкой на одной прямой и на одинаковом расстоянии:

В качестве прямых, на которых лежат точки Ci – 1(2), Pi и Ci(1), целесообразно взять касательные к графику интерполируемой функции в точках Pi. Это гарантирует отсутствие ложных экстремумов, так как кривая Безье оказывается ограниченной ломаной, построенной на её контрольных точках (если эта ломаная не имеет самопересечений).
Методом проб и ошибок эвристика для расчёта расстояния от точки интерполируемой последовательности до промежуточной контрольной получилась такой:

Первая и последняя промежуточные контрольные точки равны первой и последней точке графика соответственно (точки C1(1) и Cn – 1(2) совпадают с точками P1 и Pn соответственно).
В этом случае получается вот такая кривая:

Как видно, ложных экстремумов уже нет. Однако если сравнивать с линейной интерполяцией, местами ошибка очень большая. Можно сделать её ещё меньше, но тут в ход пойдут ещё более хитрые эвристики.
К текущему варианту мы пришли, уменьшив гладкость на один порядок. Можно сделать это ещё раз: пусть сплайн будет иметь дефект 3. По факту, тем самым формально функция не будет гладкой вообще: даже первая производная может терпеть разрывы. Но если рвать её аккуратно, визуально ничего страшного не произойдёт.
Отказываемся от требования равенства расстояний от точки Pi до точек Ci – 1(2) и Ci(1), но при этом сохраняем их все лежащими на одной прямой:
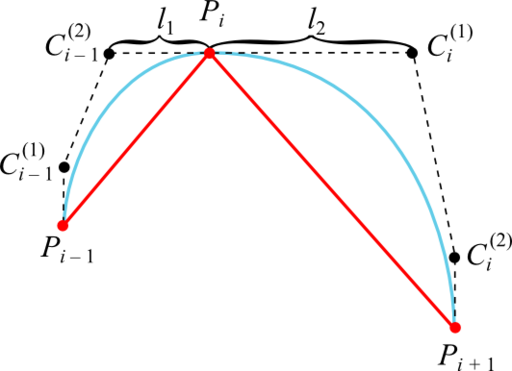
Эвристика для вычисления расстояний будет такой:
При этом, однако, стоит ещё проверять, не совпали ли точки Pi и Pi + 1 по ординате, и, если совпали, полагать l1 = l2 = 0. Это защитит от «вспухания» графика на плоских отрезках (что тоже немаловажно с точки зрения правдивого отображения данных).
Результат получается такой:
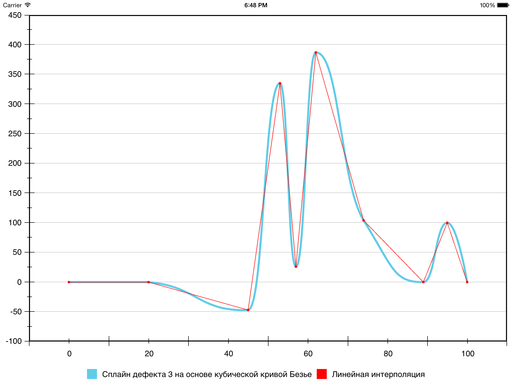
В результате на шестом сегменте ошибка уменьшилась, а на седьмом — увеличилась: кривизна у Безье на нём оказалась больше, чем хотелось бы. Исправить ситуацию можно, принудительно уменьшив кривизну и тем самым «прижав» Безье ближе к отрезку прямой, которая соединяет граничные точки сегмента. Для этого используется следующая эвристика:
Результат следующий:
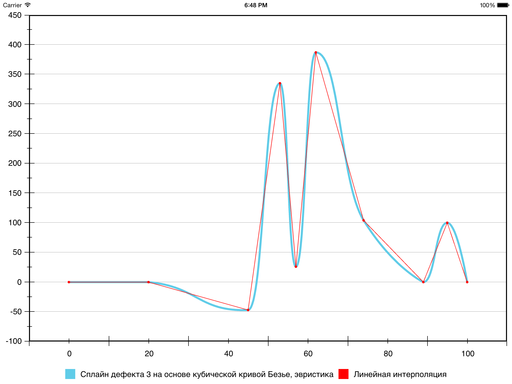
На этом было принято решение признать цель достигнутой.
Может быть, кому-то пригодится код.
А как люди-то делают?
Обещанный обзор. Конечно, перед решением задачи мы посмотрели, кто чем может похвастаться, а уже потом начали разбираться, как сделать самим и по возможности лучше. Но вот как только сделали, не без удовольствия ещё раз прошлись по доступным инструментам и сравнили их результаты с плодами наших экспериментов. Итак, поехали.
MS Excel

Это очень похоже на рассмотренный выше сплайн дефекта 1, основанный на кривых Безье. Правда, в отличие от него в чистом виде, тут всего два ложных экстремума — первый и второй сегменты (у нас было четыре). Видимо, к классическому поиску промежуточных контрольных точек тут добавляются ещё какие-то эвристики. Но ото всех ложных экстремумов они не спасли.
LibreOffice Calc
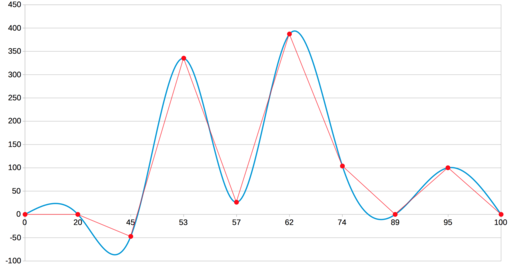
В настройках это названо кубическим сплайном. Очевидно, он тоже основан на Безье, и вот тут уже точная копия нашего результата: все четыре ложных экстремума на месте.
Есть там ещё один тип интерполяции, который мы тут не рассматривали: B-сплайн. Но для нашей задачи он явно не подходит, так как даёт вот такой результат :)

Highcharts, одна из самых популярных JS-библиотек для построения диаграмм

Тут налицо «метод касательных» в варианте равенства расстояний от точки интерполируемой последовательности до промежуточных контрольных. Ложных экстремумов нет, зато есть сравнительно большая ошибка относительно линейной интерполяции (седьмой сегмент).
amCharts, ещё одна популярная JS-библиотека

Картина очень похожа на экселевскую, те же два ложных экстремума в тех же местах.
Coreplot, самая популярная библиотека построения графиков для iOS и OS X

Есть ложные экстремумы и видно, что используется сплайн дефекта 1 на основе Безье.
Библиотека открытая, так что можно посмотреть в код и убедиться в этом.
aChartEngine, вроде как самая популярная библиотека построения графиков для Android

Больше всего похоже на кривую Безье степени n – 1, хотя в самой библиотеке график называется «cubic line». Странно! Как бы то ни было, тут не только присутствуют ложные экстремумы, но и в принципе не выполняются условия интерполяции.
Вместо заключения
В конечном счёте получается, что из «больших ребят» лучше всех проблему решили Highcharts. Но метод, описанный в этой статье, обеспечивает ещё меньшую ошибку относительно линейной интерполяции.
Вообще, заняться этим пришлось по просьбе покупателей, которые зарепортили нам «острые углы» в качестве бага в нашем движке диаграмм. Будем рады, если описанный опыт кому-то пригодится.
Комментарии (43)

BubaVV
05.08.2015 14:18Откуда взялся такой странной полином Лагранжа при сравнении с линейной интерполяцией? Он же должен быть вырожденным, с нулевыми коэффициентами

Ixtaccihuatl
05.08.2015 14:53Почему с нулевыми? Он построен по тем же точкам, которые даны в начале статьи.

k0ldbl00d
05.08.2015 15:08+6Тыщу лет ждал такую статью. Я понимаю что вся эта информация есть в других источниках, но в заметке всё ближе к практике.

irezvov
05.08.2015 15:09Ещё было бы интересно услышать, как растеризуется линия интерполирующего полинома.
Вот у нас есть параметр t в промежутке [0,1] и мы можем получать значения интерполирующей функции от этого параметра (x,y) = f(t).
Но как выбрать шаг изменения параметра, что бы закрасить все нужные пиксели?
Ixtaccihuatl
05.08.2015 15:36Выбор шага — вопрос сложный, да :) По-хорошему, надо подобрать для текущего dpi некоторую длину аппроксимирующей линии и корректировать шаг так, чтобы эту длину не превышать. Но мы пока этот вопрос решили просто выносом параметра в публичный API. По умолчанию на один сегмент приходится 32 аппроксимирующих линии, а если результат пользователю не понравится (будут видны изломы), число линий можно увеличить.

boeing777
06.08.2015 12:12Возможно, нужно для этого использовать идею Алгоритма Брезенхэма. Если «на пальцах», то результирующую кривую придется рисовать попиксельно, и для каждого пикселя определять из всех его соседей (соседей будет 7 штук, т.к. 8-й — это предыдущий пиксель) наиболее подходящий, у которого геометрический центр имеет наименьшее расхождение с аналитической кривой.
mayorovp
06.08.2015 12:57Алгоритм Брезенхэма прекрасно подходит для рисования кривых, заданных как уравнение — но не для параметрических.
mayorovp
05.08.2015 16:03+2Шаг в 1 / max(|x'(t1)|, |y'(t1))|) достаточен, чтобы закрасить все нужные пиксели, кроме, возможно, точек где функция меняет направление и тех где функция резко «ускоряется».
Точки, где функция меняет направление, можно при желании закрасить отдельно, приравняв вторую производную каждой координаты нулю и решив это уравнение.
Точки, где функция «ускоряется», ловятся явной проверкой на «перепрыгивание» пикселя с уменьшением шага.
Но я с трудом представляю себе задачу, где нужна такая точность )

KvanTTT
06.08.2015 21:18Достаточно, чтобы шаг был приблизительно равен коэффициенту кривизны в данной точке, который для декартовых координат вычисляется так:
 (или 1 / R, где R — радиус кривизны в данной точке).
(или 1 / R, где R — радиус кривизны в данной точке).mayorovp
06.08.2015 21:20Это вы шаг по x или по t привели? Впрочем, формула получилась странная в любом случае…

kashey
05.08.2015 16:32Больше всего понравился вариант aChartEngine — по таким кривым хорошо текст рисовать и другие обводки.
Жаль в топике форум нет, надо будет исходники поковырять.

ornic
05.08.2015 17:31+2Есть еще D3.js
Там есть хорошее решение интерполяции, которое называется monotone.
Скрытый текст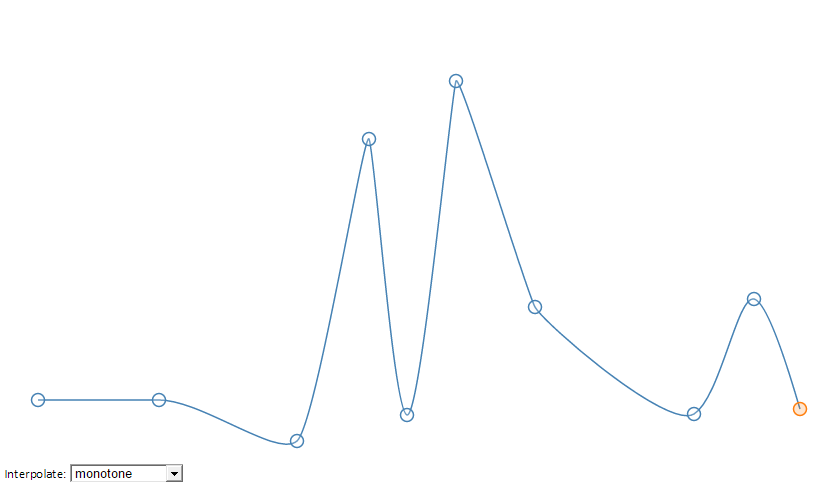

grasshoppergn
05.08.2015 17:48+1А еще есть AnyChart, который делает интерполяцию по таким точкам так:
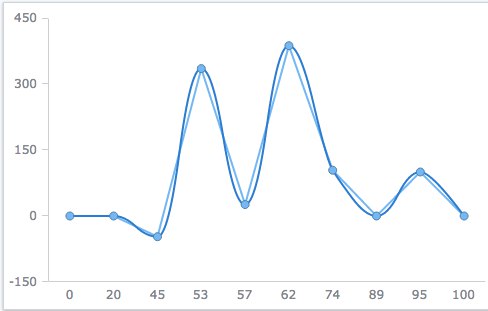

grasshoppergn
05.08.2015 17:55Кстати, в примере про amCharts та же ошибка — шкала по оси Х на картинке не линейная

Ixtaccihuatl
05.08.2015 19:09Она и у экселя с кальком не линейная :) Бог его знает, зачем они это делают.
mayorovp
05.08.2015 19:29Это зависит от типа графика. В «нелинейном» варианте попросту подписываются абсциссы указанных точек.
Строго говоря, в этом типе графиков оси абсцисс нет вообще. Вместо нее есть «ось категорий». Подписи этой оси — любые строки (а число — это тоже строка).
barabanus
05.08.2015 19:09Мне вот нужно было строить график температуры, чтобы входные и выходные точки кривых были зафиксированы, для этого я использовал простой усредняющий цифровой фильтр.

iroln
05.08.2015 20:52+3Есть ещё такая штука как «Piecewise Cubic Hermite Interpolating Polynomial». Кусочно-полиномиальная интерполяция кубическими сплайнами Эрмита. Может дать лучшие результаты в некоторых случаях. Вот пример из Matlab: www.mathworks.com/help/matlab/ref/pchip.html

DmitrySolomennikov
06.08.2015 07:55+1Можно еще посмотреть в сторону центростремительных сплайнов Catmull-Rom.

Ixtaccihuatl
06.08.2015 10:13Чо-т с ними как-то печально получается:
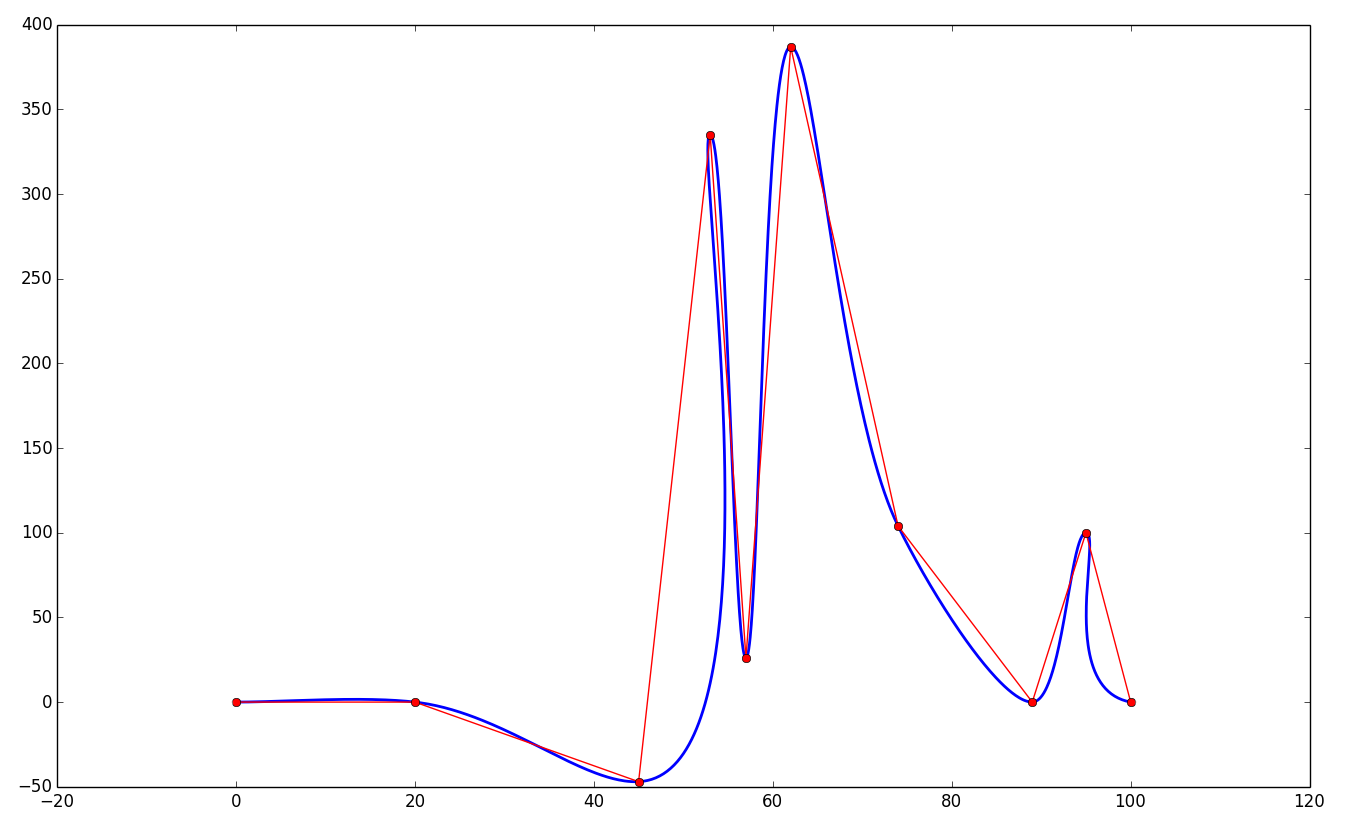
Это вот прям код из той статьи в Википедии. Может, там что-то напутано с реализацией?
iroln
06.08.2015 10:53Похоже, у вас в реализации где-то ошибка. Я писал когда-то реализацию на Matlab этих сплайнов для интерполяции 2D-кривых. Проверил на своей реализации, вроде всё правильно работает.
Картинка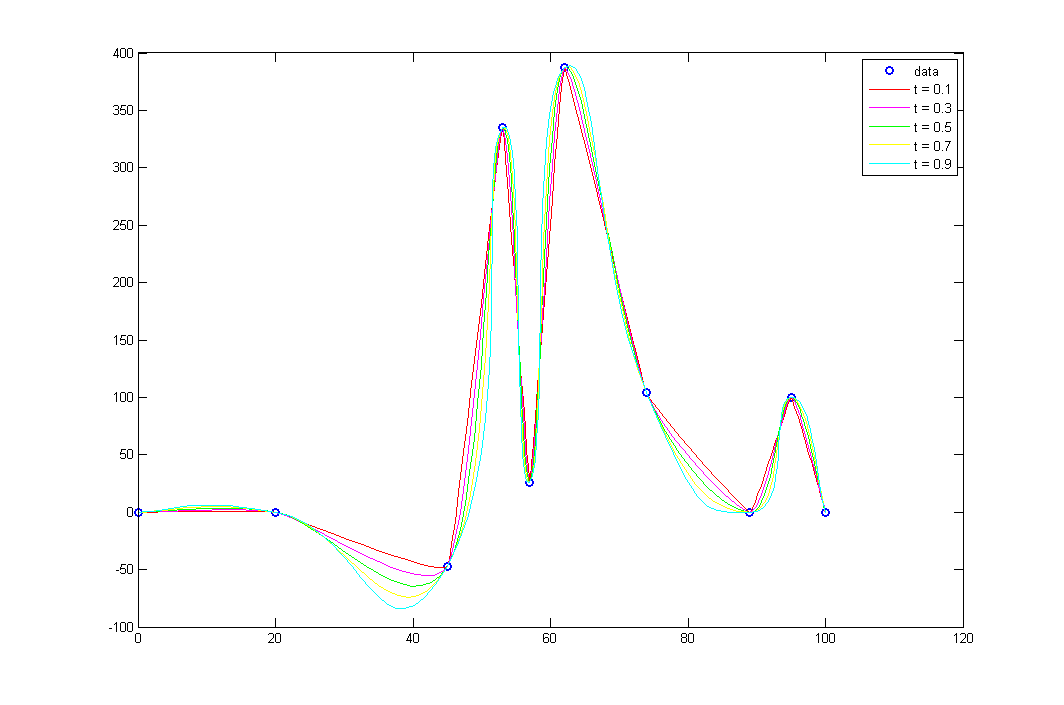

DmitrySolomennikov
06.08.2015 10:53+1А если просто Catmull-Rom? У них, по идее, таких сильных всплесков быть не должно.
therndguy.com/papers/curves.pdf

Sayonji
05.08.2015 23:14Расскажите, пожалуйста, как были выбраны точки для примеров (почти с потолка).

Ixtaccihuatl
06.08.2015 10:33Постарались для демонстрации собрать такой набор, чтобы покрыть основные сложности: участки, параллельные оси X, пики с острыми углами и изломы с тупыми.

MrShoor
06.08.2015 04:47aChartEngine, вроде как самая популярная библиотека построения графиков для Android
Больше всего похоже на кривую Безье степени n – 1, хотя в самой библиотеке график называется «cubic line».
Поже на NURBS со степенью 2 и clamped knot вектором, где входные точки для интерполяции принимались за контрольные точки.

PsyHaSTe
06.08.2015 10:48+3Вопрос, а почему мы считаем линейную интерполяцию идеальной? Такое ощущение, что мы её построили, а затем занимаемся тем, что пытаемся получить точно такую же, «но другую», более гладкую.

KoGor
06.08.2015 15:00Ага, так и есть. Линейная интерполяция хороша тем, что она не так сильно вводит нас в заблуждение.
Но обычно ситуация развивается примерно так…
Разговор крутого спеца по data science и его начальника:
— У нас тут набор пар чисел есть, я накидал их на координатную плоскость, но есть одна проблемка: я понятия не имею, что происходит между ними. Поэтому я решил соединить их ломанной, чтобы можно было хоть проследить взглядом в какой последовательности на них смотреть.
— Молодец! Только вот выглядит это не круто и не убедительно, не похоже ведь на «красивую» функцию. Надо что-то с этим сделать.
— Нууу даа, согласен… Хм, а давайте тогда её сгладим, ну чтоб солиднее выглядела.
— Давай, попробуй.
Некоторое время спустя:
— Ну что, лучше стало?
— Ну вот, сразу бы так, теперь и в презентацию не стыдно вставить! И в фэйсбук с твиттером запостить можно.
P.S. Интерполяция штука полезная, главное понимать что за ней стоит. А статья была познавательная, спасибо автору.
PsyHaSTe
06.08.2015 15:10Ага, а потом оказывается, что нужно было интерполировать экспонентой по МНК.
Нужно понимать физический смысл рисуемых кривых, а так это пальцем в небо, график с КДПВ прекрасно иллюстрирует то же, что и остальные картинки, просто они сильнее это маскируют. Если график нужен для модной инфографики и не должен отображать хоть погоду на Марсе, лишь бы было прикольно — тогда ладно.
iroln
06.08.2015 15:19интерполировать экспонентой по МНК
Это уже аппроксимация получается. :)
Интерполяцию часто применяют, чтобы напихать промежуточных точек если их не хватает, а аппроксимацию как раз для приближения функций и моделирования, нахождения неизвестных параметров.
PsyHaSTe
06.08.2015 15:30Окей, согласен. Тогда такой вопрос — у вас в целом решение лучше получается, чем у экселей и ко или только на данных входных данных? А то есть мысль, что подогнали эвристики для конкретного случая, а в общем может оказаться большая ошибка по сравнению с тем же экселем.

iroln
06.08.2015 15:51Ну, это, наверное, вопрос всё же к авторам статьи.
Я думаю, что придумывать и подгонять эвристики под конкретные данные при интерполяции — это не очень хорошо. Лучше использовать кусочную интерполяцию известными сплайнами, для которых есть точное математическое определение. Тогда будет понятно, как интерполяция будет себя вести на любых данных.
Если же цель — найти закон и параметры модели для приближения данных, про которые вам что-то известно, то тут нет никаких ограничений, берёте регрессионный анализ и аппроксимируете чем угодно, хоть линейным МНК (если получается), хоть нелинейным с придуманной вами моделью (функцией).
PsyHaSTe
06.08.2015 16:36Я уже согласился, что у нас задача интерполяции — пройтись по конкретным точкам, так что регрессия сразу отпадает :)
Тут именно вопрос в том, проверяли ли на разных наборах данных или «нарисовали красивый график и получили финансирование».

Olm
11.08.2015 19:36Именно. Практика сглаживания вообще порочна в любых точных науках или инженерии.
Измеренные точки — это единственное, что вам достоверно известно о системе. Без знания или какого-то понимания процесса любая интерполяция обманчива, а иногда просто не допустима. Линейная в этом плане лучше всего, потому что она используется по умолчанию и не нужно уточнять модель и коэффициенты, используемые для сглаживания. Но красота требует плавных линий. По хорошему же надо отображать отдельно точки и отдельно линией регрессионную модель, которая не обязательно должна проходить по всем точкам.
У меня был смешной случай на эту тему — после выпуска очередного продукта дизайнер попросил у меня пару графиков для рекламной брошюры о продукте. Я ему выслал несколько графиков с точками и линейной интерполяцией для наглядности. Графики были временные, что важно. Он, я так понимаю, засунул это в какой-то редактор и скруглил. Прислал на утверждение — я смотрю, а там линия так скруглена, что изгибы дают местами по две одновременных точки в один момент времени. Такой вот кот Шрёдингера.mayorovp
11.08.2015 20:51Он, я так понимаю, засунул это в какой-то редактор и скруглил. Прислал на утверждение — я смотрю, а там линия так скруглена, что изгибы дают местами по две одновременных точки в один момент времени.
Ну, такой график здесь тоже рассмотрен. Это B-сплайн, его даже в КДПВ автор вынес…

romy4
06.08.2015 15:44+2

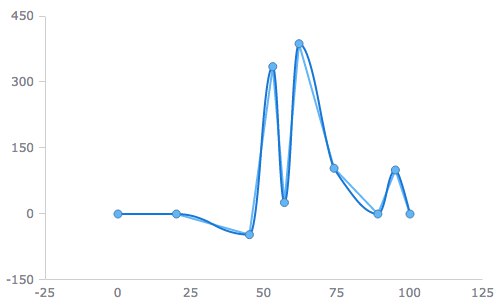
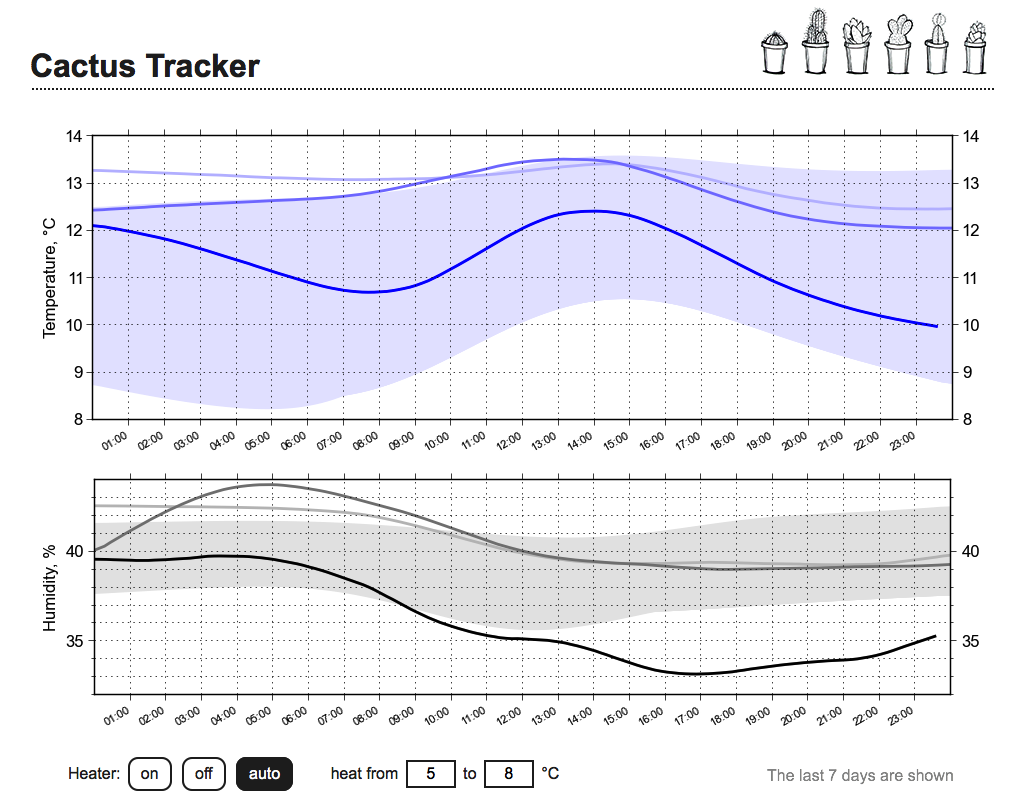

DancingOnWater
Я для сглаживания использую сплайн Акима, он более устойчив к выбросам.
Ixtaccihuatl
Более устойчив, да, но не безгрешен. По крайней мере, вот в этой реализации он явно «вспухает» на первом сегменте, ну и на пиках тоже — глобальный максимум составляет 388.018, хотя в данных это 387.0. Впрочем, наверное, и его можно отпатчить, чтобы косяков не было :)
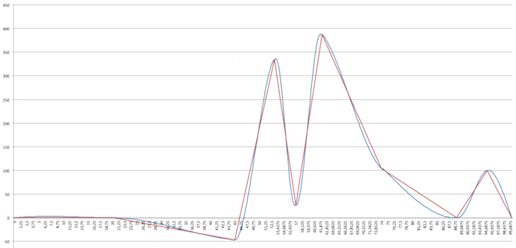
Пруфпик (из кликабл, там хорошо видно косяки сверху):
DancingOnWater
Скажем так, если бы я это вспучивание увидел бы у себя в коде в том виде, в котором оно есть здесь. Я бы стал искать ошибку в вычислениях.
Large
Не подскажите хорошее описание как его строить? А то сложно найти даже в спец. литературе.
iroln
Посмотрите код на Matlab: www.mathworks.com/matlabcentral/fileexchange/36800-interpolation-utilities/content/cakima.m
А вообще вот, информации довольно много: stackoverflow.com/a/4637884/419926