Три физика хотели обсчитать процесс изменения нейтрино. В итоге они обнаружили неожиданное взаимоотношение между одними из самых распространённых объектов математики.

Однажды в августе, утром после завтрака математик Теренс Тао открыл емейл, написанный тремя физиками, с которыми он не был знаком. Троица объяснила ему, что наткнулась на простую формулу, которая в случае, если она окажется верной, опишет неожиданное взаимоотношение между одними из наиболее базовых и важных объектов линейной алгебры.

Формула «выглядела слишком хорошо, чтобы быть правдой», сказал Тао, профессор из Калифорнийского университета в Лос-Анджелесе, лауреат Филдсовской премии, один из ведущих математиков мира. «Нечто настолько короткое и простое уже давно должно было оказаться в учебниках, — сказал он. – Поэтому сначала я подумал – нет, этого не может быть».

А потом он подумал ещё немного.

Физики – Стивен Парк из Национальной ускорительной лаборатории им. Ферми, Синин Чжан из Чикагского университета и Питер Дентон из Брукхейвенской национальной лаборатории – получили это математическое тождество за два месяца до этого, пытаясь разобраться со странным поведением элементарных частиц под названием нейтрино.

Они заметили, что "собственные векторы", сложные для подсчёта величины, описывавшие в их случае то, как нейтрино распространяются в материи, приравниваются к комбинации членов, известных как «собственные числа», вычислять которые гораздо проще. Более того, они поняли что эта взаимосвязь между собственными векторами и собственными числами – очень часто встречающимися в математике, физике и инженерных расчётах объектами, которые изучают ещё с XVIII века – судя по всему, более общего порядка.

Хотя физики не могли поверить, что они открыли новый факт, относящийся к такой базовой математике, они не смогли найти такого взаимоотношения ни в книгах, ни в статьях. Поэтому они решили рискнуть и связаться с Тао, несмотря на то, что на его сайте была размещена просьба не беспокоить его по подобным случаям.

«К нашему удивлению он ответил через два часа, и сказал, что никогда не видел раньше ничего подобного», — сказал Парк. А кроме этого, в ответе Тао были три независимых доказательства этого тождества.


Синин Чжан, Питер Дентон и Стивен Парк с открытой ими формулой

Полторы недели спустя физики и Тао, которого Парк называет «пожарным шлангом математики», опубликовали в интернете работу, сообщающую о новой формуле. Сейчас эту работу оценивают специалисты журнала Communications in Mathematical Physics. В отдельной работе, опубликованной в журнале Journal of High Energy Physics, Дентон, Парк и Чжан используют эту формулу для упрощения уравнений, описывающих поведение нейтрино.

Эксперты говорят, что у этой формулы может появиться больше способов применения, поскольку в огромном количестве задач требуется подсчёт собственных векторов и собственных чисел. «Она обладает широчайшим применением, — сказал Джон Биком, специалист по физике частиц из Университета Огайо. – Кто знает, какие двери она сможет открыть».

Математики думают так же. «Это и удивительно, и интересно, — сказал Ван Вю, математик из Йельского университета. – Не подозревал, что можно вычислять собственные векторы, используя только лишь информацию о собственных числах».

Вю и Тао доказали близкое по смыслу тождество в 2009 году (поэтому-то Дентон, Парк и Чжан и решили связаться с Тао), однако новая формула не следует очевидным образом из старой. И хотя похожая формула по случайности появилась в математической работе в мае этого года, её авторы не связали её с собственными векторами и собственными числами.

В каком-то смысле неудивительно, что новая идея по поводу математических объектов возрастом в несколько столетий, исходит от физиков. Природа вдохновляла математические изыскания с тех пор, как люди начали считать на 10 пальцах. «Чтобы математика процветала, ей нужно быть связанной с природой, — сказал Вю. – Другого способа нет».

Фокусы преобразований

Собственные векторы и собственные числа так часто встречаются, поскольку характеризуют линейные преобразования: операции, растягивающие, сжимающие, вращающие или ещё каким-либо образом меняющие все части одного объекта одинаково. Эти преобразования представлены прямоугольными массивами чисел, именуемыми матрицами. Одна матрица поворачивает объект на 90 градусов; другая переворачивает его вверх ногами и уменьшает в два раза.


Применение данной матрицы к данному объекту зеркально отразит его относительно плоскости, а также удвоит его высоту. Собственные векторы матрицы описывают направления, по которым объект не меняется, за исключением масштабирования. Собственные числа матрицы описывают, насколько объект масштабируется вдоль этих собственных векторов.
Собственный вектор А параллелен вертикальной оси. Его собственное число равно 2, поскольку объект увеличивает высоту в два раза.
Собственный вектор В находится в плоскости отражения. Его собственное число равно 1, поскольку вдоль него объект не меняется.
Собственный вектор С перпендикулярен плоскости отражения. Его собственное число равно -1, что означает отражение относительно плоскости.
Удаляя строки и столбцы матрицы, можно создавать матрицы меньших размеров. Их собственные числа вместе с собственными числами оригинальных матриц можно использовать для расчёта собственных векторов оригинальных матриц.

Делают это матрицы, изменяя «векторы» объектов – математические стрелки, указывающие на каждое физическое место объекта. Собственные векторы матрицы – это такие векторы, которые продолжают указывать в том же направлении, что и раньше, после применения матрицы. Допустим, мы возьмём матрицу, поворачивающую объект на 90 градусов вокруг оси х: собственные векторы направлены вдоль оси х, поскольку расположенные по этой оси точки не поворачиваются, когда все остальные вращаются вокруг них.

Похожая матрица может вращать объекты вокруг оси х и сжимать их в два раза. Как сильно матрица сжимает или растягивает собственные векторы объекта, описывают соответствующие собственные числа – в данном случае, 1/2 (если собственный вектор не меняется, его собственное число равняется 1).


Теренс Тао

Собственные векторы и собственные числа независимы, и обычно их приходится подсчитывать отдельно, начиная со строк и столбцов самой матрицы. Студенты учатся делать это для простых матриц. Но новая формула отличается от существующих методов. «Что интересно по поводу этого тождества, так это что вам не нужно знать никаких значений, содержащихся в матрице, чтобы что-то вычислить», — сказал Тао.

Тождество применяется к эрмитовым матрицам, осуществляющим вещественные преобразования собственных векторов (по контрасту с мнимыми числами), и, следовательно, применимым к ситуациям, происходящим в реальности. Формула выражает каждый собственный вектор эрмитовой матрицы через собственные числа этой матрицы и её «минорной матрицы» – такой матрицы меньшего размера, которая получается удалением строки и столбца из оригинальной.

Оглядываясь назад, формула кажется разумной, сказал Тао, поскольку собственные числа минорной матрицы кодируют в себе скрытую информацию. Однако «к примеру, лично я о таком бы никогда не подумал».

Он сказал, что в математике редко появляется инструмент, не связанный с задачей. Однако он считает, что взаимосвязь собственных векторов и собственных чисел обязана иметь значение. «Это настолько красиво, что я уверен, что формула найдёт какое-то применение в ближайшем будущем, — сказал он. – Пока что у нас для неё есть только одно применение».

Частицы-оборотни

И это применение связано с нейтрино: самыми странными, наименее изученными и самыми скрытными из известных фундаментальных частиц. Каждую секунду через тело человека проходят триллионы таких частиц, но поскольку они практически не обнаруживают своего присутствия, многие их свойства остаются неизвестными.

Что интересно, теория утверждает, что именно различия в поведении нейтрино и антинейтрино могут быть причиной доминирования во Вселенной материи над антиматерией. Если бы эти две противоположности появились после Большого взрыва в равных количествах, они бы аннигилировали друг с другом, и в космосе не осталось бы ничего, кроме света. Разница между нейтрино и антинейтрино могла послужить появлению жизненно важного избытка материи. «Если они ведут себя по-разному, это даст нам некое представление о том, почему Вселенная заполнена материей», — сказала Дебора Харрис, физик из Йоркского университета и Фермилаб, работающая в эксперименте с нейтрино DUNE (Deep Underground Neutrino Experiment, глубокий подземный нейтринный эксперимент), предназначенном для измерения подобных различий.

Эксперимент, который будет измерять характеристики нейтрино, запущенных из Фермилаб в Иллинойсе в подземный детектор, расположенный в Южной Дакоте в 1300 км от источника, использует тот факт, что нейтрино бывают трёх разных типов – электронное, мюонное и тау. Однако каждый тип представляет собой квантовомеханическую смесь, и нейтрино осциллируют, меняя свои типы на ходу. По мере путешествия нейтрино из Фермилаб их смесь меняется, поэтому мюонное нейтрино может превратиться в электронное или тау-нейтрино.

Эти осцилляции описывает чрезвычайно сложная матрица размера 3х3. Исходя из собственных векторов и собственных чисел физики могут подсчитать выражение, описывающее вероятность того, что мюонное нейтрино превратится в электронное к тому времени, когда оно прибудет в Южную Дакоту. Они также подсчитывают вероятность того, что мюонное нейтрино станет электронным антинейтрино.


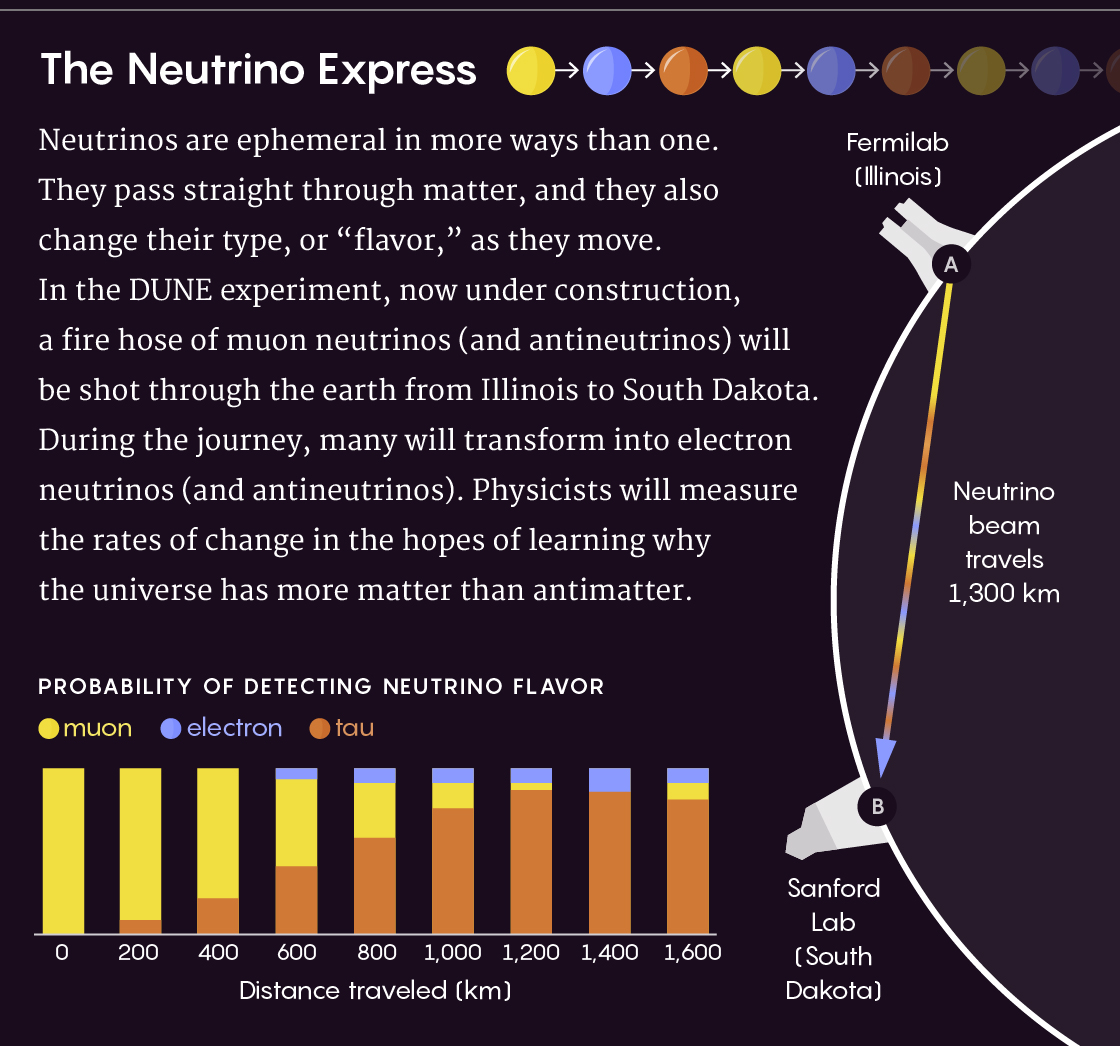
Эфемерные частицы нейтрино не только проходят сквозь материю, но ещё и меняют свой тип на лету. В эксперименте DUNE будет запущен луч нейтрино, многие из которых по пути от источника к цели поменяют свои типы. Эти изменения и будут измерять физики.
На диаграмме указана вероятность обнаружения нейтрино разного типа в зависимости от дальности их путешествия в км. Жёлтый – мюонные, синий – электронные, коричневый – тау.

В этих выражениях есть неизвестное: «фаза нарушения CP-инвариантности», показывающее, насколько отличаются друг от друга закономерности осцилляции нейтрино и антинейтрино. Измеряя и сравнивая реальные соотношения осцилляции, учёные с DUNE могут вычислить это неизвестное. Если фаза нарушения окажется достаточно большой, это поможет объяснить, почему Вселенная заполнена материей.

И как будто этих сложностей недостаточно, один странный эффект, предпосылки которого впервые были обнаружены в 1978 году физиком Линкольном Вольфенштейном, делает матрицу нейтрино ещё более сложной. Нейтрино редко взаимодействуют с материей в обычном смысле, но Вольфенштейн обнаружил, что их прохождение через материю, в отличие от пустого космоса, всё же изменяет то, как они распространяются. Иногда нейтрино, проникающий сквозь материю, взаимодействует с электронами в атоме, по сути меняясь с ним местами: электронное нейтрино превращается в электрон и наоборот.

Такие подмены вводят в матрицу новый член, влияющий на электронные нейтрино, что чрезвычайно усложняет математику. Именно этот эффект Михеева — Смирнова — Вольфенштейна [который был предсказан и теоретически исследован советскими физиками Станиславом Михеевым и Алексеем Смирновым в 1985 году на основе рассмотренного в Вольфенштейном случая осцилляций нейтрино в среде с постоянной плотностью] толкнул Парка, Чжана и Дентона на поиски способа упростить вычисления.

Выражение для вычисления собственных чисел проще выражения для собственных векторов, поэтому Парк, Чжан и Дентон использовали это как отправную точку. До этого они разработали новый метод приблизительного вычисления собственных чисел. Отталкиваясь от него они заметили, что длинные выражения для собственных векторов из предыдущих работ равнялись комбинациям этих собственных чисел. Связав всё это вместе, «можно легко и быстро подсчитать осцилляции нейтрино в материи», сказал Чжан.

Касательно того, как именно они углядели закономерность, из которой вытекает формула, физики не совсем уверены. Парк говорит, что они просто заметили отдельные проявления закономерности и обобщили её. Также он признаёт, что хорошо умеет решать загадки. Он является соавтором ещё одной важной закономерности, обнаруженной в 1986 году, и облегчившей вычисления в области физики частиц, а также по сей день вдохновляющей учёных на новые открытия.

И всё же, то, что странное поведение нейтрино могло привести к появлению новых идей, связанных с матрицей, шокировало многих. «Люди решали задачи линейной алгебры уже очень, очень долгое время, — сказал Парк. – Я всё жду, что кто-нибудь пришлёт мне емейл, где будет написано: Если вы посмотрите на эту малоизвестную работу Коши, то там в примечании к третьему приложению есть эта формула».

Минорное отличие

На самом деле похожая формула уже была известна, однако её никто не заметил, поскольку она была замаскирована.

В сентябре Тао получил ещё один неожиданный емейл, в этот раз от Цзиюаня Чжана, аспиранта по математике из Мельбурнского университета в Австралии. Чжан указал на наличие эквивалентной формулы в работе, написанной им вместе с его куратором Питером Форестером в мае, до появления работ Тао и трёх физиков. Чжан и Форрестер работали в области чистой математики, теории случайных матриц. Они применили эту формулу, исследуя задачу, связанную с решённой Тао и его коллегами в 1999 году.

Форестер объяснил нам, что впервые эта формула появилась ещё в одном виде в работе 2001 года за авторством Юлия Барышникова, математика, сейчас работающего в Иллинойсском университете в Урбане-Шампейне, на работе которого основывались Форестер и Чжан. Но эти математики описывали объекты своего тождества не как собственные векторы, а как члены, необходимые для вычисления собственных чисел определённых минорных матриц, появляющихся в ходе решения их задачи.

Форестер назвал формулу в их с Чжаном работе «идентичной» той, что использовали Тао и три физика. Тао назвал формулы «почти идентичными», относящимися друг к другу так же, как две стороны иллюзии «кролик/утка». «Некоторые люди искали кроликов, другие искали только уток», — сказал он.



Дентон в емейле написал, что существовавшая до этого формула «близка к нашему результату, но не подходит к нему идеально». Он добавил, что «в свете важности собственных векторов для многих задач, мы всё же думаем, что наш результат достаточно отличается от остальных, чтобы считать его новым».

Возможно, не так уж странно, что в данной области за одно-единственное лето после нескольких столетий может подняться такое внезапное волнение. «В математике есть много примеров одновременных открытий, — сказал Тао. – Результаты каким-то образом висят в воздухе. И люди просто начинают искать их в правильных местах».