Реплика калькулятора Sinclair Scientific демонстрирует, как заставить дешёвый чип творить чудеса

Был ли калькулятор Sinclair Scientific элегантным? Он определённо стал хитом, и после выхода в 1974 украсил обложки журналов — к примеру, Popular Mechanics. Хитроумная прошивка заставляла его весьма ограниченный процессор, способный лишь на базовые арифметические действия, выходить за пределы своих возможностей. Это позволило Sinclair продавать научный калькулятор тысячам людей, которые в ином случае просто не смогли бы себе его позволить. Он работал медленно, иногда выдавал ошибки, и его набора функций едва хватало, чтобы он считался научным калькулятором; кроме того, непосвящённым пользователям было трудно его использовать.
Я слышал о нём краем уха благодаря тому, что он стал вехой на пути к зарождению британской индустрии микрокомпьютеров и такой обожаемой многими машине, как Sinclair ZX Spectrum. И когда я увидел реплику калькулятора в магазине Tindie от Криса Чанга, внутри у меня что-то щёлкнуло. Потом я прочёл описание работы оригинального калькулятора (научная запись, и никакой клавиши «равно»?), и как реплика воспроизводит его поведение. Там используется эмулятор с прошивкой, которую получили реверс-инжинирингом путём визуального изучения металла оригинального процессора. И мне, конечно, захотелось попробовать такую штуку.

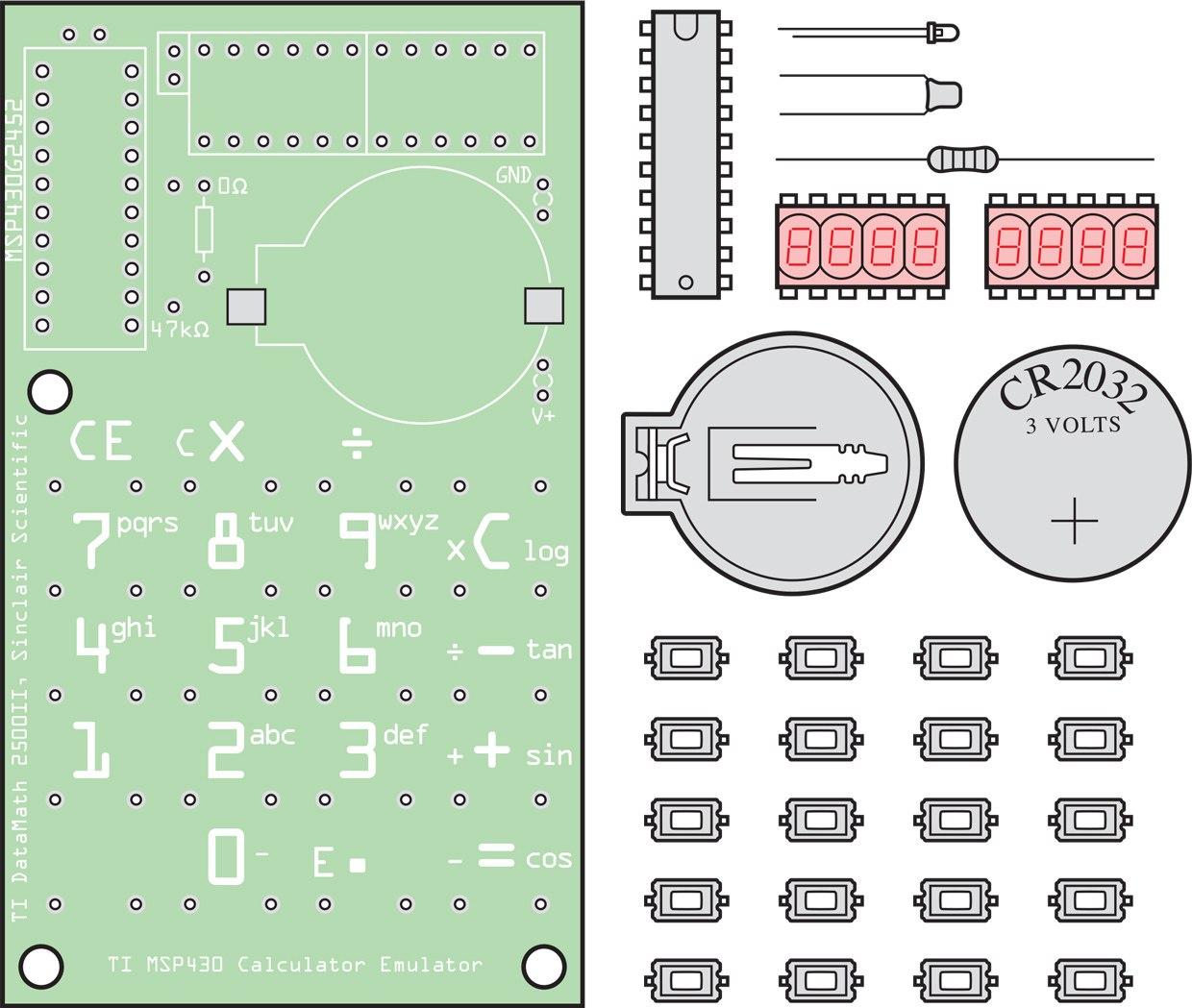
Реплика после рефакторинга. Кстати, оригинальный Sinclair Scientific тоже продавали в виде модели для сборки. Версия Криса Чанга меньше, использует меньше компонентов, и может воспроизводить поведение сразу двух калькуляторов на чипах семейства TMS080x: TI Datamath, простого арифметического калькулятора, и Sinclair Scientific. Поэтому трафарет на плате подходит под оба калькулятора.
Сначала рассмотрим железо. Набор представляет собой один из нескольких вариантов реплики Sinclair Scientific, однако это один из наиболее простых наборов. Всего один чип и плата размером с кредитку в комплекте с небольшим количеством компонентов. Чанг предлагает два варианта: оригинальный, разработанный в 2014 году и выложенный на Tindie в конце 2019, показывает цифры при помощи выпуклых светодиодных модулей QDSP-6064. Они выглядят как цифры с классических калькуляторов 1970-х, однако уже давно не выпускаются и их тяжело найти. Его обновление набора от 2020 года использует современные семисегментные светодиоды. Раритетная версия стоит дороже: $79 против $39 за вариант 2020 года. Однако у оригинальной версии есть одна приятная особенность: размеры отверстий платы подобраны так, что светодиоды вставляются просто с усилием, без пайки. Их можно вынуть и использовать в других проектах.
Функционально оба варианта одинаковы и основаны на микроконтроллере MSP430. Он устраняет необходимость в использовании почти всех остальных компонентов, которые использовались в Sinclair Scientific, и на нём работает эмулятор семейства чипов TMS080x. Семейство TMS080x производила компания Texas Instruments (TI), а конкретные версии чипов, например, TMS0805, использовавшийся в Sinclair Scientific, отличались содержимым их ROM на 3520 бит.

В стиле 70-х: в ранних калькуляторах часто использовались такие выпуклые светодиодные модули. Сферы служили линзами, увеличивавшими небольшие сегменты.
Много лет загадка того, как Sinclair заставила этот чип творить волшебство, оставалась запертой в ROM чипа TMS0805. Ситуация изменилась в 2013, когда Кен Ширрифф прослышал об Sinclair Scientific, пообщавшись с командой Visual 6502. Эта группа занимается реверс-инжинирингом классических чипов, оригинальные чертежи которых уже утеряны. Иногда для этого приходится растворять корпус чипа кислотой и аккуратно фотографировать открывшиеся кристаллы в микроскоп, изучая отдельные транзисторы. Ширрифф смог создать обобщённый симулятор чипов TMS080x на JavaScript, просто изучая заявки на патенты от TI. Однако конкретный код от Sinclair, использовавшийся в ROM чипа TMS0805, ему не давался до тех пор, пока один из членов команды Visual 6502, Джон Макмастер, не сделал фотографии кристалла в 2014.
Ширрифф активно изучает и описывает историю вычислительных машин, поэтому я написал ему вопрос о том, как ему удалось перейти от микрофотографий к рабочему коду. Он написал, что изучая, как были расположены вентили на том участке чипа, где у него был ROM, «я сразу смог извлечь необработанные биты. Фил Майнваринг, Эд Спиттлс и я ещё один день потратили на то, чтобы понять, как эти биты связаны с кодом. Код состоял из 320 слов по 11 бит, однако физически в ROM было 55 строк и 64 столбца. Изучая схему, анализируя закономерности битов, пробуя прямым перебором различные комбинации, мы разобрались в том, как там всё было устроено, и смогли извлечь код».
Когда Ширрифф загрузил код в симулятор, он смог разобраться в принципах его работы. Он, по сути, использовал «простейшие алгоритмы перебора, способные дать ответ. Однако для большей точности использовались некоторые математические хитрости, не говоря уже о программных хитростях», — пояснил он. Ширрифф поддерживает онлайн-версию симулятора, где можно отладчиком идти по коду построчно.

Вот это поворот: Sinclair Scientific подсчитывал тригонометрические функции, последовательно поворачивая изначальный вектор до тех пор, пока он не доходил до цели. Для большинства углов это занимало несколько секунд.
Sinclair Scientific смогли уменьшить сложность кода используя обратную польскую запись, в которой математические операторы идут после чисел, над которыми производится действия – к примеру, действие «5 + 4» пишется как «5 4 +». Тригонометрические функции использовали технику итерационного приближения, которая могла подсчитывать результат по нескольку секунд, и иногда давала точность максимум до третьего числа после запятой. Калькулятор использовал фиксированную научную запись для всего – десятичный разделитель ввести было нельзя. То есть, вместо ввода 521.4 нужно вводить 5214, а на дисплее это выглядит, как 5.214. Затем нужно нажать E и ввести 2, что даст число 5.214 ? 102. За один раз можно вводить только одно число.
В таком описании это выглядит ужасно. К такому можно было бы привыкнуть, только если бы вы не могли позволить себе, допустим, HP-35, создатели которого гордились его точностью и функциональностью (хотя HP-35 тоже использовал обратную польскую запись, в нём всё было немного хитрее).
Однако Sinclair пыталась конкурировать не с другими калькуляторами, а с логарифмической линейкой. Я читал об этом, но реально осознал только тогда, когда получил набор. Случайно я недавно как раз купил винтажную логарифмическую линейку Pickett, и научился выполнять на ней базовые математические операции по урокам, доступным на сайте международного музея логарифмических линеек. Потом, попробовав в деле Sinclair Scientific, я поразился тому, насколько он был концептуально похож на мою логарифмическую линейку. Для неё точность до двух-трёх цифр после запятой – вещь нормальная, вы выставляете скользящее окошко линейки так, чтобы между шкалами было всего одно число, без учёта порядка. Вы работаете со значимыми цифрами, а потом проставляете запятую у конечного результата – поэтому, например, 52 ? 2 и 5200 ? 20 вычисляются абсолютно одинаково.
Поэтому наборы для воссоздания реплик так важны – подобное понимание принципов работы устройства можно получить, только подержав его в руках. Это напомнило мне высказывание о том, что хороший дизайн – это не абстрактный идеал, он существует только в конкретном контексте. Так был ли калькулятор Sinclair Scientific элегантным? С моей точки зрения, ещё каким.

dvsx86
отличная статья! но вот в одном месте перевод режет ухо:
я так понимаю что имеется в виду Brute-force, и это можно было бы перевести немного понятнее:
Talkerbox
Еще можно сказать «влоб»