Непростые простые числа

Автор статьи предлагает заглянуть в то, что представляют собой множества простых чисел, если взглянуть на них геометрическим образом. Это не профессиональная работа, а простое, любительское исследование некоторых любопытных закономерностей. Поэтому, в статье не будет сложной математики, и мы не будем забираться глубоко в ее дебри. В общем, если вы не очень близко знакомы с простыми числами, их структурой и многовековыми исследованиями в области теории чисел, эта статья — для вас.

Подчеркну особенно, для квалифицированных математиков и тех читателей, кто себя к ним относит: статья не является профессиональной работой. Это иллюстрация некоторых свойств и закономерностей составных чисел, исключительно для наглядности и выявлении акцента на закономерности структуры, которые в дальнейшем можно выражать аналитически
Вероятно, читателю известны многие проблемы, связанные с простыми числами. Их расположение в множестве натуральных чисел неочевидно. Большие простые числа трудно находить, нужно много усилий, чтобы проверить большое число на простоту. На этой трудности основаны многие современные методы криптографии. Мы можем легко перемножить да многозначных простых числа, но зная результат найти исходные множители – очень сложная задача.
Есть множество способов оптимизации, которые намного быстрее простого перебора, однако даже если оптимизация ускорит поиск в 10 раз, достаточно увеличить число на 2 десятичных знака (т.е., в 100 раз), чтобы замедлить поиск в 100 раз.
Это и значит, что сложность алгоритма является экспоненциальной, и поэтому какой бы быстрый ни был суперкомпьютер, мы можем подобрать длину числа еще больше, чтобы таких суперкомпьютеров потребовалось миллиард. Правда, стоит уточнить еще раз: находить простые числа для перемножения при этом становится так же все труднее и труднее.
К слову, математики не нашли ни доказательства, ни опровержения того, что нельзя найти алгоритм факторизации, сложность которого не была бы экспоненциально зависящей от длины числа. А доказав или опровергнув это, как верят некоторые математики, может быть получится, заодно, решить математическую проблему, известную как гипотеза Римана. За ее доказательство математический институт Клея обещает миллион долларов. Хотя может так оказаться, что задача факторизации окажется полиномиальной, но гипотезу Римана это ни докажет, ни опровергнет.
Отбрасывают ли числа тени?
Раз уж мы не знаем закономерности, по которой бы легко находились простые числа, может быть, посмотрим внимательнее на закономерности чисел составных? Говоря математически, рассмотрим множество натуральных чисел, дополнительное к множеству простых.
Идея составных чисел очень проста. Возьмем несколько натуральных чисел и перемножим их. Тем самым, мы получаем составное число.
Мы легко найдем бесконечность составных чисел, просто умножив n на 2.

То же касается умножения на 3.

Далее следует 4, но здесь мы новых чисел не найдем, все они уже равны 2n. Далее следуют 5n, потом 6n, которые нами найдены уже дважды, как 2n и 3n одновременно. Это не увеличивает количества составных чисел, но наводит нас на мысль, что закономерность составных чисел заключена в произведении простых.
Но если мы пройдем немного дальше, то обнаружим интересную закономерность: число 6 это произведение 2 и 3. Это значит, что у нас будет сразу много удобно расположенных в таблице составных чисел:
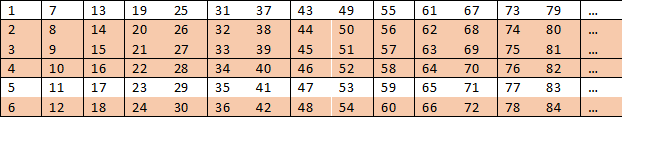
Глядя на таблицу, мы понимаем, что в строках 2, 3, 4 и 6 никогда не может быть простых чисел. А это значит, что вероятность найти простое число не может превышать 2/6. Мы понимаем, что чисел эта вероятность еще меньше, но как сильно?
Попробуем и дальше поискать удобную структуру составных чисел, а для этого, подумаем, что значит 2х3=6? Что если мы возьмем произведение из 2х3х5 за основу? Мы получаем следующую интересную таблицу (чтобы она не занимала много места, уменьшим шрифт):
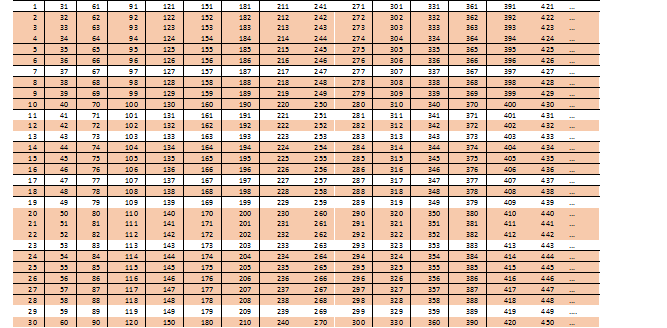
Мы видим, что:
— 15 строк вида 2n,
— 5 строк вида 3n (плюс 5 вида 6n уже учтены в 2n)
— и 2 строки вида 5n (еще три вида 10n уже вычеркнуты в числах 2n и одна 15n среди строк 3n)
не могут содержать простых чисел (мы же этого и ожидали, верно?)
Остаются лишь восемь строк вида 30n + i, где i = 1, 7, 11, 13, 17, 19, 23, 29. Если приглядеться, в них можно увидеть симметрию. 1+29=7+23=11+19=13+17.
Поэтому компактно можно записать как 30n +- i, где i = 1, 7, 11, 13,17
И мы понимаем, что вероятность найти произвольное простое число не больше 8/30. На 2/30 стало меньше…
Что же дальше? Следуя логике, в следующей таблице должно быть 2х3х5х7=210 строк. Еще дальше 210х11=2310, потом 2310х13, и так мы будем последовательно перемножать простые числа, получая все большую и большую базу «строчной развертки», которая будет сохранять свою полосатость.
Это выглядит так, будто бы простые числа отбрасывают «тени» в бесконечность кратных им чисел, если их располагать в ряд соответственно базе числа, обозначим его П(i), равного последовательному произведению i простых чисел.
Можно заметить, что полоса строк, лежащих между первой и следующей, где могут содержаться простые числа, растет по очень простому закону: если строк 6, то есть 2х3, то простые числа могут быть в строке 5, если 2х3х5, то начиная со строки 7, что логично. Таким образом, в матрице с количеством строк 30 030 (2х3х5х7х11х13) после первой строки будет широкая полоса составных чисел, до строки, следующей от числа 17. А если мы возьмем матрицу на 9 699 690 строк (2х3х5х7х11х13х17х19), то полоса, где простых чисел нет, протянется до строки 21. Что характерно, из-за симметрии, внизу матрицы так же будет 20 строк с исключительно составными числами.
Многомерные матрицы и гиперреалистичные фракталы?
Но что такое эти произведения? 2х3 – это прямоугольник, площадью 6. 2х3х5 – параллелепипед, объемом 30. А дальше? 2х3х5х7 – гиперпараллелепипед в 4 измерениях, с гиперобъемом 210? А потом? 5 измерений, 6,… Бесконечность?
Только подумайте, что могли бы себе вообразить многомерный мир, в которых простые числа отбрасывают свои тени во всех измерениях…
Мы можем представить себе четыре и более измерений, проекциями их на плоскость или в трехмерное пространство, например, раскладывая матрицу, словно перекатывая многомерный гиперкуб с грани на грань и рассматривая получающиеся на бумаге отпечатки (а так же получая отпечатки сечений).
Вот начальная грань:

А вот ее развертка с двух сторон:

Очень удачно, что во всей правой гиперплоскости у нас исключительно составные числа. Можем в нее даже не путешествовать. Можно взглянуть и на другую развертку, взгляд «сверху», но далее мы пойдем в более интересном направлении.
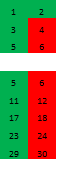
Попробуем теперь развернуть картинку в четвертое измерение, в интересующую нас сторону, где можно находить простые числа:

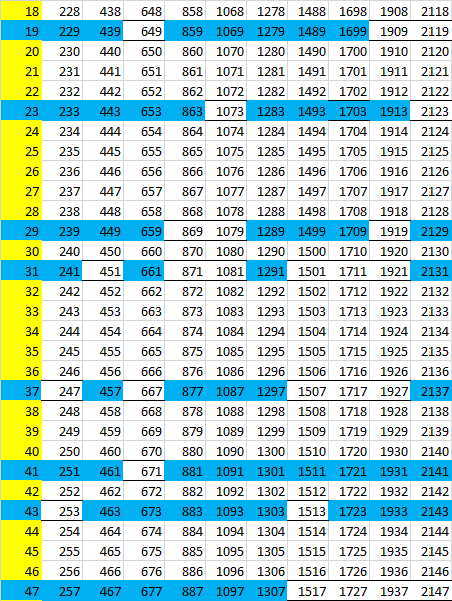
Здесь коричневым цветом обозначены числа вида mn, которые составлены произведениями чисел от 11 до 19 (ближайшее целое, меньшее 210/11). Особенность этих чисел в том, что они сами не являясь простыми числами не «отбрасывают тени» вглубь следующего измерения.
Как мы видим, средний слой развертки снова становится тривиальным – здесь и далее простых чисел нет. А вот внешние грани гиперпаллелепипеда можно рассматривать и дальше. Каждый столбец раскладывается в матрицу 7х11, получаем 5 таких матриц для каждого из трех слоев матрицы 3х5 (здесь показана развертка одного столбца и фрагмент матрицы для второго столбца):

Дальше углубляться в измерения на примере развертке мы не будем, в рамках статьи было бы неблагоразумно. В конце статьи Вы можете посмотреть на еще несколько иллюстраций. Надеюсь, это исследование немножко разбудило Ваше воображение, и путешествие в мир непростых и простых чисел Вам понравилось и показалось полезным.
Заключение
В дополнение, автор хочет заметить, что продолжает исследование этого метода. Например, вопросы появления в более крупных матрицах произведений третьих, четвертых и далее степеней чисел, которые добавляют все новые простые числа в глубоких и объемных проекциях, как отбрасывающих тень в следующие измерения, так и остающиеся «точечными» вкраплениями.
Но, пожалуй, наибольший интерес вызывает возможность уточнения оценки вероятности нахождения простых чисел все дальше и дальше. Если рассматривать матрицы, то мы видим, как вероятность падает, начиная с 4/6, далее до 7/24 (или усредненно 11/30), потом 36/180 (или 47/210), и т.д.
Кроме того, у автора есть алгоритм факторизации, оптимизация которого в многомерной матрице может заметно его ускорить (но он от этого не перестает иметь экспоненциальную степень сложности от количества знаков разлагаемого числа).
Сам алгоритм в основе очень прост.
Берем два последовательные нечетные числа, p и q, такие, что pq близко к X (используется округление корня из X до большего и меньшего нечетных чисел, при условии, что Х не является квадратом). Предварительно мы устраняем четность Х (делим на 2 до тех пор, пока результат четный), получая множитель 2^K. Далее же, в цикле, проверяем разницу между Х и pq. Если она равна нулю – результат получен. Если она больше нуля, мы уменьшаем q на 2. Если меньше нуля, увеличиваем p на 2q. В цикле используется только сложение, поэтому алгоритм довольно быстрый (зависит лишь от реализации функций работы с BigInteger).
Однако, у автора есть гипотеза, что шаг пересчета можно значительно увеличить, не теряя в аккуратности, если использовать базу кратности. Всякое число Х находится между двумя последовательными П(i) и П(i+1), где П(i) – произведение первых i простых чисел, поэтому можно определить, к какому из ребер число Х находится ближе и какой диапазон свободы у p и q в каждой из проекций) и тем самым образуемый p и q прямоугольник из одной плоскости развернуть в сечение гиперпараллелепипеда.
P.S. А при чем здесь тайное общество ткачей, спросит читатель, которого привлек оригинальный заголовок? Возможно, читатель помнит фильм «Особо опасен» В этом году обещают даже продолжение… В этом фильме ткацкий станок делает предсказания, укладывая нити и узелки… Посмотрите, как похоже это делают ниточки простых чисел…
В матрице 30х7:

И кусочек матрицы 210х11:
А управляют узелками этой машиной вот такие матрицы-перфокарты. Развертка матрицами 2х3:

И побольше, матрицами 6х5:

Комментарии (27)

oleg1977
11.04.2015 19:56+3К слову, математики не нашли ни доказательства, ни опровержения того, что нельзя найти алгоритм факторизации, сложность которого не была бы экспоненциально зависящей от длины числа.
А как же субэкспоненциальные алгоритмы факторизации? Да и о «классической архитектуре» следуем упомянуть
realbtr Автор
12.04.2015 15:52На мой взгляд, субэкспоненциальные — это экспоненциальные с оптимизацией. То есть, экспонента от длины числа в знаках в субэкспоненциальных никуда не исчезает.
А что касается классической архитектуры, то статья, это просто способ проиллюстрировать наглядно введение в некоторые классические идеи. Я сам разбираюсь с теорией чисел и проникаю в некоторые затейливые компактные формулы, разворачивая их для себя наглядно.
В статье нет особенной новизны, кроме, разве что, введения произведения последовательности простых чисел как самоподобной базы и намеков на возможное аналитическое изучение самоподобных областей симметрии в регулярности множества составных чисел (дополнительного к множеству простых)
brainick
11.04.2015 20:25+7Всякое открытие терзает меня как гвоздик в спине. Хотя я невежда и старосветский помещик, а все же таки
негодник старый занимаюсь наукой и открытиями, которые собственными руками
произвожу и наполняю свою нелепую головешку, свой дикий череп мыслями и
комплектом величайших знаний. Матушка природа есть книга, которую надо
читать и видеть. Я много произвел открытий своим собственным умом, таких
открытий, каких еще ни один реформатор не изобретал.
Господ-минусаторов прошу объяснить научную ценность данных измышлений

Bodigrim
11.04.2015 20:47+10Есть множество способов оптимизации, которые намного быстрее простого перебора, однако даже если оптимизация ускорит поиск в 10 раз, достаточно увеличить число на 2-3 десятичных знака (например, в 100 раз), чтобы замедлить поиск в 10^100 раз. Это и значит, что сложность алгоритма является экспоненциальный...
Это ложное утверждение: если умножить число на 100, то поиск замедлится не более, чем в 100 раз. У вас неверные представления об экспоненциальный сложности: она экспоненциальная относительно битовой длины числа, а не относительно самого числа.
К слову, математики не нашли ни доказательства, ни опровержения того, что нельзя найти алгоритм факторизации, сложность которого не была бы экспоненциально зависящей от длины числа. А доказав или опровергнув это, можно, заодно, решить математическую проблему, известную как гипотеза Римана.
Можно ссылку на то, что гипотеза Римана следует из указанного вами утверждения?
realbtr Автор
12.04.2015 16:01Спасибо, про увеличение сложности — исправил.
Про связь гипотезы Римана и экспоненциальности возможных алгоритмов факторизации — предположение неточное и вопрос спорный. Если говорить о практике, то я не встречал предложенных алгоритмов факторизации полиномиальной сложности, отсутствие ошибки в которых бы доказывалось справедливостью Гипотезы Римана.
Bodigrim
12.04.2015 16:12+2Построение вашего последнего предложения завело меня в тупик.
На уровне идей: справедливость гипотезы Римана означает, что простые числа распределены в некотором смысле наиболее регулярным способом, т. е. в асимптотическом законе простых чисел остаточный член мажорируется корневой оценкой. Это может повлиять на оценки сложности алгоритмов проверки на простоту (и влияет), но у нас они и так полиномиальны. Связь же гипотезы Римана именно с алгоритмами факторизации идейно ничем не обусловлена.

Bodigrim
11.04.2015 21:04+2Но, пожалуй, наибольший интерес вызывает возможность уточнения оценки вероятности нахождения простых чисел все дальше и дальше. Если рассматривать матрицы, то мы видим, как вероятность падает, начиная с 4/6, далее до 7/24 (или усредненно 11/30), потом 36/180 (или 47/210), и т.д.
Не понял, о какой вероятности идет речь. Насколько я понял, выше в таком же смысле упоминалась вероятности 2/6 и 8/30.
Вероятность того, что число не делится на последовательные простые p1, ..., pn, есть (1-1/p1)...(1-1/pn), что по теореме Мертенса равно e-? / ln pn, где ? — константа Эйлера-Маскерони.
realbtr Автор
12.04.2015 16:04Если брать разные интервалы, то и вероятность в них — разная. Если мы берем интервал от 1 до 30, то вероятность 11/30. Если же мы исключаем первую группу из 6 чисел, то получаем отрезок 1..6 (где вероятность 4/6) и 7..30 (где вероятность 8/24)
Есть много формул оценки вероятности, но их появление нужно разобрать. В данной же статье — лишь иллюстрация подхода, идея о том, какова структура, как устроены составные числа, как можно показать в этой структуре симметрию и уровни самоподобия.
Bodigrim
12.04.2015 16:28+3Позволите говорить прямо?
Факт «отбрасывание теней» (он же метод решета) в различных ипостасях является очень популярным в любительских исследованиях по теории чисел. Я регулярно встречаю эссе, претендующие на открытие нового алгоритма факторизации, основанные на его применении. Вашу статью от них выгодно отличает неплохой стиль и отсутствие завышенного ЧСВ. Однако фактический уровень математического содержания — такой же.
Читайте книжки по теории чисел и развивайтесь. Когда одолеете стандартный учебник для первого курса (лучше забугорный Hardy & Wright), можете переходить к литературе по методу решета, раз уж оно вам интересно. Например, «Распределение простых чисел» Прахара будет неплохим стартом.
realbtr Автор
12.04.2015 17:02Вы совершенно правы, увлечение — лишь стартовая мотивация. За Прахара — отдельное спасибо.

valplo
12.04.2015 01:18+9Автор, вы сперва заявляете «в статье не будет сложной математики, и мы не будем забираться глубоко в ее дебри», а потом начинаете сыпать терминами, вроде «Многомерные матрицы и гиперреалистичные фракталы», причем я не уверен, что вы сами поняли что сказали. И так далее в том же духе. Короче, пока мне кажется, что статья — фричество и ересь.

realbtr Автор
12.04.2015 16:06-3Статья совершенно любительская, Вы совершенно правы (я, правда, не очень склонен начальный уровень сложности введения в проблему дискредетировать словами фричество и ересь). Математика — не догматическая наука, а точная. Поэтому слово «ересь» в математике — ересь.

valplo
12.04.2015 17:59+2Слово «ересь», в данном случае, означает, что автор не следует соглашениям, выработанным для облегчения понимания подобных статей, изобретает собственные термины вместо использования общепринятых, не работает с источникам по данной теме. Как следствие этого — статья малополезна, и автору лучше бы научиться писать не-ересь.

realbtr Автор
12.04.2015 19:11-3Окей, с такой формулировкой согласен. Но всегда есть вопрос баланса — изобретать велосипеды (так же, как это делали многие «отцы-основатели», придумывая свою нотацию, свои методы), или изучать существующие. Когда существующие не решают поставленные задачи, можно и «пофричить» в пределах разумного. Хотя, немало примеров, когда простые числа или деление на ноль сводят с ума и съедают все время у «подсевших» на довольно тривиальные расчеты.
Меня изобретение велосипедов не пугает. Но, в одном Вы правы — публиковать изобретение велосипедов затея спорная. На будущее остерегусь спешить.
Может и эту убрать в черновики? Из 20 тысяч прочитавших не так много проголосовали «за». И много против…
Но, если честно, мне помогла критика. Когда я играл с числами — у меня было большое вдохновение, чувство чего-то значительного. Сейчас я понимаю, что это не дает новизны (но надеюсь, что может немного вдохновить таких же нубов, как и я)
dtestyk
12.04.2015 19:43мне понравилась идея многомерного представления простых чисел, о которой узнал из вашей статьи

valplo
12.04.2015 20:08+1Попробуйте переработать статью. Почитайте источники (для начала — хотя бы английскую википедию, там есть ссылки на серьезные статьи), переформулируйте в общепринятых терминах, проставьте ссылки. Может чего и найдете интересного. Вы извините, что я вас так резко раскритиковал, но, к сожалению, такие малопонятные и малополезные стати пишут все чаще, а исправляться их авторы не желают. Рад знать, что вы — приятное исключение.
Вот вам антипримеры «как не надо писать». Почитайте и ужаснитесь:
habrahabr.ru/post/225175 — по вашей теме, между прочим. Идеи похожи на ваши, насколько я смог понять — а понять тяжело. Если бы автор этой стати писал понятнее, а вы поискали бы что по этой теме уже написано хотя бы на ГТ, возможно почерпнули бы у него какие-то идеи. Но поскольку его статья написана и оформлена безграмотно, никому, кроме автора, вообще не понятно о чем идет речь.
sohabr.net/gt/post/242548, geektimes.ru/post/242214 — это, конечно, экстремальный пример, но публикация сырых идей без проработки источников может закончится и так.
habrahabr.ru/post/205900 — там все кончилось натуральным мошенничеством. Я вас не в коем случае приравниваю к мошенникам, да и в математике запутаться куда легче, чем в физике, но правила исследований для того и придумывали, чтобы фильтровать подобных граждан.
В общем: вы хотите исправиться — уже хорошо. Еще раз говорю, почитайте серьезную литературу по теме, возможно найдете что-то полезное и сможете оформить ваши идеи в теорию. А скорее всего — окажется, что ваши идеи никакой новизны не содержат, но это — не страшно, придумаете что-нибудь новое. И опубликуете уже без отсебятской терминологии и каши.

dtestyk
12.04.2015 09:52+1растет по очень простому закону
какому?
realbtr Автор
12.04.2015 15:44-2Простому закону, но невыразимому аналитически. Легко эту закономерность заметить, но чтобы написать формулу, снова старая проблема — неопределенность метрики в множестве простых чисел.
База развертки матрицы увеличивается каждый раз на уже известное небольшое простое последовательное число, размер матрицы быстро растет, в начале и конце матрицы образуются растующие медленно, но устойчиво симметричные зоны составных чисел.
Вообще мне очень интересны осевые симметрии во вложенных диапазонах, например, если база 30030, то внутри имеем 13 симметричных областей по 2310 строк, в каждой из которых 11 симметричных областей по 210 строк, в каждой из которых 7 симметричных областей по 30 строк, в каждой из которых 5 симметричных областей по 6 строк.
Как бы мы ни увеличивали базу, умножая ее на последовательные уже известные простые числа, все области симметрии сохраняются, добавляются при этом новые.
Такая закономерность очевидна. И то, что широкая зона строк с составными числами в начале и конце каждой базы растет, определяя регулярную структуру максимального расстояния между двумя простыми числами — можно заметить, аналитически же надо записать формулу вроде
...13 х (11 x (7 x (5 x (6n | {p mod 6}) | {q mod 30}) | {r mod 210}) | {s mod 2310}) | {t mod 30030} ...,
где сокращение вида "| {p mod 6}" значит исключение строк в данной области симметрии, по соответствующему модулю, например {p mod 6} это {0, 2, 3, 4}.

Ambassadorik
12.04.2015 11:16+1Помню в детстве/юности неплохо увлекался математикой, получал дипломы на разных олимпиадах, и действительно думал что когда-нибудь позже докажу что-нибудь подобное. Сейчас сижу и понимаю как далек от этого я стал спустя 5-7 лет…

realbtr Автор
12.04.2015 15:13-2Да, согласен. Теория чисел мое небольшое большое увлечение, которое откладывалось много-много лет. Понадобилось разобраться с факторизацией чисел, полез в учебники и статьи и обнаружил, что требуется множество времени, чтобы понять, что значат те или другие формулы. Попробовал это нарисовать сам себе наглядно (что-то на листочке, что-то в экселе) и обнаружил, что наглядность помогает. Поработав со структурами наглядно стал хорошо понимать суть многих статей, стало легче разбираться. Правда, не ко всему еще смог подступиться

brainick
Ксепня